Influences of site conditions and ground-motion frequency characteristics on structural fragility
-
摘要: 场地土层条件及地震动频谱特性对地震中结构响应及其震害具有显著影响，而现阶段结构易损性分析多未考虑场地条件以及地震动特性的作用。根据地震动频谱特性参数，即峰值位移与峰值加速度比值（Rd2a），将输入地震动分为4组；同时，基于场地土层平均剪切波速将场地分为基岩、硬场地、中硬场地和软场地等4类。采用OpenSees软件，建立坐落于单一土层场地上的6层钢筋混凝土（RC）框架结构概化模型。在不同场地条件下输入不同分组地震动，采用增量动力分析法（IDA）分别计算结构响应及结构破坏状态，探讨地震动特性和场地条件对结构易损性的影响规律。结果显示：①不同分组地震动输入下结构的易损性曲线差别显著，Rd2a值越大结构破坏的概率越大；②场地条件对结构易损性曲线存在一定的影响，该影响与结构的破坏状态相关，即结构破坏状态越严重，越硬场地的破坏概率趋于增大；③相对于地震动特性对结构易损性的影响，场地条件的影响较小；④在结构的易损性分析中既要考虑场地条件的影响也要考虑地震动特性的影响，特别是输入地震动的选取，对结构易损性分析结果影响较大。通过简化模型评价场地条件和地震动特性对结构易损性的影响，以期为结构易损性评价以及震害预测提供参考。Abstract: Site conditions and ground-motion frequency characteristics play a significant role in structural response and seismic damage distribution. However, the current structure fragility analysis techniques have hardly considered such effects. Taking the ratio of peak displacement to peak acceleration (i.e., Rd2a) as an index, the ground-motion records collected are subdivided into four groups. Meanwhile, based on the site average shear-wave velocity (Vs), the site conditions are classified into four categories which are bedrock, hard site, medium-hard site, and soft site. Using the OpenSees software, a simplified model for a six-story reinforced concrete (RC) frame structure on a single soil-layer site is built. The effects of ground-motion characteristics and site conditions on the fragility curves of structures for different structure damage stages controlled by the maximum structural inter-story drift angles are investigated using the incremental dynamic analysis methods. The analytical results indicate that: (1) The frequency characteristics of ground-motion greatly impact the fragility curves of structures, that is, the probability of structural damage under ground-motion loading of large Rd2a values stays higher than that of small Rd2a values. (2) The site conditions, nevertheless, impose definite influences on the structural fragility curves. Such influences correlate with the structural damage states, e.g., when the structure is seriously damaged, the possibility of structure damage tends to increase with the increasing stiffness of sites. (3) The site conditions maintain relatively smaller influences on the structure fragility curves than the ground-motion frequency characteristics. (4) The influences of the ground-motion characteristics and site conditions should be necessarily considered in the structure fragility analysis, especially during selecting input ground-motion. The investigation of the influences of the site conditions and ground motion characteristics on structural fragility herein by a simplified model provides a reference for the structure fragility analysis and seismic damage prediction techniques.
-
Keywords:
- RC frame structure /
- fragility analysis /
- peak ratio /
- site condition /
- simplified model
-
0. 引言
地震易损性是一种描述建筑物达到或超过某个设定破坏状态的超越概率，反映建筑物受到地震作用后的伤害或损失程度的表现形式[1-2]。现阶段结构地震易损性分析技术成熟、实用方法较多，然而对于易损性的研究多倾向于结构模型的多样化和精细化，对于地震动特性以及场地条件影响考虑尚少。
地震动是地震作用于结构的载荷形式，其幅值、频率、持时、相位等特征会直接影响结构的响应和破坏状态。所以，结构地震易损性分析需要考虑输入地震动的频谱特性。另一方面，地震波在传播过程中会受到场地土层的作用，其主要表现为土层对地震波的滤波和幅值放大（或缩小）效应，即场地效应，场地效应甚至会直接影响地震震害的分布。就物理机制来看，场地土层的滤波和放大作用改变地震波的频谱特性，进而影响结构地震响应和破坏状态，这些作用在历史震害调查中均得到了证实。例如，软土场地一般会放大地震动的中长周期成分，对于中长周期结构的破坏作用较大，而硬土场地上低矮房屋的震害较大。Cetin等[3]发现，在2020年萨莫斯岛（爱琴海）发生的里氏7.0级地震中，伊兹密尔湾上由于场地效应的放大和延长作用，导致795座建筑倒塌或严重损坏，而萨莫斯岛上建筑物则较少受到影响。Ademovic等[4]根据58次地震震害资料及区域场地条件资料数据分析，指出软土场地上的建筑易受到中等到高强度地震是震害较重，而硬土场地以及基岩场地上的建筑则相对较轻。所以，结构易损性分析或者震害预测技术势必考虑地震动特性及场地土层条件的影响。
结构地震易损性常用分析方法可以根据结构破坏数据来源分为经验统计法[5]和数值模拟法[6]。经验统计法主要是依据历史地震的震害调查数据和资料，通过统计分析，得到不同类型的结构在不同强度地震动作用下的破坏概率。数值模拟法（或称理论分析法）是利用结构动力数值分析工具，对结构进行一系列非线性动力分析计算，得到结构的响应和性能，采用数值模拟结果，计算不同类型的结构在不同强度地震动作用下的破坏概率。由于现阶段大部分地区的实际地震观测数据和结构震害数据尚不足以进行统计分析，所以数值模拟法依然是结构易损性分析的主流方法。从近期发表的成果来看，国内外学者开始重视场地土层条件对结构易损性的影响。Karafagka等[7]采用随机有限元法和蒙特卡罗模拟方法，研究了饱和土壤上非延性RC框架结构在考虑液化和土-结构相互作用情况下的易损性曲线，发现饱和土壤上非延性RC框架结构在地震作用下的易损性受到液化和土-结构相互作用的影响显著，指出土壤液化导致结构的基底剪力和位移增大，从而使得结构的损伤概率、预期损失均增大。Forcellini[8]研究了土壤液化对砌体填充钢筋混凝土结构（MIRC）地震性能的影响，分析了考虑液化侧移与沉降对易损性曲线影响，分析结果表明土壤液化会导致MIRC结构的刚度降低、延性增加和承载力下降，从而增加了结构的易损性。Pitilakis等[9]研究了土-结构相互作用和场地放大效应对现有RC框架结构易损性的影响，提出场地效应校正因子来修正地震易损性曲线，指出场地放大效应会显著增加土-结构系统的易损性，而土-结构相互作用效应主要在软土场地上表现出来，且对不同建筑结构的影响存在差异。
从科学合理的角度而言，结构易损性计算不仅要考虑结构本身特性，也需要考虑地震动特性以及场地条件影响[10]。采用OpenSees软件以一栋6层钢筋混凝土（RC）框架结构为例，建立简化结构和土层模型，通过数值模拟和数学分析手段，分析场地条件和输入地震动频谱特征对结构易损性曲线的影响，认识二者对结构易损性曲线的影响规律，为更合理的结构易损性分析以及震害预测技术发展提供参考。
1. 分析模型
1.1 概化模型
OpenSees是一款适用于结构和岩土工程的动力分析的开源有限元软件，因其具有数值模拟准确、便于二次开发与交流，以及计算速度快等优点，被广泛应用于地震工程领域科研及工程实践。OpenSees内嵌程序能够考虑结构和土壤的非线性行为，可以更合理地模拟土-结构相互作用模型在地震动作用下的响应和破坏过程。为了能够揭示场地条件以及地震动频谱特性对结构易损性的影响规律，这里从简化模型入手，使复杂的问题尽量简化，但保证其问题的物理本质不变。首先基于OpenSees软件平台，构建一个2跨6层的钢筋混凝土（RC）框架结构概化模型，通过输入地震荷载计算结构的动力响应。现阶段，中国城市（群）是人员和社会财富高度集中的地区，新老建（构）筑物并存，且呈现复杂、多样、密集等特点。在这些地区中，6至10层的多层房屋框架建筑物依然普遍存在，特别是在城镇地区，所占比重较大，所以建立的6层RC框架结构模型具有现实基础和一般性。
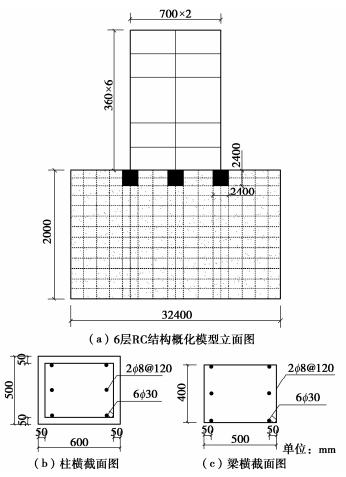
概化模型分为上部结构、基础和地基土层3部分，模型各部分尺寸如图 1（a）所示。该框架结构单跨宽7 m、层高3.6 m。地基模型部分简化为单一土层，厚度为20 m。考虑基础宽度和土层节点单元尺寸的协调性以及降低边界条件的影响，土层模型宽度为32.4 m。结构部分采用梁和柱为结构基本单元，分别用于模拟楼板及柱子的受力和变形特征。梁和柱单元之间的连接点设为固结，即不考虑相对滑动和转动。图 1（b），（c）分别给出了柱和梁的截面尺寸及配筋点分布情况，其中柱截面尺寸为600 mm×500 mm，梁截面尺寸为400 mm×400 mm。本文旨在分析地震动频谱特性以及场地条件对结构易损性的影响规律，而非结构本身特性，所以结构模型尺寸及材料特性均为常用的材料模型及参数。
1.2 结构模型
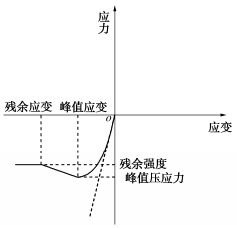
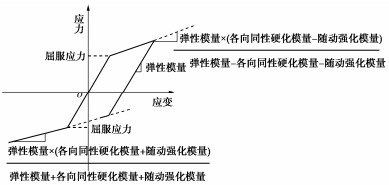
对于结构构件的材料模拟，RC框架模型中利用Concrete01材料模拟混凝土材料的本构关系，该材料模型是基于Kent等[11]提出的单轴受压混凝土模型开发，其骨架曲线忽略了混凝土的抗拉强度，但考虑了箍筋对核心区混凝土抗压强度和屈服强度的影响。因该材料模型具有形式简单、参数少、精度高等优点，是目前有限元分析建模中最常用的单轴混凝土材料模型之一。该材料模型需要输入4个参数，即混凝土的峰值压应力、峰值应变、屈服后残余强度和残余应变。本文模型参数主要参考Barbato等[12]根据混凝土的设计强度和试验数据给出的参数建议值（表 1）。模型中非核心区、核心区混凝土均采用Concrete01模拟，该材料模型的应力-应变骨架曲线如图 2所示，但核心区混凝土添加考虑箍筋对抗压强度和屈服强度提升的计算。框架模型中利用Hardening材料模型来模拟钢筋的单轴本构关系，其应力-应变骨架曲线如图 3所示，该材料模型可兼顾材料的线性变形和各向同性硬化，模型参数包括钢筋的弹性模量、屈服强度、各向同性硬化模量和随动强化模量，参数取值见表 2。
表 1 混凝土材料参数Table 1. Material parameters for concrete区域 峰值压应力/kPa 峰值应变 屈服后残余强度/kPa 残余应变 非核心区 27588 0.002 0 0.008 核心区 34485 0.004 20691.4 0.014 表 2 钢筋材料参数Table 2. Material parameters for steel参数 弹性模量/kPa 屈服强度/kPa 各向同性硬化模量/kPa 随动强化模量/kPa 配筋 2.0×108 248200 0 1.6129×106 RC框架模型中的梁柱截面采用纤维梁柱截面（即section fiber），该截面模型是目前利用OpenSees平台完成非线性分析中最精细的分析模型之一[13]，能够综合考虑截面上各个纤维的非线性本构关系，得到截面双向滞回曲线。本文根据RC框架结构模型特点，对梁柱截面进行纤维划分，即模型构建时将截面沿两个主轴方向划分成网格（纤维），每一根纤维可以是混凝土或钢筋，对应于上述建立的不同材料模型。纤维截面的细化使每个网格独立，运用不同的本构关系，提高数值模拟精度。
梁、柱采用基于位移的二维dispBeamColumn单元模拟，因其在计算时利用位移差值函数计算构件变形，而非直接使用截面力-变形关系，可实现塑性分布方向与单元长度方向保持协同，相较于其它单元模型，该单元模型具有较高的精度和效率。实际计算中，单元设置的基本假定是所有梁柱构件皆为均质，即每个积分点处截面模型相同。模型假定构件曲率分布为线性，即构件在弹性范围内服从欧拉-伯努利梁理论，在塑性范围内服从线性硬化理论，这样可以提高计算效率，且保证结果的准确性。
1.3 基础及地基土层模型
工程场地的覆盖土层复杂、多样、且空间分布不均匀，为使计算简化、且能一定程度上反应场地特性对结构易损性的影响，这里将场地土层简化成单一土层的概化模型。地基土本构模型则采用多屈服面粘塑性本构模型，即Multi-Yield-Surface model（简称MYS）。该模型由Mróz[14]和Iwan[15]于1967年提出，并经过多位研究者的改进和修改，具有稳定、可用于模拟非线性行为、相对容易实现等优点。Yang等[16]在2003年对该模型进行了改进，引入双线性卸载刚度，提高了其准确性和适用范围。随后Gu等[17]又对模型进行了修正，使其与OpenSees平台更加兼容。该模型通过引入多个同心圆形的屈服面来描述土体在不同应力状态下的弹塑性行为，能够较好地反映土体的应力-应变关系和滞回特征，适用于水平成层场地的土体动力分析。模型参数包括土材料的剪切模量、体积模量和最大切应变，参数取值见表 3。土层剪切波速能够反映场地土层的力学特性，已被多国规范作为划分场地类别的参数指标。为区分场地条件，根据场地土层平均剪切波速Vs将场地分为4类，即软土（Vs=100 m/s）、中硬土（Vs=350 m/s）、硬土（Vs=500 m/s）以及基岩（Vs=1000 m/s）。
表 3 模拟土体材料的参数Table 3. Material parameters for soil土材料名称 土层厚度/m 剪切模量/kPa 体积模量/kPa 最大切应变 软土 20 2.0×104 1.8×105 0.1 中硬土 20 2.45×105 1.8×105 0.1 硬土 20 5.0×0105 1.8×105 0.1 基岩 20 2.00×106 1.0×106 — 为了实现场地模型的二维平面离散，在建立场地模型时，土体单元使用一种基于双线性等参变换的二维四节点平面单元Quad with Sensitivity单元。该单元模型使用直接微分法进行响应灵敏度分析，区别于普通的平面单元，该单元与MYS材料本构模型具有更好的兼容性，且因其可以计算出单元的灵敏度参数用于优化设计及可靠性分析，已被广泛用于桥梁、隧道、地基等领域的数值模拟中。另外，土体阻尼的确定较为复杂，因其具有非线性、频率相关和压力相关性等特性。单独使用材料本构内置设置的滞回阻尼（即与应变幅值成正比的阻尼）不能准确地反映土体在不同频率和应力水平下的损耗行为。因此，本文在材料本构中除了设置滞回阻尼，还采用一种简化阻尼设定方式，即在场地模型中补偿设置5%的Rayleigh阻尼比。
1.4 边界条件
模型边界分为底部边界、侧向边界和内部边界3部分。底部边界即场地土与基岩的交界面，为模拟半无限地基的效应，采用固定边界条件，即将底部节点的水平向位移约束为零。侧向边界是场地土与周围土体的交界面，本文采用剪切边界为模拟地震波在侧向边界处的入射和反射效应。模型利用OpenSees平台中特有的equalDOF命令，将两侧边界处纵坐标相同的节点的水平方向位移约束为相等，使侧向节点施加与场地土相同的剪切运动，即剪切边界条件。内部边界即上部结构与场地土之间的接触面，为兼顾准确性与计算效率，模型的内部边界采用先区别设置，再进行强制组合的简化方式处理。先将结构的地下部分节点和土体对应坐标相同的节点分别定义，再使用equalDOF命令强制将其组合在一起，使坐标相同的节点保持位移一致。
2. 输入地震动
日本K-net和KiK-net地震观测台网记录高质量数字型强震数据，并且实现数据共享，为地震工程研究提供基础数据。本文搜集整理K-net和KiK-net地震观测数据库中峰值加速度（PGA）大于0.05 g（1 g =10 m/s2）的地震记录，以保证选取的地震记录具有工程意义。共计搜集了1594条地震动加速度时程，然后对加速度时程进行了基线校正和0.1~25 Hz带通滤波等常规处理。选取地震动数据的PGA在0~0.8g均有分布，但小于0.2 g数据占比83.5%。
工程上常用地震动PGA和峰值位移（PGD）作为地震动强度定量指标，物理意义明确，直观且简单方便。而实际上，峰值比，即Rd2a = PGD/PGA，不仅可以反应地震动强度，还可以反映地震动的频谱特征[18]。计算所选地震动数据的Rd2a值，结果显示所选地震动Rd2a值主要分布在0~0.19，其中小于0.04的数据最多，占比98.6%。这里PGA和PGD单位分别为m/s2和m，所以Rd2a值的单位为“s2”，而非无量纲量。确定Rd2a与地震动频谱特征的相关性，这里通过Rd2a与以往学者提出的地震动低频成分丰富程度指数RL[19]的拟合优度来验证，RL计算公式为
RL=∫f10F(f)df∫f20F(f)df。 (1) 式中：F(f)为加速度记录的傅里叶谱幅值；采用f1为低频部分频率上限，文献[19]中建议取值1.0 Hz；f2为傅里叶谱频率上限，与加速度记录采样频率相关。通过对搜集的全部强震数据的Rd2a与RL相关性分析发现，二者具有较好的相关性，拟合优度为0.82，即Rd2a值物理意义上包含地震动低频特性。相对于RL，Rd2a具有计算方便、参数物理意义明确、与工程应用结合密切等优点，所以采用Rd2a作为地震动频谱特性的表征指标。研究地震动频谱特性对结构易损性的影响，通过Rd2a值对地震动进行分组，对比分析不同地震动分组下RC框架结构地震易损性曲线。根据地震动数据的Rd2a值分布，将地震动分为4组，记为Ⅰ~Ⅳ组（表 4）。
针对结构易损性输入地震动数量的问题，国内外相关规范尚未有统一的规定。中国的《建筑抗震设计规范》（GB50011—2010）[20]和日本的《建筑基准法施行令》要求选取至少3条地震动记录来进行分析校核，美国的FEMA 356[21]和ATC-58[22]规范也建议至少选择7条或11条地震动记录来完成结构以不同强度指标调幅的地震动作用下超越概率的估计。鉴于计算效率，这里在每个地震动分组中随机选取50条加速度时程作为输入，以满足结构易损性计算的需求。
表 4 不同地震动分组Rd2a值Table 4. Rd2a values of different ground-motion groups地震动分组 Rd2a值范围 加速度记录数 Ⅰ < 0.0025 50 Ⅱ 0.0025~0.005 50 Ⅲ 0.005~0.02 50 Ⅳ 0.02~0.04 50 3. 结构易损性分析
3.1 结构破坏等级及量化指标
在进行结构地震易损性分析之前，需要对结构的破坏状态进行定量划分。最大层间位移角θmax作为表征结构性能的指标和损伤程度，可以用来衡量结构的变形和破坏情况。参考《建筑抗震设计规范》（GB50011—2010）中规定的结构竖向构件在不同破坏状态下的最大层间位移角限值，将结构的破坏状态划分为5个等级，即完好、轻微破坏、中等破坏、不严重破坏和严重破坏，其对应的结构最大层间位移角数值如表 5所示。计算结构破坏等级时，不考虑完好的情况，仅对其它4个破坏等级下结构的易损性进行分析。
表 5 《建筑抗震设计规范GB50011—2010》中结构不同破坏等级下最大层间位移角控制标准Table 5. Maximum inter-story drift angles in Chinese seismic design code for buildings (GB 50011—2010)等级 完好 轻微破坏 中等破坏 不严重破坏 严重破坏 θmax < 1/550 1/550~1/250 1/250~1/120 1/120~1/60 > 1/60 3.2 结构地震易损性
结构地震易损性曲线反映了结构在不同地震动强度下的失效概率，是进行易损性分析和风险评估的重要依据。为更系统、直观的表现不同工况下结构响应，需将地震动强度指标-破坏概率散点转化为更准确、直观的易损性曲线图。在数据结果分析中，首先采用IDA计算分析结构动力响应，提取不同地震动强度下结构最大层间位移角数据，利用数学模型进行拟合得到结构的地震易损性曲线。具体过程如下：通过OpenSees软件对模型结构进行动力计算，得到结构的最大层间位移角与输入地震动强度指标的相关性的计算散点图，然后采用基于对数正态分布模型的倒塌易损性分析工具[23]（即collapse fragility tool，简CFT）拟合得到结构易损性曲线。CFT工具是一种基于结构动力分析结果进行估计的高效易损性函数拟合工具，由斯坦福大学科技人员研发，可通过办公软件计算。
3.3 地震动频谱特性对结构易损性影响
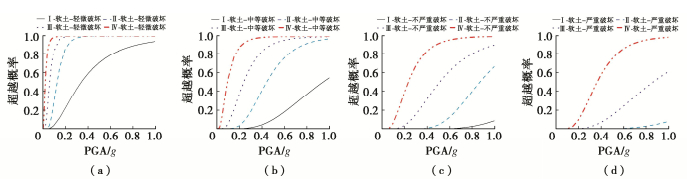
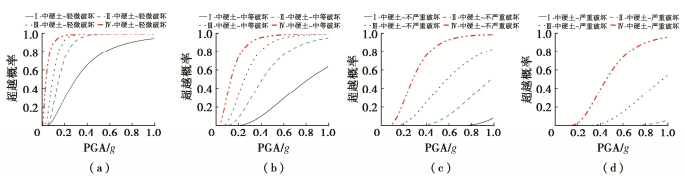
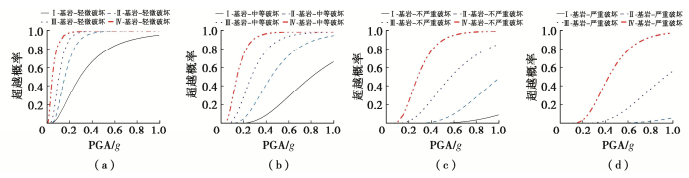
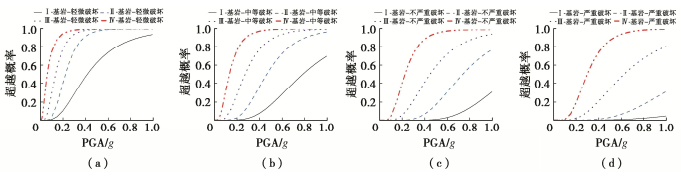
通过数值计算，图 4~7分别给出了软场地、中硬场地、硬场地和基岩，不同组地震动输入时易损性曲线对比。由图 4可以看出，不同分组地震动输入下软土场地上RC结构的易损性曲线有明显差异，即结构易损性曲线随着Rd2a的增大而升高，而且这种差异性与结构的破坏状态相关。图 5~7分别为中硬场地、硬场地和基岩场地不同分组地震动输入下，RC结构的易损性曲线对比。与软土场地工况类似，不同场地的结构易损性曲线均随着Rd2a的增大而升高，而且Rd2a对结构易损性的影响明显。值得注意的是，在第I组地震动输入下结构未发生严重破坏，如图 4（d）中，严重破坏的易损性曲线为零。但在基岩场地，第I组地震动输入下，结构可以发生严重破坏，但破坏概率值很小。
![]()
图 4 不同分组地震动输入下软土场地结构易损性曲线对比Figure 4. Comparison of structural fragility curves on soft soil site under different ground-motion groups![]()
图 5 不同分组地震动输入下中硬土场地结构易损性曲线对比Figure 5. Comparison of structural fragility curves on medium-hard soil site under different ground-motion groups![]()
图 6 不同分组地震动输入下硬土场地结构易损性曲线对比Figure 6. Comparison of structural fragility curves on hard soil site under different ground-motion groups![]()
图 7 不同分组地震动输入下基岩场地结构易损性曲线对比Figure 7. Comparison of structural fragility curves on rock site under different ground-motion groups3.4 场地条件对结构易损性影响
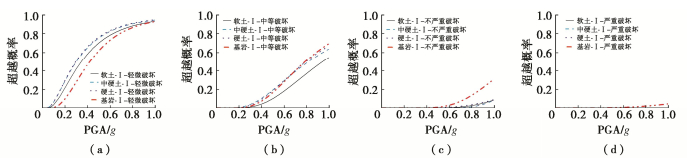
对比不同场地条件对结构易损性的影响，图 8~11显示不同分组地震动输入、相同场地条件下结构的易损性曲线对比。
![]()
图 8 第Ⅰ组地震动输入时不同类型场地上结构易损性曲线对比Figure 8. Comparison of structural fragility curves obtained by inputting ground-motion group Ⅰ for different site classes![]()
图 9 第Ⅱ组地震动输入时不同类型场地上结构易损性曲线对比Figure 9. Comparison of structural fragility curves obtained by inputting ground-motion group Ⅱ for different site classes![]()
图 10 第Ⅲ组地震动输入时不同类型场地上结构易损性曲线对比Figure 10. Comparison of structural fragility curves obtained by inputting ground-motion group Ⅲ for different site classes![]()
图 11 第Ⅳ组地震动输入时不同类型场地上结构易损性曲线对比Figure 11. Comparison of structural fragility curves obtained by inputting ground-motion group Ⅳ for different site classes由图 8可以看出，在第Ⅰ组地震动输入下，即Rd2a值较小，不同类别场地的结构易损性曲线差别不显著。图 8（a）中，轻微破坏状态下基岩场地结构易损性曲线最小，硬土场地和中硬土场地的结构易损性曲线基本一样。软土场地的结构易损性曲线处在基岩场地和硬土场地之间，这一现象与其他分组地震动输入情况下不同。其他分组情况下轻微破坏时软土场地的破坏概率最高。在中等破坏状态下（图 8（b）），软土场地的结构易损性曲线最小，其它3种场地的结构易损性曲线基本重合。但在不严重破坏状态下（图 8（c）），基岩场地的结构易损性曲线最大，其它场地的结构易损性曲线基本一致。图 8（d）可知，在第Ⅰ组地震动输入下，结构发生严重破坏的概率很小。
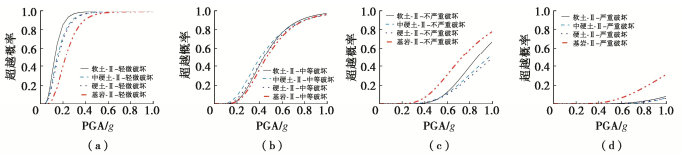
在第Ⅱ组（图 9）和第Ⅲ组地震动（图 10）输入下，场地条件对结构易损性曲线的影响呈现近似的规律。首先，结构处于轻微破坏状态时（图 9（a），10（a）），软土场地结构的破坏概率最大、基岩场地结构破坏概率最小。硬场地和中硬场地上结构的易损性曲线基本一致。从场地的平均剪切波速来看，中硬场地的平均剪切波速为350 m/s，而硬场地的平均剪切波速为500 m/s，二者差别不显著，所以结构的易损性曲线差别不大。在结构处于中等破坏状态时（图 9（b），图 10（b）），不同场地上结构的易损性曲线基本一致，此时结构的破坏概率与场地条件相关性较小。在结构处于不严重破坏和严重破坏状态下，软土场地上结构超越概率最高。
在第Ⅳ组（图 11）地震动输入下，不同场地上结构的易损性曲线与其它3组地震动输入时呈现相似的规律性，即结构处于轻微和中等破坏状态下，软土场地的结构易损性曲线最高，而在不严重和严重破坏状态下，基岩场地上结构的易损性曲线最高。第Ⅲ组和第Ⅳ组地震动输入下，结构能够发生严重破坏的概率明显增大。
从物理过程来看，场地条件对结构易损性的影响，主要通过场地土层对地震波的放大和滤波作用，进而改变地震波的频谱特性来实现。现有认识表明，软场地对地震动中低频成分具有放大作用，所以相对于较硬场地，软场地发生结构破坏的概率较大，即在相同强度地震动输入下，软土场地结构发生轻微破坏的概率要小于硬场地、严重破坏的概率要高于硬场地情况。
通过以上计算得到的RC结构易损性曲线对比可以看出，地震动频谱特征、场地条件对结构的易损性均有影响，且地震动频谱特征的影响更显著，场地条件的影响与结构的破坏状态相关。对于结构的地震易损性分析，一方面输入地震动需要根据当地的地震地质条件进行选取；另一方面，结构进行地震易损性分析时宜考虑不同场地土层条件对结构易损性的作用。
4. 结论
通过建立简化的单一土层场地条件上RC框架结构的概化模型，输入不同地震动加速度时程计算得到结构的易损性曲线，分析地震动频谱特性和场地条件对该类结构易损性曲线的影响规律。得到4点结论。
（1）根据地震动峰值位移与峰值加速度比（Rd2a）值将输入地震动数据分为4组，实际数据分析验证了Rd2a值与地震动的频率特性的相关性。
（2）输入不同分组地震动时程，对比研究了地震动频谱特性对结构易损性的影响规律，分析结果显示不同分组地震动输入下结构易损性曲线差别显著，且Rd2a值越大的地震动分组得到的结构易损性曲线越高。
（3）采用场地平均剪切波速将场地分为软场地、中硬场地、硬场地和基岩，分析了不同类别场地上结构的易损性曲线，探讨了场地条件对结构易损性的影响规律，结果显示不同场地条件结构的易损性曲线存在差异，其差异大小与结构的破坏状态相关。
（4）相对于地震动频谱特性对结构易损性的影响，场地条件的影响较小。从易损性曲线对比结果来看，二者对结构易损性均有重要作用，即结构的易损性计算须要考虑场地条件以及地震动频谱特性的影响，以期更合理预测结构破坏概率和等级，这方面工作尚需进一步研究。
-
![]()
图 4 不同分组地震动输入下软土场地结构易损性曲线对比
Figure 4. Comparison of structural fragility curves on soft soil site under different ground-motion groups
![]()
图 5 不同分组地震动输入下中硬土场地结构易损性曲线对比
Figure 5. Comparison of structural fragility curves on medium-hard soil site under different ground-motion groups
![]()
图 6 不同分组地震动输入下硬土场地结构易损性曲线对比
Figure 6. Comparison of structural fragility curves on hard soil site under different ground-motion groups
![]()
图 7 不同分组地震动输入下基岩场地结构易损性曲线对比
Figure 7. Comparison of structural fragility curves on rock site under different ground-motion groups
![]()
图 8 第Ⅰ组地震动输入时不同类型场地上结构易损性曲线对比
Figure 8. Comparison of structural fragility curves obtained by inputting ground-motion group Ⅰ for different site classes
![]()
图 9 第Ⅱ组地震动输入时不同类型场地上结构易损性曲线对比
Figure 9. Comparison of structural fragility curves obtained by inputting ground-motion group Ⅱ for different site classes
![]()
图 10 第Ⅲ组地震动输入时不同类型场地上结构易损性曲线对比
Figure 10. Comparison of structural fragility curves obtained by inputting ground-motion group Ⅲ for different site classes
![]()
图 11 第Ⅳ组地震动输入时不同类型场地上结构易损性曲线对比
Figure 11. Comparison of structural fragility curves obtained by inputting ground-motion group Ⅳ for different site classes
表 1 混凝土材料参数
Table 1 Material parameters for concrete
区域 峰值压应力/kPa 峰值应变 屈服后残余强度/kPa 残余应变 非核心区 27588 0.002 0 0.008 核心区 34485 0.004 20691.4 0.014 
下载: 导出CSV
表 2 钢筋材料参数
Table 2 Material parameters for steel
参数 弹性模量/kPa 屈服强度/kPa 各向同性硬化模量/kPa 随动强化模量/kPa 配筋 2.0×108 248200 0 1.6129×106
下载: 导出CSV
表 3 模拟土体材料的参数
Table 3 Material parameters for soil
土材料名称 土层厚度/m 剪切模量/kPa 体积模量/kPa 最大切应变 软土 20 2.0×104 1.8×105 0.1 中硬土 20 2.45×105 1.8×105 0.1 硬土 20 5.0×0105 1.8×105 0.1 基岩 20 2.00×106 1.0×106 —
下载: 导出CSV
表 4 不同地震动分组Rd2a值
Table 4 Rd2a values of different ground-motion groups
地震动分组 Rd2a值范围 加速度记录数 Ⅰ < 0.0025 50 Ⅱ 0.0025~0.005 50 Ⅲ 0.005~0.02 50 Ⅳ 0.02~0.04 50
下载: 导出CSV
表 5 《建筑抗震设计规范GB50011—2010》中结构不同破坏等级下最大层间位移角控制标准
Table 5 Maximum inter-story drift angles in Chinese seismic design code for buildings (GB 50011—2010)
等级 完好 轻微破坏 中等破坏 不严重破坏 严重破坏 θmax < 1/550 1/550~1/250 1/250~1/120 1/120~1/60 > 1/60
下载: 导出CSV
-
[1] WISNER B. Vulnerability as concept, model, metric, and tool[M]. Oxford: University Press, 2016.
[2] NAIR S S, HEMALATHA G, MUTHUPRIYA P. Vulnerability assessment using fragility curves[J]. International Journal of Applied Engineering Research, 2017, 12(9): 1867-1873.
[3] CETIN K O, PAPADIMITRIOU A G, ALTUN S, et al. The role of site effects on elevated seismic demands and corollary structural damage during the October 30, 2020, M7.0 Samos Island (Aegean Sea) Earthquake[J]. Bulletin of Earthquake Engineering, 2022, 20(14): 7763-7792. doi: 10.1007/s10518-021-01265-z
[4] ADEMOVIC N, HADZIMA-NYARKO M, ZAGORA N. Influence of site effects on the seismic vulnerability of masonry and reinforced concrete buildings in Tuzla (Bosnia and Herzegovina)[J]. Bulletin of Earthquake Engineering, 2022, 20(5): 2643-2681. doi: 10.1007/s10518-022-01321-2
[5] GARDONI P, DER KIUREGHIAN A, MOSALAM K M. Probabilistic capacity models and fragility estimates for reinforced concrete columns based on experimental observations[J]. Journal of Engineering Mechanics, 2002, 128(10): 1024-1038. doi: 10.1061/(ASCE)0733-9399(2002)128:10(1024)
[6] SHINOZUKA M, FENG M Q, LEE J, et al. Statistical analysis of fragility curves[J]. Journal of Engineering Mechanics, 2000, 126(12): 1224-1231. doi: 10.1061/(ASCE)0733-9399(2000)126:12(1224)
[7] KARAFAGKA S, FOTOPOULOU S, PITILAKIS D. Fragility curves of non-ductile RC frame buildings on saturated soils including liquefaction effects and soil-structure interaction[J]. Bulletin of Earthquake Engineering, 2021, 19(15): 6443-6468. doi: 10.1007/s10518-021-01081-5
[8] FORCELLINI D. Seismic fragility for a masonry-infilled RC (MIRC) building subjected to liquefaction[J]. Applied Sciences, 2021, 11(13): 6117. doi: 10.3390/app11136117
[9] PITILAKIS D, PETRIDIS C. Fragility curves for existing reinforced concrete buildings, including soil–structure interaction and site amplification effects[J]. Engineering Structures, 2022, 269: 114733. doi: 10.1016/j.engstruct.2022.114733
[10] KUMAR P, MAHAJAN A K, SHARMA M. Site effect assessment and vulnerability analysis using multi- geophysical methods for Kangra city, NW Himalaya, India[J]. Journal of Earth System Science, 2023, 132(1): 14. doi: 10.1007/s12040-022-02032-7
[11] KENT D C, PARK R. Flexural members with confined concrete[J]. Journal of the Structural Division, 1971, 97(7): 1969-1990. doi: 10.1061/JSDEAG.0002957
[12] BARBATO M, GU Q, CONTE J P. Probabilistic push-over analysis of structural and soil-structure systems[J]. Journal of Structural Engineering, 2010, 136(11): 1330-1341. doi: 10.1061/(ASCE)ST.1943-541X.0000231
[13] 杜轲, 孙景江, 许卫晓. 纤维模型中单元、截面及纤维划分问题研究[J]. 地震工程与工程振动, 2012, 32(5): 39-46. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201205007.htm DU Ke, SUN Jingjiang, XU Weixiao. The division of element, section and fiber in fiber model[J]. Journal of Earthquake Engineering and Engineering Vibration, 2012, 32(5): 39-46. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201205007.htm
[14] MROZ Z. On the description of anisotropic workhardening[J]. Journal of the Mechanics and Physics of Solids, 1967, 15(3): 163-175. doi: 10.1016/0022-5096(67)90030-0
[15] IWAN W D. On a class of models for the yielding behavior of continuous and composite systems[J]. Journal of Applied Mechanics, 1967, 34(3): 612. doi: 10.1115/1.3607751
[16] YANG Z H, ELGAMAL A, PARRA E. Computational model for cyclic mobility and associated shear deformation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(12): 1119-1127. doi: 10.1061/(ASCE)1090-0241(2003)129:12(1119)
[17] GU Q, CONTE J P, ELGAMAL A, et al. Finite element response sensitivity analysis of multi-yield-surface J2 plasticity model by direct differentiation method[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198(30/31/32): 2272-2285.
[18] 费扬, 陈龙伟. 考虑地基侧向永久位移的钢筋混凝土框架结构地震反应分析[J]. 力学与实践, 2023, 45(5): 1067-1078. https://www.cnki.com.cn/Article/CJFDTOTAL-LXYS202305012.htm FEI Yang, CHEN Longwei. Seismic response analysis of reinforced concrete frame structure considering permanent lateral displacement of foundation[J]. Mechanics in Engineering, 2023, 45(5): 1067-1078. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXYS202305012.htm
[19] MIYAJIMA M. Detective method of liquefaction using strong ground motion records[C]//Proc 3rd China-Japan-US Trilateral Symp. On Lifeline Earthquake Engineering. Kunming, 1998.
[20] 建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010. Code for Seismic Design of Buildings: GB 50011—2010[S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)
[21] FEMA. Prestandard and Commentary for the Seismic Rehabilitation of Buildings[R]. Washington D C: FEMA, 2000.
[22] ATC. Guidelines for seismic performance assessment of buildings[R]. Draft: ATC, 2009.
[23] BAKER J W. Efficient analytical fragility function fitting using dynamic structural analysis[J]. Earthquake Spectra, 2015, 31(1): 579-599. doi: 10.1193/021113EQS025M
-
期刊类型引用(0)
其他类型引用(1)
计量
- 文章访问数: 98
- HTML全文浏览量: 24
- PDF下载量: 17
- 被引次数: 1
