桩靴插桩动力过程的数值模拟方法研究

沈晓鹏; 李书兆; 李伟; 梁文州; 曹添铭; 刘润

doi:10.11779/CJGE2023S20029

桩靴插桩动力过程的数值模拟方法研究 English Version

1.
中海油研究总院有限责任公司, 北京 100028
2.
天津大学水利工程智能建设与运维全国重点实验室, 天津 300072

基金项目:

渤海油气田水下生产系统国产化研究与示范项目 CNOOC-KJ 135 ZDXM 36 TJ 07 ZY

详细信息

作者简介:
沈晓鹏(1980—)，男，高级工程师，主要从事海洋工程技术研究设计工作。E-mail: shenxp2@cnooc.com.cn

通讯作者:
曹添铭, E-mail: zncyx123456@126.com

中图分类号: TU43
计量
- 文章访问数: 122
- HTML全文浏览量: 26
- PDF下载量: 15
出版历程
- 收稿日期: 2023-11-29
- 网络出版日期: 2024-04-19
- 刊出日期: 2023-11-30

Numerical simulation method for dynamic process of spudcan penetration

1.
CNOOC Research Institute Co., Ltd., Beijing 100028, China
2.
State Key Laboratory of Hydraulic Engineering Intelligent Construction and Operation, Tianjin University, Tianjin 300072, China

摘要

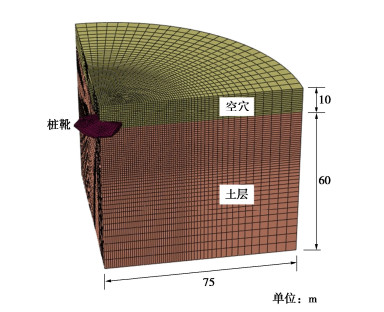
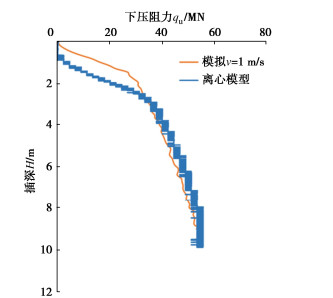
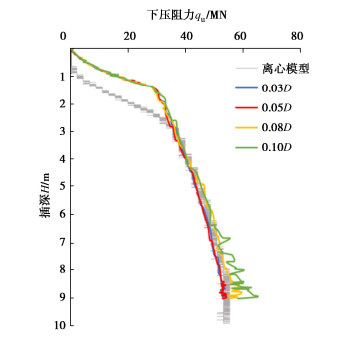
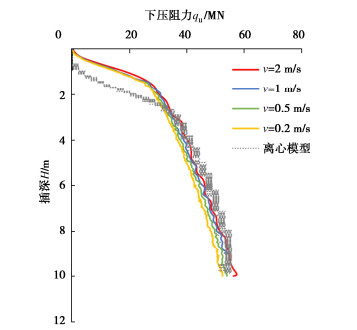
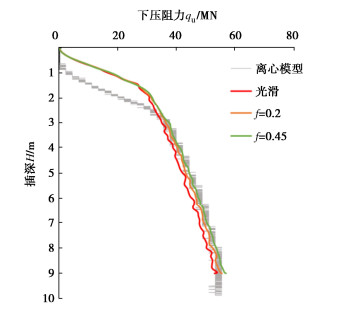
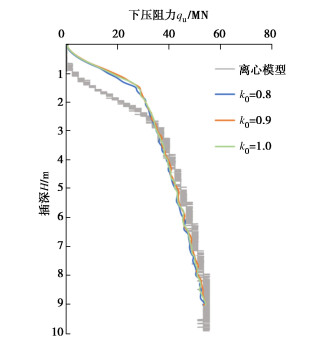
摘要: 基于耦合的欧拉-拉格朗日方法（CEL），模拟黏土中自升式钻井船桩靴插桩过程，并对计算中的参数进行敏感性分析。结果表明：CEL方法中选取合理参数可有效模拟离心模型试验下压阻力结果；模型中最小网格尺寸较大会使计算结果产生震荡，建议取0.05倍桩靴直径；桩靴插桩速率v速度较慢时对下压阻力影响较小，建议取为1 m/s；桩靴与土摩擦系数f对桩靴下压阻力影响较小，黏土中建议设置为0即光滑接触；地应力步中侧压力系数K₀应与其他土体参数协调，黏土中建议取值为1。
- 桩靴插桩 /
- CEL方法 /
- 网格尺寸 /
- 插桩速率 /
- 侧压力系数
Abstract: Based on the coupled Euler-Lagrange (CEL) method, the process of spudcan penetration is simulated, and several parameters affecting the calculated results are analyzed. The results show that the reasonable parameters in the CEL method can effectively simulate the penetration resistance results of centrifugal model tests. The large mesh size in the model will cause the calculated results to shake, so it is recommended to take 0.05 times the diameter of spudcan. Slow spudcan penetration speed v, has small influences on the lower penetration resistance, and it is recommended to be 1 m/s. The friction coefficient f between spudcan and soil has small influences on the penetration resistance, and smooth contact is recommended in clay. The lateral pressure coefficient K₀ of the geostress step should be coordinated with other soil parameters, and it is recommended to be 1 for clay.
- spudcan penetration /
- coupled Eulerian-Lagrangian method /
- mesh size /
- penetration rate /
- lateral pressure coefficient

HTML全文

0. 引言

钙质砂是由珊瑚骨骼、贝类、虫黄藻类等海洋生物残骸沉积而成，其主要组成成分是碳酸钙^[1-3]，是我国南海岛礁吹填的主要材料。因其生成环境、成因以及物质组成等因素影响，钙质砂具有颗粒易破碎、形状极不规则、内孔隙发育、微观结构复杂等显著区别于陆源石英砂的特点^[4-6]。随着“一带一路”国家战略和建设“海洋强国”政策方针的推进，研究钙质砂工程力学特性具有重要意义^[7-9]。

钙质砂作为填方工程的天然材料，其应力状态复杂多变，土体受到各向异性应力状态影响而产生初始静剪应力，在建（构）筑物的自重和动荷载（波浪、地震和交通荷载等）作用下，易引起地基强度降低、变形过大以及液化失稳等灾害。实际上，动荷载作用下剪切应力做功将导致材料损伤效应的累积，不排水条件下表现为孔压增长。因此，可以将孔压的升高与土体颗粒在运动或重排过程中所耗损的能量建立关联。损耗能作为标量，相较于应力、应变等矢量，可直接数学叠加，大幅度降低分析难度。Nemat-Nasser等^[10]首先提出了耗散能量的概念，建立其与残余孔压的关系，来有效地评估孔隙水压力的产生和发展过程。Kokusho^[11]和Pan等^[12]提出了土骨架破坏产生的单位体积耗散能与应变和残余孔压累积直接相关，为评价砂土在不规则循环应力条件下的抗液化能力提供了有效方法。总体而言，上述研究主要针对石英砂，能否适用于钙质砂仍需进一步探究。

本文以饱和钙质砂为研究对象，开展不排水条件下循环剪切三轴试验，探究相对密实度、初始静剪应力以及循环应力对其孔压发展的影响；同时，引入能量法，建立钙质砂孔压与损耗能之间联系，提出基于能量损耗的液化评价方法，为钙质砂地基稳定性分析提供理论依据和技术支撑。

1. 试验材料与方案

1.1 试验材料

本文试验材料为中国南海某岛礁的天然钙质砂，颗粒多呈灰白色，形状有片状、块状、棒状等，颗粒内孔隙多、微观结构复杂，如图 1所示。

图 1 典型钙质砂颗粒电镜扫描（SEM）图像

Figure 1. SEM image of typical calcareous sand particles

下载: 全尺寸图片幻灯片

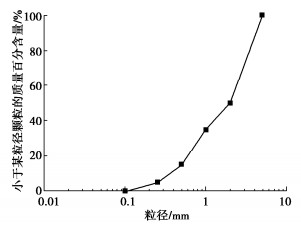
经过现场取材、清水冲洗、烘干等过程后，对粒径大于5 mm的颗粒进行剔除，处理后颗粒分布级配曲线如图 2所示，主要基本物理性质参数见表 1。不难发现，试样基本不含0.1 mm以下的细颗粒，不均匀系数和曲率系数分别为6.84和0.78，属于不良级配砂土。

图 2 钙质砂颗分级配曲线

Figure 2. Grain-size distribution curve of calcareous sand

下载: 全尺寸图片幻灯片

表 1 钙质砂物理性质指标

Table 1. Physical properties of calcareous sand

相对质量密度	d₅₀/ mm	不均匀系数	曲率系数	最大孔隙比	最小孔隙比
2.79	2.0	6.84	0.78	1.15	0.87

下载: 导出CSV

| 显示表格

1.2 试验方案

结合实际工况，采用CKC三轴试验系统模拟复杂应力条件下饱和钙质砂循环剪切试验，先进行有效围压为100 kPa的等向固结后再根据试验设计的初始静偏应力状态进行非等向固结，具体方案如表 2所示。初始静剪应力比SSR和循环应力比CSR可通过式（1）和（2）计算。

表 2 不排水循环剪切试验方案

Table 2. Summary of undrained cyclic triaxial tests

试验系列	相对密实度 D_r	${q_{\text{s}}}$ / kPa	${q_{{\text{cyc}}}}$ / kPa	SSR	CSR	N_f
Ⅰ	70% （密砂）	0	20	0	0.1	232
		0	25	0	0.125	74
		0	30	0	0.15	17
		0	40	0	0.2	6
		20	30	0.1	0.15	168
		20	45	0.1	0.225	19
		20	50	0.1	0.25	3
		50	50	0.25	0.25	53
		50	60	0.25	0.3	11
		50	70	0.25	0.35	6
		80	70	0.4	0.35	14
		80	80	0.4	0.4	7
		-10	25	-0.05	0.125	78
		-10	30	-0.05	0.15	39
		-10	35	-0.05	0.175	8
		-20	20	-0.1	0.1	210
		-20	25	-0.1	0.125	11
		-20	30	-0.1	0.15	8
		-40	20	-0.2	0.1	57
		-40	25	-0.2	0.125	16
		-40	30	-0.2	0.15	8
Ⅱ	30% （松砂）	0	15	0	0.075	943
		0	20	0	0.1	120
		0	25	0	0.125	37
		0	30	0	0.15	18
		24	30	0.12	0.15	61
		24	35	0.12	0.175	16
		24	40	0.12	0.2	5
		40	15	0.2	0.075	175
		40	20	0.2	0.1	9
		50	12.5	0.25	0.0625	17
		50	15	0.25	0.075	2
		-10	12.5	-0.05	0.0625	382
		-10	15	-0.05	0.075	180
		-10	20	-0.05	0.1	11
		-20	10	-0.1	0.05	246
		-20	12.5	-0.1	0.0625	202
		-20	15	-0.1	0.075	12
		-40	5	-0.2	0.025	104
		-40	7.5	-0.2	0.0375	13
		-40	10	-0.2	0.05	2

下载: 导出CSV

| 显示表格

${\text{SSR}} = \frac{{{q_{\text{s}}}}}{{2{{p'}_0}}}\text{，}$

(1)

${\text{CSR}} = \frac{{{q_{{\text{cyc}}}}}}{{2{{p'}_0}}}。$

(2)

式中： ${q_{\text{s}}}$ 为初始静剪偏应力； ${q_{{\text{cyc}}}}$ 为循环偏应力； ${p'_0}$ 为平均有效正应力。

2. 试验结果与分析

2.1 孔压特性发展规律

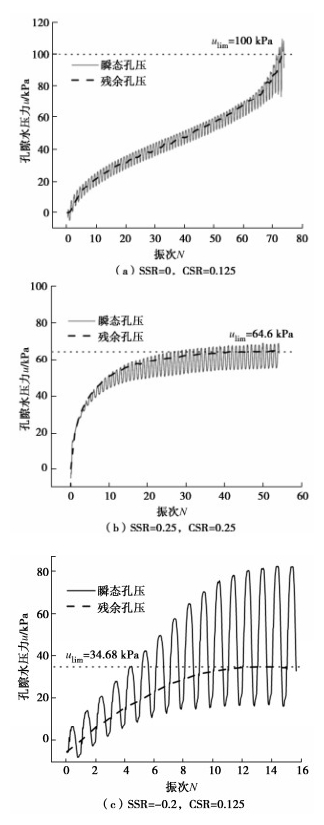
图 3给出不同初始偏应力作用下饱和密砂的孔压发展规律曲线。孔隙水压力可分为两类：①随着循环荷载作用实时变化的孔压，即实线所示的瞬态孔压，这种孔压会随着循环荷载的卸载而快速消散；②每个循环加载结束，试样未及时恢复的孔压，即虚线所示的残余孔压。从图 3（a）中可以看出，对于等向固结的试样，残余孔压在前期随着荷载的施加而逐渐累积，而在后期快速增长，直至达到荷载施加前的有效围压，u_lim=100 kPa。如图 3（b）所示，在压缩静偏应力作用下，孔压在加载初期迅速累积，随着循环荷载持续进行，残余孔压逐渐趋于稳定，u_lim=64.6 kPa。在拉伸静偏应力作用下，孔压发展与压缩静偏应力时有类似的变化趋势，孔压在加载初期累积较快而后基本保持不变，u_lim=34.68 kPa。

图 3 钙质砂孔压增长变化规律

Figure 3. Development of pore water pressure of calcareous sand

下载: 全尺寸图片幻灯片

同时，通过式（3）和（4）定义固结应力比K_c和残余孔压比u_r。

${K_{\text{c}}} = \frac{{{\sigma _{{\text{v}}0}}}}{{{\sigma _{{\text{h}}0}}}}\text{，}$

(3)

${u_{\text{r}}} = \frac{u}{{{\sigma _{{\text{h}}0}}}}。$

(4)

式中： ${\sigma _{{\text{v}}0}}$ 和 ${\sigma _{{\text{h}}0}}$ 分别为初始有效竖向应力和水平应力，u为残余孔压。

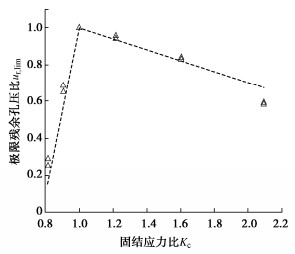
图 4给出了饱和密砂的极限残余孔压比和固结应力比的关系曲线。从图中可以看出，饱和密砂的极限残余孔压比随着固结应力比的增大呈先增大后减小的趋势，在K_c=1（等向固结）时，极限残余孔压比达到最大值u_{r, lim}=1，且大致上呈线性分布，与循环应力幅值大小无明显关系。

图 4 极限残余孔压比与固结应力比的关系

Figure 4. Relationship between ultimate residual pore pressure ratio and consolidation stress ratio

下载: 全尺寸图片幻灯片

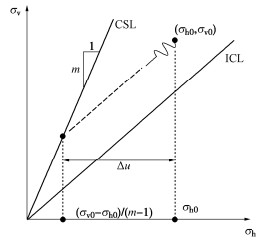
对于同一材料的砂土，其在循环荷载作用下有效应力路径将沿着平行于等向固结线（ICL）的方向逐渐靠近临界状态线（CSL），而与循环应力幅值无关，如图 5所示。因此，对于给定的初始应力状态（σ_h0，σ_v0），会与临界状态线相交于一点，且理论上初始应力点与最终应力点之间的水平距离 $\Delta u$ 为试验中的极限残余孔压，如式（5）所示。根据u_r和K_c定义，可得到两者关系如式（6），符合图 4所示的线性关系。

${u_{\lim }} = \Delta u = {\sigma _{{\text{h}}0}} - \frac{{{\sigma _{{\text{v}}0}} - {\sigma _{{\text{h}}0}}}}{{m - 1}}\text{，}$

(5)

${u_{{\text{r, lim}}}} = \frac{{{u_{\lim }}}}{{{\sigma _{{\text{h0}}}}}} = 1 - \frac{{{K_{\text{c}}} - 1}}{{m - 1}}。$

(6)

图 5 初始静剪应力状态对残余孔压影响示意图

Figure 5. Influences of initial static shear stress on residual pore pressure

下载: 全尺寸图片幻灯片

2.2 损耗能演化规律

动荷载作用下饱和砂土损耗的能量主要用于颗粒的相对运动和重新排列。因此，引入能量法，提出基于损耗能的砂土液化评价方法。循环加载过程中一个振次的损耗能W可用应力-应变滞回圈的面积表示，即：

$W = \sum\limits_{i = 1}^{n - 1} {\frac{1}{2}} ({q_{i + 1}} + {q_i})({\varepsilon _{{\text{a, }}i + 1}} - {\varepsilon _{{\text{a, }}i}}) 。$

(7)

式中：n为计算增量的总个数， ${q_i}$ 和 ${\varepsilon _{{\text{a, }}i}}$ 分别为第i个增量的偏应力和轴向应变。

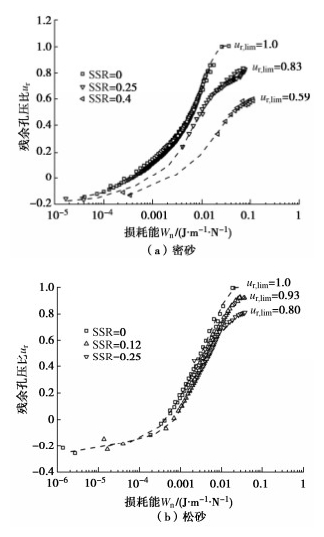
图 6分别给出饱和钙质砂在不同初始静偏应力作用下残余孔压比与正交化损耗能的内在关系，正交化损耗能W_n为损耗能W与初始有效水平正应力 ${\sigma _{{\text{h0}}}}$ 的比值。结果显示：饱和密砂的残余孔压初期增长缓慢，随着W_n的增大而较快增长，最后趋于稳定；在饱和松砂中也观察到类似的变化趋势。这说明残余孔压与损耗能的关系主要取决于初始应力条件。

图 6 残余孔压比与损耗能的关系

Figure 6. Relationship between residual pore pressure ratio and dissipated energy

下载: 全尺寸图片幻灯片

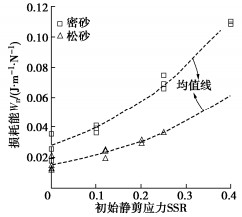
从图 7可以看出，饱和钙质砂在失稳破坏时所积累的损耗能随着初始静剪应力的增加而增加；对于同一初始应力状态，密砂所需能量始终大于松砂。研究表明^[13-14]，饱和砂土在循环荷载作用下损耗能主要与初始应力和相对密实度有关，受循环荷载幅值影响极小，具体可用式（8）表示：

${W'_{\text{n}}} = {10^{a\left( {{D_{\text{r}}} - 0.78} \right)}}{10^{b\left( {{\text{SSR}} - 1.0} \right)}}。$

(8)

图 7 损耗能与初始静剪应力比的关系

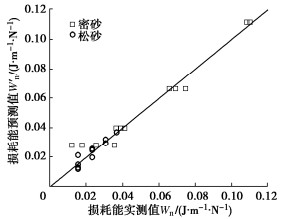
Figure 7. Relationship between dissipated energy and initial static shear stress ratio

下载: 全尺寸图片幻灯片

式中：a和b为经验参数，根据本次试验数据可分别取0.65，1.5。图 8对损耗能的试验实测值与通过式（8）所得的预测值进行对比，发现两者基本落在斜率为1的对角线两侧，表明能量模型可较好地预测不同试验条件下饱和钙质砂的损耗能。

图 8 损耗能实测值与预测值

Figure 8. Measured and predicted values of dissipated energy

下载: 全尺寸图片幻灯片

3. 结论

（1）饱和钙质砂的极限残余孔压比随固结应力比呈先增大后减小的趋势，在K_c=1时存在最大值，临界状态理论可以解释此现象。

（2）不排水循环加载条件下饱和钙质砂的损耗能与试样的初始静剪应力比和相对密实度有关，受循环应力比影响极小，可通过构建的能量模型较好地预测不同试验条件下饱和钙质砂所累积的损耗能。

图 1 桩靴模型

Figure 1. Spudcan model

下载: 全尺寸图片幻灯片

图 2 有限元模型

Figure 2. Finite element model

下载: 全尺寸图片幻灯片

图 3 离心模型

Figure 3. Centrifuge model

下载: 全尺寸图片幻灯片

图 4 桩靴下压阻力与插深关系图

Figure 4. Relationship between penetration resistance and depth

下载: 全尺寸图片幻灯片

图 5 不同网格尺寸对桩靴下压阻力影响

Figure 5. Effects of mesh size on penetration resistance

下载: 全尺寸图片幻灯片

图 6 插桩速率对下压阻力影响

Figure 6. Effects of penetration rate on penetration resistance

下载: 全尺寸图片幻灯片

图 7 不同摩擦系数对下压阻力影响

Figure 7. Effects of friction coefficient on penetration resistance

下载: 全尺寸图片幻灯片

图 8 不同侧压力系数对下压阻力影响

Figure 8. Effects of lateral pressure coefficient on penetration resistance

下载: 全尺寸图片幻灯片

图 9 侧压力系数K₀=0.9时地应力

Figure 9. Geostresses when lateral pressure coefficient K₀=0.9

下载: 全尺寸图片幻灯片

图 10 不同时间地应力的波动

Figure 10. Vibration of geostress at different time

下载: 全尺寸图片幻灯片

表 1 网格尺寸和单元数量

Table 1 Mesh size and number of cells

相对桩靴直径D的网格尺寸单元边长/m 土单元数量

0.1D 1.60 245290

0.08D 1.28 366700

0.05D 0.80 751830

0.03D 0.50 1898290

下载: 导出CSV

参考文献(24)

[1]	SICILIANO R J, HAMILTON J M, MURFF J D, et al. Effect of jackup spud cans on piles[C]//Proceedings of the Offshore Technology Conference. Houston, 1990.
[2]	CRAIG W H. Spud-can foundations: installation with deep penetration and subsequent removal[J]. Proceedings of the Institution of Civil Engineers: Geotechnical Engineering, 1998, 131(3): 146-151. doi: 10.1680/igeng.1998.30470
[3]	HOSSAIN M S, HU Y, RANDOLPH M F. Bearing behaviour of spudcan foundation on uniform clay during deep penetration[C]//International Conference on Offshore Mechanics and Arctic Engineering. Vancouver, 2004.
[4]	XIE Y. Centrifuge Model Study on Spudcan-pile Interaction[D]. Singapore: National University of Singapore, 2009.
[5]	QIU G, GRABE J. Numerical simulation of the deep penetration process of spudcans into sand overlying caly using the extended hypoplastic models[C]// International Offshore and Polar Engineering Conference. Rhodes, 2012.
[6]	QIU G, HENKE S, GRABE J. Application of a Coupled Eulerian–Lagrangian approach on geomechanical problems involving large deformations[J]. Computers and Geotechnics, 2011, 38(1): 30-39. doi: 10.1016/j.compgeo.2010.09.002
[7]	QIU G, HENKE S. Controlled installation of spudcan foundations on loose sand overlying weak clay[J]. Marine Structures, 2011, 24(4): 528-550. doi: 10.1016/j.marstruc.2011.06.005
[8]	QIU G, GRABE J. Explicit modeling of cone and strip footing penetration under drained and undrained conditions using a visco-hypoplastic model[J]. geotechnik, 2011, 34(3): 205-217. doi: 10.1002/gete.201100004
[9]	THO K K, LEUNG C F, CHOW Y K, et al. Eulerian finite element simulation of spudcan–pile interaction[J]. Canadian Geotechnical Journal, 2013, 50(6): 595-608. doi: 10.1139/cgj-2012-0288
[10]	HU P, WANG D, CASSIDY M J, et al. Predicting the resistance profile of a spudcan penetrating sand overlying clay[J]. Canadian Geotechnical Journal, 2014, 51(10): 1151-1164. doi: 10.1139/cgj-2013-0374
[11]	LEE K K. Investigation of Potential Spudcan Punch Through Failure on Sand Overlying Clay Soils[D]. Perth: The University of Western Australia, 2009.
[12]	周龙, 刘润, 郭绍曾, 等. 桩靴连续贯入过程的动态模拟方法研究[J]. 地震工程学报, 2015, 37(2): 460-466. doi: 10.3969/j.issn.1000-0844.2015.02.0460 ZHOU Long, LIU Run, GUO Shaozeng, et al. A dynamic simulation method for continuous spudcan penetration[J]. China Earthquake Engineering Journal, 2015, 37(2): 460-466. (in Chinese) doi: 10.3969/j.issn.1000-0844.2015.02.0460
[13]	王建华, 兰斐. 钻井船插桩对邻近桩影响的耦合欧拉-拉格朗日有限元方法研究[J]. 岩土力学, 2016, 37(4): 1127-1136. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201604028.htm WANG Jianhua, LAN Fei. A coupled Eulerian-Lagrange FEM method for analyzing the effects of spudcan penetration on an adjacent pile[J]. Rock and Soil Mechanics, 2016, 37(4): 1127-1136. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201604028.htm
[14]	ZHANG H, LIU R, YUAN Y. et al. Numerical analysis of lateral behaviour of large-diameter monopile in saturated clay[C]// The 29th International Ocean and Polar Engineering Conference. Hawaii, 2019.
[15]	冯加伟, 周立臣, 梁思颖. 钻井船插桩对海洋平台桩基影响的数值研究[J]. 中国海洋平台, 2022, 37(1): 43-47, 83. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGHY202201008.htm FENG Jiawei, ZHOU Lichen, LIANG Siying. Numerical study on influence of drilling ship piling on offshore platform pile foundation[J]. China Offshore Platform, 2022, 37(1): 43-47, 83. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGHY202201008.htm
[16]	闫澍旺, 林澍, 霍知亮, 等. 桶形基础液压下沉过程的耦合欧拉-拉格朗日有限元法分析[J]. 岩土力学, 2017, 38(1): 247-252. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201701032.htm YAN Shuwang, LIN Shu, HUO Zhiliang, et al. Coupled Eulerian-Lagrangian finite element analysis of suction caisson penetration processes under hydraulic pressure[J]. Rock and Soil Mechanics, 2017, 38(1): 247-252. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201701032.htm
[17]	郝心童, 李书兆, 李伟, 等. 黏土中大直径钢圆筒在桩靴贯入时的稳定性研究[J/OL]. 工程力学, doi: 10.6052/j.issn.1000-4750.2022.05.0428. 1-10. HAO Xintong, LI Shuzhao, LI Wei, et al. Study on Stability of Large-Diameter Steel Cylinder During Spudcan Penetration[J/OL]. Engineering Mechanics, doi: 10.6052/j.issn.1000-4750.2022.05.0428. (in Chinese)
[18]	戴笑如, 王建华, 范怡飞. 钻井船插桩CEL数值模拟中的若干问题分析[J]. 岩土力学, 2018, 39(6): 2278-2286. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201806044.htm DAI Xiaoru, WANG Jianhua, FAN Yifei. Issues of numerical simulation of the spudcan penetration based on CEL method[J]. Rock and Soil Mechanics, 2018, 39(6): 2278-2286. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201806044.htm
[19]	HOSSAIN M S, RANDOLPH M F, HU Y, et al. Cavity stability and bearing capacity of spudcan foundations on clay[C]// Offshore Technology Conference. Houston, Texas, USA. Offshore Technology Conference, 2006: OTC-17770.
[20]	THO K K, LEUNG C F, CHOW Y K, et al. Eulerian finite-element technique for analysis of jack-up spudcan penetration[J]. International Journal of Geomechanics, 2012, 12(1): 64-73. doi: 10.1061/(ASCE)GM.1943-5622.0000111
[21]	YI J T, HUANG L Y, LI D Q, et al. A large-deformation random finite-element study: failure mechanism and bearing capacity of spudcan in a spatially varying clayey seabed[J]. Géotechnique, 2020, 70(5): 392-405. doi: 10.1680/jgeot.18.P.171
[22]	ZHENG J B, HOSSAIN M S, WANG D. Estimating spudcan penetration resistance in stiff-soft-stiff clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2018, 144(3): 04018001. doi: 10.1061/(ASCE)GT.1943-5606.0001820
[23]	李大勇, 王召龙, 吴宇旗. 均质黏土中桩靴基础贯入阻力系数Nc的解析解[J/OL]. 工程力学, doi: 10.6052/j.issn.1000-4750.2022.11.0930. LI Dayong, WANG Zhaolong, WU Yuqi. Analytical solution of resistance factor nc for spudcan foundation penetrating into uniform undrained Clay[J/OL]. Engineering Mechanics, doi: 10.6052/j.issn.1000-4750.2022.11.0930. (in Chinese)
[24]	张海洋, 刘润, 贾沼霖. 自升式平台插桩对邻近平台桩基础的影响研究[J]. 岩土工程学报, 2021, 43(5): 867-876. doi: 10.11779/CJGE202105010 ZHANG Haiyang, LIU Run, JIA Zhaolin. Investigation of effect of spudcan penetration on adjacent platform piles[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(5): 867-876. (in Chinese) doi: 10.11779/CJGE202105010