考虑土-结构相互作用倾斜状态文峰塔地震响应分析

安一劲; 韩鹏举; 秦健栋; 白向灵; 何斌; 王效渊

doi:10.11779/CJGE2023S20028

考虑土-结构相互作用倾斜状态文峰塔地震响应分析 English Version

太原理工大学土木工程学院, 山西太原 030024

基金项目:

山西省文物局科技项目 RH2100001662

详细信息

作者简介:
安一劲(1999—)，男，博士，主要从事建筑遗产健康评估等方面的科研工作。E-mail: anyijing0020@163.com

通讯作者:
韩鹏举, E-mail: 13834569544@163.com

中图分类号: TU311.3
计量
- 文章访问数: 160
- HTML全文浏览量: 23
- PDF下载量: 14
出版历程
- 收稿日期: 2023-11-29
- 网络出版日期: 2024-04-19
- 刊出日期: 2023-11-30

Seismic response analysis of leaning Wenfeng Pagoda considering soil-structure interaction

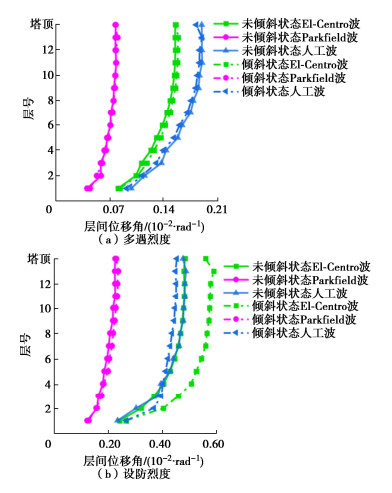
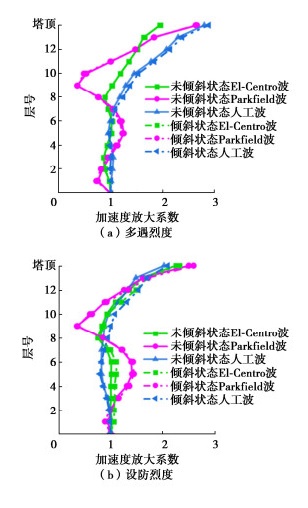
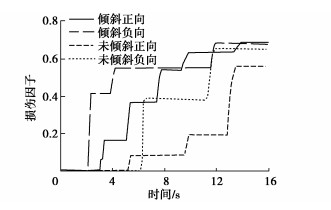
College of Civil Engineering, Taiyuan University of Technology, Taiyuan 030024, China

摘要

摘要: 为研究在土-结构相互作用下倾斜状态古塔地震响应，利用ABAQUS有限元软件，采用等效线性化地基土及非线性化砖石材料，考虑土体与结构分离滑移的几何非线性，借助python语言添加黏弹性人工边界，建立了倾斜及未倾斜状态永祚寺文峰塔两种有限元模型，通过时程分析方法对比研究倾斜因素对古塔抗震性能影响。结果表明：多遇地震作用下，文峰塔历史最大倾斜量对其抗震性能影响较小，峰值位移、层间位移角及加速度放大系数较未倾斜状态增加较小；设防地震作用下，倾斜状态文峰塔残余位移大幅增加，下层层间位移角普遍放大，加速度放大系数有所提高，塔身在倾斜侧损伤面积及损伤程度急剧增大，同时基础损伤也不容忽视。分析结果可为同类倾斜状态高层密檐砖塔抗震保护提供借鉴作用。
- 土-结构相互作用 /
- 倾斜砖塔 /
- 地震响应 /
- 黏弹性边界
Abstract: In order to study the seismic response of the leaning pagoda under soil-structure interaction, two kinds of finite element models for the leaning and un-leaning Wenfeng Pagoda of Yongzuo Temple are established by using the ABAQUS finite element software, adopting the equivalent linearization of foundation soils and non-linearization of masonry materials, considering the geometric non-linearities of the soil-structure separation and slip, and adding the visco-elastic artificial boundaries with the help of python language. By comparing the two models through the time-range analysis method, the effects of inclination factor on the seismic performance of the pagoda are investigated. The results show that under the action of small earthquakes, the historical maximum tilt has less impact on its seismic performance, and the peak displacement, section displacement angle and acceleration amplification coefficient have small increase. Under the action of middle earthquakes, the residual displacement of the leaning pagoda increases greatly, the lower layer of the pagoda section displacement angle is generally enlarged, the acceleration amplification coefficient increases, the damage area and degree of the pagoda in the leaning side increase dramatically, and the foundation damage should not be neglected. The analysis results can provide a reference for the seismic protection of similar leaning high-rise dense eaves brick pagodas.
- soil-structure interaction /
- leaning masonry pagoda /
- seismic response /
- viscoelastic boundary

HTML全文

0. 引言

无论是寒区工程^[1-2],还是人工冻结技术应用中^[3-7],都会遇到冻土的融化。冻土在融化过程中,会产生显著沉降变形或者累积超静孔隙水压力,这些均会造成附近建筑物及土层的变形破坏。与土体冻结过程中的冻胀破坏^[8-10]类似,冻土融化过程也严重威胁冻土相关工程的安全。

许多学者进行了冻土融化过程相关的研究,除了试验和测试外^[11-14],也有一些模型方面的成果。Morgenstern等^[15-16],Nixon等^[17]基于相变热传导纽曼解答以及太沙基一维固结理论建立了冻土的一维融化固结模型（以下简称MN模型）,并给出了模型解析解答；试验对比表明,模型对低含冰量冻土预测结果较好,而对高含冰量冻土则偏差较大。Zhou等^[18]在MN模型基础上,考虑了冻土中未冻水对传热的影响以及外部变荷载条件,建立了改进的融化固结模型,并给出了模型的解析解答。对于高含冰量冻土,小变形固结理论体系下的MN模型及其改进并不适用。Foriero等^[19]在Gibson大变形固结理论^[20]的基础上建立了一维大变形融化固结理论,考虑的相界面位置是时间的幂函数。实际上,相界面位置变化是与传热过程相关联的,基于此,Yao等^[21-22]建立了三维大变形融化固结理论；Qi等^[23],Wang等^[24],Wang等^[25]对Yao等的大变形融化固结理论进行了改进,并计算了寒区工程中的冻土融化过程。Yao等的模型并未考虑大变形对传热控制方程的影响,Dumais等^[26]做出了改进,给出了大变形坐标系下的传热方程,并建立了新的一维大变形融化固结模型。

在人工冻结技术应用中,冻结壁在完成临时使命后会逐渐融化,而自然融化过程往往较长,长时间沉降及孔压消散会带来许多不确定因素。因而常采用人工强制解冻的方式,即利用高温热水强制融化冻土（70℃或更高）^[27-28]；在天然冻土区,为了方便施工,有时也采用高温热水强制融化冻土。人工强制融化过程与天然融化过程有所不同,前者由于高温作用,融区内土颗粒、水的热膨胀不可忽视,融区内发生的不是普通固结,而是热固结^[29-32]。因此,冻土在高温融化过程中,超静孔压、沉降等的演变与普通融化过程是不同的,上述的模型均不适用。本文考虑饱和冻土在高温下的一维融化热固结过程,推导建立过程的理论模型,并给出模型的解析解答。

1. 模型基本方程

图1为饱和冻土在高温下一维融化过程的示意图。冻土初始温度为均匀T₀,低于冻结温度T_f；开始融化时,上表面z = 0迅速升温到某一高温T_w。冻土融化过程中,融化锋面S(t)逐渐向下移动,热固结发生在上表面与融化界面之间,而上表面荷载一次施加,作用在单位面积上的大小为P_ob。

图 1 高温下饱和冻土一维融化过程示意图

Figure 1. Schematic diagram of 1-D thawing process of saturated frozen soil under high temperature

下载: 全尺寸图片幻灯片

MN模型的基本假设也在本文模型中采用：①冻土含冰量较少,过程是小变形过程；②冻土融化过程中,融土处于饱和状态,即不考虑空气相的影响；③不考虑固结水流对流作用对传热的影响,传热部分近似为半无限大物体相变热传导；④忽略冰水相变体积变化对传热、热固结过程的影响,而只在最后计算沉降时加以讨论。

传热部分的控制方程为

$C_{v} \frac{\partial T}{\partial t} = \frac{\partial}{\partial z} (k_{h} \frac{\partial T}{\partial z}) - L ρ_{w} \frac{\partial θ_{u}}{\partial t} (0 < z < \infty)$ ,

(1)

$T (z, 0) = T_{0}$ ,

(2)

$T (0, t) = T_{w}$ ,

(3)

式中,T为温度,z为位置坐标,t为时间,C_v为土体体积热容,k_h为土体导热系数,L为冰相变的潜热,θ_u为体积未冻水含量, $ρ_{w}$ 为水的密度。

式（1）中C_v,k_h均随土体成分变化而变化,一般可用各成分的算术或几何平均表示^[18]；冻土中未冻水与负温的关系即为冻结特性,可以用下式描述（不考虑滞后效应^[33]）：

$\begin{matrix} θ_{u} = \frac{ρ_{d}}{100 ρ_{w}} \exp (0.2618 + 0.5519 \ln S_{a} - \\ 1.4495 S_{a}^{- 0.2640} \ln | T |) \end{matrix}$ ,

(4)

式中,ρ_d为土的干密度,S_a为土的比表面积。

热固结发生在融化区0< z <S(t)内,在建立热固结方程时,主要考虑土颗粒、水的热膨胀性,而不考虑它们的压缩性。土颗粒部分体积变化率为

$\frac{1}{V} \frac{\partial V_{s}}{\partial t} = (1 - n) a_{s} \frac{\partial T}{\partial t} (0 < z < S (t))$ ,

(5)

式中,V为总体积,V_s为土颗粒体积,n为孔隙率,a_s为土颗粒的热膨胀系数。

孔隙的变形主要包括水流的净流入和水的热膨胀两部分,可以描述为

$\frac{1}{V} \frac{\partial V_{e}}{\partial t} = - \frac{\partial q_{w}}{\partial z} + n a_{w} \frac{\partial T}{\partial t} (0 < z < S (t))$ ,

(6)

式中,V_e为孔隙体积,q_w为固结水流速度,a_w为水的热膨胀系数。

结合式（5）,（6）得到^[29]：

$\begin{matrix} \frac{\partial ε_{v}}{\partial t} = \frac{1}{V} \frac{\partial V_{s}}{\partial t} + \frac{1}{V} \frac{\partial V_{e}}{\partial t} \\ = - \frac{\partial q_{w}}{\partial z} + [n a_{w} + (1 - n) a_{s}] \frac{\partial T}{\partial t} (0 < z < S (t)) \end{matrix}$ ,

(7)

式中, $ε_{v}$ 为体应变。

融化区中固结水流满足达西定律

$q_{w} = - \frac{k_{g}}{γ_{w}} \frac{\partial P}{\partial z}$ ,

(8)

式中,P为超静孔压,k_g为渗透系数, $γ_{w}$ 为水的重度。

将式（8）代入式（7）得到

$\frac{\partial ε_{v}}{\partial t} = \frac{k_{g}}{γ_{w}} \frac{\partial^{2} P}{\partial z^{2}} + \bar{a} \frac{\partial T}{\partial t} (0 < z < S (t))$ ,

(9)

式中, $\bar{a} = n a_{w} + (1 - n) a_{s}$ 。

考虑热应力作用时,土体有效应力形式表达的一维本构方程为^[29]

${σ^{'}}_{z z} = E_{s} ε_{z z} - β (T - T_{f})$ ,

(10)

式中, ${σ^{'}}_{z z}$ 为z方向土体有效应力, $ε_{z z}$ 为z方向土体应变,均以拉为正（而孔压则以压为正）,E_s为土体压缩模量,β为土体热应力系数,都可以表示为土体的变形模量E和泊松比 $ν$ 的关系式^{[29, 31]}

$\begin{array}{l} E_{s} = \frac{1 - ν}{1 + ν} \frac{E}{1 - 2 ν} ， \\ β = \frac{E}{1 - 2 ν} a_{sm} ， \end{array}}$

(11)

其中, $a_{sm}$ 为土体的热膨胀系数,一般可取 $a_{sm} = \bar{a}$ 。

在深度z处,由太沙基有效应力原理得到

${σ^{'}}_{z z} = - P_{ob} - γ^{'} z + P$ ,

(12)

式中, $γ^{'} = γ - γ_{w}$ , $γ$ 为土的重度。

由式（10）,（12）可以得到：

$\begin{array}{l} \frac{\partial P}{\partial t} = E_{s} \frac{\partial ε_{z z}}{\partial t} - β \frac{\partial T}{\partial t} & (0 < z < S (t)) \end{array}$ 。

(13)

在一维问题中 $ε_{v} = ε_{z z}$ ,利用式（9）,（13）可以得到融化区热固结方程：

$C_{g} \frac{\partial^{2} P}{\partial z^{2}} = \frac{\partial P}{\partial t} + A \frac{\partial T}{\partial t} (0 < z < S (t))$ ,

(14)

式中, $A = β - E_{s} \bar{a}$ , $C_{g}$ 为固结系数, $C_{g} = k_{g} E_{s} / γ_{w}$ 。

如图1所示,考虑融化界面上的单元 $V =$ $Δ S (t) \times A_{c}$ , $A_{c}$ 为横截面积。Δt时间间隔内该单元体积变化量为ΔV,ΔV由水流净流入及温度膨胀两部分组成；融化界面下方为冻土,无水流,所以有

$Δ V = - \frac{k_{g}}{γ_{w}} {\frac{\partial P}{\partial z} |}_{S (t)} A_{c} Δ t + \bar{a} Δ T V$ 。

(15)

根据式（10）界面单元应变为

$ε_{z z} = \frac{Δ {σ^{'}}_{z z} + β Δ T}{E_{s}}$ 。

(16)

在融化界面z = S(t)上,土体有效应力为

${σ^{'}}_{z z} = - P_{ob} - γ^{'} S (t) + P (S (t), t)$ 。

(17a)

式（16）中增量对应的初始状态为冻土融化但未发生体积变化时的状态,此时外荷载尚未传递给土骨架,有效应力一般取为0^[15]。

因此式（16）中有效应力增量为

$Δ {σ^{'}}_{z z} = {σ^{'}}_{z z} = - P_{ob} - γ^{'} S (t) + P (S (t), t)$ 。

(17b)

由式（15）,（16）得到的应变应相等,同时相界面温度恒定即增量 $Δ T$ 为0,从而有

$- \frac{k_{g}}{γ_{w}} {\frac{\partial P}{\partial z} |}_{S (t)} \frac{Δ t}{Δ S (t)} = \frac{- P_{ob} - γ^{'} S (t) + P (S (t), t)}{E_{s}}$ 。

(18)

式（18）经整理后得到

$[P_{ob} + γ^{'} S (t) - P (S (t), t)] \frac{d S (t)}{d t} = C_{g} {\frac{\partial P}{\partial z} |}_{S (t)}$ 。

(19)

土体上边界为完全透水边界,因此有

$P (0, t) = 0$ 。

(20)

式（14）,（19）,（20）构成融化区热固结作用的基本方程。

2. 模型解析求解

2.1 融化界面及温度场部分解答

MN模型传热部分应用了纽曼相变热传导的解答,且由于不考虑热膨胀,模型仅需要确定融化界面的位置；文献[18]进一步考虑了冻土融化与普通相变热传导的不同,采用式（1）～（4）为基本方程,给出了融化界面及温度场的解析解答,下面介绍并直接应用该解答。

在融化区内,温度场解答为

$T (z, t) = a_{1} + b_{1} erfc (\frac{z}{2 \sqrt{α_{1} t}}) (0 < z < S (t))$ ,

(21)

$S (t) = α_{thaw} \sqrt{t}$ ,

(22)

式中, $α_{1}$ 为融化区中土的热扩散系数,参数a₁,b₁, $α_{thaw}$ 均可以表示为常数 $λ_{1}$ 的表达式,

$\begin{array}{l} a_{1} = \frac{T_{f} - T_{w} erfc (λ_{1})}{erf (λ_{1})} ， \\ b_{1} = \frac{T_{w} - T_{f}}{erf (λ_{1})} ， \\ α_{thaw} = 2 λ_{1} \sqrt{α_{1}} ， \end{array}}$

(23)

其中,erf(•),erfc(•)分别为误差函数和误差补函数,而 $λ_{1}$ 的求解过程详见文献[18]。

2.2 热固结部分解答

对于融化区域0 < z < S(t) 内的热固结问题,引入如下变量：

$u (z, t) = P (z, t) - P_{ob} - C z$ ,

(24)

式中, $C = 2 R^{2} γ^{'} / (1 + 2 R^{2})$ ,R为融化固结比, $R = α_{thaw} /$ $2 \sqrt{C_{g}}$ ^[15]。

由式（14）,（19）,（20）,变量u(z, t)的控制方程为

$\begin{array}{l} C_{g} \frac{\partial^{2} u}{\partial z^{2}} = \frac{\partial u}{\partial t} + A \frac{\partial T}{\partial t} & (0 < z < S (t) = α_{thaw} \sqrt{t}) \end{array}$ ,

(25)

$u (0, t) = - P_{ob}$ ,

(26)

$C_{g} \frac{\partial u}{\partial z} [S (t), t] = - u [S (t), t] \frac{d S (t)}{d t}$ 。

(27)

融区内热物性均为常数,温度场满足如下方程：

$\frac{\partial T}{\partial t} = α_{1} \frac{\partial^{2} T}{\partial z^{2}} (0 < z < S (t) = α_{thaw} \sqrt{t})$ 。

(28)

定义如下变量

$Ω = u + \frac{A α_{1}}{α_{1} - C_{g}} T$ 。

(29)

由式（25）,（28）可知,变量 $Ω$ 满足如下控制方程：

$C_{g} \frac{\partial^{2} Ω}{\partial z^{2}} = \frac{\partial Ω}{\partial t} (0 < z < S (t) = α_{thaw} \sqrt{t})$ 。

(30)

在融化界面S(t)上,变量 $Ω$ 满足

$\begin{matrix} - [Ω (S (t), t) - \frac{A α_{1}}{α_{1} - C_{g}} T_{f}] \frac{d S (t)}{d t} \\ = C_{g} {[\frac{\partial Ω}{\partial z} - \frac{A α_{1}}{α_{1} - C_{g}} \frac{\partial T}{\partial z}] |}_{S (t)} \end{matrix}$ 。

(31)

引入相似变量 $η = z / 2 \sqrt{C_{g} t}$ ,可将关于 $Ω$ 的偏微分方程变为如下常微分方程^[34-35]：

$\frac{d^{2} Ω}{d η^{2}} + 2 η \frac{d^{2} Ω}{d η} = 0 (0 < η < R) ，$

(32a)

$Ω (0) = - P_{ob} + \frac{A α_{1}}{α_{1} - C_{g}} (a_{1} + b_{1})$ ,

(32b)

${(2 R Ω + \frac{d Ω}{d η}) |}_{η = R} = \frac{A α_{1}}{α_{1} - C_{g}} [2 R T_{f} - \frac{2 b_{1}}{\sqrt{π} F} \exp (- λ_{1}^{2})] ，$

(32c)

式中,F为导温固结比, $F = \sqrt{α_{1} / C_{g}}$ 。

式（32a）的通解为^[34-35]

$Ω = a + b erfc (η)$ ,

(33)

式中,系数a,b由边界条件式（32b）,（32c）确定。

根据式（32b）,（32c）可以得到：

$a = \frac{A α_{1}}{α_{1} - C_{g}} (a_{1} + b_{1}) - P_{ob} - b$ ,

(34)

$\begin{matrix} b = - \frac{\sqrt{π} R P_{ob}}{\exp (- R^{2}) + \sqrt{π} R erf (R)} + \\ \frac{A α_{1}}{α_{1} - C_{g}} b_{1} \frac{\exp (- λ_{1}^{2}) + \sqrt{π} F R \erf (λ_{1})}{F \exp (- R^{2}) + \sqrt{π} F R \erf (R)} \end{matrix}$ 。

(35)

将a,b代入式（33）,利用式（21）,（24）,（29）可以得到超静孔隙压力的解析解答,将解答整理成无量纲形式为

$\begin{array}{l} \bar{P} = ε \frac{F^{2}}{F^{2} - 1} \frac{\erf (λ_{1} \bar{z})}{\erf (λ_{1})} - ε \frac{F^{2}}{F^{2} - 1} \frac{\erf (R \bar{z})}{\erf (λ_{1})} \cdot \\ \frac{\sqrt{π} F R \erf (λ_{1}) + \exp (- λ_{1}^{2})}{\sqrt{π} F R \erf (R) + F \exp (- R^{2})} + \frac{\sqrt{π} R \erf (R \bar{z})}{\sqrt{π} R \erf (R) + \exp (- R^{2})} + \\ W_{r} \bar{z} \frac{2 R^{2}}{2 R^{2} + 1} (0 < \bar{z} < 1) \end{array}$ ,

(36)

式中

$\begin{array}{l} \bar{P} = \frac{P (z, t)}{P_{ob}} ， \\ \bar{z} = \frac{z}{S (t)} ， \\ ε = \frac{A (T_{w} - T_{f})}{P_{ob}} ， \\ W_{r} = \frac{γ^{'} S (t)}{P_{ob}} 。 \end{array}}$

(37)

式（36）表明无量纲超静孔压 $\bar{P}$ 是无量纲变量 $\bar{z}$ ,W_r, $ε$ ,R,F的函数,式中虽然包含 $λ_{1}$ ,但 $λ_{1}$ =R/F并不是独立变量。W_r是融土浮自重与外荷载之比,也正比于t^0.5,称之为自重时间因子； $ε$ 为热固结强度与外荷载之比,称之为热固结强度因子。

获得超静孔压后,沉降变形可以由下式计算^[31]：

$\begin{matrix} S_{t} = - \int_{0}^{S (t)} ε_{z z} d z = - \int_{0}^{S (t)} [{σ^{'}}_{z z} + β (T - T_{f})] / E_{s} d z \\ = \int_{0}^{S (t)} [P_{ob} + γ^{'} z - P - β (T - T_{f})] / E_{s} d z \end{matrix}$ ,

(38)

式中,S_t为融化热固结沉降。

将超静孔压代入式（38）,积分后可以整理成如下的无量纲形式：

${\bar{S}}_{t} = {\bar{S}}_{t 1} + {\bar{S}}_{t 2} - {\bar{S}}_{t 3}$ ,

(39)

式中, ${\bar{S}}_{t} = S_{t} / S (t)$ ,右侧各项为

$\begin{matrix} {\bar{S}}_{t 1} = δ (1 + \frac{W_{r}}{2}) - \frac{\sqrt{π} δ [ierfc (R) + R - ierfc (0)]}{\exp (- R^{2}) + \sqrt{π} R \erf (R)} - \\ \frac{δ W_{r} R^{2}}{2 R^{2} + 1} \end{matrix}$ ,

(40)

$\begin{array}{l} {\bar{S}}_{t 2} = δ ε \frac{F^{2}}{F^{2} - 1} [\frac{ierfc (R) + R - ierfc (0)}{R \erf (λ_{1})} \cdot \\ \frac{\exp (- λ_{1}^{2}) + \sqrt{π} F R \erf (λ_{1})}{F \exp (- R^{2}) + \sqrt{π} F R \erf (R)} - \frac{ierfc (λ_{1}) + λ_{1} - ierfc (0)}{λ_{1} \erf (λ_{1})}] ， \end{array}$

(41)

${\bar{S}}_{t 3} = δ ζ \frac{- λ_{1} erfc (λ_{1}) - ierfc (λ_{1}) + ierfc (0)}{λ_{1} \erf (λ_{1})}$ ,

(42)

其中, $ierfc (ε) = \int_{ε}^{+ \infty} erfc (z) d z$ 。

式（40）～（42）中无量纲量 $ζ$ , $δ$ 为

$\begin{array}{l} ζ = \frac{β (T_{w} - T_{f})}{P_{ob}} ， \\ δ = \frac{P_{ob}}{E_{s}} ， \end{array}}$

(43)

式中, $ζ$ 为热应力强度与荷载之比,称为热应力因子, $δ$ 为荷载压缩变形。

式（39）中 ${\bar{S}}_{t 1}$ 为普通固结引起的沉降, ${\bar{S}}_{t 2}$ 为由热固结引起的孔压变化导致的沉降（称为热压作用）,而 ${\bar{S}}_{t 3}$ 是热膨胀作用引起的膨胀变形。对于冻土中冰融化体积变化造成的直接沉降则为0.1n,而本文主要讨论式（39）给出的融化热固结变形。

3. 算例及分析

3.1 与相关模型及解答的一致性

可以用于热固结模型及解答对比的完整试验结果较少,这也是文献[29～32]热固结计算未进行试验对比的原因；而冻土在高温下融化热固结过程则更为特殊,因此本文主要通过与已有模型及解答的一致性来阐述本文结果的正确性。

MN模型是冻土一维融化过程的经典模型,常被用于对比参照,如文献[26]中融化大变形固结理论、文献[18]中考虑未冻水及变荷载的融化固结理论均是通过与MN模型的对比来说明结果的正确性的。

在不考虑温度对融化区的作用时,热应力系数β = 0,参数 $\bar{a} = 0$ ,从而式（14）中温度变化率项系数A = 0,式（36）直接退化为

$\bar{P} = \frac{\sqrt{π} R \erf (R \bar{z})}{\sqrt{π} R \erf (R) + \exp (- R^{2})} + W_{r} \bar{z} \frac{2 R^{2}}{2 R^{2} + 1} (0 < \bar{z} < 1)$ 。

(44)

容易看出,退化后的模型与MN模型是一致的,且式（44）与MN模型的解答一致^[15]。

另一方面,在融化区0 < z < S(t)内,热固结控制方程与文献[31]中的热固结方程相同,文献[32]中热固结方程在忽略对流换热并考虑瞬时荷载后也与本文一致。

3.2 孔压计算结果

式（36）中温度对超静孔压的影响主要在前两项,而前两项正比于如下函数：

$\begin{array}{l} g (\bar{z}, F, R) = \frac{F^{2}}{F^{2} - 1} \frac{\erf (λ_{1} \bar{z})}{\erf (λ_{1})} - \\ \frac{F^{2}}{F^{2} - 1} \frac{\erf (R \bar{z})}{\erf (λ_{1})} \frac{\sqrt{π} F R \erf (λ_{1}) + \exp (- λ_{1}^{2})}{\sqrt{π} F R \erf (R) + F \exp (- R^{2})} \end{array}$ 。

(45)

图2给出了不同条件下g函数随F的变化。从图2中可以看出,g函数始终为负值,且在F=1处的间断点是可去间断点。由式（36）,温度的作用会增加还是减小超静孔压主要取决于A的正负,下面就A的取值作一些讨论。

图 2 超静孔压解答中g函数的变化

Figure 2. g function in analytical solution of excessive pore water pressure

下载: 全尺寸图片幻灯片

表1给出了文献[29]中两种材料的相关参数及由这些参数计算得到的A值,两种材料的A均为负值。从式（36）可知,A为负值时,高温作用会增加超静孔压,文献[29]中热固结的计算结果确实如此。

表 1 文献[29]中材料参数及A的计算值

Table 1. Material parameters and computed values of A in Ref.[29]

材料	a_w/(10^-4℃^-1)	a_s/(10^-6℃^-1)	a_sm/(10^-6℃^-1)	n	E/MPa	v	A/(10^-4MPa℃^-1)
A	3	3	3	0.25	5.0	0.2	-4.2083
B	3	3	3	0.375	2.880	0.2	-3.6120

下载: 导出CSV

| 显示表格

文献[29]中土体的热膨胀系数a_sm并未取 $\bar{a}$ ,一般情况下若a_sm取为 $\bar{a}$ ,则可以根据式（11）得到

$A = \frac{2 ν v}{1 + ν} \frac{E}{1 - 2 ν} \bar{a}$ 。

(46)

通常材料泊松比小于0.5,因而A为正值,根据式（36）可知此时高温作用会降低超静孔压,文献[31]中的计算A取为正值,确实也出现了超静孔压降低到负值的结果。

参数A的取值不影响解答的应用,本文在下面的算例中A取为正值,此时ε也为正值。根据相关文献中的数据^[36],导温固结比F一般小于10,而其他的无量纲参数则没有明显范围限制。

图3分别给出了R为20,5,2时不同 $ε$ 下 $\bar{P}$ 随 $\bar{z}$ 的变化曲线。从图中可以看出,A为正值时高温作用造成了超静孔压的下降,并且形成了一定的负压区,这与前述分析是一致的；该特征也可以通过控制方程式（14）解释,由于融区内温度的上升,抵消了部分本应造成的超静孔压的上升,从而导致实际超静孔压与忽略高温作用时相比有所降低。随着热固结强度因子 $ε$ 的增加,热压作用引起的孔压下降愈加显著,但热压作用影响的相对范围（ $\bar{z}$ 的范围）没有明显改变。

图 3 ε对

$\bar{P}$ 影响

Figure 3. Effects of ε on

$\bar{P}$

下载: 全尺寸图片幻灯片

对比图3可知,随着R的减小,热压作用的相对影响范围增大,即减小融化界面速度或增加土的固结系数会导致热压作用影响到相对深处（ $\bar{z}$ 较大的位置）。

图4给出了不同R下 $\bar{P}$ 随 $\bar{z}$ 的变化曲线。在R=20时,热压作用影响集中在 $\bar{z} < 0.1$ 的范围；在R=10时,热压作用的影响扩大到 $\bar{z} < 0.3$ ；在R = 5时,该影响范围增大到 $\bar{z} < 0.6$ ；而在R进一步减小到2,1时,热压作用的影响范围已扩大到整个融区。随着R减小,另一个变化特征是热压作用影响的峰值强度逐渐减弱；当R减小为1时,负压区已经消失。这表明减小融化界面速度或增加土的固结系数会使得热压作用的影响在融区内变得更均匀。

图 4 R对

$\bar{P}$ 影响

Figure 4. Effects of R on

$\bar{P}$

下载: 全尺寸图片幻灯片

图5给出了不同F下 $\bar{P}$ 随 $\bar{z}$ 的变化曲线。导温固结因子F表示热扩散与固结的相对强弱,F增大代表热扩散相对变强,融区的温度更高且温度影响扩散更远,这也导致热压作用变强且逐渐影响到相对深处,这与图5中的结果是一致的。

图 5 F对

$\bar{P}$ 影响

Figure 5. Effects of F on

$\bar{P}$

下载: 全尺寸图片幻灯片

图6给出了不同W_r下 $\bar{P}$ 随 $\bar{z}$ 的变化曲线。W_r代表了时间和自重的作用,W_r增加表示融化区域增加,自重作用增强,因此 $\bar{P}$ 也增加；图中结果还表明W_r增加对热压作用强度影响不大,同时也基本不改变热压作用的相对影响范围。

图 6 W_r对

$\bar{P}$ 影响

Figure 6. Effects of W_r on

$\bar{P}$

下载: 全尺寸图片幻灯片

3.3 沉降量计算结果

因为P_ob可以很小,沉降量计算时两个无量纲变量ζ, ε是没有上限的,但是δζ与δε却有一定的限制,根据定义有

$\begin{array}{l} δ ζ = \frac{β (T_{w} - T_{f})}{E_{s}} ， \\ δ ε = \frac{A (T_{w} - T_{f})}{E_{s}} 。 \end{array}}$

(47)

若冻土在高温T_w=T_f+80℃下融化,采用文献[32]中的参数,土体E=3 MPa, $ν$ = 0.45,土颗粒热膨胀系数为2.5×10^-5℃^-1,水的热膨胀系数2×10^-4℃^-1,则计算得到的δζ大约为10^-2；材料泊松比一般小于0.5,此时δε与δζ的比值小于2/3,该比值在泊松比为0.45时约为0.62。下面算例中考虑δ = 0.03, $ζ$ = 1/3,ε = 0.62ζ。

图7给出了各部分无量纲沉降随W_r的变化,热压作用部分和热膨胀作用部分基本不随W_r变化,而普通固结和总沉降部分随着W_r增加而线性增加,该变化规律也可以直接从式（39）得出；从图中还可以看出,热膨胀作用强于热压作用,因此温度的净效果是膨胀变形,该膨胀变形会抵消部分普通固结沉降,因而总沉降较普通固结沉降略有降低。

图 7 各部分无量纲沉降随W_r的变化

Figure 7. Variation of different dimensionless settlements with W_r

下载: 全尺寸图片幻灯片

图8给出了各部分无量纲沉降随F变化的曲线,普通固结部分不随F变化,而热膨胀作用、热压作用均随F增加而近似线性增长,且热膨胀作用始终强于热压作用；在F变化范围内,普通固结部分强于温度引起的净膨胀变形,因而总沉降为正值,它随F增大而减小。随着F增大,热扩散相对增强,融区内温度整体提高,这是热膨胀作用、热压作用均增强的原因。

图 8 各部分无量纲沉降随F的变化

Figure 8. Variation of different dimensionless settlements with F

下载: 全尺寸图片幻灯片

图9给出了各部分无量纲沉降随R变化的曲线,随着R增加,热压作用早期增加后又逐渐减小,热膨胀作用则一直减小,后者始终强于前者；普通固结沉降也逐渐减小,且它始终强于温度引起的净膨胀变形,因而逐渐减小的总沉降始终为正值。R的增加代表融化界面推进速度相对于固结速度的增加,即融区迅速扩大,而固结及热扩散则相对缓慢,因此各部分无量纲沉降基本随R的增加而逐渐减小。

图 9 各部分无量纲沉降随R的变化

Figure 9. Variation of different dimensionless settlements with R

下载: 全尺寸图片幻灯片

上述结果表明,温度的净效果是膨胀变形,该效果弱于普通固结沉降,因此总的效果是沉降。实际上,如果δ增大,普通固结沉降会增加,而温度净效果由于δζ值的限制仍然弱于普通固结作用；另一方面,冰相变体积变化会造成无量纲沉降0.1n,因此一般不会出现温度引起的净膨胀变形占优势的情形。

4. 结论与展望

人工冻土融化过程中,常采用高温热水强制加速解冻,该方法在寒区工程施工中也有应用。本文针对饱和冻土在高温下的一维融化过程,开展了理论建模及解析计算研究,得到5点结论。

（1）建立了饱和冻土在高温作用下一维融化过程的理论模型,该模型包含传热部分与热固结部分。前者为全区域考虑冻土中未冻水的相变热传导过程,而后者为融化区土体在高温、荷载及自重作用下产生的热固结过程。模型在忽略了温度引起的土颗粒、水热膨胀作用后退化为Morgenstern和Nixon的经典一维融化固结模型。

（2）考虑初始温度T₀和表面融化温度T_w,对上述冻土一维融化热固结模型进行了解析求解,其中传热部分解答为已有结果,而热固结部分解答则为本文推导获得。该解析解在忽略高温热膨胀作用后退化为Morgenstern和Nixon模型的解答。

（3）利用解析解对融区内的超静孔压进行了计算。温度对 $\bar{P}$ 的影响即热压作用取决于热固结强度因子ε,本文ε为正值,因此热压作用为负值,且随着ε增加热压作用增强；随着R的减小,热压作用逐渐影响到 $\bar{z}$ 较大的位置,且热压作用强度在融化区内趋于均匀；随着F的增大,热压作用同样逐渐影响到 $\bar{z}$ 较大的位置,而热压作用在融区内会整体增强（该点与R的影响不同）；W_r的增加会增加 $\bar{P}$ ,但基本不改变热压作用强度及相对影响范围。

（4）利用解析解答对融化区内的沉降进行了计算。热压作用会增加沉降,但热膨胀作用会减小沉降,温度的净效果为膨胀变形；温度作用的净效果小于普通固结沉降,因而融化热固结总体表现为沉降；考虑到冰相变体积缩小引起的沉降,冻土在高温下融化时温度引起的净膨胀变形不会占主导。

（5）对于工程实际中复杂条件下的融化热固结问题,需要对本文模型进行数值求解,而本文建立的解析解答为发展模型高精度数值方法提供了对比基准。

图 1 黏弹性边界示意图

Figure 1. Schematic diagram of viscoelastic boundary

下载: 全尺寸图片幻灯片

图 2 文峰塔土-结构相互作用模型

Figure 2. Model for soil-structure interaction of Wenfeng Pagoda

下载: 全尺寸图片幻灯片

图 3 地震波加速度时程曲线

Figure 3. Seismic acceleration-time curves

下载: 全尺寸图片幻灯片

图 4 多遇烈度El-Centro波作用下文峰塔x向位移时程曲线

Figure 4. Time-history curves of x-directional displacement under action of El-Centro wave with small intensities

下载: 全尺寸图片幻灯片

图 5 设防烈度El-Centro波作用下文峰塔x向位移时程曲线

Figure 5. Time-history curves of x -directional displacement under action of El-Centro wave with middle intensities

下载: 全尺寸图片幻灯片

图 6 层间位移角

Figure 6. Section displacement angles

下载: 全尺寸图片幻灯片

图 7 加速度放大系数

Figure 7. Acceleration amplification factors

下载: 全尺寸图片幻灯片

图 8 El-Centro波作用下未倾斜状态古塔损伤云图

Figure 8. Damage cloud of Wenfeng Pagoda in untilted state under action of El-Centro wave

下载: 全尺寸图片幻灯片

图 9 El-Centro波作用下倾斜状态古塔损伤云图

Figure 9. Damage cloud of Wenfeng Pagoda in inclined state under.action of El-Centro wave

下载: 全尺寸图片幻灯片

图 10 古塔基础受拉损伤因子时程

Figure 10. Time histories of tensile damage factors of foundation

下载: 全尺寸图片幻灯片

表 1 土层物理力学参数

Table 1 Physical and mechanical parameters of soil layer

土类	密度/(kg·m^-3)	泊松比	黏聚力/kPa	内摩擦角/(°)	弹性模量/MPa
粉土	1950	0.29	16	24	217.76

下载: 导出CSV

表 2 文峰塔两种模型前二阶自振频率及差值

Table 2 First two natural frequencies and differences of three models for Wenfeng Pagoda

模态阶数	非倾斜模型			倾斜模型
模态阶数	实测频率 ${f_0}$ /Hz	频率 ${f_1}$ /Hz	误差e_1-0/%	频率 ${f_2}$ /Hz	差值e_1-0/%
一阶X向	0.732	0.718	-1.91	0.662	-7.80
一阶Z向	0.732	0.719	-1.78	0.700	-2.64
二阶X向	3.125	3.393	8.58	3.391	-0.06
二阶Z向	3.125	3.410	9.12	3.407	-0.09
注： ${e_{i - j}} = {{({f_i} - {f_j})} \mathord{\left/ {\vphantom {{({f_i} - {f_j})} {{f_j}}}} \right. } {{f_j}}}$ 。

下载: 导出CSV

参考文献(19)

[1]	李犇. 倾斜砖石古塔的有限元模拟及危险性分析[D]. 南京: 东南大学, 2022. LI Ben. Finite Element Simulation and Risk Analysis of Inclined Masonry Ancient Tower[D]. Nanjing: Southeast University, 2022. (in Chinese)
[2]	崔晓玲, 李凯, 卢俊龙, 等. 倾斜砖石古塔随机振动测试分析[J]. 建筑结构, 2017, 47(2): 70-74. https://www.cnki.com.cn/Article/CJFDTOTAL-JCJG201702013.htm CUI Xiaoling, LI Kai, LU Junlong, et al. Analysis of random vibration test of an inclined ancient masonry pagoda[J]. Building Structure, 2017, 47(2): 70-74. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JCJG201702013.htm
[3]	严绍军, 方云, 唐朝晖. 云南大理崇圣寺南北塔倾斜成因研究[J]. 岩土力学, 2012, 33(11): 3367-3373. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201211031.htm YAN Shaojun, FANG Yun, TANG Zhaohui. Research on inclination reason of north and south pagodas of Chongsheng Temple, Dali, Yunnan Province[J]. Rock and Soil Mechanics, 2012, 33(11): 3367-3373. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201211031.htm
[4]	李宏男, 徐静. 考虑桩–土–结构动力相互作用的输电塔线体系简化抗震计算模型[J]. 岩土工程学报, 2009, 31(11): 1763-1767. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200911024.htm LI Hongnan, XU Jing. Simplified aseismic calculation model for transmission tower-line system considering pile-soil dynamic interaction[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(11): 1763-1767. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200911024.htm
[5]	CASOLO S, DIANA V, UVA G. Influence of soil deformability on the seismic response of a masonry tower[J]. Bulletin of Earthquake Engineering, 2017, 15(5): 1991-2014. doi: 10.1007/s10518-016-0061-y
[6]	刘羽. 汶川地震中龙护舍利塔的损伤特征研究[D]. 扬州: 扬州大学, 2012. LIU Yu. Research on Seismic Damage Feature of Longhu Pagoda in Wenchuan Earthquake[D]. Yangzhou: Yangzhou University, 2012. (in Chinese)
[7]	BAO X, LIU J B, LI S T, et al. A new viscoelastic artificial boundary with improved numerical stability in explicit calculation of wave propagation problems in infinite domains[J]. Computers and Geotechnics, 2022, 145: 104698. doi: 10.1016/j.compgeo.2022.104698
[8]	马笙杰, 迟明杰, 陈红娟, 等. 黏弹性人工边界在ABAQUS中的实现及地震动输入方法的比较研究[J]. 岩石力学与工程学报, 2020, 39(7): 1445-1457. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202007013.htm MA Shengjie, CHI Mingjie, CHEN Hongjuan, et al. Implementation of viscous-spring boundary in ABAQUS and comparative study on seismic motion input methods[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(7): 1445-1457. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202007013.htm
[9]	沈继美. 砌体匀质化过程的数值模拟方法与应用研究[D]. 长沙: 长沙理工大学, 2012. SHEN Jimei. Study on Homogenization Process of Masonry and its Applications using Numerical Simulation[D]. Changsha: Changsha University of Science & Technology, 2012. (in Chinese)
[10]	杨卫忠. 砌体受压本构关系模型[J]. 建筑结构, 2008, 38(10): 80-82. https://www.cnki.com.cn/Article/CJFDTOTAL-JCJG200810026.htm YANG Weizhong. Constitutive relationship model for masonry materials in compression[J]. Building Structure, 2008, 38(10): 80-82. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JCJG200810026.htm
[11]	郑妮娜, 李英民, 潘毅. 芯柱式构造柱约束的低层砌体结构抗震性能[J]. 西南交通大学学报, 2011, 46(1): 24-29, 55. https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT201101006.htm ZHENG Nina, LI Yingmin, PAN Yi. Seismic behavior of low masonry structure with core-tie-columns[J]. Journal of Southwest Jiaotong University, 2011, 46(1): 24-29, 55. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT201101006.htm
[12]	李世温, 李庆玲. 太原永祚寺东塔维修后的抗震能力初探[C]//建筑物鉴定与加固改造第五届全国学术讨论会. 南京, 2000. LI Shiwen, LI Qinglin. A preliminary investigation of the seismic resistance of the repaired Yongzuo Temple East Pagoda in Taiyuan[C]// Proceedings of the Fifth National Symposium on Building Identification and Strengthening and Renovation. Nanjing, 2000. (in Chinese)
[13]	施楚贤. 砌体结构理论与设计[M]. 2版. 北京: 中国建筑工业出版社, 2003: 78-80. SHI Chuxian. Theory and Design of Masonry Structure[M]. 2nd ed. Beijing: China Architecture & Building Press, 2003: 78-80. (in Chinese)
[14]	杜修力, 许紫刚, 许成顺, 等. 基于等效线性化的土–地下结构整体动力时程分析方法研究[J]. 岩土工程学报, 2018, 40(12): 2155-2163. doi: 10.11779/CJGE201812001 DU Xiuli, XU Zigang, XU Chengshun, et al. Time-history analysis method for soil-underground structure system based on equivalent linear method[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(12): 2155-2163. (in Chinese) doi: 10.11779/CJGE201812001
[15]	BARDET J, ICHII K, LIN C. EERA-A Computer Program for Equivalent-linear Earthquake Site Response Analyses of Layered Soil Deposits[R]. Los Angeles: University of Southern California, 2000.
[16]	魏剑伟, 李铁英. 古砖塔动力特性测试与分析研究[J]. 山西建筑, 2002, 28(1): 18-19. https://www.cnki.com.cn/Article/CJFDTOTAL-JZSX200201010.htm WEI Jianwei, LI Tieying. Research on the test and analysis of ancient brick tower dynamic characteristics[J]. Shanxi Agchitecture, 2002, 28(1): 18-19. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZSX200201010.htm
[17]	FLORA A, CHIARADONNA A, DE SANCTIS L, et al. Understanding the Damages Caused by the 1999 Kocaeli Earthquake on One of the Towers of the Theodosian Walls of Constantinople[J]. International Journal of Architectural Heritage, 2022, 16(7): 1076-1100. doi: 10.1080/15583058.2020.1864512
[18]	BI Z H, CUI B H, ZHAI Y F. Research on seismic input method of layered ground foundation[J]. IEEE Access, 2021, 9: 54820-54830. doi: 10.1109/ACCESS.2021.3070479
[19]	JIANLI Y, SHENGCAI L. Study of the seismic damage regularity of ancient masonry pagodas in the 2008 Wenchuan Earthquake[C]// WIT Transactions on The Built Environment", "Earthquake Resistant Engineering Structures IX. A Coruña, 2013.