考虑土-结构动力相互作用的小型核反应堆楼层反应谱

刘浩; 李波; 周孟

doi:10.11779/CJGE2023S20018

考虑土-结构动力相互作用的小型核反应堆楼层反应谱 English Version

刘浩^{1, 2,},
李波^{1, 2, ,},
周孟¹

1.
哈尔滨工业大学(深圳), 广东深圳 518055
2.
广东省土木工程智能韧性结构重点实验室, 广东深圳 518055

基金项目:

广东省自然科学基金面上项目 2023A1515012887

国家自然科学基金面上项目 52178471

详细信息

作者简介:
刘浩(2000—)，男，硕士研究生，主要从事地震工程方面的研究工作。E-mail: 273792506@qq.com

通讯作者:
李波（E-mail: boli@hit.edu.cn）

中图分类号: TU411
计量
- 文章访问数: 94
- HTML全文浏览量: 15
- PDF下载量: 20
出版历程
- 收稿日期: 2023-11-29
- 网络出版日期: 2024-04-19
- 刊出日期: 2023-11-30

Floor response spectra of small nuclear reactor considering seismic soil-structure interaction

LIU Hao^{1, 2,},
LI Bo^{1, 2, ,},
ZHOU Meng¹

1.
Harbin Institute of Technology Shenzhen, Shenzhen 518055, China
2.
Guangdong Provincial Key Laboratory of Intelligent and Resilient Structures for Civil Engineering, Shenzhen 518055, China

摘要

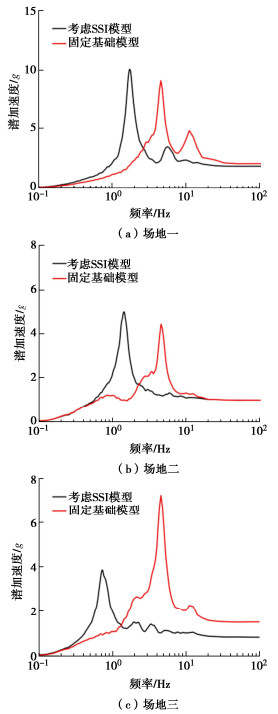
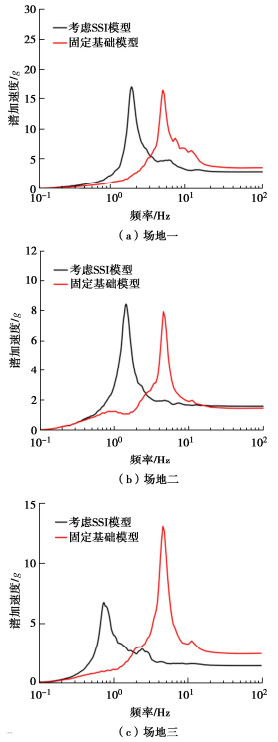
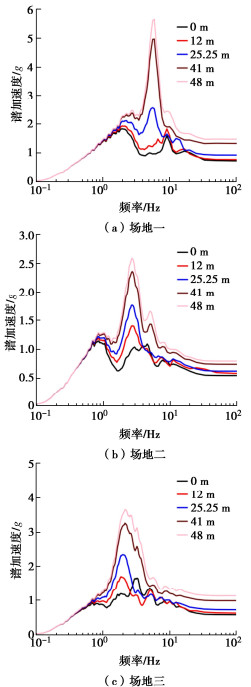
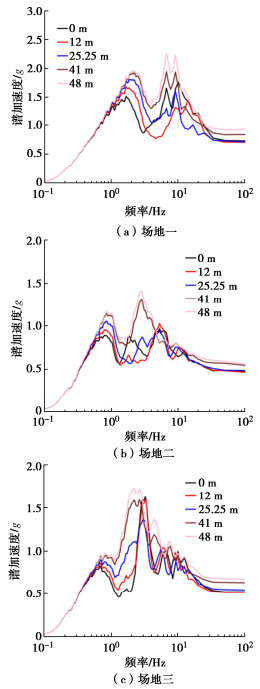
摘要: 小型核反应堆因其广泛的应用前景而成为研发热点。然而，小型核反应堆通常部分或完全埋入地下，这使得土-结构相互作用对其地震响应产生深远的影响。考虑土-结构动力相互作用可更为真实反映非基岩场地核电厂房在地震作用下的响应特性，进而有助于评估核电设备在地震作用下的安全性，对确保核电站系统的可靠性和安全性至关重要。采用数值模拟方法，选取了3个典型场地和1个代表性的小型核反应堆结构作为研究对象，探讨在不同结构埋深和不同楼层高度等条件下小型核反应堆的楼层反应谱特性。研究结果表明，考虑土-结构动力相互作用后，小型核反应堆楼层反应谱的峰值频率会向低频偏移。研究还发现场地土层的刚度对结构楼层反应谱的影响显著。考虑土-结构相互作用后，楼层反应谱随结构楼面高度减小，幅值在低频段有减小的趋势，在中高频段有先减小后增大的趋势。
- 小型核反应堆 /
- 地震波动输入方法 /
- 土-结构动力相互作用 /
- 楼层反应谱
Abstract: Small nuclear reactors have become a research hotspot due to their wide range of applications. However, tehy are usually partially or completely buried, which makes soil-structure interaction have a profound impact on their seismic responses. Considering the soil-structure dynamic interaction can more realistically reflect the response characteristics of nuclear power plant buildings on soil sites under earthquakes, which can help evaluate the safety of nuclear power equipments under earthquakes, and is crucial to ensure the reliability and safety of the nuclear power plant system. By using the numerical simulation methods, three typical sites and a representative small nuclear reactor structure are selected as the research objects, and the floor response spectral characteristics of small nuclear reactors are explored under different structural burial depths and different floor heights. The research results show that after considering the soil-structure dynamic interaction, the peak frequency of the floor response spectra of small nuclear reactors will shift to low frequency. The stiffness of the site soil layer has a significant impact on the floor response spectra. After considering the soil-structure interaction, the amplitudes of floor response spectra decrease with the decrease of the structural floor height, and the amplitude decreases in the low-frequency range and increases first and then decreases in the medium-high-frequency range.
- small nuclear reactor /
- seismic wave input method /
- dynamic soil-structure interaction /
- floor response spectrum

HTML全文

0. 引言

近年来，随着“交通强国”战略和“一带一路”倡议的实施，大量的超高层建筑、大跨度桥梁、超长海底隧道等工程项目相继出现，桩基础因其承载力高、稳定性好、变形小等优点^[1-2]，在季节性冻土、湿陷性黄土、软土等复杂恶劣地质环境中和山区交通^[3-4]、海上风电^[5-6]、跨海大桥等重要项目设施中得到了广泛应用，因此，对桩基承载力进行科学评估，并合理选择其设计参数，是目前亟待解决的问题。

传统的桩基载荷试验有两种方法，一种是高应变法^[7-8]，另一种是静压法^[9-14]。高应变动测分析具有快速方便的特点，但测试时桩身弹性的假定与实际不符，因此得到的Q-S曲线有一定误差^[15]。静压法可采用堆载法、锚桩横梁法和拉压锚法，堆载法要解决成百上千吨堆载材料的来源、存储和运输及吊装，费时费力；而锚桩横梁法和拉压锚法由于需要设置多个锚桩、反力梁等，设备成本较高，并且容易受到场地、吨位等因素的制约，在试验过程中，基桩的潜能无法完全被挖掘出来，很难获得可靠的试验数据，从而无法科学、合理地评估基桩的承载力。

桩基自平衡载荷试验是基于改进传统载荷试验的反力系统发展而来的，称之为O-Cell法^[16-18]，国内称为自平衡法^[19-21]；作为一种新的桩基承载力检测手段，因该技术受场地条件限制较少，故而特别适用于一些特殊工程，如深基坑工程的桩基承载力检测试验。但该测试技术的主要缺陷在于，主要设备荷载箱是一种特别设计可用于加载的设备，造价高昂；使用时焊接在钢筋笼上，试验完毕后无法回收^[22]。

本文研发了一种可回收自平衡法桩基承载力检测装置，具有适用范围广、造价低廉、测试周期短等优点，并根据荷载传递特性模型分析了该新型测试装置的工作机理，并通过现场实测结果和三维有限元计算进行了验证，结合桩身荷载沉降、轴力等数据，揭示了可回收自平衡法桩基承载力检测装置的工作机理。

1. 新型检测结构的提出及工作机理

1.1 新型可回收检测结构的提出及构造

针对现有测试技术周期长、受地形影响大等原因，基于自平衡法的测试原理和开瓶器受力方式，从节能减排、绿色低碳等角度出发，提出一种可回收自平衡法桩基承载力检测装置^[22]，装置主要包括试验桩、液压千斤顶、反力梁、反力锚筋、反力钢板、位移监测系统，结构原理及装置如图 1所示。

图 1 新型检测结构

Figure 1. New detection structure

下载: 全尺寸图片幻灯片

该装置采用分离桩体和加载系统的方式，实现了一种可回收自平衡法桩基承载力检测，主要做法是在桩身中性点下放置反力钢板，上段桩预设孔洞并安设受压钢柱，钢柱顶安装液压千斤顶和反力梁，并通过反力锚筋与桩身连接形成整体测试装置，试验时，液压加载系统控制千斤顶沿垂直方向同时施加荷载，得到上段挖孔桩向上、下段实心桩向下的位移，绘制Q-S曲线，进而得到桩基承载力、桩基沉降等参数。

1.2 工作机理及主要优点

该装置工作的主要技术原理为：①作用力与反作用力原理：在实心桩和挖孔桩交界处设置钢板，将桩身分为上下两部分，液压千斤顶加载时锚筋受向上拉力，同时通过预留孔洞内插入的受压杆对钢板产生向下压力。②检测原理：在作用力与反作用力原理下，液压千斤顶通过受压杆和钢板下压使实心桩产生向下位移，由于锚筋和钢梁组成的反力系统使得挖孔桩产生向上位移，绘制对应的“Q-S曲线”，判断桩基承载力。③回收原理：测量结束以后，拆除钢梁、液压千斤顶、扩大盘，按照设计高度切割锚筋，运用起重设备将受压杆从挖孔桩的预留孔洞中分段吊出回收，拆除各构件以便再次组装利用，上端桩体的预留孔洞内填筑混凝土并振捣填实后可作为承载桩使用。

其主要的优点是：①该装置使用空间小，特别适用于坡地、水上、基坑底、狭窄场地；②该装置利用桩的侧阻力与端阻力互为反力，可清楚区分侧阻力与端阻力分布以及各自的荷载-位移曲线；③该装置使用液压千斤顶提供荷载，费用低，可多根桩同时测试，测试周期短，有利于增加试桩数量，扩大检测范围；④试验结束后，组合钢柱吊出回收再利用，大量节约资源；⑤在试验桩预留孔洞注浆后，试验桩仍可作为工程承载桩使用，经济效益显著。

2. 工作机理分析

2.1 荷载传递函数微分方程

基本假设如下：

（1）桩为弹性体，忽略受压钢柱、反力钢板的变形及反力锚筋与上段桩之间的相对位移。

（2）可由单元上下两面的轴向力和平均截面刚度来计算各单元应变。

（3）桩端承载力-沉降量关系及不同深度的桩侧摩阻力-变形量关系与标准试验方法相同。

新型可回收检测结构的工作机理及微单元受力分析如图 2所示。

图 2 荷载传递模型

Figure 2. Load transfer model

下载: 全尺寸图片幻灯片

由微单元受力可得

$\frac{{{\text{d}}{s^2}(z)}}{{{\text{d}}{z^2}}} = \frac{U}{{EA}}q(z) \text{, }\;$

(1)

式中： $U$ 为桩周长； $E$ 和 $A$ 分别为桩的弹性模量和横截面积。根据剪切位移法，假设桩周土的位移为

$s(z) = \frac{{q(z){r_0}}}{{{G_{\text{s}}}}}\ln ({r_{\text{m}}}/{r_0}) \text{, }\;$

(2)

式中：q(z)为桩侧摩阻力； ${r_0}$ 为桩半径； ${r_{\text{m}}}$ 为有效影响半径， ${r_{\text{m}}}$ =2.5L(1- ${\nu _{\text{s}}}$ )，L为桩长； ${G_{\text{s}}}$ 为桩侧土剪切模量； ${\nu _{\text{s}}}$ 为土体泊松比。

将式（2）代入式（1）可得

$\frac{{{{\text{d}}^2}s(z)}}{{{\text{d}}{z^2}}} - \frac{U}{{EA}} \cdot \frac{{s(z) \cdot {G_{\text{s}}}}}{{{r_0} \cdot \ln ({r_{\text{m}}}/{r_0})}} = 0 。$

(3)

令 $k = (2{\rm{ \mathsf{ π} }} \cdot {G_{\text{s}}})/\ln ({r_{\text{m}}}/{r_0})$ ，定义为桩土剪切刚度系数， $\alpha = \sqrt {k/EA}$ ，可得

$\frac{{{{\text{d}}^2}s(z)}}{{{\text{d}}{z^2}}} - {\alpha ^2} \cdot s(z) = 0 。$

(4)

2.2 上段桩荷载传递规律

自平衡法检测中，上段桩自重对端承载力有一定影响，因此，考虑上段桩自重影响时，其桩侧荷载传递基本微分方程为

$\frac{{{\text{d}}{s_1}^2(z)}}{{{\text{d}}{z^2}}} - {\alpha ^2}{s_1}(z) = \frac{\gamma }{E} \text{, }\;$

(5)

式中， $\gamma$ 为桩体重度。

上段桩顶的边界条件为

${Q_1}(z) = - {\left. {EA\frac{{{\text{d}}{s_1}(z)}}{{{\text{d}}z}}} \right|_{z = 0}} = 0 \text{, }\;$

(6)

上段桩底的边界条件为

${Q_1}(z) = - {\left. {EA\frac{{{\text{d}}{s_1}(z)}}{{{\text{d}}z}}} \right|_{z = {L_1}}} = {Q_{\text{u}}}, {s_1}(z) = {\left. {{s_1}(z)} \right|_{z = {L_1}}} = {s_{\text{u}}} 。$

(7)

式中： ${Q_{\text{u}}}$ 和 ${s_{\text{u}}}$ 分别为液压千斤顶施加的向上的荷载与产生的位移。

根据式（5）可得，上段桩的桩身位移和轴力为

$\left\{ \begin{array}{l} {s_1}(z) = {C_1}{{\text{e}}^{\alpha z}} + {C_2}{{\text{e}}^{ - \alpha z}} - \frac{\gamma }{{{\alpha ^2}E}} \hfill \\ {Q_1}(z) = - {C_1}EA\alpha {{\text{e}}^{\alpha z}} + {C_2}EA\alpha {{\text{e}}^{ - \alpha z}} \hfill \end{array} \right. \text{, }\;$

(8)

式中：C₁和C₂为常数，可由式（6），（7）确定。

将式（8）用矩阵形式表达为

$\left\{ {\begin{array}{*{20}{l}} {{s_1}(z)} \\ {{Q_1}(z)} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {{{\text{e}}^{\alpha z}}}&{{{\text{e}}^{ - \alpha z}}} \\ { - EA\alpha {{\text{e}}^{\alpha z}}}&{EA\alpha {{\text{e}}^{ - \alpha z}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{l}} {{C_1}} \\ {{C_2}} \end{array}} \right\} - \left\{ {\begin{array}{*{20}{c}} {\frac{\gamma }{{{\alpha ^2}E}}} \\ 0 \end{array}} \right\} 。$

(9)

试验桩侧地基土层按照单元厚度为h_i进行划分，可得桩单元顶部的内力和位移表达为

$\left\{ {\begin{array}{*{20}{c}} {{s_1}({z_i})} \\ {{Q_1}({z_i})} \end{array}} \right\} = {T^1}(z)\left\{ {\begin{array}{*{20}{l}} {{C_1}} \\ {{C_2}} \end{array}} \right\} - \left\{ {\begin{array}{*{20}{c}} {\frac{\gamma }{{{\alpha ^2}E}}} \\ 0 \end{array}} \right\} \text{, }\;$

(10)

其中，

${T^1} = \left[ {\begin{array}{*{20}{c}} {\cosh (\alpha {h_i})}&{ - {{(EA\alpha )}^{ - 1}}\sinh (\alpha {h_i})} \\ { - EA\alpha \sinh (\alpha {h_i})}&{\cosh (\alpha {h_i})} \end{array}} \right] 。$

(11)

根据位移连续性条件可得：

$\left\{ {\begin{array}{*{20}{l}} {{s_1}(z = {L_1})} \\ {{Q_1}(z = {L_1})} \end{array}} \right\} = \left[ {{T^1}} \right]\left\{ {\begin{array}{*{20}{l}} {{s_1}(z = 0)} \\ {{Q_1}(z = 0)} \end{array}} \right\} - \left\{ {\begin{array}{*{20}{c}} {\frac{\gamma }{{{\alpha ^2}E}}} \\ 0 \end{array}} \right\} \text{, }\;$

(12)

式中， ${L_1}$ 为上段桩长。

荷载试验过程中，上段桩侧土体出现塑性区，第i段桩单元侧摩阻力达到土体剪切强度 ${q_{{f_{\text{u}}}}}$ 后，假定该单元进入塑性状态后摩阻力保持稳定状态，后期增加的荷载将转移到上部弹性区域的桩单元承担，第i段桩单元微分方程为

$\frac{{{\text{d}}{s_1}^2(z)}}{{{\text{d}}{z^2}}} - \frac{U}{{EA}}{q_{{f_{\text{u}}}}} = \frac{\gamma }{E} 。$

(13)

求解并表达为增量形式为

$\left\{ {\begin{array}{*{20}{l}} {\Delta {s_{1i}}} \\ {{Q_{1i}}} \end{array}} \right\} = \left[ {{T_f}} \right]\left\{ {\begin{array}{*{20}{l}} {\Delta {s_{1i}}} \\ {\Delta {Q_{1i}}} \end{array}} \right\} - \left\{ {\begin{array}{*{20}{c}} {\frac{\gamma }{{{\alpha ^2}E}}} \\ 0 \end{array}} \right\} \text{, }\;$

(14)

其中，

${\left[ {{T_f}} \right]_i} = \left[ {\begin{array}{*{20}{c}} 1&{ - \frac{{{h_i}}}{{EA}}} \\ 0&1 \end{array}} \right] 。$

(15)

2.3 下段桩荷载传递规律

对于下段桩受压加载时，不需要克服桩自重，桩侧受正摩阻力作用，受力特征与传统受压桩相同，同理可得

$\frac{{{\text{d}}{s_2}^2(z)}}{{{\text{d}}{z^2}}} - {\alpha ^2}{s_2}(z) = 0 \text{, }\;$

(16)

式中，s₂(z)与Q₂(z)分别表示下段桩z位置处的位移与轴力。同理可得

${\left\{ {\begin{array}{*{20}{l}} {{s_2}({z_i})} \\ {{Q_2}({z_i})} \end{array}} \right\}_b} = \left[ {{T^2}({z_i})} \right]\left\{ {\begin{array}{*{20}{l}} {{s_2}({z_i})} \\ {{Q_2}({z_i})} \end{array}} \right\} \text{, }\;$

(17)

其中，

${T^2}({z_i}) = \left[ {\begin{array}{*{20}{c}} {\cosh (\alpha {h_i})}&{ - {{{\text{(}}EA\alpha {\text{)}}}^{ - 1}}\sinh (\alpha {h_i})} \\ { - EA\alpha \sinh (\alpha {h_i})}&{\cosh (\alpha {h_i})} \end{array}} \right] 。$

(18)

2.4 Q-S曲线等效转换方法

以反力钢板位置为起点，将上段桩分割为n个单元，桩身任意处的内力与变形量如下：

$Q(i)=Q(0)+\sum\limits_{m=1}^{i}q(m)\{U(m)+U(m+1)\}q(m)/2 \text{, }\;$

(19)

$s(i)=s(0)+\sum\limits_{m=1}^{i}\frac{Q(m)+Q(m+1)}{E(m)A(m)+E(m+1)A(m+1)}h(m) 。$

(20)

式中：Q(0)为i=0处桩的轴力（kN），即上部液压千斤顶的加载值；s(0)为i=0处桩的位移（m），即上段桩的位移；q(m)为m处的桩侧摩阻力（kPa）。

上段桩等效转换桩顶i=n时的荷载和位移如下：

$Q(n)=Q(0)+\sum\limits_{m=1}^{n}q(m)\{U(m)+U(m+1)\}q(m)/2 \text{, }\;$

(21)

$\begin{array}{l}s(n)=s(0)+\frac{h(n)}{E(n)A(n)+E(n-1)A(n-1)}\cdot \\ \{2Q(0)+\sum\limits_{m=1}^{n-1}q(m)[U(m)+U(m+1)]h(m)+\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {\begin{array}{*{20}{c}} {} \\ {} \end{array}q(n)[U(n) + U(n - 1)]h(n)/2} \right\} 。 \end{array}$

(22)

根据上文建立的荷载传递模型，采用MATLAB编程可得到多层地基中上、下段桩的轴力、位移值，根据式（21），（22）将测试结果进行转换，在利用等荷载法将试桩的Q-S曲线转换为传统静压桩的Q-S曲线，可得到试桩的极限承载力：

${Q}_{\text{u}}={Q}_{\text{u}}{}_{上}+{Q}_{\text{u}}{}_{下} 。$

(23)

3. 工程对比与数值模拟分析

3.1 工程概况与数值模拟建模

以润扬长江大桥桩基承载力检测工程^[23]为参考，基于ABAQUS建立了大型三维有限元分析模型（如图 3），由于篇幅限制，详细参数与测试方法见文献[23]。

图 3 数值分析模型

Figure 3. Numerical model

下载: 全尺寸图片幻灯片

3.2 试桩Q-S曲线对比分析

荷载箱加载现场实测结果、数值模拟分析结果与新型检测结构加载时的对比曲线如图 4所示，可以看出，三者上段桩与下段桩的Q-S曲线发展趋势基本一致，加载分为15个等级，每级8000 kN，加载结束后，上段桩位移18.26 mm，下端桩位移7.91 mm，因此取上、下段桩极限承载力分别为62771 kN和56436 kN。就数值大小而言，本文理论计算结果比现场实测结果大0.16%~12.49%，可认为该新型可回收桩基检测结构在合理评价桩基承载力方面具有优势；数值分析结果略小于现场实测结果，可能与现场土层非均匀性、桩-土相对位移、边界条件等的简化分析有关。

图 4 试桩Q-S曲线

Figure 4. Q-S curves of test piles

下载: 全尺寸图片幻灯片

3.3 桩身轴力分析

各级加载下，桩身轴力对比如图 5所示，可以看出理论计算结果、数值模拟结果与实测结果均比较吻合；下段桩轴力出现衰减，表明荷载较小时，施加荷载主要由桩身下部土层承担，荷载逐级增大时，上部土层逐渐发挥作用；从曲线疏密程度来看，曲线越稀疏轴力衰减越大，从钢板位置向上25 m范围内曲线较疏，可认为该部分土层承担的荷载较大。

图 5 各级加载下试桩轴力分布

Figure 5. Distribution of axial force of test piles under different loads

下载: 全尺寸图片幻灯片

3.4 等效转换结果分析

从图 6可以看出，现场实测结果、理论计算结果和数值模拟结果基本吻合，现场实测桩基承载力比数值模拟结果大3.5%，本文理论计算结果为119207 kN，可见新型可回收结构检测结果优于荷载箱结构，精度提高3.5%。

图 6 试桩等效荷载曲线

Figure 6. Equivalent load curves of test piles

下载: 全尺寸图片幻灯片

4. 结论

本文研发了一种可回收自平衡桩基承载力检测装置，建立了荷载传递模型，分析了新型结构的工作机理，并与现场实测结果、数值模拟结果进行了对比分析，主要结论如下：

（1）通过分离桩体和加载系统的方式，提出一种可回收自平衡法桩基承载力检测装置，主要做法是在桩身中性点下放置反力钢板，替代荷载箱进行加载，特别适用于坡地、水上、基坑底、狭窄场地，结构巧妙，装配化程度高，具备可回收、低耗能等优点，为桩基承载力检测提供了新的思路。

（2）建立了新型结构作用下的桩体荷载传递模型，本文理论结果分析表明，解析模型能够合理反映新型结构作用下的上、下段桩的荷载沉降特性以及桩身轴力等分布规律，与现场实测结果、数值模拟结果吻合程度较好，承载力检测精度提高3.5%，可认为该新型结构具有一定的适用性和推广价值。

（3）本文仅针对新型检测装置作用的等截面试桩进行了荷载传递机理分析，但对湿陷性黄土、冻土等特殊地层桩和变截面桩未进行研究，以待下一步进行现场试验，综合分析该新型结构的工作原理。

图 1 二维土-结构相互作用模型

Figure 1. Two-dimensional soil-structure interaction model

下载: 全尺寸图片幻灯片

图 2 自由场及对应内部子结构模型

Figure 2. Free field and corresponding internal substructure model

下载: 全尺寸图片幻灯片

图 3 小型核反应堆厂房剖面图

Figure 3. Cross-sectional view of a small nuclear reactor building

下载: 全尺寸图片幻灯片

图 4 土-结构相互作用模型

Figure 4. Soil-structure interaction model

下载: 全尺寸图片幻灯片

图 5 X, Y水平方向输入地震动加速度反应谱

Figure 5. Response spectra of horizontally input motions in X and Y direction

下载: 全尺寸图片幻灯片

图 6 3个场地

Figure 6. Three sites

下载: 全尺寸图片幻灯片

图 7 土体动剪切模量比和阻尼比曲线

Figure 7. Dynamic shear modulus and damping ratios of soil

下载: 全尺寸图片幻灯片

图 8 X方向固定基础结构楼层反应谱

Figure 8. Fixed-base FRS in X direction

下载: 全尺寸图片幻灯片

图 9 Y方向固定基础结构楼层反应谱

Figure 9. Fixed-base FRS in Y direction

下载: 全尺寸图片幻灯片

图 10 土-结构相互作用与固定基础结构于楼面高度25.25 m处X方向楼层反应谱

Figure 10. X-direction FRS of soil-structure interaction model and fixed-base model at floor height of 25.25 m

下载: 全尺寸图片幻灯片

图 11 土-结构相互作用与固定基础结构于楼面高度48 m处X方向楼层反应谱

Figure 11. X-direction FRS of soil-structure interaction model and fixed-base model at floor height of 48 m

下载: 全尺寸图片幻灯片

图 12 在结构25 m埋深下楼层反应均值谱

Figure 12. Average FRS under embedment depth of 25 m

下载: 全尺寸图片幻灯片

图 13 结构在48 m埋深下楼层反应均值谱

Figure 13. Average FRS under embedment depth of 48 m

下载: 全尺寸图片幻灯片

表 1 场地二的土层参数

Table 1 Layer parameters for Site 2

土层编号	土层厚度/m	密度/(kg·m^-3)	初始剪切波速/(m·s^-1)
S1	9	2050	481.6
S2	14	2053.4	378.0
S3	15	2050	365.8
S4	20	1973.2	476.7
S5	4	2117.6	656.2
S6	14	2117.6	524.3
S7	9	2021.3	431.3
S8	7	2117.6	510.5
S9	21	2101.6	614.2

下载: 导出CSV

参考文献(13)

[1]	LOCATELLI G, BINGHAM C, MANCINI M. Small modular reactors: a comprehensive overview of their economics and strategic aspects[J]. Progress in Nuclear Energy, 2014, 73: 75-85. doi: 10.1016/j.pnucene.2014.01.010
[2]	JIANG W, LI B, XIE W C, et al. Generate floor response spectra: part 1. Direct spectra-to-spectra method[J]. Nuclear Engineering and Design, 2015, 293: 525-546. doi: 10.1016/j.nucengdes.2015.05.034
[3]	DE BORBÓN F, DOMIZIO M, AMBROSINI D, et al. Influence of various parameters in the seismic soil-structure interaction response of a nuclear power plant[J]. Engineering Structures, 2020, 217: 110820. doi: 10.1016/j.engstruct.2020.110820
[4]	EL HOSENY M, MA J X, DAWOUD W, et al. The role of soil structure interaction (SSI) on seismic response of tall buildings with variable embedded depths by experimental and numerical approaches[J]. Soil Dynamics and Earthquake Engineering, 2023, 164: 107583. doi: 10.1016/j.soildyn.2022.107583
[5]	TAKEWAKI I, TAKEDA N, UETANI K. Fast practical evaluation of soil–structure interaction of embedded structures[J]. Soil Dynamics and Earthquake Engineering, 2003, 23(3): 13-20. doi: 10.1016/S0267-7261(02)00225-7
[6]	PARK S, SAMADDAR S. Seismic soil-structure interactionanalysis of deeply embedded smrs and associated challenges[C]// The 24th International Conference in Structural Mechanics in Reactor Technology. Busan, 2017.
[7]	谭辉. 土-结构动力相互作用分析中地震波输入方法研究及应用[D]. 北京: 清华大学, 2018: 106-112. TAN Hui. Research and Application of the Seismic Wave Input Method for Soil-Structure Dynamic Interaction Analysis[D]. Beijing: Tsinghua University, 2018: 106-112. (in Chinese)
[8]	刘晶波, 谷音, 杜义欣. 一致黏弹性人工边界及黏弹性边界单元[J]. 岩土工程学报, 2006, 28(9): 1070-1075. https://www.cnki.com.cn/Article/CJFDTOTAL-CQJT202209012.htm LIU Jingbo, GU Yin, DU Yixin. Consistent viscous-spring artificial boundaries and viscous-spring boundary elements[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1070-1075. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CQJT202209012.htm
[9]	谷音, 刘晶波, 杜义欣. 三维一致黏弹性人工边界及等效黏弹性边界单元[J]. 工程力学, 2007, 24(12): 31-37. https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB200905031.htm GU Yin, LIU Jingbo, DU Yixin. 3d consistent viscous-spring artificial boundary and viscous-spring boundary element[J]. Engineering Mechanics, 2007, 24(12): 31-37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB200905031.htm
[10]	SOLBERG J, HOSSAIN Q, BLINK J, et al. Development of a Generalized Methodology for Soil-Structure Interaction Analysis Using Nonlinear Time-Domain TechniquesNEAMS Program, DOE Office of Nuclear Energy (NE-41)[R]. Livermore: Lawrence Livermore National Lab. (LLNL), 2013.
[11]	李述涛, 刘晶波, 宝鑫, 等. 人工边界子结构地震动输入方法在ABAQUS中的实现[J]. 自然灾害学报, 2020, 29(4): 133-141. https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH202004014.htm LI Shutao, LIU Jingbo, BAO Xin, et al. Implementation for seismic wave input method based on the artificial boundary substructure in ABAQUS[J]. Journal of Natural Disasters, 2020, 29(4): 133-141. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH202004014.htm
[12]	刘晶波, 宝鑫, 谭辉, 等. 土-结构动力相互作用分析中基于内部子结构的地震波动输入方法[J]. 土木工程学报, 2020, 53(8): 87-96. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC202008009.htm LIU Jingbo, BAO Xin, TAN Hui, et al. Seismic wave input method for soil-structure dynamic interaction analysis based on internal substructure[J]. China Civil Engineering Journal, 2020, 53(8): 87-96. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC202008009.htm
[13]	SOLBERG J M, HOSSAIN Q, MSEIS G. Nonlinear time-domain soil–structure interaction analysis of embedded reactor structures subjected to earthquake loads[J]. Nuclear Engineering and Design, 2016, 304: 100-124. doi: 10.1016/j.nucengdes.2016.04.026