复杂循环应力路径下冻结粉质黏土的变形特性与安定性行为研究

王亚鹏; 李国玉; 陈敦; 马巍; 张轩

doi:10.11779/CJGE2023S20017

复杂循环应力路径下冻结粉质黏土的变形特性与安定性行为研究 English Version

王亚鹏^{1, 2, 3,},
李国玉^{1, 2, 3},
陈敦^{1, 3, ,},
马巍^{1, 2},
张轩⁴

1.
中国科学院西北生态环境资源研究院冻土工程国家重点实验室, 甘肃兰州 730000
2.
中国科学院大学, 北京 100049
3.
中国科学院西北生态环境资源研究院大兴安岭冻土工程与环境观测研究站, 黑龙江加格达奇 165000
4.
西北民族大学土木工程学院, 甘肃兰州 730030

基金项目:

国家自然科学基金青年基金项目 42201162

甘肃省青年科技基金计划项目 22JR5RA089

科技基础资源调查专项项目 2022FY100703

国家自然科学基金面上项目 42272339

国家电网公司总部科技项目 5200-202230098A-1-1-ZN

详细信息

作者简介:
王亚鹏(1997—)，男，博士，主要从事冻土力学与寒区工程方面的研究工作。E-mail: wangyapeng@nieer.ac.cn

通讯作者:
陈敦, E-mail: chendun@1zb.ac.cn

中图分类号: TU43
计量
- 文章访问数: 128
- HTML全文浏览量: 17
- PDF下载量: 25
出版历程
- 收稿日期: 2023-11-29
- 网络出版日期: 2024-04-19
- 刊出日期: 2023-11-30

Deformation characteristics and shakedown behaviors of frozen silty clay under complex cyclic stress paths

WANG Yapeng^{1, 2, 3,},
LI Guoyu^{1, 2, 3},
CHEN Dun^{1, 3, ,},
MA Wei^{1, 2},
ZHANG Xuan⁴

1.
Northwest Institute of Eco-environment and Resources, CAS, Lanzhou 730000, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China
3.
Da Xing'anling Observation and Research Station of Frozen Ground Engineering and Environment, Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences, Jagdaqi 165000, China
4.
School of Civil Engineering, Northwest MinZu University, Lanzhou 730030, China

摘要

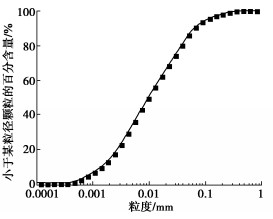
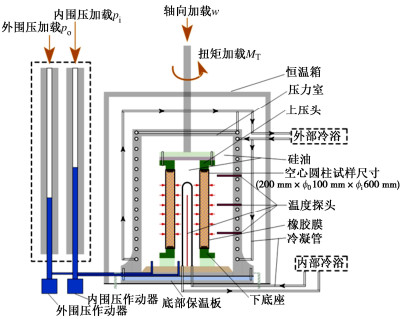
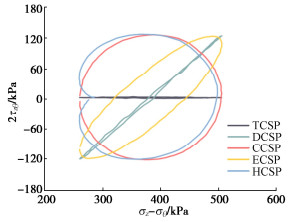
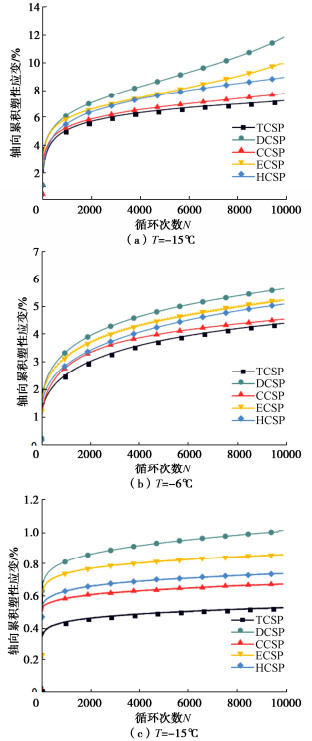
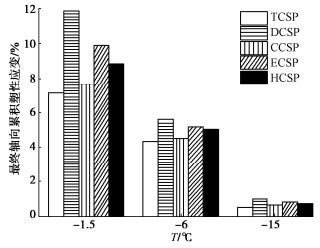
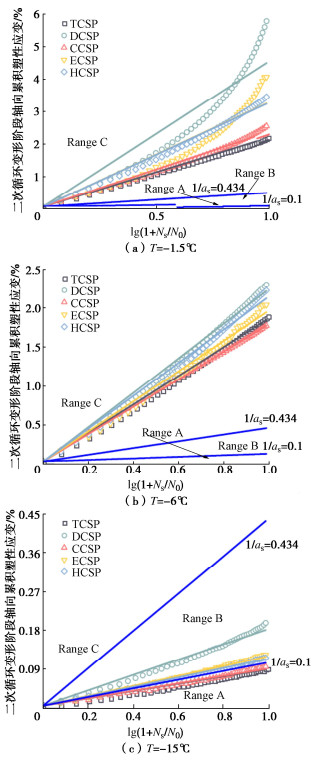
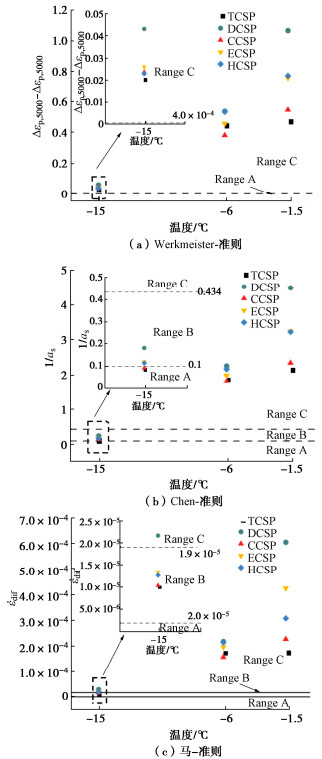
摘要: 复杂循环应力路径下冻土的变形特性与安定性行为研究对寒区工程的长期稳定性具有重要作用。为分析不同复杂循环应力路径对冻土变形特性与安定性行为的影响，设计不同温度同一水平下的5种循环应力路径，即三轴循环应力路径（TCSP）、定向循环应力路径（DCSP）、圆形循环应力路径（CCSP）、椭圆循环应力路径（ECSP）和心形循环应力路径（HCSP），分析了粉质黏土的轴向累积塑性应变，同时利用3种安定性评价准则对结果进行评估。研究结果表明：不同温度5种循环应力路径下的轴向累积塑性应变满足DCSP > ECSP > HCSP > CCSP > TCSP。安定性评价结果表明，定向循环应力路径对土体的安定性行为影响最大，在3种准则下都属于增量破坏。在-15℃时，心形循环应力路径与椭圆循环应力路径试验结果在Chen-准则评估下也属于增量破坏。
- 复杂循环应力路径 /
- 冻结粉质黏土 /
- 变形特性 /
- 安定性行为
Abstract: The deformation characteristics and stability behaviors of frozen soil under complex cyclic stress paths play an important role in the long-term stability of cold region engineering. To analyze the influences of different complex cyclic stress paths on the deformation characteristics and shakedown behaviors of frozen soil, five cyclic stress paths are designed at the same level, namely triaxial cyclic stress path (TCSP), directional cyclic stress path (DCSP), circular cyclic stress path (CCSP), elliptical cyclic stress path (ECSP) and heart-shaped cyclic stress path (HCSP). The axial cumulative plastic strains of the samples are analyzed, and the results are evaluated by three shakedown evaluation criteria. The axial cumulative plastic strains under five cyclic stress paths at different temperatures satisfy the following: DCSP > ECSP > HCSP > CCSP > TCSP. The directional cyclic stress path has the greatest influences on the shakedown behaviors of the soil, and the failure belongs to the incremental one under the three criteria. At the temperature of -15℃, the results of the HCSP and ECSP tests also belong to the incremental failure under the evaluation of Chen criterion.
- complex cyclic stress path /
- frozen silty clay /
- deformation characteristic /
- shakedown behavior

HTML全文

0. 引言

高桩码头是一种典型的沿海水工建筑物。高桩码头的岸坡在地震期间可能发生整体失稳、产生较大的侧向位移进而导致结构损坏。

在进行高桩码头抗震设计时，需对岸坡地震稳定性进行验算，并可采用拟静力法^[1]开展。在拟静力分析方法中，地震引起的荷载通过等效静态水平力施加，边坡的拟静力地震稳定性常用临界地震系数表示。针对边坡拟静力地震稳定性问题，Sarma^[2]在1973年提出了一种使用极限平衡法确定边坡临界地震系数的方法。Chang等^[3]采用极限分析法，确定了平面和对数螺旋两种破坏机制下边坡临界地震系数的严格上限解。Sloan^[4-5]基于有限元法将土体离散进行极限分析，并开发了适用于边坡稳定性分析的数值极限分析程序。Loukidis等^[6]使用有限元极限分析方法，评估了地震作用下边坡的稳定性。

考虑排桩稳定效果的高桩码头岸坡稳定性分析可采用有限元方法开展，但其计算较为复杂。Ito等^[7-8]使用塑性变形理论计算抗滑桩受到的极限侧向力，提出了多排抗滑桩边坡的设计方法。Lee等^[9]基于非耦合公式，分别考虑桩的响应和边坡稳定性，使用简化Bishop法寻找边坡的临界滑动面。Hassiotis等^[10]推广摩擦圆法，将反作用力纳入到边坡稳定性分析中，从而确定了边坡临界滑动面和安全系数。Ausilio^[11]采用极限分析上限法分析抗滑桩边坡稳定性，得出了给定安全系数条件下所需抗滑力的理论表达式。

针对考虑排桩加固的高桩码头岸坡稳定性，使用梯形分布抗滑力考虑排桩对岸坡的稳定作用，假设临界破坏面为穿过坡脚的对数螺旋面，基于极限分析上限法推导了岸坡临界地震系数的表达式。通过变量优化，得到临界地震系数最小上限解和对应的临界破坏面。进一步地，采用强度折减法计算给定水平地震加速度下高桩码头岸坡的安全系数，并分析不同因素对岸坡地震稳定安全系数和破坏模式的影响规律。

1. 高桩码头岸坡临界地震系数

根据极限分析上限定理，对于任何假定的破坏机制，若外力功率超过内部能量耗散速率，则土体不能承受施加的荷载。

。

${{\displaystyle \int }}_{S}{T}_{i}{v}_{i}\text{d}S+{{\displaystyle \int }}_{V}{X}_{i}{v}_{i}\text{d}V\le {{\displaystyle \int }}_{V}{\sigma }_{ij}{\epsilon }_{ij}\text{d}V\text{ }i,j=1,2,3 。$

(1)

式中：T_i为作用在边界S上的牵引力；X_i为作用在体积V上的体力；v_i为运动学容许的速度场； ${\varepsilon _{ij}}$ 为与v_i相容的应变速率场； ${\sigma _{ij}}$ 为与T_i和X_i相对应的应力场。

对岸坡地震稳定性的分析基于以下条件开展：土体为均质、各向同性；平面应变条件；拟静力地震荷载；土体服从莫尔-库伦破坏准则及关联流动法则。

使用极限分析上限法计算临界水平地震系数，假设破坏面为穿过坡脚的对数螺旋面，破坏面方程为

。

$r = {r_0}{{\text{e}}^{\left( {\theta - {\theta _0}} \right)\tan \varphi }}。$

(2)

式中：r为对数螺旋线的半径；φ为土体内摩擦角；r₀为对数螺旋线与坡顶面相交处的半径；θ₀和θ为r₀和r与水平线的夹角。

建立岸坡地震稳定性极限分析模型，如图 1所示。水位线与坡顶平齐，岸坡坡高为H，坡角为β。土体的总重度和有效重度分别为 $\gamma$ 和 $\gamma '$ 。破坏时ABC区域的土体作为刚体绕点O以角速度ω旋转，L为滑动土体顶面宽度，参数θ₀和θ_h用于确定滑动面的具体位置，θ_f1至θ_fn分别代表码头从近海侧到陆地侧的第i排桩在对数螺旋破坏机制中所处的位置(i=1, 2, $\cdots$ , n)。最靠近坡脚的一排桩与坡脚的距离为l，桩间距为d。

图 1 上限分析破坏机制

Figure 1. Failure mechanism of upper bound analysis

下载: 全尺寸图片幻灯片

破坏模式的几何关系如下：

$\frac{H}{{{r_0}}} = \left[ {\sin {\theta _{\text{h}}}{{\text{e}}^{\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi }} - \sin {\theta _0}} \right]\text{，}$

(3)

$\frac{L}{{{r_0}}} = \frac{{\sin (\beta + {\theta _0}) - {{\text{e}}^{\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi }}\sin ({\theta _{\text{h}}} + \beta )}}{{\sin \beta }}\text{，}$

(4)

$\begin{array}{c} \begin{gathered} {r_0}{{\text{e}}^{\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi }}\cos {\theta _{\text{h}}} + l = {r_0}{{\text{e}}^{\left( {{\theta _{{\text{f1}}}} - {\theta _0}} \right)\tan \varphi }}\cos {\theta _{{\text{f1}}}}， \\ \text{······} \end{gathered} \\ {r_0}{{\text{e}}^{\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi }}\cos {\theta _{\text{h}}} + l + (n - 1)d = {r_0}{{\text{e}}^{\left( {{\theta _{{\text{fn}}}} - {\theta _0}} \right)\tan \varphi }}\cos {\theta _{{\text{fn}}}} 。 \end{array}$

(5)

速度不连续面AC上能量耗散速率为

$D = \frac{{c{r_0}^2\omega }}{{2\tan \varphi }}\left( {{{\text{e}}^{2\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi }} - 1} \right) 。$

(6)

极限状态下，作用在排桩上的侧向力可由Ito等^[7]提出的公式确定。排桩对单位宽度岸坡的反作用力可由排桩受力除以桩间距得到，故可将高桩码头岸坡稳定性问题简化为平面应变问题。将排桩对岸坡稳定作用等效为梯形分布力，表达为

$p = {\alpha _{\text{m}}}(a + bz)\text{，}$

(7)

式中：a和b为使用Ito等^[7]提出的公式计算出的参数； ${\alpha _{\text{m}}}$ 为群桩抗滑力系数；z为计算点距地表的深度。

近海侧到陆地侧排桩在滑动面以上产生抗滑力的有效深度z₁至 ${z_n}$ 分别为：

$\begin{array}{c}{z}_{1}={r}_{0}{\text{e}}^{\left({\theta }_{\text{f1}}-{\theta }_{0}\right)\mathrm{tan}\phi }\mathrm{sin}{\theta }_{\text{f1}}-{r}_{0}{\text{e}}^{\left({\theta }_{\text{h}}-{\theta }_{0}\right)\mathrm{tan}\phi }\mathrm{sin}{\theta }_{\text{h}}+l\mathrm{tan}\beta \text{ }，\\ \text{……}\\ {z}_{n}={r}_{0}{\text{e}}^{\left({\theta }_{\text{f}n}-{\theta }_{0}\right)\mathrm{tan}\phi }\mathrm{sin}{\theta }_{\text{f}n}-{r}_{0}{\text{e}}^{\left({\theta }_{\text{h}}-{\theta }_{0}\right)\mathrm{tan}\phi }\mathrm{sin}{\theta }_{\text{h}}+\\ \left[ {l + {\text{(}}n - 1{\text{)}}d} \right]\tan \beta 。 \end{array}$

(8)

近海侧到陆地侧排桩的抗滑力做功功率W_f1至 ${W_{{\text{f}}n}}$ 分别为：

$\begin{array}{c}{W}_{\text{f1}}=-\omega {\alpha }_{\text{m}}\{\left(a{z}_{1}+\frac{b{z}_{1}{}^{2}}{2}\right)\left[{r}_{0}{\text{e}}^{\left({\theta }_{\text{h}}-{\theta }_{0}\right)\mathrm{tan}\phi }\mathrm{sin}{\theta }_{\text{h}}-l\mathrm{tan}\beta \right]+\\ \left(\frac{a{z}_{1}{}^{2}}{2}+\frac{b{z}_{1}{}^{3}}{3}\right)\}\text{ }，\\ \text{……}\\ {W_{{\text{f}}n}} = - \omega {\alpha _{\text{m}}}\left\{ {\left( {a{z_n} + \frac{{bz_n^2}}{2}} \right)\left[ {{r_0}{{\text{e}}^{\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi }}\sin {\theta _{\text{h}}} - } \right.} \right. \\ \left. {\left[ {l + (n - 1)d} \right]\tan \beta } \right] + \left. {\left( {\frac{{az_n^2}}{2} + \frac{{bz_n^3}}{3}} \right)} \right\} 。 \end{array}$

(9)

ABC区滑动土体重力做功功率可由OAC、OBC和OAB区土体重力的功率（W₁-W₂-W₃）得到：

$\begin{array}{c} {W_1} = \frac{{\gamma 'r_0^3\omega }}{{3(1 + 9{{\tan }^2}\varphi )}}\left\{ {(3\tan \varphi \cos {\theta _{\text{h}}} + \sin {\theta _{\text{h}}}){{\text{e}}^{\left[ {3\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi } \right]}} - } \right.\\ \left. {\mathop {}\limits_{} 3\tan \varphi \cos {\theta _0} - \sin {\theta _0}} \right\}\text{，} \end{array}$

(10)

${W_2} = \frac{{\gamma 'r_0^3\omega }}{6}\frac{L}{{{r_0}}}\left( {2\cos {\theta _0} - \frac{L}{{{r_0}}}} \right)\sin {\theta _0}\text{，}$

(11)

$\begin{array}{c} {W_3} = \frac{{\gamma 'r_0^3\omega }}{6}{{\text{e}}^{\left[ {\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi } \right]}}\left[ {\sin {\text{(}}{\theta _{\text{h}}} - {\theta _0}{\text{)}} - \frac{L}{{{r_0}}}\sin {\theta _{\text{h}}}} \right] \cdot \\ \left\{ {\cos {\theta _0} - \frac{L}{{{r_0}}} + \cos {\theta _{\text{h}}}{{\text{e}}^{\left[ {\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi } \right]}}} \right\}。 \end{array}$

(12)

ABC区域土体单位重力加速度的水平惯性力做功功率可同理可表示为（W₄-W₅-W₆）：

$\begin{array}{c} {W_4} = \frac{{\gamma r_0^3\omega }}{{3(1 + 9{{\tan }^2}\varphi )}}\left\{ {(3\tan \varphi \sin {\theta _{\text{h}}} - \cos {\theta _{\text{h}}}) \cdot \mathop {}\limits_{} } \right. \\ {\text{e}}^{\left[3\left({\theta }_{\text{h}}-{\theta }_{0}\right)\mathrm{tan}\phi \right]}-3\mathrm{tan}\phi \mathrm{sin}{\theta }_{\text{h}}+\mathrm{cos}{\theta }_{0}\}\text{ }\text{，} \end{array}$

(13)

${W_5} = \frac{{\gamma r_0^3\omega }}{6}\frac{L}{{{r_0}}}\sin {\theta _0}\sin {\theta _0}\text{，}$

(14)

$\begin{array}{c} {W_6} = \frac{{\gamma r_0^3\omega }}{6}{{\text{e}}^{\left[ {\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi } \right]}}\left[ {\sin ({\theta _{\text{h}}} - {\theta _0}) - \frac{L}{{{r_0}}}\sin {\theta _{\text{h}}}} \right] \cdot \\ \left\{ {{\text{sin}}{\theta _0} + \sin {\theta _{\text{h}}}{{\text{e}}^{\left[ {\left( {{\theta _{\text{h}}} - {\theta _0}} \right)\tan \varphi } \right]}}} \right\}。 \end{array}$

(15)

将内部能量耗散速率与外力做功的功率相等，可得到岸坡的临界地震系数k_c。

${k_{\text{c}}} = \frac{{D - {W_{{\text{f1}}}} - \ldots \ldots - {W_{{\text{f}}n}} - ({W_1} - {W_2} - {W_3})}}{{({W_4} - {W_5} - {W_6})}}。$

(16)

前述分析表明，临界地震系数k_c中有n+2个未知参数θ₀, θ_h, θ_f1, …, θ_fn。将式（5）中的n个几何关系作为非线性约束条件，对k_c进行优化，从而得到临界地震系数k_c的最小上限解和破坏模式参数θ₀和θ_h。

2. 高桩码头地震稳定性极限有限元分析

2.1 计算案例

地震作用下高桩码头岸坡断面如图 2所示，水位与坡顶地表平齐，岸坡坡高H = 10 m，坡度为1∶2。高桩码头在垂直海岸线的方向上有四排桩，近海排桩与坡脚的距离为2.5 m，排桩间距为5 m。在平行海岸线方向上，桩间距D₁ = 5 m，桩间净距D₂ = 3.8 m。岸坡土的黏聚力c = 5 kPa，内摩擦角φ = 30°重度γ = 20 kN/m³。群桩抗滑力系数α_m取0.5。

图 2 高桩码头结构断面

Figure 2. Cross section of pile-supported wharf

下载: 全尺寸图片幻灯片

使用本文理论方法求出临界地震系数k_c= 0.2521，对应的破坏面形态参数θ₀ = 1.3763、θ_h = 1.9883。

2.2 计算结果

为验证本文方法所得结果的合理性，使用有限元极限分析软件OPTUM G2对案例进行计算。OPTUM G2通过网格自适应迭代技术来获得更为精确的上、下限解，有限元极限分析网格如图 3所示。

图 3 有限元极限分析网格

Figure 3. Meshes of finite element limit analysis

下载: 全尺寸图片幻灯片

通过极限分析有限元上、下限分析计算得到的临界地震系数k_c分别为0.2493和0.2473。将上、下限解平均值作为精确解的估计，本文理论方法与有限元极限分析结果误差约为1.2%，这表明本文理论方法在计算岸坡临界地震系数方面的有效性。岸坡在拟静力地震荷载作用下的破坏模式可根据极限分析有限元上限分析得到的剪切耗散云图确定。理论方法得到的对数螺旋破坏面与有限元极限分析得到的剪切耗散分布如图 4所示，可看到对数螺旋破坏面与剪切耗散集中区域接近重合，证明了假设的破坏机制的合理性。

图 4 岸坡破坏机制对比

Figure 4. Comparison of failure mechanisms

下载: 全尺寸图片幻灯片

为进一步验证本文理论方法的合理性，分析了不同桩间净距与桩间距之比D₂/D₁、土体强度指标c和φ条件下理论分析方法与极限分析有限元方法得到的临界地震系数k_c，如表 1所示。从表 1可知，理论分析方法得到的临界地震系数k_c略大于极限分析上限有限元解，与本文方法上、下限解平均值误差均为1%左右，表明采用本文理论分析方法所得的岸坡临界地震系数合理。

表 1 临界地震系数对比

Table 1. Comparison of critical seismic coefficients

D₂/D₁	c/kPa	φ/(°)	k_c
D₂/D₁	c/kPa	φ/(°)	有限元下限解	有限元上限解	本文理论方法
0.76	5	30	0.2473	0.2493	0.2521
0.80	5	30	0.2269	0.2287	0.2303
0.84	5	30	0.2107	0.2122	0.2131
0.76	2.5	30	0.1722	0.1747	0.1760
0.76	7.5	30	0.3040	0.3061	0.3101
0.76	5	27.5	0.2164	0.2181	0.2201
0.76	5	32.5	0.2810	0.2837	0.2870

下载: 导出CSV

| 显示表格

3. 岸坡地震稳定性影响因素分析

强度折减法被广泛应用于边坡稳定性分析中，其通过安全系数 ${{F}_\text{S}}$ 折减土体强度指标c和φ，直至边坡达到临界状态，安全系数与土体强度参数的关系为

${{F}_\text{S}} = \frac{c}{{c{\text{'}}}} = \frac{{\tan \varphi }}{{\tan \varphi {\text{'}}}}\text{，}$

(17)

式中：c和φ为土体的黏聚力和内摩擦角， $c{\text{'}}$ 和 $\varphi {\text{'}}$ 为折减后的黏聚力和内摩擦角。

为分析土体强度参数c，φ和影响抗滑力的排桩布置参数D₂/D₁对稳定性和临界破坏面的影响，在岸坡拟静力稳定性分析中，使用临界地震系数k_c和0.15g水平地震作用下岸坡安全系数F_S评估其抗震性能。

3.1 排桩布置影响

排桩抗滑力受桩间净距与桩间距之比D₂/D₁影响。分别计算不同D₂/D₁条件下岸坡临界地震系数k_c和在0.15g水平地震加速度条件下的安全系数，桩间净距与桩间距之比D₂/D₁分别为0.84，0.80，0.76，0.72，0.68。得到D₂/D₁对岸坡稳定性影响如图 5所示，临界地震系数k_c和安全系数F_S随D₂/D₁增大而减小。

图 5 D₂/D₁对地震稳定性的影响

Figure 5. Influences of D₂/D₁ on seismic stability

下载: 全尺寸图片幻灯片

不同D₂/D₁对应的临界破坏面如图 6所示，图 6表明随着D₂/D₁增大，滑动土体在上部范围缩小而在中下部范围扩大，破坏面曲率增大，但D₂/D₁对破坏机制的影响并不显著。

图 6 D₂/D₁对破坏机制的影响

Figure 6. Influences of D₂/D₁ on failure mechanism

下载: 全尺寸图片幻灯片

3.2 黏聚力的影响

计算不同黏聚力条件下岸坡临界地震系数k_c和在0.15g水平地震加速度条件下的安全系数F_S，其中，土体黏聚力c分别为1，3，5，7，9 kPa。黏聚力c的影响如图 7所示，图 7表明k_c和F_S随黏聚力c增大呈非线性增大，且随着黏聚力c增大，k_c和F_S增长速率降低。

图 7 黏聚力对地震稳定性的影响

Figure 7. Influences of cohesion on seismic stability

下载: 全尺寸图片幻灯片

不同黏聚力c对应的岸坡破坏面如图 8所示，从图 8可知，随着黏聚力c增大，临界破坏面以上滑动土体的范围明显增大，这表明土体黏聚力对岸坡的破坏机制有较显著的影响。

图 8 黏聚力对破坏模式的影响

Figure 8. Influences of cohesion on failure mechanism

下载: 全尺寸图片幻灯片

3.3 内摩擦角的影响

计算不同内摩擦角的岸坡临界地震系数k_c和在0.15g水平地震加速度条件下的安全系数F_S，内摩擦角φ分别为25°，27.5°，30°，32.5°，35°，内摩擦角φ对岸坡地震稳定性的影响如图 9所示，图 9表明k_c和F_S均随内摩擦角增大而增大。

图 9 内摩擦角对地震稳定性的影响

Figure 9. Influences of friction angle on seismic stability

下载: 全尺寸图片幻灯片

不同内摩擦角对应的临界破坏面如图 10所示。从图 10可知随着内摩擦角增大，滑动土体在岸坡中下部范围减小，对数螺旋面曲率减小。内摩擦角对岸坡临界破坏面形态的影响在三个因素中最小。

图 10 内摩擦角对破坏机制的影响

Figure 10. Influences of friction angle on failure mechanism

下载: 全尺寸图片幻灯片

4. 结论

针对地震条件下高桩码头岸坡稳定性提出了一种理论分析方法，分析了高桩码头岸坡的破坏模式和安全系数及随主要因素的变化规律。

（1）将排桩对码头岸坡的稳定作用简化为梯形分布力，采用对数螺旋破坏机制推导出岸坡的临界地震系数，并确定临界地震系数的最小上限解和对应的临界破坏面，建立了适用于高桩码头岸坡地震稳定性的理论分析方法。

（2）采用提出的理论分析方法分析了一个高桩码头案例的临界地震系数和破坏机制，并与极限分析有限元结果进行对比，所得结果与有限元极限分析结果相符，验证了理论分析方法的合理性。

（3）采用建立的理论分析方法，分析得出排桩布置、黏聚力、内摩擦角等对临界地震系数和破坏机制的影响规律，并通过强度折减法计算0.15g水平地震加速度条件下岸坡的安全系数。

（4）高桩码头岸坡的临界地震系数和安全系数随桩间净距与桩间距之比增大而减小，随着土体黏聚力和内摩擦角增大而增大。桩间净距与桩间距之比、土体黏聚力和内摩擦角均影响岸坡的临界破坏模式，但土体黏聚力对破坏面模式的影响更明显。

图 1 颗粒级配曲线

Figure 1. Grain-size distribution curves of test soil

下载: 全尺寸图片幻灯片

图 2 冻土空心圆柱仪装置示意图

Figure 2. Schematic representation of hollow cylinder apparatus for frozen soil

下载: 全尺寸图片幻灯片

图 3 室内复杂循环应力路径实现

Figure 3. Implementation of complex cyclic stress paths in laboratory

下载: 全尺寸图片幻灯片

图 4 不同温度下不同循环应力路径轴向累积塑性应变随循环次数的变化

Figure 4. Axial cumulative plastic strain versus number of vibrations under various cyclic stress paths at different temperatures

下载: 全尺寸图片幻灯片

图 5 不同温度下不同循环应力路径最终轴向累积塑性应变

Figure 5. Axial cumulative plastic strains under various cyclic stress paths at different temperatures

下载: 全尺寸图片幻灯片

图 6 不同温度下5种循环应力路径二次循环压实阶段的轴向累积塑性应变变化

Figure 6. Change of cumulative plastic strain during second-cycle compaction stage under five cyclic stress paths at different temperatures

下载: 全尺寸图片幻灯片

图 7 不同温度5种循环应力路径轴向累积塑性应变的3种安定性准则评估

Figure 7. Evaluation of three shakedown criteria for axial cumulative plastic strain under five cyclic stress paths at different temperatures

下载: 全尺寸图片幻灯片

表 1 试验土体基本物理性质

Table 1 Physical properties of test soil

最大干密度ρ_dmax/(g·cm^-3) 最优含水率w_opt/% 饱和含水率w_sat/% 液限w_L/% 塑限w_P/% 塑性指数I_P

1.84 17.51 20.12 31.17 17.20 13.97

下载: 导出CSV

表 2 试验方案

Table 2 Test schemes

试样编号温度/℃ CSR 应力路径

TN1~5 -1.5 0.875 TCSP, DCSP, CCSP, ECSP, HCSP

TN6~10 -6 1.750 TCSP, DCSP, CCSP, ECSP, HCSP

TN11~15 -15 1.750 TCSP, DCSP, CCSP, ECSP, HCSP

下载: 导出CSV

参考文献(13)

[1]	NIE R S, LI Y F, LENG W M, et al. Deformation characteristics of fine-grained soil under cyclic loading with intermittence[J]. Acta Geotechnica, 2020, 15(11): 3041-3054. doi: 10.1007/s11440-020-00955-3
[2]	LIN T S, ISHIKAWA T, MARUYAMA K, et al. Pavement design method in Japan with consideration of climate effect and principal stress axis rotation[J]. Transportation Geotechnics, 2021, 28: 100552. doi: 10.1016/j.trgeo.2021.100552
[3]	WU T Y, JIN H X, GUO L, et al. Predicting method on settlement of soft subgrade soil caused by traffic loading involving principal stress rotation and loading frequency[J]. Soil Dynamics and Earthquake Engineering, 2022, 152: 107023. doi: 10.1016/j.soildyn.2021.107023
[4]	董彤, 郑颖人, 孔亮, 等. 考虑主应力轴方向的砂土各向异性强度准则与滑动面研究[J]. 岩土工程学报, 2018, 40(4): 736-742. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201804024.htm DONG Tong, ZHENG Yingren, KONG Liang, et al. Strength criteria and slipping planes of anisotropic sand considering direction of major principal stress[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(4): 736-742. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201804024.htm
[5]	陈敦, 马巍, 王大雁, 等. 定向剪切应力路径下冻结黏土变形特性试验[J]. 岩土力学, 2018, 39(7): 2483-2490. CHEN Dun, MA Wei, WANG Dayan, et al. Experimental study of deformation characteristics of frozen clay under directional shear stress path[J]. Rock and Soil Mechanics, 2018, 39(7): 2483-2490. (in Chinese)
[6]	张斌龙, 王大雁, 马巍, 等. 主应力轴旋转条件下冻结黏土累积塑性应变与临界动应力特性研究[J]. 岩土工程学报, 2023, 45(3): 551-560. doi: 10.11779/CJGE20211149 ZHANG Binlong, WANG Dayan, MA Wei, et al. Characteristics of cumulative plastic strain and critical dynamic stress of frozen clay under principal stress rotation[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(3): 551-560. (in Chinese) doi: 10.11779/CJGE20211149
[7]	QIAN J G, WANG Y G, YIN Z Y, et al. Experimental identification of plastic shakedown behavior of saturated clay subjected to traffic loading with principal stress rotation[J]. Engineering Geology, 2016, 214: 29-42. doi: 10.1016/j.enggeo.2016.09.012
[8]	ZHOU Z W, MA W, LI G Y, et al. A novel evaluation method for accumulative plastic deformation of granular materials subjected to cyclic loading: taking frozen subgrade soil as an example[J]. Cold Regions Science and Technology, 2020, 179: 103152. doi: 10.1016/j.coldregions.2020.103152
[9]	王庆志, 周志伟, 张淑娟. 青藏铁路路基粗颗粒填料动力特性和安定性行为研究[J]. 冰川冻土, 2022, 44(2): 566-582. https://www.cnki.com.cn/Article/CJFDTOTAL-BCDT202202020.htm WANG Qingzhi, ZHOU Zhiwei, ZHANG Shujuan. Study on dynamic properties and shakedown behaviors of coarse-grained fillers in Qinghai-Tibet Railway subgrade[J]. Journal of Glaciology and Geocryology, 2022, 44(2): 566-582. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BCDT202202020.htm
[10]	CHEN D, WANG D Y, MA W, et al. A strength criterion for frozen clay considering the influence of stress Lode angle[J]. Canadian Geotechnical Journal, 2019, 56(11): 1557-1572. doi: 10.1139/cgj-2018-0054
[11]	GU F, ZHANG Y Q, LUO X, et al. Characterization and prediction of permanent deformation properties of unbound granular materials for Pavement ME Design[J]. Construction and Building Materials, 2017, 155: 584-592. doi: 10.1016/j.conbuildmat.2017.08.116
[12]	WERKMEISTER S, DAWSON A R, WELLNER F. Pavement design model for unbound granular materials[J]. Journal of Transportation Engineering, 2004, 130(5): 665-674. doi: 10.1061/(ASCE)0733-947X(2004)130:5(665)
[13]	CHEN W B, FENG W Q, YIN J H, et al. Characterization of permanent axial strain of granular materials subjected to cyclic loading based on shakedown theory[J]. Construction and Building Materials, 2019, 198: 751-761. doi: 10.1016/j.conbuildmat.2018.12.012

施引文献

资源附件(0)

图(7) / 表(2)

计量

文章访问数: 128
HTML全文浏览量: 17
PDF下载量: 25
被引次数: 0

0. 引言
1. 高桩码头岸坡临界地震系数
2. 高桩码头地震稳定性极限有限元分析
2.1 计算案例
2.2 计算结果
3. 岸坡地震稳定性影响因素分析
3.1 排桩布置影响
3.2 黏聚力的影响
3.3 内摩擦角的影响
4. 结论

最大干密度ρ_dmax/(g·cm^-3)	最优含水率w_opt/%	饱和含水率w_sat/%	液限w_L/%	塑限w_P/%	塑性指数I_P
1.84	17.51	20.12	31.17	17.20	13.97

试样编号	温度/℃	CSR	应力路径
TN1~5	-1.5	0.875	TCSP, DCSP, CCSP, ECSP, HCSP
TN6~10	-6	1.750	TCSP, DCSP, CCSP, ECSP, HCSP
TN11~15	-15	1.750	TCSP, DCSP, CCSP, ECSP, HCSP

复杂循环应力路径下冻结粉质黏土的变形特性与安定性行为研究 English Version

作者简介: 王亚鹏(1997—)，男，博士，主要从事冻土力学与寒区工程方面的研究工作。E-mail: wangyapeng@nieer.ac.cn

通讯作者: 陈敦, E-mail: chendun@1zb.ac.cn

计量

出版历程