WIB在动力机器荷载激励下的远场被动隔振分析

陈娟; 吴昱洁; 高广运; 宋耀

doi:10.11779/CJGE2023S20016

WIB在动力机器荷载激励下的远场被动隔振分析 English Version

陈娟^{1, 2,},
吴昱洁^{1, 2},
高广运^3, ,,
宋耀^{1, 2}

1.
山东建筑大学土木工程学院, 山东济南 250101
2.
山东建筑大学建筑结构加固改造与地下空间工程教育部重点实验室, 山东济南 250101
3.
同济大学土木工程学院, 上海 200092

基金项目:

国家自然科学基金面上项目 51978510

国家自然科学基金面上项目 42277130

山东省自然科学基金青年项目 ZR2020QE264

山东省高等学校青年创新团队发展计划项目 2023KJ123

详细信息

作者简介:
陈娟(1989—)，女，博士，讲师，硕士生导师，主要从事环境振动控制与屏障隔振方面的研究工作。E-mail: chenjuanjk@126.com

通讯作者:
高广运, E-mail: gaoguangyun@263.net

中图分类号: TU411
计量
- 文章访问数: 108
- HTML全文浏览量: 20
- PDF下载量: 16
出版历程
- 收稿日期: 2023-11-29
- 网络出版日期: 2024-04-19
- 刊出日期: 2023-11-30

Far-field passive vibration isolation of WIB under dynamic machine loads

CHEN Juan^{1, 2,},
WU Yujie^{1, 2},
GAO Guangyun^3, ,,
SONG Yao^{1, 2}

1.
School of Civil Engineering, Shandong Jianzhu University, Jinan 250101, China
2.
Key Laboratory of Building Structural Retrofitting and Underground Space Engineering (Shandong Jianzhu University), Ministry of Education, Jinan, 250101, China
3.
College of Civil Engineering, Tongji University, Shanghai, 200092, China

摘要

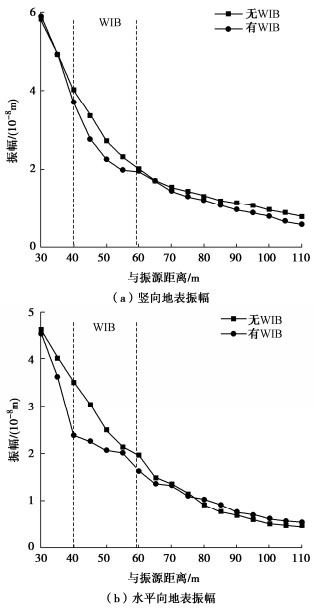
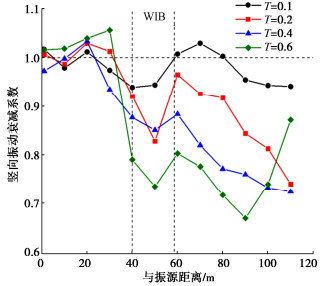
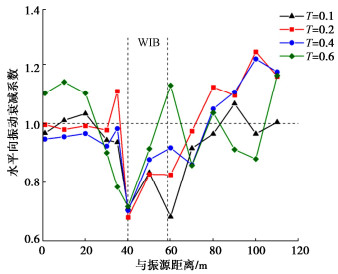
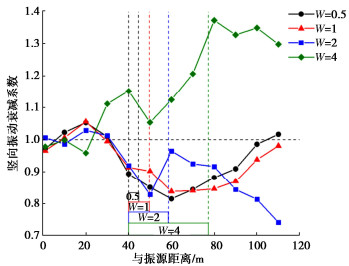
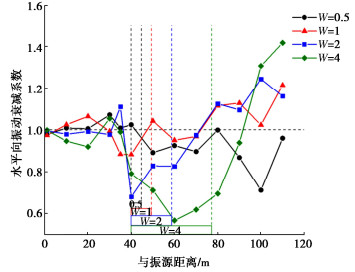
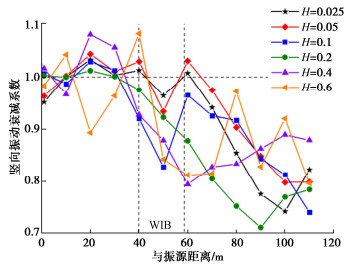
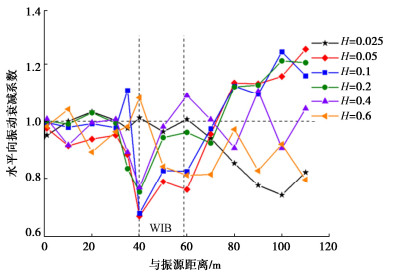
摘要: 为研究波阻板在动力机器荷载作用下的被动隔振效果，通过数值模拟的方法，建立了动力机器基础-WIB-土体的三维有限元模型，计算分析动力机器激振作用下埋置波阻板对远场地表振动传递阻隔的效果，研究不同参数条件对波阻板隔振效果的影响。结果表明：竖向动力机器荷载作用下，在被保护体下方地基中设置波阻板对地表竖向和水平向振动具有一定的阻隔作用，整体隔振效果竖向优于水平向；调整波阻板厚度、宽度及埋深均对被动隔振效果有影响，随波阻板厚度增加，波阻板上方地表的隔振效果基本呈增加趋势；波阻板宽度增大对上方地表振动的阻隔区域有扩张趋势，达到4倍瑞利波长则会明显放大波阻板区域的地表振动；波阻板浅埋时能够有效阻隔振动波，波阻板后方地表的隔振效果明显优于波阻板上方。
- 动力机器基础 /
- WIB /
- ABAQUS /
- 三维有限元模型 /
- 隔振
Abstract: In order to study the passive vibration isolation effects of wave impeding block(WIB) under dynamic machine load, a 3D finite element model for power machine foundation-WIB-soil is established by using the numerical simulation method. The effects of the buried WIB used for dynamic machine excitation on far field surface vibration transmission barrier are calculated and analyzed, and the influences of different parameters on the vibration isolation effects of the WIB are studied. The results show that under the vertical dynamic machine loads, the WIB installed in the foundation under the protected body has certain barrier effects on the vertical and horizontal vibrations of the surface, and the overall vibration isolation effects is better in the vertical than in the horizontal. Adjusting the thickness, width and buried depth of the WIB has effects on the passive vibration isolation effects. With the increase of the thickness of the WIB, the vibration isolation effects of the surface above the WIB basically increase. When the width of the WIB increases, the barrier region of the surface vibration above the WIB expands. When the depth of the WIB up to 4 times the Rayleigh wavelength, the surface vibration in the region of the WIB will be amplified obviously. When it is shallowly buried, the WIB can effectively block the vibration waves, and the vibration isolation effects behind the WIB are obviously better than those above the WIB.
- dynamic machine foundation /
- WIB /
- ABAQUS /
- 3D finite element model /
- vibration isolation

HTML全文

0. 引言

钙质砂是由珊瑚骨骼、贝类、虫黄藻类等海洋生物残骸沉积而成，其主要组成成分是碳酸钙^[1-3]，是我国南海岛礁吹填的主要材料。因其生成环境、成因以及物质组成等因素影响，钙质砂具有颗粒易破碎、形状极不规则、内孔隙发育、微观结构复杂等显著区别于陆源石英砂的特点^[4-6]。随着“一带一路”国家战略和建设“海洋强国”政策方针的推进，研究钙质砂工程力学特性具有重要意义^[7-9]。

钙质砂作为填方工程的天然材料，其应力状态复杂多变，土体受到各向异性应力状态影响而产生初始静剪应力，在建（构）筑物的自重和动荷载（波浪、地震和交通荷载等）作用下，易引起地基强度降低、变形过大以及液化失稳等灾害。实际上，动荷载作用下剪切应力做功将导致材料损伤效应的累积，不排水条件下表现为孔压增长。因此，可以将孔压的升高与土体颗粒在运动或重排过程中所耗损的能量建立关联。损耗能作为标量，相较于应力、应变等矢量，可直接数学叠加，大幅度降低分析难度。Nemat-Nasser等^[10]首先提出了耗散能量的概念，建立其与残余孔压的关系，来有效地评估孔隙水压力的产生和发展过程。Kokusho^[11]和Pan等^[12]提出了土骨架破坏产生的单位体积耗散能与应变和残余孔压累积直接相关，为评价砂土在不规则循环应力条件下的抗液化能力提供了有效方法。总体而言，上述研究主要针对石英砂，能否适用于钙质砂仍需进一步探究。

本文以饱和钙质砂为研究对象，开展不排水条件下循环剪切三轴试验，探究相对密实度、初始静剪应力以及循环应力对其孔压发展的影响；同时，引入能量法，建立钙质砂孔压与损耗能之间联系，提出基于能量损耗的液化评价方法，为钙质砂地基稳定性分析提供理论依据和技术支撑。

1. 试验材料与方案

1.1 试验材料

本文试验材料为中国南海某岛礁的天然钙质砂，颗粒多呈灰白色，形状有片状、块状、棒状等，颗粒内孔隙多、微观结构复杂，如图 1所示。

图 1 典型钙质砂颗粒电镜扫描（SEM）图像

Figure 1. SEM image of typical calcareous sand particles

下载: 全尺寸图片幻灯片

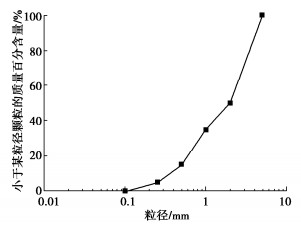
经过现场取材、清水冲洗、烘干等过程后，对粒径大于5 mm的颗粒进行剔除，处理后颗粒分布级配曲线如图 2所示，主要基本物理性质参数见表 1。不难发现，试样基本不含0.1 mm以下的细颗粒，不均匀系数和曲率系数分别为6.84和0.78，属于不良级配砂土。

图 2 钙质砂颗分级配曲线

Figure 2. Grain-size distribution curve of calcareous sand

下载: 全尺寸图片幻灯片

表 1 钙质砂物理性质指标

Table 1. Physical properties of calcareous sand

相对质量密度	d₅₀/ mm	不均匀系数	曲率系数	最大孔隙比	最小孔隙比
2.79	2.0	6.84	0.78	1.15	0.87

下载: 导出CSV

| 显示表格

1.2 试验方案

结合实际工况，采用CKC三轴试验系统模拟复杂应力条件下饱和钙质砂循环剪切试验，先进行有效围压为100 kPa的等向固结后再根据试验设计的初始静偏应力状态进行非等向固结，具体方案如表 2所示。初始静剪应力比SSR和循环应力比CSR可通过式（1）和（2）计算。

表 2 不排水循环剪切试验方案

Table 2. Summary of undrained cyclic triaxial tests

试验系列	相对密实度 D_r	${q_{\text{s}}}$ / kPa	${q_{{\text{cyc}}}}$ / kPa	SSR	CSR	N_f
Ⅰ	70% （密砂）	0	20	0	0.1	232
		0	25	0	0.125	74
		0	30	0	0.15	17
		0	40	0	0.2	6
		20	30	0.1	0.15	168
		20	45	0.1	0.225	19
		20	50	0.1	0.25	3
		50	50	0.25	0.25	53
		50	60	0.25	0.3	11
		50	70	0.25	0.35	6
		80	70	0.4	0.35	14
		80	80	0.4	0.4	7
		-10	25	-0.05	0.125	78
		-10	30	-0.05	0.15	39
		-10	35	-0.05	0.175	8
		-20	20	-0.1	0.1	210
		-20	25	-0.1	0.125	11
		-20	30	-0.1	0.15	8
		-40	20	-0.2	0.1	57
		-40	25	-0.2	0.125	16
		-40	30	-0.2	0.15	8
Ⅱ	30% （松砂）	0	15	0	0.075	943
		0	20	0	0.1	120
		0	25	0	0.125	37
		0	30	0	0.15	18
		24	30	0.12	0.15	61
		24	35	0.12	0.175	16
		24	40	0.12	0.2	5
		40	15	0.2	0.075	175
		40	20	0.2	0.1	9
		50	12.5	0.25	0.0625	17
		50	15	0.25	0.075	2
		-10	12.5	-0.05	0.0625	382
		-10	15	-0.05	0.075	180
		-10	20	-0.05	0.1	11
		-20	10	-0.1	0.05	246
		-20	12.5	-0.1	0.0625	202
		-20	15	-0.1	0.075	12
		-40	5	-0.2	0.025	104
		-40	7.5	-0.2	0.0375	13
		-40	10	-0.2	0.05	2

下载: 导出CSV

| 显示表格

${\text{SSR}} = \frac{{{q_{\text{s}}}}}{{2{{p'}_0}}}\text{，}$

(1)

${\text{CSR}} = \frac{{{q_{{\text{cyc}}}}}}{{2{{p'}_0}}}。$

(2)

式中： ${q_{\text{s}}}$ 为初始静剪偏应力； ${q_{{\text{cyc}}}}$ 为循环偏应力； ${p'_0}$ 为平均有效正应力。

2. 试验结果与分析

2.1 孔压特性发展规律

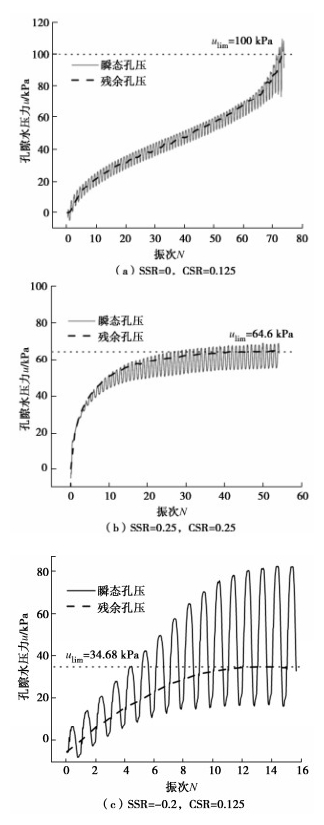
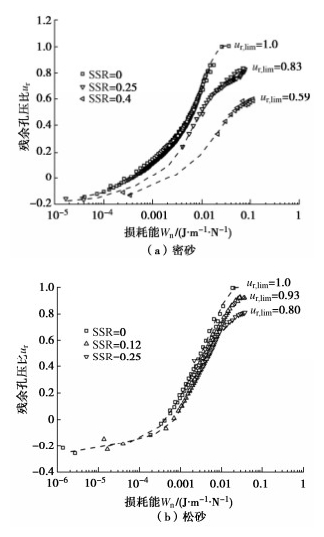
图 3给出不同初始偏应力作用下饱和密砂的孔压发展规律曲线。孔隙水压力可分为两类：①随着循环荷载作用实时变化的孔压，即实线所示的瞬态孔压，这种孔压会随着循环荷载的卸载而快速消散；②每个循环加载结束，试样未及时恢复的孔压，即虚线所示的残余孔压。从图 3（a）中可以看出，对于等向固结的试样，残余孔压在前期随着荷载的施加而逐渐累积，而在后期快速增长，直至达到荷载施加前的有效围压，u_lim=100 kPa。如图 3（b）所示，在压缩静偏应力作用下，孔压在加载初期迅速累积，随着循环荷载持续进行，残余孔压逐渐趋于稳定，u_lim=64.6 kPa。在拉伸静偏应力作用下，孔压发展与压缩静偏应力时有类似的变化趋势，孔压在加载初期累积较快而后基本保持不变，u_lim=34.68 kPa。

图 3 钙质砂孔压增长变化规律

Figure 3. Development of pore water pressure of calcareous sand

下载: 全尺寸图片幻灯片

同时，通过式（3）和（4）定义固结应力比K_c和残余孔压比u_r。

${K_{\text{c}}} = \frac{{{\sigma _{{\text{v}}0}}}}{{{\sigma _{{\text{h}}0}}}}\text{，}$

(3)

${u_{\text{r}}} = \frac{u}{{{\sigma _{{\text{h}}0}}}}。$

(4)

式中： ${\sigma _{{\text{v}}0}}$ 和 ${\sigma _{{\text{h}}0}}$ 分别为初始有效竖向应力和水平应力，u为残余孔压。

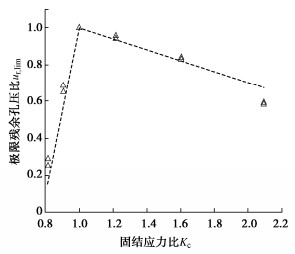
图 4给出了饱和密砂的极限残余孔压比和固结应力比的关系曲线。从图中可以看出，饱和密砂的极限残余孔压比随着固结应力比的增大呈先增大后减小的趋势，在K_c=1（等向固结）时，极限残余孔压比达到最大值u_{r, lim}=1，且大致上呈线性分布，与循环应力幅值大小无明显关系。

图 4 极限残余孔压比与固结应力比的关系

Figure 4. Relationship between ultimate residual pore pressure ratio and consolidation stress ratio

下载: 全尺寸图片幻灯片

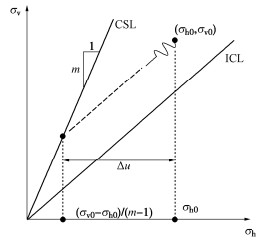
对于同一材料的砂土，其在循环荷载作用下有效应力路径将沿着平行于等向固结线（ICL）的方向逐渐靠近临界状态线（CSL），而与循环应力幅值无关，如图 5所示。因此，对于给定的初始应力状态（σ_h0，σ_v0），会与临界状态线相交于一点，且理论上初始应力点与最终应力点之间的水平距离 $\Delta u$ 为试验中的极限残余孔压，如式（5）所示。根据u_r和K_c定义，可得到两者关系如式（6），符合图 4所示的线性关系。

${u_{\lim }} = \Delta u = {\sigma _{{\text{h}}0}} - \frac{{{\sigma _{{\text{v}}0}} - {\sigma _{{\text{h}}0}}}}{{m - 1}}\text{，}$

(5)

${u_{{\text{r, lim}}}} = \frac{{{u_{\lim }}}}{{{\sigma _{{\text{h0}}}}}} = 1 - \frac{{{K_{\text{c}}} - 1}}{{m - 1}}。$

(6)

图 5 初始静剪应力状态对残余孔压影响示意图

Figure 5. Influences of initial static shear stress on residual pore pressure

下载: 全尺寸图片幻灯片

2.2 损耗能演化规律

动荷载作用下饱和砂土损耗的能量主要用于颗粒的相对运动和重新排列。因此，引入能量法，提出基于损耗能的砂土液化评价方法。循环加载过程中一个振次的损耗能W可用应力-应变滞回圈的面积表示，即：

$W = \sum\limits_{i = 1}^{n - 1} {\frac{1}{2}} ({q_{i + 1}} + {q_i})({\varepsilon _{{\text{a, }}i + 1}} - {\varepsilon _{{\text{a, }}i}}) 。$

(7)

式中：n为计算增量的总个数， ${q_i}$ 和 ${\varepsilon _{{\text{a, }}i}}$ 分别为第i个增量的偏应力和轴向应变。

图 6分别给出饱和钙质砂在不同初始静偏应力作用下残余孔压比与正交化损耗能的内在关系，正交化损耗能W_n为损耗能W与初始有效水平正应力 ${\sigma _{{\text{h0}}}}$ 的比值。结果显示：饱和密砂的残余孔压初期增长缓慢，随着W_n的增大而较快增长，最后趋于稳定；在饱和松砂中也观察到类似的变化趋势。这说明残余孔压与损耗能的关系主要取决于初始应力条件。

图 6 残余孔压比与损耗能的关系

Figure 6. Relationship between residual pore pressure ratio and dissipated energy

下载: 全尺寸图片幻灯片

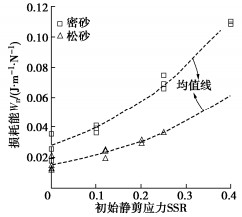
从图 7可以看出，饱和钙质砂在失稳破坏时所积累的损耗能随着初始静剪应力的增加而增加；对于同一初始应力状态，密砂所需能量始终大于松砂。研究表明^[13-14]，饱和砂土在循环荷载作用下损耗能主要与初始应力和相对密实度有关，受循环荷载幅值影响极小，具体可用式（8）表示：

${W'_{\text{n}}} = {10^{a\left( {{D_{\text{r}}} - 0.78} \right)}}{10^{b\left( {{\text{SSR}} - 1.0} \right)}}。$

(8)

图 7 损耗能与初始静剪应力比的关系

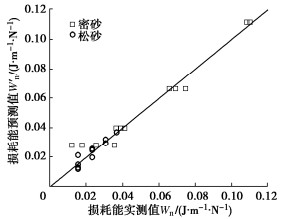
Figure 7. Relationship between dissipated energy and initial static shear stress ratio

下载: 全尺寸图片幻灯片

式中：a和b为经验参数，根据本次试验数据可分别取0.65，1.5。图 8对损耗能的试验实测值与通过式（8）所得的预测值进行对比，发现两者基本落在斜率为1的对角线两侧，表明能量模型可较好地预测不同试验条件下饱和钙质砂的损耗能。

图 8 损耗能实测值与预测值

Figure 8. Measured and predicted values of dissipated energy

下载: 全尺寸图片幻灯片

3. 结论

（1）饱和钙质砂的极限残余孔压比随固结应力比呈先增大后减小的趋势，在K_c=1时存在最大值，临界状态理论可以解释此现象。

（2）不排水循环加载条件下饱和钙质砂的损耗能与试样的初始静剪应力比和相对密实度有关，受循环应力比影响极小，可通过构建的能量模型较好地预测不同试验条件下饱和钙质砂所累积的损耗能。

图 1 动力机器基础-WIB-土体三维模型

Figure 1. Three-dimensional model for power machine foundation-WIB-soil

下载: 全尺寸图片幻灯片

图 2 模型网格划分

Figure 2. Model meshing

下载: 全尺寸图片幻灯片

图 3 模型验证结果对比

Figure 3. Verification of proposed model

下载: 全尺寸图片幻灯片

图 4 竖向激振作用下设置WIB前后地表振幅对比

Figure 4. Comparison of surface amplitudes before and after WIB set under vertical excitation

下载: 全尺寸图片幻灯片

图 5 不同WIB厚度时竖向A_R随距离的变化曲线

Figure 5. Variation curves of vertical A_R with distance under different WIB thicknesses

下载: 全尺寸图片幻灯片

图 6 不同WIB厚度时水平向A_R随距离的变化曲线

Figure 6. Variation curves of horizontal A_R with distance under different WIB thicknesses

下载: 全尺寸图片幻灯片

图 7 不同WIB宽度时竖向A_R随距离的变化曲线

Figure 7. Variation curves of vertical A_R with distance under different WIB widths

下载: 全尺寸图片幻灯片

图 8 不同WIB宽度时水平向A_R随距离的变化曲线

Figure 8. Variation curves of horizontal A_R with distance under different WIB widths

下载: 全尺寸图片幻灯片

图 9 不同WIB埋深时竖向A_R随距离的变化曲线

Figure 9. Variation curves of vertical A_R with distance under different WIB depths

下载: 全尺寸图片幻灯片

图 10 不同WIB埋深时水平向A_R随距离的变化曲线

Figure 10. Variation curves of horizontal A_R with distance under different WIB depths

下载: 全尺寸图片幻灯片

表 1 模型材料参数表

Table 1 Parameters of model materials

材料密度/(kg·m^-3) 泊松比弹性模量/MPa α β/10^-4

土体 1800 0.35 124 2.42 1.53

基础 2500 0.2 28 1.45 0.92

WIB 2400 0.22 2240 1.45 0.92

下载: 导出CSV

表 2 WIB基本参数

Table 2 Basic parameters of WIB

参数无量纲尺寸(单位：1) 模型尺寸/m

波阻板埋深 0.1 0.9

波阻板厚度 0.2 1.9

波阻板厚度 2 18.7

下载: 导出CSV

参考文献(21)

[1]	CHOUW N, LE R, SCHMID G. Propagation of vibration in a soil layer over bedrock[J]. Engineering Analysis with Boundary Elements, 1991, 8(3): 125-131. doi: 10.1016/0955-7997(91)90021-K
[2]	SCHMID G, CHOU W N, LE R. Shielding of structures from soil vibrations[C]// Soil Dynamic and Earthquake Engineering V, Proc Int Conf on Soil Dynamics and Earthquake Engineering. Southampton: Computational Mechanics Publications, 1991: 651-662.
[3]	TAKEMIYA H, JIANG J Q. Wave impeding effect by buried rigid block and response reduction of dynamically excited pile foundation[J]. Doboku Gakkai Ronbunshu, 1993, 1993(477): 45-52. doi: 10.2208/jscej.1993.477_45
[4]	PEPLOW A T, JONES C J C, PETYT M. Surface vibration propagation over a layered elastic half-space with an inclusion[J]. Applied Acoustics, 1999, 56(4): 283-296. doi: 10.1016/S0003-682X(98)00031-0
[5]	高广运, 李伟. 二维地基波阻板隔振分析[J]. 地震工程与工程振动, 2005, 25(2): 130-135. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC20050200M.htm GAO Guangyun, LI Wei. 2-D analysis of ground vibration isolation using wave impeding block[J]. Earthquake Engineering and Engineering Vibration, 2005, 25(2): 130-135. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC20050200M.htm
[6]	高广运, 冯世进, 李伟, 等. 二维层状地基波阻板隔振分析[J]. 振动工程学报, 2007, 20(2): 174-179. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC200702012.htm GAO Guangyun, FENG Shijin, LI Wei, et al. 2-D analysis of vibration isolation by wave impeding block in layered ground[J]. Journal of Vibration Engineering, 2007, 20(2): 174-179. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC200702012.htm
[7]	高广运, 冯世进, 李伟, 等. 三维层状地基竖向激振波阻板主动隔振分析[J]. 岩土工程学报, 2007, 29(4): 471-476. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200704001.htm GAO Guangyun, FENG Shijin, LI Wei, et al. 3D analysis of active vibration isolation with wave impeding block in layered ground under vertical loading[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(4): 471-476. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200704001.htm
[8]	高广运, 陈功奇, 张博. 列车荷载下竖向非均匀地基波阻板主动隔振分析[J]. 振动与冲击, 2013, 32(22): 57-62. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201322011.htm GAO Guangyun, CHEN Gongqi, ZHANG Bo. Active vibration isolation using WIB in non-uniform ground under train loadings[J]. Journal of Vibration and Shock, 2013, 32(22): 57-62. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201322011.htm
[9]	GAO G Y, LI N, GU X Q. Field experiment and numerical study on active vibration isolation by horizontal blocks in layered ground under vertical loading[J]. Soil Dynamics and Earthquake Engineering, 2015, 69: 251-261. doi: 10.1016/j.soildyn.2014.11.006
[10]	GAO G Y, CHEN J, GU X Q, et al. Numerical study on the active vibration isolation by wave impeding block in saturated soils under vertical loading[J]. Soil Dynamics and Earthquake Engineering, 2017, 93: 99-112. doi: 10.1016/j.soildyn.2016.12.006
[11]	李宁, 高广运, 郑建国. 水平激振下波阻板主动隔振试验与数值计算[J]. 地下空间与工程学报, 2010, 6(1): 90-95. doi: 10.3969/j.issn.1673-0836.2010.01.017 LI Ning, GAO Guangyun, ZHENG Jianguo. Field experimental and numerical study on active vibration isolation by WIB under horizontal loading[J]. Chinese Journal of Underground Space and Engineering, 2010, 6(1): 90-95. (in Chinese) doi: 10.3969/j.issn.1673-0836.2010.01.017
[12]	周凤玺, 马强, 周志雄. 二维地基中空沟-波阻板联合隔振屏障分析[J]. 岩土力学, 2020, 41(12): 4087-4092, 4115. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202012029.htm ZHOU Fengxi, MA Qiang, ZHOU Zhixiong. 2D analysis of vibration-isolation efficiency of an open trench-wave impedence block barrier[J]. Rock and Soil Mechanics, 2020, 41(12): 4087-4092, 4115. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202012029.htm
[13]	MA Q, ZHOU F X. Analysis of isolation ground vibration by graded wave impeding block under a moving load[J]. Journal of Engineering, 2018, 2018: 4989584.
[14]	ZHOU F X, ZHOU Z X, MA Q. Study on the vibration isolation performance of an open trench–wave impedance block barrier using perfectly matched layer boundaries[J]. Journal of Vibration and Control, 2022, 28(3/4): 329-338.
[15]	高盟, 张致松, 王崇革, 等. 竖向激振力下WIB-Duxseal联合隔振试验研究[J]. 岩土力学, 2021, 42(2): 537-546. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202102026.htm GAO Meng, ZHANG Zhisong, WANG Chongge, et al. Field test on vibration isolation performance by WIB-Duxseal under vertical excitation[J]. Rock and Soil Mechanics, 2021, 42(2): 537-546. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202102026.htm
[16]	江烨, 马强. 非饱和土地基中波阻板隔振屏障对P波的隔离效应[J/OL]. 工程力学, 1-12[2023-10-23]. http://kns.cnki.net/kcms/detail/11.2595.O3.20230510.1320.002.html. JIANG Ye, MA Qiang. Isolation effect of wave impeding barrier on P-wave in unsaturated ground foundation[J/OL]. Engineering Mechanics, 1-12[2023-10-2]. http://kns.cnki.net/kcms/detail/11.2595.O3.20230510.1320.002.html. (in Chinese)
[17]	时刚, 李永辉. 弹性地基中波阻板对入射Rayleigh波的远场被动隔振研究[J]. 世界地震工程, 2019, 35(2): 11-17. https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC201902002.htm SHI Gang, LI Yonghui. Passive vibration isolation effectiveness of wave impedance block under incident Rayleigh wave in elastic foundation[J]. World Earthquake Engineering, 2019, 35(2): 11-17. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC201902002.htm
[18]	邓亚虹, 夏唐代, 陈敬虞. 车辆荷载作用下隔震沟隔震效率影响因素分析[J]. 岩土力学, 2007, 28(5): 883-887, 894. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200705006.htm DENG Yahong, XIA Tangdai, CHEN Jingyu. Analysis of efficiency of vibration isolating groove subjected to vehicle load[J]. Rock and Soil Mechanics, 2007, 28(5): 883-887, 894. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200705006.htm
[19]	谷音, 刘晶波, 杜义欣. 三维一致黏弹性人工边界及等效黏弹性边界单元[J]. 工程力学, 2007, 24(12): 31-37. https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB200905031.htm GU Yin, LIU Jingbo, DU Yixin. 3d consistent viscous-spring artificial boundary and viscous-spring boundary element[J]. Engineering Mechanics, 2007, 24(12): 31-37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB200905031.htm
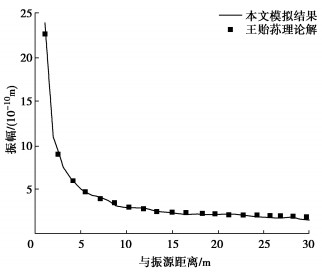
[20]	王贻荪. 半无限体表面在竖向集中谐和力作用下表面竖向位移的精确解[J]. 力学学报, 1980, 12(4): 386-391. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB198004007.htm WANG Yisun. Exact solution for the dynamic vertical surface displacement of the elastic half-space under vertical harmonic point load[J]. Acta Mechanica Sinica, 1980, 12(4): 386-391. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB198004007.htm
[21]	WOODS R D. Screening of surface wave in soils[J]. Journal of the Soil Mechanics and Foundations Division, 1968, 94(4): 951-979. doi: 10.1061/JSFEAQ.0001180