Bounding surface plastic p-y model for a single laterally loaded pile in sand
-
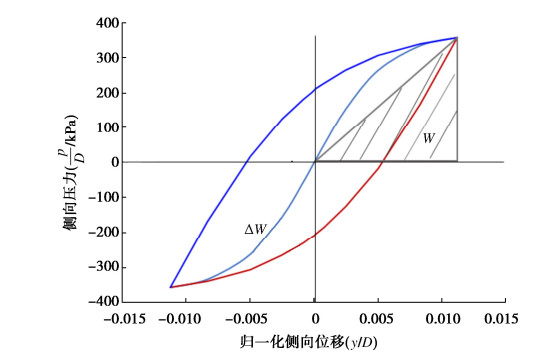
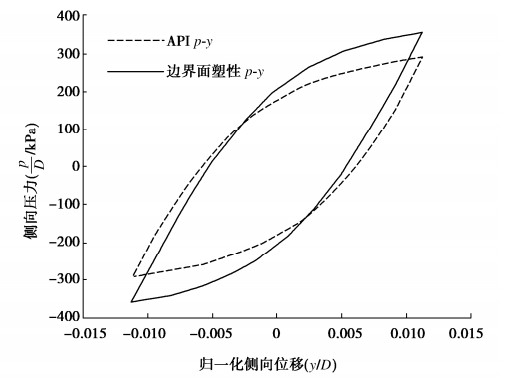
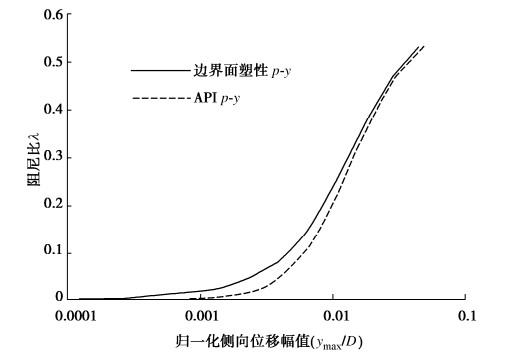
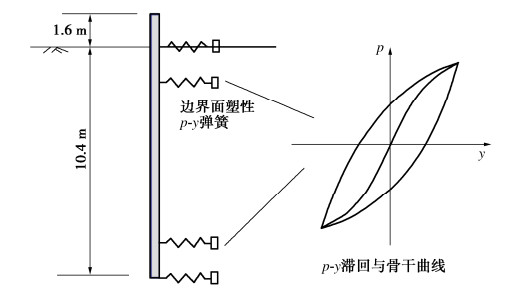
摘要: 在海洋工程实践中，横向承载桩通常采用非线性温克尔地基梁法进行分析，其中土与结构相互作用通过p-y曲线进行模拟，但目前API/DNV规范的p-y模型仅适用少量的土性和桩型，没有给出循环荷载下的p-y滞回曲线。提出了一个适用单调和循环荷载的简化砂土边界面塑性剪应力-剪应变模型，介绍了一种从剪应力-应变响应构建p-y曲线的方法，该方法将应力和应变分别比例换算为相应的土反力p和桩挠度y，具有较好的理论基础。根据API规范中砂土的p-y曲线，采用Masing法则构建了API p-y滞回曲线，并与边界面塑性p-y曲线进行了对比，分析了割线刚度、阻尼比等随位移幅值的变化特性。最后采用模型试验结果验证了所提出的p-y曲线的有效性。Abstract: In ocean engineering practice, laterally loaded piles are usually analyzed using the nonlinear Winkler foundation beam method, in which the soil-structure interaction is modelled by means of the p-y curve, but now the API/DNV rules are only valid for few soils and pile conditions, and the p-y hysteresis curve is not given under cyclic loading. A simplified bounding surface plastic shear stress-shear strain model for sandy soil under monotonic and cyclic loads is proposed, and a method is introduced for the establishment of p-y curves from the proposed model. Based on the scaling of stress and strain into compatible soil reaction p and pile deflection y respectively, the proposed method has good theoretical basis. According to the p-y curve of sand in the API rule, the API p-y hysteresis curve is established using the Masing rule and compared with the bounding surface plastic p-y curve, and the variation characteristics of secant stiffness and damping ratio with displacement amplitude are analyzed. Finally, the validity of the proposed p-y curve is verified by the model test results.
-
Keywords:
- bounding surface plasticity /
- p-y curve /
- laterally loaded pile /
- cyclic loading
-
0. 引言
对于海洋采油平台、港口码头等结构物，由于受到风、波浪、地震等水平荷载的作用，其桩基础的横向承载特性是其设计的重要内容，在过去40 a中横向受荷桩的特性受到了相当多的关注。因为桩侧土体的应力-应变特性复杂，该问题可以使用三维数值模拟进行分析，但土/桩相互作用非线性的模拟非常复杂、参数标定工作量大和计算成本的高昂等使得数值分析在多数情况下不可行、也不经济。在实践中横向受荷桩的最简单实用的分析方法仍是采用非线性温克尔地基梁模型，即p-y曲线法。目前有多种方法用于构建p-y曲线，如基于现场横向载荷试验数据的反分析及室内三轴试验的应力-应变曲线的半经验方法(API 2014[1]，DNV 2001[2]，Reese等[3])、从钻孔压力测试参数推演p-y曲线法等[4-5]。
p-y方法的有效性是基于宏观上桩的荷载-变形响应与细观上桩侧土体的剪切应力-应变响应之间具有相似性假设，理论上可以通过应用适当的比例因子将应力、应变分别转换为等效的土反力p和桩土相对位移y。Bouzid等[6]认为这些比例因子可以从被称为“可动员强度设计”(MSD)(Vardanega等[7])的方法中推出。Lombardi等介绍了一种从应力-应变模型构建液化后土p-y曲线的比例系数法[8]。
API(2014)或DNV规范(DNV 2001)提供了软黏土、硬黏土、砂土等少量土体的p-y曲线，且是半经验的。然而，在实践中经常遇到“非规范化”的土体，这种情况下的p-y曲线需要从具体的土的应力-应变特性中得出。随着对复杂本构关系问题的计算能力不断增强，p-y曲线的建立可以更有理论依据。传统的p-y曲线虽然能考虑桩周土体的非线性特性，但一般只能用于分析单调水平荷载，苏栋[9]基于边界塑性的概念，直接建立了地基反力p与位移y的增量弹塑性模型，能模拟往复荷载作用的桩土响应。黄茂松等[10]引入土体不排水强度与塑性累积位移间的关系和Masing准则，获得了考虑荷载循环影响的p-y曲线。Zhang等[11]基于直接单剪试验数据，取归一化的抗剪强度与地基反力相等，剪应变比例缩放为归一化的侧向位移，建立循环p-y曲线。目前API/DNV规范中对于砂土循环荷载作用，采用0.9倍折减极限承载力的简单方法，从整体上调整p-y曲线，没有卸载-再加载描述。上述研究多是根据桩土模型试验提出经验的p-y曲线，或是基于土单元体试验的应变比例缩放，缺乏可靠的应力应变理论基础，不能描述桩土相互作用的连续的滞回曲线和复杂的强度、刚度弱化特性。
本文基于弹塑性应力应变理论，提出了模拟循环荷载作用下砂土剪切变形特性的简化边界面塑性本构模型，进而介绍了根据砂土剪应力-应变关系建立横向受荷桩p-y曲线的比例系数法。对往复水平荷载作用下的单桩模型试验进行分析，结果表明本文的边界面塑性p-y模型能有效的模拟水平荷载作用下单桩基础的刚度非线性、强度衰减和滞回响应。
1. 砂土的边界面塑性应力应变关系
为了简便起见，本文仅介绍剪切应力-剪应变关系。增量剪应变dγ被分解为弹性和塑性两部分，其与剪应力增量dτ的关系可写为
dγ=dγe+dγp， (1) dγe=1Gdτdγp=2Hdτ。 (2) 式中：G，H为弹、塑性剪切模量；上标‘e’和‘p’表示弹性、塑性分量；d表示增量。
弹性剪切模量G与孔隙比和平均正应力有关，采用如下经验公式[12]：
G=G0(2.973−e)21+e√p′pa。 (3) 式中：G0为模型参数；e为初始孔隙比；p′为初始平均有效应力；pa为大气压。
在弹性模量中引入考虑非线性特性的附加项，可建立塑性模量表达式。基于Wang等[12]提出的边界面亚塑性理论，塑性剪切模量H，考虑与密实状态的相关性，本文采用如下形式：
H=Ghf(ξ)[τfτm(ˉρρ)m−1]。 (4) 式中：f(ξ)=(ρ/ˉρ)n+e−αξ[1−(ρ/ˉρ)n]为与塑性剪应变相关的软化系数，用以模拟周期荷载作用下的模量退化现象，累积塑性剪应变ξ=∫|dγp|，α，h为模型参数，n可取任意较大的整数，软化系数的这种表述使其主要对非初始加载有影响；m=2τm/ˉρ非模型参数，τm为土体历史上的最大剪应力，τf为土的抗剪强度，ρ，ˉρ分别为投影中心与当前应力状态、边界面上“像应力”的距离，如图 1所示。
在简单单调剪切、排水条件下，平均体应力p为常数时，对增量关系式(1)，(2)积分，不考虑软化系数和模量变化时，可得这种条件下模型的全量剪应力剪应变关系如下：
对于原始加载：
γ=f(τ)=τG−2τfhG[ττf+ln(1−ττf)]； (5) 对于卸载：
γ2=γ1+τ2−τ1G−4τfhG[τ2−τ12τf−ln(2τf+τ2−τm2τf+τ1−τm)]； (6) 对于重新加载(反向卸载)：
γ2=γ1+τ2−τ1G−4τfhG[τ2−τ12τf+ln(τ2+τm−2τfτ1+τm−2τf)]。 (7) 在不排水条件下，剪胀会引起平均有效应力变化，式(3)中p被视为当前平均有效应力，需结合有效应体力-体应变关系使用。
在循环加载时，由应力-应变滞回曲线式(6)，(7)可求阻尼比λ为
λ=−2π τfhGτmγm[(4τf−2τm)ln(1−τmτf)+4τm]。 (8) 上述边界面塑性模型的剪应力和剪应变，通过两个比例系数，可分别转化为地基反力p和侧向变形y，进而得到计算横向承载桩响应的p-y塑性模型。
2. 边界面塑性p-y模型
横向土-桩相互作用的p-y曲线通常从现场桩荷载试验中得出[13]，但经验公式p-y的适用性通常仅限于与现场试验的土性、桩的几何特征及荷载条件等相同的基础设计。Bransby[14]和Klar[15]从数值和理论上证明，横向荷载作用下桩的p-y曲线与其侧面土的应力应变曲线的非线性特性具有相似性。因此，可以根据应力-应变响应按一定比例系数缩放得到桩-土相互作用的p-y响应。Osman等[16]首次将这一概念用于推导不排水黏土地基上圆形基础的荷载-沉降曲线，被称之为动员强度设计法(MSD)。近年来，这一概念已成功应用于开发特定场地的横向承载桩的p-y曲线。从剪应力-应变曲线估算p-y曲线的方法如图 2所示，需要3个参数：MC，NC和D(桩径)，坐标比例变换如下：
pD=Nc⋅τmob=Nc⋅√32τ， (9a) yD=1Mc⋅εs=1Mc⋅√32γ， (9b) yD=0.866Mc⋅f(1.15pDNc)。 (10) ![]()
图 2 从应力-应变曲线获取p-y曲线的比例方法Figure 2. Scaling method for constructing p-y curve from shear stress-strain curve很多学者对比例系数MC和NC进行了研究。根据Bouzid等[6]的研究，在弹性介质中，对于光滑界面MC和NC分别为3.15和11.23，对于粗糙界面分别为2.59和17.86。对于均匀黏土，在达到最大剪应力后，可以使用完全塑性条件的解，即MC=2.6和NC=9。根据Martin等[17]，塑性条件下桩在黏土中的极限侧阻力系数Nc在9.14(完全光滑)与11.92(完全粗糙)之间变化。对于砂土，由于塑性力学机制复杂，桩侧极限阻力分析更难，在小于5倍桩径深度时，几种极限阻力公式计算结果很接近，在深度较大时API 2014曲线看似更合理[18]。Prasad等[19]提供了靠近地表的临界区域内的侧向压力试验数据，与经验系数N=kp2非常一致。
假设砂土摩擦角φ′=35°，有效重度γ′=7.5 kN/m3，桩径D=0.6 m，取静止土压力系数k0=0.6，考虑深度z/D=3处的p-y曲线。根据API 2014，k=22 MPa/m，c1=3，c2=3.4，pu=247.5 kN/m，kz=66000 kPa。对于边界面模型，Gmax=2688 kPa，h=2.8，τf=34.94 kPa，取Mc=2.6，Nc=10(Barton系数：2kp2/(kp-1)，kp为被动土压力系数)构建边界面塑性p-y曲线，与API曲线对比如图 3。
对于原始加载情况，根据式(5)可得边界面塑性p-y模型的割线刚度衰减方程为
KKmax=GGmax=[1−2h(τfτln(1−ττf)+1)]−1。 (11) 3. 与API砂土p-y模型对比
根据API 2014建议，砂土侧向阻力与位移p-y关系呈现为非线性，在缺少可靠的信息时，某一深度z处的p-y曲线可近似采用双曲正切函数描述为
p=Apu⋅tanh(kzApuy)。 (12) 式中：A是一个取决于荷载类型的系数：循环荷载为A=0.9，静态荷载为A=(3−0.8z/D) ≥ 0.9。这意味着循环荷载只会导致土层深度小于2.6D时的承载力降低；kz等于p-y曲线初始刚度，即初始刚度随深度线性增加，k值是砂土内摩擦角的函数，可以查图求取；pu为p-y弹簧的极限强度。式(12)显示API p-y曲线为仅含两个模型参数k和pu的单调增加函数。从式(12)可得API p-y模型的刚度衰减曲线，与前述边界面塑性p-y模型对比如图 4所示，可以看出两者衰减趋势一致，但后者衰减更快，在位移小于某个门槛值时, 可以不考虑刚度衰减(G/Gmax > 0.99)。
![]()
图 4 边界面塑性p-y模型与API模型的刚度衰减曲线Figure 4. Stiffness reduction of bounding surface plastic p-y curve and API model对于土体在循环荷载下的应力应变响应，一般认为Masing法则真实地描述了土体滞后特性。当用于目前的API p-y曲线设计时，初始加载或骨干曲线采用式(12)的双曲正切曲线模式，对于y方向上的稳态循环加载，采用Masing二倍法则确定滞后响应的卸载和重新加载曲线如下：
p−pm2=−0.9puD⋅tanh(kz0.9puy−ym2)。 (13) 该滞回圈曲线在几何上类似初始加载曲线，但尺度放大一倍，并反向移到荷载反向点(p0，u0)处，这些不同位移振幅的稳态滞回线如图 5所示，与边界面塑性p-y滞回圈形态相似如图 6，后者稍平缓(刚度较小)。
![]()
图 5 采用Masing法则的API砂土p-y滞回曲线Figure 5. API p-y hysteresis loop of sand using Masing rule![]()
图 6 边界面塑性p-y模型与API模型的滞回圈Figure 6. Hysteresis loop of bounding surface plastic p-y curve and API model从API p-y滞回曲线式(13)可求其阻尼比λ为
λ=Δw4π w=2π 2ln(cosh(y∗))−y∗⋅tanh(y∗)y∗⋅tanh(y∗)。 (14) 式中：y* = ymkz/(Apu)。
API p-y曲线与边界面塑性p-y模型的阻尼比对比如图 7所示，可以看出两者随位移幅值发展趋势一致，后者阻尼比略大。
![]()
图 7 边界面塑性与API p-y模型的阻尼与位移幅值的关系Figure 7. Damping ratio and displacement amplitudes relation for bounding surface plastic p-y curve and API model从以上刚度衰减曲线、滞回圈和阻尼比曲线等比较可知，本文提出的边界面塑性p-y模型与API p-y模型一致性较好，但前者具有较好的理论基础，可以描述p-y滞回特性的具体发展过程，后者在API规范中并无滞回圈方程，因此只能描述平均发展趋势，且折减系数固定为0.9，适应性较差。
4. 实例分析
文献[20]进行了砂土中单桩的离心模型试验，相似比取40，原型桩直径0.72 m、入土深度10.4 m，抗弯刚度476 MN.m2，加载点位于地面上1.6 m处。模型试验采用干砂，粒径集中于0.125~0.315 mm，土体的干重度16.34 kN/m3，相对质量密度2.65，相对密实度约86%，内摩擦角38°。模型只施加水平力，采用力控制循环加载，荷载速率10 N/s，最大载荷960 kN，载荷幅值960 kN，允许桩头自由转动。
如图 8，分析时桩长取12 m，均分为30个梁单元(每个单元长度为0.4 m)，在地面下的梁单元节点处设置边界面塑性p-y弹簧支座。采用力控制分析，荷增量为±96 N。模型参数取值为：h=0.5，α=1.5，Rf = 0.895(τf=Rfp′，p′为平均有效体应力)，G0=50，Mc=2.75，Nc=17。
![]()
图 8 p-y曲线法模拟侧向受荷桩计算模型图Figure 8. Schematic of laterally loaded pile model in the p-y method采用API p-y模型计算，结果显示计算刚度偏大、极限强度偏小。估计是桩周砂土在打桩过程中存在挤密效应，为此根据挤密前的内摩擦角计算Rf，但Nc取较大的值(> 11.92[17])，仍可视为在合理的范围(弹塑性过渡段，< 17.86[6])。在深度z =1.8 m处，边界面塑性p-y数值模拟与试验结果如图 9所示。
![]()
图 9 循环荷载下桩侧土反力与位移关系曲线Figure 9. Relationship between lateral soil reaction force and displacement under cyclic loading从图 9可以看出，对加载和重加载情况，计算刚度较大，但整体上计算结果较好地重现了模型试验测得的桩侧水平力-位移关系曲线的非线性特性，计算和测得的水平力最大值也较为接近。在往复加载阶段，数值结果也较好地反映了桩头水平力-位移关系曲线的滞回和软化特性。这些分析结果表明本文提出的边界面弹塑性p-y模型能可靠地模拟单桩在水平循环荷载作用下的力-位移响应。
5. 结论
针对目前API等规范中缺乏循环荷载下桩土作用的p-y滞回曲线，本文基于“动员强度设计”概念，提出了一种由砂土的剪应力-应变关系构造桩土作用的p-y曲线的方法，主要得到以下3点结论。
(1) 边界面塑性p-y曲线与Masing法则构造的API p-y滞回曲线形态相似，且骨干曲线的刚度衰减、滞回圈的阻尼比增加规律一致。
(2) 边界面塑性p-y模型保留了循环剪应力-应变关系的特征，通过模型4个参数的不同取值，能模拟不同非线性特性的单调p-y关系和循环荷载下桩土作用的滞回和软化特性，较2个参数的API p-y曲线具有更广的适应性。
(3) 对横向荷载作用下的桩土模型试验进行实例分析表明，边界面塑性p-y曲线计算结果和模型试验测试的非线性和滞回特性结果吻合较好。
-
![]()
图 2 从应力-应变曲线获取p-y曲线的比例方法
Figure 2. Scaling method for constructing p-y curve from shear stress-strain curve
![]()
图 4 边界面塑性p-y模型与API模型的刚度衰减曲线
Figure 4. Stiffness reduction of bounding surface plastic p-y curve and API model
![]()
图 5 采用Masing法则的API砂土p-y滞回曲线
Figure 5. API p-y hysteresis loop of sand using Masing rule
![]()
图 6 边界面塑性p-y模型与API模型的滞回圈
Figure 6. Hysteresis loop of bounding surface plastic p-y curve and API model
![]()
图 7 边界面塑性与API p-y模型的阻尼与位移幅值的关系
Figure 7. Damping ratio and displacement amplitudes relation for bounding surface plastic p-y curve and API model
![]()
图 8 p-y曲线法模拟侧向受荷桩计算模型图
Figure 8. Schematic of laterally loaded pile model in the p-y method
-
[1] AMERICAN PETROLEUM INSTITUTE. Recommended practice 2GEO/ISO 19901—4: Geotechnical and Foundation Design Considerations[S]. Washington: API Publishing Services, 2014.
[2] DET NORSKE VERITAS. Support Structures for Wind Turbines: DNVGL—ST—0126[S]. Oslo: Det Norske Veritas, 2018.
[3] REESE L C, IMPE W F V. Single Piles and Pile Groups under Lateral Loading[M]. London: Taylor & Francis Group, 2001.
[4] BOUAFIA A. Single piles under horizontal loads in sand: determination of P-Y curves from the prebored pressuremeter test[J]. Geotechnical and Geological Engineering, 2007, 25(3): 283-301 doi: 10.1007/s10706-006-9110-7
[5] 朱斌, 朱瑞燕, 罗军, 等. 海洋高桩基础水平大变位性状模型试验研究[J]. 岩土工程学报, 2010, 32(4): 521-530. http://cge.nhri.cn/cn/article/id/12426 ZHU Bin, ZHU Ruiyan, LUO Jun, et al. Model tests on characteristics of ocean and offshore elevated piles with large lateral deflection[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(4): 521-530. (in Chinese) http://cge.nhri.cn/cn/article/id/12426
[6] BOUZID D J, BHATTACHARYA S, DASH S R. Winkler Springs (p–y curves) for pile design from stress-strain of soils: FE assessment of scaling coefficients using the mobilized strength design concept[J]. Geomechnics and Engineering, 2013, 5(5): 379-399. doi: 10.12989/gae.2013.5.5.379
[7] VARDANEGA P J, BOLTON M D. Strength mobilization in clays and silts[J]. Canadian Geotechnical Journal, 2011, 48(10): 1485-1503. doi: 10.1139/t11-052
[8] LOMBARDI D, DASH S R, BHATTACHARYA S et al. A Construction of simplified design p-y curves for liquefied soils[J]. Géotechnique, 2016, 66(9): 115-127.
[9] 苏栋. 弹塑性p-y模型及非线性地基梁的增量有限元法[J]. 岩土工程学报, 2012, 34(8): 1469-1474. http://cge.nhri.cn/cn/article/id/14665 SU Dong. Elasto-plastic p-y model and incremental finite element method for beams on nonlinear foundation[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(8): 1469-1474. (in Chinese) http://cge.nhri.cn/cn/article/id/14665
[10] 黄茂松, 马昊, 李森, 等. 软黏土中水平受荷桩的静力和循环p-y曲线[J]. 岩土工程学报, 2017, 39(增刊2): 9-12. doi: 10.11779/CJGE2017S2003 HUANG Maosong, MA Hao, LI Sen, et al. Static and cyclic p-y curves for laterally loaded piles in soft clay[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(S2): 9-12. (in Chinese) doi: 10.11779/CJGE2017S2003
[11] ZHANG Y, ANDERSEN K H, JEANJEAN P, et al. Validation of a monotonic and cyclic p-y framework by lateral pile load tests in a stiff over-consolidated clay at the Haga site[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(9): 04020080. doi: 10.1061/(ASCE)GT.1943-5606.0002318
[12] WANG Z L, DAFALIAS Y F, SHEN C K. Bounding surface hypoplasticity model for sand[J]. Jouranl of Engineering Meachnics, 1990, 116(5): 983-1001.
[13] 李洪江, 刘松玉, 童立元. 基于应力增量的单桩p-y曲线分析方法[J]. 岩土力学, 2017, 38(10): 2916-2922, 2930. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201710020.htm LI Hongjiang, LIU Songyu, TONG Liyuan. A method for p-y curve of a single pile based on stress increment[J]. Rock and Soil Mechanics, 2017, 38(10): 2916-2922, 2930. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201710020.htm
[14] BRANSBY M F. Selection of p-y curves for the design of single laterally loaded piles[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1999, 23: 1909-1926. doi: 10.1002/(SICI)1096-9853(19991225)23:15<1909::AID-NAG26>3.0.CO;2-L
[15] KLAR A. Upper bound for cylinder movement using elastic fields and its possible application to pile deformation analysis[J]. International Journal of Geomechanics, 2008, 8(2): 162-167. doi: 10.1061/(ASCE)1532-3641(2008)8:2(162)
[16] OSMAN A S, BOLTON M D. Simple plasticity-based prediction of the undrained settlelment of shallow circular foundations on clay [J] Géotechnique, 2005, 55(6): 435-447.
[17] MARTIN C M, RANDOLPH M F. Upper bound analysis of lateral pile capacity in cohesive soil[J]. Géotechnique, 2006, 56(2): 141-145. doi: 10.1680/geot.2006.56.2.141
[18] RANDOLPH M F, GOURVENEC S. Offshore Geotechnical Engineering[M]. New York: Spon press, 2011
[19] PRASAD, Y S V, CHARI T R. Lateral capacity of model rigid piles in cohesionless soils[J]. Soils and Foundations, 1999, 39(2): 21-29. doi: 10.3208/sandf.39.2_21
[20] ROSQUOET F, THOREL L, GARNIER J, et al. Lateral cyclic loading of sand-installed piles[J]. Soils and Foundations, 2007, 47(5): 821-832.
下载:
计量
- 文章访问数: 119
- HTML全文浏览量: 13
- PDF下载量: 24
