水平荷载作用下饱和土与单桩的相互作用动力响应分析

曹小林; 周凤玺; 戴国亮

doi:10.11779/CJGE2023S20004

水平荷载作用下饱和土与单桩的相互作用动力响应分析 English Version

曹小林^{1, 2,},
周凤玺^{1, 2},
戴国亮³

1.
兰州理工大学土木工程学院, 甘肃兰州 730050
2.
兰州理工大学西部土木工程防灾减灾教育部工程研究中心, 甘肃兰州 730050
3.
东南大学土工程学院, 江苏南京 211189

基金项目:

国家自然科学基金项目 11962016

国家自然科学基金项目 51978320

兰州理工大学红柳优秀青年人才支撑计划项目

甘肃省高校教师创新技能基金项目

详细信息

作者简介:
曹小林(1990—)，男，讲师，硕士生导师，主要从事岩土工程方面的教学与科研工作。E-mail: xlcao@lut.edu.cn

中图分类号: TU43
计量
- 文章访问数: 150
- HTML全文浏览量: 42
- PDF下载量: 23
出版历程
- 收稿日期: 2023-11-29
- 网络出版日期: 2024-04-19
- 刊出日期: 2023-11-30

Dynamic response analysis of saturated soils and single pile under horizontal loads

CAO Xiaolin^{1, 2,},
ZHOU Fengxi^{1, 2},
DAI Guoliang³

1.
School of Civil Engineering, Lanzhou University of Technology, Lanzhou 730050, China
2.
Engineering Research Center of Disaster Mitigation in Civil Engineering of Ministry of Education, Lanzhou University of Technology, Lanzhou 730050, China
3.
School of Civil Engineering, Southeast University, Nanjing 211189, China

摘要

摘要: 为了研究饱和土的特性对桩的水平动力刚度的影响，建立了饱和土与桩的相互作用计算模型。首先，基于饱和多孔介质的Biot理论，考虑土体的竖向位移和竖向应变的存在，使用Helmholtz分解定律引入势函数，得到饱和土的位移和应力的解析解。其次，利用饱和土与桩的相互作用关系，建立桩-饱和土耦合的振动微分方程，进而得到桩的阻抗和阻尼的解析解。通过数值算例，与现有计算模型进行比较，验证了本文计算模型的结果；并通过参数分析，研究了饱和土的孔隙率、压缩系数和液体体积模量对桩头的动力阻抗及其对应的阻尼的影响。研究发现饱和土的孔隙率、压缩系数和液体体积模量对桩头的动力刚度及其对应的阻尼影响较大。
- 饱和土 /
- 水平振动 /
- 桩基础 /
- 动力刚度
Abstract: To study the influences of the characteristics of saturated soils on the horizontal dynamic impedance of a pile, a computational model for the interaction between the saturated soils and the pile is established. First, based on the Biot theory of saturated porous media, considering the existence of the vertical displacement and vertical strain of the soil, using the Helmholtz decomposition law to introduce a potential function, the analytical solutions for the displacement and stress of the saturated soils are obtained. Secondly, using the interaction between the saturated soils and the pile, the vibration differential equation for the pile-saturated soil coupling is established, and then the analytical solutions for the impedance and damping of the pile are obtained. Through a numerical example, compared with those of the existing models, the results of the proposed model are verified. Through the parameter analysis, the influences of porosity, compressibility, and liquid bulk modulus of the saturated soil on the dynamic impedance of the pile head are studied and its corresponding damping effects. It is found that the porosity, compressibility and liquid bulk modulus of the saturated soils have a great influence on the dynamic impedance of the pile head and its corresponding.
- saturated soil /
- horizontal vibration /
- pile foundation /
- dynamic impedance

HTML全文

0. 引言

桩作为上部结构的基础，受到各种动力荷载以及地震波的作用，动力荷载作用下，要求桩基础具有更高的承载能力；此外，当振动荷载的频率等于桩-土的自振频率后会产生共振，削弱桩-土刚度，使桩的承载性能降低。桩基础设计过程中，考虑动力荷载的存在至关重要。

为了明确水平动力荷载下桩在土中的振动响应，学者们做了大量的研究。目前，分析桩基础动力响应的经典模型主要有Winkler模型^[1]、平面应变模型^[2]和3D连续介质模型^[3]。基于上述研究成果，针对桩基础水平动力响应存在大量研究^[4-10]。上述理论研究均假定土体为单相介质，而在实际工程中，土体为三相介质，由土骨架、孔隙中的液体和空气组成，当孔隙中的空气中充满液体，则称为饱和土。基于Biot饱和多孔理论，基于Biot理论，针对不同的侧重点做了大量的研究，揭示饱和土与桩的相互动力作用规律^[11-15]。

考虑竖向位移和应变的存在，基于用Biot波动理论建立了桩-土相互作用计算模型，并通过公式推导得到了桩的水平动力阻抗的解析，其中阻抗的实部为桩的桩头刚度，虚部为阻尼。通过数值算例验证了计算模型的正确性，并分析了饱和土的参数对桩的水平动力阻抗的影响。

1. 计算模型

1.1 建立模型

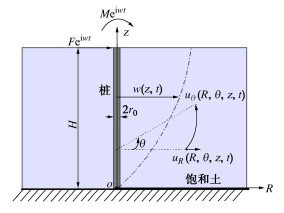
桩与饱和土的相互作用计算模型见图 1，采用柱坐标进行分析。桩半径为r₀，桩长为H，桩头受到水平力Fe^iωt或者力偶Me^iωt。t为时间变量，ω为动力荷载的圆频率， ${\text{i}} = \sqrt { - 1}$ 是虚数。桩与桩侧饱和土完全接触，考虑饱和土在桩的作用下产生的变形为小变形，界面之间满足力与位移协调。假定桩侧土为均质、各向同性的黏弹性材料。

图 1 计算模型示意图

Figure 1. Computational model

下载: 全尺寸图片幻灯片

1.2 饱和土的基本方程

根据Biot的理论，沿径向和切向方向作用在任意土体单元上的力的平衡表示为

$\frac{{\partial {\sigma _R}}}{{\partial R}} + \frac{{\partial {\tau _{Rz}}}}{{\partial z}} + \frac{1}{R}\frac{{\partial {\tau _{R\theta }}}}{{\partial \theta }} + \frac{{{\sigma _R} - {\sigma _\theta }}}{R} = {\rho _{\text{s}}}{\ddot u_R} + {\rho _{\text{f}}}{\ddot w_R} \text{，}$

(1)

$\frac{{\partial {\tau _{R\theta }}}}{{\partial R}} + \frac{{\partial {\tau _{\theta z}}}}{{\partial z}} + \frac{1}{R}\frac{{\partial {\sigma _\theta }}}{{\partial \theta }} + \frac{2}{R}{\tau _{R\theta }} = {\rho _{\text{s}}}{\ddot u_\theta } + {\rho _{\text{f}}}{\ddot w_\theta }\text{，}$

(2)

$- \frac{{\partial {p_{\text{f}}}}}{{\partial R}} = {\rho _{\text{f}}}{\ddot u_R} + {m_1}{\ddot w_R} + \frac{{{\rho _{\text{f}}}g}}{{{k_{\text{d}}}}}{\dot w_R}\text{，}$

(3)

$- \frac{{\partial {p_{\text{f}}}}}{{R\partial \theta }} = {\rho _{\text{f}}}{\ddot u_\theta } + {m_1}{\ddot w_\theta } + \frac{{{\rho _{\text{f}}}g}}{{{k_{\text{d}}}}}{\dot w_\theta }。$

(4)

对于含液饱和多孔均匀的各向同性介质，饱和土的本构关系可表示为

${\sigma _{ij}} = 2\mu {\varepsilon _{ij}} + (\lambda {\text{e}} - \alpha {p_{\text{f}}}){\delta _{ij}}\text{，}$

(5)

${p_{\text{f}}} = M(\zeta - \alpha {\text{e}})。$

(6)

式中：u_i = u_i(R, θ, z, t)和w_i = w_i(R, θ, z, t) 为土骨架和流体的位移(i, j = R, θ, z)。 ${\sigma _i}$ = ${\sigma _i}$ (R, θ, z, t)和 ${\tau _{ij}}$ = ${\tau _{ij}}$ (R, θ, z, t)分别为土骨架的正应力和剪应力。 $\lambda$ 和 $\mu$ 为拉梅常数。 ${\mu _{\text{s}}}$ =G_s(1+2iξ)； $\lambda$ =2 ${\mu _{\text{s}}}{\nu _{\text{s}}}$ /(1-2 ${\nu _{\text{s}}}$ )。G_s， ${\nu _{\text{s}}}$ 和ξ分别为土体的剪切模量、泊松比和阻尼比。 $\alpha$ 和M为Biot参数。 ${\rho _{\text{s}}}$ 和 ${\rho _{\text{f}}}$ 分别为固体和液体的密度。 ${p_{\text{f}}}$ 为孔隙压力。k_d为土体的达西渗透系数。

水平动力荷载作用下，桩的动力微分控制方程可以表示为

${E_{\text{p}}}{I_{\text{p}}}\frac{{{\partial ^4}{u_{\text{p}}}}}{{\partial {z^4}}} + {m_{\text{p}}}\frac{{{\partial ^2}{u_{\text{p}}}}}{{\partial {t^2}}} = - p(z, t)。$

(7)

式中： ${E_{\text{p}}}{I_{\text{p}}}$ 为桩的抗弯刚度； ${m_{\text{p}}}$ 为单位桩长的桩质量；p (z, t)是土体的侧向土抗力。

2. 饱和土与桩的水平振动求解

2.1 饱和土的水平振动

基于正应力 ${\sigma _z}$ 为零的假定，通过式（5）可得

$\left. \begin{array}{l}{\sigma }_{R}={\mu }_{\text{s}}\left[{\eta }_{\sigma }^{2}({\varepsilon }_{R}+{\varepsilon }_{\theta })-2{\varepsilon }_{\theta }\right]-\alpha \frac{1-2{\nu }_{\text{s}}}{1-{\nu }_{\text{s}}}{p}_{\text{f}}\text{ }\text{，}\\ {\sigma }_{\theta }={\mu }_{\text{s}}\left[{\eta }_{\sigma }^{2}({\varepsilon }_{R}+{\varepsilon }_{\theta })-2{\varepsilon }_{R}\right]-\alpha \frac{1-2{\nu }_{\text{s}}}{1-{\nu }_{\text{s}}}{p}_{\text{f}}\text{ }。\end{array} \right\}$

(8)

式中： $\eta _\sigma ^2 = \frac{2}{{1 - {\nu _{\text{s}}}}}$ 。将极坐标下的几何方程，式（5），式（8）代入方程（1），（2）可得

$\begin{array}{c} \eta _{\text{s}}^2\frac{\partial }{{\partial R}}\left[ {\frac{1}{R}\left( {\frac{{\partial (R{u_R})}}{{\partial R}} + \frac{{\partial {u_\theta }}}{{\partial \theta }}} \right)} \right] - \frac{1}{{{R^2}}}\frac{\partial }{{\partial \theta }}\left[ {\frac{{\partial (R{u_\theta })}}{{\partial R}} - \frac{{\partial {u_R}}}{{\partial \theta }}} \right] + \\ \frac{{{\partial ^2}{u_r}}}{{\partial {z^2}}}{\text{ + }}{\kappa _1}{\left( {\frac{\omega }{{{V_{\text{s}}}}}} \right)^2}{u_R} - {\kappa _2}\frac{{\partial {p_{\text{f}}}}}{{\partial R}} = 0 \text{，} \end{array}$

(9)

$\begin{array}{c} \frac{\partial }{{\partial R}}\left[ {\frac{1}{R}\left( {\frac{{\partial (R{u_\theta })}}{{\partial R}} - \frac{{\partial {u_R}}}{{\partial \theta }}} \right)} \right] + \eta _{\text{s}}^{\text{2}}\frac{1}{{{R^2}}}\frac{\partial }{{\partial \theta }}\left[ {\frac{{\partial (R{u_R})}}{{\partial R}} + \frac{{\partial {u_\theta }}}{{\partial \theta }}} \right] +\\ \frac{{{\partial ^2}{u_\theta }}}{{\partial {z^2}}}{\text{ + }}{\kappa _1}{\left( {\frac{\omega }{{{V_{\text{s}}}}}} \right)^2}{u_\theta } - {\kappa _2}\frac{{\partial {p_{\text{f}}}}}{{R\partial \theta }} = 0 。 \end{array}$

(10)

式中： ${\kappa _1} = 1{\text{ + }}\frac{{{\omega ^2}\rho _{\text{f}}^2}}{{{\rho _{\text{s}}}\vartheta }}$ ， ${\kappa _2} = \frac{\alpha }{{2{\mu _{\text{s}}}}}\frac{{1 - 2{\nu _{\text{s}}}}}{{1 - {\nu _{\text{s}}}}} + \frac{{{\rho _{\text{f}}}{\omega ^2}}}{{{\mu _{\text{s}}}\vartheta }}$ ， $\eta _{\text{s}}^2 =$ $\frac{{2 - {\nu _{\text{s}}}}}{{1 - {\nu _{\text{s}}}}}$ ； ${V_{\text{s}}} = \sqrt {{\mu _{\text{s}}}/{\rho _{\text{s}}}}$ 为土体的剪切波速。忽略流体的垂向位移，由式（6）可得如下表达式：

$\left(\frac{{\omega }^{2}{\rho }_{\text{f}}}{\vartheta }-\alpha \frac{1-2{\nu }_{\text{s}}}{1-{\nu }_{\text{s}}}\right)\left(\frac{\partial {u}_{R}}{\partial R}\text{+}\frac{{u}_{R}}{R}\text{+}\frac{1}{R}\frac{\partial {u}_{\theta }}{\partial \theta }\right)=\frac{{\nabla }^{2}{p}_{\text{f}}}{\vartheta }\text{+}\left(\frac{{\alpha }^{2}}{\lambda }\frac{{\nu }_{\text{s}}}{1-{\nu }_{\text{s}}}+\frac{1}{M}\right){p}_{\text{f}}。$

(11)

根据Helmholtz分解定律，通过方程（9），（10）和（11）可得

$\eta _{\text{s}}^{\text{2}}{\nabla ^2}\Phi + \frac{{{\partial ^2}\Phi }}{{\partial {z^2}}}{\text{ + }}{\kappa _1}{\left( {\frac{\omega }{{{V_{\text{s}}}}}} \right)^2}\Phi = {\kappa _2}{p_{\text{f}}} \text{，}$

(12)

${\nabla ^2}\varPsi + \frac{{{\partial ^2}\varPsi }}{{\partial {z^2}}}{\text{ + }}{\kappa _1}{\left( {\frac{\omega }{{{V_{\text{s}}}}}} \right)^2}\varPsi = 0 \text{，}$

(13)

${\nabla }^{2}{p}_{\text{f}}\text{+}\left(\frac{\vartheta {\alpha }^{2}}{\lambda }\frac{{\nu }_{\text{s}}}{1-{\nu }_{\text{s}}}+\frac{\vartheta }{M}\right){p}_{\text{f}}=\left({\omega }^{2}{\rho }_{\text{f}}-\alpha \vartheta \frac{1-2{\nu }_{\text{s}}}{1-{\nu }_{\text{s}}}\right){\nabla }^{2}\Phi \text{ }。$

(14)

式中： ${\nabla ^2}{\text{ = }}\frac{{{\partial ^2}}}{{\partial {R^2}}} + \frac{1}{R}\frac{\partial }{{\partial R}} + \frac{1}{{{R^2}}}\frac{{{\partial ^2}}}{{\partial {\theta ^2}}}$ ，将式（15）代入式（13）可得

${\nabla ^4}\Phi + {d_{11}}{\nabla ^2}\Phi + {d_{12}}\Phi {\text{ = }}0 。$

(15)

采用分离变量法通过式（14）可得

$\begin{array}{c} {\varPhi _{11}} = \left[ {{A_{11}}{{\text{I}}_n}({\zeta _{11}}R) + {B_{11}}{{\text{K}}_n}({\zeta _{11}}R)} \right]\left[ {{C_{11}}\sin (n\theta ) + {D_{11}}\cos (n\theta )} \right] \cdot \\ \left[ {{E_1}\cos (az) + {F_1}\sin (az)} \right] \text{，} \end{array}$

(16)

$\begin{array}{c} {\varPhi _{12}} = \left[ {{A_{12}}{{\text{I}}_n}({\zeta _{12}}R) + {B_{12}}{{\text{K}}_n}({\zeta _{12}}R)} \right]\left[ {{C_{12}}\sin (n\theta ) + {D_{12}}\cos (n\theta )} \right] \cdot \\ \left[ {{E_1}\cos (az) + {F_1}\sin (az)} \right] \text{，} \end{array}$

(17)

$\begin{array}{c} \varPsi = \left[ {{A_2}{{\text{I}}_n}({\zeta _2}R) + {B_2}{{\text{K}}_n}({\zeta _2}R)} \right]\left[ {{C_{11}}\sin (n\theta ) + {D_2}\cos (n\theta )} \right] \cdot \\ \left[ {{E_2}\cos (az) + {F_2}\sin (az)} \right] 。 \end{array}$

(18)

式中： $\varPhi = {\varPhi _{11}} + {\varPhi _{12}}$ ， $\zeta _{11}^{}$ ， $\zeta _{12}^{}$ ， $\zeta _{12}^{}$ ， ${\zeta _2}$ ， ${d_{11}}$ 和 ${d_{12}}$ 为常数。I_n()和K_n()为修正的第一类和第二类n阶Bessel函数，A₁₁, A₁₂, A₂, B₁₁, B₁₂, B₂, C₁₁, C₁₂, C₂, D₁₁, D₁₂, D₂, E₁, E₂, F₁和F₂为待定常数，通过边界条件得到。

考虑在距离桩无穷远处的土体位移为零，则I_n ()对应的系数须为零，即A₁₁= A₁₂ = A₂ = 0；考虑桩荷载方向沿θ=0，径向和切向位移分量必须满足条件 ${\left. {{u_R}} \right|_{\theta = {\text{π }}/2}} =$ ${\left. {{u_\theta }} \right|_{\theta = 0}} = 0$ ，即C₁₁=C₁₂=D₂=0，且n=0；土层底部固定无位移，土体表面无应力则使E₁ = E₂ =0，且cos(aH)= 0。由此可得

${\varPhi _m}{\text{ = }}\cos (\theta )\left[ {{B_{11m}}{{\text{K}}_1}({\zeta _{11m}}R) + {B_{12m}}{{\text{K}}_1}({\zeta _{12m}}R)} \right]\sin ({a_m}z) \text{，}$

(20)

${\varPsi _m}{\text{ = }}{B_{2m}}\sin (\theta ){{\text{K}}_1}({\zeta _{2m}}R)\sin ({a_m}z) \text{，}$

(21)

$a_m=\frac{(2 m-1) \pi}{2 H}, m=1, 2, 3, \cdots 。$

(22)

将式（20），（21）代入式（12）即可土体的位移如下所示：

$\begin{array}{l} {u_R} = \cos (\theta )\sum\limits_{m = 0}^\infty {\left[ { - {B_{11m}}\left( {{\zeta _{11m}}{{\text{K}}_0}({\zeta _{11m}}R){\text{ + }}\frac{{{{\text{K}}_1}({\zeta _{11m}}R)}}{R}} \right)} \right.}\\ -{B}_{12m}\left({\zeta }_{12m}{K}_{0}\text{(}{\zeta }_{12m}R\text{)+}\frac{{\text{K}}_{1}({\zeta }_{12m}R)}{r}\right)+{B}_{2m}\frac{{\text{K}}_{1}({\zeta }_{2m}R)}{R}]\mathrm{sin}({a}_{m}z)\text{，} \end{array}$

(23)

$\begin{array}{c} {u_\theta }{\text{ = sin(}}\theta {\text{)}}\sum\limits_{m = 0}^\infty {\left[ { - {B_{11m}}\frac{{{{\text{K}}_1}({\zeta _{11m}}R)}}{R} - {B_{12m}}\frac{{{{\text{K}}_1}({\zeta _{12m}}R)}}{R}} \right.} {\text{ + }}\\ \left. {{B_{2m}}\left( {{\zeta _{2m}}{{\text{K}}_0}({\zeta _{2m}}R){\text{ + }}\frac{{{{\text{K}}_1}({\zeta _{2m}}r)}}{R}} \right)} \right]\cos ({a_m}z) 。 \end{array}$

(24)

根据式（23），（24）可得到饱和土的径向位移和环向位移，借助结合几何方程和式（8）的本构关系即可求得饱和土体的应力和应变。

2.2 饱和土-桩耦合的水平振动

水平荷载作用下，桩产生水平变形，而土产生抗力阻止桩产生变形。抗力通过下式得到

$p(z, w) = - \int_0^{2{\text{π }}} {\left[ {{\sigma _R}({R_0})\cos \theta - {\tau _{R\theta }}({R_0})\sin \theta } \right]{R_0}} {\text{d}}\theta 。$

(25)

式中： ${\sigma _R}({R_0}) = {\sigma _R}({R_0}, \theta , z, \omega )$ 和 ${\tau _{R\theta }}({R_0}){\text{ = }}$ ${\tau _{R\theta }}({R_0}, \theta ,$ $z, \omega )$ 分别为土体桩身接触面上的正应力与剪应力。

将式（23），（24）得到的位移和环向位移与柱坐标的应变关系结合，通过本构关系即可得到

$p(z, w)=\text{π}\mu {\displaystyle \sum _{i=0}^{n}{R}_{m}}(\omega ){W}_{m}(\omega )=\text{π}\mu {\displaystyle \sum _{i=0}^{n}{R}_{m}}(\omega ){W}_{m}(\omega )\mathrm{sin}({a}_{m}z)。$

(26)

式中：R_m(ω)为饱和土的抗力系数。

将式（26）代入桩的振动微分方程式（7）可得

${E}_{\text{p}}{I}_{\text{p}}\frac{{\partial }^{4}U(z, \omega )}{\partial {z}^{4}}-{m}_{\text{p}}{\omega }^{2}U(z, \omega )=-\text{π}\mu {\displaystyle \sum _{i=0}^{n}{R}_{m}}(\omega ){W}_{m}(\omega )\mathrm{sin}({a}_{m}z)。$

(27)

式（27）的解可以分解为通解 ${U_{\text{h}}}$ 和特解 ${U_{\text{p}}}$ ，U= ${U_{\text{h}}}$ + ${U_{\text{p}}}$ 。通解的表达式为

${U_{\text{h}}} = E\sin \lambda z + F\cos \lambda z + G\sinh \lambda z + H\cosh \lambda z。$

(29)

取特解的表达式如下所示：

${U_{\text{p}}} = \sum\limits_{m = 1}^\infty {{p_m}} (\omega )\sin {a_m}z。$

(30)

将式（30）代入方程（28）可得p_m为

${p_m}(\omega ) = - {\text{π }}\mu \frac{{{R_m}(\omega ){W_m}(\omega )}}{{{E_{\text{p}}}{I_{\text{p}}}(a_m^4 - {\lambda ^4})}}。$

(31)

因此，桩身位移的幅值可表示为

$\begin{align} U(z, \omega )&{\text{ = }}A\sin \lambda z + B\cos \lambda z + C\sinh \lambda z + \\ &D\cosh \lambda z - {\text{π }}\mu \sum\limits_{m = 1}^\infty {\frac{{{R_m}(\omega ){W_m}(\omega )}}{{{E_{\text{p}}}{I_{\text{p}}}(a_m^4 - {\lambda ^4})}}} \sin {a_m}z。 \end{align}$

(32)

考虑饱和土与桩身完全接触，将sin $\lambda z$ ，cos $\lambda z$ ，sinh $\lambda z$ 和cosh $\lambda z$ 展开为自变量a_mz的傅里叶正弦级数，通过式（32）可得

${W_m}(\omega ) = \frac{{A{F_{1m}} + B{F_{2m}} + C{F_{3m}} + D{F_{4m}}}}{{\left[ {{\text{1 + }}{{{\text{π }}\mu {R_m}(\omega )} \mathord{\left/ {\vphantom {{{\text{π }}\mu {R_m}(\omega )} {{E_{\text{p}}}{I_{\text{p}}}(a_m^4 - {\lambda ^4})}}} \right. } {{E_{\text{p}}}{I_{\text{p}}}(a_m^4 - {\lambda ^4})}}} \right]}}。$

(33)

式中： ${F_{1m}}$ ， ${F_{2m}}$ ， ${F_{3m}}$ 和 ${F_{4m}}$ 为常数。将式（33）代入式（32）即可得到桩身位移的表达式为

$\begin{array}{l} U(z, \omega ) = A\left( {\sin \lambda z - \sum\limits_{m = 1}^\infty {{f_{1m}}} \sin {a_m}z} \right){\text{ + }}B\left( {\cos \lambda z - \sum\limits_{m = 1}^\infty {{f_{2m}}} \sin {a_m}z} \right){\text{ + }}\\ C\left( {\sinh \lambda z - \sum\limits_{m = 1}^\infty {{f_{3m}}} \sin {a_m}z} \right){\text{ + }}D\left( {\cosh \lambda z - \sum\limits_{m = 1}^\infty {{f_{4m}}} \sin {a_m}z} \right)。 \end{array}$

(34)

式（34）给出了桩的位移幅值，将桩的位移幅值带入位移幅值与转角幅值、弯矩幅值和剪力幅值之间的关系，即可得到转角幅值、弯矩幅值和剪力幅值的解析解，位移幅值与转角幅值、弯矩幅值和剪力幅值之间的关系如下所示：

$\left. \begin{array}{l}\varphi (z, \omega )=\frac{\text{d}U}{\text{d}z}\text{ }\text{，}\\ M(z, \omega )={E}_{\text{p}}{I}_{\text{p}}^{\text{s}}\frac{{\text{d}}^{2}U}{\text{d}{z}^{2}}\text{ }\text{，}\\ S(z)={E}_{\text{p}}{I}_{\text{p}}^{\text{s}}\frac{{\text{d}}^{3}U}{\text{d}{z}^{3}}\text{ }。\end{array} \right\}$

(35)

取桩头的位移和转角分别为 $W_{\text{0}}^{\text{s}}$ 和 $\varPsi _{\text{0}}^{\text{s}}$ 将式（34）代入式（35）可得

${\left[ B \right]_j} = {\left[ E \right]_j}{\left[ C \right]_j}。$

(36)

其中，[C]_j = [A_j B_j C_j D_j]，矩阵[B]_j = [ $W_{{\text{0}}j}^{\text{s}}\varPsi _{{\text{0}}j}^{\text{s}}$ 0 0]。通过式（36）可得

${\left[ C \right]_j}{\text{ = }}{\left[ E \right]_j}^{{\text{ - }}1}{\left[ B \right]_j}。$

(37)

转角为零的情况下，在桩头处施加一个单位水平位移，可得到水平荷载作用下桩的剪切刚度 $K_{S{\text{u}}}^{\text{s}}$ 和弯-剪动刚度 $K_{M{\text{u}}}^{\text{s}}$ 。转动角度为零的情况下，在桩头处施加一个单位旋转，我们可以得到弯曲刚度 $K_{M\varphi }^{\text{s}}$ 和弯-剪刚度 $K_{S\varphi }^{\text{s}}$ 。

通过下式对 $K_{S{\text{u}}}^{\text{s}}$ ， $K_{M{\text{u}}}^{\text{s}}$ ， $K_{M\varphi }^{\text{s}}$ 进行无量纲化，可得无量纲刚度和阻尼因子如下：

$K_{\text{h}}^{\text{s}} = \frac{{Re(K_{S{\text{u}}}^{\text{s}})}}{{{E_{\text{p}}}{r_0}}}\begin{array}{*{20}{c}} {}&{} \end{array}C_{\text{h}}^{\text{s}} = \frac{{{Im} (K_{S{\text{u}}}^{\text{s}})}}{{{E_{\text{p}}}{r_0}}}\text{，}$

(38)

$K_{\text{c}}^{\text{s}} = \frac{{Re(K_{M{\text{u}}}^{\text{s}})}}{{{E_{\text{p}}}r_0^3}}\begin{array}{*{20}{c}} {}&{} \end{array}C_{\text{c}}^{\text{s}} = \frac{{{Im} (K_{M{\text{u}}}^{\text{s}})}}{{{E_{\text{p}}}r_0^3}}\text{，}$

(39)

$K_{\text{r}}^{\text{s}} = \frac{{Re(K_{M\varphi }^{\text{s}})}}{{{E_{\text{p}}}r_0^2}}\begin{array}{*{20}{c}} {}&{} \end{array}C_{\text{r}}^{\text{s}} = \frac{{{Im} (K_{M\varphi }^{\text{s}})}}{{{E_{\text{p}}}r_0^2}} 。$

(40)

通过式（38），（39）和式（40）即可得到水平荷载作用饱和土-桩的无量纲化剪切刚度及其阻尼。

3. 数值算例及其结果分析

3.1 验证

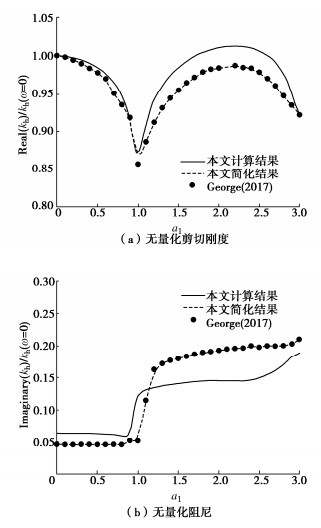
为了将本节得到的结果与Anoyatis等^[13]得到的结果进行比较，以桩端为铰接条件为例，取H = 40r₀，α = 0.9， ${\rho _{\text{s}}}$ = 2200 kg/m³， ${\rho _{\text{f}}}$ = 1000 kg/m³，G_s = 2.5 MPa，ξ = 0.01，v_s = 0.4，k_d = 1×10^-8 m/s，K_f = 33 MPa，K_s = 370 MPa。在分析中，频率通过a₁ = r₀ω / V_s转换为无量纲频率。

从图 2中可以发现，本文计算模型结果与Anoyatis等^[13]计算得到的无量化刚度和阻尼的结果总体趋势一致；将本文计算模型进行简化，其结果与Anoyatis等^[13]计算的结果完全一致，验证了本文计算结果的正确性。

图 2 本文模型与现有方法比较

Figure 2. Comparison between proposed model and existing method

下载: 全尺寸图片幻灯片

3.2 参数分析

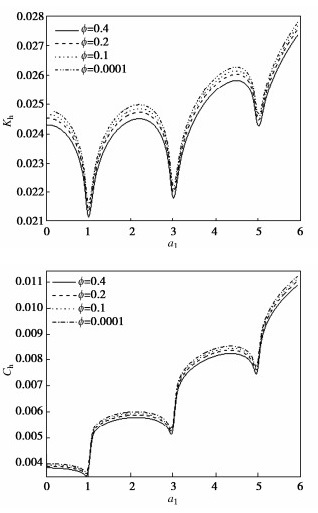
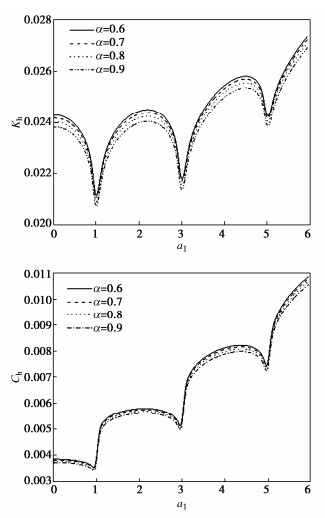
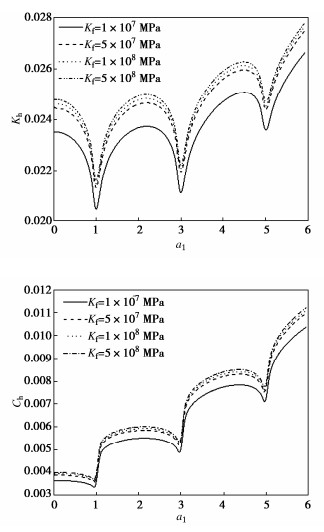
图 3~5给出了前3个共振区域（0 < ω < 6a₁），无量纲化刚度和阻尼随着无量纲化频率和饱和土参数的变化规律。以剪切刚度为例进行分析，由图 3~5发现它们的共同规律为：由于共振，剪切刚度在共振区域被削弱，而阻尼增加。

图 3 孔隙率对桩的剪切刚度和阻尼的影响

Figure 3. Influences of porosity on stiffness and damping of pile head during swaying

下载: 全尺寸图片幻灯片

图 4 压缩系数对桩的剪切刚度和阻尼的影响

Figure 4. Influences of compression coefficient on stiffness and damping of pile head during swaying

下载: 全尺寸图片幻灯片

图 5 液体体积模量对桩的剪切刚度和阻尼的影响

Figure 5. Influences of bulk modulus of interstitial fluid on stiffness and damping of pile head during swaying

下载: 全尺寸图片幻灯片

图 3给出了饱和土的孔隙率对桩的剪切刚度和阻尼的影响。从图中可以发现，随着饱和土孔隙率的增加，桩剪切刚度降低。共振前随着孔隙率的增大，阻尼减小。在共振区域，随着无量钢化频率的增大，阻尼突然增大然后保持稳定。

压缩系数对桩的剪切和对应阻尼的影响如图 4所示。从图中可以发现，随着饱和土压缩系数的增加，桩的剪切刚度减小。随着孔隙率的增大，桩头阻尼减小。

图 5给出了饱和土的液体体积模量对桩的剪切刚度和对应的阻尼的影响规律。随着液体体积模量的增大，桩的剪切刚度增大，同时阻尼也随着液体体积模量的增大而增大。

4. 结论

本文推导了水平动力合作作用下饱和土-桩相互作用的分析模型。基于流体饱和多孔介质的Biot模型，给出了桩的剪切刚度和对应的阻尼的解析解。通过对比现有计算模型来验证本文结果的正确性，主要得到以下4点结论。

（1）由于共振，剪切刚度在共振区域被削弱，而共振区域的阻尼增加。刚度和阻尼的变化规律可以很好地反映共振对桩的刚度和阻尼的影响。

（2）在饱和土中，随着孔隙率的降低，压缩系数和液体体积模量的增加，桩剪切刚度增加。

（3）在饱和土中，共振前剪切阻尼随着频率的增加而增加的较小。在共振区域，桩的剪切阻尼突然增加，随后并保持较小的增大，直到下一次共振。

（4）随着饱和土的孔隙率的减小、压缩系数和间隙流体体积模量的增大，桩的剪切阻尼减小。

图 1 计算模型示意图

Figure 1. Computational model

下载: 全尺寸图片幻灯片

图 2 本文模型与现有方法比较

Figure 2. Comparison between proposed model and existing method

下载: 全尺寸图片幻灯片

图 3 孔隙率对桩的剪切刚度和阻尼的影响

Figure 3. Influences of porosity on stiffness and damping of pile head during swaying

下载: 全尺寸图片幻灯片

图 4 压缩系数对桩的剪切刚度和阻尼的影响

Figure 4. Influences of compression coefficient on stiffness and damping of pile head during swaying

下载: 全尺寸图片幻灯片

图 5 液体体积模量对桩的剪切刚度和阻尼的影响

Figure 5. Influences of bulk modulus of interstitial fluid on stiffness and damping of pile head during swaying

下载: 全尺寸图片幻灯片

参考文献(13)

[1]	YAO S, NOGAMI T. Lateral cyclic response of pile in viscoelastic winkler subgrade[J]. J Eng Mech, ASCE, 1994(120): 758-775.
[2]	NOVAK M, ABOUL-ELLA F, NOGAMI T J J o t E M D. Dynamic soil reactions for plane strain case[J]. Journal of the Engineering Mechanics Division, 1978(104): 953-959.
[3]	GAZETAS G, DOBRY R. Simple radiation damping model for piles and footings[J]. J Eng Mech, ASCE, 1984(110): 937-956.
[4]	庄海洋, 赵畅, 于旭, 等. 液化地基上隔震结构群桩与土动力相互作用振动台模型试验研究[J]. 岩土工程学报, 2022, 44(6): 979-987. doi: 10.11779/CJGE202206001 ZHUANG Haiyang, ZHAO Chang, YU Xu, et al. Earthquake responses of piles-soil dynamic interaction system for base-isolated structure system based on shaking table tests[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(6): 979-987. (in Chinese) doi: 10.11779/CJGE202206001
[5]	张小玲, 赵景玖, 孙毅龙, 等. 基于圆孔扩张理论的桩基水平承载力计算方法[J]. 工程力学, 2021, 38(2): 232-241, 256. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202102025.htm ZHANG Xiaoling, ZHAO Jingjiu, SUN Yilong, et al. An analysis method for the horizontal bearing capacity of pile foundation based on the cavity expansion theory[J]. Engineering Mechanics, 2021, 38(2): 232-241, 256. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202102025.htm
[6]	梁发云, 袁强, 李家平, 等. 堆载作用下土体分层特性对地铁隧道纵向变形的影响研究[J]. 岩土工程学报, 2020, 42(1): 63-71. doi: 10.11779/CJGE202001007 LIANG Fayun, YUAN Qiang, LI Jiaping, et al. Influences of soil characteristics on longitudinal deformation of shield tunnels induced by surface surcharge[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(1): 63-71. (in Chinese) doi: 10.11779/CJGE202001007
[7]	赵密, 黄义铭, 王丕光, 等. 桩顶水平动荷载作用下水-桩-土相互作用的解析解[J]. 岩土工程学报, 2022, 44(5): 907-915. doi: 10.11779/CJGE202205014 ZHAO Mi, HUANG Yiming, WANG Piguang, et al. Analytical solution of water pile soil interaction under horizontal dynamic load at pile top[J]. Journal of Geotechnical Engineering, 2022, 44(5): 907-915. (in Chinese) doi: 10.11779/CJGE202205014
[8]	崔春义, 辛宇, 许成顺, 等. Pasternak层状地基中群桩水平动力响应解析解答[J]. 岩土工程学报, 2023, 45(5): 893-902. doi: 10.11779/CJGE20220235 CUI Chunyi, XIN Yu, XU Chengshun, et al. Analytical solution of horizontal dynamic response of pile groups in Pasternak layered foundation[J]. Journal of Geotechnical Engineering, 2023, 45(5): 893-902. (in Chinese) doi: 10.11779/CJGE20220235
[9]	陆建飞. 频域内半空间饱和土中水平受荷桩的动力分析[J]. 岩石力学与工程学报, 2002, 21(4): 577-581. doi: 10.3321/j.issn:1000-6915.2002.04.026 LU Jianfei. Dynamic frequency domain analysis on laterally loaded pile in saturated soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(4): 577-581. (in Chinese) doi: 10.3321/j.issn:1000-6915.2002.04.026
[10]	余俊, 尚守平, 李忠, 等. 饱和土中端承桩水平振动动力响应分析[J]. 岩土工程学报, 2009, 31(3): 408-415. doi: 10.3321/j.issn:1000-4548.2009.03.017 YU Jun, SHANG Shouping, LI Zhong et al. Dynamic response analysis of horizontal vibration of middle-end bearing piles in saturated soil[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(3): 408-415. (in Chinese) doi: 10.3321/j.issn:1000-4548.2009.03.017
[11]	ZHENG C, LIU H, DING X, et al. Torsional dynamic response of a large-diameter pipe pile in viscoelastic saturated soil[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015(38): 1724-1743.
[12]	DING X, LUAN L, ZHENG C, et al. Influence of the second-order effect of axial load on lateral dynamic response of a pipe pile in saturated soil layer[J]. Soil Dynamics and Earthquake Engineering, 2017, 103: 86-94.
[13]	ANOYATIS G, LEMNITZER A. Dynamic pile impedances for laterally-loaded piles using improved Tajimi and Winkler formulations[J]. Soil Dynamics and Earthquake Engineering, 2017(92): 279-297.