空沟-波阻板联合隔振屏障的试验研究与数值分析

周凤玺; 周志雄; 梁玉旺; 刘佳; 马强

doi:10.11779/CJGE2023S20001

空沟-波阻板联合隔振屏障的试验研究与数值分析 English Version

周凤玺^1,,
周志雄^1, ,,
梁玉旺¹,
刘佳¹,
马强²

1.
兰州理工大学土木工程学院, 甘肃兰州 730050
2.
青海大学土木工程学院, 青海西宁 810016

基金项目:

国家自然科学基金项目 12362032

国家自然科学基金项目 51978320

甘肃省重点研发计划项目 23YFFA0063

详细信息

作者简介:
周凤玺(1979—)，男，博士，教授，主要从事岩土力学、结构振动方面的研究工作。E-mail: geolut@163.com

通讯作者:
周志雄, E-mail: zzx_0603@163.com

中图分类号: TU435
计量
- 文章访问数: 117
- HTML全文浏览量: 24
- PDF下载量: 18
出版历程
- 收稿日期: 2023-11-29
- 网络出版日期: 2024-04-19
- 刊出日期: 2023-11-30

Experimental research and numerical analysis of an open Trench-WIB barrier

1.
School of Civil Engineering, Lanzhou University of Technology, Lanzhou 730050, China
2.
School of Civil Engineering, Qinghai University, Xining 810016, China

摘要

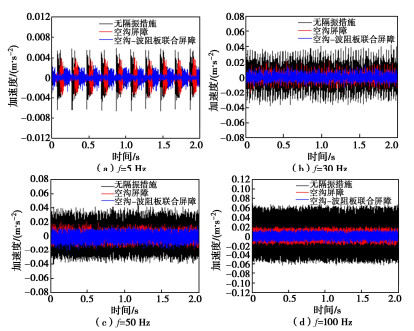
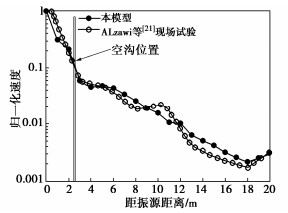
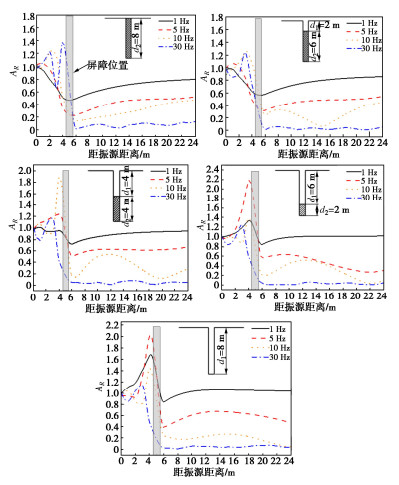
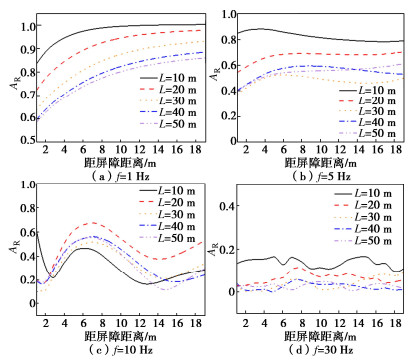
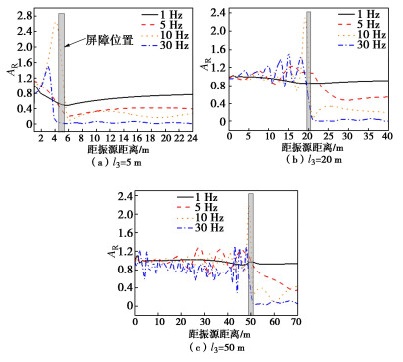
摘要: 采用模型试验和数值模拟相结合的方法研究了空沟-波阻板联合隔振屏障对竖向简谐荷载的隔振效果。首先，对比了空沟-波阻板联合屏障与空沟屏障的隔振效果，试验结果表明：空沟-波阻板联合屏障在各个激振频率下的隔振效果均优于空沟屏障，在低频段最为明显。然后，结合完全匹配层吸收边界，利用COMSOL建立了简谐荷载作用下弹性半空间中设置空沟-波阻板联合隔振屏障的三维有限元模型，并通过加速度振幅衰减系数来评价隔振效果，研究了空沟-波阻板联合屏障的几何参数对其隔振效果的影响。结果表明：空沟-波阻板联合屏障的几何参数对其隔振效果影响较大。其中，空沟深度越大，隔振效果越好，但在频率较低时有所不同；波阻板深度以及屏障长度越大，联合屏障的隔振效果越好。此外，空沟-波阻板联合屏障更适用于近场主动隔振。
- 地基隔振 /
- 空沟-波阻板联合屏障 /
- 模型试验 /
- 相似理论 /
- 数值模拟
Abstract: The vibration isolation effects of an open trench-WIB barrier on the vertical harmonic loads are studied by using the combined method of model tests and numerical simulations. Firstly, the vibration isolation effects of the open trench-WIB barrier and the open trench are compared. The experimental results show that the vibration isolation effects of the combined barrier are better than those of the open trench barrier at each excitation frequency and the most obvious in the low frequency. Then, combined with the perfectly matched layer absorption boundary, a three-dimensional finite element model is established using the COMSOL to set up the open trench-WIB barrier in an elastic half space under harmonic loads. The vibration isolation effects are evaluated through the acceleration amplitude attenuation coefficient, and the influences of the geometric parameters of the combined barrier on the isolation effects are studied. The results show that the geometric parameters of the combined barrier have a great influence on the vibration isolation effects. The larger the depth of the open trench, the better the isolation effects, but different in the low frequency. Meanwhile, the larger the depth and length of the WIB, the better the vibration isolation effects of the combined barrier. Moreover, the open trench-WIB barrier is more suitable for the near-field active vibration isolation.
- vibration isolation of foundation /
- open trench-WIB barrier /
- model test /
- similarity theory /
- numerical simulation

HTML全文

0. 引言

非饱和状态下的土体具有很高的强度^[1]，然而遇水湿化强度会迅速降低，局部可能达到饱和，该状态下的土压力值与非饱和条件下的值差别很大。多名学者统计显示大部分基坑事故都与水有关，此外，2019年6月8日南宁绿地中心基坑塌陷也是因为场地管道爆裂，非饱和土遇水湿化，作用在支护结构的土压力增大^[2]。因此，亟需定量评估浸湿作用对非饱和土侧向土压力的影响，提出计算方法，减少此类事故发生。

目前，对非饱和土压力研究获得了很大进展，但现有研究多从理论出发进行公式推导，1961年Coleman等^[3]提出双变量理论，Fredlund便得到净应力与吸力的双变量理论，之后得到了扩展的朗肯土压力理论，但是在平时的设计和研究中，仍然采用朗肯土压力理论^[4]计算非饱和土压力。姚攀峰等^[5]提出了与扩展型朗肯土压力不同的计算方法广义朗肯土压力计算方法，陈铁林等^[6]解决水位变化及降水条件下的土压力计算问题，根据K₀定义推导K₀求解式。任传健等^[7]结合Fredlund非饱和土抗剪切与强化准则和经典的朗肯土压计算公式，得出考虑降水变化的土压计算公式。汪丁建等^[8]在饱和土朗肯土压力分析基础上，推导出降雨条件下非饱和朗肯土压力。王晓亮等^[9]将降雨和蒸发对基质吸力的影响引入到非饱和土抗剪强度公式中，得到K₀随降雨定性变化，但没有定量结果。

已有的大量研究充分表明水对静止土压力的影响不可忽略，但已有的计算公式复杂不实用，结果有待验证。导致现有非饱和土体仍采用饱和土理论的计算结果加安全储备来设计计算^[10]，安全系数是否足够不明确。为了使湿化条件下静止土压力增量的演化规律更明确，本文通过室内试验确定了其相关的变化规律、建立相应的计算模型，减小对安全施工的威胁。

1. 试验材料与方法

1.1 土料特性

取北京延庆地区原状粉质黏土进行烘干、碾碎、过0.25 mm筛备用，进行基本物理性质测试，依据《土工试验方法标准：GB/T50123—2019》^[11]，结果见表 1。

表 1 土的基本物理性质

Table 1. Basic physical properties of soil

最大干密度/ (g·cm^-3)	最优含水率/%	液限 w_L/%	塑限w_P/%	塑性指数I_P	土粒相对密度G_S
1.80	16.5	30.7	15.2	15.5	2.73

下载: 导出CSV

| 显示表格

1.2 试验方案

选择干密度1.53 g/cm³（压实度0.85）、高度40 mm的标准环刀试样开展K₀压缩试验，设5个不同的初始饱和度与4个不同的上覆荷载，具体方案见表 2。

表 2 浸水条件下非饱和粉质黏土试验方案

Table 2. Test schemes under water immersion conditions

上覆荷载/kPa	加载过程	初始饱和度
100/200/ 300/400	100(200/300/400)kPa→湿化→逐级加载至1600kPa	0.2/0.3/0.4/ 0.5/0.6

下载: 导出CSV

| 显示表格

1.3 试验过程

（1）仪器标定。本文采用JCY型K₀固结仪来完成K₀压缩试验，在气囊中充入与试样等体积的水，利用水各向等压特性标定仪器在竖向压力下对土压力的测量，根据试验数据拟合得到两仪器的标定系数^[12]。

（2）制样并养护得到不同初始含水率试样。用饱和再风干的土样模拟经过了干湿循环的天然非饱和土，通过7 d密闭养护保证孔隙水分布均匀，见图 1。

图 1 准备不同初始含水率的试样

Figure 1. Preparation of samples with different initial moisture contents

下载: 全尺寸图片幻灯片

（3）加上覆荷载待稳定后进行湿化饱和，湿化稳定后养护7 d，再完成后续设定加载至试验结束。

（4）卸压并整理仪器装置，将不同初始饱和度湿化前与湿化压缩后试样进行对比，如图 2所示。

图 2 试验前后对比图

Figure 2. Comparison of soil samples before and after tests

下载: 全尺寸图片幻灯片

2. 试验结果及规律

K₀固结仪连接压力传感器采集数据，得到侧压力随时间变化关系^[12]，从而得到粉质黏土在5个不同初始饱和度S_r和4个不同上覆荷载P作用下发生湿化与湿化后继续加载的水平静止土压力-竖向压力的关系曲线，见图 3，因篇幅关系只展示S_r=0.2结果^[12]。对于非饱和土一般采用水土合算计算土压力，此时侧压力传感器测量得到的相当于水土合算下的土压力。

图 3 静止土压力随竖向压力变化关系(S_r=0.2)

Figure 3. Variation of static earth pressure with vertical pressure (S_r=0.2)

下载: 全尺寸图片幻灯片

湿化静止土压力增量 $\Delta {\sigma _{{\text{h}}}}$ 统计见表 3，计算式为

$\Delta {\sigma _{{\text{h}}}} = {\sigma _{{\text{w}}}} - {\sigma _{{\text{d}}}} 。$

(1)

表 3 湿化静止土压力增量计算值统计

Table 3. Statistics of calculated increment static earth pressure

初始饱和度S_r	0.2	0.3	0.4	0.5	0.6
100 kPa下增量值	35.14	25.10	17.41	12.5	3.53
200 kPa下增量值	68.95	48.38	33.32	22.97	6.31
300 kPa下增量值	95.01	68.95	47.86	29.99	8.98
400 kPa下增量值	118.02	90.00	60.99	35.97	10.11

下载: 导出CSV

| 显示表格

式中： ${\sigma _{{\text{d}}}}$ 为上覆荷载作用下湿化前静止土压力大小； ${\sigma _{{\text{w}}}}$ 湿化饱和后静止土压力大小。

3. 静止土压力增量计算模型

3.1 湿化过程中静止土压力演变规律

不同初始饱和度湿化过程的增湿水平不同，可使用湿化前初始饱和度表示增湿水平，即：S_r=1的增湿水平为0，S_r越小增湿水平越大。

由表 3可以看到湿化时静止土压力都有不同程度的增大，且初始饱和度S_r越低或上覆荷载P越大，静止土压力增量越大。图 3数据显示，湿化后继续加载呈线性且斜率基本一致，表明K₀值大小近似一致，S_r与P的不同不会影响湿化饱和后K₀大小。可能原因是：静止土压力系数主要由有效内摩擦角决定，饱和后有效内摩擦角接近，因此湿化饱和后K₀近似一致。

土体强度理论认为土颗粒间存在综合作用，包括吸力、胶结作用、德华力以及化学键等^[4]，非饱和土研究学者^[13]一般认为土骨架受压为保证完整性依靠两部分力平衡：一是土颗粒间的基质吸力，取决于土体的含水量；另外是土颗粒间的胶结力，取决于土体内部的黏粒微量物质。静止土压力增量是由颗粒间胶结作用的减弱和基质吸力减小两方面原因引起的^[14]。为推导计算模型引出中间变量0.65-S_r，如图 4所示，初始饱和度越小，湿化导致基质吸力减少量就越大，静止土压力增量就越大；湿化饱和后上覆荷载越大，对土体胶结力破坏就越大，如图 5所示，湿化饱和后的静止土压力增量，随上覆荷载增加而变大。

图 4 静止土压力增量与初始饱和度关系

Figure 4. Variation of increment of static earth pressure increment with initial saturation

下载: 全尺寸图片幻灯片

图 5 静止土压力增量与上覆荷载关系

Figure 5. Variation of increment of static earth pressure with load

下载: 全尺寸图片幻灯片

3.2 湿化过程中静止土压力增量计算模型

土压力增量 $\Delta {\sigma _{{\text{h}}}}$ 与上覆荷载P，初始饱和度S_r都呈线性关系，双线性模型见式（2），P和S_r确定时有一次函数式（3），（4）。当变量 $n=（{S}_{\text{r}}{\text{+}}{b}_{1}）{\text{=0}}{\text{.65}}-{S}_{{\text{r}}}$ 时，土压力增量 $\Delta {\sigma _{{\text{h}}}}$ 与n成正比例， ${k_1}{k_2}m$ 为斜率，见图 4。

$\Delta {\sigma _{{\text{h}}}} = {k_1}n \times {k_2}m {\text{，}}$

(2)

${k}_{1}n={k}_{1}（{S}_{{\text{r}}}{\text{+}}{b}_{1}） {\text{，}}$

(3)

${k}_{2}m={k}_{2}（P{\text{+}}{b}_{2}）。$

(4)

P与其对应的 ${k_1}{k_2}m$ 拟合得 ${k_1}{k_2}m{{\text{ = 0}}}{{\text{.60}}}P + {{\text{19}}}{{\text{.76}}}$ ，再将 $n$ 代入式（2）中，得到式（5）。当初始饱和度S_r较大接近饱和土时，静止土压力增量为0，观察式（5），当饱和度S_r＞0.65时，湿化不会引起静止土压力增加。

$\Delta {\sigma _{{\text{h}}}} = \left\{ \begin{array}{l} (0.60P{{\text{ + 19}}}{{\text{.76}}}){{\text{(}}}0.65 - {S_{{\text{r}}}}{{\text{)}}} \;\;\;\;{{\text{(}}}{S_{{\text{r}}}} \leqslant 0.65{{\text{)}}} \hfill \\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\text{ (}}}{S_{{\text{r}}}} > 0.65{{\text{)}}} \hfill \\ \end{array} \right. 。$

(5)

为了更直观的表现增量的含义，将 $\Delta {S_{{\text{r}}}} = 1 - {S_{{\text{r}}}}$ 代入式（5），得到最终的增量表达式如下：

$\begin{equation} \Delta \sigma_{\mathrm{h}}=\left\{\begin{array}{ll} (0.60 P+19.76)\left(\Delta S_{\mathrm{r}}-0.35\right) & \left(\Delta S_{\mathrm{r}} \geqslant 0.35\right) \\ 0 & \left(\Delta S_{\mathrm{r}}<0.35\right) \end{array}\right. 。 \end{equation}$

(6)

4. 挡土墙静止土压力计算案例分析

以延庆某深基坑为背景，结合勘察数据，对上文的模型进行试算。该基坑开挖深度23 m，上表面有8 kPa的均布荷载，施工阶段饱和度0.25，已勘测到自然地面以下34 m地层特性，土体基本为粉质黏土。

根据划分土层的重度与厚度计算出土层下表面荷载，并根据K₀算出湿化前静止土压力 ${\sigma _{{\text{h}}}}_i$ ，K₀按经验值取0.3。根据式（6）算出静止土压力增量 $\Delta {\sigma _{{\text{h}}}}_i$ ，接着计算出湿化后静止土压力 ${\sigma _{{\text{w}}}}_i$ 和 ${\sigma _{{\text{w}}}}_i$ / ${\sigma _{{\text{h}}}}_i$ 比值，计算值随深度变化绘制在图 6中，发现比值随深度增大而减小，但始终大于1.8，说明湿化对静止土压力影响较大。

图 6 不同累计深度处静止土压力与其相关计算值关系

Figure 6. Static earth pressures and their correlation with depth

下载: 全尺寸图片幻灯片

由于本文采用重塑土进行试验，和天然土体湿化时侧压力变化结果不同，特别是黄土等结构性非饱和土，其湿化可能发生湿陷等行为，导致土压力演化较为复杂。本文研究结果仅适用于非结构性的非饱和土。

5. 结论

本文通过开展室内试验，定量评估浸湿作用对非饱和土侧向土压力的影响，实测浸湿饱和作用下静止土压力增量的变化规律，建立相应的计算模型，通过应用发现设计时必须重视湿化的影响，并得到以下3点结论。

（1）湿化饱和后，土体的静止土压力系数K₀值与初始饱和度、上覆荷载无关。推测土体静止土压力系数K₀值主要由有效内摩擦角决定，饱和后有效内摩擦角基本一致，故K₀值大小近似一致。

（2）湿化前的初始饱和度越低，湿化饱和后的静止土压力增量越大；且湿化饱和后的静止土压力增量，随湿化时的上覆荷载增加而变大。

（3）基于试验数据和机理分析，得到了湿化条件下考虑上覆荷载与初始饱和度的双线性土压力增量计算模型；将其应用于某支挡工程，发现湿化后的土压力可达初始土压力1.8倍以上，设计时必须予以重视。

图 1 试验仪器

Figure 1. Test instruments

下载: 全尺寸图片幻灯片

图 2 模型试验布置图

Figure 2. Layout of model tests

下载: 全尺寸图片幻灯片

图 3 不同频率下地表振动加速度时程曲线

Figure 3. Time-history curves of surface vibration acceleration at different frequencies

下载: 全尺寸图片幻灯片

图 4 有限元模型示意图

Figure 4. Schematic diagram of finite element model

下载: 全尺寸图片幻灯片

图 5 退化模型验证

Figure 5. Verification of degradation model

下载: 全尺寸图片幻灯片

图 6 相对深度对隔振效果的影响

Figure 6. Effects of relative depth on vibration isolation

下载: 全尺寸图片幻灯片

图 7 屏障长度对隔振效果的影响

Figure 7. Effects of barrier length on vibration isolation

下载: 全尺寸图片幻灯片

图 8 屏障距振源距离对隔振效果的影响

Figure 8. Effects of distance between barrier and vibration source on vibration isolation

下载: 全尺寸图片幻灯片

表 1 物理参数的模型缩放

Table 1 Model scaling of physical parameters

参数	相似系数	模型/原型
几何尺寸	$\lambda_l$	1/20
密度	$\lambda_\rho$	1/1
弹性模量	$\lambda_E$	1/20
外力	$\lambda_F=\lambda_E \cdot \lambda_l \cdot \lambda_u$	1/8000
应变	$\lambda_{\varepsilon}=\lambda_l \cdot \lambda_\rho \cdot \lambda_E^{-1}$	1/1
应力	$\lambda_\sigma=\lambda_E \cdot \lambda_{\varepsilon}$	1/20
加速度	$\lambda_a=a_m / a_p$	1/1
速度	$\lambda_v=\lambda_E^{0.5} \cdot \lambda_\rho^{-0.5}$	1/4.47
位移	$\lambda_u=\lambda_l \cdot \lambda_{\varepsilon}$	1/20
动力时间	$\lambda_t=\lambda_l \cdot \lambda_\rho^{0.5} \cdot \lambda_E^{-0.5}$	1/4.47
频率	$\lambda_\omega=\lambda_t^{-1}$	1/0.224

下载: 导出CSV

表 2 土的物理力学参数

Table 2 Physical and mechanical parameters of soils

项目	${\rho _{\text{s}}}$ /(kg·m^-3)	${E_{\text{s}}}$ /MPa	${G_{\text{s}}}$ /MPa	${\nu _{\text{s}}}$
原型	2000	60	23.08	0.3
模型	2000	3	1.15	0.3

下载: 导出CSV

表 3 波阻板的物理力学参数

Table 3 Physical and mechanical parameters of WIB

项目	${\rho _{\text{w}}}$ /(kg·m^-3)	${E_{\text{w}}}$ /GPa	${G_{\text{w}}}$ /GPa	${\nu _{\text{w}}}$
原型	2400	30	11.54	0.3
模型	2400	1.5	0.58	0.3

下载: 导出CSV

表 4 模型试验方案设计

Table 4 Plan for model tests

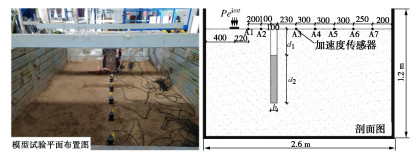
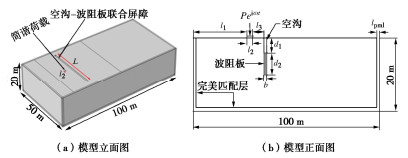
工况	工况编号	空沟深度d₁/cm	波阻板深度d₂/cm	屏障厚度b/cm	屏障长度L/cm
无隔振	1	0	0	0	0
空沟屏障	2	30	0	10	80
联合屏障	3	30	40	10	80

下载: 导出CSV

表 5 物理力学性质

Table 5 Physical and mechanical characteristics

参数	E_s/(kN·m^-2)	${\nu _{\text{s}}}$	ρ_s/(kg·m^-3)	E_w/(kN·m^-2)	${\nu _{\text{w}}}$	${\rho _{\text{w}}}$ /(kg·m^-3)	ξ
量值	5.0×10⁴	0.3	2000	5.0×10⁷	0.3	2700	0.05

下载: 导出CSV

参考文献(21)

[1]	徐平, 周新民, 夏唐代. 应用屏障进行被动隔振的研究综述[J]. 地震工程学报, 2015, 37(1): 88-93. https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ201501015.htm XU Ping, ZHOU Xinmin, XIA Tangdai. Review on passive vibration isolation using barriers[J]. China Earthquake Engineering Journal, 2015, 37(1): 88-93. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ201501015.htm
[2]	杨先健. 工业环境振动中的土动力学问题[J]. 岩土工程学报, 1992, 114(2): 82-88. http://cge.nhri.cn/cn/article/id/9570 YANG Xianjian. Soil dynamics problems in industrial environment vibration[J]. Chinese Journal of Geotechnical Engineering, 1992, 114(2): 82-88. (in Chinese) http://cge.nhri.cn/cn/article/id/9570
[3]	WOODS R D. Screening of surface wave in soils[J]. Journal of the Soil Mechanics and Foundations Division, 1968, 94: 951-980. doi: 10.1061/JSFEAQ.0001180
[4]	KLEVIN R, ANTES H, LE HOUE'DEC D. Efficient 3D modelling of vibration isolation by open trenches[J]. Computers and Structures, 1997, 64(1-4): 809-817. doi: 10.1016/S0045-7949(96)00418-X
[5]	HASAN A A, HAIDER S A, JAAFAR K A. An experimental study on vibration isolation by open and in-filled trenches[J]. Open Engineering, 2022, 12(1): 555-569. doi: 10.1515/eng-2022-0011
[6]	孙立强, 李嘉, 刘彬, 等. 空沟、碎石填充沟和排桩隔振效果试验研究[J]. 地震工程学报, 2015, 37(2): 342-348. https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ201502010.htm SUN Liqiang, LI Jia, LIU Bin, et al. Experimental study on vibration-isolation effects of open trench, gravel-filled trench, and piles in a row[J]. China Earthquake Engineering Journal, 2015, 37(2): 342-348. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ201502010.htm
[7]	TAKEMIYA H. Field vibration mitigation by honeycomb WIB for pile foundations of a high-speed train viaduct[J]. Soil Dynamics and Earthquake Engineering, 2004, 24(1): 69-87. doi: 10.1016/j.soildyn.2003.07.005
[8]	李宁, 高广运, 郑建国. 水平激振下波阻板主动隔振试验与数值计算[J]. 地下空间与工程学报, 2010, 6(1): 90-95. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201001018.htm LI Ning, GAO Guangyun, ZHENG Jianguo, et al. Field experimental and numerical study on active vibration isolation by WIB under horizontal loading[J]. Chinese Journal of Underground Space and Engineering, 2010, 6(1): 90-95. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201001018.htm
[9]	AHMAD S, AL-HUSSAINI T. Simplified design for vibration screening by open and in-filled trenches[J]. Journal of Geotechnical Engineering, 1991, 117(1): 67-88. doi: 10.1061/(ASCE)0733-9410(1991)117:1(67)
[10]	TAN Y, LU Y, PENG F, et al. Isolation of DDC impact to sheet pile walls by open trenches[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(1): 110-114. doi: 10.1061/(ASCE)GT.1943-5606.0000544
[11]	ADAM M, PFLANZ G, SCHMID G. Two-and three- dimensional modelling of half-space and train-track embankment under dynamic loading[J]. Soil Dynamics and Earthquake Engineering, 2000, 19(8): 559-573. doi: 10.1016/S0267-7261(00)00068-3
[12]	PEPLOW A T, JONES C, PETYT M. Surface vibration propagation over a layered elastic half-space with an inclusion[J]. Applied Acoustics, 1999, 56(4): 283-296. doi: 10.1016/S0003-682X(98)00031-0
[13]	高广运, 张博, 李伟. 层状和竖向非均匀地基中水平-摇摆耦合激振波阻板三维隔振分析[J]. 岩土力学, 2012, 33(2): 349-353, 421. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201202007.htm GAO Guangyun, ZHANG Bo, LI Wei. 3D analysis of vibration isolation using wave impeding block in layered and vertical heterogeneous foundation under horizontal-rocking coupled excitation[J]. Rock and Soil Mechanics, 2012, 33(2): 349-353, 421. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201202007.htm
[14]	LUAN L B, ZHENG C J, KOURETZIS G, et al. A new dynamic interaction factor for the analysis of pile groups subjected to vertical dynamic loads[J]. Acta Geotechnica, 2020, 15(12): 3545-3558. doi: 10.1007/s11440-020-00989-7
[15]	周凤玺, 马强, 周志雄. 二维地基中空沟-波阻板联合隔振屏障分析[J]. 岩土力学, 2020, 41(12): 4087-4092, 4115. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202012029.htm ZHOU Fengxi, MA Qiang, ZHOU Zhixiong. 2D analysis of vibration-isolation efficiency of an open trench-wave impedence block barrier[J]. Rock and Soil Mechanics, 2020, 41(12): 4087-4092, 4115. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202012029.htm
[16]	黄强, 叶斌, 黄宏伟, 等. 饱和软土二维-三维列车振动响应对比分析[J]. 西南交通大学学报, 2017, 2017(6): 1121-1129. https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT201706012.htm HUANG Qiang, YE Bin, HUANG Hongwei, et al. Comparison of 2D and 3D Dynamic Responses of Saturated Soft Soil due to Metro Train Load[J]. Journal of Southwest Jiaotong University, 2017, 2017(6): 1121-1129. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT201706012.htm
[17]	IAI S, TOBITA T, NAKAHARA T. Generalised scaling relations for dynamic centrifuge tests[J]. Géotechnique, 2005, 55(5): 355-362.
[18]	YANG W, YUAN R, WANG J. Vibration induced by subway trains: open-trench mitigation analysis in the time and frequency domains[J]. Shock and Vibration, 2018, 2018(8): 1-16.
[19]	杨文波, 徐朝阳, 陈子全, 等. 列车振动荷载作用下管片接缝对盾构隧道衬砌结构与周围软土地层动力响应影响研究[J]. 岩石力学与工程学报, 2017, 36(8): 1977-1988. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201708017.htm YANG Wenbo, XU Zhaoyang, CHEN Ziquan, et al. Influence of segment joints on dynamic response of shield tunnel and surrounding soft soil due to train induced vibration[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(8): 1977-1988. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201708017.htm
[20]	KUHLMEYER R L, LYSMER J. Finite element method accuracy for wave propagation problems[J]. ASCE Soil Mechanics and Foundation Division Journal, 1973, 99(5): 421-427.
[21]	ALZAWI A, NAGGAR M H E. Full scale experimental study on vibration scattering using open and in-filled (GeoFoam) wave barriers[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(3): 306-317.