Creep tests and creep model for reconstituted over-consolidated saturated clay
-
摘要: 采取杭州地区黏土制备重塑超固结土样（OCR=1.00，1.25，1.67，2.00，3.00）进行三轴剪切蠕变试验，研究超固结饱和黏土的时间变形特性和蠕变模型，对模型参数取值进行了分析。结果表明，重塑超固结饱和黏土的应力应变曲线具有应变硬化特征，在恒定偏应力下土样的时间变形曲线具有双曲线特征；超固结比越大，施加偏应力初始阶段试样中产生的超静孔压越小，试样变形进入蠕变阶段的时间越早，且在一定时间内试样的蠕变量发展越小。基于“孔压消散法”确定了超固结土的蠕变起始时间，采用双曲线蠕变模型可以高度拟合超固结饱和黏土剪切蠕变发展规律，曲线拟合分析表明：在相同的偏应力下，不同超固结比试样的最终蠕变量大致相等，但是超固结比越大时，土样蠕变发展越缓慢，表现为双曲线蠕变模型参数As在超固结比变化时几乎保持为常量，参数Bs则随超固结比的增大近似呈线性增长。Abstract: The triaxial shear creep tests are carried out on the reconstituted over-consolidated clay samples (OCR=1.00, 1.25, 1.67, 2.00, 3.00) from Hangzhou, China. The time-dependent deformation characteristics and creep model for the over-consolidated saturated clay are studied, and the values of model parameters are analyzed. The results show that the stress-strain curve of the reconstituted over-consolidated saturated clay has strain-hardening characteristics. The time-deformation curves of the over-consolidated clays under constant deviator stress are of hyperbolic characteristics. The larger the over-consolidation ratio, the smaller the excess pore pressure generated at the initial stage of the deviator stress application, the earlier the creep stage starts, and the smaller the creep evolution of the sample within a certain time. Based on the "pore pressure dissipation method", the tEOP of the over-consolidated clay is determined. The hyperbolic creep model can highly fit the shear creep curves of the over-consolidated saturated clay. The curve fitting analysis shows that under the same deviator stress, the final creep values of the samples with different over-consolidation ratios are roughly equal. However, the larger the over-consolidation ratio, the slower the creep development of clay. The hyperbolic creep model parameter As almost remains constant when the over-consolidation ratio changes, while the parameter Bs approximately linearly increases with the increase of the over-consolidation ratio.
-
0. 引言
由于地基的工后长期变形沉降而引发的建（构）筑物损坏和功能失效问题在工程界一直备受关注，土的蠕变是引起地基工后长期变形的主要原因之一。在地下工程建设中，开挖卸土引起了土的固结状态的改变，如建筑基坑开挖导致的开挖面土体卸载，地铁隧道挖掘引起的深部土体卸载，地下管廊开挖产生的土体卸载效应等。在后续工程建设和运维中，这些地基土往往具有超固结行为。因此，研究超固结土的时间变形特性对评估地下工程结构的长期变形具有重要的工程意义。
通过室内一维压缩试验和三轴剪切试验针对正常固结黏土蠕变（亦称次固结变形）特性开展的研究表明[1-2]，土样的孔隙特征以及加载时的应力路径、应力水平、排水条件等因素对土的时间变形效应都会产生较大影响。在试验的基础上研究者提出了一些非线性经验蠕变模型[3-6]，但是模型和模型参数的取值仍是研究的难点。在超固结土方面，高彦斌[7]对上海超固结黏土样进行了一维次压缩试验，发现超固结土的次压缩指数小于正常固结土。韩剑等[8]针对不同超固结比的重塑黏土试样开展了三轴不排水蠕变试验，结果表明具有强超固结比的试样在整个蠕变过程中都处于剪胀状态，且超固结比越大土样达到最大剪胀状态的蠕变时间越长。Yin等[9]提出了适用于正常固结和超固结黏土时变应力-应变特性的黏弹塑性本构模型，是一个可以考虑超固结条件下土体“延时变形”的非线性蠕变模型。胡亚元等[10]认为超固结土的次固结系数取值与时间相关，在Bjerrum蠕变图中将Yin模型[9]中的等效时间进行几何转化，通过添加超固结比参数ROCR改进模型以适用于超固结土，建立了相应的次固结系数随时间增长的双曲线模型。
上述研究表明超固结土的蠕变特性受到超固结比的影响，适用于超固结土的蠕变模型和参数取值方法尚未统一。本文选取杭州地区的黏性土进行不同超固结比土样的三轴剪切蠕变试验，分析不同程度超固结重塑土的蠕变特征；探讨适合描述超固结黏土的蠕变模型并对模型参数进行分析，以明确超固结比对黏土蠕变发展快慢和最终蠕变量大小的影响规律。
1. 试样与试验方案
试验土样取自杭州市区某基坑工程现场，取土深度15~25 m，土样呈黑灰色，含有一定量的腐殖质，原状土样基本物理指标如表 1所示，为饱和黏土。本文采用重塑土开展研究。制样前将原状土样烘干并碾碎，按照含水率控制制备土样，将称量好的土分4层填入制样器，圆柱形试样的尺寸为H×D=78 mm×39.1 mm。本文制备重塑土试样参照国家标准[11]中的方法。
表 1 原状土的基本物理性质指标Table 1. Index parameters of intact soil samples取土深度/m Gs 含水率w/kPa 天然密度ρ/(g·cm-3) 液限wL/% 塑限
wP/%塑性指数Ip 液性指数IL 15~25 2.72 36.21 1.87 40.27 20.26 20.01 0.79 本文试验共制备了5组不同超固结比试样（OCR= 1.0，1.25，1.67，2.0，3.0），见表 2。蠕变试验前，饱和后的各重塑土样在不同先期有效固结压力下等压固结，待固结稳定后卸载至初始固结压力（σ0=p=200 kPa），围压加卸载速率均为Δp=10 kPa/min。试样卸载固结完成后进行偏应力加载和蠕变试验。各超固结试样在相同的围压（p=200 kPa）下固结稳定后，以相同的偏应力加载速率Δq=10 kPa/min加载到预定值（q=155 kPa）进行蠕变。在蠕变过程中始终打开排水阀，室温维持21±3ºC。
表 2 超固结土三轴试验方案Table 2. Test schemes of over-consolidated ratio试样编号 OCR σ'c/kPa σ'0/kPa q/kPa K ① 1.00 200 200 155 0.68 ② 1.25 250 200 155 0.58 ③ 1.67 334 200 155 0.52 ④ 2.00 400 200 155 0.47 ⑤ 3.00 600 200 155 0.37 注：σ'c为试样先期有效固结压力；σ '0为初始有效围压；q为偏应力，q=σ1-σ3；K为蠕变偏应力和剪切强度qf的比值。 2. 试验结果与分析
2.1 超固结土的固结不排水剪切强度
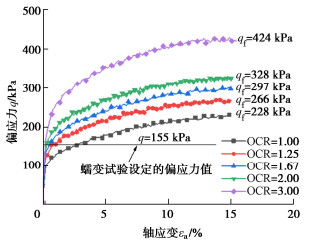
图 1给出了不同超固结比土样在同一有效围压（200 kPa）下的固结不排水（CU）试验应力应变曲线。由图可见，在轴向应变达到15%之前，各重塑超固结土的固结不排水试验曲线均呈应变硬化型，这与传统土力学中对超固结土具有应变软化特性的认识有所不同。因为本文试验采用的是重塑土，不具有天然超固结土的结构性，因此，可以推断土体沉积过程中形成的结构性是引起土的应变软化行为的内因，而由先期固结压力形成的超固结状态可能仅是“加剧”土的应变软化行为的外因。图 1同时给出了各超固结试样对应于轴向应变εa=15%的剪切强度qf值，可见超固结比越大，土的剪切强度越高。
![]()
图 1 不同超固结比试样的应力应变曲线Figure 1. Stress-strain curves for over-consolidated clay in CU test2.2 超固结土偏应力加载曲线分析
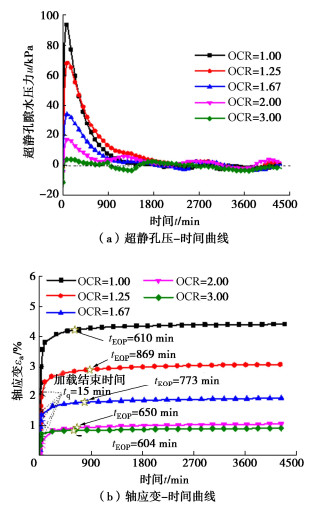
图 2给出了各超固结土样施加相同偏应力（q＝155 kPa）并保持稳定过程中孔压u和轴应变εa随时间的发展曲线。
由图 2（a）可见，在偏应力加载阶段，各试样内超静孔压逐渐上升并达到峰值；在稳定阶段（偏应力q达到目标值155 kPa以后保持稳定），超静孔压逐渐消散。土样的超固结比越大，偏应力加载阶段产生的超静孔压峰值越小。由图 2（b）可见，在偏应力加载阶段，各土样的轴应变逐渐增加，超固结比越大，土样的轴应变增加量越小，但是当OCR > 2.00时，超固结比对土样轴应变增量的影响开始减弱。
2.3 超固结土样的蠕变分析
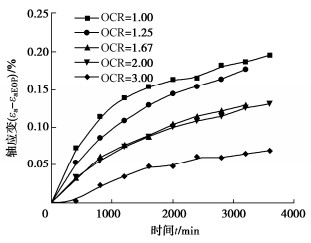
本文采用孔压消散法确定次固结（蠕变）起始时间tEOP，tEOP取为超静孔压消散达到80%时对应的时间[12]。据此，图 3给出了各不同超固结比试样的蠕变曲线，可见超固结土样的蠕变曲线亦具有非线性特征。
![]()
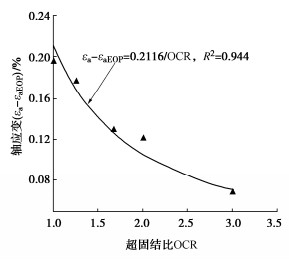
图 3 不同超固结比试样的蠕变曲线Figure 3. Creep deformations of samples with different over-consolidation ratios为了对比各土样的等时蠕变量，图 4给出了各土样72 h蠕变量与超固结比的关系曲线。由图可见，超固结比越大，土样的72 h蠕变量越小，同时可见各土样等时蠕变量随超固结比的变化是非线性衰减的。
![]()
图 4 蠕变量与超固结比的关系（t=4320 min）Figure 4. Relationship between over-consolidation ratio and creep deformation of samples3. 重塑超固结饱和黏土蠕变模型讨论
3.1 双曲线蠕变模型
εs(t)−εs(tEOP)=Ast−tEOPBs+(t−tEOP)。 (1) 式中：εs(t)为试样在t时刻的轴向应变；tEOP为蠕变起始时间；As为拟合参数，其物理意义为土样的最终蠕变应变量，即当t→∞时，As=εs(∞)-εs(tEOP)；Bs为拟合参数，其物理意义为试样蠕变应变量达到50%时所经历的时间，即Bs是一个时间参数，量纲为T。
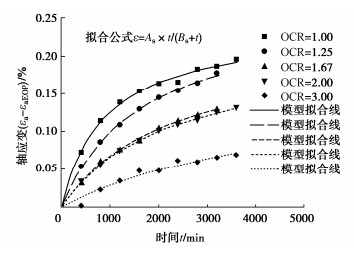
超固结黏土剪切蠕变模型拟合结果如图 5所示。由图 5可见，该模型对超固结黏土蠕变拟合度高，具有良好地适用性。
![]()
图 5 超固结土双曲线蠕变模型拟合曲线Figure 5. Fitting of shear creep curves of samples with different over-consolidation ratios3.2 模型参数分析
根据图 5的拟合结果，可以获得双曲线蠕变模型用于超固结土的模型参数As和Bs的取值，如表 3所列。
表 3 剪切蠕变双曲线模型参数Table 3. Fitting parameters of hyperbolic creep model超固结比 偏应力/
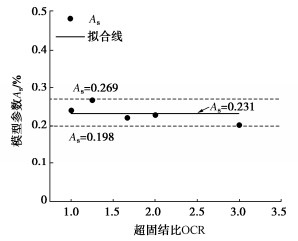
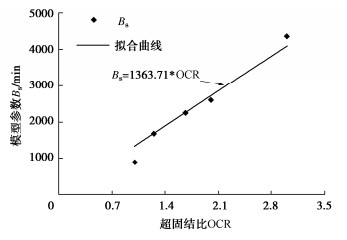
kPaAs/% Bs/min 相关系数R2/% 1.00 155 0.2397 904.33 99.64 1.25 155 0.2659 1685.06 99.89 1.67 155 0.2202 2248.02 99.78 2.00 155 0.2279 2602.10 99.74 3.00 155 0.2011 4352.29 95.64 根据表 3可以得到As值和Bs值与OCR的变化关系。由图 6可见，在同一偏应力作用下，As（试样最终蠕变应变量）受OCR的影响甚微，即不同超固结比土样的最终蠕变量大小并无明显差别。由图 7可见，Bs随OCR的增大近似呈线性增加，说明超固结黏土的蠕变发展速率随OCR的增大而趋缓慢，即OCR越大试样蠕变量达到50%时所需的时间越长。
综上所述，超固结比的大小对重塑饱和黏土的最终蠕变变形量影响较小，但是超固结比增大将延缓蠕变的发展。这可以解释图 4（3 d蠕变量）与图 6（最终蠕变量）给出的OCR产生的影响不一致的原因，表明土的应力历史不会影响其最终蠕变量的大小，但是会影响其蠕变变形发展的快慢。这个结论将有助于通过少量的室内试验确定超固结土的蠕变模型参数。
4. 结论与建议
本文采用杭州市地区黏土开展了重塑超固结饱和黏土的三轴剪切蠕变试验，分析了超固结黏土偏应力蠕变的特征，验证了双曲线蠕变模型对超固结黏土的适用性，分析了模型参数的取值特点。
（1）重塑超固结黏土的固结不排水剪切曲线具有应变硬化特征；在中等偏应力水平下，超固结黏土的时间变形曲线具有双曲线特征。
（2）以超静孔压消散达到80%确定试样的蠕变起始时间，获得了重塑超固结饱和黏土的剪切蠕变曲线。采用双曲线蠕变模型能很好地拟合不同超固结比下黏土剪切蠕变规律。
（3）双曲线蠕变模型参数与OCR的相关性良好，在相同的偏应力下，不同超固结比土样的最终蠕变应变量大致相等，As可取为常量；但超固结比越大，蠕变发展时间越长，Bs随OCR近似呈线性增加。
-
![]()
图 1 不同超固结比试样的应力应变曲线
Figure 1. Stress-strain curves for over-consolidated clay in CU test
![]()
图 3 不同超固结比试样的蠕变曲线
Figure 3. Creep deformations of samples with different over-consolidation ratios
![]()
图 4 蠕变量与超固结比的关系（t=4320 min）
Figure 4. Relationship between over-consolidation ratio and creep deformation of samples
![]()
图 5 超固结土双曲线蠕变模型拟合曲线
Figure 5. Fitting of shear creep curves of samples with different over-consolidation ratios
表 1 原状土的基本物理性质指标
Table 1 Index parameters of intact soil samples
取土深度/m Gs 含水率w/kPa 天然密度/(g·cm-3) 液限wL/% 塑限
wP/%塑性指数Ip 液性指数IL 15~25 2.72 36.21 1.87 40.27 20.26 20.01 0.79 
下载: 导出CSV
表 2 超固结土三轴试验方案
Table 2 Test schemes of over-consolidated ratio
试样编号 OCR σ'c/kPa σ'0/kPa q/kPa K ① 1.00 200 200 155 0.68 ② 1.25 250 200 155 0.58 ③ 1.67 334 200 155 0.52 ④ 2.00 400 200 155 0.47 ⑤ 3.00 600 200 155 0.37 注：σ'c为试样先期有效固结压力；σ '0为初始有效围压；q为偏应力，q=σ1-σ3；K为蠕变偏应力和剪切强度qf的比值。
下载: 导出CSV
表 3 剪切蠕变双曲线模型参数
Table 3 Fitting parameters of hyperbolic creep model
超固结比 偏应力/
kPaAs/% Bs/min 相关系数R2/% 1.00 155 0.2397 904.33 99.64 1.25 155 0.2659 1685.06 99.89 1.67 155 0.2202 2248.02 99.78 2.00 155 0.2279 2602.10 99.74 3.00 155 0.2011 4352.29 95.64
下载: 导出CSV
-
[1] 王者超, 乔丽苹, 李术才. 荷载水平和孔隙比对土次压缩性质影响研究[J]. 土木工程学报, 2013, 46(1): 112-118. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201301013.htm WANG Zhechao, QIAO Liping, LI Shucai. Influences of load level and void ratio on secondary compressibility of soil[J]. China Civil Engineering Journal, 2013, 46(1): 112-118. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201301013.htm
[2] 曾玲玲, 洪振舜, 刘松玉, 等. 重塑黏土次固结性状的变化规律与定量评价[J]. 岩土工程学报, 2012, 34(8): 1496-1500. http://www.cgejournal.com/cn/article/id/14669 ZENG Lingling, HONG Zhenshun, LIU Songyu, et al. Variation law and quantitative evaluation of secondary consolidation behavior for remolded clays[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(8): 1496-1500. (in Chinese) http://www.cgejournal.com/cn/article/id/14669
[3] YIN J H. Non-linear creep of soils in oedometer tests[J]. Géotechnique, 1999, 49(5): 699-707. doi: 10.1680/geot.1999.49.5.699
[4] SINGH A, MITCHELL J K. General stress-strain-time function for soils[J]. Journal of the Soil Mechanics and Foundations Division, 1968, 94(1): 21-46. doi: 10.1061/JSFEAQ.0001084
[5] MESRI G, FEBRES-CORDERO E, SHIELDS D R, et al. Discussion: shear-stress-strain time behaviour of clays[J]. Géotechnique, 1982, 32(4): 407-411. doi: 10.1680/geot.1982.32.4.407
[6] XIAO B, HU M Y, ZHOU P J, et al. Creep behavior of saturated clay in triaxial test and a hyperbolic model[J]. Geofluids, 2021: 1-12.
[7] 高彦斌. 超固结土一维次压缩特性实验研究[C]// 2004年度上海市土力学与岩土工程学术年会. 上海, 2004. Yanbin. Experimental study on one-dimensional compression characteristics of over-consolidated soil[C]// 2004 Annual Conference of Soil mechanics and Geotechnical Engineering in Shanghai. Shanghai, 2004. (in Chinese))
[8] 韩剑, 姚仰平, 尹振宇. 超固结度对超固结饱和黏土不排水蠕变特性的影响研究[J]. 岩土工程学报, 2018, 40(3): 426-430. doi: 10.11779/CJGE201803005 HAN Jian, YAO Yangping, YIN Zhenyu. Influences of overconsolidation ratio on undrained creep behavior of overconsolidated saturated clay[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(3): 426-430. (in Chinese) doi: 10.11779/CJGE201803005
[9] YIN J H, ZHU J G, GRAHAM J. A new elastic viscoplastic model for time-dependent behaviour of normally and overconsolidated clays: theory and verification[J]. Canadian Geotechnical Journal, 2002, 39(1): 157-173. doi: 10.1139/t01-074
[10] 胡亚元, 杨平, 余启致. 超固结土次固结系数的时间效应[J]. 中国公路学报, 2016, 29(9): 29-37. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201609003.htm HU Yayuan, YANG Ping, YU Qizhi. Time effect of secondary consolidation coefficient of over-consolidated soil[J]. China Journal of Highway and Transport, 2016, 29(9): 29-37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201609003.htm
[11] 土工试验方法标准: GB/T 50123—2019[S]. 北京: 中国计划出版社, 2019. Standard for Soil Test Method: GB/T 50123—2019[S]. Beijing: China Planning Press, 2019. (in Chinese)
[12] 肖斌. 重塑粉质黏土的蠕变特性及蠕变模型研究[D]. 杭州: 浙江工业大学, 2017. XIAO Bin. Study on Creep Characteristics and Creep Model of Reconstituted Silty Clay[D]. Hangzhou: Zhejiang University of Technology, 2017. (in Chinese)
-
期刊类型引用(1)
1. 李飞霞，方彪，刘庆，杨洋，邓亚虹. Q_3重塑黄土三维非线性流变本构模型试验研究. 地下空间与工程学报. 2024(S2): 638-645 . 
百度学术
其他类型引用(2)
计量
- 文章访问数: 207
- HTML全文浏览量: 37
- PDF下载量: 71
- 被引次数: 3
