Experimental study on mechanical properties and constitutive relation of CSG materials
-
摘要: 通过大型三轴试验得到了胶凝堆石料应力-应变关系曲线,分析了其力学性能,并针对关系曲线存在明显的非线性及软化特性,采用分段描述的方法建立了胶凝堆石料的本构关系,即破坏强度前考虑剪切所引起的体积变化采用双模量K-G模型描述,峰值强度后软化曲线的数学模型通过数据的回归分析和参数反演方式分析得到,各模型参数均可通过大三轴试验获取,方便可靠。Abstract: The stress-strain relationship curve of cementitious CSG materials is obtained through the large-scale triaxial tests, and its mechanical properties are analyzed. In response to the obvious nonlinear and softening characteristics of the relationship curve, a segmented description method is used to establish the constitutive relation of cementitious CSG materials. The volume change caused by shear is considered in the curve before failure strength, and a two-modulus K-G model is used to describe it. The mathematical model for the softening curve after the peak strength is obtained through the regression analysis of data and parameter inversion analysis.The parameters of each model can be easily determined through the large-scale triaxial tests.
-
Keywords:
- CSG material /
- stress and strain /
- age /
- constitutive relation /
- large-scale triaxial test
-
0. 引言
胶凝堆石料作为一种新型的筑坝材料备受工程界关注[1-5]。由于胶凝材料用料少、施工工艺粗放,其材料特性介于碾压堆石和混凝土之间,受胶凝含量、骨料级配、含砂率等诸多因素影响,具有明显的非线性应力-应变特征。然而目前已发表文献中,胶凝堆石料本构模型的研究大致可分为线弹性模型和非线性模型两类[4, 6],但很多学者重在描述应力-应变关系非线性和软化特征,并未考虑试验过程中体积变形的影响。
本文以双模量K-G模型为基础来分析胶凝堆石料的应力-应变关系。由已有研究成果可知,K-G模型在描述切线剪切模量Gt时,假定了曲线形状,当采用驼峰曲线(即软化曲线)时,在剪应力达到最大值,曲线开始下降时,Gt出现负值,致使劲度矩阵对角线出现了负值,此时矩阵将出现异常,致使方程可能无解。即使是采用对应于相同剪切应力时上升段的劲度矩阵或其它方法来替代此时的劲度矩阵,仍与实测关系曲线存在很大差异。为简化计算,本文将针对胶凝堆石料力学性能,根据在简单应力状态下获得的试验资料,利用双模量K-G模型推导方法,分段建立考虑软化特性的胶凝堆石料本构模型。
1. 胶凝堆石料力学性能
1.1 材料选型
试验材料采用胶凝含量为65 kg/m3的胶凝堆石料,胶凝剂采用P.O42.5普通硅酸盐水泥,Ⅰ级粉煤灰:细度9.3%,需水量比92%,含水率0.7%,烧失量2.8%,水灰比为1:1,含水率75 kg/m3。堆石料级配为直径40~60 mm的砂砾石占8.75%,20~40 mm的占18.83%,10~20 mm的占18.61%,5~10 mm的占14.16%,5 mm以下的占39.65%。
1.2 试验方案
试样尺寸按300 mm×700 mm的标准,依据《水工混凝土试验规程》要求进行制备,试样密度为2.05 g/m3。制样时在成模筒内先套两层橡皮膜,橡皮膜内侧垫0.4 mm的橡胶板,用振动碾分5层装填压实,成型后带模养护。制备好的试样在承台上安放到位后,把橡皮膜绑扎在上下透水承压板上,然后真空饱和。
试样真空饱和固结完成后,在100 t电液伺服粗粒土动静三轴试验机上,以0.02 mm/s的加荷速度进行排水剪切(CD)试验,试验围压分别为400,600,800 kPa,固结比1.0。试验过程中记录轴向压力、轴向位移、排水量和孔隙压力,以峰值强度作为破坏标准,以轴向应变值达到15%或试样完全破坏作为试验结束条件。
1.3 应力-应变关系
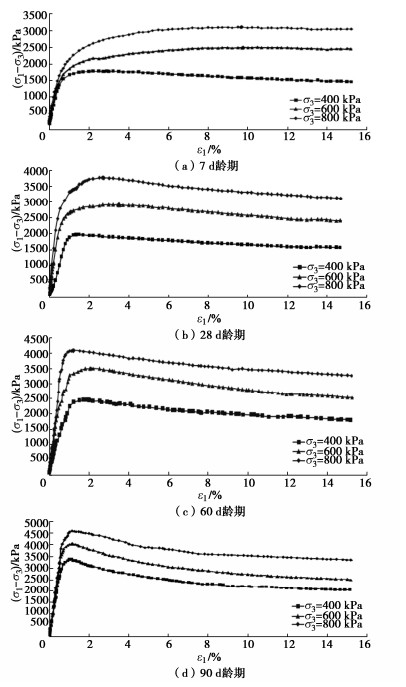
根据大型三轴试验资料成果[7],不同龄期试样的应力-应变曲线较为相似,各龄期不同围压下的应力-应变关系曲线见图 1所示。可知,在应力水平较低情况下,胶凝堆石料的应力-应变关系曲线近似直线发展。一般围压越高直线斜率越大;随着轴向应力进一步增加,材料塑性变形增大,曲线向应变轴偏转,并逐步达到材料强度极限;随后材料塑性变形迅速发展,应力水平难以维持,并逐步下降;当应力水平达到残余强度时,基本维持不变,材料应变继续发展。
从图 1可知,在三向受压情况下,胶凝材料具有应力峰值,而且关系曲线可大致分为3个阶段:①弹性变形阶段。从开始加载到试样应力达到胶凝堆石料极限强度的65%~84%左右时,试样的变形与应力成正比,应力-应变关系曲线基本呈直线,在此阶段内,胶凝堆石料可近似为线弹性材料。②塑性变形阶段。当试样的应力超过材料弹性极限强度后,胶凝堆石料的应变增加速率大于应力增长速率,应力-应变关系曲线开始逐渐向应变轴弯曲;试样应力接近胶凝堆石料极限强度时,应变增加速率急剧增大,塑性变形明显。③试样破坏阶段。当试样应力达到极限强度时,因试样发生剪切破坏不能承受更大的外荷载,此时的极限强度为峰值抗压强度,相应的应变值为峰值应变。大三轴试验试样的破坏多表现为上中部隆起,围压较小时,变形较大部位在试样上端,随着围压的增加,逐渐表现为试样中部破坏。当超过峰值抗压强度后,试样材料间破坏而剪切滑移增大,变形越来越大,承载能力下降。继续对试样施压,随着变形的增大,剪切位移克服了颗粒之间的咬合作用,颗粒结构崩解变松,黏聚力很快减低,而颗粒之间的内摩擦力还在起作用,使试件仍然能够承受一定的外荷载;当应变达到15%左右时,材料强度趋于一个定值,即残余强度。峰值强度和残余强度随着围压增长基本呈现增长趋势。
2. 胶凝堆石料本构关系特性
2.1 本构关系基本特性
根据对胶凝堆石料大三轴试验资料的分析,其应力-应变关系呈现明显的非线性和软化特性,不满足邓肯-张本构模型中的双曲线假设,且随着龄期的增长,越接近材料破坏,应力-应变关系曲线的切线斜率越高。本文采用应用较为广泛的双模量K-G模型来描述胶凝堆石料的应力-应变本构关系。该模型在确定参数时所用的剪切应变包含了正应力增加所引起的剪缩,也包括了剪切所引起的体积变化。在描述胶凝堆石料应力-应变关系的数学表达时,分为以下两个阶段:①峰值强度前曲线用双模量模型描述,考虑剪切所引起的体积变化;②峰值强度后软化曲线的数学模型通过数据的回归分析和参数反演等方式进行挖掘分析。
2.2 峰值强度前本构关系的建立
(1)切线体积模量Kt的测定
试验采用各向等压固结,根据增量广义Hooke定律,有
Kt=ΔpΔεv。 (1) 式(1)表明p - εv关系曲线的切线斜率具有Kt的物理意义。基于这一点,求得孔隙比e与压力p的e - p关系曲线,即可由此曲线推出dp/dεv=Kt。
以60 d龄期胶凝堆石料为例,各向等压固结的试验结果如表 1所示。
表 1 60 d龄期胶凝堆石料各向等压固结试验结果Table 1. Results of isotropic isobaric consolidation tests on CSG materials at age of 60 d压力p/kPa 试样初始体积Vc/cm3 固体颗粒体积Vs/cm3 排水量Vf/cm3 孔隙比e 400 44405.70 36400 1506.9 4.14 600 44836.02 36400 1335.8 3.67 800 44193.49 36400 1187.5 3.26 由表 1可获得孔隙比e与压力p的对应关系,并在半对数纸上点绘e - lnp关系曲线,e - p关系可用下式表示:
e=ea0−λlnp, (2) 式中,ea0,λ为试验常数。
进而推得切线体积模量Kt的表达式:
Kt=dpdεv=1+e0λp, (3) 式中,e0为起始孔隙比。
(2)切线剪切模量Gt的测定
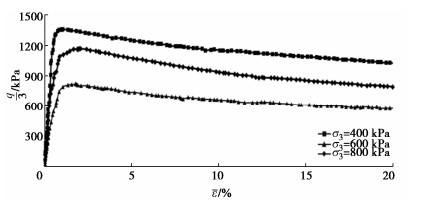
60 d龄期胶凝堆石料大型三轴试验的(q/3) - ˉε曲线如图 2所示。(q/3) - ˉε关系曲线(峰值前)与双曲线近似,但本次试验为各向等压固结,与Domaschuk等的假设不同,试验条件为σ3不变,Gt的表达式计算过程考虑用邓肯-张双曲线的推算过程。根据增量广义Hooke定律可知,Gt=Δ(q/3)/Δˉε,体现了(q/3) - ˉε关系曲线的切线斜率具有Gt的物理意义。
对于某一剪切应力q/3,(q/3) - ˉε关系可表示为
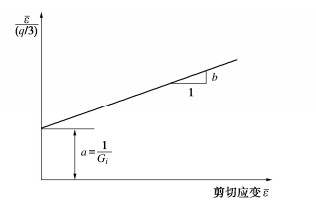
ˉε(q/3)=a+bˉε, (4) 式中,a,b为试验常数。
以ˉε/(q/3)为纵坐标,ˉε为横坐标,构成新的坐标系,则双曲线转换为直线。参照常用的E-B模型中参数a、b的求取方法(见图 3),通过对胶凝堆石料试验资料的整理与分析,取应力水平70%和80%两点的连线求得a、b较合适,其中a为直线在纵坐标上的截距,b为直线的斜率。由a和b即可求得初始切线剪切模量Gi和主应力差的渐近值(q/3)ult。
根据增量广义Hooke定律,得
Gt=Δq3Δˉε=∂(q3)∂ˉε。 (5) 将式(4)代入式(5),可求得
Gt=1a[1−b(q/3)]2 。 (6) 当ˉε→∞时,
b=1(q/3)b→∞=1(q/3)ult 。 (7) 定义破坏比Rf=(q/3)f/(q/3)ult(其中(q/3)f为试样破坏时的应力差,kPa),则
b=1/(q3)ult=Rf/(q3)f。 (8) 可得切线剪切模量:
Gt=Gi[1−Rf(q3)/(q3)f]2 。 (9) 可见,Gi,(q/3)f,Rf的值均随着σ3的变化而有所变化。结合胶凝堆石料大三轴试验结果可进一步确定式中参数Gi,(q/3)f,Rf与围压σ3的关系,进而得到
Gt=k1Paen(σ3Pa)[1−Rf(q/3)k2Pa(σ3Pa)m−1]2 。 (10) 即求得了剪切模量Gt的函数表达,从式(10)中可以看出,Gt随应力水平的增加而降低,随围压的增加而增加,这一规律与邓肯-张模型得到的结论是一致的,但Gt的表达则较邓肯-张模型简单。该函数仅包含k1,n,k2,m四个无量纲试验参数。
2.3 峰值强度后本构关系的建立
定义ˉεf为破坏强度(q/3)f对应的剪切应变值,此典型曲线满足以下数学条件:①当ˉε=ˉεf时,d(q3)/d(ˉε)=0,且q/3=(q/3)f,曲线单峰;②当ˉε→+∞时,q/3→(q/3)u,(q/3)u为残余强度的渐进值。
对不同围压下的剪切破坏强度q/3进行回归分析,考虑q/3随ˉε的变化规律。在对比分析的基础上,考虑最优数学模型(q/3Pa)=Ae−ˉε/t1+k0,其中A,t1,k0为待求的回归系数,均与围压存在一定关系:A(σ3)=(A1ln(σ3Pa)+A2)/(σ3Pa)2,t1(σ3)=t2(σ3Pa)+t3,k0(σ3)=k01ea(σ3Pa),其中A1,A2,t2,t3,k01,a均为无量纲试验常数。各式代入后即可得到胶凝堆石料破坏强度后剪应力q/3与ˉε关系的数学表达式:
q3=Pa[A1ln(σ3Pa)+A2(σ3Pa)2e−ˉεt2(σ3Pa)+t3+k01ea(σ3Pa)] (11) 2.4 剪切应变峰值点的确定
胶凝堆石料应力-应变关系曲线具有明显的应力峰值,应力峰值前表现出非线性的本构关系特性;达到峰值后应变继续增大,而应力水平逐渐减小并逐步趋于一个定值,表现出明显的软化特征。分界点剪切应力峰值(q/3)f对应的剪切应变为ˉεf。由试验结果可知,剪切应变ˉεf与围压和龄期有关,并呈现非线性变化关系,可表示成围压和龄期的函数:
¯εf=f1(σ′3,t′) 。 (12) 式中:f1为剪切应变函数;为了便于计算,σ′3,t′分别为无量刚化围压和龄期的对应值。
利用基因自动编程算法(GEP)函数挖掘,取σ′3=σ3/10 Pa,t′=t/180。得到胶凝堆石料破坏强度预测函数为
¯εf=1σ′3t′(0.52−0.19/σ′3) 。 (13) 3. 结论
(1)根据大型三轴试验资料分析了胶凝堆石料力学性能,其应力-应变关系表现出明显的非线性和软化特性;在低应力水平下表现为线弹性性质;当应力达到其峰值强度的65%~84%后塑性变形明显,直至达到其峰值强度;其后应力随着应变的增长而降低,表现出明显的软化特性,当应变达到15%左右时趋近于材料的残余强度。
(2)采用分段建模的方法分别建立了胶凝堆石料应力-应变本构关系,达到破坏强度前关系曲线采用双模量K-G模型建立了包含4个无量纲参数的胶凝堆石料非线性本构关系模型,并考虑了试验过程中体积变形的影响;通过试验数据的回归分析,建立了包含6个无量纲参数达到破坏强度后软化曲线的本构关系模型,各参数均可由大三轴试验确定,方便可靠。
-
表 1 60 d龄期胶凝堆石料各向等压固结试验结果
Table 1 Results of isotropic isobaric consolidation tests on CSG materials at age of 60 d
压力p/kPa 试样初始体积Vc/cm3 固体颗粒体积Vs/cm3 排水量Vf/cm3 孔隙比e 400 44405.70 36400 1506.9 4.14 600 44836.02 36400 1335.8 3.67 800 44193.49 36400 1187.5 3.26 -
[1] 何蕴龙, 刘俊林, 李建成. Hardfill筑坝材料应力-应变特性与本构模型研究[J]. 四川大学学报(工程科学版), 2011, 43(6): 40-47. https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH201106008.htm HE Yunlong, LIU Junlin, LI Jiancheng. Study on the stress-strain property and constitutive model of hardfill material[J]. Journal of Sichuan University (Engineering Science Edition), 2011, 43(6): 40-47. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH201106008.htm
[2] 贾金生, 马锋玲, 李新宇, 等. 胶凝砂砾石坝材料特性研究及工程应用[J]. 水利学报, 2006, 37(5): 578-582. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200605009.htm JIA Jinsheng, MA Fengling, LI Xinyu, et al. Study on material characteristics of cement-sand-gravel dam and engineering application[J]. Journal of Hydraulic Engineering, 2006, 37(5): 578-582. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200605009.htm
[3] 黄虎, 李坡, 霍文龙, 等. 胶凝砂砾石材料宏细观参数及破坏模式研究[J]. 华北水利水电大学学报(自然科学版), 2020, 41(4): 27-38. https://www.cnki.com.cn/Article/CJFDTOTAL-HBSL202004005.htm HUANG Hu, LI Po, HUO Wenlong, et al. Study on relationship between mesoscopic and macroscopic mechanical parameters and failure model of cemented sand and gravel material[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2020, 41(4): 27-38. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HBSL202004005.htm
[4] 蔡新, 武颖利, 李洪煊, 等. 胶凝堆石料本构特性研究[J]. 岩土工程学报, 2010, 32(9): 1340-1344. http://www.cgejournal.com/cn/article/id/13520 CAI Xin, WU Yingli, LI Hongxuan, et al. Constitutive equation for CSG materials[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(9): 1340-1344. (in Chinese) http://www.cgejournal.com/cn/article/id/13520
[5] 颉建军. 300m级浇筑式沥青混凝土面板胶凝堆石坝设计研究[J]. 水力发电, 2017, 43(2): 54-59. https://www.cnki.com.cn/Article/CJFDTOTAL-SLFD201702015.htm XIE Jianjun. Design study of jellification rockfill dam for 300m-high level pouring asphalt concrete face[J]. Water Power, 2017, 43(2): 54-59. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLFD201702015.htm
[6] T F, A N, H K, et al. Material properties of CSG for the seismic design of trapezoid-shaped CSG dam: Proceedings of the Thirteenth World Conference on Earthquake Engineering[C]// Vancouver, 2004.
[7] 李娜, 何鲜峰, 张斌, 等. 基于大型三轴试验的胶凝堆石料力学特性试验研究[J]. 水力发电学报, 2014, 33(6): 202-208. https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201406031.htm LI Na, HE Xianfeng, ZHANG Bin, et al. Study of mechanical properties of cemented sand and rockfill material based on large-scale triaxial tests[J]. Journal of Hydroelectric Engineering, 2014, 33(6): 202-208. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201406031.htm



 下载:
下载: