探讨低围压条件下如何准确测试土体强度

李小梅; 凌小东; 王芳; 米占宽; 占鑫杰

doi:10.11779/CJGE2023S10023

探讨低围压条件下如何准确测试土体强度 English Version

1.
南京水利科学研究院岩土工程研究所, 江苏南京 210024
2.
南京工业大学海外教育学院, 江苏南京 211816

详细信息

作者简介:
李小梅(1986—)，女，河南新乡人，博士，高级工程师，从事土的基本特性、测试技术及标准化研究。E-mail：xmli@nhri.cn

中图分类号: TU411
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
出版历程
- 收稿日期: 2023-07-04
- 网络出版日期: 2023-11-23
- 刊出日期: 2023-10-31

On how to accurately testing compressive strength of soils under low confining pressure

1.
Geotechnical Engineering Department, Nanjing Hydraulic Research Institute, Nanjing 210024, China
2.
College of Overseas Education, Nanjing Tech University, Nanjing 211816, China

摘要

摘要: 准确测试土体的强度指标对地基基础的受力变形分析、稳定计算具有重要意义，对低围压（小于100 kPa）条件下的三轴试验而言，压力室传力杆的活塞摩阻、橡皮膜的径向约束不可忽视，同时设备的测试精度及量程也是应当考虑的重要影响因素。试图通过开展不同条件下的无侧限抗压强度试验、不同设备的三轴剪切试验等测试方案探讨活塞摩阻、橡皮膜等因素对测试结果的影响程度，探讨根据现有的测试条件如何测得试样的抗压及抗剪强度，为设计施工及数值计算提供可靠数据。针对国产三轴测试设备存在的不足提出了合理化建议，期望三轴测试设备从机械制造上进一步改造升级，推动中国精密三轴测试设备的研发。
- 低围压 /
- 活塞摩阻 /
- 橡皮膜 /
- 量程 /
- 三轴试验
Abstract: It is important to study the stress deformation and stability of foundation by accurately testing the strength index of soils. For the triaxial tests under low confining pressures (less than 100 kPa), the influences of the piston friction and the rubber membrane can not be ignored. At the same time, the test accuracy and measuring range of equipments are also the important factors that should be considered. This study attempts to explore the influences of factors such as the piston friction and the rubber membrane on the test results by carrying out unconfined compressive strength tests under different conditions and triaxial consolidated undrained shear tests of different equipments, and to explore how to measure the compressive and shear strengths of samples according to the existing test conditions, so as to provide reliable data for design, construction and numerical calculation. In view of the shortcomings of domestic triaxial test equipments, reasonable suggestions are put forward, and it is expected that the triaxial test equipments should be further transformed and upgraded from mechanical manufacturing so as to promote the researches and development of precise triaxial test equipments in China.
- low confining pressure /
- piston friction /
- rubber membrane /
- measuring range /
- triaxial test

HTML全文

0. 引言

沿海地区的水下地下工程建设不可避免地会受到的地下水渗流影响^[1]，将导致施工区域软土地基沉降，造成周围建筑物和地面的不均匀沉降。为保持原有地层稳定，人工冻结技术在岩土工程中广泛应用^[2]，包括海底隧道和城市地铁建设^[3]。流速较大条件下易出现冻结壁不闭合的现象^[4]，不能满足施工设计的要求。

在人工冻结过程中，确定地层的冻结范围是非常重要的。基于热势叠加理论，Hu等^[5]和Pimentel等^[6]推导了静水和渗流条件下不同冻结形式下的稳态温度场的理论公式，用来预测圆形冻结壁的厚度和平均温度^[7]。地下水渗流的存在使等温线向下游移动，下游冻结壁厚度大于上游^[8]。但现有的解析解不能揭示多孔介质冻结过程中渗流与各物理场的耦合机制。

当存在地下水渗流时，水流携带的热量导致冻结区的解冻^[9]，研究渗流条件下冻结过程中的多场耦合机制是必要的。考虑冻结过程中多场耦合变化，建立了渗流条件下人工冻结过程多场耦合数值模型^[10]。饱和土的冻结过程涉及多场、多相，针对沿海地区地下水含盐量高的问题^[11]，在多孔介质理论框架下建立多场宏观模型，模拟地下水渗流条件下的冻结过程。

本文建立了渗流条件下砂地层在人工冻结时的水-盐-热-力耦合模型。充分考虑非对流通量对传热传质的影响，固体颗粒对盐的解吸和吸附作用，以准确模拟人工冻结过程。采用Navier-Stokes方程来考虑渗流过程中流体的动量守恒，研究了单管冻结条件下，不同渗流速度下滨海砂地层中各组分的分布规律。

1. 控制方程

1.1 固体基质质量守恒方程

多孔介质中固体基质的质量守恒方程为^[12]：

$\frac{1}{{(1 - n)}}\frac{{\partial n}}{{\partial t}} + \frac{1}{{(1 - w_{\text{p}}^{\text{s}})}}\frac{{\partial w_{\text{p}}^{\text{s}}}}{{\partial t}} + {\beta _{{\text{sT}}}}\frac{{\partial T}}{{\partial t}} = {\beta _{{\text{sP}}}}\frac{{\partial {P_{\text{l}}}}}{{\partial t}} + \frac{{\partial {\varepsilon _{\text{v}}}}}{{\partial t}} 。$

(1)

式中： $w_{\text{p}}^{\text{s}}$ 为固体颗粒吸附盐的质量分数；T为温度； ${P_{\text{l}}}$ 为孔隙水力压力。

1.2 水分守恒方程

多孔介质中水分质量守恒方程的展开式为

$\begin{array}{l} n{S^{\text{l}}}(1 - w_{\text{p}}^{\text{l}}){\beta _{{\text{lp}}}}{\rho ^{\rm{l}}}\frac{{\partial {P_{\text{l}}}}}{{\partial t}} + {\text{div}}(\rho _{\text{w}}^{\text{l}}{{\boldsymbol{q}}^{\text{l}}}) - {\text{div}}({\boldsymbol{j}}_{\text{p}}^{\text{l}}) \hfill \\ = - \frac{{\partial {m_i}}}{{\partial t}} - \frac{{\partial m_{\text{p}}^{\text{l}}}}{{\partial t}} + n\rho _{\text{w}}^{\text{l}}\frac{{\partial {S^i}}}{{\partial t}} + n\rho _{\text{w}}^{\text{l}}\frac{{{S^{\text{p}}}}}{{\partial t}} - {S^{\text{l}}}\rho _{\text{w}}^{\text{l}}\frac{{\partial n}}{{\partial t}} + \hfill \\ n{S^{\text{l}}}{\rho ^{\text{l}}}\left[ {(1 - w_{\text{p}}^{\text{l}}){\beta _{{\text{lw}}}} + 1} \right]\frac{{\partial w_{\text{p}}^{\text{l}}}}{{\partial t}} - n{S^{\text{l}}}\rho _{\text{w}}^{\text{l}}\frac{{\partial {\varepsilon _{\text{v}}}}}{{\partial t}} + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;(1 - w_{\text{p}}^{\text{l}})n{S^{\text{l}}}{\beta _{{\text{lT}}}}{\rho ^{\text{l}}}\frac{{\partial T}}{{\partial t}} 。 \end{array}$

(2)

式中： ${\beta _{{\rm{lp}}}}$ 为液相压缩率； ${\beta _{{\text{lT}}}}$ 为液体热膨胀系数； ${\beta _{{\text{lw}}}}$ 为浓度依赖系数； $\partial {m_i}/\partial t$ 为冰的结晶速率； $\partial m_{\text{p}}^{\text{l}}/\partial t$ 为结晶盐水合物的形成速率； ${\boldsymbol{j}}_{\text{p}}^{\text{l}}$ 为盐在液相中的非对流通量； $\rho _{\text{w}}^{\text{l}}$ 为液态的水密度； ${\rho ^{\text{l}}}$ 为液相的密度； $w_{\text{p}}^{\text{l}}$ 溶解盐的质量分数。

冰的质量守恒方程为^[13]

$\frac{1}{n}\frac{{\partial n}}{{\partial t}} + \frac{1}{{{S^{\text{i}}}}}\frac{{\partial {S^{\text{i}}}}}{{\partial t}} + \frac{{\partial {\varepsilon _{\text{v}}}}}{{\partial t}} = \frac{1}{{n{S^{\text{i}}}{\rho ^{\text{i}}}}}\frac{{\partial {m_{\text{i}}}}}{{\partial t}} \text{, }\;$

(3)

式中， ${\rho ^{\text{i}}}$ 为冰的密度。

1.3 盐分守恒方程

考虑冻结多孔介质液相中盐溶液的非对流通量，溶液的质量守恒为

$\frac{{\partial (n{S^{\text{l}}}\rho _{\text{p}}^{\text{l}})}}{{\partial t}} + {\text{div}}(n{S^{\text{l}}}\rho _{\text{p}}^{\text{l}}{{\boldsymbol{v}}^{\text{l}}}) + {\text{div}}({\boldsymbol{j}}_{\text{p}}^{\text{l}}) = - \frac{{\partial {m_{\text{p}}}}}{{\partial t}} - \frac{{\partial m_{\text{p}}^{\text{l}}}}{{\partial t}} 。$

(4)

式中： ${\boldsymbol{j}}_{\text{p}}^{\text{l}}$ 为冻土中盐的非对流通量； $\partial {m_{\text{p}}}/\partial t$ 为结晶盐的相变速率。

可得到展开的溶液质量守恒方程：

$\begin{array}{l} \frac{1}{n}\left( {1 - \frac{{{\rho ^{\text{s}}}w_{\rm{p}}^{\rm{s}}}}{{{\rho ^{\text{l}}}w_{\text{p}}^{\text{l}}}}} \right)\frac{{\partial n}}{{\partial t}} - \frac{1}{{{S^{\text{l}}}}}\frac{{\partial {S^{\text{i}}}}}{{\partial t}} - \frac{1}{{{S^{\text{l}}}}}\frac{{{S^{\text{p}}}}}{{\partial t}} + \frac{{\partial {\varepsilon _{\text{v}}}}}{{\partial t}} + \\ \left[ {{\beta _{{\text{lp}}}} + \frac{{(1 - n)w_{\text{p}}^{\text{s}}{\rho ^{\text{s}}}}}{{n{S^{\text{l}}}{\rho ^{\text{l}}}w_{\text{p}}^{\text{l}}}}{\beta _{{\text{sP}}}}} \right]\frac{{\partial {P^{\text{l}}}}}{{\partial t}} + \frac{{(1 - w_{\text{p}}^{\text{l}}{\beta _{{\text{lw}}}})}}{{w_{\rm{p}}^{\rm{l}}}}\frac{{\partial w_{\text{p}}^{\text{l}}}}{{\partial t}} + \\ \frac{1}{{w_{\text{p}}^{\text{l}}}}\frac{{(1 - n){\rho ^{\text{s}}}}}{{n{S^{\text{l}}}{\rho ^{\text{l}}}}}\frac{{\partial w_{\text{p}}^{\text{s}}}}{{\partial t}} - \left[ {\frac{{(1 - n)w_{\text{p}}^{\text{s}}{\rho ^{\text{s}}}}}{{n{S^{\text{l}}}{\rho ^{\text{l}}}w_{\text{p}}^{\text{l}}}}{\beta _{{\text{sT}}}} + {\beta _{{\text{lT}}}}} \right]\frac{{\partial T}}{{\partial t}} \\ \;\; = \frac{{{\text{div}}({\rho ^{\text{l}}}w_{\text{p}}^{\text{l}}{{\boldsymbol{q}}^{\text{l}}}) + {\text{div}}({\boldsymbol{j}}_{\text{p}}^{\text{l}}) - \frac{{\partial {m_{\text{p}}}}}{{\partial t}} - \frac{{{\upsilon _{\text{l}}}{M_{\text{l}}}}}{{{M_{\text{p}}}}}\frac{{\partial {m_{\text{p}}}}}{{\partial t}}}}{{n{S^{\text{l}}}{\rho ^{\text{l}}}w_{\text{p}}^{\text{l}}}} 。 \end{array}$

(5)

式中： $w_{\text{p}}^{\text{l}}$ 为液相中盐的质量分数； ${\boldsymbol{j}}_{\text{p}}^{\text{l}}$ 冻为土中盐的非对流通量； ${{\boldsymbol{q}}^{\text{l}}}$ 为液相相对流动体积； ${M_{\text{l}}}$ 为液体的摩尔质量； ${M_{\text{p}}}$ 为结晶盐的摩尔质量。

考虑多孔介质中盐的吸附-解吸效应，冻土中盐分的沉积动力学公式为

$\begin{array}{l} (1 - n){\rho ^{\text{s}}}\frac{{\partial w_{\text{p}}^{\text{s}}}}{{\partial t}}{\text{ + div}}\left[ {(1 - n){\rho ^{\text{s}}}{{\boldsymbol{v}}^{\text{s}}}} \right] \\ = {k_{ad}}n{S^l}{\rho ^l}w_p^l - {k_{de}}(1 - n){\rho ^s}w_p^s \text{, }\; \end{array}$

(6)

式中， ${k_{{\text{ad}}}}$ 和 ${k_{{\text{de}}}}$ 分别为吸附系数和解吸系数。

结晶盐的质量守恒方程为^[13]

$\frac{1}{n}\frac{{\partial n}}{{\partial t}} + \frac{1}{{{S^{\text{p}}}}}\frac{{\partial {S^{\text{p}}}}}{{\partial t}} + \frac{{\partial {\varepsilon _{\text{v}}}}}{{\partial t}} = \frac{1}{{n{\rho ^{\text{p}}}{S^{\text{p}}}}}\frac{{\partial {m_{\text{p}}}}}{{\partial t}} \text{, }\;$

(7)

式中： ${\rho ^{\text{p}}}$ 为结晶盐的密度。

1.4 能量守恒方程

多孔介质冻结过程中的能量守恒与热容和热传导度有关，能量守恒方程表示为

$\begin{array}{l} \left[ {(1 - n){\rho ^{\text{s}}}{c_{\text{s}}} + n{S^{\text{l}}}{\rho ^{\text{l}}}{c^{\text{l}}} + n{S^{\text{i}}}{\rho ^{\text{i}}}c_{\text{i}}^{\text{i}} + n{S^{\text{p}}}{\rho ^{\text{p}}}c_{\text{p}}^{\text{p}}} \right]\frac{{\partial T}}{{\partial t}} + \hfill \\ {\text{div}}\left[ {(c_{\text{p}}^{\text{l}}{\boldsymbol{j}}_{\text{p}}^{\text{l}} - {\rho ^{\text{l}}}{c^{\rm{l}}}{{\boldsymbol{q}}^{\text{l}}})(T - {T_0}) - {\lambda _{{\text{eff}}}}\nabla T} \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;= {L_{{\text{wi}}}}\frac{{\partial {m_{\text{i}}}}}{{\partial t}} + {L_{{\text{sc}}}}\frac{{\partial {m_{\text{p}}}}}{{\partial t}} + {L_{{\text{lp}}}}\frac{{{\upsilon _{\text{l}}}{M_{\text{l}}}}}{{{M_{\text{p}}}}}\frac{{\partial {m_{\text{p}}}}}{{\partial t}} 。\end{array}$

(8)

式中：g为重力加速度矢量； ${\lambda _{{\text{eff}}}}$ 为冻土有效导热系数； ${c_{\text{s}}}$ ， ${c^{\text{l}}}$ ， $c_{\text{i}}^{\text{i}}$ 和 $c_{\text{p}}^{\text{p}}$ 分别代表固体颗粒、液相、冰和结晶盐的热容； ${L_{{\text{wi}}}}$ ， ${L_{{\text{lp}}}}$ ， ${L_{{\text{sc}}}}$ 分别为水、冰的相变潜热、自由水、结合水相变潜热和溶液-结晶盐的相变潜热。

1.5 动量守恒方程

人工冻结过程中的各向异性和渗流状态影响着砂土地层的冻结状态，在动量守恒中引入Navier-Stokes方程来描述渗流的动量守恒。土体冻结过程中π相的动量守恒方程为

${\rho ^\pi }{n^\pi }\frac{{d{{\boldsymbol{v}}^\pi }}}{{dt}} - div({n^\pi }{{\boldsymbol{\sigma }}^\pi }) - {\rho ^\pi }{n^\pi }{{\boldsymbol{g}}^\pi } = {\dot m^\pi } 。$

(9)

式中： ${{\boldsymbol{\sigma}} ^\pi }$ 为π相的应力张量； ${\dot m^\pi }$ 为π相与其他相的动量交换， ${{\boldsymbol{g}}^\pi }$ 为π相的体积密度。

可得到土体的动量守恒方程：

$\begin{array}{l} n{\rho ^{\rm{l}}}\left( {{F_{\rm{g}}} - \frac{{\nabla {P^{\rm{l}}}}}{{{\rho ^{\rm{l}}}}} + {\mu _{\rm{l}}}{\nabla ^2}{{\boldsymbol{v}}^{\rm{l}}}} \right) - {\rm{div}}({\boldsymbol{\sigma}} ' + {S^{\rm{l}}}{P^{\rm{l}}} + {S^{\rm{i}}}{P^{\rm{i}}} + {S^{\rm{p}}}{P^{\rm{p}}}) - \\ \left[ {(1 - n){\rho ^{\rm{s}}} + n{S^{\rm{l}}}{\rho ^{\rm{l}}} + n{S^{\rm{i}}}{\rho ^{\rm{i}}} + n{S^{\rm{p}}}{\rho ^{\rm{p}}}} \right]{\boldsymbol{g}} = {\dot m^\pi } 。 \end{array}$

(10)

式中：F_g为单位质量力；μ_l为液相的动力黏度； ${P^{\rm{i}}}$ 为冰压力； ${P^{\rm{p}}}$ 为孔隙中盐结晶压力； ${\boldsymbol{\sigma}} '$ 为有效应力。

1.6 边界条件

将耦合方程（1）~（3），（5）~（8），（10）代入COMSOL Multiphysics进行求解。边界与外部存在热对流和热交换和水、盐供应。要解耦合方程，必须满足下列边界条件：

$\left. \begin{array}{l} ({\rho }_{\text{w}}^{\text{l}}{{\boldsymbol{q}}}^{\text{l}}-{{\boldsymbol{j}}}_{\text{p}}^{\text{l}})\cdot {\boldsymbol{n}}={\overline{P}}^{\text{l}}\text{ }\text{, }\;\\ ({\rho }^{\text{l}}{w}_{\text{p}}^{\text{l}}{{\boldsymbol{q}}}^{\text{l}}+{{\boldsymbol{j}}}_{\text{p}}^{\text{l}})\cdot {\boldsymbol{n}}={\overline{w}}_{\text{p}}^{\text{l}}\text{ }\text{, }\;\\ \left[({\rho }_{\text{w}}^{\text{l}}{c}_{\text{w}}^{\text{l}}{{\boldsymbol{q}}}^{\text{l}}+{c}_{\text{p}}^{\text{l}}{{\boldsymbol{j}}}_{\text{p}}^{\text{l}})\cdot (T-{T}_{0})-{\lambda }_{\text{eff}}\nabla T\right]\cdot {\boldsymbol{n}}=\overline{T}\text{ }\text{, }\;\\ \sigma \cdot {\boldsymbol{n}}={\overline{\varepsilon }}_{\text{v}}\text{ }。 \end{array} \right\}$

(11)

2. 理论验证

结合Wang等^[14]的渗流条件下人工冻结过程温度场验证本文理论模型。模型试验如图 1所示，箱体中间设置一根外径为42 mm的冷冻管。整个模型的初始温度为10℃，冻结管的初始温度为-30℃。在箱体0.4 m处设置D轴。表 1给出了本研究使用的物理参数，模型试验所用砂土的干密度为1612 kg/m³，孔隙率为0.33，渗透系数为2.28×10⁻⁴ m/s。理论模型中D轴的温度分布结果与试验结果对比如图 2所示。可以看出理论分析结果与模型试验结果基本一致。

图 1 Wang等^[14]的模型试验示意图

Figure 1. Sketch of model tests conducted by Wang et al.^[14]

下载: 全尺寸图片幻灯片

表 1 数值模型中物理参数^[12]

Table 1. Physical parameters for numerical simulation^[12]

名称	符号	值	单位	名称	符号	值	单位
吸附系数	k_ad	2.5×10^-4	s^-1	水冰相变潜热	L_wi	6.01	kJ·mol^-1
解吸系数	k_de	1.5×10^-4	s^-1	液相压缩率	β_lp	1×10^-7	kPa^-1
固相热膨胀系数	β_sT	7.8×10^-6	K^-1	液体热膨胀系数	β_lT	2.1×10^-4	K^-1
浓度依赖系数	β_lw	0.6923	—	液态水密度	$\rho _{\text{w}}^{\text{l}}$	1000	kg·m^-3
冰的密度	$\rho _{}^{\text{l}}$	917	kg·m^-3	摩尔气体常数	R	8.2	J·mol^-1·K^-1
结晶盐密度	$\rho _{}^{\text{p}}$	1460	kg·m^-3	结晶盐的物质的量	M_p	0.142	kg·mol^-1
盐的动力学参数	K_p	1.8×10^-3	s^-1	液相的物质的量	M_l	0.018	kg·mol^-1
吸湿膨胀系数	β_s	1.5×10^-4	—	固体热容	c_s	850	J·kg^-1·K^-1
冰的动力学参数	K_i	5.82×10^-3	s^-1	冰的热容	$c_{\text{i}}^{\text{i}}$	2090	J·kg^-1·K^-1
自由水结合水相变潜热	L_lp	73.04	kJ·mol^-1	结晶盐的热容	$c_{\text{p}}^{\text{p}}$	1743	J·kg^-1·K^-1
盐、结晶盐相变潜热	L_sc	2.34	kJ·mol^-1	固相压缩率	β_sp	2×10^-4	kPa^-1

下载: 导出CSV

| 显示表格

图 2 不同渗流速度下D轴上Wang等^[14]的试验中温度分布与理论验证

Figure 2. Verification of proposed theory with model tests conducted by Wang et al^[14] and spatial temperature distribution at (a) 0 m/d and (b) 3 m/d seepage velocity on D axis

下载: 全尺寸图片幻灯片

3. 参数研究

通过参数化研究，分析了不同渗流速度和温度梯度下各组分在砂层中的空间分布。砂土层模型试验渗流如所示。模型边界目标参数如所示，砂层中 $w_{{\text{p0}}}^{\text{l}}$ 和T₀的初始值分别为0.005和10℃。冻结管壁温度设为-27℃，渗流只存在于砂层底部。冰饱和度Sⁱ、结晶盐饱和度S^p、吸收盐含量 $w_{{\text{p0}}}^{\text{s}}$ 的初始条件和边界条件均为0。选取图 2中位于砂层中4条轴线D_c，D_s，I_c，I_s，绘制温度、冰、盐、位移分布图。

图 3 砂地层模型

Figure 3. Sketch of sand stratum model

下载: 全尺寸图片幻灯片

表 2 参数分析中使用的目标参数

Table 2. Target parameters used in parametric studies

项目	P_l0/kPa	T_p/℃	T₀/℃	$w_{{\text{p0}}}^{\text{l}}$	$w_{\text{p}}^{\text{l}}$	渗流/(m·d^-1)
试验	$\gamma _{\text{w}}^{}\Delta H$	-30	10	—	—	0, 3
渗流	$\gamma _{\text{w}}^{}\Delta H$	-27	13	0.005	0.005	0, 5, 10

下载: 导出CSV

| 显示表格

不同渗流速度的下部砂层中温度沿D轴和I轴分布情况如图 4所示。随着渗流速度从0 m/d增加到10 m/d，在人工冻结70 h后，在沿着D轴方向上的砂层上游的温度增加8.8℃，下游最高降低了13.2℃，如图 4（a）所示。当渗流速度从0 m/d增加到10 m/d，人工冻结70 h后，冻结管左右两侧的沿着I轴的温度升高了6.2℃，如图 4（b）所示。

图 4 在不同渗流速度下，冻结10，75 h后，砂层中温度分布

Figure 4. Distribution of temperature along (a) D axis and (b) I axis in sand stratum after 10 and 75 hours of freezing under different seepage velocities

下载: 全尺寸图片幻灯片

不同渗流速度对下部砂层中含冰量沿D轴和I轴分布情况如图 5所示。渗流导致水分开始冻结的位置沿着D轴向下游移动。随着渗流速度从0 m/d增加到10 m/d，在人工冻结70 h后，在沿着D轴方向上的砂层上游水分冻结的位置向下游移动了63.5%，下游中水分冻结的位置向下游移动了173.2%，如图 5（a）所示。当渗流速度从0 m/d增加到10 m/d，即人工冻结70 h后，冻结管左右两侧的沿着I轴的水分冻结范围缩减了37.8%，如图 5（b）所示。

图 5 在不同渗流速度下，冻结10，75 h后，砂层中冰含量分布

Figure 5. Distribution of ice content along (a) D axis and (b) I axis in sand stratum after 10 and 75 hours of freezing under different seepage velocities

下载: 全尺寸图片幻灯片

不同渗流速度对下部砂层中结晶盐量沿D轴和I轴分布情况如图 6所示。图 6（a）给出了沿着渗流方向上结晶盐含量随着渗流和冻结时间变化的分布情况，盐分析出的位置沿着D轴向下游移动。随着渗流速度从0 m/d增加到10 m/d，在人工冻结70 h后，在沿着D轴方向上的砂层上游盐分开始析出的位置向下游移动了65.1%，下游中盐分开始析出的位置向下游移动了182.7%。当渗流速度从0 m/d增加到10 m/d，即人工冻结70 h后，冻结管左右两侧的沿着Ⅰ轴的盐分的析出范围缩减了42.7%，如图 6（b）所示。

图 6 在不同渗流速度下，冻结10，75 h后，砂层中结晶盐含量分布

Figure 6. Distribution of crystalline salt content along (a) D axis and (b) I axis in sand stratum after 10 and 75 hours of freezing under different seepage velocities

下载: 全尺寸图片幻灯片

不同渗流速度对下部砂层吸附盐含量沿D轴和I轴分布的影响如图 7所示。渗流削弱了下游的盐分吸附能力。随着渗流速度从0 m/d增加到10 m/d，在人工冻结70 h后，在沿着渗流的D轴方向上，砂层上游的吸附盐突变位置向下游移动了52%，下游的吸附盐突变位置向下游移动了32%，如图 7（a）所示。当渗流速度从0 m/d增加到10 m/d，即人工冻结70 h后，冻结管左右两侧的沿着I轴的吸附盐突变范围向冻结管方向缩小了16.2%，如图 7（b）所示。

图 7 在不同渗流速度下，冻结10，75 h后，砂层中吸附盐含量分布

Figure 7. Distribution of adsorbed salt content along (a) D axis and (b) Ⅰ axis in sand stratum after 10 and 75 hours of freezing under different seepage velocities

下载: 全尺寸图片幻灯片

不同渗流速度对下部砂层中土体位移沿D轴和I轴分布情况如图 8所示。随着冻结时间的增加，砂地层在冻胀和盐胀的作用下土体位移逐渐增加。随着渗流速度从0 m/d增加到10 m/d，在人工冻结70 h后，在沿着D轴方向上的砂层上游的土体位移降低了33.4%，下游的土体位移降低了14.3%，如图 8（a）所示。当渗流速度从0 m/d增加到10 m/d，即人工冻结70 h后，冻结管左右两侧的沿着I轴的土体位移降低了23.1%，如图 8（b）所示。

图 8 在不同渗流速度下，冻结10，75 h后，砂层中位移分布

Figure 8. Distribution of soil displacement along (a) D axis and (b) I axis in sand stratum after 10 and 75 hours of freezing under different seepage velocities

下载: 全尺寸图片幻灯片

4. 结论

本文推导了渗流条件滨海砂土层人工冻结的水-盐-热-力学耦合模型。利用COMSOL Multiphysics软件对导出的微分方程进行求解。理论计算结果与文献中实验室模型试验结果吻合较好，验证了模型的准确性。通过参数分析，研究了不同渗流速度下的砂地层中各组分的空间分布情况。得出以下3点结论。

（1）在砂层冻结后，地层中的孔隙被堵塞，砂层底部上游的高温流体穿过地层的左右两侧下游流动。随着渗流速度从0 m/d增加到10 m/d，在人工冻结70 h后，砂层上游的最高温度增加8.8℃。冻结管左右两侧的土体位移降低了23.1%，渗流削弱了冻结效果，减小了冻结导致的土体位移。

（2）在垂直于渗流方向上，冻结管左右两侧的冰、结晶盐对称分布。在人工冻结70 h后，随着渗流速度从0 m/d增加到10 m/d，砂层上游水分冻结位置向下游移动63.5%，下游中水分冻结位置向下游移动173.2%，冻结管左右两侧的水分冻结范围缩减37.8%。

（3）冻结区域中盐分的吸附能力是被抑制的。随着渗流速度从0 m/d增加到10 m/d，在人工冻结70h后，砂层上游的吸附盐突变位置向下游移动52%，下游的吸附盐突变位置向下游移动32%，冻结管左右两侧的吸附盐突变范围向冻结管方向缩小16.2%。

图 1 试验土样颗粒级配曲线

Figure 1. Grain-size distribution curves of soil samples

下载: 全尺寸图片幻灯片

图 2 三轴仪

Figure 2. Triaxial apparatus

下载: 全尺寸图片幻灯片

图 3 不同条件下抗压强度应力应变曲线

Figure 3. Stress-strain curves of compressive strength under different conditions

下载: 全尺寸图片幻灯片

图 4 试样1-1-4和1-1-5的应力应变曲线

Figure 4. Stress-strain curves of samples 1-1-4 and 1-1-5

下载: 全尺寸图片幻灯片

图 5 试样1-2-1和1-2-2的应力应变曲线

Figure 5. Stress-strain curves of samples 1-2-1 and 1-2-2

下载: 全尺寸图片幻灯片

图 6 总应力强度包络线

Figure 6. Envelopes of total stress intensity

下载: 全尺寸图片幻灯片

表 1 试验土样物理指标汇总表

Table 1 Physical indices of soil samples

试样编号	G_s	w_L/%	w_P/%	I_P	ρ_dmax/(g·cm^-3)	w_op/%	工程分类
1-1	2.72	33.6	19.8	13.8	1.54	21.0	SM
1-2	2.70	32.6	18.7	13.9	1.78	17.8	CLS

下载: 导出CSV

表 2 试验方案汇总表

Table 2 Summary of test scheme

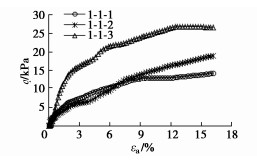
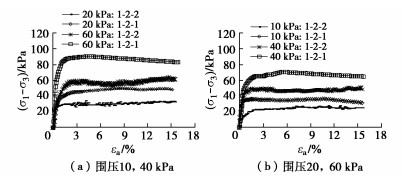
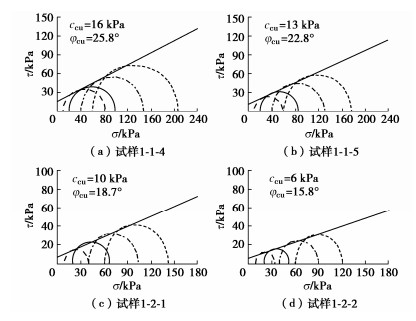
方案序号	试样编号	压实度	干密度ρ_d/(g·cm^-3)	围压σ₃/kPa	试验条件
1	1-1-1	0.9	1.39	—	无侧限抗压
2	1-1-2	0.9	1.39	—	压力室内无侧限
3	1-1-3	0.9	1.39	—	压力室内套橡皮膜
4	1-1-4	0.9	1.39	10，20，40，60	三轴CU，国产三轴
5	1-1-5	0.9	1.39		三轴CU，GDS三轴
6	1-2-1	0.9	1.60		三轴CU，国产三轴
7	1-2-2	0.9	1.60		三轴CU，GDS三轴

下载: 导出CSV

表 3 三轴试验结果汇总表

Table 3 Summary of triaxial test results

试样编号	总应力强度指标		不同围压下破坏点强度q/kPa
试样编号	c_cu/kPa	φ_cu/(°)	10 kPa	20 kPa	40 kPa	60 kPa
1-1-4	16	25.8	71.3	78.5	108.5	147.4
1-1-5	13	22.8	48.9	65.7	90.8	117.5
1-2-1	10	18.7	31.1	48.0	65.0	83.5
1-2-2	6	15.8	23.8	32.0	49.0	60.8

下载: 导出CSV

参考文献(13)

[1]	宁祚良, 陈刚, 陈旭. 多轴试验测试技术的发展与应用[J]. 机械工程学报, 2021, 57(16): 16-36. https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB202116003.htm NING Zuoliang, CHEN Gang, CHEN Xu. Development and application of multiaxial testing technique[J]. Journal of Mechanical Engineering, 2021, 57(16): 16-36. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB202116003.htm
[2]	蔡正银, 周宏磊, 蔡国军, 等. 土工测试与勘察技术研究进展[J]. 土木工程学报, 2020, 53(5): 100-117. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC202005009.htm CAI Zhengyin, ZHOU Honglei, CAI Guojun, et al. Review of the geotechnical testing and exploration techniques[J]. China Civil Engineering Journal, 2020, 53(5): 100-117. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC202005009.htm
[3]	郭万里, 朱俊高, 王俊杰, 等. 粗粒土静力特性及室内测试技术研究进展[J]. 岩石力学与工程学报, 2020, 39(增刊2): 3570-3585. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2020S2035.htm GUO Wanli, ZHU Jungao, WANG Junjie, et al. Research progress on static properties and laboratory testing technology of coarse-grained soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(S2): 3570-3585. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2020S2035.htm
[4]	肖晓, 冯秀丽, 林霖, 等. 低围压下埕北海域重塑粉土振动孔压模型试验研究[J]. 海洋地质与第四纪地质, 2020, 40(4): 214-222. https://www.cnki.com.cn/Article/CJFDTOTAL-HYDZ202004018.htm XIAO Xiao, FENG Xiuli, LIN Lin, et al. An experimental research of vibration pore water pressure of remolded silt under low confining pressure: a case from Chengbei Sea area[J]. Marine Geology & Quaternary Geology, 2020, 40(4): 214-222. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HYDZ202004018.htm
[5]	GU L L, WANG Z, HOSOYA A H, et al. Dilatancy and liquefaction behaviour of clean sand at wide range of confining stresses[J]. Journal of Central South University, 2020, 27(8): 2394-2407. doi: 10.1007/s11771-020-4457-0
[6]	聂如松, 董俊利, 程龙虎, 等. 重载铁路基床填料低围压静三轴试验研究[J]. 铁道科学与工程学报, 2019, 16(11): 2707-2715. https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD201911009.htm NIE Rusong, DONG Junli, CHENG Longhu, et al. The study on static triaxial test of heavy haul railway filler of subgrade roadbed under low confining pressure[J]. Journal of Railway Science and Engineering, 2019, 16(11): 2707-2715. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD201911009.htm
[7]	方涤华, 夏怀祖. 三轴压缩试验中活塞摩阻和橡皮膜的影响[J]. 大坝观测与土工测试, 1989(5): 27-32, 36. https://www.cnki.com.cn/Article/CJFDTOTAL-DBGC198905004.htm FANG Dihua, XIA Huaizu. Influence of piston friction and rubber membrane in triaxiao tests[J]. Hydropower Automation and Dam Monitoring, 1989(5): 27-32, 36. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DBGC198905004.htm
[8]	郭爱国, 茜平一. 三轴压缩试验中橡皮膜约束影响的校正[J]. 岩土力学, 2002, 23(4): 442-445. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200204011.htm GUO Aiguo, QIAN Pingyi. Corrections for influence of membrane restraint in triaxial test[J]. Rock and Soil Mechanics, 2002, 23(4): 442-445. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200204011.htm
[9]	肖杰, 杨和平, 林京松, 等. 模拟干湿循环及含低围压条件的膨胀土三轴试验[J]. 中国公路学报, 2019, 32(1): 21-28. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201901004.htm XIAO Jie, YANG Heping, LIN Jingsong, et al. Simulating wet-dry cycles and low confining pressures triaxial test on expansive soil[J]. China Journal of Highway and Transport, 2019, 32(1): 21-28. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201901004.htm
[10]	FUKUSHIMA S, TATSUOKA F. Strength and deformation characteristics of saturated sand at extremely low pressures[J]. Soils and Foundations, 1984, 24(4): 30-48.
[11]	邹维列, 陈轮, 张俊峰, 等. 低围压水平下QH-E模拟月壤三轴试验技术与力学特性[J]. 岩土工程学报, 2015, 37(8): 1418-1425. doi: 10.11779/CJGE201508009 ZOU Weilie, CHEN Lun, ZHANG Junfeng, et al. Techniques for triaxial compression tests on simulant lunar soil QH-E and its mechanical behaviors under low confining stress[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(8): 1418-1425. (in Chinese) doi: 10.11779/CJGE201508009
[12]	王鹏鹏. 土工三轴试验系统非线性补偿控制与变形场测量[D]. 大连: 大连理工大学, 2020. WANG Pengpeng. Nonlinear Compensation Control and Deformation Field Measurement in Geotechnical Triaxial Experiment System[D]. Dalian: Dalian University of Technology, 2020. (in Chinese)
[13]	刘潇. 三轴试验土样全表面变形测量方法及其应用[D]. 大连: 大连理工大学, 2012. LIU Xiao. Method of Whole Surface Deformation Measurement for Soil Specimen In Triaxial Tests and its Application[D]. Dalian: Dalian University of Technology, 2012. (in Chinese)