基于随机动力分析的高土石坝极限抗震能力研究

庞锐; 卢韵竹; 季睿; 徐斌

doi:10.11779/CJGE20230690

基于随机动力分析的高土石坝极限抗震能力研究 English Version

庞锐^{1, 2,},
卢韵竹¹,
季睿¹,
徐斌^{1, 2, ,}

1.
大连理工大学建设工程学院, 辽宁大连 116024
2.
海岸和近海工程国家重点试验室(大连理工大学), 辽宁大连 116024

基金项目:

国家自然科学基金项目 52279096

国家自然科学基金项目 52279125

国家自然科学基金项目 52379117

详细信息

作者简介:
庞锐(1989—)，男，博士，副教授，硕士生导师，主要从事水利工程和岩土工程抗震风险评价等方面的工作。E-mail: pangrui@dlut.edu.cn

通讯作者:
徐斌, E-mail: xubin@dlut.edu.cn

中图分类号: TU43
计量
- 文章访问数: 412
- HTML全文浏览量: 55
- PDF下载量: 86
出版历程
- 收稿日期: 2023-07-19
- 网络出版日期: 2023-12-19
- 刊出日期: 2024-09-30

Ultimate a seismic capacity of high earth-rock dams based on stochastic dynamic analysis

PANG Rui^{1, 2,},
LU Yunzhu¹,
JI Rui¹,
XU Bin^{1, 2, ,}

1.
School of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China
2.
The State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China

摘要

摘要: 地震动的随机性对大坝的动力响应影响较大，极限抗震能力作为大坝抗震安全性能的重要环节，在评估过程中也应该充分考虑荷载随机性的影响。基于大量高土石坝随机动力有限元计算，探究坝顶震陷率和坝坡累计滑移量两个重要坝体变形指标之间的关系，并建议了土石坝安全控制标准。利用概率密度演化法对高土石坝进行极限抗震能力分析。结果表明：震陷率随着累计滑移量的增大而增大，二者之间符合逻辑斯蒂增长模型；取10%的超越概率，以250 m规则高面板堆石坝和高心墙堆石坝为例，极限抗震能力分别为0.7g~0.75g和0.8g~0.85g；从概率角度提出了评估大坝极限抗震能力的新方法。
- 随机动力分析 /
- 高土石坝 /
- 极限抗震能力 /
- 谱表达-随机函数法 /
- 概率密度演化法
Abstract: The randomness of seismic motion significantly affects the dynamic response of dams. The ultimate capacity is a critical factor for the seismic safety of dams, thus during the assessment process the influences of load randomness should be thoroughly considered. Based on a large number of random dynamic finite element calculations for high earth-rock dams, the relationship between the settlement rate of dam crest and the cumulative sliding displacement of slope, two important deformation indices of dams is studied. Additionally, the safety control standards for earth-rock dams are proposed. The probabilistic density evolution method is used to analyze the ultimate a seismic capacity of dams. The results indicate that the settlement rate increases with the cumulative sliding displacement and follows a logistic growth model. Taking the exceedance probability of 10% as an example, the ultimate a seismic capacities for a 250 m-high faced rockfill dam and a high-core rockfill dam are approximately 0.7g~0.75g and 0.8g~0.85g, respectively. A new probabilistic approach is proposed for evaluating the ultimate a seismic capacities of dams.
- stochastic dynamic analysis /
- high earth-rock dam /
- ultimate a seismic capacity /
- spectral expression-random function method /
- probability density evolution methed

HTML全文

0. 引言

为了适应国家经济发展要求，推动清洁低碳的新能源体系建设，在水资源丰富的西部高烈度地区修建高坝大库是国家水电开发战略的大势所趋^[1]。土石坝对地形适应能力强、抗震性能好，得到了广泛的应用。为了适应地形特征，土石坝的坝高逐渐增加，例如200 m级的长河坝（240 m）、300 m级的双江口（315 m）^[2]。高坝的抗震安全成为工程建设过程中不可忽视的问题。

随着工程安全意识的提升，大坝的极限抗震能力成为评估其抗震安全性能的关键焦点，众多学者在该领域进行了广泛研究^[3-4]。然而迄今为止，相关研究主要依赖于确定的地震动输入。赵剑明等^[5]采用设计和校核地震场地波提出了基于稳定、变形、面板防渗体系安全的极限抗震能力分析方法并建议了安全评价标准；陈生水等^[6]基于有限元动力时程法，通过调整峰值加速度实现对地震动强度的控制，并结合震害调查建议了高土石坝地震安全控制标准。邹德高等^[7]输入实际工程场地谱的人工波，结合实测资料建议了土石坝的极限抗震能力评价量化指标。上述研究均未考虑地震动不确定性对极限抗震能力的影响，但是研究表明随机荷载对大坝动力响应影响较大^[8-9]。因此，将可靠度理念引入大坝极限抗震能力研究有重要意义。

本文利用谱表达-随机函数的方法生成非平稳随机地震动，建立面板堆石坝和心墙堆石坝二维有限元模型。将等价极值思想和概率密度演化法相结合获取了大坝随机动力响应极值的概率信息。最后，以坝顶震陷率和坝坡累计滑移量为安全控制指标，基于超越概率等值线图以及安全控制指标-PGA-超越概率关系表，从概率角度进行高土石坝的极限抗震能力评估。

1. 随机地震动模拟及概率密度演化

1.1 谱表达-随机函数模型

梁建文^[10]根据Priestly提出的非平稳渐进功率谱理论，直接推导出实非平稳地震动加速度时程模拟的谱表示方法：

${\ddot X_{\text{g}}}(t) = \sum\limits_{k = 1}^N {\sqrt {2{S_{{X_{\text{g}}}}}(t,{\omega _k})\Delta \omega } \left[ {\cos ({\omega _k}t){X_k} + \sin ({\omega _k}t){Y_k}} \right]} 。$

(1)

式中： ${\omega _k}$ =kΔω；N为截断级数。Liu等^[11]在该模型中引入随机函数的思想，将随机变量的数量减少至2个，提高了计算效率。所需的两个基本随机变量Θ₁和Θ₂服从均匀分布且相互独立，其构造的两个标准正交随机变量 ${\bar X_k}$ 和 ${\bar Y_k}$ 可以写为

${\bar X_k} = {\text{cas}}(k{\Theta _1}) \text{，}$

(2)

${\bar Y_k} = {\text{cas}}(k{\Theta _2}) 。$

(3)

式中：n=1, 2, …, N；cas(x)=sin(x)+cos(x)是Hartley正交基函数。将{ ${\bar X_k}$ , ${\bar Y_k}$ }做映射可以得到唯一确定的正交随机变量{X_k，Y_k}，功率谱采用C-P谱^[12]，并在此基础上考虑地震动频率和强度随时间的变化特性，得到强度-频率全非平稳地震动的演化功率谱密度函数：

$\begin{aligned} S_{\ddot{X}_{\mathrm{g}}}(t, \omega)= & A^2(t) \frac{\omega_{\mathrm{g}}(t)+4 \xi_{\mathrm{g}}^2(t) \omega_{\mathrm{g}}^2(t) \omega^2}{\left[\omega^2-\omega_{\mathrm{g}}^2(t)\right]^2+4 \xi_{\mathrm{g}}^2(t) \omega_{\mathrm{g}}^2(t) \omega^2}\cdot \\ & \frac{\omega^4}{\left(\omega^2-\omega_{\mathrm{f}}^2\right)^2+4 \xi_{\mathrm{f}}^2(t) \omega_{\mathrm{f}}^2(t) \omega^2} \cdot S_0(t)。 \end{aligned}$

(4)

式中：ω_g(t)和ξ_g(t)分别为场地土的卓越圆频率和阻尼比，可由式（5），（6）确定；ω_f和ξ_f为二次滤波频率参数和阻尼比参数，ω_f=0.1ω_g，ξ_f=ξ_g；A(t)见式（7）。

${\omega _{\text{g}}}(t) = {\omega _{\text{0}}} - a\frac{t}{T} \text{，}$

(5)

${\xi _{\text{g}}} = {\xi _{\text{0}}} + b\frac{t}{T} \text{，}$

(6)

$A(t) = {\left[ {\frac{t}{c}\exp (1 - \frac{t}{c})} \right]^d} 。$

(7)

a和b为描述场地圆频率和阻尼比随时间变化的常数；T为地震动持时；c和d分别为控制峰值加速度到达时刻和包络函数形状的参数；S₀为谱强度因子：

${S_{\text{0}}}(t) = \frac{{2a_{{\text{max}}}^2}}{{{\gamma ^2}{\text{π }}{\omega _{\text{g}}}(t)\left[ {2{\xi _{\text{g}}}(t) + \frac{1}{{2{\xi _{\text{g}}}(t)}}} \right]}} 。$

(8)

式中：a_max为峰值加速度的平均值； $\gamma$ 为峰值因子。

1.2 非平稳随机地震动生成

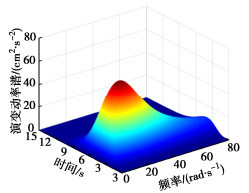
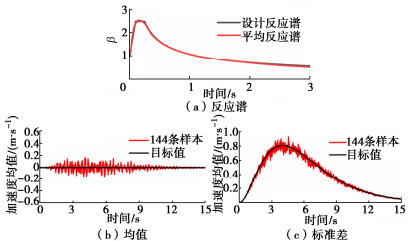
以《水工建筑物抗震设计标准：GB51247—2018》^[13]中划分的I₀场地为例，识别了演化功率谱密度函数的参数（表 1），并通过迭代提高了反应谱拟合精度。基于数论法生成的144个随机点，对应144条随机地震动样本^[14]。演化功率谱密度函数如图 1所示，样本平均反应谱与标准中的设计反应谱的拟合效果以及前两阶统计矩时程与目标值的对比见图 2。

表 1 I₀场地演化功率谱密度函数的参数

Table 1. Parameters of power spectral density function of I₀ site

参数	ω₀/s^-1	ξ₀	a/s^-1	b	c/s	d	γ	T/s
I₀场地	27.5	0.65	20	0.65	4	2	2.5	15

下载: 导出CSV

| 显示表格

图 1 I₀场地的演化功率谱函数

Figure 1. Evolution power spectral function of I₀ site

下载: 全尺寸图片幻灯片

图 2 样本反应谱、均值和标准差与目标值对比

Figure 2. Comparison between response spectrum, mean and standard deviation and target values

下载: 全尺寸图片幻灯片

经计算，均值和标准差的相对误差分别为6.69%，9.25%，平均反应谱的相对误差为2.40%，满足精度要求，拟合效果较好，可以为结构随机响应分析提供有效的随机激励。

1.3 概率密度演化法

一般的多自由度体系的运动方程可以写为

$M\ddot X(t) + C\dot X(t) + KX(t) = - M{\ddot X_{\text{g}}}(\Theta ,t) 。$

(9)

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；Ẍ(t)，Ẋ(t)和X(t)分别为结构的相对加速度、速度和位移；Ẍ_g(Θ, t)表示地面运动的加速度，荷载的随机性包含在Θ中。该系统为概率守恒系统，服从概率守恒定律，可以推导出概率密度演化方程^[15]：

$\frac{{\partial {P_{Z\Theta }}(z,\theta ,t)}}{{\partial t}} + \ddot Z(\theta ,t)\frac{{\partial {P_{Z\Theta }}(z,\theta ,t)}}{{\partial z}} = 0 。$

(10)

式中：Z为结构的动力响应； ${P_{Z\Theta }}$ (z, θ, t)是(Z, Θ)的联合概率密度函数。在输入随机变量Θ的概率空间上积分，得到动力响应Z的概率密度函数（PDF）的表达式：

${P_Z}(z,t) = \int_{{\Omega _\Theta }} {{P_{Z\Theta }}(z,\theta ,t){\text{d}}\theta } 。$

(11)

对于复杂的非线性结构，需要利用数值的方法进行求解。首先划分输入随机变量空间Ω_Θ并利用数论法^[16]选取代表点，采用TVD格式差分^[17]求解式（11），结构响应Z的PDF即为各个代表点处求解结果之和：

${P_Z}(z,t) = \sum\limits_{q = 1}^N {{P_{Z\Theta }}(z,{\theta _q},t)} 。$

(12)

将上述概率密度演化的理论与等价极值分布思想^[18]相结合，构造与极值向量E(Θ，T)有关的虚拟随机过程V(τ)=φ(Θ, T, τ)，得到虚拟随机过程的概率密度演化方程（式(14)）。

$E(\Theta ,T) = {\text{ex}}{{\text{t}}_{t \in [0,T]}}(Z(t)) \text{，}$

(13)

$\frac{{\partial {P_{V\Theta }}(v,\theta ,t)}}{{\partial t}} + \dot \varphi (\theta ,t)\frac{{\partial {P_{V\Theta }}(v,\theta ,t)}}{{\partial v}} = 0 。$

(14)

式中：P_VΘ(v, θ, τ)为V(τ)和Θ的联合概率密度函数。虚拟随机函数在τ_c=1处与极值相等，数值求解得到的虚拟随机函数的PDF等价于极值的PDF，积分得到累计概率分布函数（CDF）以及对应的超越概率。

2. 高土石坝有限元模型及安全控制指标

2.1 有限元模型

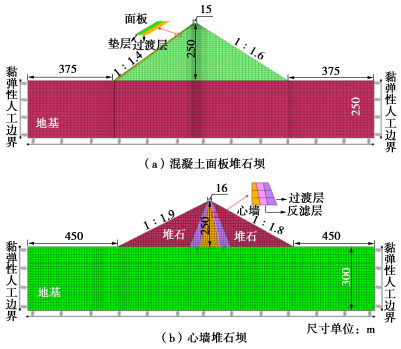
实际工程中坝体最大变形位置常位于最大断面内，而且坝体最大剖面与三维模型的变形计算结果的规律一致^[19]。为了减少计算量，分别建立了200，250 m的高面板堆石坝模型和200，250，300 m高的心墙堆石坝二维有限元模型（图 3）。地基的底边和两侧设置粘弹性边界单元，同时输入激发水平向地面运动和竖向地面运动的地震波，水平向峰值加速度以0.1g为间隔从0.1g增至1.0g，竖向地震动加速度峰值取水平向的2/3，进行1440次随机动力有限元计算。坝坡稳定计算采用有限元动力时程分析法^[20]。

图 3 典型混凝土面板堆石坝、心墙堆石坝二维有限元模型

Figure 3. 2D finite element models for typical concrete face rockfill dam and core wall rockfill dam

下载: 全尺寸图片幻灯片

2.2 安全控制标准

高土石坝在地震动作用下，坝顶塌陷变形严重时会导致坝顶高程低于上游库水位，出现“漫顶”的重大灾害。同时坝顶的震陷也是坝体出现裂缝的主要诱因，甚至会导致渗透破坏。根据邹德高等^[7]和刘君等^[21]的统计，实际工程中土石坝震陷率与地震动峰值加速度（PGA）之间有明显的正相关性。坝顶震陷直接反映了大坝的受到地震作用后的永久变形程度，因此坝顶竖向变形可以作为评估坝体极限抗震能力的指标之一。工程界一般使用坝顶沉降量与坝高之比（坝顶震陷率δ）来表示坝体在地震动作用下的变形情况。

在有关土石坝安全控制标准的研究中，前期研究常根据工程经验、震害数据以及有限的数值计算划定安全范围，确定极限抗震标准。表 2所示为部分土石坝极限抗震能力指标研究成果。综合考虑国内外数十座土石坝的实际震陷率数据^[21]，高面板堆石坝大多在坝顶震陷率大于0.8%时，出现比较严重的变形破坏。心墙坝的震陷率一般高于高面板坝，美国的AMBUKLAO心墙坝坝高120 m，在0.49g地震动作用下出现严重损害，坝顶震陷率达到0.88%^[22]。另外根据对不同坝高的心墙坝进行数值计算的结果表明，坝高的增加会导致震陷率的增大，因此可以推断，对于坝高超过200 m的心墙坝在震陷率达到0.9%时将处于严重破坏状态。综上，建议分别将0.8%，0.9%作为高面板堆石坝和高心墙坝的安全控制标准。

表 2 部分土石坝极限抗震能力指标研究成果

Table 2. Research results of ultimate a seismic capacity index of some earth-rock dams

研究者	坝顶震陷率	坝坡稳定
邹德高等^[7]	高面板坝1.1% 高心墙坝1.3%	高面板坝1.2 m 高心墙坝1.4 m
赵剑明等^[5]	高面板坝： 0.6%~0.8%	动力时程法，安全系数1.0 动力等效值法，安全系数1.1
陈生水等^[6]	面板坝0.6% 心墙坝1%	拟静力法，安全系数1.0 有限元时程分析法，安全系数小于1.2的累计时间 < 2 s
李国英等^[25]	高心墙坝1%	拟静力法，安全系数1.0 有限元时程分析法，安全系数小于1.2的累计时间 < 2 s
田景元等^[4]	以100，200，250，300 m坝高为分界：2%，1.5%，1%，0.85%，0.75%	拟静力法，安全系数 > 1.0 有限元时程分析法，安全系数小于1的累计时间 < 1 s
刘君等^[21]	小于0.6g的地震震陷率不超过1%	—
邵磊等^[26]	高心墙坝震陷率 < 1.2%，且设计工况震陷 < 1 m	滑移变形 > 滑体长度的2%
Swaisgood^[22]	0.5%及以上严重破坏	—

下载: 导出CSV

| 显示表格

结合紫坪铺面板堆石坝的震害情况^[23]以及其他土石坝的地震变形响应，发现坝坡滑移是一种常见的震害形式。近年来有限元动力时程法在高土石坝极限抗震能力评估领域得到了广泛的应用。徐斌等^[20]基于有限元动力时程稳定的分析方法，引入累计滑移量指标进行抗震安全性评价。孔宪京等^[24]考虑了堆石料软化，基于最小安全系数、安全系数超限累计时间以及累计滑移量进行了土石坝坝坡可靠度评价。邹德高等^[7]基于实际的震害数据统计结果提出坝顶震陷率和坝坡累计滑移量之间存在线性关系，但有限的震害数据限制了两个指标之间相关性的研究。因此，本文基于大量的随机动力有限元模拟结果，建立了二者之间的统计关系，以便利用震陷率安全控制标准确定累计滑移量安全控制标准。

2.3 震陷率与累计滑移量的关系

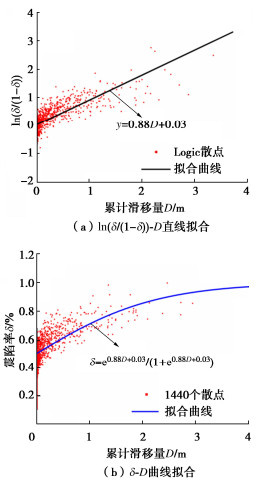
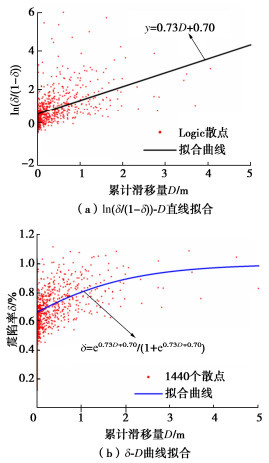
以坝体的最大累计滑移量为横坐标，最终震陷率为纵坐标，绘制散点图并进行拟合。对比最小二乘法拟合、二次函数拟合以及逻辑斯蒂回归拟合的拟合效果，最终认为采用逻辑斯蒂增长模型的拟合效果最佳。拟合过程中先将震陷率δ做如下对数变换：

$y = \ln \left( {\frac{\delta }{{1 - \delta }}} \right)。$

(15)

变换后离散点（简称Logistic散点）的分布呈现较好的线性关系，即y=a+bD（D为坝坡累计滑移量）。陷率与累计滑移量之间的拟合曲线如图 4，5所示，曲线数学表达式如下：

图 4 面板堆石坝震陷率与累计滑移量拟合

Figure 4. Fitting of settlement rate and cumulative sliding displacement of concrete face rockfill dam

下载: 全尺寸图片幻灯片

图 5 心墙堆石坝震陷率与累计滑移量拟合

Figure 5. Fitting of settlement rate and cumulative slding displacement of core wall rockfill dam

下载: 全尺寸图片幻灯片

$\delta = \frac{{{{\text{e}}^{a + bD}}}}{{1 + {{\text{e}}^{a + bD}}}}。$

(16)

面板堆石坝和心墙坝的逻辑斯蒂拟合结果见式（17），（18），均方误差分别为0.0046，0.0128，可以认为拟合效果良好。

${\delta _{\text{f}}} = \frac{{{{\text{e}}^{0.0343 + 0.8827{D_{\text{f}}}}}}}{{1 + {{\text{e}}^{0.0343 + 0.8827{D_{\text{f}}}}}}} \text{，}$

(17)

${\delta _{\text{c}}} = \frac{{{{\text{e}}^{0.7045 + 0.7268{D_{\text{c}}}}}}}{{1 + {{\text{e}}^{0.7045 + 0.7268{D_{\text{c}}}}}}} 。$

(18)

式中：D为坝坡滑移量；δ为坝顶震陷率；下标f和c分别表示面板坝指标和心墙坝指标。心墙坝的两个变形指标相关性比面板坝变形指标相关性弱，散点相对比较分散。但是总体来看，两种坝型震陷率与累计滑移量两个指标之间均为正相关，震陷率随着累计滑移量的增大而增大，且增速逐渐变慢，累计滑移量和震陷率指标之间的逻辑斯蒂拟合关系。

将2.2节确定的高面板坝和高心墙坝抗震安全控制标准：δ_f=0.8%和δ_c=0.9%分别代入式（17），（18），计算得到基于坝坡累计滑移量的安全控制标准分别为153，205 cm。

3. 极限抗震能力评估

结合目前工程界广泛应用的概率密度演化法和等价极值分布^[18]的思想，在考虑随机荷载作用下结构响应随机性的基础上，获取结构最大响应的概率信息，即累计概率密度曲线（CDF）或者超越概率曲线。超越概率指的是超过某一响应值的概率。参考核电厂“高裕度（95%）”的评估依据^[27]，水工结构的安全裕度可以在此基础上适当降低，本文建议选用90%作为高土石坝极限抗震评估的安全裕度（超越概率10%）。

在不同的超越概率曲线上，每隔0.1%震陷率取一个超越概率值，制作面板堆石坝和心墙堆石坝的震陷率-PGA-超越概率关系表（表 3，4）。根据确定好的震陷率安全控制指标及安全裕度，在表 3中查得大坝的极限抗震能力在0.7g~0.8g。同理，可以确定高心墙坝的极限抗震能力在0.8g~0.9g。采用同样的方法可以得到两种坝型累计滑移量-PGA-超越概率关系表（表 5，6）。用线性插值的方法在表中补充出153，205 cm的超越概率值，得到文中高面板堆石坝和高心墙堆石坝模型的极限抗震能力分别为0.8g~0.9g和0.9g~1.0g。

表 3 高面板堆石坝震陷率-PGA-超越概率的关系表

Table 3. Relationship of settlement rate-PGA-exceedance probability of high concrete face rockfill dam

地震动峰值加速度/g	坝顶相对震陷率/%
	0.1		0.2		0.3		0.4		0.5		0.6		0.7		0.8		0.9		1.0		1.1		1.2
	超越概率/%
0.1		92.44		19.81		0		0		0		0		0		0		0		0		0		0
0.2		100		87.67		23.63		0.61		0		0		0		0		0		0		0		0
0.3		100		99.07		73.18		18.86		1.14		0		0		0		0		0		0		0
0.4		100		100		94.06		56.49		13.63		1.51		0		0		0		0		0		0
0.5		100		100		98.87		83.18		41.74		10.60		1.46		0		0		0		0		0
0.6		100		100		100		94.92		68.65		31.91		7.04		1.56		0		0		0		0
0.7		100		100		100		98.54		86.27		55.34		21.98		5.07		1.38		0		0		0
0.8		100		100		100		100		94.60		74.78		41.11		15.66		3.30		1.08		0		0
0.9		100		100		100		100		97.93		87.49		59.65		31.08		9.89		2.39		0.96		0
1.0		100		100		100		100		99.16		93.95		74.86		46.19		20.84		5.23		1.73		0.87

下载: 导出CSV

| 显示表格

表 4 高心墙堆石坝震陷率-PGA-超越概率的关系表

Table 4. Relationship of settlement rate-PGA-exceedance probability of high core wall rockfill dam

地震动峰值加速度/g	坝顶相对震陷率/%
	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0	1.1	1.2
	超越概率/%
0.1	97.93	32.37	0	0	0	0	0	0	0	0	0	0
0.2	100	98.31	45.47	1.71	0	0	0	0	0	0	0	0
0.3	100	100	94.10	35.63	2.90	0	0	0	0	0	0	0
0.4	100	100	100	80.46	25.70	2.08	0	0	0	0	0	0
0.5	100	100	100	96.91	63.31	17.25	1.68	0	0	0	0	0
0.6	100	100	100	100	88.17	45.18	10.37	1.19	0	0	0	0
0.7	100	100	100	100	97.19	72.17	30.91	7.17	1.00	0	0	0
0.8	100	100	100	100	99.37	89.83	55.79	22.68	6.12	0.91	0	0
0.9	100	100	100	100	100	96.99	77.21	43.14	18.38	5.81	0.68	0
1.0	100	100	100	100	100	98.73	90.54	64.95	35.23	15.03	4.54	0.18

下载: 导出CSV

| 显示表格

表 5 高面板堆石坝累计滑移量-PGA-超越概率的关系表

Table 5. Relationship of cumulative sliding displacement-PGA-exceedance probability of high concrete face rockfill dam

峰值加速度/g	累积滑移量/cm
	0	1	5	10	20	50	80	100	120	153	200	250
	超越概率/
0.4	8.63	3.99	1.39	0.69	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
0.5	33.00	29.04	14.84	10.11	5.83	1.24	0.76	0.00	0.00	0.00	0.00	0.00
0.6	68.48	57.13	31.02	20.55	12.07	6.64	5.83	1.06	0.00	0.00	0.00	0.00
0.7	90.44	81.82	58.80	44.44	19.39	13.36	8.66	6.67	1.98	1.16	0.00	0.00
0.8	92.32	90.87	80.95	64.20	41.20	18.75	14.43	12.21	8.64	6.08	2.43	1.07
0.9	94.07	91.96	88.76	85.77	59.95	37.24	21.80	16.26	13.36	11.36	8.51	7.22
1.0	95.59	93.23	90.24	85.51	76.69	55.34	39.04	26.49	17.07	14.96	11.97	10.35

下载: 导出CSV

| 显示表格

表 6 高心墙堆石坝累积滑移量-PGA-超越概率的关系表

Table 6. Relationship cumulative sliding displacement-PGA-exceedance probability of high core wall rockfill dam

峰值加速度/g	累积滑移量/cm
	0	1	5	10	20	50	80	100	120	200	205	250
	超越概率/%
0.4	12.5	6.94	1.42	0	0	0	0	0	0	0	0	0
0.5	29.86	18.75	13.19	7.64	2.78	0.69	0	0	0	0	0	0
0.6	57.64	37.5	25.01	20.83	12.5	2.08	1.39	0.65	0	0	0	0
0.7	75.69	60.42	47.22	33.33	23.61	7.64	4.17	2.78	1.37	0.43	0.387	0
0.8	86.11	72.92	61.81	54.17	39.58	17.36	9.03	6.25	2.1	1.44	1.373	0.77
0.9	95.14	85.42	73.61	65.97	52.08	34.47	20.49	15.32	8.89	5.79	5.453	2.42
1.0	98.61	90.28	81.94	72.55	63.89	39.58	29.64	20.04	16.36	12.69	12.186	7.65

下载: 导出CSV

| 显示表格

对比由震陷率确定的极限抗震能力，可以发现基于累计滑移量指标确定的大坝极限抗震能力较高。综合考虑大坝整体的变形情况，极限抗震能力应该以震陷率指标为准。

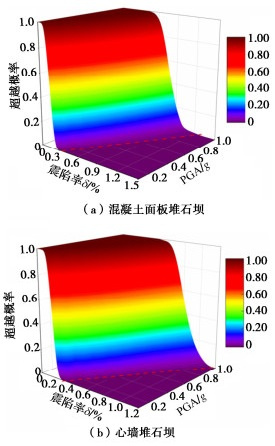
采用绘制超越概率等值线图的方法进一步缩小极限抗震能力区间。图 6为坝顶震陷率的超越概率曲面图，由10条不同的超越概率曲线决定。随着峰值加速度的增大，超越概率曲线逐渐向震陷率增大的方向移动。对于某一特定的震陷率值来说，随着PGA的增大，超越概率也逐渐增大。图中红色虚线表示超越概率曲面与水平坐标平面的交线，线上的点表示不同峰值加速度的作用下土石坝坝顶从概率意义上有可能达到的震陷率值。

图 6 混凝土面板堆石坝和心墙堆石坝震陷率超越概率曲面图

Figure 6. Exceedance probability surfaces of settlement rate of concrete face rockfill dam and core wall rockfill dam

下载: 全尺寸图片幻灯片

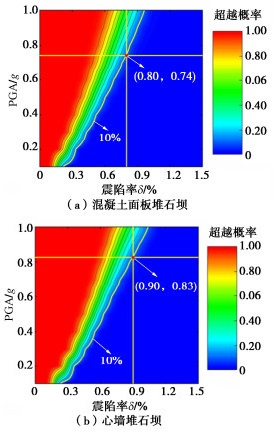
震陷率的超越概率等值线图为超越概率密度曲面图的投影，10%超越概率等值线与直线δ_f=0.8%（或δ_c=0.9%）交点所处的峰值加速度范围即为大坝极限抗震能力：0.7g~0.75g（面板坝）和0.8g~0.85g（心墙坝）。

经计算，坝型相同时，本文建立的5种不同高度的土石坝模型在概率意义上有着相近的极限抗震能力，均可采用上述结论作为其极限抗震能力评估结果。由于篇幅限制，本文仅针对250 m的面板坝和心墙坝极限抗震能力评估过程进行了详细说明。

图 7 面板堆石坝和心墙堆石坝震陷率超越概率等值线图

Figure 7. Contours of exceedance probability of settlement rate of concrete face rockfill dam and core wall rockfill dam

下载: 全尺寸图片幻灯片

4. 结论

本文在随机动力分析的基础上，探究了坝顶震陷率和坝坡累计滑移量两个变形指标的相关关系，建议了大坝安全控制标准。利用概率密度演化法，从概率意义上提出了评估土石坝极限抗震能力的新方法。主要得到以下3点结论。

（1）大量的随机动力有限元模拟结果表明，震陷率与累计滑移量指标之间符合逻辑斯蒂增长模型。

（2）结合工程震害实例，高面板堆石坝和高心墙堆石坝的安全控制标准建议采用0.8%和0.9%的震陷率，依据震陷率与累计滑移量之间的拟合曲线可以确定两种坝型的累计滑移量的安全控制标准分别为153，205 cm。

（3）利用安全控制标准-PGA-超越概率表和超越概率等值线图，确定了250 m规则面板坝和心墙坝模型的极限抗震能力分别为0.7g~0.75g和0.8g~0.85g。基于震陷率指标确定的极限抗震能力更严格，是高土石坝极限抗震能力的主要控制因素。

需要注意的是，本文提出了评估大坝极限抗震能力的新方法，实际工程的极限抗震能力还受到模型参数、地震动参数等因素影响，还需要结合实际情况计算、检验。在后续的研究中，将坝体堆石料参数的不确定性引入大坝极限抗震能力评估也具有重要意义。

图 1 I₀场地的演化功率谱函数

Figure 1. Evolution power spectral function of I₀ site

下载: 全尺寸图片幻灯片

图 2 样本反应谱、均值和标准差与目标值对比

Figure 2. Comparison between response spectrum, mean and standard deviation and target values

下载: 全尺寸图片幻灯片

图 3 典型混凝土面板堆石坝、心墙堆石坝二维有限元模型

Figure 3. 2D finite element models for typical concrete face rockfill dam and core wall rockfill dam

下载: 全尺寸图片幻灯片

图 4 面板堆石坝震陷率与累计滑移量拟合

Figure 4. Fitting of settlement rate and cumulative sliding displacement of concrete face rockfill dam

下载: 全尺寸图片幻灯片

图 5 心墙堆石坝震陷率与累计滑移量拟合

Figure 5. Fitting of settlement rate and cumulative slding displacement of core wall rockfill dam

下载: 全尺寸图片幻灯片

图 6 混凝土面板堆石坝和心墙堆石坝震陷率超越概率曲面图

Figure 6. Exceedance probability surfaces of settlement rate of concrete face rockfill dam and core wall rockfill dam

下载: 全尺寸图片幻灯片

图 7 面板堆石坝和心墙堆石坝震陷率超越概率等值线图

Figure 7. Contours of exceedance probability of settlement rate of concrete face rockfill dam and core wall rockfill dam

下载: 全尺寸图片幻灯片

表 1 I₀场地演化功率谱密度函数的参数

Table 1 Parameters of power spectral density function of I₀ site

参数	ω₀/s^-1	ξ₀	a/s^-1	b	c/s	d	γ	T/s
I₀场地	27.5	0.65	20	0.65	4	2	2.5	15

下载: 导出CSV

表 2 部分土石坝极限抗震能力指标研究成果

Table 2 Research results of ultimate a seismic capacity index of some earth-rock dams

研究者	坝顶震陷率	坝坡稳定
邹德高等^[7]	高面板坝1.1% 高心墙坝1.3%	高面板坝1.2 m 高心墙坝1.4 m
赵剑明等^[5]	高面板坝： 0.6%~0.8%	动力时程法，安全系数1.0 动力等效值法，安全系数1.1
陈生水等^[6]	面板坝0.6% 心墙坝1%	拟静力法，安全系数1.0 有限元时程分析法，安全系数小于1.2的累计时间 < 2 s
李国英等^[25]	高心墙坝1%	拟静力法，安全系数1.0 有限元时程分析法，安全系数小于1.2的累计时间 < 2 s
田景元等^[4]	以100，200，250，300 m坝高为分界：2%，1.5%，1%，0.85%，0.75%	拟静力法，安全系数 > 1.0 有限元时程分析法，安全系数小于1的累计时间 < 1 s
刘君等^[21]	小于0.6g的地震震陷率不超过1%	—
邵磊等^[26]	高心墙坝震陷率 < 1.2%，且设计工况震陷 < 1 m	滑移变形 > 滑体长度的2%
Swaisgood^[22]	0.5%及以上严重破坏	—

下载: 导出CSV

表 3 高面板堆石坝震陷率-PGA-超越概率的关系表

Table 3 Relationship of settlement rate-PGA-exceedance probability of high concrete face rockfill dam

地震动峰值加速度/g	坝顶相对震陷率/%
	0.1		0.2		0.3		0.4		0.5		0.6		0.7		0.8		0.9		1.0		1.1		1.2
	超越概率/%
0.1		92.44		19.81		0		0		0		0		0		0		0		0		0		0
0.2		100		87.67		23.63		0.61		0		0		0		0		0		0		0		0
0.3		100		99.07		73.18		18.86		1.14		0		0		0		0		0		0		0
0.4		100		100		94.06		56.49		13.63		1.51		0		0		0		0		0		0
0.5		100		100		98.87		83.18		41.74		10.60		1.46		0		0		0		0		0
0.6		100		100		100		94.92		68.65		31.91		7.04		1.56		0		0		0		0
0.7		100		100		100		98.54		86.27		55.34		21.98		5.07		1.38		0		0		0
0.8		100		100		100		100		94.60		74.78		41.11		15.66		3.30		1.08		0		0
0.9		100		100		100		100		97.93		87.49		59.65		31.08		9.89		2.39		0.96		0
1.0		100		100		100		100		99.16		93.95		74.86		46.19		20.84		5.23		1.73		0.87

下载: 导出CSV

表 4 高心墙堆石坝震陷率-PGA-超越概率的关系表

Table 4 Relationship of settlement rate-PGA-exceedance probability of high core wall rockfill dam

地震动峰值加速度/g	坝顶相对震陷率/%
	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0	1.1	1.2
	超越概率/%
0.1	97.93	32.37	0	0	0	0	0	0	0	0	0	0
0.2	100	98.31	45.47	1.71	0	0	0	0	0	0	0	0
0.3	100	100	94.10	35.63	2.90	0	0	0	0	0	0	0
0.4	100	100	100	80.46	25.70	2.08	0	0	0	0	0	0
0.5	100	100	100	96.91	63.31	17.25	1.68	0	0	0	0	0
0.6	100	100	100	100	88.17	45.18	10.37	1.19	0	0	0	0
0.7	100	100	100	100	97.19	72.17	30.91	7.17	1.00	0	0	0
0.8	100	100	100	100	99.37	89.83	55.79	22.68	6.12	0.91	0	0
0.9	100	100	100	100	100	96.99	77.21	43.14	18.38	5.81	0.68	0
1.0	100	100	100	100	100	98.73	90.54	64.95	35.23	15.03	4.54	0.18

下载: 导出CSV

表 5 高面板堆石坝累计滑移量-PGA-超越概率的关系表

Table 5 Relationship of cumulative sliding displacement-PGA-exceedance probability of high concrete face rockfill dam

峰值加速度/g	累积滑移量/cm
	0	1	5	10	20	50	80	100	120	153	200	250
	超越概率/
0.4	8.63	3.99	1.39	0.69	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
0.5	33.00	29.04	14.84	10.11	5.83	1.24	0.76	0.00	0.00	0.00	0.00	0.00
0.6	68.48	57.13	31.02	20.55	12.07	6.64	5.83	1.06	0.00	0.00	0.00	0.00
0.7	90.44	81.82	58.80	44.44	19.39	13.36	8.66	6.67	1.98	1.16	0.00	0.00
0.8	92.32	90.87	80.95	64.20	41.20	18.75	14.43	12.21	8.64	6.08	2.43	1.07
0.9	94.07	91.96	88.76	85.77	59.95	37.24	21.80	16.26	13.36	11.36	8.51	7.22
1.0	95.59	93.23	90.24	85.51	76.69	55.34	39.04	26.49	17.07	14.96	11.97	10.35

下载: 导出CSV

表 6 高心墙堆石坝累积滑移量-PGA-超越概率的关系表

Table 6 Relationship cumulative sliding displacement-PGA-exceedance probability of high core wall rockfill dam

峰值加速度/g	累积滑移量/cm
	0	1	5	10	20	50	80	100	120	200	205	250
	超越概率/%
0.4	12.5	6.94	1.42	0	0	0	0	0	0	0	0	0
0.5	29.86	18.75	13.19	7.64	2.78	0.69	0	0	0	0	0	0
0.6	57.64	37.5	25.01	20.83	12.5	2.08	1.39	0.65	0	0	0	0
0.7	75.69	60.42	47.22	33.33	23.61	7.64	4.17	2.78	1.37	0.43	0.387	0
0.8	86.11	72.92	61.81	54.17	39.58	17.36	9.03	6.25	2.1	1.44	1.373	0.77
0.9	95.14	85.42	73.61	65.97	52.08	34.47	20.49	15.32	8.89	5.79	5.453	2.42
1.0	98.61	90.28	81.94	72.55	63.89	39.58	29.64	20.04	16.36	12.69	12.186	7.65

下载: 导出CSV

参考文献(27)

[1]	靳聪聪. 基于性能的高土石坝地震易损性分析与地震风险评估方法研究[D]. 大连: 大连理工大学, 2020. JIN Congcong. Performance-Based Seismic Fragility Analysis and Seismic Risk Assessment Method Research of High Earth-Rockfill Dam[D]. Dalian: Dalian University of Technology, 2020. (in Chinese)
[2]	孔宪京, 陈健云, 邹德高. 高坝抗震安全理论发展趋势研究[J]. 水力发电学报, 2020, 39(7): 1-11. KONG Xianjing, CHEN Jianyun, ZOU Degao. Study on development trend of seismic safety theory for high dams[J]. Journal of Hydroelectric Engineering, 2020, 39(7): 1-11. (in Chinese)
[3]	朱亚林, 孔宪京, 朱大勇, 等. 高心墙堆石坝的动力反应及加固极限抗震能力研究[J]. 岩土工程学报, 2013, 35(增刊2): 184-190. ZHU Yalin, KONG Xianjing, ZHU Dayong, et al. Dynamic response and reinforcement ultimate aseismic capacity of high core rockfill dams[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 184-190. (in Chinese)
[4]	田景元, 刘汉龙, 伍小玉. 高土石坝极限抗震能力的评判角度及标准述评[J]. 防灾减灾工程学报, 2013, 33(增刊1): 128-131, 137. TIAN Jingyuan, LIU Hanlong, WU Xiaoyu. Evaluation perspectives and criteria of maximum aseismic capability for high earth-rock dam[J]. Journal of Disaster Prevention and Mitigation Engineering, 2013, 33(S1): 128-131, 137. (in Chinese)
[5]	赵剑明, 刘小生, 杨玉生, 等. 高面板堆石坝抗震安全评价标准与极限抗震能力研究[J]. 岩土工程学报, 2015, 37(12): 2255-2263. ZHAO Jianming, LIU Xiaosheng, YANG Yusheng, et al. Criteria for seismic safety evaluation and maximum aseismic capability of high concrete face rockfill dams[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(12): 2255-2263. (in Chinese)
[6]	陈生水, 李国英, 傅中志. 高土石坝地震安全控制标准与极限抗震能力研究[J]. 岩土工程学报, 2013, 35(1): 59-65. CHEN Shengshui, LI Guoying, FU Zhongzhi. Safety criteria and limit resistance capacity of high earth-rock dams subjected to earthquakes[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(1): 59-65. (in Chinese)
[7]	邹德高, 孔宪京, 刘京茂, 等. 高土石坝极限抗震能力评价量化指标研究[J]. 中国科学: 技术科学, 2022, 52(12): 1831-1838. ZOU Degao, KONG Xianjing, LIU Jingmao, et al. Safety criteria and limit resistance capacity of high earth-rock dams subjected to earthquakes[J]. Scientia Sinica (Technologica), 2022, 52(12): 1831-1838. (in Chinese)
[8]	LI Y C, PANG R, XU B, et al. GPDEM-based stochastic seismic response analysis of high concrete-faced rockfill dam with spatial variability of rockfill properties based on plastic deformation[J]. Computers and Geotechnics, 2021, 139: 104416. doi: 10.1016/j.compgeo.2021.104416
[9]	CHEN K H, PANG R, XU B. Stochastic dynamic response and seismic fragility analysis for high concrete face rockfill dams considering earthquake and parameter uncertainties[J]. Soil Dynamics and Earthquake Engineering, 2023, 167: 107817. doi: 10.1016/j.soildyn.2023.107817
[10]	梁建文. 非平稳地震动过程模拟方法(Ⅰ)[J]. 地震学报, 2005, 27(2): 213-224. doi: 10.3321/j.issn:0253-3782.2005.02.012 LIANG Jianwen. Simulation of non-stationary ground motion processes (Ⅰ)[J]. Acta Seismologica Sinica, 2005, 27(2): 213-224. (in Chinese) doi: 10.3321/j.issn:0253-3782.2005.02.012
[11]	LIU Z, ZENG B. Aseismatic design code of hydraulic structures-based probabilistic model for non-stationary ground motion[J]. China Civil Engineering Journal, 2014, 47: 312-316.
[12]	CLOUGH R W, PENZIEN J. Dynamics of Structures[M]. 2nd ed. New York: McGraw-Hill, 1993.
[13]	水工建筑物抗震设计标准: GB 51247—2018[S]. 北京: 中国计划出版社, 2018. Standard for Seismic Design of Hydraulic Structures: GB 51247—2018[S]. Beijing: China Planning Press, 2018. (in Chinese)
[14]	LU Y Z, PANG R, DU M Z, et al. Simulation of non-stationary ground motions and its applications in high concrete faced rockfill dams via direct probability integral method[J]. Engineering Structures, 2024, 298: 117034. doi: 10.1016/j.engstruct.2023.117034
[15]	PANG R, XU B, ZHOU Y, et al. Seismic time-history response and system reliability analysis of slopes considering uncertainty of multi-parameters and earthquake excitations[J]. Computers and Geotechnics, 2021, 136: 104245. doi: 10.1016/j.compgeo.2021.104245
[16]	KENG H L, YUAN W. Applications of Number Theory to Numerical Analysis[M]. Berlin: Springer Berlin Heidelberg, 1981.
[17]	CHEN J B, LI J. Dynamic response and reliability analysis of non-linear stochastic structures[J]. Probabilistic Engineering Mechanics, 2005, 20(1): 33-44. doi: 10.1016/j.probengmech.2004.05.006
[18]	LI J, CHEN J B, FAN W L. The equivalent extreme-value event and evaluation of the structural system reliability[J]. Structural Safety, 2007, 29(2): 112-131. doi: 10.1016/j.strusafe.2006.03.002
[19]	LYSMER J, KUHLEMEYER R L. Finite dynamic model for infinite media[J]. Journal of the Engineering Mechanics Division, 1969, 95(4): 859-877. doi: 10.1061/JMCEA3.0001144
[20]	徐斌, 邹德高, 孔宪京, 等. 高土石坝坝坡地震稳定分析研究[J]. 岩土工程学报, 2012, 34(1): 139-144. XU Bin, ZOU Degao, KONG Xianjing, et al. Seismic stability of slopes of high rockfiU dams[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(1): 139-144. (in Chinese)
[21]	刘君, 刘博, 孔宪京. 地震作用下土石坝坝顶沉降估算[J]. 水力发电学报, 2012, 31(2): 183-191. LIU Jun, LIU Bo, KONG Xianjing. Estimation of earthquake-induced crest settlements of earth and rock-fill dams[J]. Journal of Hydroelectric Engineering, 2012, 31(2): 183-191. (in Chinese)
[22]	SWAISGOOD J R. Embankment dam deformations causedby earthquakes[C]// 7th Pacific Conference on Earthquake Engineering. Christchurch, 2003.
[23]	叶亚三, 陈国兴, 王志华, 等. 汶川大地震中广元市水库震害调查与分析[J]. 世界地震工程, 2011, 27(4): 73-85. YE Yasan, CHEN Guoxing, WANG Zhihua, et al. Investigation and analysis of seismic damage of reservoirs in Guangyuan City during Wenchuan great earthquake[J]. World Earthquake Engineering, 2011, 27(4): 73-85. (in Chinese)
[24]	孔宪京, 庞锐, 徐斌, 等. 考虑堆石料软化的坝坡随机地震动力稳定分析[J]. 岩土工程学报, 2019, 41(3): 414-421. KONG Xianjing, PANG Rui, XU Bin, et al. Stochastic seismic stability analysis of dam slopes considering softening of rockfills[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(3): 414-421. (in Chinese)
[25]	李国英, 沈婷, 赵魁芝. 高心墙堆石坝地震动力特性及抗震极限分析[J]. 水利水运工程学报, 2010(1): 1-8. doi: 10.3969/j.issn.1009-640X.2010.01.001 LI Guoying, SHEN Ting, ZHAO Kuizhi. Seismic dynamic behavior and limit a seismic analysis on high earth core rockfill dams[J]. Hydro-Science and Engineering, 2010(1): 1-8. (in Chinese) doi: 10.3969/j.issn.1009-640X.2010.01.001
[26]	邵磊, 迟世春, 李红军, 等. 高心墙堆石坝极限抗震能力初探[J]. 岩土力学, 2011, 32(12): 3827-3832, 3838. doi: 10.3969/j.issn.1000-7598.2011.12.046 SHAO Lei, CHI Shichun, LI Hongjun, et al. Preliminary studies of ultimate aseismic capacity of high core rockfill dam[J]. Rock and Soil Mechanics, 2011, 32(12): 3827-3832, 3838. (in Chinese) doi: 10.3969/j.issn.1000-7598.2011.12.046
[27]	郑志. 核安全壳双向地震反应分析及易损性评估[D]. 哈尔滨: 哈尔滨工业大学, 2018. ZHENG Zhi. Bi- directional Seismic Analysis and Fragility Evaluation of A Nuclear Containment Building[D]. Harbin: Harbin Institute of Technology, 2018. (in Chinese)