Estimation of pipeline responses induced by shield tunnelling considering gap formation and soil yielding
-
摘要: 大量试验证实盾构隧道开挖可引起管线与土体界面脱空和土体屈服现象。基于无拉力Winkler地基及管线地基承载力理论，将界面脱空和土体屈服判据条件引入管土线弹性相互作用分析；由此推导了考虑界面脱空和土体屈服影响的管土非线性相互作用计算方法，并与模型试验结果对比验证了其适用性。参数分析发现，界面脱空范围随管线抗弯刚度增大而拓宽；受管土分离和地基屈服影响，管线响应随地层损失呈非线性变化；在土体脱空和屈服范围较大时，其对管线响应影响显著，忽略该效应将导致计算管线挠度和弯矩过于保守。
-
关键词:
- 盾构隧道开挖 /
- 管土相互作用 /
- 界面脱空 /
- 土体屈服 /
- 无拉力Winkler地基
Abstract: The extensive tests confirm gap formation and soil yielding at the pipe-soil interface during shield tunnelling. By incorporating the tension-free Winkler foundation model and the theory of pull-out and compressive bearing capacity of pipeline, the criteria for gap formation and soil yielding are introduced into the pipe-soil linear elastic interaction theory. A method for calculating the nonlinear pipe-soil interaction, accounting for gap formation and soil yielding, is derived and validated against the model tests. The parametric studies reveal that interface gap gets wider with the increasing flexural stiffness of pipeline. The pipeline response exhibits nonlinear changes as an increase in the volume loss due to pipe-soil separation and subgrade yielding. When the interface gap and yielding range are large in width, it significantly affects the pipeline response. Ignoring this effect may lead to overly conservative calculations of deflection and bending moments of pipeline. -
0. 引言
近10年来，盾构下穿诱发管土相互作用问题，在工程界和学术界均引起了极大关注。在以往研究中，通常假设土与管线完全接触，从而便于管线挠曲计算。然而，管土界面脱空，已被大量试验证实。在工程实践中，管线脱空后将失去地基支撑，通常视为危及其结构安全的严重问题。然而目前大部分数值模拟和理论方法都没有考虑间隙形成的影响。
近3年来，国内一些学者就管土界面脱空开展了一些探索性工作。笔者等[1]基于无拉力Pasternak地基和Winkler地基模型，提出了考虑界面脱空的隧道开挖上覆管线变形计算方法。程霖[2]基于双层弹簧弹性地基梁模型，推导了管土接触与脱空区的荷载表达式。除接触界面脱空之外，管土相互作用中地基非线性响应，包括土体刚度弱化和局部屈服等，目前研究尚有待深入。Klar等[3]将地基极限抗拔承载力融入线弹性解答，推导了管土相互作用的弹塑性解。
综上，就隧道开挖引起管土相互作用问题，目前考虑管土界面接触及管土响应非线性的研究相对较少。本文基于管土线弹性相互作用理论，推导了同时考虑局部界面脱空和土体屈服的管土相互作用迭代算法，并经模型试验验证了其适用性；此外，参数分析了管线抗弯刚度和地层损失对管线形变响应的影响。
1. 理论推导
1.1 力学模型与基本假定
隧道开挖地层损失引起上覆地层位移，进而导致地下管线挠曲，部分工况下管土界面存在局部脱空和土体屈服。本文推导基于以下假定和简化：①隧道与管线轴线均呈水平且垂直交叉；②管线和周围地层分别假定为Euler-Bernoulli梁和无拉力Winkler地基；③管土界面脱空前上下两侧及脱空区段地基受压侧满足管土变形协调条件；④管土界面上土体抗拉强度为0；⑤管线与周围土体形变响应分别为线弹性和理想弹塑性；⑥管线的存在不影响隧道的掘进过程。
就本文理论推导，在管土界面脱空之前仍沿用完全接触假定；在管线一侧界面间隙形成之后，进一步增加的载荷仅由仍与管线保持接触的另一侧土体承担。此外，考虑到实际工程中地基屈服常见于管土界面脱空之后，故本文就地基屈服区段的评判仅在该区段被判定为界面脱空之后，且潜在地基屈服位置处于脱空界面的另一侧。
1.2 管土初始线弹性相互作用分析
基于Winkler地基模型和Euler-Bernoulli梁理论，结合管土变形协调条件，可推得关于管线挠度、弯矩及地基反力的控制微分方程，并应用有限差分方法将其转化为代数方程组，进而整合成矩阵形式[4]，分别如下：
([C][λ]−1)−1([Kp]+[C][λ]−1){w}={s} ， (1) {M}=−1l[Kp]{w}， (2) {P}=[C]−1[Kp]{w}。 (3) 式中：{w}，{M}和{P}分别为管线挠曲向量、管线弯矩向量和地基反力向量；[Kp]为管线刚度矩阵；[C]为系数矩阵； \left[ \boldsymbol\lambda \right] 为地基柔度矩阵，其中（i, j）元素λij为地基柔度系数，表示作用于第j个差分结点位置的单位力在第i个差分结点位置产生的地层沉降；{s}为隧道开挖引起的地层沉降向量；l为管线差分单元长度。以上方程推导及各矩阵的展开式详见Lin等[4]。
使用Winkler地基模型时，地基柔度矩阵 \left[ \boldsymbol\lambda \right] 为对角矩阵[5]，如下所示：
{\lambda _{ij}} = \left\{ \begin{gathered} \frac{1}{{k{D_{\text{p}}}l}}{\text{ (}}i = j) \hfill \\ 0{\text{ (}}i \ne j) \hfill \\ \end{gathered} \right. \text{，} (4a) k = \frac{{3.08}}{\varsigma }\frac{{{E_{\text{s}}}}}{{1 - {v_{\text{s}}}}}\sqrt[8]{{\frac{{{E_{\text{s}}}}}{{{E_{\text{p}}}{I_{\text{p}}}D{{\text{p}}^4}}}}} \text{，} (4b) \varsigma = \left\{ \begin{gathered} 2.18{\text{ (}}{z_{\text{p}}}/{D_{\text{p}}} \leqslant 0.5) \hfill \\ 1 + \frac{1}{{1.7{z_{\text{p}}}/{D_{\text{p}}}}}{\text{ (}}{z_{\text{p}}}/{D_{\text{p}}} > 0.5) \hfill \\ \end{gathered} \right. 。 (4c) 式中：k为地基反力系数；Dp为管线外径；Es和vs分别为土体弹性模量和泊松比；Ep和Ip分别为管线弹性模量和截面惯性矩；zp为管线轴线埋深。
隧道开挖引起的横断面地面沉降s(x)符合高斯曲线分布形态[6]，即
s(x)=\frac{\text{π}{R}^{2}{V}_{\text{l}}}{\sqrt{2\text{π}}K({z}_{0}-{z}_{\text{p}})}\mathrm{exp}\left[-\frac{{x}^{2}}{2{K}^{2}{({z}_{0}-{z}_{\text{p}})}^{2}}\right]\text{ }\text{，} (5a) K = {K_{\text{s}}}\left( {1 + \xi \frac{{{z_{\text{p}}}/{z_0}}}{{1 - {z_{\text{p}}}/{z_0}}}} \right) 。 (5b) 式中：R为隧道半径；Vl为隧道开挖地层损失；K和Ks分别为管线轴线和地表位置的地层沉降槽宽度参数；z0为隧道轴线埋深；ξ为反映K随埋深变化速率的经验参数。
综上，联立式（1）~（5），即可求得管线挠度向量{w}、弯矩向量{M}及地基反力向量{P}。
1.3 界面脱空评判及土体柔度系数调整
在式（4）的推导过程中[5]，地基反力系数k为管线上覆和下卧地基刚度的联合体现，即
k = {k_{\text{u}}} + {k_{\text{d}}} 。 (6) 式中：ku和kd分别为管线上覆与下卧地基反力系数。
然而，ku和kd对k的具体贡献比例，Yu等[5]并未明确。本文假定ku=kd=0.5k；结合上下两侧土体与管线完全接触的变形协调条件，可得在管周间隙形成之前地基反力由上下土层平均提供。
本文对Poulos等[7]的桩土脱开近似处理方法加以改进并应用于管土相互作用分析，详述如下。
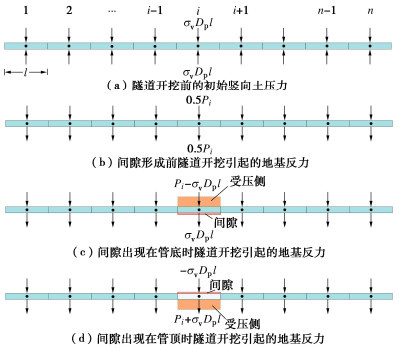
（1）假设作用于每个管线单元顶部初始垂直土压力为σvDpl，其中σv为管线上覆土体自重应力。忽略管线自重，作用在管线底部的初始竖向土压力大小也是σvDpl，但方向相反（见图 1（a））。作用于管线的土压力以向下为正。使用上述Winkler解进行初始线弹性分析，获得每个管线单元的地基反力（在第i个管线单元上记为Pi）。如上所述，Pi由管线上下土体平均施加（见图 1（b）），由此确定在管线底部作用力合力（0.5Pi-σvDpl）为正（即受拉），以及在管线顶部作用力合力（0.5Pi+σvDpl）为负（即受拉）的管线单元。
![]()
图 1 管线竖向土压力与地基反力示意Figure 1. Illustration of vertical force and subgrade reaction force acting on a pipeline（2）由于假定管土界面土体无抗拉强度，因此在上述所确定的管线单元的受拉侧将发生管土分离，需重新计算该位置处土体位移。在这些管线单元的受压侧，仍满足管线与土体的变形协调，可用于重新计算。在管土分离之前，管土相互作用所引起的地面沉降可计算为
{s_{{\text{u}}i}} = {s_{{\text{d}}i}} = {\lambda _{ii}}{P_i} = \frac{1}{{k{D_{\text{p}}}l}}{P_i} 。 (7) 式中：sui和sdi分别为第i个管线单元因管土相互作用而引起的上覆和下卧土体的沉降。
在某管线单元界面脱空之后，进一步增加的负载将仅由受压侧土体承担。若管土分离出现在管线底部，则下卧土体所承担的地基反力为σvDpl；而剩余部分，(Pi-σvDpl)，则由上覆土体承担（见图 1（c））。结合式（7）和ku=0.5k，此时受压侧（即管线上方）土体沉降可计算为
{{s}^{\prime }}_{\text{u}i}=\frac{{P}_{i}-{\sigma }_{\text{v}}{D}_{\text{p}}l}{{k}_{\text{u}}{D}_{\text{p}}l}=\frac{{P}_{i}-{\sigma }_{\text{v}}{D}_{\text{p}}l}{0.5k{D}_{\text{p}}l}=2(1-\frac{{\sigma }_{\text{v}}{D}_{\text{p}}l}{{P}_{i}}){\lambda }_{ii}{P}_{i}=\zeta {\lambda }_{ii}{P}_{i}\text{ }。 (8) 式中： {s'_{{\text{u}}i}} 为管底间隙形成后管线上覆土体沉降；ζ为土体柔度系数的调整系数，当间隙出现在管线底部时， \zeta = 2\left( {1 - \frac{{{\sigma _{\text{v}}}{D_{\text{p}}}l}}{{{P_i}}}} \right) 。
另一方面，当管线顶部出现管土分离时，同理，下方土体沉降值可计算为
\begin{aligned} s_{\mathrm{d} i}^{\prime} & =\frac{P_i+\sigma_{\mathrm{v}} D_{\mathrm{p}} l}{k_{\mathrm{d}} D_{\mathrm{p}} l}=\frac{P_i+\sigma_{\mathrm{v}} D_{\mathrm{p}} l}{0.5 k D_{\mathrm{p}} l} \\ & =2\left(1+\frac{\sigma_{\mathrm{v}} D_{\mathrm{p}} l}{P_i}\right) \lambda_{i i} P_i=\zeta \lambda_{i i} P_i。 \end{aligned} (9) 式中： {s'_{{\text{d}}i}} 为管顶间隙形成后管线下卧土体沉降。当管线顶部满足管土分离判别条件时， \xi = 2\left( {1 + \frac{{{\sigma _{\text{v}}}{D_{\text{p}}}l}}{{{P_i}}}} \right) 。
整合以上两种情况，对所有满足脱空判别条件的管线单元进行土体柔度系数调整，从而获得更新的地基柔度矩阵 {\left[ \boldsymbol\lambda \right]^\prime } ，其内部元素为
{\lambda '_{ij}} = \left\{ \begin{gathered} \zeta \frac{1}{{k{D_{\text{p}}}l}}{\text{ (}}i = j) \hfill \\ 0{\text{ (}}i \ne j) \hfill \\ \end{gathered} \right. \text{，} (10a) \zeta =\{\begin{array}{l}2\left(1-\frac{{\sigma }_{\text{v}}{D}_{\text{p}}l}{{P}_{i}}\right)\text{ }\\ \left(当\frac{1}{2}{P}_{i}-{\sigma }_{\text{v}}{D}_{\text{p}}l > 0\text{，}管底脱空时\right)\\ 2\left(1+\frac{{\sigma }_{\text{v}}{D}_{\text{p}}l}{{P}_{i}}\right)\text{ }\\ \left(当\frac{1}{2}{P}_{i}+{\sigma }_{\text{v}}{D}_{\text{p}}l < 0\text{，}管顶脱空时\right)\\ 1\text{ (}不满足以上条件\text{，}无脱空\text{)}\end{array}\text{ }。 (10b) （3）将调整后的 {\left[ \boldsymbol\lambda \right]^\prime } 代入式（1）~（3），算得{w}，{M}及{P}的新一轮解答；重复上述过程，直至管线上下两侧在所有单元位置均无净拉力为止。
1.4 脱空区段地基屈服评判及计算方程调整
经前述步骤确定管土界面脱空区段后，基于计算所得脱空收敛后的地基反力，进一步评判该区段地基屈服的可能。
参照油气管线抗震设计指南[8]和Shi等[9]的数值和试验研究，管线地基抗拔和抗压承载力分别为
{q}_{\text{u}}={N}_{\text{v}}r{z}_{\text{p}}{D}_{\text{p}}\text{ }\text{，} (11) {q}_{\text{d}}={N}_{\text{q}}r{z}_{\text{p}}{D}_{\text{p}}+\frac{1}{2}{N}_{\text{r}}r{D}_{\text{p}}^{2}\text{ }。 (12) 式中：qu和qd分别为管线顶部和底部土体的抗拔和抗压承载力；r为土体重度；Nv为上拔承载力系数；Nq和Nr为抗压承载力系数，取值与土体内摩擦角有关。
式（1）为管土位移协调方程，式（3）是Euler- Bernoulli梁处于线弹性阶段的位移方程[4]。当管土界面地基受力达到其承载极限时，地基开始进入塑性阶段，其在管线反力作用下的位移不再遵从线弹性阶段的荷载-位移关系，故式（1）不再适用。对于界面地基屈服区段，地基反力将维持在极限水平，即Pi已确定；此时，假定管线仍处于线弹性阶段，因此该区段管线位移方程，即式（3），仍满足。因此，当管土界面地基屈服时，仍可使用式（1）求解管线挠度{w}，只需把地基屈服区段的管土位移协调方程式（1）调整为管线位移方程式（3）。
（1）对于已确定的管底界面脱空单元i，可知管线上部和下部地基提供的地基反力分别为Pui=Pi- {\sigma _{\text{v}}} Dpl和Pdi= {\sigma _{\text{v}}} Dpl；若Pui≥qul，则判定该单元上部地基屈服，此时Pui=qul，Pi也相应调整为（qul+ {\sigma _{\text{v}}} Dpl）。式（1）中，令 {\left( {\left[ C \right]{{\left[ \boldsymbol\lambda \right]}^{ - 1}}} \right)^{ - 1}} \left( {\left[ {{K_{\text{p}}}} \right] + \left[ C \right]{{\left[ \boldsymbol\lambda \right]}^{ - 1}}} \right) =[Ze]，则式（1）转化为
\left[{Z}_{\text{e}}\right]\left\{w\right\}=\left\{s\right\}\text{ }。 (13) 式（3）中，令[C]-1[Kp]=[Zp]，则式（3）转化为
\left[{Z}_{\text{p}}\right]\left\{w\right\}=\left\{P\right\}\text{ }。 (14) 如前述，若管线单元i处地基屈服，在进行管线挠度{w}的求解时，需将该单元对应的代数方程由式（1）调整为式（3），即
\begin{aligned} & \left\{\begin{array}{l} Z_{\mathrm{e}}(i,:)=Z_{\mathrm{p}}(i,:) \\ s(i)=P_i=q_{\mathrm{u}} l+\sigma_{\mathrm{v}} D_{\mathrm{p}} l \end{array}\right. \\ && \text { (当 } \frac{1}{2} P_i-\sigma_{\mathrm{v}} D_{\mathrm{p}} l>0, P_i \geqslant q_{\mathrm{u}} l+\sigma_{\mathrm{v}} D_{\mathrm{p}} \text { 时)。 } \end{aligned} (15) 式中：Ze(i, : )和Zp(i, : )分别为[Ze]和[Zp]第i行所对应的元素；s(i)为地层沉降向量{s}第i行所对应的元素。
（2）对于已确定的管顶界面脱空单元i，可知管线上部和下部地基提供的地基反力分别为Pui=- {\sigma _{\text{v}}} Dpl和Pdi=Pi+ {\sigma _{\text{v}}} Dpl；若Pdi≤-qdl，则判定该单元底部地基屈服，此时Pdi=-qdl，Pi也相应调整为(-qdl- {\sigma _{\text{v}}} Dpl)。同理，将管线单元i所对应的管土变形协调方程调整为管线位移方程，即
\begin{aligned} & \left\{\begin{array}{l} Z_{\mathrm{e}}(i,:)=Z_{\mathrm{p}}(i,:) \\ s(i)=P_i=-q_{\mathrm{d}} l-\sigma_{\mathrm{v}} D_{\mathrm{p}} l \end{array}\right. \\ && \text { (当 } \frac{1}{2} P_i <-\sigma_{\mathrm{v}} D_{\mathrm{p}} l, P_i+\sigma_{\mathrm{v}} D_{\mathrm{p}} l \leqslant-q_{\mathrm{d}} \text { 时)。 } \end{aligned} (16) （3）经前述两步，完成管线屈服区段计算方程调整后，即可统一使用式（13）的矩阵方程形式进行{w}的求解，进而代入式（2），（3）可分别求得{M}和{P}。基于新求得的{P}，即可重复以上步骤，直到所有管线单元无地基反力大于地基承载极限的情况。
（4）为提高上述迭代效率，在每一轮计算中，当判定某管线单元i地基屈服后，按地基受力临界状态调整地基柔度系数[ \lambda ]，得到更新的[ \lambda ]''以作为下一轮计算的初始地基柔度系数。地基柔度系数的调整思路同前，仍是根据单元上下地基真实分担的荷载计算受压侧地基位移，并计算对应于荷载Pi的柔度系数取值。具体推导不再累述，调整过程如下所示：
{\lambda ''_{ij}} = \left\{ \begin{gathered} \zeta \frac{1}{{k{D_{\text{p}}}l}}{\text{ (}}i = j) \hfill \\ 0{\text{ (}}i \ne j) \hfill \\ \end{gathered} \right. \text{，} (17a) \zeta =\{\begin{array}{l}\frac{2{q}_{\text{u}}l}{{q}_{\text{u}}l+{\sigma }_{\text{v}}{D}_{\text{p}}l}\\ \left(当\frac{1}{2}{P}_{i}-{\sigma }_{\text{v}}{D}_{\text{p}}l > 0\text{，}\text{ }{P}_{i}\ge {q}_{\text{u}}l+{\sigma }_{\text{v}}{D}_{\text{p}}l时\right)\\ \frac{2{q}_{\text{d}}l}{{q}_{\text{d}}l+{\sigma }_{\text{v}}{D}_{\text{p}}l}\text{ }\\ \left(当\frac{1}{2}{P}_{i} < -{\sigma }_{\text{v}}{D}_{\text{p}}l\text{，}\text{ }{P}_{i}+{\sigma }_{\text{v}}{D}_{\text{p}}l\le -{q}_{\text{d}}l时\right)\\ 1\text{ (}不满足以上条件\text{，}脱空区段无地基屈服\text{)}。\end{array} (17b) 2. 算法流程与实现
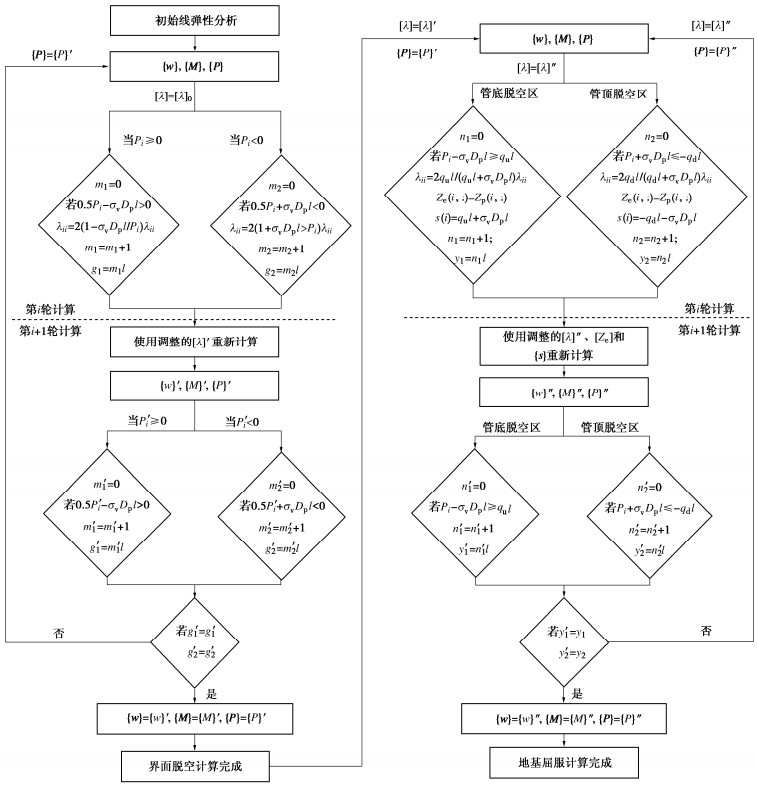
图 2概述了融合界面脱空和地基屈服的计算流程，其中[λ]0是在线弹性分析中使用的初始土体柔度矩阵。在界面脱空计算时，{w}'，{M}'和{P}'是每次迭代的第二轮计算结果，分别与{w}，{M}和{P}对应；m1和m2分别是在每次迭代的第一轮计算中在管线下方和上方发生脱空的管线单元数量；g1和g2分别是与m1和m2相对应的间隙宽度；m1'和m2'是在每次迭代的第二轮计算结果，分别与m1和m2对应；g1'和g2'是在每次迭代的第二轮计算结果，分别对应于g1和g2。在界面脱空区域计算收敛后，随后开展地基屈服计算，{w}''，{M}''和{P}''是每次迭代的第二轮计算结果；n1和n2分别是在每次迭代的第一轮计算中在管线上方和下方发生地基屈服的管线单元数量；y1和y2分别是与n1和n2相对应的屈服宽度；n1'和n2'是在每次迭代的第二轮计算结果，分别与n1和n2对应；y1'和y2'是在每次迭代的第二轮计算结果，分别对应于y1和y2。
如图 2所示，界面脱空迭代的收敛准则是在某一次迭代过程中第一轮和第二轮计算所得管线上方和下方的间隙宽度相等，由此即可满足管线上下两侧静拉力均为0的要求。同理，地基屈服收敛的判断标准是某次迭代中前后两轮计算得到的管线上下地基屈服宽度均相等，由此实现地基反力无超过其承载极限的情况。以上矩阵和迭代运算由Matlab编程实现。
3. 试验验证与参数分析
3.1 试验验证
![]()
图 2 考虑界面脱空与地基屈服的管土相互作用计算流程Figure 2. Flow chart for calculation of pipeline responses considering gap formation and soil yielding程霖[2]和Shi等[9]分别使用TK-C500型土工离心机开展了加速度为80g和60g的独立平行试验，研究了砂土中盾构隧道开挖上覆管线响应。下面分别针对这两个试验的原型工况开展理论计算，并与模型试验所对应的原型结果对比分析。
（1）80g离心机模型试验
程霖[2]开展了3组工况下的模型试验，表 1列出了其所对应的原型尺寸与基本物理力学参数。工况A预设地层损失为5%，工况B和C为10%；工况A和B主要探究地层损失的影响，工况B和C主要探究管线抗弯刚度的影响。
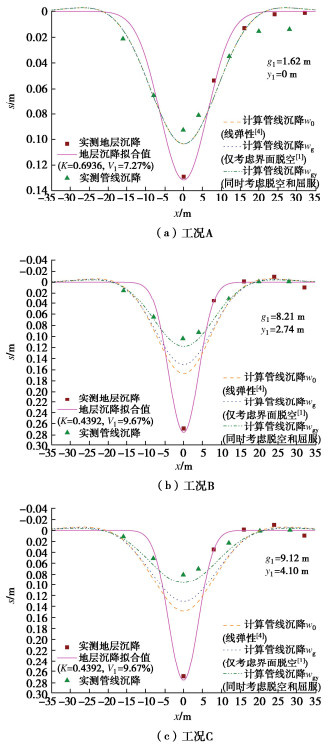
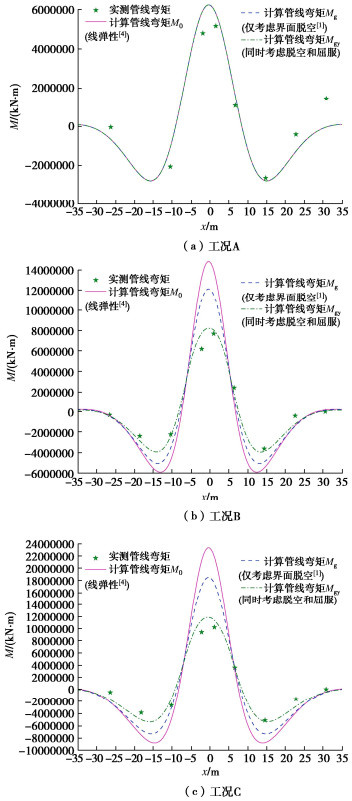
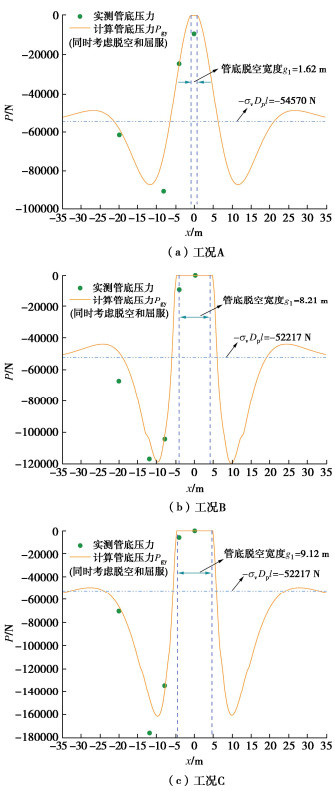
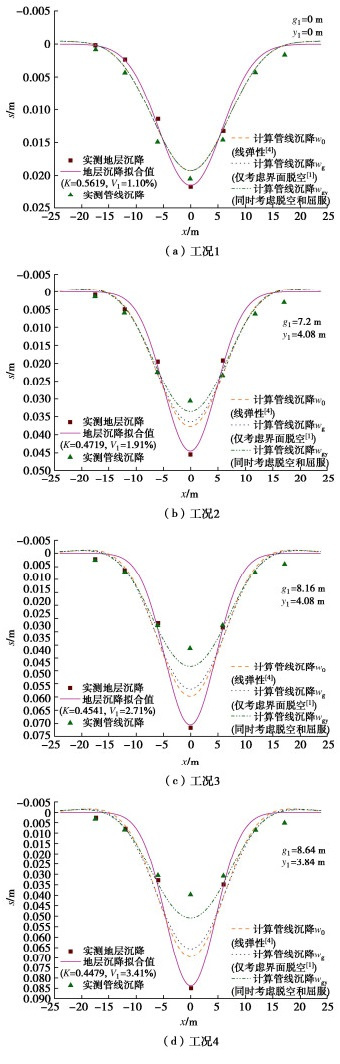
表 1 80g离心机模型试验原型尺寸和物理力学参数[2]Table 1. Dimensions and characteristics of prototype (80g)分类 管线 隧道 土体 L/m Dp/m tp/m Ep/GPa zp/m R/m z0/m Es/MPa vs φ/(°) K0 \gamma /(kN∙m-3) 工况A 91.2 1.422 0.0191 210 5.384 3 14.384 39.49 0.3 32 0.43 15.631 工况B 91.2 1.422 0.0191 210 5.168 3 14.168 38.47 0.3 32 0.43 15.582 工况C 91.2 1.626 0.0286 210 5.168 3 14.168 38.47 0.3 32 0.43 15.582 注：tp为管线壁厚；K0为静止侧向土压力系数；φ为土体内摩擦角。 图 3~5分别为3种工况下地层沉降及管线挠曲、弯矩和管底压力的实测和计算值。图中，w0和M0分
![]()
图 3 地面沉降与管线挠度的实测值与计算值(80g)Figure 3. Observed and calculated ground settlements and pipe deflections (80g)别表示由初始线弹性解[4]计算得到的管线挠度和弯矩；相应地，wg和Mg表示仅考虑界面脱空的计算结果（计算方法详见文献[1]），wgy和Mgy表示本文理论计算结果。仅考虑界面脱空的计算方法[1]系基于线弹性解[4]补充了管土界面脱空的影响，本文计算理论则是在其基础上进一步考虑了管周地基局部屈曲。参数取值见表 2。
表 2 计算参数取值(80g)Table 2. Values of parameters used for calculation (80g)由图 3~5可见，本文理论方法可较好地预测管线挠曲、弯矩和管底压力。对于工况A，计算管底脱空宽度1.62 m（仅占管线全长的1.78%），无地基屈服；此时界面脱空对管线响应影响较小，考虑脱空和屈服的计算结果与初始线弹性计算结果差别不大。对于工况B和C，伴随地层损失增大，管底脱空区域不断拓宽（计算脱空宽度分别为8.21，9.12 m），管顶地基发生屈服（计算屈服宽度分别为2.74，4.1 m），此时线弹性计算结果远大于实测；仅考虑界面脱空的计算结果较线弹性计算更趋于实测，但仍较实际偏大；本文同时考虑脱空和屈服的计算结果则与实测更为接近。此外，程霖[2]通过管底压力变化反推管底脱空宽度，工况A管土无明显脱空，工况B和C脱空宽度约8 m，与本文计算脱空宽度较为吻合。
![]()
图 5 管线底部地基反力实测值与计算值(80g)Figure 5. Observed and calculated subgrade reaction forces acting on pipe bottom (80g)（2）60g离心机模型试验
Shi等[9]开展了4组工况模型试验，表 3列出了其所对应的原型尺寸与基本物理力学参数。工况1~4仅变化地层损失，预设值分别为1%，2%，3%，4%。
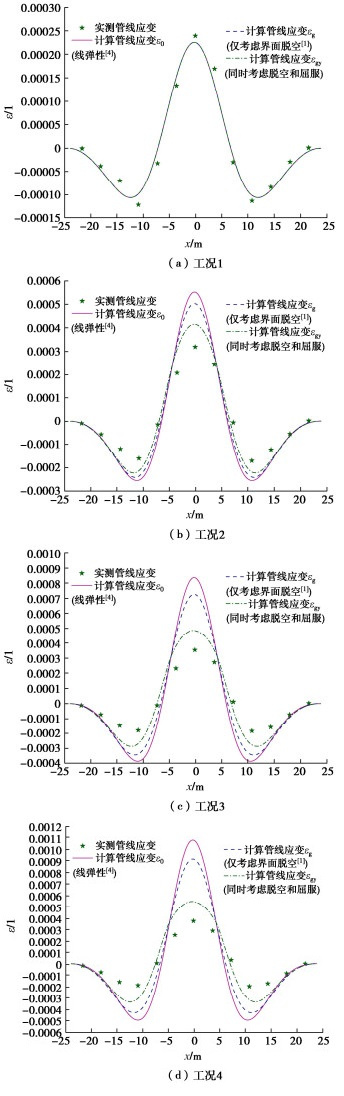
管线 隧道 土体 L/m Dp/m tp/m Ep/GPa Ip/(105 m4) zp/m R/m z0/m φ/(°) K0 \gamma /(kN∙m-3) 48 1.08 0.06 70 17563 1.74 3 6 31 0.49 14.602 图 6，7分别为4种工况下地层沉降及管线挠曲和应变的实测和计算值。由式（2）算得任意差分结点位置管线弯矩M后，对应的管线应变 \varepsilon = \frac{{M{D_{\text{p}}}}}{{2{E_{\text{p}}}{I_{\text{p}}}}} 。图 7中， {\varepsilon _0} 表示由线弹性解算得管线弯曲应变；相应地， {\varepsilon _{\text{g}}} 和 {\varepsilon _{{\text{gy}}}} 分别表示仅考虑界面脱空和本文理论计算结果。计算参数取值见表 4。
![]()
图 6 地面沉降与管线挠度的实测值与计算值(60g)Figure 6. Observed and calculated ground settlements and pipe deflections (60g)表 4 计算参数取值(60g)Table 4. Values of parameters used for calculation (60g)K k (kN∙m-3) qu (kN∙m-1) qd (kN∙m-1) 工况1 工况2 工况3 工况4 0.5619 0.4719 0.4541 0.4479 17287 36.4 2290 Vl/% 工况1 工况2 工况3 工况4 1.10 1.91 2.71 3.41 注：①K和Vl取值由各工况实测管线轴线位置自由场沉降经式（5a）拟合所得；②K，qu和qd取值由文献[9]计算给出。 由图 6，7亦可见，本文理论方法可以较好地预测管线挠曲和弯曲应变。在工况1地层损失较小时，经计算界面无脱开、地基无屈服，本文计算结果等同初始线弹性结果；在工况2~4中，伴随地层损失增大，初始线弹性和仅考虑脱空的计算结果与实测偏差增大；这反映了在地层损失较大时，地基屈服对管线响应的显著影响。此外，本文计算结果虽与实测管线挠度和应变虽较为接近，但仍普遍大于实测值，可能原因是本文假定管线上下地基刚度相同，高估了上覆地基在屈服前的地基反力分担比例。
3.2 参数分析
（1）管线抗弯刚度的影响
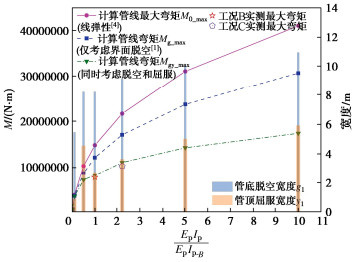
80g离心机模型试验工况B和C探究了管线抗弯刚度对管线响应的影响。以工况B为基准，分别取管线EpIp为工况B抗弯刚度EpIp-B的0.01，0.1，0.5，1（工况B），2.21（工况C），5，10倍，计算所得管线最大弯矩及管底脱空和管顶屈服宽度见图 8。
![]()
图 8 管线最大弯矩及脱空与屈服宽度随EpIp变化Figure 8. Variations of maximum bending moment of pipeline and width of gap and yielding with EpIp由图 8可见，伴随管线抗弯刚度增大，界面脱空宽度和管线最大弯矩均递增，但增速递减；而地基屈服宽度的变化相对无规律。当管线刚度较大时，界面脱空较宽，且伴随地基屈服，此时若忽略脱空和屈服影响，或仅计脱空影响，计算结果都与实际偏差较大。
（2）地层损失的影响
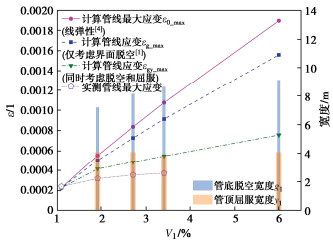
60g离心机模型试验工况1~4探究了地层损失对管线响应的影响。取该试验计算参数，变化Vl取值，算得管线最大弯曲应变及管底脱空和管顶屈服宽度见图 9。
![]()
图 9 管线最大应变及脱空与屈服宽度随Vl变化Figure 9. Variations of maximum strain of pipeline and width of gap and yielding with Vl由图 9可见，随地层损失增大，管底脱空宽度呈增大趋势，而管顶地基屈服宽度变化规律不明显；由于界面脱空和地基屈服，使得管线响应随地层损失的变化呈非线性，因此忽略脱空和屈服效应的线弹性计算或仅考虑脱空影响的近似线性计算均偏保守，且随地层损失增大计算偏差越大。
对比图 8，9可以发现，就部分试验数据与计算结果的对比可见，本文计算理论在80g离心机模型试验（算例1）中取得了更好的计算效果，而在60g离心机模型试验（算例2）中较大地层损失（大于1%）下的计算值较试验值明显偏大。本文计算理论假定地基刚度由管线上覆和下卧地基平均提供，即ku=kd=0.5k。对于算例1[2]，ku=2670 kN∙m-3，kd=3560 kN∙m-3，ku/k=0.43，kd/k=0.57，近似满足上述假定；而对于算例2[9]，ku=1546 kN∙m-3，kd=15741 kN∙m-3，ku/k=0.09，kd/k=0.91，明显偏离以上假定。算例1试验值和本文理论计算值的吻合程度优于算例2，可能原因是算例1试验中地基模量的取值更符合ku=kd=0.5k的假定。
4. 结论
（1）计算理论适用于盾构隧道开挖引起上覆管线的挠曲和弯矩计算，可准确预估管土界面脱空宽度；当界面脱空区域较宽且局部地基屈服时，本文计算理论较线弹性解或仅考虑界面脱空影响的计算更符合实际。
（2）当地层损失较小时，因管土界面未发生脱空和地基屈服或发生范围较小，此时线弹性计算结果较符合实际；伴随地层损失增大，管土界面脱空范围递增，界面脱空和地基屈服对管线响应的影响愈发显著，管线挠曲和弯矩呈非线性增长，此时线弹性计算和仅考虑脱空影响的计算均因高估了地基承载能力而较实际偏大。
（3）管线抗弯刚度是影响管土界面脱空行为的重要因素；随管线抗弯刚度提升，管土界面更易脱空，且管线最大弯矩呈递增趋势。
本文盾构穿越管线挠曲计算方法，引入了管线砂土地基承载理论，且仅就砂土地基进行了模型试验验证；其尚待拓展至黏土地层并开展试验验证。此外，本文计算理论忽略了不同管土相对位移方向下地基反力系数的差异，尚待进一步完善管线地基模型。
-
![]()
图 1 管线竖向土压力与地基反力示意
Figure 1. Illustration of vertical force and subgrade reaction force acting on a pipeline
![]()
图 2 考虑界面脱空与地基屈服的管土相互作用计算流程
Figure 2. Flow chart for calculation of pipeline responses considering gap formation and soil yielding
![]()
图 3 地面沉降与管线挠度的实测值与计算值(80g)
Figure 3. Observed and calculated ground settlements and pipe deflections (80g)
![]()
图 5 管线底部地基反力实测值与计算值(80g)
Figure 5. Observed and calculated subgrade reaction forces acting on pipe bottom (80g)
![]()
图 6 地面沉降与管线挠度的实测值与计算值(60g)
Figure 6. Observed and calculated ground settlements and pipe deflections (60g)
![]()
图 8 管线最大弯矩及脱空与屈服宽度随EpIp变化
Figure 8. Variations of maximum bending moment of pipeline and width of gap and yielding with EpIp
![]()
图 9 管线最大应变及脱空与屈服宽度随Vl变化
Figure 9. Variations of maximum strain of pipeline and width of gap and yielding with Vl
表 1 80g离心机模型试验原型尺寸和物理力学参数[2]
Table 1 Dimensions and characteristics of prototype (80g)
分类 管线 隧道 土体 L/m Dp/m tp/m Ep/GPa zp/m R/m z0/m Es/MPa vs φ/(°) K0 /(kN∙m-3) 工况A 91.2 1.422 0.0191 210 5.384 3 14.384 39.49 0.3 32 0.43 15.631 工况B 91.2 1.422 0.0191 210 5.168 3 14.168 38.47 0.3 32 0.43 15.582 工况C 91.2 1.626 0.0286 210 5.168 3 14.168 38.47 0.3 32 0.43 15.582 注：tp为管线壁厚；K0为静止侧向土压力系数；φ为土体内摩擦角。 
下载: 导出CSV
管线 隧道 土体 L/m Dp/m tp/m Ep/GPa Ip/(105 m4) zp/m R/m z0/m φ/(°) K0 /(kN∙m-3) 48 1.08 0.06 70 17563 1.74 3 6 31 0.49 14.602
下载: 导出CSV
-
[1] LIN C G, ZHENG J J, YE Y W, et al. Analytical solution for tunnelling-induced response of an overlying pipeline considering gap formation[J]. Underground Space, 2024, 15: 298-311. doi: 10.1016/j.undsp.2023.07.006
[2] 程霖. 地铁隧道开挖引起地下管线变形的理论分析和试验研究[D]. 北京: 北京交通大学, 2021. CHENG Lin. Theoretical Analysis and Experimental Research on Deformation of Buried Pipelines Due to Subway Tunnel Excavation[D]. Beijing: Beijing Jiaotong University, 2021. (in Chinese)
[3] KLAR A, VORSTER T, SOGA K, et al. Elastoplastic solution for soil-pipe-tunnel interaction[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(7): 782-792. doi: 10.1061/(ASCE)1090-0241(2007)133:7(782)
[4] LIN C G, HUANG M S. Tunnelling-induced response of a jointed pipeline and its equivalence to a continuous structure[J]. Soils and Foundations, 2019, 59(4): 828-839. doi: 10.1016/j.sandf.2019.02.009
[5] YU J, ZHANG C R, HUANG M S. Soil-pipe interaction due to tunnelling: assessment of Winkler modulus for underground pipelines[J]. Computers and Geotechnics, 2013, 50: 17-28. doi: 10.1016/j.compgeo.2012.12.005
[6] LIN C G, HUANG M S, NADIM F, et al. Embankment responses to shield tunnelling considering soil-structure interaction: case studies in Hangzhou soft ground[J]. Tunnelling and Underground Space Technology, 2020, 96: 103230. doi: 10.1016/j.tust.2019.103230
[7] POULOS H G, DAVIS E H. Pile Foundation Analysis and Design[M]. New York: Wiley, 1980.
[8] ASCE Committee on Gas and Liquid Fuel Lifeline. Guidelines for the Seismic Design of Oil and Gas Pipeline Systems[M]. New York: American Society of Civil Engineers, 1984.
[9] SHI J W, CHEN Y H, LU H, et al. Centrifuge modeling of the influence of joint stiffness on pipeline response to underneath tunnel excavation[J]. Canadian Geotechnical Journal, 2022, 59(9): 1568-1586. doi: 10.1139/cgj-2020-0360
-
期刊类型引用(0)
其他类型引用(2)
-
其他相关附件
计量
- 文章访问数: 331
- HTML全文浏览量: 45
- PDF下载量: 67
- 被引次数: 2
