Fractional-order plasticity model for sand-silt mixtures
-
摘要: 砂-粉混合料是自然界和岩土工程中常见的非均质土，密实程度、应力水平和细粒含量等因素对其颗粒接触状态和力学性能具有显著影响。为了能够较为全面地描述砂-粉混合料在细粒含量阈值内的复杂力学特性（FC＜FCthre），基于分数阶微积分理论确定了能够统一描述相关联和非相关联的塑性流动法则，并采用等效骨架孔隙比的概念，将等效骨架状态参数嵌入剪胀方程和塑性模量中，进而建立了考虑细粒含量和状态相关的分数阶塑性本构模型。模型预测结果与试验数据对比分析表明，所建立的分数阶塑性模型能够有效反映砂-粉混合料在排水剪切条件下的应变软化（应变硬化）和剪胀（剪缩）等特性。同时，不排水条件下的关键特征，如流动和非流动行为也可以得到合理地描述。Abstract: The sand-silt mixtures, as common heterogeneous soils, are ubiquitous in nature and geotechnical engineering, and their particle contact state and mechanical properties are significantly affected by the factors such as density, stress level and fines content. In order to comprehensively describe the complex mechanical properties of the sand-silt mixtures within the fines content threshold (FC<FCthre), the plastic flow rules that can uniformly describe association and non-association are determined based on the fractional calculus theory. Using the concept of equivalent skeleton void ratio, the equivalent skeleton state parameter is embedded in the dilatancy equation and plastic modulus, and then a fractional-order plasticity model considering the fines content and state-dependent behavior is established. The comparison between the predicted results and the experimental data shows that the proposed fractional-order plasticity model can effectively reflect the strain-softening (strain-hardening) and dilatancy (contraction) behaviors of the sand-silt mixtures under drained conditions. Meanwhile, the key characteristics of undrained conditions, such as flow and non-flow behaviors, can also be reasonably described.
-
Keywords:
- sand-silt mixture /
- fines content /
- state-dependence /
- fractional calculus /
- constitutive model
-
0. 引言
砂-粉混合料在长江三角洲、渤海湾和南海等地区表层普遍存在，通常由不同比例的粗颗粒和细颗粒组成。此外，人工吹填造陆、软土地基处理、高速铁路路基等工程的建设也会形成类似的二元颗粒混合料[1-3]。砂-粉混合料的颗粒接触状态和力学行为受初始密实度、应力水平、细粒含量和粒度分布等因素的影响。细粒含量作为砂-粉混合料的重要级配参数，对混合料强度、应力-剪胀、临界状态和静态液化等特性的影响得到广泛关注。试验结果表明[4-5]，细颗粒的存在，即使其所占的比例小于10%，对砂土的应力变形和静态液化行为也起着不可忽视的影响。Monkul等[6]指出在沉积过程中细颗粒与粗颗粒的接触状态并不固定，混合料结构性的强弱，取决于细颗粒的贡献程度。Gobbi等[7]分析了不同细粒含量对松散、中、致密粉砂抗液化能力的影响，发现混合料的力学行为很大程度上取决于粗颗粒和细颗粒的堆积结构。Yilmaz等[3]指出细粒含量对砂-粉混合料的应力-应变响应、最大剪胀角、峰值摩擦角、临界状态摩擦角以及应力-剪胀特性有着显著影响。
为了更好地描述砂-粉混合料的力学特性，Chang等[8]考虑细颗粒对临界状态摩擦角和颗粒间滑动量的影响，建立了砂-粉混合料的微观力学模型。Rahman等[9]引入等效骨架孔隙比的概念，修正了Li等[10]的无黏性土本构模型。Xu等[11]采用等效骨架孔隙比和等效骨架状态参数，建立了一种应力比控制的砂-粉混合料状态相关本构模型。考虑细粒含量对临界状态的影响，Wei等[12]采用全局孔隙比建立了状态相关模型对混合料的静态液化特性进行预测。Sun等[13]将等效骨架状态参数引入Rowe应力剪胀方程和塑性模量，结合临界状态与细粒含量的相关性，建立了砂-粉混合料的细粒-状态相关本构模型。
岩土材料在加载过程中，塑性应变增量的方向通常由塑性势函数的正交梯度决定。对于具有压硬性和剪胀性的岩土材料，塑性流动方向与加载方向并不一致，具有非相关联特性。非正交塑性应变增量的获取通常有两种方法[14-15]：①构造新的塑性势函数，但合理的塑性势函数难以通过试验数据构建，还会引入一些没有明确物理含义的参数；②由屈服函数的非正交梯度直接确定塑性应变增量方向。近年来，分数阶塑性理论在岩土材料的本构模型中得到广泛应用[16-19]。分数阶导数具有调节可微函数非正交梯度方向的能力，通过对屈服函数进行分数阶求导能够得到统一描述相关联和非相关联流动特性的塑性流动法则。本文在临界状态土力学和分数阶塑性理论框架下，假设部分细颗粒可以参与接触力的传递，引入等效骨架孔隙比和状态参数对剪胀方程和弹/塑性模量进行修正，建立考虑细粒含量和状态相关的砂-粉混合料分数阶塑性本构模型。最后，采用砂-粉混合料的三轴排水和不排水剪切试验结果对模型的合理性进行验证。
1. 等效骨架孔隙比和状态参数
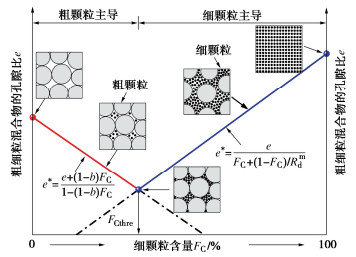
临界状态土力学框架中，孔隙比e是一个十分重要的状态变量，可用于量化土体的应力-应变响应。细颗粒的影响与主砂的级配、细颗粒的矿物成分和含量以及细颗粒在砂基质中的分布有关。Thevanayagam等[20]指出由于微观结构特征的改变，粉砂、砂质粉土与纯砂土的物理力学特性有较大差异。混合料的力学响应对细粒含量具有一定依赖性，当细粒含量低于阈值时，粗颗粒是影响其整体行为的决定性因素；当细粒含量超过阈值后，细粒-细粒接触作用显著，细颗粒在混合料力学响应中占据主导地位。在此基础上，提出了二元混合料的颗粒接触状态理论，如图 1所示。
![]()
图 1 二元混合料的颗粒接触状态和孔隙比[20]Figure 1. Schematic diagram of particle contact state and void ratio of binary mixtures当细粒含量${F_{\text{C}}}$小于细粒含量阈值FCthre时，粗颗粒占主导地位，等效骨架孔隙比${e^ * }$可表示为
$$ {e^ * } = \frac{{e + (1 - b){F_{\text{C}}}}}{{1 - (1 - b){F_{\text{C}}}}}。 $$ (1) 式中：b为细颗粒在粗粒骨架中参与粒间接触或接触力传递的贡献程度，取值范围为0~1。当b=0时意味着细颗粒填充在粗颗粒间的孔隙中，对接触力的传递无贡献；当b=1时表明所有细颗粒均被激活，参与接触力的传递，即${e^ * } = e$。参数b值可通过对试验数据的反演分析或经验方程计算得到，Chang等[21]、Gobbi等[7]探讨了不同估算方法对参数b取值的影响。
当${F_{\text{C}}}$≥FCthre时，细颗粒占主导地位，等效骨架孔隙比${e^ * }$可表示为
$$ {e^ * } = \frac{e}{{{F_{\text{C}}} + (1 - {F_{\text{C}}})/R_{\text{d}}^c}} 。 $$ (2) 式中：Rd为粒径比；c为与颗粒特征相关的材料参数。
对于不同砂-粉混合料来说，FCthre取值不同，可以根据混合料最大/最小孔隙比随${F_{\text{C}}}$的变化规律确定。此外，Rahman等[5]提出了FCthre的经验表达式为
$$ {F_{{\text{Cthre}}}} = 0.4\left( {\frac{1}{{1{\text{ + }}\exp (0.5 - 0.13\chi )}} + \frac{1}{\chi }} \right) 。 $$ (3) 式中：$ \chi $为主砂有效粒径D10与细颗粒平均粒径d50的比值。
根据状态参数$\psi = e - {e_{{\text{cs}}}}$的定义[22]，将${e^ * }$代替e，采用等效骨架状态参数${\psi ^ * }$描述混合料的状态依赖行为，可表示为
$$ {\psi ^ * } = {e^ * } - e_{{\text{cs}}}^ * 。 $$ (4) 在等效骨架孔隙比${e^ * }$-平均有效应力$p'$平面中，等效临界状态线（EG-CSL）的幂函数表达式为[13]
$$ e_{{\text{cs}}}^ * = {e_\Gamma } - {\lambda _{\text{c}}}{(p'/{p_{\text{a}}})^\xi }。 $$ (5) 式中：${e_\Gamma }$和${\lambda _{\text{c}}}$分别为EG-CSL的截距和斜率；${p_{\text{a}}}$为大气压力；$\xi $为材料参数，控制着EG-CSL的曲率，在0.6~0.8变化。
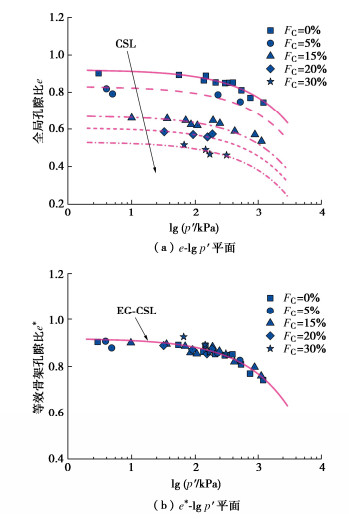
图 2（a）为悉尼砂-粉混合料在$e{\text{ - }}\lg p'$平面内的临界状态线。可以看出，CSL与细粒含量具有相关性，随细粒含量的增加逐渐向下移动。当采用${e^ * }$代替e后，4种混合料（即FC=5%，15%，20%，30%）在${e^ * }{\text{ - }}\lg p'$平面中的临界状态点可由纯砂试样的CSL进行描述，不受细粒含量的影响，如图 2（b）所示。需要说明的是，CSL随细粒含量的增加不仅会向下移动，还可能发生旋转，这与粒度分布、矿物成分、颗粒形状及试样制备方法等因素有关[23-25]。根据前期研究[8, 9, 26]，为降低模型复杂程度，未考虑CSL随细粒含量增加的旋转特性，仅采用等效骨架孔隙比表征不同细粒含量下混合料的临界状态特性。
2. 状态相关分数阶塑性本构模型
2.1 本构关系
在弹塑性理论中，应力应变增量关系表示为[27]
$$ \mathrm{d} \boldsymbol{\varepsilon}=\mathrm{d} \boldsymbol{\varepsilon}^{\mathrm{e}}+\mathrm{d} \boldsymbol{\varepsilon}^{\mathrm{p}} \text{，} $$ (6a) $$ \mathrm{d} \boldsymbol{\sigma}=\boldsymbol{D}^{\mathrm{e}}:\left(\mathrm{d} \boldsymbol{\varepsilon}-\mathrm{d} \boldsymbol{\varepsilon}^{\mathrm{p}}\right)=\boldsymbol{D}^{\mathrm{ep}}: \mathrm{d} \boldsymbol{\varepsilon} 。 $$ (6b) 式中：$ {\text{d}}{\boldsymbol{\varepsilon}^{\text{e}}} $和$ {\text{d}}{\boldsymbol{\varepsilon}^{\text{p}}} $分别为弹性和塑性应变增量；$ {\boldsymbol{D}^{{\text{ep}}}} $为弹塑性刚度矩阵；$ {\boldsymbol{D}^{\text{e}}} $为弹性刚度矩阵，
$$\boldsymbol{D}^{\mathrm{e}}=\left(K-\frac{2}{3} G\right) \boldsymbol{\delta} \otimes \boldsymbol{\delta}+2 G \boldsymbol{I}。 $$ (7) 式中：$ G $和$ K $分别为弹性剪切模量和体积模量；$ \boldsymbol{\delta} $和I分别为二阶和四阶等同张量。
Rahman等[9]和Goudarzy等[28]指出采用${e^ * }$代替e，Hardin方程能够较好地反映细粒含量对剪切模量的影响，可以表示为
$$ G = {G_0}\frac{{{{(2.97 - {e^ * })}^2}}}{{1 + {e^ * }}}\sqrt {p'{p_{\text{a}}}} \text{，} $$ (8a) $$ K = {G_0}\frac{{2(1 + \nu )}}{{3(1 - 2\nu )}}\frac{{{{(2.97 - {e^ * })}^2}}}{{1 + {e^ * }}}\sqrt {p'{p_{\text{a}}}} 。 $$ (8b) 式中：$ {G_0} $为材料参数；$ \nu $为泊松比。
弹塑性刚度矩阵$ {\boldsymbol{D}^{{\text{ep}}}} $和塑性乘子$ \varLambda $可表示为
$$\boldsymbol{D}^{\mathrm{ep}}=\boldsymbol{D}^{\mathrm{e}}-\frac{\boldsymbol{D}^{\mathrm{e}}: \boldsymbol{m} \otimes \boldsymbol{n}^{\mathrm{T}}: \boldsymbol{D}^{\mathrm{e}}}{H+\boldsymbol{n}^{\mathrm{T}}: \boldsymbol{D}^{\mathrm{e}}: \boldsymbol{m}}\text{，} $$ (9a) $$ \varLambda=\frac{\boldsymbol{n}^{\mathrm{T}}: \boldsymbol{D}^{\mathrm{e}}: \mathrm{d} \boldsymbol{\varepsilon}}{H+\boldsymbol{n}^{\mathrm{T}}: \boldsymbol{D}^{\mathrm{e}}: \boldsymbol{m}} 。 $$ (9b) 式中：H为塑性模量；$ m $和$ n $分别为塑性流动方向和加载方向向量。根据塑性流动方向向量$ m $，塑性应变增量可表示为
$$ \mathrm{d} \boldsymbol{\varepsilon}^{\mathrm{p}}=\varLambda \cdot \boldsymbol{m}。 $$ (10) 2.2 屈服面方程
屈服面方程$f$采用修正椭圆形式来描述当前应力状态下砂-粉混合料的屈服特性[16, 29]：
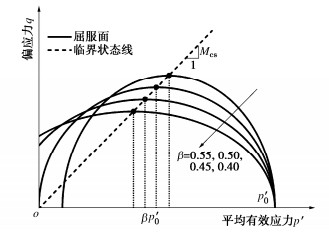
$$ f=\left(\frac{p^{\prime}-\beta p_0^{\prime}}{1-\beta}\right)^2+\left(\frac{q}{M_{\mathrm{cs}} \beta}\right)^2-p_0^{\prime 2}=0。 $$ (11) 式中：$q$为偏应力；${p'_0}$为平均有效应力轴与椭圆屈服面的交点；${M_{{\text{cs}}}}$为临界状态应力比；$\beta $为长短轴比值，$0 < \beta < 1$，控制着屈服面的形状。不同$\beta $值时，$q{\text{ - }}p'$平面内屈服面的形状如图 3所示。当$\beta = $0.5时，屈服面的形状为椭圆，与修正剑桥模型一致。
砂-粉混合料的试验结果表明[3, 7, 30]，FC对临界状态应力比有显著的影响，可用线性关系表示：
$$ {M_{{\text{cs}}}} = M + {\vartheta _{{\text{cs}}}}{F_{\text{C}}}。 $$ (12) 式中：M为纯砂的临界状态应力比；${\vartheta _{cs}}$为材料参数。
对式（11）进行微分可得
$$ \frac{{\partial f}}{{\partial p'}} = \frac{{2(\rho - \beta ){{p'}_0}}}{{{{(1 - \beta )}^2}}} \text{，} $$ (13a) $$ \frac{{\partial f}}{{\partial q}} = \frac{{2\rho \eta {{p'}_0}}}{{M_{{\text{cs}}}^2{\beta ^2}}} 。 $$ (13b) 式中：$ \eta $（=$q/p'$）为应力比；$\rho $为加载标量，可以表示为
$$ \rho = \frac{{\beta + \sqrt {{\beta ^2} + (1 - 2\beta )\left[ {1 + {{({\beta ^{ - 1}} - 1)}^2}{{(\eta /M)}^2}} \right]} }}{{1 + {{({\beta ^{ - 1}} - 1)}^2}{{(\eta /M)}^2}}} 。 $$ (14) 加载方向向量$\boldsymbol{n} = {\left[ {{n_{\text{v}}},{n_{\text{s}}}} \right]^{\text{T}}} $可以表示为
$$ {n_{\text{v}}} = \frac{{\partial f}}{{\partial p'}}/\sqrt {{{\left( {\frac{{\partial f}}{{\partial p'}}} \right)}^2} + {{\left( {\frac{{\partial f}}{{\partial q}}} \right)}^2}} \text{，} $$ (15a) $$ {n_{\text{s}}} = \frac{{\partial f}}{{\partial q}}/\sqrt {{{\left( {\frac{{\partial f}}{{\partial p'}}} \right)}^2} + {{\left( {\frac{{\partial f}}{{\partial q}}} \right)}^2}} 。 $$ (15b) 2.3 剪胀与塑性流动法则
常用的分数阶微分定义主要包括Caputo型和Riemann-Liouville型两种。其中，Caputo型分数阶微分具有弱奇异性，对常数C的分数阶微分为0，定义形式相对简单，在实际物理、力学问题建模等方面得到广泛应用。参考Sun等[16]和Lu等[17]的工作，Caputo型分数阶微分的定义如下：
$$ {}_a^CD_t^\alpha f(t) = \frac{1}{{\Gamma (n - \alpha )}}\int_a^t {{{(t - \tau )}^{n - \alpha - 1}}{f^{\left( n \right)}}(\tau ){\text{d}}\tau } 。 $$ (16) 式中，${}^C{D^\alpha }$为Caputo型$\alpha $阶微分；a和t为积分上下限；n为大于$\alpha $的最小整数；$\Gamma ( \cdot )$为伽马函数。
将屈服面方程（式（11））代入式（16），分别对$p'$与$q$进行$\alpha $阶求导可得
$$ \frac{{{\partial ^\alpha }f}}{{\partial {{(p')}^\alpha }}} = \frac{{2\left[ {\rho - (2 - \alpha )\beta } \right]{\rho ^{1 - \alpha }}{{({{p'}_0})}^{2 - \alpha }}}}{{\Gamma (3 - \alpha ){{(1 - \beta )}^2}}} \text{，} $$ (17a) $$ \frac{{{\partial ^\alpha }f}}{{\partial {q^\alpha }}} = \frac{{2{{(\rho \eta )}^{2 - \alpha }}{{({{p'}_0})}^{2 - \alpha }}}}{{\Gamma (3 - \alpha ){{({M_{{\text{cs}}}}\beta )}^2}}} 。 $$ (17b) 塑性流动方向向量$ m = {\left[ {{m_{\text{v}}},{m_{\text{s}}}} \right]^{\text{T}}} $可以表示为
$$ {m_{\text{v}}} = \frac{{{\partial ^\alpha }f}}{{\partial {{(p')}^\alpha }}}/\sqrt {{{\left( {\frac{{{\partial ^\alpha }f}}{{\partial {{(p')}^\alpha }}}} \right)}^2} + {{\left( {\frac{{{\partial ^\alpha }f}}{{\partial {q^\alpha }}}} \right)}^2}} \text{，} $$ (18a) $$ {m_{\text{s}}} = \frac{{{\partial ^\alpha }f}}{{\partial {q^\alpha }}}/\sqrt {{{\left( {\frac{{{\partial ^\alpha }f}}{{\partial {{(p')}^\alpha }}}} \right)}^2} + {{\left( {\frac{{{\partial ^\alpha }f}}{{\partial {q^\alpha }}}} \right)}^2}} 。 $$ (18b) 剪胀方程d可以表示为
$$ d = - \frac{{{\text{d}}\varepsilon _{\text{v}}^{\text{p}}}}{{{\text{d}}\varepsilon _{\text{s}}^{\text{p}}}} = \frac{{{\partial ^\alpha }f/\partial {{(p')}^\alpha }}}{{{\partial ^\alpha }f/\partial {q^\alpha }}} $$ $$ = \frac{{\left[ {\rho - (2 - \alpha )\beta } \right]{\rho ^{1 - \alpha }}{{({M_{cs}}\beta )}^2}}}{{{{(\rho \eta )}^{2 - \alpha }}{{(1 - \beta )}^2}}} 。 $$ (19) 当分数阶次$\alpha = $1.0，$\beta = $0.5时，式（19）与修正剑桥模型的剪胀方程完全一致。此时，塑性流动方向与加载方向一致，能够退化为相关联流动法则。为反映土体在加载过程中的状态相关性，将${\psi ^ * }$嵌入分数阶次$\alpha $中，可表示为
$$ \alpha = \exp (m{\psi ^ * })\text{，} $$ (20) 式中，m为材料参数。
当应力达到临界状态时，由式（19）可知，剪胀方程d满足条件：
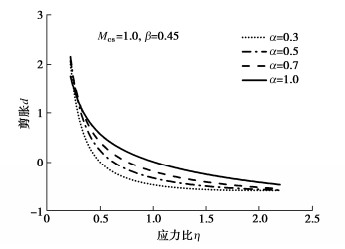
$$ d\left| {_{\eta = {M_{{\text{cs}}}},e = {e_{{\text{cs}}}},\alpha = 1}} \right. = \frac{{\left[ {\rho - (2 - \alpha )\beta } \right]{\rho ^{1 - \alpha }}{{({M_{{\text{cs}}}}\beta )}^2}}}{{{{(\rho \eta )}^{2 - \alpha }}{{(1 - \beta )}^2}}} = 0 。 $$ (21) 当土体为密实状态时，${\psi ^ * } < $0，$\alpha $随剪切应力的增大而增大，土体表现出应变软化和体积膨胀行为，达到临界状态时，${\psi ^ * } = $0和d=0。当土体为松散状态时，${\psi ^ * } > $0，随剪切应力增大$\alpha $逐渐减小，土体表现出应变硬化和体积收缩行为，达到临界状态时，${\psi ^ * } = $0和d=0。应力-剪胀关系随$\alpha $的演化规律如图 4所示。可以看出，随着$\alpha $的增加，$d{\text{ - }}\eta $曲线逐渐向上移动。当$\alpha $值较小时，在相同应力水平下剪胀性更加显著。
![]()
图 4 应力-剪胀关系随分数阶次的变化规律Figure 4. Evolution of stress-dilatancy curves with fractional order2.4 塑性模量
土体在临界状态线的“湿侧”和“干侧”分别表现出应变硬化和应变软化行为，材料状态是影响其行为转变的决定性因素。合理的塑性模量是反映土体力学特性的关键，塑性模量的确定方法有两种：一是严格按照屈服函数的一致性条件确定；二是构造满足下述条件的表达式：①当$\eta = $0时，$H = + \infty $；②当$\eta = $ ${M_{{\text{cs}}}}$以及$e = {e_{{\text{cs}}}}$时，$H = $0；③当峰值状态（$\eta = {M^p}$）时，$H = $0。砂-粉混合料的塑性模量受$ G $、$ {e^ * } $、$ {\psi ^ * } $和$ \eta $等因素的影响，参考Li等[10]的工作，提出了细粒-状态相关的塑性模量表达式：
$$ H = \frac{{{\chi _0}G{e^{\zeta {\psi ^ * }}}}}{\eta }({M^{\text{p}}} - \eta ) 。 $$ (22) 式中：$ {\chi _0} = {\chi _a} - {\chi _b}{e^ * } $，${\chi _a}$和${\chi _b}$为塑性模量参数。
为了描述砂-粉混合料的峰值破坏应力和峰后软化行为，将等效骨架状态参数$ {\psi ^ * } $嵌入峰值破坏应力比${M^p}$中，可表示为
$$ {M^p} = {M_{{\text{cs}}}}\exp ( - \zeta {\psi ^ * }) \text{，} $$ (23) 式中，$ \zeta $为峰值状态参数。
3. 模型参数
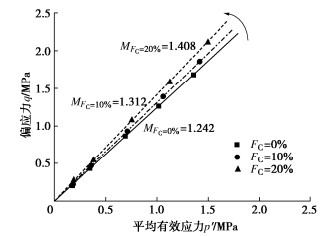
砂-粉混合料的分数阶塑性模型共有12个材料参数，可分为5种类型：①弹性参数${G_0}$和$ \nu $；②临界状态参数M，${\vartheta _{{\text{cs}}}}$，${e_\Gamma }$，${\lambda _{\text{c}}}$和$\xi $；③剪胀参数$\beta $和m；④峰值强度参数$ \zeta $；⑤塑性模量参数${\chi _a}$和${\chi _b}$。其中，临界状态参数M和${\vartheta _{{\text{cs}}}}$可通过式（12）拟合不同细粒含量下砂-粉混合料在$p'{\text{ - }}q$平面内的试验数据获得，如图 5所示。临界状态参数${e_\Gamma }$、${\lambda _{\text{c}}}$和$\xi $可通过式（5）拟合不同细粒含量下混合料在${e^ * }{\text{ - }}\lg p'$平面内的试验数据确定。
形状参数$\beta $控制土体的剪胀性，根据剪胀比$d$与应力比$\eta $的关系，结合式（19），通过调整参数$\beta $的大小获得$(d,\eta )$平面内试验数据的最佳拟合结果，即可确定参数$\beta $的取值[16, 31]。分数阶次$\alpha $反映材料非相关联流动的程度，根据相变状态时土体的剪胀比d=0，结合式（19），参数m可通过下式计算得到：
$$ m = \frac{1}{{({\psi ^ * })_{\text{d}}^{{\text{ob}}}}}\ln \left( {2 - \frac{{\rho _{\text{d}}^{{\text{ob}}}}}{\beta }} \right) 。 $$ (24) 式中：$ ({\psi ^ * })_{\text{d}}^{{\text{ob}}} $和$ \rho _{\text{d}}^{{\text{ob}}} $分别为相变状态下等效骨架状态参数和标量的实测值。
峰值状态时塑性模量$H = $0，参数$ \zeta $可通过峰值状态时的应力比和等效骨架状态参数计算确定[10, 29]。塑性模量参数${\chi _a}$和${\chi _b}$可通过拟合三轴排水或不排水剪切条件下$q{\text{ - }}{\varepsilon _{\text{s}}}$平面内的应力-应变关系确定。对于排水条件（${\text{d}}p' = {\text{d}}q/3$）和不排水条件（${\text{d}}{\varepsilon _{\text{v}}} = 0$），结合式（6）~（10），（15），（18）和（22）可计算得到参数$ {\chi _0} $的值[13]。参数$ {\chi _0} $确定后，根据最小二乘法拟合得到参数$ {\chi _a} $和$ {\chi _b} $的值。
4. 模型验证
针对粗颗粒占主导地位（FC < FCthre）的情况，分别对Xiao等[30]和Rahman等[5, 9]的砂-粉混合料试验数据进行模拟来验证分数阶塑性本构模型的合理性和适用性。模型参数取值如表 1所示。
表 1 模型验证参数Table 1. Parameters of model validation4.1 模型的试验验证Ⅰ
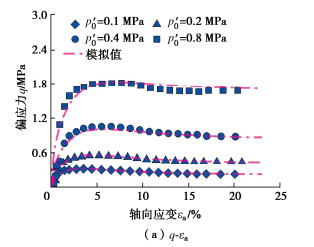
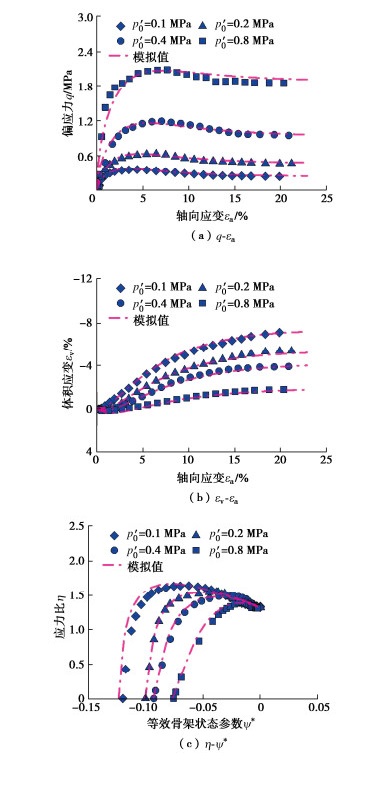
Xiao等[30]在不同初始围压（${p'_{\text{c}}}$=100，200，400，800 kPa）和细粒含量（非塑性细粒FC=0%，10%，20%）条件下对福建砂-粉混合料开展了一系列三轴排水剪切试验。主砂和非塑性细粒的矿物成分均为石英，试样的初始全局孔隙比${e_0}$在0.318~0.549的范围内变化。通过对试验数据的反演分析，得到FC=10%和20%时对应的b值分别为0.422和0.381。
图 6~8为福建砂-粉混合料模型预测结果与试验数据的对比。从图 6~8中可以看出，FC对混合料的应力-应变关系有着显著影响，剪切强度随FC的增大显著增大。所有试样在剪切过程中均先表现出轻微的收缩，到达相变状态后出现体积膨胀，最后达到临界状态。需要说明的是，FC=10%时混合料的剪胀性比FC=20%时更为明显，这可能是试样的密实程度不同造成的。从偏应力-轴向应变（$q{\text{ - }}{\varepsilon _{\text{a}}}$）、体积应变-轴向应变（${\varepsilon _{\text{v}}}{\text{ - }}{\varepsilon _{\text{a}}}$）和应力比-等效骨架状态参数（$\eta {\text{ - }}{\psi ^ * }$）3个角度来看，模型预测结果与试验数据整体上吻合较好，表明所建立的分数阶塑性模型能够合理地反映福建砂-粉混合料在不同有效围压和细粒含量下的应变软化和剪胀特性。
![]()
图 6 FC=0%时福建砂-粉混合料模型预测结果与试验数据对比Figure 6. Comparisons between simulations and test data of Fujian sand-silt mixtures with FC=0%![]()
图 7 FC=10%时福建砂-粉混合料模型预测结果与试验数据对比Figure 7. Comparisons between simulations and test data of Fujian sand-silt mixtures with FC =10%![]()
图 8 FC =20%时福建砂-粉混合料模型预测结果与试验数据对比Figure 8. Comparisons between simulations and test data of Fujian sand-silt mixtures with FC =20%4.2 模型的试验验证Ⅱ
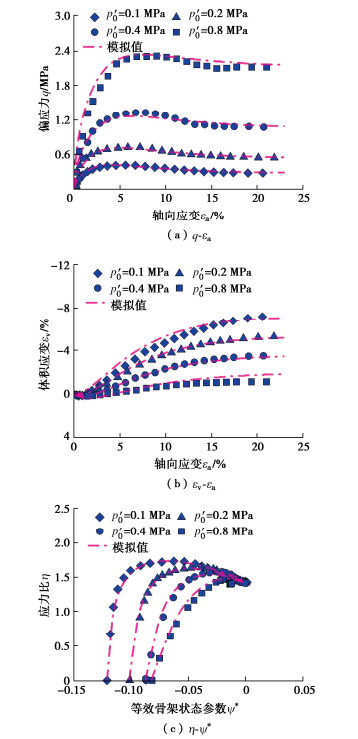
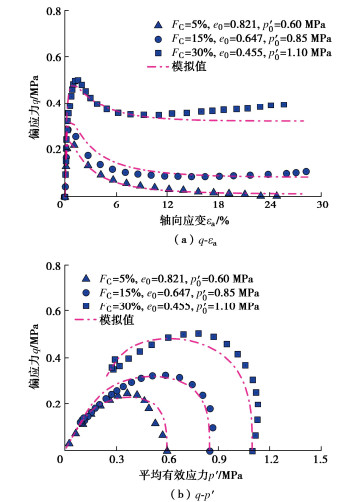
Rahman等[5, 9]以含非塑性细粒的悉尼砂为研究对象，开展了三轴不排水剪切试验。有效围压、细粒含量和孔隙比变化范围分别为0.35~1.1 MPa，0~30%，0.535~0.821。通过经验公式计算得到FC=5%，15%，30%时对应的b值分别为0.052，0.150，0.280。模型预测结果与试验数据对比如图 9~11所示。
![]()
图 9 悉尼砂-粉混合料模型预测与试验数据（非流动行为）Figure 9. Comparisons between simulations and test data (non-flow behavior) of Sydney sand-silt mixtures![]()
图 10 悉尼砂-粉混合料模型预测与试验数据（流动行为）Figure 10. Comparisons between simulations and test data (flow behavior) of Sydney sand-silt mixtures![]()
图 11 FC=15%时悉尼砂-粉混合料模型预测与试验数据Figure 11. Comparisons between simulations and test data of Sydney sand-silt mixtures with FC=15%砂-粉混合料的不排水剪切特性可分为两大类，即流动行为（收缩）和非流动行为（膨胀）。流动行为可能会表现出不同的特征，如不稳定或准稳定状态，这取决于试样的密实程度和初始有效应力。非流动行为不具有不稳定或准稳定状态。但是在达到临界状态之前，可能存在相变状态。对于具有非流动行为试样的应力-应变曲线和有效应力路径如图 9所示。从图 9中可以看出，虽然预测得到的应力-应变曲线和试验数据之间存在一定的差异，但考虑到试验结果的误差以及剪切过程中试样难以达到理论膨胀状态，模型整体上能够反映悉尼砂-粉混合料的非流动行为。
选取3种细粒含量（5%、15%和30%）的试验结果来验证模型预测流动行为的能力，如图 10所示。其中，FC=5%和15%的试样在${e_0}$和${p'_0}$方面具有不同的初始状态，但表现出相似的不排水响应，这是由于两种混合料的初始骨架状态参数$\psi _0^ * $几乎相同，分别为0.101和0.106。结果表明，不同细粒含量的试样不排水响应主要受$\psi _0^ * $控制，初始状态接近时，无论细粒含量如何，不排水响应趋于相似。因此，建立的模型能够合理反映砂-粉混合料的状态参数相关性。
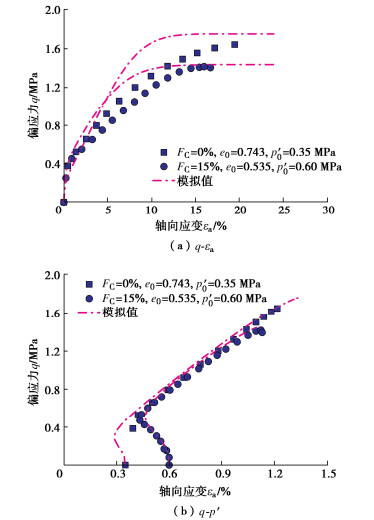
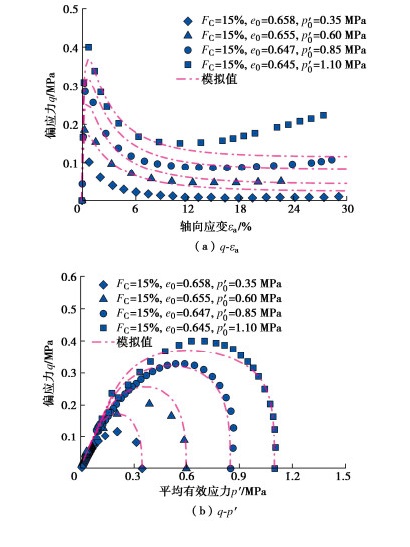
图 11为细粒含量FC=15%时悉尼砂-粉混合料模型预测结果与试验数据的对比。从图 11中可以看出，在细粒含量和孔隙比基本一致的条件下，随着有效围压的增加，试样逐渐从流动状态向限制流动状态（${e_0}$=0.645，${p'_0}$=1.10 MPa）转变，模型能够较好地捕捉到这种趋势。但是，模型在描述限制流动状态方面仍然存在一定的局限性。通过上述对比分析可知，模型预测得到的应力-应变曲线和有效应力路径与试验数据整体上吻合较好，表明建立的模型能够反映不同初始状态下砂-粉混合料的不排水剪切特性。
5. 结论与展望
本文针对砂-粉混合料在细粒含量阈值内的强度和变形特性（FC$ ＜ $FCthre），基于临界状态理论和分数阶塑性理论，建立了能够反映细粒含量和状态相关的分数阶塑性本构模型，并通过三轴排水和不排水剪切试验数据进行了验证，得到以下4点结论。
（1）随着细颗粒的加入临界状态线的位置逐渐向下移动，通过引入等效骨架孔隙比的概念，能够表征不同细粒含量下砂-粉混合料的临界状态特性，从而更好地描述其应力变形和液化失稳特性。
（2）基于分数阶微分理论，在不引入塑性势函数的情况下，通过屈服面方程的非正交梯度可以直接确定塑性应变增量方向，得到统一描述相关联和非相关联的塑性流动法则。
（3）在临界状态理论和分数阶塑性流动法则基础上，引入等效骨架孔隙比和状态参数对剪胀方程和弹/塑性模量进行修正，建立了考虑细粒含量和状态相关的分数阶塑性本构模型。
（4）模型预测结果与试验数据对比分析表明，所建立的模型能够有效反映砂-粉混合料在排水剪切条件下的应变软化（应变硬化）和剪胀（剪缩）等特性。同时，不排水条件下的关键特征，如流动和非流动行为也能够得到合理地描述。
-
![]()
图 1 二元混合料的颗粒接触状态和孔隙比[20]
Figure 1. Schematic diagram of particle contact state and void ratio of binary mixtures
![]()
图 4 应力-剪胀关系随分数阶次的变化规律
Figure 4. Evolution of stress-dilatancy curves with fractional order
![]()
图 6 FC=0%时福建砂-粉混合料模型预测结果与试验数据对比
Figure 6. Comparisons between simulations and test data of Fujian sand-silt mixtures with FC=0%
![]()
图 7 FC=10%时福建砂-粉混合料模型预测结果与试验数据对比
Figure 7. Comparisons between simulations and test data of Fujian sand-silt mixtures with FC =10%
![]()
图 8 FC =20%时福建砂-粉混合料模型预测结果与试验数据对比
Figure 8. Comparisons between simulations and test data of Fujian sand-silt mixtures with FC =20%
![]()
图 9 悉尼砂-粉混合料模型预测与试验数据（非流动行为）
Figure 9. Comparisons between simulations and test data (non-flow behavior) of Sydney sand-silt mixtures
![]()
图 10 悉尼砂-粉混合料模型预测与试验数据（流动行为）
Figure 10. Comparisons between simulations and test data (flow behavior) of Sydney sand-silt mixtures
![]()
图 11 FC=15%时悉尼砂-粉混合料模型预测与试验数据
Figure 11. Comparisons between simulations and test data of Sydney sand-silt mixtures with FC=15%
-
[1] 吴琪, 陈国兴, 周正龙, 等. 基于颗粒接触状态理论的粗细粒混合料液化强度试验研究[J]. 岩土工程学报, 2018, 40(6): 475-485. doi: 10.11779/CJGE201803011 WU Qi, CHEN Guoxing, ZHOU Zhenglong, et al. Experimental investigation on liquefaction resistance of fine-coarse-grained soil mixtures based on theory of intergrain contact state[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(6): 475-485. (in Chinese) doi: 10.11779/CJGE201803011
[2] 李涛, 赵洪扬, 翁勃航, 等. 细颗粒形状和含量对钙质混合砂强度的影响试验研究[J]. 岩土工程学报, 2023, 45(7): 1517-1525. doi: 10.11779/CJGE20220535 LI Tao, ZHAO Hongyang, WENG Bohang, et al. Experimental study on effects of shape and content of fine particles on strength of calcareous mixed sand[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(7): 1517-1525. (in Chinese) doi: 10.11779/CJGE20220535
[3] YILMAZ Y, DENG Y, CHANG CS, et al. Strength-dilatancy and critical state behaviours of binary mixtures of graded sands influenced by particle size ratio and fines content[J]. Géotechnique, 2023, 73(3): 202-217. doi: 10.1680/jgeot.20.P.320
[4] LADE P V, YAMAMURO J A. Effects of nonplastic fines on static liquefaction of sands[J]. Canadian Geotechnical Journal, 1997, 34(6): 918-928. doi: 10.1139/t97-052
[5] RAHMAN M M, LO S R, BAKI MAL. Equivalent granular state parameter and undrained behaviour of sand-fines mixtures[J]. Acta Geotechnica, 2011, 6(4): 183-194. doi: 10.1007/s11440-011-0145-4
[6] MONKUL M M, ETMINAN E, ŞENOL A. Coupled influence of content, gradation and shape characteristics of silts on static liquefaction of loose silty sands[J]. Soil Dynamics and Earthquake Engineering, 2017, 101: 12-26. doi: 10.1016/j.soildyn.2017.06.023
[7] GOBBI S, SANTISI D M P, LENTI L, et al. Effect of active plastic fine fraction on undrained behavior of binary granular mixtures[J]. International Journal of Geomechanics, 2022, 22(1): 06021035. doi: 10.1061/(ASCE)GM.1943-5622.0002242
[8] CHANG C S, YIN Z Y. Micromechanical modeling for behavior of silty sand with influence of fine content[J]. International Journal of Solids and Structures, 2011, 48(19): 2655-2667. doi: 10.1016/j.ijsolstr.2011.05.014
[9] RAHMAN M M, LO S R, DAFALIAS Y F. Modelling the static liquefaction of sand with low-plasticity fines[J]. Géotechnique, 2014, 64(11): 881-894. doi: 10.1680/geot.14.P.079
[10] LI X S, DAFALIAS Y F. Dilatancy for cohesionless soils[J]. Géotechnique, 2000, 50(4): 449-460. doi: 10.1680/geot.2000.50.4.449
[11] XU L Y, ZHANG J Z, CAI F, et al. Constitutive modeling the undrained behaviors of sands with non-plastic fines under monotonic and cyclic loading[J]. Soil Dynamics and Earthquake Engineering, 2019, 123: 413-424. doi: 10.1016/j.soildyn.2019.05.021
[12] WEI X, YANG J. A critical state constitutive model for clean and silty sand[J]. Acta Geotechnica, 2019, 14(2): 329-345.
[13] SUN Z C, CHU J, XIAO Y. Formulation and implementation of an elastoplastic constitutive model for sand-fines mixtures[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2021, 45(18): 2682-2708. doi: 10.1002/nag.3282
[14] 李晓强, 梁靖宇, 路德春, 等. 非饱和土的非正交弹塑性本构模型[J]. 中国科学: 技术科学, 2022, 52(7): 1048-1064. https://www.cnki.com.cn/Article/CJFDTOTAL-JEXK202207006.htm LI Xiaoqiang, LIANG Jingyu, LU Dechun, et al. Non- orthogonal elastoplastic constitutive model for unsaturated soil[J]. SCIENTIA SINICA Technologica, 2022, 52(7): 1048-1064. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JEXK202207006.htm
[15] YAO Y P, HE G, LUO T. Study on determining the plastic flow direction of soils with dilatancy[J]. Acta Geotechnica, 2023, 18(5): 2411-2425. doi: 10.1007/s11440-022-01770-8
[16] SUN Y F, SHEN Y. Constitutive model of granular soils using fractional-order plastic-flow rule[J]. International Journal of Geomechanics, 2017, 17(8): 04017025. doi: 10.1061/(ASCE)GM.1943-5622.0000904
[17] LU D C, LIANG J Y, DU X L, et al. Fractional elastoplastic constitutive model for soils based on a novel 3D fractional plastic flow rule[J]. Computers and Geotechnics, 2019, 105: 277-290. doi: 10.1016/j.compgeo.2018.10.004
[18] 路德春, 金辰逸, 梁靖宇, 等. 考虑状态相关的砂土非正交弹塑性本构模型[J]. 岩土工程学报, 2023, 45(2): 221-231. doi: 10.11779/CJGE20211457 (LU Dechun, JIN Chenyi, LIANG Jingyu, et al. State-dependent non-orthogonal elastoplastic constitutive model for sand[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(2): 221-231. doi: 10.11779/CJGE20211457
[19] 汪成贵, 束善治, 肖杨, 等. 考虑钙质砂颗粒破碎的分数阶边界面本构模型[J]. 岩土工程学报, 2023, 45(6): 1162-1170. doi: 10.11779/CJGE20220229 WANG Chenggui, SHU Shanzhi, XIAO Yang, et al. Fractional-order bounding surface model considering breakage of calcareous sand[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(6): 1162-1170. (in Chinese) doi: 10.11779/CJGE20220229
[20] THEVANAYAGAM S, SHENTHAN T, MOHAN S, et al. Undrained fragility of clean sands, silty sands, and sandy silts[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(10): 849-859. doi: 10.1061/(ASCE)1090-0241(2002)128:10(849)
[21] CHANG C S, DENG Y. Revisiting the concept of inter- granular void ratio in view of particle packing theory[J]. Géotechnique Letters, 2019, 9(2): 121-129. doi: 10.1680/jgele.18.00175
[22] BEEN K, JEFFERIES M G. A state parameter for sands[J]. Géotechnique, 1985, 35(2): 99-112. doi: 10.1680/geot.1985.35.2.99
[23] MURTHY T G, LOUKIDIS D, CARRARO J A H, et al. Undrained monotonic response of clean and silty sands[J]. Géotechnique, 2007, 57(3): 273-288. doi: 10.1680/geot.2007.57.3.273
[24] GOUDARZY M, SARKAR D, LIESKE W, et al. Influence of plastic fines content on the liquefaction susceptibility of sands: monotonic loading[J]. Acta Geotechnica, 2022, 17(5): 1719-1737. doi: 10.1007/s11440-021-01283-w
[25] ZHU Z H, DUPLA J C, CANOU J, et al. Experimental study of liquefaction resistance: effect of non-plastic silt content on sand matrix[J]. European Journal of Environmental and Civil Engineering, 2022, 26(7): 2671-2689. doi: 10.1080/19648189.2020.1765198
[26] LÜ X L, XUE D W, ZHANG B, et al. Experimental studies and constitutive modeling of static liquefaction instability in sand-clay mixtures[J]. International Journal of Geomechanics, 2022, 22(9): 04022149. doi: 10.1061/(ASCE)GM.1943-5622.0002472
[27] YAO Y P, HOU W, ZHOU A N. UH model: Three- dimensional unified hardening model for overconsolidated clays[J]. Géotechnique, 2009, 59(5): 451-469. doi: 10.1680/geot.2007.00029
[28] GOUDARZY M, RAHEMI N, RAHMAN M M, et al. Predicting the maximum shear modulus of sands containing nonplastic fines[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2017, 143(9): 06017013. doi: 10.1061/(ASCE)GT.1943-5606.0001760
[29] 孙增春, 汪成贵, 刘汉龙, 等. 粗粒土边界面塑性模型及其积分算法[J]. 岩土力学, 2020, 41(12): 3957-3967. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202012015.htm SUN Zengchun, WANG Chenggui, LIU Hanlong, et al. Bounding surface plasticity model for granular soil and its integration algorithm[J]. Rock and Soil Mechanics, 2020, 41(12): 3957-3967. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202012015.htm
[30] XIAO Y, SUN Y F, LIU H L, et al. Model predictions for behaviors of sand-nonplastic-fines mixtures using equivalent- skeleton void-ratio state index[J]. Science China Technological Sciences, 2017, 60(6): 878-892. doi: 10.1007/s11431-016-9024-9
[31] XIAO Y, LIU H L, CHEN Y M, et al. Bounding surface model for rockfill materials dependent on density and pressure under triaxial stress conditions[J]. Journal of Engineering Mechanics, 2014, 140(4): 04014002. doi: 10.1061/(ASCE)EM.1943-7889.0000702
-
期刊类型引用(2)
1. 吴彦燊，徐博远，刘璐，薄昭，吴琪. 砂-粉混合料不排水剪切相变强度特性试验研究. 人民长江. 2025(01): 187-192 . 
百度学术
2. 王钰轲，蒋睿，郭成超，王复明. 考虑相变状态及温度效应的冻结砂土非关联弹塑性本构模型. 岩石力学与工程学报. 2025(04): 1026-1039 . 百度学术
其他类型引用(0)
-
其他相关附件
下载:
计量
- 文章访问数: 553
- HTML全文浏览量: 59
- PDF下载量: 123
- 被引次数: 2
