岩土离心模型试验软接触式微型土压计研制及性能评价

王永志; 杨阳; 徐光明; 汤兆光; 张雪东; 孙锐; 周燕国

doi:10.11779/CJGE20230642

岩土离心模型试验软接触式微型土压计研制及性能评价 English Version

王永志^{1, 2,},
杨阳^{1, 2},
徐光明³,
汤兆光^{1, 2, ,},
张雪东⁴,
孙锐^{1, 2},
周燕国⁵

1.
中国地震局工程力学研究所地震工程与工程振动重点实验室, 黑龙江哈尔滨 150080
2.
地震灾害防治应急管理部重点实验室, 黑龙江哈尔滨 150080
3.
南京水利科学研究院岩土工程研究所, 江苏南京 210024
4.
中国水利水电科学研究院, 北京 100038
5.
浙江大学岩土工程研究所, 浙江杭州 310058

基金项目:

中国地震局工程力学研究所基本科研业务费专项项目 2023B08

国家自然科学基金项目 52278374

国家自然科学基金项目 519786131

黑龙江省自然科学基金项目 LH2023E019

详细信息

作者简介:
王永志(1984—)，男，研究员，主要从事土工离心机设计理论与试验方法、岩土工程防灾方面的研究工作。E-mail: yong5893741@163.com

通讯作者:
汤兆光, E-mail: tzg158135@163.com

中图分类号: TU432
计量
- 文章访问数: 319
- HTML全文浏览量: 37
- PDF下载量: 62
出版历程
- 收稿日期: 2023-07-09
- 网络出版日期: 2023-12-19
- 刊出日期: 2024-07-31

Development and performance evaluation of a soft-contact earth pressure transducer for geotechnical centrifuge modeling

WANG Yongzhi^{1, 2,},
YANG Yang^{1, 2},
XU Guangming³,
TANG Zhaoguang^{1, 2, ,},
ZHANG Xuedong⁴,
SUN Rui^{1, 2},
ZHOU Yanguo⁵

1.
Key Laboratory of Earthquake Engineering and Engineering Vibration, Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China
2.
Key Laboratory of Earthquake Disaster Mitigation, Ministry of Emergency Management, Harbin150080, China
3.
Geotechnical Engineering Department, Nanjing Hydraulic Research Institute, Nanjing 210024, China
4.
State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Institute of Water Resources and Hydropower Research, Beijing 100038, China
5.
Institute of Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China

摘要

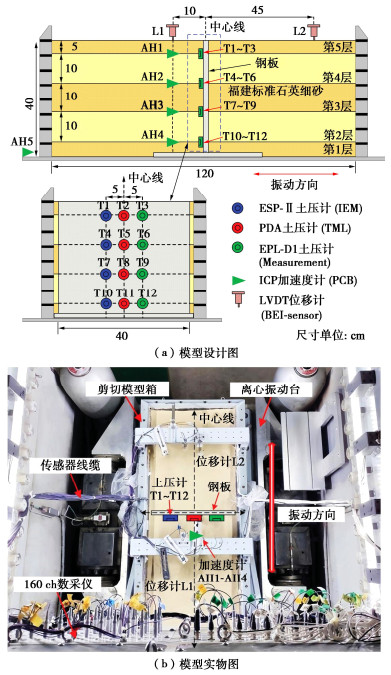
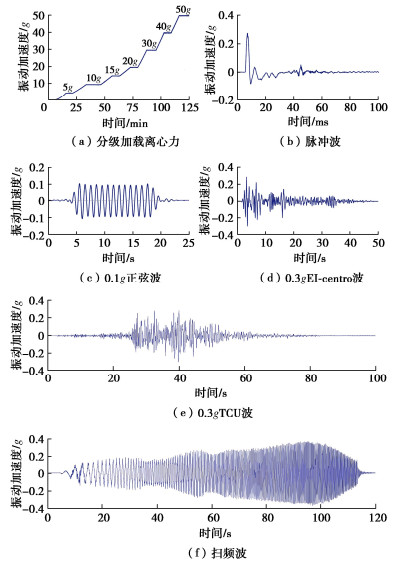
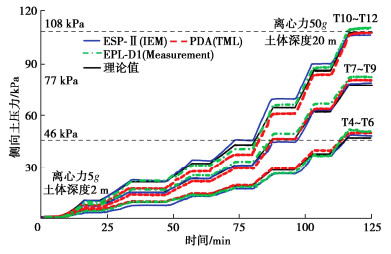
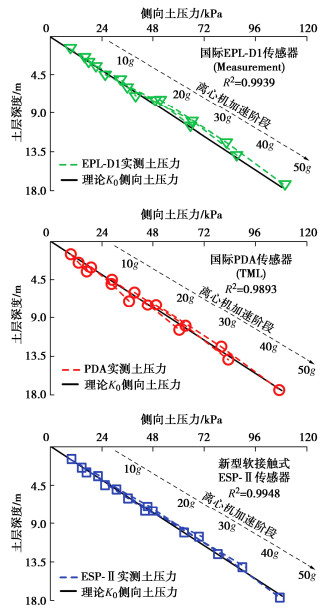
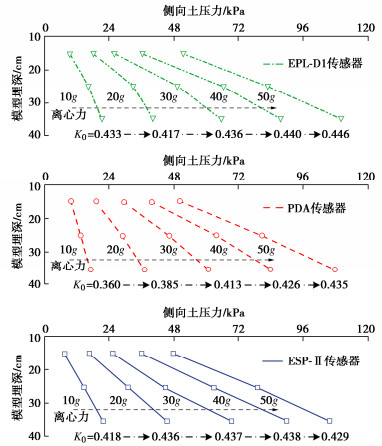
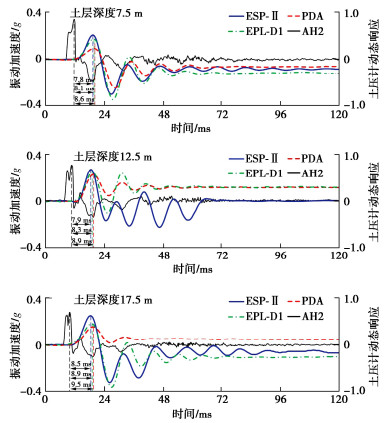
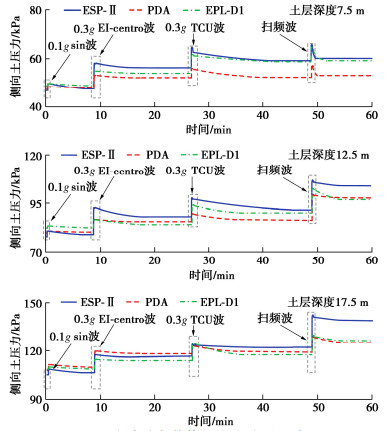
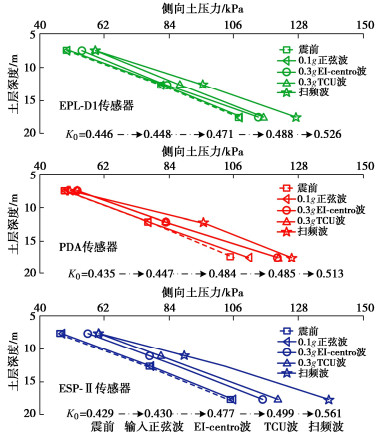
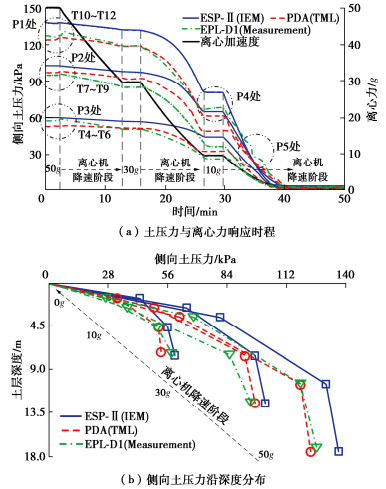
摘要: 微型土压计是岩土离心模型试验的重要测量技术之一。为解决刚性土压计测量中拱效应、尺寸效应、厚径比等经典误差问题及提升频响速率和精度，尝试开发了一种全新软接触式微型土压计ESP-Ⅱ，介绍了其技术创新和设计方法。以两种国际代表性土压计为参考，设计开展一系列离心模型试验，对其感应精度、速率和适用性进行评价。主要结论：①逐级加载离心加速度5g~50g试验下，各深度ESP-Ⅱ和两种参考传感器测试结果与理论值的平均误差分别为5.16%，6.70%，4.85%，三者沿深度拟合K₀优度系数R²均≥0.9893。②脉冲荷载试验中ESP-Ⅱ最大响应时间约7.8 ms，略优于两种参考传感器，具有良好的频响速率。③不同幅值正弦、地震等动荷载试验下，3种传感器测得土压力均呈一致增量趋势，K₀约由0.43~0.45增至0.51~0.56，与既有规律认识吻合。④离心机下降卸荷过程中，ESP-Ⅱ测得时程表现良好连续性和光滑性，反映软接触式设计有利于保障土体与传感器良好接触和稳定响应。研究成果，初步证明了软接触式土压计适应于静、动力离心试验需求，具有重要价值与应用前景。
- 岩土离心模型试验 /
- 微型土压计 /
- 设计方法 /
- 软接触式 /
- 性能评价
Abstract: The miniature earth pressure transducer is one of the key testing tools in geotechnical centrifuge modeling. Aiming at solving the classical problems such as arching effects, size effects and thickness-diameter ratio in the measurement of rigid transducers, and improving the frequency response rate and induction accuracy, a soft-contact pressure transducer ESP-Ⅱ is developed, and its innovations and design methods are introduced. Taking two internationally representative earth pressure transducers as reference, a series of centrifugal model tests are designed and carried out to evaluate its accuracy, frequency response and applicability. The main conclusions are as follows: (1) In the static centrifugal acceleration tests spinning up from 5g to 50g, the difference between the theoretical values and the test results of ESP-Ⅱ and the two reference transducers at each depth is small, and the average deviations are 5.16%, 6.70% and 4.85%, respectively. The coefficient R² of the three curves K₀ fitted along the depth is≥0.9893. (2) In the pulse load tests, the maximum response time of ESP-Ⅱ is about 7.8 ms, which is slightly better than that of the two reference transducers and has a satisfactory frequency response. (3) In the dynamic load tests of sine and seismic with different amplitudes, the incremental trend of earth pressure measured by the three transducers is basically consistent. The variation range of K₀ increases from 0.43~0.45 before the seismic to 0.51~0.56 after the seismic, which is consistent with the existing theory. (4) At the decelerating stage of the centrifuge, the good continuity and smoothness of the time history measured by the ESP-Ⅱ, which reflects the soft-contact design, is conducive to ensuring good contact and stable response between the soil and the transducer. The research results have preliminarily proved that the developed soft-contact transducer ESP-Ⅱ satisfies the requirements of static and dynamic centrifugal tests, with significant application value and immense potential.
- geotechnical centrifuge modeling /
- miniature earth pressure transducer /
- design method /
- soft-contact type /
- performance evaluation

HTML全文

0. 引言

维持开挖面稳定性是确保盾构施工安全的关键，在盾构施工中若开挖面支护力等施工参数设置不当，将会诱发开挖面失稳，造成地表的沉降^[1]。近年来，中国城市地下工程建设迅速发展，出现了越来越多的新建隧道近接既有隧道施工案例^[2]。盾构隧道近接施工的力学行为更加复杂，施工风险更加突出。与常规单一隧道不同，近接施工中的盾构开挖面稳定性分析受既有结构、近接形式和近接距离等因素的影响，因而呈现出多体、多形式、多过程的特点。当前针对近接施工盾构开挖面稳定性分析的研究成果匮乏，理论依据尚不完善，给盾构近接施工带来较大风险。

盾构隧道开挖面稳定性问题已成为地下工程施工安全研究的重点。国内外学者从模型试验、理论分析和数值模拟等方面开展了大量的研究。模型试验是研究盾构开挖面失稳破坏的主要手段之一，基于离心模型试验、大尺寸模型试验和小尺寸透明土模型试验等方法，学者们得到了砂土地层的烟囱状破坏模式^[3]和黏土地层的盆状破坏模式^[4]。在理论分析方面，学者们基于极限状态分析方法(极限平衡法和极限分析法)提出了二维及三维的失稳破坏模型，包括二维锥形模型^[5]、二维对数螺旋线模型^[6]、三维对数螺旋体模型^[7]、经典三维楔形体模型^[8]、各类改进的棱柱体-楔形体模型^[9-11]、Torus模型^[12]和三维水平球缺形模型^[13]等。二维模型和楔形体模型由于过于简化，因而计算结果误差较大，而三维旋转破坏理论考虑了破坏体三维空间形态，并且可用于砂土和黏土地层，因而具有明确的物理意义，准确性高，适用性广。近年来已有研究考虑不同影响因素对三维旋转破坏理论进行了改进，如Zou等^[14]考虑土拱效应影响，将对数螺旋线旋转模型在隧道拱顶以上部分修正为半椭球体；Ibrahim等^[15]考虑开挖面位于成层土地基，采用分段的对数螺旋形进行修正；Li等^[16]考虑渗流的影响，将水头方程引入三维旋转模型。然而，考虑近接既有隧道条件下的盾构开挖面稳定性问题及其相关计算方法还鲜见报道，因而本文基于近接既有隧道条件下开挖面破坏模式，对三维旋转模型的截面形状进行修正，可用于深入分析近接施工的盾构开挖面稳定性。

数值模拟是确定盾构隧道开挖面破坏模式的主要手段之一，主要包括有限元法(FEM)、有限差分法(FDM)和离散元法(DEM)等。有限元法在计算大变形时可能会出现网格畸变导致计算不收敛。离散元法虽然对大变形问题处理较好，但计算效率较低，并且对于足尺模型无法还原土体的真实粒径。有限差分法作为隧道围岩变形计算的常用方法，具有求解速度快，计算精度高和可处理大变形等优势而被广泛应用。

本文基于FLAC^3D有限差分软件揭示了近接既有隧道条件下的盾构开挖面破坏模式，构建了考虑水平方向破坏扩展不均匀性的对数螺旋体+椭圆柱的开挖面稳定性三维理论分析模型，给出了考虑土体黏聚力和重度影响系数的开挖面极限支护力表达式。分析了近接距离、隧道埋深和地层参数等因素对近接既有隧道条件下的盾构开挖面极限支护力的影响。

1. FLAC^3D数值模拟

1.1 数值模型建立

对于单隧道条件，可以建立半模型以节约计算资源，但本文主要考虑近接施工条件，若采用半模型会截断既有隧道，不利于设置边界条件，因此采用全模型进行数值模拟分析。为尽可能地削减边界效应，模型尺寸取为10倍盾构直径(D = 6 m)，如图 1所示。

图 1 FLAC^3D数值模型

Figure 1. Numerical model in FLAC^3D

下载: 全尺寸图片幻灯片

模型边界条件设置为：地表为自由边界，侧面为固定水平位移边界，底面为固定边界。土体选用基于Mohr–Coulomb准则的弹塑性本构模型。数值模型物理力学参数如表 1所示。不同地层条件下的土体参数根据Mollon等^[17]的建议取为4种，分别对应松砂、密砂、软黏和硬黏。土体的弹性模量根据不同土性分类进行取值^[18]。隧道结构(新建隧道与既有隧道)均采用衬砌结构单元(Liner)，厚度取为0.35 m。注浆层采用泥浆的相关参数。利用六面体单元划分网格，模型建立完成后，共有79360个单元，83681个节点。

表 1 数值模型参数(引自文献[17-18])

Table 1. Parameters of numerical model (data from References [17-18])

类别		重度γ/(kN·m^-3)	弹性模量E/MPa	泊松比 $\nu$	黏聚力c/kPa	内摩擦角φ/(°)
土体	松砂	17.0	17.5	0.397	0	20
	密砂	19.5	65.0	0.263	0	40
	软黏	16.0	3.5	0.414	7	17
	硬黏	18.0	12.5	0.366	10	25
衬砌	混凝土	25.0	33500	0.20	—	—
注浆层	泥浆	12.0	50	0.49	—	—

下载: 导出CSV

| 显示表格

模型生成后，首先施加重力加速度，使模型整体达到初始地应力平衡状态。其次，开挖既有隧道并施加衬砌，并再次进行地应力平衡。随后，开挖新建隧道至既有隧道附近并在开挖面处施加与初始水平地应力持平的支护力。本文针对盾构开挖面失稳破坏这一特定阶段进行研究，因此简化盾构施工过程，采用一次性开挖到位的形式。最后采用逐渐降低支护力的手段模拟开挖面失稳，这是由于在实际工程中，开挖面失稳往往是由于支护力不足导致的，即主动破坏模式。通过逐级降低开挖面支护力(共取20级)，待每级支护力下模型运算至平衡状态或出现塑性流动后方可调整为下一级支护力^[19]，直至支护力降为0。具体模拟过程如图 2所示。近接条件下由于设定既有隧道在新建隧道上方，限制了土体的变形发展，因而此时破坏模式的主要影响因素应为隧道间距，而非埋深，故在近接条件下暂不考虑埋深的影响。具体模拟方案如表 2所示。

图 2 数值模拟过程

Figure 2. Process of numerical simulations

下载: 全尺寸图片幻灯片

表 2 数值模拟方案

Table 2. Scheme of numerical simulations

土体类别	近接形式	新建隧道埋深比C/D	隧道垂直净距比d/D	开挖面水平间距比s/D
松砂	无	1.0，1.5，2.0	—	—
密砂	无	1.0，1.5，2.0	—	—
松砂	新建隧道垂直下穿既有隧道	2.0	0.25，0.50，0.75	-1，-0.5，0，0.5
密砂
软黏
硬黏
注：隧道垂直净距比d/D为新建隧道上表面与既有隧道下表面的垂直距离d与新建隧道直径D之比；开挖面水平间距比s/D为新建隧道开挖面与既有隧道中心轴线的水平距离s与新建隧道直径D之比，负值表示盾构尚未穿越既有隧道中心轴线。

下载: 导出CSV

| 显示表格

在模拟过程中，由于盾构开挖面支护力逐渐降低，开挖面土体产生朝向隧道内部的位移，但位移分布并不均匀，为了统一量化开挖面位移随支护力的变化情况，通过FISH函数获取开挖面各节点位移的平均值，以此作为盾构开挖面的代表性位移。

1.2 数值模型建立

为了验证数值模拟中采用的本构模型和参数的适用性和正确性，选取Kirsch等^[3]开展的离心模型试验结果进行对比分析。图 3所示为单隧道条件下，埋深比C/D = 1.5时的变形区域对比。可以看出，离心模型试验中沿开挖面前方和上方的主要变形范围与本文数值模拟结果基本一致，结果相差均在5%以内，因此可以认为数值模型可以较好地还原真实情况。

图 3 失稳变形区域对比^[3]

Figure 3. Comparison of instability areas^[3]

下载: 全尺寸图片幻灯片

图 4为不同埋深条件下开挖面支护力-位移关系对比结果，其中，虚线为本文单隧道条件下的开挖面极限支护力，取值原则为：当支护力变化不大时，开挖面位移显著增加，认为开挖面发生失稳，此时的支护力即为极限支护力。通过对比可以发现，松砂条件下数值模拟结果和离心试验结果^[3]相差不大；而密砂条件下，数值模拟结果未显现出支护力曲线回弹的现象，这是由于离心试验^[3]中采用“位移法”(控制开挖面的支护面板以一定速度后退模拟失稳的方法)，初始阶段由于土拱效应使得支护力迅速下降，超过临界位移后，周围土体出现“应变软化”，导致所需支护力回升^[20]。而在实际盾构施工中，开挖面失稳的直接原因是支护力的不足，因而采用“力法”(即本文中控制支护力逐级降低的方法)模拟开挖面失稳更加符合实际。

图 4 无量纲化开挖面支护力–位移关系曲线

Figure 4. Relationship between normalized displacement and normalized support force of tunnel face

下载: 全尺寸图片幻灯片

1.3 数值模拟结果

近接条件下(松砂，d/D = 0.5)盾构开挖面失稳变形模式如图 5所示。由于黏性土层失稳滑移时没有明显的剪切带，因此多通过采用位移轮廓线来确定破坏模式的范围^[21]。本文参考Li等^[22]数值模拟结果，取位移值大于1%盾构直径的区域为破坏模式包络面。由模拟结果可见，随着盾构开挖面接近→穿越→远离既有隧道(s/D逐渐增加)，失稳区呈现出沿开挖方向不对称的特点，这是由于既有隧道与土体刚度差异很大，限制了土体的位移发展。除s/D =-0.5外，其余3种条件下开挖面变形模式均与单隧道情况类似，即由开挖面前方对数螺旋体和上方筒仓状滑动体组合而成。当s/D =-0.5时，开挖面变形呈现出沿既有隧道方向扩展的形态。

图 5 近接既有隧道条件下开挖面变形模式(不同s/D)

Figure 5. Deformation characteristics of shield tunnel face adjacent to an existing tunnel under different s/D

下载: 全尺寸图片幻灯片

不同隧道垂直净距下(松砂，s/D = -0.5)的盾构开挖面失稳模式如图 6所示。垂直净距对破坏模式的影响较小，随着净距的增加，上方破坏影响范围有所增加。不同土性条件下的开挖面失稳模式(d/D = 0.5，s/D = -0.5)如图 7所示，可以发现不同土性中的失稳模式基本一致，只是沿开挖面前方和两侧的扩展范围有所不同：密砂相比松砂向两侧扩展范围更小，黏土相比砂土向前方扩展更大。

图 6 近接既有隧道条件下开挖面变形模式(不同d/D)

Figure 6. Deformation characteristics of shield tunnel face adjacent to an existing tunnel under different d/D

下载: 全尺寸图片幻灯片

图 7 近接既有隧道条件下开挖面变形模式(不同土性)

Figure 7. Deformation characteristics of shield tunnel face adjacent to an existing tunnel under different soil properties

下载: 全尺寸图片幻灯片

近接条件下的开挖面极限支护力如图 8所示。图 8(a)中虚线为相应地层中的单隧道开挖面极限支护力，可以看出既有隧道的存在使开挖面极限支护力有所降低，这是由于既有隧道的刚度远大于土体，在开挖面失稳过程中起到了“支撑”的作用。对于同种地层，随着隧道垂直净距的增加，开挖面极限支护力略有增加，这是由于隧道净距越大，隧道间松动土柱越高，导致松动土压力越大，也就需要更大的支护力。图 8(b)为盾构穿越既有隧道过程中的开挖面极限支护力，可以看出随着开挖面水平间距比s/D逐渐增加，开挖面极限支护力呈现先降低后升高的趋势，在s/D = -0.5时最低，这是由于此时失稳破坏区域与既有隧道的重合区域最大，既有隧道对开挖面前方土体的“支撑”作用最显著，因此所需的极限支护力越低。对于同一工况，软黏土地层的极限支护力最大，这是由于软黏土强度低且破坏范围较大。

图 8 不同近接距离下开挖面极限支护力

Figure 8. Limit support pressures on tunnel face under different adjacent distances

下载: 全尺寸图片幻灯片

2. 三维旋转破坏模型

2.1 理论模型描述

基于数值模拟结果，构建近接既有隧道条件下的开挖面三维旋转破坏模型。对于近接工况，当s/D = -0.5时，开挖面破坏模式受既有隧道的影响最大，因而先依据此工况建立理论模型进行推导。影响开挖面破坏模式的主要因素为隧道净距，但若垂直净距过大，则不符合近接施工条件。因此，为体现近接施工特点，同时参考相关规范中对于近接施工的定义^[23]，本文假定隧道垂直净距不大于1倍盾构直径。

根据数值模拟结果，将开挖面破坏模式简化为对数螺旋体+筒仓体，如图 9所示。对于筒仓体部分，为体现沿开挖面前方和两侧扩展范围的差异性，假设其为半长轴、半短轴和高度分别设为a，b和h的椭圆柱；对数螺旋体由对数螺旋线旋转得到，对数螺旋线又称等角螺旋线，曲线上每个点的切向量与对数螺旋线极点至该点所成的向量均成一固定角度^[21]，满足

$r = {r_0} \cdot \exp \left[ {(\theta - {\theta _0})\tan \varphi } \right] 。$

(1)

图 9 改进的三维旋转破坏模型

Figure 9. Improved three-dimensional rotational failure mode

下载: 全尺寸图片幻灯片

目前已有一些学者基于对数螺旋体模型开展了盾构开挖面稳定性的相关研究^{[14, 17]}，但其截面被假定为圆形，这在多数情况下与实际不符，且无法与本模型中的上部椭圆体对应，因此本文采用截面为椭圆形的对数螺旋体作为破坏体模型。对数螺旋体具体生成方式为：极角为θ的射线OG与对数螺旋线AH、BE分别相交，以两条对数螺旋线之间线段长度的一半为椭圆半短轴b。假定同一地层中椭圆离心率保持不变，即椭圆长短轴之比不变，设a = kb。则

$a = k\frac{{{r_2} - {r_1}}}{2}, {\text{ }}b = \frac{{{r_2} - {r_1}}}{2} 。$

(2)

其中，

${r_1} = D\tan {\beta _B} \cdot \exp \left[ {(\theta - {\text{π }}/2)\tan \varphi } \right] \text{，}$

(3a)

${r_2} = D\sec {\beta _B} \cdot \exp \left[ {{\text{(}}\theta - {\beta _B}{\text{)}}\tan \varphi } \right] 。$

(3b)

令射线OG与对数螺旋线BE相交于G点，与开挖面中心线AB相交于F点，过F点作平行于x轴的直线F₁F₂与开挖面圆周分别相交于F₁、F₂点，截去椭圆F₁GF₂外侧部分得到椭圆缺形截面，该截面关于FG两侧对称。令极角θ由 ${\beta _B}$ 增加至π/2，则生成的所有截面叠加即形成对数螺旋体。图 10为近接既有隧道条件下盾构开挖面失稳变形区域的数值模拟结果与理论模型对比，可以看出，所提出的对数螺旋体+筒仓体模型在各个方向上均可较好地拟合实际位移包络面。

图 10 数值模拟结果与理论模型对比

Figure 10. Comparison between FDM simulation and theoretical model

下载: 全尺寸图片幻灯片

2.2 理论模型求解

首先，求解椭圆柱对下部对数螺旋体的土压力。根据图 9所示条分法，并假设土体服从Mohr–Coulomb破坏准则，建立垂直方向受力平衡方程：

${\text{π }}{a_0}{b_0}\gamma {\text{d}}z = {\text{π }}{a_0}{b_0}{\text{d}}{\sigma _{\text{v}}} +\\ \left[ {2{\text{π }}{b_0} + 4({a_0} - {b_0})} \right]{\text{(}}c + K\tan \varphi {\sigma _{\text{v}}}{\text{)d}}z \text{，}$

(4)

$\gamma = \sum\limits_{i = 1}^n {{\gamma _i}{h_i}} /({C_0} + {D_0}) 。$

(5)

式中：a₀，b₀分别为椭圆柱的半长轴和半短轴；γ为椭圆柱体上方考虑既有隧道空心影响的土体加权平均重度；γ_i，h_i分别为既有隧道上方各层土体的重度和层厚；c，φ分别为土体黏聚力和内摩擦角； $K = 1 - \sin \varphi$ 为土体侧压力系数； ${\sigma _{\text{v}}}$ 为竖向土压力。

椭圆柱体上表面压力为既有隧道底部处的土体自重应力，即 ${\sigma _{\text{v}}}$ (0) = γ(C₀+D₀)，其中，C₀，D₀分别为既有隧道埋深和直径。由式(4)及a = kb可得

${\sigma }_{\text{v}}(z)=\frac{\left[\text{π}k{b}_{0}\gamma -2(\text{π}+2k-2)c\right]\left(1-{\text{e}}^{-\frac{2\left(\text{π}+2k-2\right)K\mathrm{tan}\varphi }{\text{π}k{b}_{0}}z}\right)}{2(\text{π}+2k-2)K\mathrm{tan}\varphi }+\gamma ({C}_{0}+{D}_{0})\text{ }。$

(6a)

进而可得椭圆柱体作用在对数螺旋体顶面的竖向力 ${\sigma _{{\text{v1}}}}$ (其中柱体高度h取为隧道垂直净距d)：

${\sigma }_{\text{v1}}=\frac{\left[\text{π}k{b}_{0}\gamma -2(\text{π}+2k-2)c\right]\left(1-{\text{e}}^{-\frac{2\left(\text{π}+2k-2\right)K\mathrm{tan}\varphi }{\text{π}k{b}_{0}}d}\right)}{2(\text{π}+2k-2)K\mathrm{tan}\varphi }+\gamma ({C}_{0}+{D}_{0})\text{ }。$

(6b)

式中，当 $c \geqslant {\text{π }}k{b_0}\gamma /(2{\text{π }} + 4k - 4)$ 时， ${\sigma _{{\text{v1}}}}$ 取0，b₀可由式(2)令θ = π/2得到。

其次，建立对数螺旋体对原点O的力矩平衡方程：

${M_{\text{w}}} + {M_{\text{v}}} - {M_{\text{T}}} - {M_{\text{c}}} = 0 \text{，}$

(7)

式中： ${M_{\text{w}}}$ 为重力力矩； ${M_{\text{v}}}$ 为上表面压力 ${\sigma _{{\text{v1}}}}$ 产生的力矩； ${M_{\text{T}}}$ 为开挖面支护力力矩； ${M_{\text{c}}}$ 为土体抗力矩。

如所示，由于直接计算 ${M_{\text{w}}}$ 较为复杂，因此采用完整对数螺旋体AHBE重力力矩减去不规则体AHB重力力矩进行计算：

${M_{\text{w}}} = {M_{AHBE}} - {M_{AHB}} 。$

(8)

图 11 M_w计算图

Figure 11. Calculation diagram for M_w

下载: 全尺寸图片幻灯片

完整对数螺旋体AHBE微元体的重力力矩为

${\text{d}}{M_{AHBE}} = \gamma \cdot {\text{π }}ab\left[ {\frac{1}{2}({r_{\text{1}}} + {r_{\text{2}}}){\text{d}}\theta } \right]({r_2} - b)\sin \theta \text{，}$

(9)

对式(9)积分得

${M_{AHBE}} = \int_{{\beta _B}}^{\frac{{\text{π }}}{2}} {\gamma \cdot {\text{π }}ab\left[ {\frac{1}{2}({r_{\text{1}}} + {r_{\text{2}}})} \right]({r_2} - b)\sin \theta {\text{d}}\theta } 。$

(10)

不规则体AHB可以近似看作底面为正方形的楔形体，根据面积等效原则，其边长为 $\sqrt {\text{π }} D/2$ ，则

${M_{AHB}} = \gamma \cdot \frac{1}{2}{\left( {\frac{{\sqrt {\text{π }} D}}{2}} \right)^2}{h_{\text{H}}} \cdot \left( {D\tan {\beta _B} - \frac{{{h_{\text{H}}}}}{3}} \right) \\ {h_{\text{H}}} = D\tan {\beta _B}\left\{ {1 - \exp \left[ {({\beta _B} - {\text{π }}/2)\tan \varphi } \right]} \right\} \text{，}$

(11)

式中， ${h_{\text{H}}}$ 为三角形AHB中底边AB的高。

上表面压力 ${\sigma _{{\text{v1}}}}$ 产生的力矩 ${M_{\text{V}}}$ 为

${M_{\text{V}}} = {\text{π }}kb_0^2{\sigma _{{\text{v}}1}}(OE - {b_0}) \text{，}$

(12)

其中， $OE = \frac{D}{{\cos {\beta _B}}} \cdot \exp \left[ {\left( {\frac{{\text{π }}}{2} - {\beta _B}} \right)\tan \varphi } \right]$ 。

开挖面支护力力矩 ${M_{\text{T}}}$ 为

${M_{\text{T}}} = {\sigma _{\text{T}}}{\text{π }}({D^2}/4)(D/2) 。$

(13)

采用条分法计算土体抗力矩 ${M_{\text{c}}}$ ，如图 12所示。

图 12 条分单元体受力平衡

Figure 12. Force equilibrium of soil slices

下载: 全尺寸图片幻灯片

假设滑动面上土体强度同时得到发挥，且服从Mohr–Coulomb破坏准则：

${\tau _{\text{f}}} = c + \sigma \tan \varphi 。$

(14)

将条分单元体近似看作圆缺形，则根据第i个土条的竖直方向受力平衡，有

${\sigma _{{\text{v1}}}}{l_i} \cdot {P_1}{P_2} + {W_i} = {T_i}\sin ({\theta _i} - \varphi ) + {N_i}\cos {\text{(}}{\theta _i} - \varphi {\text{)}} \text{，}$

(15)

${T}_{i}=c{l}_{i}\stackrel{⌢}{{P}_{1}Q{P}_{2}}+{N}_{i}\mathrm{tan}\varphi 。$

(16)

其中： ${l_i} = {r_i}{\text{d}}\theta$ ； ${W_i} = \gamma \cdot \Delta {S_i}{l_i}\cos ({\theta _i} - \varphi )$ 为第i个土条的重力；T_i，N_i分别为第i个土条的滑动面摩擦力合力和支持力合力。

ΔS_i，P₁P₂和 $\stackrel{⌢}{{P}_{1}Q{P}_{2}}$ 可根据几何性质进行求解：

$\begin{array}{l}\Delta {S}_{i}=\frac{\mathrm{arccos}\left(\frac{{P}_{1}{P}_{2}{}^{2}-4P{Q}^{2}}{{P}_{1}{P}_{2}{}^{2}+4P{Q}^{2}}\right)\cdot \left(PQ+\frac{{P}_{1}{P}_{2}{}^{2}}{4PQ}\right)+{P}_{1}{P}_{2}\left(PQ-\frac{{P}_{1}{P}_{2}{}^{2}}{4PQ}\right)}{4}\text{，}\\ {P}_{1}{P}_{2}=2{a}_{0}\sqrt{1-{\left(\frac{{r}_{i}\mathrm{sin}\theta -D\mathrm{tan}{\beta }_{B}-{b}_{0}}{{b}_{0}}\right)}^{2}}\text{，}\\ PQ={r}_{i}\mathrm{cos}\theta \end{array} \\ \stackrel{⌢}{{P}_{1}Q{P}_{2}}=\mathrm{arccos}\left(\frac{{P}_{1}{P}_{2}{}^{2}-4P{Q}^{2}}{{P}_{1}{P}_{2}{}^{2}+4P{Q}^{2}}\right)\cdot \left(PQ+\frac{{P}_{1}{P}_{2}{}^{2}}{4PQ}\right) 。$

(17)

由式(15)~(17)可得

$\begin{array}{l}{N}_{i}=\frac{{\sigma }_{\text{v}1}{r}_{i}\mathrm{cos}({\theta }_{i}-\varphi ){P}_{1}{P}_{2}\text{d}\theta +{W}_{i}-c{r}_{i}\stackrel{⌢}{{P}_{1}Q{P}_{2}}\mathrm{sin}({\theta }_{i}-\varphi )\text{d}\theta }{\mathrm{tan}\varphi \mathrm{sin}({\theta }_{i}-\varphi )+\mathrm{cos}({\theta }_{i}-\varphi )}\text{ }\text{，}\\ {T}_{i}=c{l}_{i}+\frac{{\sigma }_{\text{v}1}{r}_{i}\mathrm{cos}({\theta }_{i}-\varphi ){P}_{1}{P}_{2}\text{d}\theta +{W}_{i}-c{r}_{i}\stackrel{⌢}{{P}_{1}Q{P}_{2}}\mathrm{sin}({\theta }_{i}-\varphi )\text{d}\theta }{\mathrm{tan}\varphi \mathrm{sin}({\theta }_{i}-\varphi )+\mathrm{cos}({\theta }_{i}-\varphi )}\mathrm{tan}\varphi 。\end{array}$

(18)

滑动面上土体抗力的微力矩为

$\left. \begin{array}{l} {\rm{d}}{M_{{\rm{cT}}}} = {T_i}{r_i}{\rm{cos}}\varphi ,\\ {M_{{\rm{cN}}}} = {N_i}{r_i}{\rm{sin}}\varphi 。 \end{array} \right\}$

(19)

则滑动面上土体抗力的总力矩为

${M_{\text{c}}} = {M_{{\text{cT}}}} + {M_{{\text{cN}}}} = \int_{{\beta _B}}^{\frac{{\text{π }}}{2}} {({T_i}{r_i}\cos \varphi + {N_i}{r_i}\sin \varphi )}\\ ={\displaystyle {\int }_{{\beta }_{B}}^{\frac{\text{π}}{2}}\left(c{r}_{i}^{2}\stackrel{⌢}{{P}_{1}Q{P}_{2}}\mathrm{cos}\varphi +\frac{2{N}_{i}{r}_{i}\mathrm{sin}\varphi }{\text{d}\theta }\right)}\text{d}\theta 。$

(20)

最后，联立式(7)，(8)，(10)~(18)和(20)，可得

${\sigma _{\text{T}}} = c{N_c} + \gamma D{N_\gamma } 。$

(21)

式中： ${\sigma _{\text{T}}}$ 为开挖面支护力； ${N_c}$ ， ${N_\gamma }$ 分别为土体黏聚力和重度对开挖面支护力的影响系数：

$\begin{array}{l}{N}_{c}=\frac{8k{b}_{0}^{2}(OE-{b}_{0})\left[\mathrm{exp}\left(-\frac{2(\text{π}+2k-2)K\mathrm{tan}\varphi }{\text{π}k{b}_{0}}d\right)-1\right]}{{D}^{3}K\mathrm{tan}\varphi }-\\ \frac{8}{\text{π}{D}^{3}}{\displaystyle {\int }_{{\beta }_{B}}^{\frac{\text{π}}{2}}\{{r}_{2}^{2}\stackrel{⌢}{{P}_{1}Q{P}_{2}}\mathrm{cos}\varphi +\frac{2\mathrm{sin}\varphi \cdot {r}_{\text{2}}{}^{2}\mathrm{cos}(\theta -\varphi ){P}_{1}{P}_{2}}{K\mathrm{tan}\varphi \left[\mathrm{tan}\varphi \mathrm{sin}(\theta -\varphi )+\mathrm{cos}(\theta -\varphi )\right]}\cdot }\\ \left[\mathrm{exp}\left(-\frac{2(\text{π}+2k-2)K\mathrm{tan}\varphi }{\text{π}k{b}_{0}}d\right)-1\right]-\end{array} \\ \frac{2\mathrm{sin}\varphi \cdot {r}_{\text{2}}{}^{2}\stackrel{⌢}{{P}_{1}Q{P}_{2}}\mathrm{sin}\text{(}\theta -\varphi \text{)}}{\mathrm{tan}\varphi \mathrm{sin}\text{(}\theta -\varphi \text{)}+\mathrm{cos}\text{(}\theta -\varphi \text{)}}\}\text{d}\theta \text{，}$

(22)

${N_\gamma } = \frac{{4\int_{{\beta _B}}^{\frac{{\text{π }}}{2}} {ab({r_{\text{1}}} + {r_{\text{2}}})({r_2} - b)\sin \theta {\text{d}}\theta } }}{{{D^4}}} - \frac{{{h_{\text{H}}} \cdot \left( {D\tan {\beta _{\text{B}}} - \frac{{{h_{\text{H}}}}}{3}} \right)}}{{{D^2}}} +\\ \begin{array}{l} \frac{{8k{b_0}^2(OE - {b_0})({C_0} + {D_0})}}{{{D^4}}} + \hfill \\ \frac{{4{\text{π }}{k^2}{b_0}^3(OE - {b_0})\left[ {1 - \exp \left( { - \frac{{2({\text{π }} + 2k - 2)K\tan \varphi }}{{{\text{π }}k{b_0}}}d} \right)} \right]}}{{{D^4}({\text{π }} + 2k - 2)K\tan \varphi }} - \hfill \\ \frac{8}{{{\text{π }}{D^4}}}\int_{{\beta _B}}^{\frac{{\text{π }}}{2}} {\left\{ \begin{array}{l} \hfill \\ \hfill \\ \hfill \\ \end{array} \right.} \frac{{2\sin \varphi \cdot {r_{\text{2}}}^2\cos (\theta - \varphi )\Delta S}}{{\tan \varphi \sin (\theta - \varphi ) + \cos (\theta - \varphi )}} + \hfill \\ \frac{{2\sin \varphi \cdot {r_{\text{2}}}^2\cos (\theta - \varphi ){P_1}{P_2}}}{{\tan \varphi \sin (\theta - \varphi ) + \cos (\theta - \varphi )}} \cdot \hfill \\ \end{array} \\ \left. {\left( {\frac{{{\text{π }}k{b_0}\left[ {1 - \exp \left( { - \frac{{2({\text{π }} + 2k - 2)K\tan \varphi }}{{{\text{π }}k{b_0}}}d} \right)} \right]}}{{2({\text{π }} + 2k - 2)K\tan \varphi }} + C + {D_0}} \right)} \right\} \text{d}\theta 。$

(23)

当s/D为其他值时，可采用线性插值对开挖面极限支护力进行求解，具体为

${\sigma }_{\text{T}}^{*}=\{\begin{array}{l}(0.5-s/D){\sigma }_{\text{Tm}}+(s/D+0.5){\sigma }_{\text{T0}}\text{ (}-0.5 < s/D < 0.5)\\ 2(s/D+1){\sigma }_{\text{Tm}}-2(s/D+0.5){\sigma }_{\text{T0}}\text{ (}-1 < s/D < -0.5)\\ {\sigma }_{\text{T0}}\text{ (}s/D\le -1或s/D\ge 0.5)\end{array}。$

(24)

式中： $\sigma _{\text{T}}^*$ 为相应s/D处的极限支护力； ${\sigma _{{\text{Tm}}}}$ 为近接条件下s/D =-0.5时的极限支护力； ${\sigma _{{\text{T0}}}}$ 为相同土性和埋深的单隧道开挖面极限支护力，可令k = 1进行计算。

3. 理论模型验证及参数分析

3.1 理论模型验证

理论模型中自定义参数为两个：OB与垂直面的夹角 ${\beta _B}$ 及椭圆长短轴之比k。根据村山公式原理^[6]，对数螺旋线在盾构底面与水平方向夹角为 ${\text{π }}/4 + \varphi /2$ ，则 ${\beta _B} = {\text{π /}}4 - \varphi /2$ 。近接条件下k值主要受地层条件和既有隧道影响，可由数值模拟结果得到(松砂：k = 1.8；密砂：k = 1.3；软黏：k = 1.9；硬黏：k = 1.6)。由于式(22)和(23)较为复杂，可代入已知参数至Matlab中进行求解。当隧道埋深较大(通常C/D > 3.0)，则盾构施工引起的土拱效应、渐进性破坏特性与常规埋深隧道完全不同^[13]，因此本文暂不考虑大埋深情况。

图 13为本文理论分析和数值模拟结果与其他学者的结果对比。单隧道条件下(图 13(a))的理论分析结果与已有试验结果和本文数值模拟结果均符合较好。图 13(b)为松砂地层近接条件下(s/D = 0)的结果对比，可以看出，本文基于三维旋转破坏模型得到的极限支护力与数值模拟结果的偏差在10%以内，表明计算结果较好，且相比于数值模拟繁琐的建模过程可以大大提高不同工况下的计算分析效率。

图 13 开挖面极限支护力结果对比

Figure 13. Comparison of limit support pressure of tunnel face

下载: 全尺寸图片幻灯片

3.2 理论模型参数分析

在本文理论模型中，参数k体现了近接工况下破坏体横截面的椭圆程度，这一现象是由于土体变形向上方的扩展被既有隧道限制而只能沿水平方向扩展，并且沿既有隧道方向的土体存在与既有隧道“剥离”的趋势，更加容易产生变形，因而与垂直方向的土体变形扩展产生差异。土体c，φ值越高，变形越不易扩展，导致土体更趋于各向同性，因此两个方向的变形范围差异(k值)随土性抗剪强度增加而降低。

如图 14所示，开挖面极限支护力随黏聚力的增加而线性降低，随土体内摩擦角φ增加呈现出先增加后降低的趋势，随埋深增加近似线性增加。极限支护力影响系数N_c、N_γ与土体内摩擦角的关系如图 15所示。由于土体黏聚力起抗力作用，因而N_c为负数。N_c随土体φ值增加而先增加后降低，随近接距离增加而降低。N_γ随φ值增加先基本不变而后逐渐降低，随近接距离增加而增加。此外，当土体内摩擦角较大(φ > 30°)时，近接距离对N_c的影响很小，这是由于内摩擦角越大，破坏范围越小，邻近的既有隧道的影响越低。

图 14 土性参数对极限支护力的影响

Figure 14. Influences of soil parameters on limit support pressure

下载: 全尺寸图片幻灯片

图 15 极限支护力系数与土体内摩擦角关系

Figure 15. Relationship between coefficient of limit support pressure and internal friction angle of soils

下载: 全尺寸图片幻灯片

4. 结论

本文揭示了近接既有隧道条件下的盾构开挖面破坏模式，构建了对数螺旋体+椭圆柱的开挖面失稳三维破坏模型并对主要参数进行了分析，得到以下3点结论。

(1) 近接既有隧道条件下盾构开挖面失稳三维变形区呈现沿隧道纵向和横向不对称的特点。当盾构开挖面与既有隧道轴线距离(s/D)在-1~0.5时，破坏模式呈现螺旋体+筒仓体形态。隧道垂直净距和土性对近接条件下开挖面破坏模式影响不大，但会改变三维方向上破坏扩展范围。

(2) 改进的对数螺旋体+椭圆柱体模型可以反映开挖面失稳扩展沿隧道纵向和横向的非均匀性，因此更加符合近接既有隧道条件下的实际开挖面破坏模式，且可以通过设置参数k使其适用于单隧道条件。基于所提出的破坏模型，推导了可以反映土体黏聚力和重度影响系数的开挖面极限支护力计算公式。

(3) 理论模型中参数k可体现开挖面失稳变形沿隧道纵向和横向扩展的非均匀性。土体强度越高(黏聚力c和内摩擦角φ越大)、隧道埋深越浅、近接距离越小，则开挖面极限支护力越低。开挖面极限支护力影响系数N_c、N_γ随土体内摩擦角φ增加呈现先增加后降低的变化趋势。内摩擦角临界值约为11°~13°。

图 1 ESP-Ⅱ微型土压计设计方案及3种传感器实物

Figure 1. Structural design of ESP-Ⅱ miniature transducer and photos of three types of transducers

下载: 全尺寸图片幻灯片

图 2 调配与选取最优刚度匹配软接触材料

Figure 2. Reconciliation and test soft-contact materials with different elastic moduli

下载: 全尺寸图片幻灯片

图 3 凹、凸、平不同接触面形态设计对比

Figure 3. Design contact surface shapes of concave, convex and plane

下载: 全尺寸图片幻灯片

图 4 DCIEM-40-300型离心机振动台系统

Figure 4. DCIEM-40-300 centrifuge shaking table test system

下载: 全尺寸图片幻灯片

图 5 砂土粒径级配曲线与实物

Figure 5. Grain-size distribution curve and photo of soil particles

下载: 全尺寸图片幻灯片

图 6 离心模型试验设计方案与实物照片

Figure 6. Design configuration and photo of test models

下载: 全尺寸图片幻灯片

图 7 施加离心力与动荷载

Figure 7. Centrifugal acceleration and dynamic loading as input

下载: 全尺寸图片幻灯片

图 8 离心机加速度阶段3种土压计响应测试结果

Figure 8. Static centrifugal test results of three types of earth pressure transducers at celebration stage of centrifuge

下载: 全尺寸图片幻灯片

图 9 离心机加载阶段侧向土压力与理论K₀分布

Figure 9. Profile of lateral earth pressure and theoretical K₀ at celebration stage of centrifuge

下载: 全尺寸图片幻灯片

图 10 不同离心力下各组土压计实测侧向土压力变化

Figure 10. Measured values of three types of earth pressure transducers at different centrifugal accelerations

下载: 全尺寸图片幻灯片

图 11 脉冲波荷载下土压计动力离心试验结果

Figure 11. Dynamic centrifugal test results of three types of earth pressure transducers under pulse wave

下载: 全尺寸图片幻灯片

图 12 连续动力荷载下土压计测量结果

Figure 12. Dynamic centrifugal test results of earth pressure transducers under different seismic amplitudes

下载: 全尺寸图片幻灯片

图 13 不同动荷载下侧向土压力分布

Figure 13. Profile of lateral earth pressure under different seismic loads

下载: 全尺寸图片幻灯片

图 14 离心力逐级下降阶段3种土压计响应结果

Figure 14. Test results of three types of earth pressure transducers at decelerating stage of centrifuge

下载: 全尺寸图片幻灯片

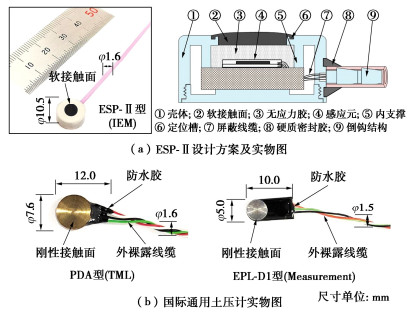
表 1 ESP-Ⅱ与国际通用土压计的主要设计参数及材料

Table 1 Main design parameters and materials of three types of earth pressure transducers

型号	量程/kPa	感应元类型	壳体/mm	线缆/mm	厚径比 $\frac{d}{h}$	接触面形式	信号类型
ESP-Ⅱ	500	压敏硅膜片	ϕ 10.5	ϕ 1.6	0.47	柔性	电压
PDA	500	电阻应变片	ϕ 7.6	ϕ 1.6	0.21	刚性	应变
EPL-D1	500	电阻应变片	ϕ 5.0	ϕ 1.5	0.32	刚性	电压

下载: 导出CSV

表 2 静力离心试验3种土压计实测土压力

Table 2 Earth pressures measured of three types of earth pressure transducers by static centrifuge spinning up 5g to 50g

离心加速度/g	土层深度/m	传感器位置/m	土压计实测值/kPa
离心加速度/g	土层深度/m	传感器位置/m	ESP-Ⅱ(IEM)	PDA(TML)	EPL-D1(Measurement)
5	2.0	0.75	3.41	4.89	4.33
		1.25	7.01	5.81	7.66
		1.75	9.97	7.48	9.23
10	4.0	1.50	7.39	9.69	9.41
		2.50	14.59	13.38	16.25
		3.50	22.15	17.08	21.41
15	6.0	2.25	12.46	14.40	13.11
		3.75	22.89	21.23	24.74
		5.25	33.69	27.32	30.28
20	8.0	3.00	16.80	19.20	18.00
		5.00	30.74	28.89	32.86
		7.00	45.51	36.92	40.06
30	12.0	4.50	25.48	29.08	25.85
		7.50	44.31	45.88	49.20
		10.50	69.51	60.65	65.54
40	16.0	6.00	36.18	39.60	36.08
		10.00	62.49	63.41	66.46
		14.00	89.81	83.54	87.41
50	20.0	7.50	47.82	49.66	51.51
		12.50	78.28	80.31	82.43
		17.50	106.89	107.35	109.85

下载: 导出CSV

参考文献(27)

[1]	张建民, 于玉贞, 濮家骝, 等. 电液伺服控制离心机振动台系统研制[J]. 岩土工程学报, 2004, 26(6): 843-845. http://cge.nhri.cn/cn/article/id/11539 ZHANG Jianmin, YU Yuzhen, PU Jialiu, el at. Development of a shaking table in electro-hydraulic servo-control centrifuge[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(6): 843-845. (in Chinese) http://cge.nhri.cn/cn/article/id/11539
[2]	陈云敏, 马鹏程, 唐耀. 土体的本构模型和超重力物理模拟[J]. 力学学报, 2020, 52(4): 901-915. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202004001.htm CHEN Yunmin, MA Pengcheng, TANG Yao. Constitutive models and hypergravity physical simulation of soils[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(4): 901-915. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202004001.htm
[3]	土工离心模型试验技术规程: DL/T 2013—2020[S]. 北京: 中国建筑工业出版社, 2020. Specification for Geotechnical Centrifuge Model Test Techniques: DL/T 2013—2020[S]. Beijing: China Architecture and Building, 2020. (in Chinese)
[4]	港口工程离心模型试验技术规程: JTS/T 231—7—2013[S]. 北京: 人民交通出版社, 2013. Code for Centrifugal Model Test for Port Engineering: JTS/T 231-7-2013[S]. Beijing: China Communications Press, 2013. (in Chinese)
[5]	曾辉, 余尚江. 岩土压力传感器匹配误差的计算[J]. 岩土力学, 2001, 22(1): 99-105. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200101026.htm ZENG Hui, YU Shangjiang. The calculation of matching error of rock-soil pressure transducer[J]. Rock and Soil Mechanics, 2001, 22(1): 99-105. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200101026.htm
[6]	MIURA K, OTSUKA N, KOHAMA E, et al. The size of earth pressure cells on measurement in granular materials[J]. The Japanese Geotechnical Society, 2003, 43(5): 133-147.
[7]	余尚江, 曾辉. 土中自由场应力与结构表面压力测量的差异[J]. 岩土工程学报, 2003, 25(6): 654-657. http://cge.nhri.cn/cn/article/id/11299 YU Shangjiang, ZENG Hui. The difference between measurements of stress in soil and pressure on wall-surface[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(6): 654-657. (in Chinese) http://cge.nhri.cn/cn/article/id/11299
[8]	JOSEPH F L, BRENT T. Laboratory calibration of earth pressure cells[J]. Geotechnical Testing Journal, 2005, 28(2): 188-196. doi: 10.1520/GTJ12089
[9]	TALESNICK M. Measuring soil contact pressure on a solid boundary and quantifying soil arching[J]. Geotechnical Testing Journal, 2005, 28(2): 171-179. doi: 10.1520/GTJ12484
[10]	徐光明, 陈爱忠, 曾友金, 等. 超重力场中界面土压力的测量[J]. 岩土力学, 2007, 28(12): 2671-2674. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200712040.htm XU Guangming, CHEN Aizhong, ZENG Youjin, et al. Measurement of boundary total stress in a multi-gravity environment[J]. Rock and Soil Mechanics, 2007, 28(12): 2671-2674. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200712040.htm
[11]	WEILER W A, KULHAWAY F H. Factors affecting stress cell measurement in soil[J]. Journal of the Geotechnical Engineering Division, ASCE, 1982, 108(12): 1529-1548. doi: 10.1061/AJGEB6.0001393
[12]	EGAN D, MERRIFIELD C K. The use of miniature earth pressure cells in a multi-gravity environment[C]// Centrifuge 98. Tokyo, 1998.
[13]	DAVE T N, DASAKA S M. In-house calibration of pressure transducers and effect of material thickness[J]. Geo-mechanics and Engineering, 2013, 5(1): 1-15.
[14]	魏永权, 罗强, 张良, 等. 离心力场中微型土压力传感器非线性响应分析[J]. 岩土力学, 2015, 36(1): 286-292. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201501039.htm WEI Yongquan, LUO Qiang, ZHANG Liang, et al. Study of nonlinear response of miniature earth pressure transducer in centrifugal force field[J]. Rock and Soil Mechanics, 2015, 36(1): 286-292. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201501039.htm
[15]	芮瑞, 吴端正, 胡港, 等. 模型试验中膜式土压力盒标定及其应用[J]. 岩土工程学报, 2016, 38(5): 837-845. doi: 10.11779/CJGE201605009 RUI Rui, WU Duanzheng, HU Gang, et al. Calibration tests on diaphragm-type pressure cells[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(5): 837-845. (in Chinese) doi: 10.11779/CJGE201605009
[16]	梁波, 厉彦君, 凌学鹏, 等. 离心模型试验中微型土压力盒土压力测定[J]. 岩土力学, 2019, 40(2): 818-826. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201902047.htm LIANG Bo, LI Yanjun, LING Xuepeng, et al. Centrifugal model test of micro box of earth pressure[J]. Rock and Soil Mechanics, 2019, 40(2): 818-826. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201902047.htm
[17]	蔡正银, 代志宇, 徐光明, 等. 离心模型试验中界面土压力盒标定方法研究[J]. 水利学报, 2020, 51(6): 695-704. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB202006007.htm CAI Zhengyin, DAI Zhiyu, XU Guangming, et al. Study on calibration method of interface soil pressure sensor in centrifugal model test[J]. Journal of Hydraulic Engineering, 2020, 51(6): 695-704. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB202006007.htm
[18]	刘开源, 许成顺, 贾科敏, 等. 薄膜压力传感器(FSR)曲面土压力测量研究[J]. 岩土工程学报, 2020, 42(3): 584-591. doi: 10.11779/CJGE202003021 LIU Kaiyuan, XU Chengshun, JIA Kemin, et al. Research on measurement of curved soil pressure using thin film pressure sensor (FSR) [J]. Journal of Geotechnical Engineering, 2020, 42(3): 584-591. (in Chinese) doi: 10.11779/CJGE202003021
[19]	GAO Y, WANG Y H. Calibration of tactile pressure sensors for measuring stress in soils[J]. Geotechnical testing journal, 2013, 36(4): 1-7.
[20]	PALMER M C, O'ROURKE, THOMAS D, OLSON N A, et al. Tactile pressure sensors for soil-structure interaction assessment[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(11): 1638-1645. doi: 10.1061/(ASCE)GT.1943-5606.0000143
[21]	MADABHUSHI S S C, HAIGH S K. Using tactile pressure sensors to measure dynamic earth pressures around du-al-row walls[J]. International Journal of Physical Modelling in Geotechnics, 2018, 19(2): 58-71.
[22]	张紫涛, 徐添华, 徐韵, 等. 薄膜压力传感器在土工试验中的适用性初探[J]. 岩土工程学报, 2016, 39(增刊1): 209-213. doi: 10.11779/CJGE2017S1041 ZHANG Zitao, XU Tianhua, XU Yun, et al. Feasibility of applying tactile pressure sensors in geotechnical tests[J]. Chinese Journal of Geotechnical Engineering, 2016, 39(S1): 209-213. (in Chinese) doi: 10.11779/CJGE2017S1041
[23]	MADABHUSHI G. Centrifuge Modelling for Civil Engineers[M]. Boca Raton: CRC Press, 2015.
[24]	汤兆光. 超重力试验动态孔压传感器设计方法、性能评价与应用[D]. 哈尔滨: 中国地震局工程力学研究所, 2022. TANG Zhaoguang. Design Method and Performance Evaluation of Dynamic Miniature Pore Water Pressure Transducer in Centrifuge Modelling and Its Application[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2022. (in Chinese)
[25]	JAKY J. The coefficient of earth pressure at rest[J]. Journal of the Society of Hungarian Architects and Engineers, 1944, 78(22): 355-358.
[26]	岩土工程仪器基本参数及通用技术条件: GB/T 15406—2007[S]. 北京: 中国标准出版社, 2007. Primary Parameter and General Specification for Geotechnical Engineering Instrument: GB/T 15406—2007[S]. Beijing: China Standards Publishing House, 2007. (in Chinese)
[27]	蔡正银, 代志宇, 徐光明, 等. 颗粒粒径和密实度对砂土K0值影响的离心模型试验研究[J]. 岩土力学, 2020, 41(12): 3882-3888. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202012007.htm CAI Zhengyin, DAI Zhiyu, XU Guangming, et al. Effect of particle size and compaction on K₀ value of sand by centrifugal model test[J]. Rock and Soil Mechanics, 2020, 41(12): 3882-3888. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202012007.htm

施引文献(15)

期刊类型引用(11)

1.	王伊立，丁景花，马力骏. 基于SSA-ENN神经网络的软岩隧道围岩变形预测模型. 广州建筑. 2025(01): 19-22 . 百度学术
2.	张林清. 基于指数平滑法的隧道围岩变形预测研究. 施工技术(中英文). 2025(04): 54-59+94 . 百度学术
3.	刘俭. 山岭隧道围岩稳定性分析及管棚支护优化研究. 施工技术(中英文). 2025(04): 67-73 . 百度学术
4.	肖时辉，王峰，何柏延，徐国元，黄伟真，李伟鹏. 基于LHS-WOA-ELM的隧道围岩参数反演分析. 矿业研究与开发. 2025(03): 91-100 . 百度学术
5.	周杜，杨遵俭，刘运雄，贺亚青，罗泽毅. 引水隧洞不良地质段超前地质预报技术及应用. 山东交通科技. 2024(04): 108-112 . 百度学术
6.	李成辉. CNN-LSTM组合模型在隧道衬砌变形预测中的应用. 国防交通工程与技术. 2024(06): 35-40 . 百度学术
7.	范明辉，杨普新，李薇，任文渊，马驰骋. 高性能混凝土的早期抗压强度预测和极值寻优. 硅酸盐通报. 2024(12): 4339-4349 . 百度学术
8.	王浩宇，李鹏飞，聂鼎. 水工隧洞衬砌混凝土多尺度开裂机理及防裂技术研究进展. 重庆交通大学学报(自然科学版). 2024(12): 27-40 . 百度学术
9.	易铭，李军，王浩，傅鹤林，易海东. 来米坡连拱隧道洞身围岩扰动与变形控制研究. 交通科学与工程. 2024(06): 25-33 . 百度学术
10.	杨春山，杨雪强，王雅甜，林永贵. 建筑敏感区隧道破除抗滑桩进洞转换体系设计与施工方案优选. 现代隧道技术. 2023(06): 220-227 . 百度学术
11.	曾淑珍. 输水隧洞开挖过程中围岩受力变形分析. 水利科技与经济. 2023(12): 60-63 . 百度学术