内外水力交互下浅埋带压盾构隧道水土压力计算模型

谢家冲; 黄昕; 金国龙; 张子新

doi:10.11779/CJGE20230603

内外水力交互下浅埋带压盾构隧道水土压力计算模型 English Version

谢家冲^{1, 3, 5,},
黄昕^{1, 2, 3, ,},
金国龙^{1, 3, 4},
张子新^{1, 3}

1.
同济大学土木工程学院地下建筑与工程系, 上海 200092
2.
新疆大学建筑工程学院, 新疆乌鲁木齐 830047
3.
同济大学岩土及地下工程教育部重点实验室, 上海 200092
4.
中船第九设计研究院工程有限公司, 上海 200063
5.
加泰罗尼亚理工大学土木与环境工程学院, 巴塞罗那 08034

基金项目:

国家自然科学基金项目 52278407

上海市科技创新行动计划项目 21DZ1201103

国家留学基金委项目 202306260053

详细信息

作者简介:
谢家冲(1996—)，男，博士研究生，主要从事隧道衬砌渗漏和结构响应方面的研究工作。E-mail：jcxie@tongji.edu.cn

通讯作者:
黄昕, E-mail: xhuang@tongji.edu.cn

中图分类号: TU432
计量
- 文章访问数: 392
- HTML全文浏览量: 45
- PDF下载量: 78
出版历程
- 收稿日期: 2023-06-29
- 网络出版日期: 2023-12-19
- 刊出日期: 2024-07-31

Model for calculating water and earth pressures of shallowly buried pressurized shield tunnels under external water infiltration and internal water exosmosis conditions

XIE Jiachong^{1, 3, 5,},
HUANG Xin^{1, 2, 3, ,},
JIN Guolong^{1, 3, 4},
ZHANG Zixin^{1, 3}

1.
Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
2.
College of Civil Engineering and Architecture, Xinjiang University, Urumchi 830047, China
3.
Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education, Tongji University, Shanghai 200092, China
4.
China Shipbuilding NDRI Engineering Co., Ltd., Shanghai 200063, China
5.
Department of Civil and Environmental Engineering, Universitat Politècnica de Catalunya (UPC), Barcelona 08034, Spain

摘要

摘要: 针对浅埋有压盾构隧道内外水力交互渗流下引起的松动水土压力变化，基于修正镜像法获得了考虑内水压的地层渗流场分布与水力梯度。随后基于考虑松动区内部应力分布的修正Terzaghi公式给出了考虑隧道内水压下的松动区任意位置的水土压力解，并与数值模拟结果进行了对比验证。主要结论如下：采用圆弧拱和抛物线拱的主应力轨迹线能够有效描述隧顶松动区应力分布情况；当地层渗透系数与衬砌渗透系数比值小于1000时，内压水头大小对水土压力的影响显著；内压水头的增加将减小松动区有效应力，引起上覆土体卸载，同时引起隧顶松动区总应力增大，表明该范围内孔隙水压的增长对水土压力的变化占据主导作用；5参数正交分析结果的线性回归分析结果表明隧道埋深和半径对土压力有显著的正向影响，土体摩擦角和黏聚力均表现为负向影响。在相对低渗透地层条件下，内压水头对隧顶有效应力和总应力分别表现为显著的负向和正向影响。
- 带压盾构隧道 /
- 衬砌渗漏 /
- 内水外渗 /
- 松动土压力 /
- 土拱 /
- 镜像法
Abstract: Focusing on the variation of relaxed water and earth pressures of shallowly shield tunnels under external water infiltration and internal water exosmosis conditions, the seepage field and hydraulic gradient considering internal water pressure are firstly, derived based on the modified image method. Then, the solutions for the water and earth pressures in arbitrary locations within the relaxed zone are obtained based on the modified Terzaghi's formula considering the horizontal distribution of stress. The effectiveness of the computational model is verified by comparing with the numerical results. It is shown that the principal stress path in either an arc or a parabola form can effectively capture the stress distribution within the relaxed zone over the tunnel crown. When the ratio of permeability of strata to that of linings is below 1000, the internal water pressure head has significant effects on the water and earth pressures. The increase of internal water pressure head will cause the reduction on the effective stress in the relaxed zone, which induces the unloading of soils. Moreover, it will also result in the increase of the total pressures at the tunnel crown of the relaxed zone, implying that the growth in pore pressure dominates the variation of the water and earth pressures. The linear regression of five-parameter orthogonal analysis suggests that the buried depth and tunnel radius have significant positive impacts on the earth pressures, while the influences of friction angle and cohesion are negative. Under the scenarios of relatively low-permeable strata, the influences of internal water head on the total and effective earth pressures at the tunnel crown are significantly negative and positive, respectively.
- pressurized shield tunnel /
- lining leakage /
- internal water exosmosis /
- relaxed earth pressure /
- soil arching /
- image method

HTML全文

0. 引言

由于接缝、手孔等薄弱防水部位的存在，盾构隧道在运营中不可避免地会出现渗漏病害^[1-2]，并引发隧道长期沉降^[3]、衬砌变形破坏^{[1, 4-5]}和地表水土流失^[6]等一系列问题。传统的市政交通隧道多关注地层向隧道内部的单向渗流问题，而近年来随着盾构隧道广泛应用于输排水和调蓄隧道^[7-9]，因内水压的存在产生的地层与隧道间的双向渗流问题逐渐引起关注。

隧道渗漏引起地层渗流场改变，进而引发松动区水土压力改变，是典型的流固耦合问题^[10]。隧道长期渗漏下的稳态渗流场分布求解主要通过保角映射^[10-12]和镜像法^[13-14]两种方法，二者分别通过映射复平面和汇源叠加的方式简化了渗流边界。

基于上述方法求得的地层渗流场解，部分学者对长期渗漏下的松动区水土压力与土与结构相互作用展开解析研究。王将等^{[12, 15]}先后针对浅埋和深埋下的隧顶松动土压力给出计算模型，指出渗流力将削弱土拱作用；刘世伟等^[13]比较了在长期渗漏条件下，海相与陆相段隧顶水土荷载的差异。除了基于Terzaghi公式给出考虑土拱效应的松动区土压力解，连续介质模型也能够有效求解衬砌渗漏下的水土压力与沉降：宋锦虎等^[10]在解析模型中考虑了土体渗透系数变化，通过对各分区的循环迭代计算给出流固耦合计算模型；张治国等^{[11, 16]}基于连续介质模型考虑了弹塑性、黏弹性地层，给出了渗流作用下围岩-隧道相互作用模型。上述两种模型在适用范围上存在差异：松动土压力模型更适用于浅埋隧道，连续介质模型则更适合围岩地层的深埋隧洞。另外，上述模型主要关注地下水外水内渗场景和隧顶位置水土压力变化，针对输水隧洞等带内水压隧道可能产生的内外水交互渗流问题的研究尚少，尤其是内水外渗对松动土压力变化影响的显著性及作用规律有待探明。

本文针对浅埋输水盾构隧道，基于镜像法推导了考虑内水外渗下的地层渗流场解析解，随后基于考虑松动区内部应力分布的修正Terzaghi解给出了考虑内水外渗下松动区任意位置的竖向有效应力与总应力，并与数值模拟结果进行了对比验证。在参数分析中探讨了埋深、隧道半径、土体强度参数和内压水头的影响，并基于线性回归进行了内压水头对隧顶土压力影响的显著性分析，可为类似带压输水盾构隧道工程设计提供参考。

1. 内外水交互下隧道渗流场解析分析

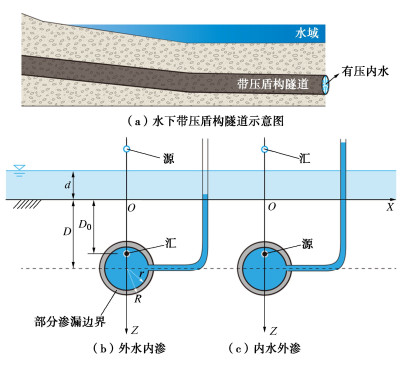
在浅埋条件下，考虑埋深远大于半径的近似解可能出现较大计算误差，而采用埋深修正的镜像法^[17]或保角变换的精确解^[18]则可以适用。图 1（a）给出水下带压盾构隧道示意图，隧道衬砌内外将同时承受地下水外水头和隧道内部水头^[8]。在隧道内水的影响下，渗流场的流线方向可能发生偏转，模拟隧道的“汇”点与虚拟的镜像“源”点也可能互相转换。为了更好地考虑带压隧道内水压的影响，有必要对现有解析解进行修正和拓展。

图 1 带压隧道渗流场计算示意图

Figure 1. Schematic diagram of seepage field calculation for pressurized tunnel

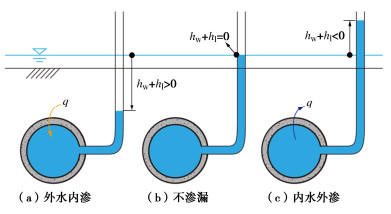
下载: 全尺寸图片幻灯片

图 1（b），分别给出上述的外水内渗和内水外渗下渗流场计算示意图。中， $D$ 为地表至隧道中心的距离， ${D_0}$ 为修正后的隧洞汇点（内水外渗下，转换为源点）距离， $R$ 和 $r$ 分别为隧道外、内径。为了便于后续土压力计算，将竖向坐标轴Z定义为向下为正。

地下水稳定渗流的控制方程为

$\frac{{{\partial ^2}\phi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\phi }}{{\partial {z^2}}} = 0。$

(1)

为了方便渗流场计算，以地表为参考给出各位置的总水头值。地表处总水头为

$\phi {|_{z = 0}} = d\text{，}$

(2)

式中， $d$ 为地表水位高度。

通常情况下（不考虑内压），隧道外水头被视为定水头，即 $\phi {|_{{x^2} + {{\left( {z - D} \right)}^2} = 0}} = {\phi _0}$ 边界，实则是对定水压（内部孔压为0）边界的近似处理，其计算中隧道外边界的压力水头 ${H_{\text{e}}}$ 被视为

${H_{\text{e}}} = {\phi _0} + z 。$

(3)

即隧道外边界水压随深度增大。而在考虑内压条件下（内水含自重），隧道内外边界水压力均沿深度增加，式（3）成为渗流场计算的精确边界。

在该种假设下，考虑埋深修正的镜像法和保角变换法均得到了一致的解答^[17-18]。以镜像法为例，修正后的隧道汇点和地表的距离^[17]：

${D_0} = \sqrt {{D^2} - {R^2}} 。$

(4)

将隧道汇源点位置的内水压力水头定义为 ${H_{\text{i}}}$ 。则隧道内水总水头为内水压力水头 ${H_{\text{i}}}$ 与 ${D_0}$ 的差值：

${\phi _i} = \phi {|_{{x^2} + {{\left( {z - D} \right)}^2} = {a^2}}} = {H_{\text{i}}} - {D_0}。$

(5)

已知隧道外总水头 $\phi_0$ 后，可由隧道外总水头与地表处总水头之差计算得到地层汇入隧道的渗漏量：

${q_{\text{s}}} = \frac{{2{\text{π }}{k_{\text{s}}}(d - {\phi _0})}}{{\ln \left[ {\frac{D}{R} + \sqrt {{{\left( {\frac{D}{R}} \right)}^2} - 1} } \right]}}{\text{ }} \text{，}$

(6)

式中， ${k_{\text{s}}}$ 为地层土体渗透系数。

由此可得到水下任意位置处的渗流场：

$\phi (x, z)=\frac{d-{\phi }_{0}}{2\mathrm{ln}\left[\frac{D}{R}+\sqrt{{\left(\frac{D}{R}\right)}^{2}-1}\right]}\mathrm{ln}\left(\frac{{x}^{2}+{(\sqrt{{D}^{2}-{R}^{2}}-z)}^{2}}{{x}^{2}+{(\sqrt{{D}^{2}-{R}^{2}}+z)}^{2}}\right)+d。$

(7)

式（7）能在给定渗流量的基础上给出准确的地层渗流场分布。但在不同内压条件下，衬砌外部水头 ${\phi _0}$ 值是不同的，渗漏量和渗流场应通过隧洞内边界水头和衬砌透水性推导得到。Fernandez等^[14]给出已知衬砌内外降深 ${h_{\text{l}}}$ 下流经隧洞衬砌的渗流量：

${q_l} = \frac{{2{\text{π }}{k_{\text{l}}}{h_{\text{l}}}}}{{\ln \left( {\frac{R}{r}} \right)}} 。$

(8)

式中， ${k_{\text{l}}}$ 为衬砌渗透系数。盾构隧道中接缝等局部薄弱防水部位为主要渗漏位置^{[1, 8]}，其水力传导能力可弥散至隧道全周，并通过实测等方法估算其等效渗透系数 ${k_{\text{l}}}$ ^[19]。据此，在渗流场解析中视 ${k_{\text{l}}}$ 为等效渗透系数^[12-13]。

由于在地层与隧洞衬砌中的水头降深 ${h_{\text{w}}}$ 和 ${h_{\text{l}}}$ 之和为地表总水头 $d$ 与隧洞内总水头 ${\phi _i}$ 之差，即 ${h_{\text{w}}} + {h_{\text{l}}} = d + {D_0} - {H_{\text{i}}}$ 。其中，降深 ${h_{\text{w}}}$ 和 ${h_{\text{l}}}$ 则可分别表示为

${h_{\text{w}}} = d - {\phi _0} \text{，}$

(9)

${h_{\text{l}}} = {\phi _0} - {H_{\text{i}}} + {D_0} 。$

(10)

由于流经衬砌与地层的渗漏量相等，因此联立式（6），（8）~（10），可以得到衬砌外侧水头 ${\phi _0}$ 的表达式：

${\phi _0} = d - \frac{{(d + {D_0} - {H_{\text{i}}})C({k_{\text{l}}}/{k_{\text{s}}})}}{{1 + C({k_{\text{l}}}/{k_{\text{s}}})}} \text{，}$

(11)

式中，

$C = \frac{{\ln \left[ {\frac{D}{R} + \sqrt {{{\left( {\frac{D}{R}} \right)}^2} - 1} } \right]}}{{\ln (R/r)}} 。$

(12)

再将式（11）代入式（6），（7），即可得到通过隧道内压计算得到的隧道渗漏量与地层渗流场分布。与基于给定渗流量计算渗流场的方式不同，在计算中地层与衬砌渗透系数的比值（相对渗透系数）是必要的。

当地下水位于地表以下的情况（陆域）时，则为上述解的特殊情况，即 $d = 0$ 。另外，考虑到隧洞内水头可能会高于外水头，即出现内水外渗的情况，定义降深 $d + {D_0} - {H_{\text{i}}}$ 大于0时为外水内渗情况，小于0时为内水外渗情况，如图 2和下式所示：

$h_{\mathrm{w}}+h_1=d+D_0-H_{\mathrm{i}}\left\{\begin{array}{ll} >0 & (\text { 外水内渗 }) \\ =0 & (\text { 不渗漏 }) \\ <0 & (\text { 内水外渗 }) \end{array} 。\right.$

(13)

图 2 衬砌隧洞内外水交互渗漏示意图

Figure 2. Schematic diagram of two-way water infiltration of tunnel linings

下载: 全尺寸图片幻灯片

2. 内外水力交互下松动区水土压力解

基于Terzaghi松动土压力分析模型和第1节给出的地层渗流场模型，建立考虑内外交互渗流情况下松动区内部水土压力（总应力）解析解。主要假设如下：①本文主要研究浅埋输水盾构隧道情况，认为松动区的滑裂面竖直且延伸至地表^[12]；②隧道内外交互渗流不改变原有滑裂面范围及土拱形态^[15]；③高地下水位下，地层土体强度均采用有效应力指标^[13]；④采用有效应力原理来考虑渗流场变化引起的外水荷载差异；⑤考虑松动区内部水平方向的应力分布差异，分别假设大主应力迹线为圆弧和抛物线拱形^[20]。

2.1 松动区内部土体应力分布模型

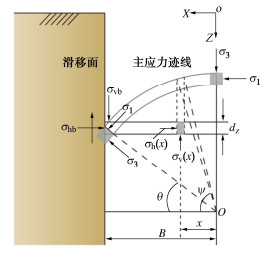
徐长节等^[20]通过引入修正系数m考虑了松动区内应力分布的特点，引入该方法可以有效考虑隧顶处水土压力明显小于两侧的特点。首先对滑裂面处的单元进行分析，由于已经达到极限平衡状态，可以得到滑裂面处的侧向土压力系数为

${K_{\text{b}}} = \frac{{{{\cos }^2}\theta + {K_{\text{p}}}{{\sin }^2}\theta }}{{{{\sin }^2}\theta + {K_{\text{p}}}{{\cos }^2}\theta }} 。$

(14)

式中： ${K_{\text{p}}}$ 为侧向土压力系数， $K_{\mathrm{p}}=\tan ^2\left(45^{\circ}+\varphi / 2\right)$ ； $\theta=45^{\circ}-\varphi / 2$ ， $\theta$ 为滑裂面位置与原点O连线与水平方向上的夹角； $\varphi$ 为土体内摩擦角。在黏性土情况下，经过坐标转换也可获得上述公式，变换后的土体法向应力 ${\sigma ^c}$ = $\sigma + c\cot \varphi$ ，其中 $\sigma$ 为原始法向应力，c为土体黏聚力。

松动区内部任意位置的竖向有效应力可由拱脚滑裂面处的竖向应力 ${\sigma '_{{\text{vb}}}}$ 来表示：

${\sigma '_{\text{v}}}(x) = \frac{{{{\cos }^2}\psi + {K_{\text{p}}}{{\sin }^2}\psi }}{{{{\sin }^2}\theta + {K_{\text{p}}}{{\cos }^2}\theta }}{\sigma '_{{\text{vb}}}} 。$

(15)

式中： $\psi$ 为土条内部任意位置与拱迹线原点O连线与水平方向的夹角，如图 3所示。

图 3 考虑土条内部应力分布的松动土压力分析模型^[20]

Figure 3. Analytical model for relaxed earth pressure considering internal distribution of soil strips

下载: 全尺寸图片幻灯片

由此可积分和坐标变换得到松动区内部平均竖向土压力 $\overline {{{\sigma '}_{\text{v}}}}$ ：

$\overline {{{\sigma '}_{\text{v}}}} = \frac{{{{\sigma '}_{{\text{vb}}}}}}{B}\int_0^B {\frac{{{{\cos }^2}\psi + {K_{\text{p}}}{{\sin }^2}\psi }}{{{{\sin }^2}\theta + {K_{\text{p}}}{{\cos }^2}\theta }}} {\text{d}}x - c\cot \varphi 。$

(16)

对于典型的圆弧拱形^[21]和抛物线拱形^[20]，分别有

$\cos \psi = \frac{x}{B}\cos \theta \text{，}$

(17)

$\cot \psi = \frac{x}{B}\cot \theta 。$

(18)

将式（17），（18）代入式（16）可积分得到

$\overline {{{\sigma '}_{\text{v}}}} = m{\sigma '_{{\text{vb}}}} - c\cot \varphi 。$

(19)

式中， $m$ 为主应力轨迹线形状系数，为式（16）中 ${\sigma '_{{\text{vb}}}}$ 的系数项。其大小与轨迹线形态、松动区宽度和土体强度等因素有关。将式（17），（18）代入式（16）并进行积分，可得

$m=\left\{\begin{array}{l}\frac{2+{\mathrm{sin}}^{2}\theta +{K}_{\text{p}}{\mathrm{cos}}^{2}\theta }{3({\mathrm{sin}}^{2}\theta +{K}_{\text{p}}{\mathrm{cos}}^{2}\theta )}\;\;\;\;\;\;\;\text{(}圆弧线\text{)}\\ \frac{{K}_{\text{p}}+(1-{K}_{\text{p}})\left(\frac{\text{π}}{2}-\theta \right)\mathrm{tan}\theta }{{\mathrm{sin}}^{2}\theta +{K}_{\text{p}}{\mathrm{cos}}^{2}\theta }\;\text{(}抛物线\text{)}\end{array} \right. 。$

(20)

2.2 考虑交互渗流的松动区水土压力模型

在渗流条件下，对松动区内部土条进行极限平衡分析，可得

$B(\gamma ' + {\gamma _{\text{w}}}{\bar i_z}){\text{d}}z = B{\text{d}}{\bar \sigma '_{\text{v}}} + {K_{\text{b}}}{\sigma '_{{\text{vb}}}}\tan \varphi {\text{d}}z 。$

(21)

需要指出的是，在平衡方程中若将渗流力考虑为随位置改变的量，则会导致平衡方程难以求解^[12-13]。考虑到浅埋隧道渗流场分布的特性，同时考虑不利情况，认为在水平方向上隧道中心线上的渗流场可代表松动区内的渗流力分布情况^[13]：

$\phi (0, z) = \frac{{d - {\phi _0}}}{{\ln \left[ {\frac{D}{R} + \sqrt {{{\left( {\frac{D}{R}} \right)}^2} - 1} } \right]}}\ln \left( {\frac{{\sqrt {{D^2} - {R^2}} - z}}{{\sqrt {{D^2} - {R^2}} + z}}} \right) + d 。$

(22)

则松动区内部竖向水力梯度可由地下水水头求导得到

${i_z} = - \frac{{\partial \phi (0, z)}}{{\partial z}} 。$

(23)

文献[12，]在对隧顶深度土压力进行求解时，将水力梯度简化为积分平均后的常值。在此基础上，将在每一个计算深度z上的水力梯度值都视为该深度以上覆土中的水力梯度 ${i_z}$ 的积分平均值：

$\overline {{i_z}} = - \frac{1}{z}\frac{{d - {\phi _0}}}{{\ln \left[ {\frac{D}{R} + \sqrt {{{\left( {\frac{D}{R}} \right)}^2} - 1} } \right]}}\ln \left( {\frac{{\sqrt {{D^2} - {R^2}} - z}}{{\sqrt {{D^2} - {R^2}} + z}}} \right) 。$

(24)

由于定义Z方向向下为正，当外水内渗情况下， $\overline {{i_z}}$ 大于0，在内水外渗情况下， $\overline {{i_z}}$ 小于0。由式（24）可知渗流方向的判别条件为 $d - {\phi _0}$ 的正负性，即地表水头与衬砌外水头的差值大小。

随后，将式（19），（24）积分得到的 $\overline {{i_z}}$ 代入式（21），得到

$\gamma ' + {\gamma _{\text{w}}}{i_z} = \frac{{{\text{d}}{{\bar \sigma '}_{\text{v}}}}}{{{\text{d}}z}} + \frac{{{K_{\text{b}}}{{\bar \sigma '}_{\text{v}}}\tan \varphi }}{{Bm}} + \frac{{c{K_{\text{b}}}}}{{Bm}} 。$

(25)

考虑到地表边界条件为

${\bar \sigma _{\text{v}}} = q 。$

(26)

在海域段地表水位高于地表时，由于采用有效应力计算方法， ${\bar \sigma _{\text{v}}} = q = 0$ 。由式（26）给出的边界条件可积分得到：

$\overline {{{\sigma '}_{\text{v}}}} = \frac{{(\gamma ' + {\gamma _{\text{w}}}\overline {{i_z}} )Bm - {K_{\text{b}}}c}}{{{K_{\text{b}}}\tan \phi }}\left[ {1 - \exp \left( { - \frac{{z{K_{\text{b}}}\tan \varphi }}{{mB}}} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;q\exp \left( { - \frac{{z{K_{\text{b}}}\tan \varphi }}{{mB}}} \right) 。$

(27)

在近海陆域段中，由于地下水位低于地表，近地表部分土层不存在渗流场，因此隧顶有效土压力需要分段计算^[13]。将地下水位处的土压力作为地表超载，积分得到

$\overline {{{\sigma '}_{\text{v}}}} = \frac{{(\gamma ' + {\gamma _{\text{w}}}\overline {{i_z}} )Bm - {K_{\text{b}}}c}}{{{K_{\text{b}}}\tan \varphi }}\left[ {1 - \exp \left( { - \frac{{z{K_{\text{b}}}\tan \varphi }}{{mB}}} \right)} \right] + \\ \frac{{\gamma }^{\prime }Bm-{K}_{\text{b}}c}{{K}_{\text{b}}\mathrm{tan}\varphi }\left[1-\mathrm{exp}\left(-\frac{{d}_{1}{K}_{\text{b}}\mathrm{tan}\varphi }{mB}\right)\right]\cdot \mathrm{exp}\left(-\frac{z{K}_{\text{b}}\mathrm{tan}\varphi }{mB}\right)\text{，}$

(28)

式中， ${d_1}$ 为陆域段地表距地下水位距离。

将式（27），（28）计算的平均竖向应力代入式（15）和（16），可得到水平方向上各个位置的竖向土压力：

${\sigma '_{\text{v}}}(x) = \frac{{{{\sin }^2}\psi + {K_{\text{p}}}{{\cos }^2}\psi }}{{{{\sin }^2}\theta + {K_{\text{p}}}{{\cos }^2}\theta }}\frac{{\overline {{{\sigma '}_{\text{v}}}} + c\cot \varphi }}{m} - c\cot \varphi 。$

(29)

据此，圆弧拱和抛物线拱下松动区内部任意位置处竖向有效土压力 ${\sigma '_{{\text{v}}x}}$ 分别为

$\sigma_{\mathrm{v}}^{\operatorname{arc}'}(x)=\frac{1+\left(K_{\mathrm{p}}-1\right)(x \cos \theta / B)^2}{\sin ^2 \theta+K_{\mathrm{p}} \cos ^2 \theta} \frac{\overline{\sigma_{\mathrm{v}}^{\prime}}+c \cot \varphi}{m}-c \cot \varphi,$

(30)

$\begin{gathered} \sigma_{\mathrm{v}}^{\text {para}'}(x)=\frac{1+K_{\mathrm{p}}(x \cot \theta / B)^2}{\left(1+(x \cot \theta / B)^2\right)\left(\sin ^2 \theta+K_{\mathrm{p}} \cos ^2 \theta\right)} \frac{\overline{\sigma_{\mathrm{v}}}+c \cot \varphi}{m}- \\ c \cot \varphi 。 \end{gathered}$

(31)

松动区内部各个位置的孔隙压力可由式（7）计算得到的地下水总水头与位置水头相加计算得到

$p(x) = (\phi (x, z) + z){\gamma _w} 。$

(32)

松动区内部土体竖向总压力可由有效应力原理计算得到

${\sigma _{\text{v}}}(x) = {\sigma '_{\text{v}}}(x) + p(x) \text{，}$

(33)

式中， $p(x)$ 为松动区计算点处的孔隙水压力。

3. 输水隧洞实例数值模型验证

3.1 数值模型

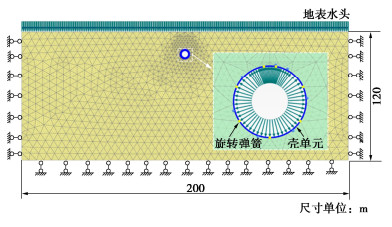
本节建立二维流固耦合数值模型以验证上述计算模型的有效性。带压盾构隧道结构形式参考文献[8]，衬砌设计过水断面直径为7.4 m，单层衬砌厚度为0.45 m，管片标准环每环管片由一块封顶块F块、2块邻接块L1、L2块、4块标准块B1、B2、B3、B4块共同组成，环宽为1.8 m。

图 4给出二维数值模型示意图，模型大小为200 m ×120 m。在地层-结构模型中将衬砌简化为壳单元模拟，材料考虑为理想弹性，弹性模量取3.45×10⁴ MPa，泊松比取0.167。衬砌分块间接触采用旋转弹簧，旋转刚度为1×10⁵ kN/rad^[7]，Laver等^[19]指出长期渗漏下的盾构隧道衬砌等效渗透系数范围在1×10^-11~1×10^-10 m/s，本文考虑不利的长期渗漏条件， ${k_l}$ 取1×10^-10 m/s。地层土体模型采用HS-small本构模型模拟，内摩擦角和黏聚力分别取35°和3 kPa，有效重度 $\gamma '$ 取16 kN/m³，根据模型参数取值方法^[22]，参考割线和加卸载模量 $E_{50}^{{\text{ref}}}$ 、 $E_{{\text{ur}}}^{{\text{ref}}}$ 和剪切模量 $G_0^{{\text{ref}}}$ 分别取10，48，148 MPa，渗透系数取1×10^-8 m/s。隧道拱顶埋深取16 m，地表以上水头为4 m且地表水视为无限供给，内压水头取0，10，20，30 m^[8]。

图 4 数值模型示意图

Figure 4. Diagram of numerical model

下载: 全尺寸图片幻灯片

数值模拟的步骤为：①初始地应力平衡，设置地层水位；②隧道开挖，设置盾构机壳支护；③隧道收缩，根据实际盾构机参数施加隧道收缩率为0.5%；④隧道支护，激活隧道衬砌与旋转弹簧（接头）；⑤流固耦合渗流分析，激活隧道内部初始水头边界（ ${H_{\text{i}}}$ = 0），设置固结时间为365 d。重复分析步⑤，依次增加隧道内边界水头，并提取各个流固耦合分析步下的渗流场、土压力结果。

3.2 结果分析与验证

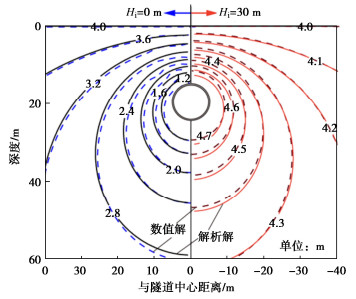
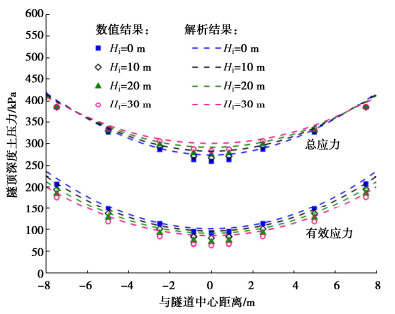
给出隧道内压水头为0和30 m下地层渗流场的数值与解析结果对比。解析与数值结果吻合良好，均反映了由于外水内渗和内水外渗下隧道周边地下水水头的显著变化。当 ${H_{\text{i}}}$ 为0时，隧道外侧地层降深显著，拱顶位置的降深 ${h_{\text{w}}}$ 约3 m。当 ${H_{\text{i}}}$ 增长至30 m，隧道周边地下水水头显著提高，此时 ${h_{\text{w}}}$ 为负值，表明了在渗漏情况下带压内水将增大隧道外水压力。

图 5

${H_{\text{i}}}$ 为0和30 m下地下水水头的结果对比

Figure 5. Comparisons of ground water head distribution when

${H_{\text{i}}}$ = 0 and 30 m, respectively

下载: 全尺寸图片幻灯片

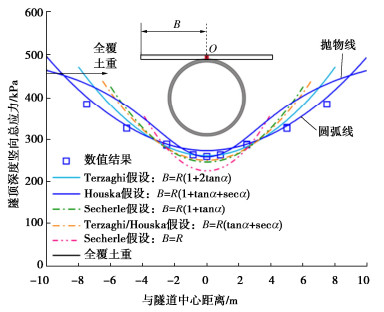
解析计算中采用不同的松动区宽度假设将影响水土压力结果的准确性。为了验证并确定松动区宽度和迹线假定，图 6，给出内压水头为0下，不同松动区宽度假设下的解析计算结果与数值解对比。由可知，松动区宽度越小，隧顶土拱效应越明显，最大水土压力也越小。在Komer假设下，即 $B$ = $R$ 时，隧顶竖向应力仅为226 kPa，为全覆土重的49.6%。从土压力水平分布趋势上看，Houska假设与数值结果更接近。除了松动区宽度假设外，不同的主应力轨迹线假设也会影响横向土条水土压力分布。图 6还给出抛物线形迹线下水土压力分布，相比于圆弧拱形，在隧顶位置抛物线拱形得到的竖向应力更小，更接近数值计算结果。而从松动区内应力分布情况看，采用圆弧拱形的水土压力分布更接近数值计算结果。

图 6 不同松动区宽度假设下松动区水土压力比较

Figure 6. Comparisons of relaxed water and earth pressures under different widths of relaxed zone

下载: 全尺寸图片幻灯片

图 7 松动区有效应力方向与偏应变云图

Figure 7. Direction of principal stress and contours of deviatoric strain in relaxed zone

下载: 全尺寸图片幻灯片

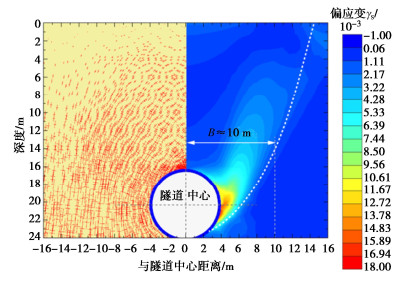
另外，数值结果显示在隧道收缩下，将会产生较大范围的松动区，如图 7给出的主应力方向与偏应变云图所示。主应力方向分布结果表明隧道上方形成较完整的土拱区，在距离隧道10~12 m处土体主应力开始偏转。根据土拱效应的机理，松动区边界可以基于偏应变^[23]来判定。结果表明在隧顶深度松动区边界出现于距离隧道中心约10 m位置处，与Houska假设计算结果一致。据此，后文均给出基于Houska松动区假设的计算结果。

图 8给出内水头影响下土压力变化情况，结果表明随着内水头增加，隧顶总应力增加而有效应力减小，数值解与解析结果均准确地反映了该行为。从数值上看，数值结果略小于解析解，产生的原因可能是在解析计算假设中过大地估计了松动区效应，实际接近地表区域土体剪切强度并未完全发挥（见图 7偏应变云图）。综上所述，本文给出的水土压力计算模型与数值结果吻合良好，在渗流场、土压力分布和松动区假设上均有较高的一致性。因此，可以基于该计算模型展开考虑隧洞内外水力交互的参数敏感性分析。

图 8 内压水头作用下土压力变化

Figure 8. Variations of earth pressures affected by internal water pressure head

下载: 全尺寸图片幻灯片

4. 内外交互渗流下参数敏感性分析

本节展开内外水力交互的参数敏感性分析，建模方式与第3节一致。

4.1 地层相对渗透系数的影响

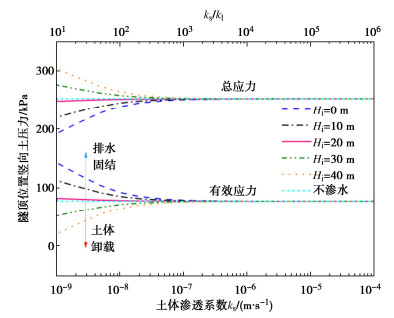
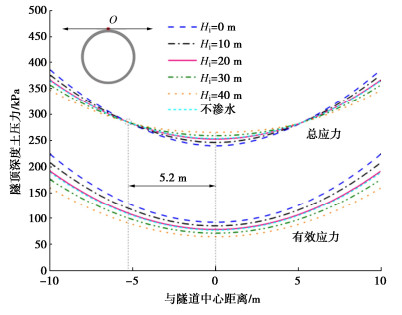
地层与衬砌相对渗透系数 ${k_{\text{s}}}/{k_{\text{l}}}$ 对隧顶水土荷载有较大影响。给出在外水内渗工况下，土体在低渗透性至强渗透性条件下，隧顶深度上的土压力分布结果。其中， $\varphi$ 取30°， $c$ 取5 kPa，埋深10 m， $\gamma '$ 取16 kN/m³，地表上覆水头d取8 m。计算结果表明随着地层相对渗透系数的上升，有效应力大幅降低，当 ${k_{\text{s}}}/{k_{\text{l}}}$ 大于1000后，其影响不再显著。相对渗透系数对总应力影响稍复杂，在距离隧道中心5.2 m（大于隧道外径4.15 m）范围内， ${k_{\text{s}}}/{k_{\text{l}}}$ 的增加将引起隧顶外荷载的增大，在5.2 m范围外则相反。这表明在隧顶区域，外荷载以相对渗透系数变化引起的水头改变占主导，在距离较远的松动区内外荷载则以有效应力的增加占据主导。随着相对渗透系数 ${k_{\text{s}}}/{k_{\text{l}}}$ 的增大，地层中的降深变化减小，土体应力也越接近于不渗水的原始状态。

图 9 地层渗透系数对拱顶土压力的影响（

${H_{\text{i}}}$ = 0）

Figure 9. Influences of seepage coefficient on earth pressures at tunnel crown (

${H_{\text{i}}}$ = 0)

下载: 全尺寸图片幻灯片

以隧顶中心的土压力为例，给出同时考虑渗透系数 ${k_{\text{s}}}$ 与内压水头 ${H_{\text{i}}}$ 影响的结果。结果表明在内水压参与作用下，渗透系数的影响范围主要位于 ${k_{\text{s}}}/{k_{\text{l}}}$ 小于1000的区域内。随着内压水头的增加，隧顶的水土荷载显著提升，而有效应力明显下降。这表明在拱顶位置处，水土荷载的大小变化主要由降深引起的水荷载导致。当 ${H_{\text{i}}}$ 为20 m时，随着 ${k_{\text{s}}}/{k_{\text{l}}}$ 变化引起的水土荷载和有效应力差异不再显著，这是因为此时衬砌内外水压基本平衡，渗漏引起的降深值较小。

图 10 地层渗透系数和内压水头对隧顶土压力的影响

Figure 10. Influences of seepage coefficient and internal water pressure head on earth pressures at tunnel crown

下载: 全尺寸图片幻灯片

4.2 隧洞内压水头的影响

长期的外水内渗将导致隧道周围土体产生固结，从而产生持续沉降^[19]。而带压内水作用下隧道可能出现内水外渗行为，导致长期变形可能并非表现为沉降模式。如，所示的有效应力变化规律，随着 ${H_{\text{i}}}$ 的增加，渗流力将引起有效应力的降低。以不渗水的初始状态为基准，定义有效应力增大和减小分别为土体排水固结和卸载趋势。这表明内水压的增大将引起隧顶上覆土体卸载，从而使隧道产生上浮趋势，甚至反转土体有效应力方向。需要指出的是，内水外渗下隧顶水土荷载的增加可能引起结构附加变形，与土体变形叠加从而产生复杂的土与结构相互作用^[8]。

提取中地层渗透系数 ${k_{\text{s}}}$ 为1×10^-8m/s时的隧顶水平方向分布的竖向土压力，如所示。结果表明 ${H_{\text{i}}}$ 对总应力的影响拐点同样位于距离隧道中心水平距离约5.2 m处，即内压水头的增加会引起隧道上方的松动区内外部水土荷载的增大，但远端的外部水土荷载则减小。

图 11 内压水头对隧顶土压力的影响

Figure 11. Influences of internal water pressure head on earth pressures at tunnel crown

下载: 全尺寸图片幻灯片

4.3 隧道埋深和土体强度参数的影响

隧道所处埋深和土体强度也会对水土压力产生较大影响。给出埋深对隧顶位置处竖向总压力的影响，计算参数与4.2节相同，同时考虑3种内摩擦角（20°，30°，40°）。结果表明随着埋深增加，隧顶水土荷载呈非线性增长（斜率逐渐降低），但始终远小于全覆土重，这表明土拱效应起到显著作用。随着埋深增加，内摩擦角 $\varphi$ 逐渐对水土压力起主要影响逐渐增大。图中以 $\varphi =$ 20°为例给出黏聚力的影响，表明 $c$ 值增加同样能显著降低隧顶水土压力。另外，内压水头 ${H_{\text{i}}}$ 对不同强度参数土体下的水土压力的影响规律一致，均表现为 ${H_{\text{i}}}$ 的增大引起隧顶总压力的上升。在 $\varphi =$ 40°下， ${H_{\text{i}}}$ 对隧顶水土荷载的影响最大。

图 12 埋深对隧顶水土压力的影响

Figure 12. Influences of burial depth on water and earth pressures at tunnel crown

下载: 全尺寸图片幻灯片

4.4 基于回归分析的关键参数影响分析

相比于常规市政交通盾构隧道，浅埋输水隧洞存在交替变换的内水头从而导致在内外水交互下隧道所受外部水土荷载发生改变。然而，该因素的作用往往不被设计考虑。为了阐明考虑内水头对隧道耐久性设计的必要性，以下针对5个相关参数展开正交分析，并基于线性回归系数评价不同因素的影响程度。

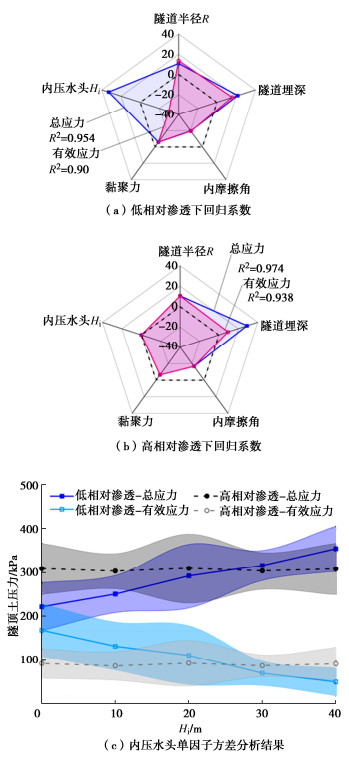
根据浅埋输水盾构隧道的性质特点，并考虑低相对渗透（ ${k_{\text{s}}}/{k_{\text{l}}} = {10^1}$ ）和高相对渗透（ ${k_{\text{s}}}/{k_{\text{l}}} = {10^5}$ ）两组地层条件，分别进行常规的25次正交分析试验，给出正交分析的5个参数与各自对应的5个水平得到的对试验结果的回归系数如所示。结果表明在高、低两组渗透条件下， ${H_{\text{i}}}$ 对土压力的回归系数呈现显著的差异：在低相对渗透条件下， ${H_{\text{i}}}$ 对总应力和有效应力分别表现为显著的正向和负向影响关系，回归系数分别为32.96，-29.77，超过了埋深的21.61，15.82；而在高相对渗透组中， ${H_{\text{i}}}$ 的回归系数仅为-0.073，-0.091，不具备显著性。给出的平均值与标准差计算结果也进一步说明了在低渗地层下，应考虑隧道水土荷载变化带来的不利影响。这也再次验证了4.2节给出的结论：在内外水力交互下，内压水头 ${H_{\text{i}}}$ 将引起隧顶松动区有效应力降低，总应力增加。

表 1 5因素5水平正交分析表

Table 1. Orthogonal analysis with 5 parameters and 5 levels

因素	参数	水平
因素	参数	1	2	3	4	5
1	隧道半径R/m	2	3	4	5	6
2	隧道埋深/m	10	12	14	16	18
3	内摩擦角 $\varphi$ /(°)	20	25	30	35	40
4	黏聚力 $c$ /kPa	0	5	10	15	20
5	隧洞内压水头 ${H_{\text{i}}}$ /m	0	10	20	30	40

下载: 导出CSV

| 显示表格

图 13 正交分析结果

Figure 13. Results of orthogonal analysis

下载: 全尺寸图片幻灯片

其他参数的回归分析如下：隧道埋深和半径始终对水土压力有正向影响，隧道埋深的影响更大。注意到隧道埋深对总应力的回归系数始终大于有效应力，这是因为埋深增加的同时也增大了外部水压。另外，土体强度参数 $\varphi$ 和 $c$ 对水土压力均为负向影响，且对总应力与有效应力的影响基本一致。其中，内摩擦角 $\varphi$ 的影响更显著，在低、高渗条件下对总应力的回归系数分别为-19.6和-16.8，黏聚力对总应力的回归系数仅为-6.03，-6.44。

总而言之，相比于其他外部荷载设计参数，带压隧道内水头大小对设计外荷载、和对地层沉降变形有不可忽略的影响，设计中应重点考虑。

5. 结论

（1）考虑松动区应力分布的水土压力模型计算结果与海域段典型剖面的数值模拟结果吻合良好，圆拱与抛物线的主应力迹线能够有效描述拱顶松动区的水平应力分布。基于Houska假设的土压力计算结果与数值模拟结果更加接近。

（2）地层渗透系数对水土压力有较大影响，主要表现为当地层与衬砌相对渗透系数小于1000时，内压水头大小对竖向有效应力与总应力影响显著。在外水内渗阶段，长期渗流将引起隧顶土体总应力降低和有效应力增加，表现为覆土长期固结沉降特点。内压水头的增大将逐渐转变为内水外渗态势，减小松动区土体的竖向有效应力，引起上覆土体卸载趋势。

（3）随着隧道埋深增加，隧顶水土压力非线性增长，增长幅度随埋深缓慢减小。内摩擦角对隧顶水土压力有显著影响，摩擦角增加将降低隧洞松动土压力，同时内压水头对水土压力的影响也越大。

（4）5参数的线性回归分析结果表明：隧道埋深和半径对水土压力有显著的正向影响；土体摩擦角和黏聚力对水土压力有显著的负向影响；在相对低渗地层条件下，内压水头对隧顶松动区竖向有效应力和总应力表现为显著的负向和正向影响。

图 1 带压隧道渗流场计算示意图

Figure 1. Schematic diagram of seepage field calculation for pressurized tunnel

下载: 全尺寸图片幻灯片

图 2 衬砌隧洞内外水交互渗漏示意图

Figure 2. Schematic diagram of two-way water infiltration of tunnel linings

下载: 全尺寸图片幻灯片

图 3 考虑土条内部应力分布的松动土压力分析模型^[20]

Figure 3. Analytical model for relaxed earth pressure considering internal distribution of soil strips

下载: 全尺寸图片幻灯片

图 4 数值模型示意图

Figure 4. Diagram of numerical model

下载: 全尺寸图片幻灯片

${H_{\text{i}}}$ 为0和30 m下地下水水头的结果对比

Comparisons of ground water head distribution when ${H_{\text{i}}}$ = 0 and 30 m, respectively

下载: 全尺寸图片幻灯片

图 6 不同松动区宽度假设下松动区水土压力比较

Figure 6. Comparisons of relaxed water and earth pressures under different widths of relaxed zone

下载: 全尺寸图片幻灯片

图 7 松动区有效应力方向与偏应变云图

Figure 7. Direction of principal stress and contours of deviatoric strain in relaxed zone

下载: 全尺寸图片幻灯片

图 8 内压水头作用下土压力变化

Figure 8. Variations of earth pressures affected by internal water pressure head

下载: 全尺寸图片幻灯片

地层渗透系数对拱顶土压力的影响（ ${H_{\text{i}}}$ = 0）

Influences of seepage coefficient on earth pressures at tunnel crown ( ${H_{\text{i}}}$ = 0)

下载: 全尺寸图片幻灯片

图 10 地层渗透系数和内压水头对隧顶土压力的影响

Figure 10. Influences of seepage coefficient and internal water pressure head on earth pressures at tunnel crown

下载: 全尺寸图片幻灯片

图 11 内压水头对隧顶土压力的影响

Figure 11. Influences of internal water pressure head on earth pressures at tunnel crown

下载: 全尺寸图片幻灯片

图 12 埋深对隧顶水土压力的影响

Figure 12. Influences of burial depth on water and earth pressures at tunnel crown

下载: 全尺寸图片幻灯片

图 13 正交分析结果

Figure 13. Results of orthogonal analysis

下载: 全尺寸图片幻灯片

表 1 5因素5水平正交分析表

Table 1 Orthogonal analysis with 5 parameters and 5 levels

因素	参数	水平
因素	参数	1	2	3	4	5
1	隧道半径R/m	2	3	4	5	6
2	隧道埋深/m	10	12	14	16	18
3	内摩擦角 $\varphi$ /(°)	20	25	30	35	40
4	黏聚力 $c$ /kPa	0	5	10	15	20
5	隧洞内压水头 ${H_{\text{i}}}$ /m	0	10	20	30	40

下载: 导出CSV

参考文献(23)

[1]	WU H N, SHEN S L, CHEN R P, et al. Three-dimensional numerical modelling on localised leakage in segmental lining of shield tunnels[J]. Computers and Geotechnics, 2020, 122(2): 103549.
[2]	XIE J, HUANG X, JIN G. Analytical model for the sealant performance of tunnel gasketed joints based on multi-scale contact and percolation theories[J]. Underground Space, 2024, 14: 319-337. doi: 10.1016/j.undsp.2023.08.004
[3]	彭益成, 龚琛杰, 丁文其, 等. 考虑管片接头渗流的盾构隧道流固耦合模型研究[J]. 土木工程学报, 2022, 55(4): 95-108. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC202204010.htm PENG Yicheng, GONG Chenjie, DING Wenqi, et al. Fluid-structure coupling model of shield tunnel considering seepage of segmental joints[J]. China Civil Engineering Journal, 2022, 55(4): 95-108. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC202204010.htm
[4]	徐国文, 卢岱岳. 接头抗弯刚度非线性及渗水影响下盾构隧道力学行为分析[J]. 岩土工程学报, 2016, 38(7): 1202-1211. doi: 10.11779/CJGE201607006 XU Guowen, LU Daiyue. Mechanical behavior of shield tunnel considering nonlinearity of flexural rigidity and leakage of joints[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(7): 1202-1211. (in Chinese) doi: 10.11779/CJGE201607006
[5]	孙雅珍, 于阳, 王金昌, 等. 考虑界面效应的内张钢圈加固盾构管片结构力学性能研究[J]. 岩土工程学报, 2022, 44(2): 343-351. doi: 10.11779/CJGE202202016 SUN Yazhen, YU Yang, WANG Jinchang, et al. Mechanical properties of linings of shield tunnel strengthened by steel plates considering interface effects[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(2): 343-351. (in Chinese) doi: 10.11779/CJGE202202016
[6]	ZHANG N, SHEN J S, ZHOU A, et al. Tunneling Induced Geohazards in Mylonitic Rock Faults with Rich Groundwater: A Case Study in Guangzhou[J]. Tunnelling and Underground Space Technology, 2018, 74: 262-272. doi: 10.1016/j.tust.2017.12.021
[7]	HUANG X, LIU W, ZHANG Z, et al. Exploring the Three-Dimensional Response of a Water Storage and Sewage Tunnel Based on Full-Scale Loading Tests[J]. Tunnelling and Underground Space Technology, 2019, 88: 156-168. doi: 10.1016/j.tust.2019.03.003
[8]	谢家冲, 黄昕, 金国龙, 等. 局部水力交互下盾构隧道渗流与力学响应研究[J]. 岩土力学, 2023, 44(4): 1179-1189. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202304023.htm XIE Jiachong, HUANG Xin, JIN Guolong, et al. Seepage characteristics and mechanical response of shield tunnels under localized leakage and exosmosis[J]. Rock and Soil Mechanics, 2023, 44(4): 1179-1189. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202304023.htm
[9]	周龙, 朱合华, 沈奕, 等. 内水压盾构隧道管片衬砌受力与变形特性分析[J]. 岩土工程学报, 2023, 45(9): 1763-1772. doi: 10.11779/CJGE20220761 ZHOU Long, ZHU Hehua, SHEN Yi, et al. Stress and deformation properties of shield segmental linings under internal water pressures[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(9): 1763-1772. (in Chinese) doi: 10.11779/CJGE20220761
[10]	宋锦虎, 缪林昌, 高学伸, 等. 基于土体渗透系数变化的管片荷载流-固耦合解析[J]. 岩土力学, 2016, 37(12): 3520-3528. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201612022.htm SONG Jinhu, MIAO Linchang, GAO Xueshen, et al. Coupled Fluid-Solid Analysis of Bearing Characteristic of Segment Based on Change of Soil Permeability Coefficient[J]. Rock and Soil Mechanics, 2016, 37(12): 3520-3528. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201612022.htm
[11]	张治国, 沈安鑫, 徐晨, 等. 黏性场地列车荷载影响下衬砌半渗透边界盾构隧道诱发地表固结沉降解[J]. 中国公路学报, 2022, 35(5): 116-127. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202205011.htm ZHANG Zhiguo, SHEN Anxin, XU Chen, et al. Analytical Solution for Surface Consolidation Settlements Induced by Shield Tunneling with Semi-permeable Boundary Conditions Under Train Loading in Viscous Field[J]. China Journal of Highway and Transport, 2022, 35(5): 116-127. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202205011.htm
[12]	王将, 袁大军, 金大龙, 等. 稳态渗流条件下盾构隧道松动土压力计算模型研究[J]. 天津大学学报: 自然科学与工程技术版, 2019, 52(增刊1): 92-98. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX2019S1014.htm WANG Jiang, YUAN Dajun, JIN Dalong, et al. Calculation model for loosening earth pressure of a shield tunnel based on the influence of steady seepage[J]. Journal of Tianjin University Science and Technology, 2019, 52(S1): 92-98. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX2019S1014.htm
[13]	刘世伟, 赵书争, 付迪, 等. 长期渗漏水条件下海陆相浅埋盾构隧道隧顶水土荷载计算[J]. 岩石力学与工程学报, 2021, 40(10): 2149-2160. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202110018.htm LIU Shiwei, ZHAO Shuzheng, FU Di, et al. Calculation of water and earth pressures on the top of shallow shield tunnels in marine and terrestrial sections under the condition of long-term water leakage[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(10): 2149-2160. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202110018.htm
[14]	FERNANDEZ G, MOON J. Excavation-Induced Hydraulic Conductivity Reduction around a Tunnel - Part 1: Guideline for Estimate of Ground Water Inflow Rate[J]. Tunnelling and Underground Space Technology, 2010, 25(5): 560-566. doi: 10.1016/j.tust.2010.03.006
[15]	王将, 袁大军, 王滕, 等. 局部渗水条件下深埋盾构隧道松动土压力计算模型研究[J]. 土木工程学报, 2020, 53(增刊1): 105-111. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2020S1018.htm WANG Jiang, YUAN Dajun, WANG Teng, et al. Calculation model for loosening earth pressure of the deeply-buried shield tunnel based on the influence of partial leakage[J]. China Civil Engineering Journal, 2020, 53(S1): 105-111. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2020S1018.htm
[16]	张治国, 程志翔, 汪嘉程, 等. 考虑渗流影响的深埋隧道围岩-衬砌相互作用研究[J]. 隧道建设(中英文): 2021, 41(增刊1): 108-121. https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD2021S1014.htm ZHANG Zhiguo, CHENG Zhixiang, WANG Jiacheng, et al. Interaction between surrounding rock and lining of deep-buried tunnel considering influence of seepage[J]. Tunnel Construction: 2021, 41(S1): 108-121. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD2021S1014.htm
[17]	LEI S. An analytical solution for steady flow into a tunnel[J]. Ground Water, 1999, 37(1): 23-26.
[18]	PARK K H, OWATSIRIWONG A, LEE J G. Analytical solution for steady-state groundwater inflow into a drained circular tunnel in a semi-infinite aquifer: a revisit[J]. Tunnelling and Underground Space Technology, 2008, 23(2): 206-209.
[19]	LAVER R G, LI Z, SOGA K. Method to evaluate the long-term surface movements by tunneling in london clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2017, 143(3): 06016023.
[20]	徐长节, 梁禄钜, 陈其志, 等. 考虑松动区内应力分布形式的松动土压力研究[J]. 岩土力学, 2018, 39(6): 1927-1934. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201806002.htm XU Changjie, LIANG Luju, CHEN Qizhi, et al. Research on loosening earth pressure considering the patterns of stress distribution in loosening zone[J]. Rock and Soil Mechanics, 2018, 39(6): 1927-1934. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201806002.htm
[21]	应宏伟, 蒋波, 谢康和. 考虑土拱效应的挡土墙主动土压力分布[J]. 岩土工程学报, 2007, 29(5): 717-722. http://cge.nhri.cn/cn/article/id/12490 YING Hongwei, JIANG Bo, XIE Kanghe. Distribution of active earth pressure against retaining walls considering arching effects[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(5): 717-722. (in Chinese) http://cge.nhri.cn/cn/article/id/12490
[22]	顾晓强, 吴瑞拓, 梁发云, 等. 上海土体小应变硬化模型整套参数取值方法及工程验证[J]. 岩土力学, 2021, 42(3): 833-845. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202103026.htm GU Xiaoqiang, WU Ruituo, LIANG Fayun, et al. On HSS model parameters for Shanghai soils with engineering verification[J]. Rock and Soil Mechanics, 2021, 42(3): 833-845. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202103026.htm
[23]	LIN X T, CHEN R P, WU H N, et al. Three-dimensional stress-transfer mechanism and soil arching evolution induced by shield tunneling in sandy ground[J]. Tunnelling and Underground Space Technology, 2019, 93: 103104.