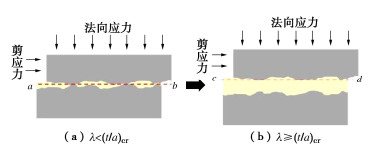
Experimental study on size effect of shear strength of joints with different infill ratios
-
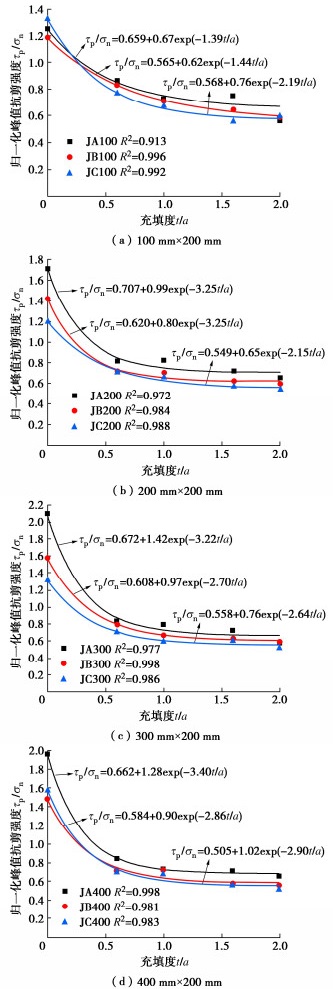
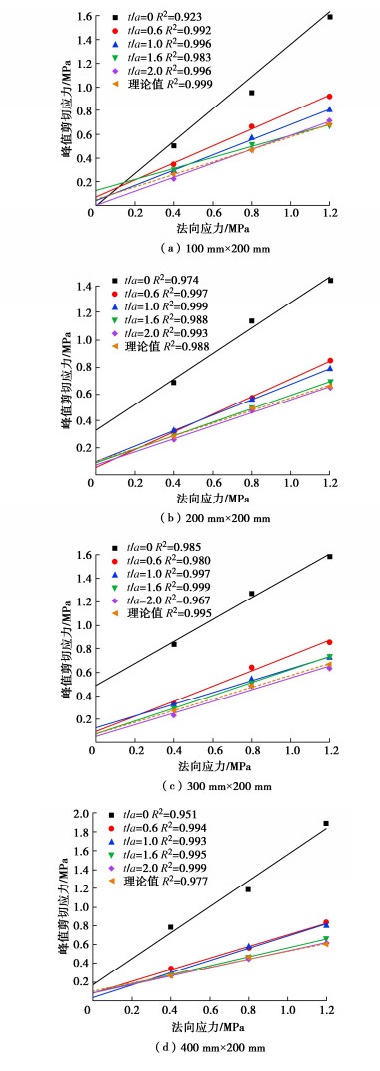
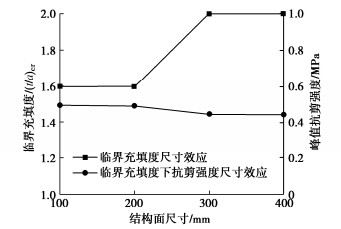
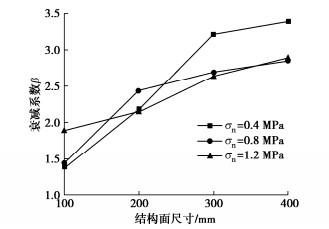
摘要: 针对现有岩体结构面抗剪强度尺寸效应研究较少考虑充填程度差异影响的不足，首先基于渐进扩大法选取平均起伏差和平均起伏角相近的4种连续尺寸天然结构面形貌，并通过3D打印技术制作结构面面板，然后结合类岩石材料配制方法和毫米级充填装置制备5种充填度的充填结构面，最后通过课题组自主研发的大型结构面直剪试验系统开展3种法向应力条件下的室内直剪试验，获得充填结构面的剪切力学与破坏特征，并分析临界充填度和抗剪强度尺寸效应特性。结果表明：随着充填度的增加，结构面剪切破坏模式主要由“岩-岩”剪断破坏逐渐转变为“岩-土界面”滑动破坏，且结构面归一化峰值抗剪强度逐渐减小，直至达到临界充填度时趋于稳定；随着结构面尺寸的增加，临界充填度逐渐增加，变化范围为1.6~2.0；无充填结构面抗剪强度存在较明显的正尺寸效应，而充填结构面抗剪强度尺寸效应较不明显。通过尺寸效应机理分析发现，在不考虑结构面平均起伏角的影响下，平均起伏高度是影响临界充填度和抗剪强度尺寸效应的主要因素。上述研究可为充填结构面抗剪强度尺寸效应模型建立奠定试验基础。Abstract: To address the shortcomings of the existing studies on the size effect of shear strength of rock joints, which do not consider the effects of differences in the filling degree. Firstly, four continuous-size natural joint morphologies with the similar average asperity height and average undulation angle are selected based on the progressively magnifying method, and the joint panels are produced by using the 3D printing technology. Secondly, the infilled joints with five infill ratios are prepared by combining the rock-like material preparation method and the millimeter-level filling devices. Finally, using the direct shear test system for large-scale joints independently developed by the anthors-research group, the laboratory direct shear tests under three normal stress conditions are carried out to obtain the shear mechanics and damage characteristics of the infilled joints. The size effects of the critical infill ratio and shear strength are analyzed. The results show that as the infill ratio increases, the shear damage mode of the joint is mainly changed from "rock-rock" shear fracture to "rock-soil interface" sliding damage, and the normalized peak shear strength gradually decreases until it reaches the critical infill ratio and tends to be stable. As the size of the joints increases, the critical infill ratio gradually increases, ranging from 1.6 to 2.0. There is a more obvious positive size effect on the shear strength of the unfilled joints, while the size effects on the shear strength of the infilled joints are not obvious. Through the analysis of the size effect mechanism, without considering the influences of the average undulation angle of the joints, it is found that the average undulation height is the main factor affecting the size effects of the critical infill ratio and shear strength. The above research can lay an experimental foundation for establishing the size effect model for shear strength of the infilled joints.
-
0. 引言
根据国家“十四五”规划中对能源体系的发展计划，至2025年非化石能源使用占比提升至20%，需建设一批风电、光电、水电等清洁能源基地，同时加快抽水蓄能电站和新型储能技术规模化应用[1]。压缩空气储能技术（compress air energy storage，简称CAES）是新型的大型能源存储技术，采用压缩空气作为工质对能量进行存储和释放，具备改善电力品质、提高电力系统稳定可靠性以及效率高，布置灵活、投资和运行费用较少等优点，一直是国内外研究热点[2]。
1969年世界上第一个商业大型CAES电站在德国Huntorf诞生[3]，20世纪70年代美国能源部开始对CAES电站进行示范性工程计划，该计划关注的两个主要问题为：①CAES长期运行过程储层稳定性标准；②尽量少用或不用化石燃料补充燃烧的CAES系统可行性[4]。直至目前CAES的研究的出发点依旧是紧密围绕CAES电站的安全可靠性和经济性这两个关键问题，针对经济性的研究主要围绕压缩热量处理[5-6]，压缩空气热力学过程[7-10]、能量计算[11-12]，系统设计及能量利用效率计算[13-14]等。针对安全可靠性的研究主要围绕地下储气库稳定性这一问题展开，其研究成果远少于经济性研究成果。
CAES电站地下储气库深处地下，本身受力影响因素众多，受力特性复杂，再加上空气在储气库中频繁循环压缩和释放，造成压力和温度载荷的频繁循环变化，使长期运行过程中地下储气库可靠性和稳定性的精准预测和评估成为难点。目前多数学者的研究成果均存在较大局限性，如Carranza-torres等[15]采用解析解和有限差分两种方法研究了浅埋圆形洞室的地质稳定性；Kim等[16]采用极限平衡法探究了储气库设计参数对地面隆起的影响；夏才初等[17]采用数值模拟方法分析了衬砌围岩受力特性。然而以上研究过程中并未对温度这一关键物理因素对储气库受力影响进行考虑。蒋中明等[18]、周舒威等[19-20]、夏才初等[21]对温度的影响进行考虑，采用热力耦合理论分别采用FLAC3D、解析解和COMSOL研究了储气库衬砌围岩的受力特性，但忽略了运行过程中气体渗漏对稳定性的影响。周瑜等[22]则考虑了储气库的渗漏问题，但忽略了温度的作用。目前仅有Kim等[23]、Rutqvist等[24]采用TOUGH-FLAC对储气库衬砌围岩进行了热流固耦合（thermo-hydro-mechanical，简称THM）研究。
以上研究成果虽有进步性，然而对多物理场耦合过程考虑的还不够全面，尤其针对有无地下水两种情况下储气库气密性和稳定性的研究仍需进一步深入。为探究地下水对CAES硬岩地下储气库运行过程中的气密性和稳定性影响，本文基于压缩空气热力学、热流固耦合理论和两相渗流理论，分别建立了非稳态边界条件下衬砌围岩单相和两相THM耦合数值模型，对比分析了地下水对CAES电站运行过程中储气库稳定性的影响，为此类工程的选址、设计、建设和运行提供科学依据。
1. 孔隙介质多物理场耦合理论和数值实现方法
当CAES电站选址位置无地下水或者地下水位较低时，运行过程中储气库不受地下水影响，考虑气体渗漏过程和压缩空气的温度变化和洞壁传热过程时，储气库衬砌围岩的受力特性可采用单相THM耦合理论进行描述。
1.1 单相THM耦合理论
基于线性热弹性假设，在考虑渗流耦合作用和温度应力作用下时，总应变为应力导致的应变、渗流压力导致的应变和热应变之和，固体总应变控制方程[25]表示如下：
σij = 2Gεij+λδijεV−βTδij(Ts−Ts0)+αδij(p−p0)。 (1) 式中：G = E/2(1+ν)；λ = 2νG/(1−2ν)；εij=(ui,j+uj,i)/2；βT=αTE/(1−2ν)。其中：σij为应力二阶张量分量（Pa）；G为岩石剪切模量（Pa）；εij为应变张量的分量；E为岩石弹性模量（Pa）；ν为泊松比；λ为拉梅系数（Pa）；δij为Kronecker符号，当i=j时，δij=1，当i≠j时，δij=0；εv为体积应变；βT为热膨胀因子；αT为热膨胀系数（K-1）；Ts为固体温度（K）；Ts0为固体初始温度（K）；α为有效应力系数，无量纲；p为孔隙渗流压力（Pa）；p0为初始孔隙压力（Pa）；ui和uj为分别为位移在i和j方向上的分量。
不考虑衬砌结构的配筋和损伤破坏，将其视作理想弹性材料，围岩屈服准则采用莫尔库仑模型：
σ1−σ3=2ccosφ−(σ1+σ3)sinφ。 (2) 式中：σ1，σ3分别为第一、三主应力（N/m2）；c为黏聚力（MPa）；φ为内摩擦角（°）。
孔隙内流体流动满足达西定理，同时考虑固体流体应力变形和温度膨胀过程，热流固耦合作用下渗流方程如下：
θβl∂p∂t=Kμg(∇p+ρfg)−α∂εV∂t+(θαl+(1−θ)αs)∂T∂t。 (3) 式中：θ为孔隙介质孔隙率；βl为流体体积模量（Pa）；K为多孔基质渗透率（m2）；μg为气体动力黏度（Pa·s）；ρf为流体密度（kg/m3）；g为重力加速度（m/s2）；αl和αs分为流体和固体组分热膨胀系数（K-1）；T为温度（K）。
其中考虑体积变形和热膨胀作用时多孔介质孔隙率和渗透率的变化如下所示[26]：
θ = 1−(1−θ0)1+εv(1−ΔpKs+αsΔT)， (4) K = K0(θ/θθ0θ0)3。 (5) 气体在多孔介质中的流动，在温度差异下产生对流传热和传导传热过程，此处采用局部热平衡假设，假设多孔基质和孔隙内气体温度在极短时间内达到热平衡状态，此时的多孔基质内传热控制方程如下所示：
(θsρsCsp+(1−θs)ρCp)∂T∂t+θsK′αTT0∂εV∂t+ρCpug⋅∇T−∇⋅(θsks+(1−θs)k)∇T=Q。 (6) 式中：θs为多孔介质内基质体积分数；ρs为基质材料密度（kg/m3）；Csp为基质材料恒压热容（J/(kg·K)）；Cp为气体恒压热容（J/(kg·K)）；∇T为温度梯度（K/m）；ks为固体基质导热率（W/(m·K)）；k为气体导热率（W/(m·K)）；Q为热源（J/(m3 s)）。
1.2 两相THM耦合理论
当储气库处于地下水影响范围内时，整个物理过程为两相热流固耦合过程，其中固体力学理论和耦合理论如上一节基本相同，但式（1）中的孔隙压力为气相和液相的平均压力；气体渗漏过程由单相渗流变为气液两相渗流，根据达西定律和毛管力驱动可得其控制方程如下：
θβl∂p∂t+∇⋅[−K(s1kr1μ1+s2kr2μ2)(∇p+(s1ρ1+s2ρ2)g)] =−α∂εV∂t+(θαl+(1−θ)αs)∂T∂t ，∂(θc1)∂t+∇⋅[−K(s1kr1μ1+s2kr2μ2)∇p⋅c1] =∇⋅[kr1μ1k(s1−1)∂pec∂s1⋅∇c1] 。} (7) 其中，βl=s1×βw+s2×βg，c1=s1ρ1kr1=s1lvg(1− (1−s11/1mvgmvg)mvg)2，kr2=(1−s1)lvg(1−s11/mvg)2mvg。
式中：s1和s2分别为湿润相和非湿润相体积分数；βw和βg分别为液体和气体体积模量（Pa）；ρ1和ρ2分别为湿润相和非湿润相流体密度（kg/m3）；kr1和kr2分别为湿润相和非湿润相流体相对渗透率；lvg和mvg分别为模型参数；c1为湿润相流体在孔隙中含量（kg/m3）。
采用局部热平衡假设，且根据体积平均理论，多孔基质内两相流体传热控制方程如下所示：
(θsρsCsp+(1−θs)ρCpef)∂T∂t+θsK′αTT0∂εV∂t+ρCpfu∇T−∇(θsks+(1−θs)kef)∇T=Q。 (8) 式中：θs为多孔介质内基质体积分数；Cpef为流体有效比热容（J/(kg·K)），Cpef=s1·Cp1+ s2·Cp2，Cp1和Cp1分为流体相1和2的比热容；kef为流体有效导热率（W/(m·K)），kef= s1·k1+ s2·k2，k1和k2分别为流体相1和2的导热系数。
1.3 储气库THM耦合动态边界模型
关于CAES电站运行过程中储气库内压缩空气热力学模型，He等[27]做出了相当有益的工作，本部分内容在其研究结果上进行了细化推导和演化，增加了渗漏项。考虑洞壁传热和气体渗漏过程的压缩空气热力学模型如下：
dm/dt=min−mout−me ，me=∮uρgDds ，dT/dt=(˙Q+minCp(Tin−T)+Vdp/dt)/mCp ，dp/dt=1/V[κRminTin−κRmoutT−κRmeT+(κ−1)hcA(Tw−T)] 。} (9) 式中：m为储气库内压缩空气质量（kg）；min和mout分别为充放气速率（kg/s）；me为储气库整体渗流渗漏速率（kg/s）；D为圆柱形储气库长度（m）；s为圆柱形储气库横断面周长（m）；V为储气库容积（m3）；Tin为充气温度（K）；R为气体常数，取值287.06 J/(K kg)；к为绝热指数；hc为储气库洞壁对流换热系数，（W/(m2·K)）；A为洞壁的对流换热面积（m2）；Tw为储气库洞壁温度（K）。
数值实现时，储气库压缩空气实时变化的压力作为应力和压力边界作用在硐室内壁边界上；压缩空气实时变化的温度则作为热传导分析的边界作用在洞壁表面。
1.4 THM耦合数值分析流程
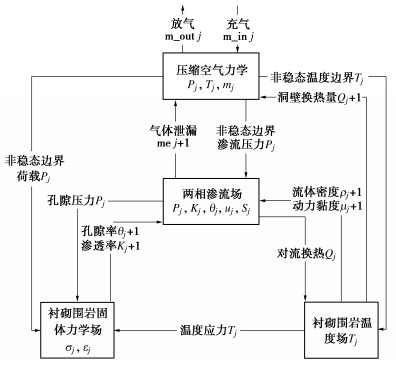
由于渗流速度u和储气库洞壁温度Tw受到压缩空气压力p和温度T影响，以COMSOL数学全局ODE（ordinary differential equation）来建立压缩空气热力学模型，将耦合时变渗漏和洞壁传热的空气温度T压力p作为储气库洞室内壁非稳态边界。流场采用弱形式PDE（partial differential equation）在达西定律与两相达西模块进行二次开发建模。耦合数值分析模型计算流程如图 1所示。
![]()
图 1 储气库衬砌围岩两相热流固耦合模型计算流程Figure 1. Calculation flow of two-phase THM coupling model for lining and surrounding rock of gas reservoir1.5 模型及程序验证
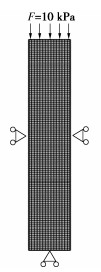
为验证热流固模型的正确性，本文采用经典的一维饱和土柱弹性热固结问题进行验证，该问题前后经过Noorisha等[28]、孙致学等[25]学者的验证。利用COMSOL建立该热流固耦合数值模型并求解，模型高为7 m，宽1 m。模型初始孔隙水压力为10 kPa，模型初始温度为10℃，土柱顶部向下施加10 kPa均布载荷，同时受60℃温度作用，且为自由渗流边界。模型左右边界和底部的力学边界为法向约束，热学边界为绝热边界，渗流边界为不透水边界。模型及网格如图 2所示，模型参数如文献[25]。
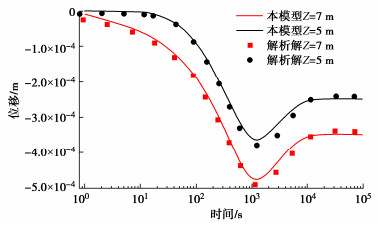
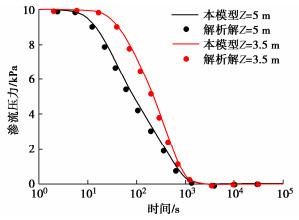
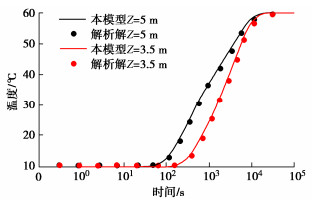
热固结数值模型计算所得到的沉降位移、渗流压力、温度验证结果分别如图 3~5所示，由图可知，本模型与数值解所得出结果在数值和规律上一致性较好，位移曲线先下降，最后开始上升，其过程代表含义为孔隙水排除后，孔隙压力消散，有效应力增加，位移增加，当孔隙水排净后，温度传递导致的膨胀作用导致位移向上。从位移、压力和温度对比可表明该数值模型的正确性。
![]()
图 4 不同高度渗流压力验证结果Figure 4. Verification results of seepage pressure at different heights2. 算例研究
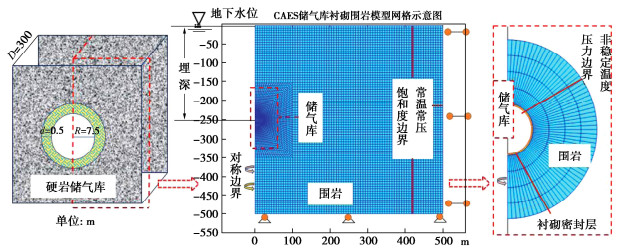
以某拟建地下硬岩CAES储气库为例，建立其横断面二维数值模型，图 6为地下储气库模型及边界设置，储气库为圆柱形横向布置，半径7.5 m，洞室长度300 m，衬砌密封层采用低渗混凝土，厚度为0.5 m，洞室埋深250 m，围岩为花岗岩。假定地下水位在地平面位置。模型采用二维轴对称模型进行建模，为尽量减弱边界尺寸对计算结果的影响，围岩研究范围定为500 m。
![]()
图 6 CAES储气库数值模型及边界示意图Figure 6. Numerical model and boundary diagram of CAES gas reservoir电站运行以1 d为一个周期，分别为充气（8 h）—高压储气（4 h）—放气（4 h）—低压储气（8 h）。入气温度为15℃，储气库的运行压力上下限为7~10 MPa。充放气速率调整结果为初始阶段以50.3 kg/s的充气速率充气24 h，正式运行时充气速率为47.5 kg/s，放气速率为95 kg/s。
依照Kim等[23]、Rutqvist等[24]提出的地下水两相THM模型计算流程，模型计算流程分4步：①初始自重应力平衡过程计算，清除初始自重位移。②地下储气库的开挖过程计算，计算开挖排水之后7 d的储气库位移变形和围岩内孔压变化。③计算衬砌施工后1 d内的衬砌围岩的变形位移和孔压变化。④计算包括初始充气阶段在内的60个运行循环过程中的压缩空气热力学过程和储气库两相THM耦合过程。
模型左侧为对称边界，对力学模型底部为固定约束、右边为法向约束、顶部为自由面；对渗流模型底部、右侧和顶部均为随埋深变化的常压和水相饱和度边界，对传热模型底部、右侧和顶部为常温边界。计算相关参数如表 1所示。
表 1 计算参数取值表Table 1. Values of calculation parameters参数 值/单位 参数 值/单位 参数 值/单位 参数 值/单位 储气库半径r 7.5 m 两相流参数lvg 0.5 围岩初始孔隙率θr0 0.02 衬砌恒压热容Cpc 880 J/(kgK) 储气库长度D 300 m 两相流参数mvg 0.595 围岩恒压热容Cpr 930 J/(kg K) 衬砌导热率λc 2 W/(m·K) 衬砌密封层厚度d 0.5 m 围岩弹性模量Er 20 GPa 围岩导热率λr 1.8 W/(m·K) 围岩热膨胀系数 5.0×10-51/K 初始压力P0 1 atm 衬砌弹性模量Ec 23 GPa 衬砌热膨胀系数 1.2×10-5 1/K 围岩内摩擦角 50 ° 初始温度T0 15 ℃ 围岩密度ρr 2650 kg/m3 衬砌初始孔隙率θc0 0.01 围岩泊松比νr 0.18 充气温度T_in 15 ℃ 衬砌密度ρc 2300 kg/m3 衬砌初始渗透率Kc0 1×10-20 m2 衬砌泊松比νc 0.2 毛细入口压力pec 1.47 MPa 围岩初始渗透率Kr0 2×10-16 m2 围岩黏聚力c 2 MPa 3. 计算成果及分析
3.1 储气库压缩空气热力学过程变化
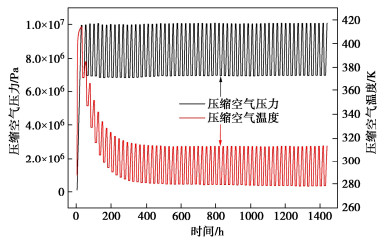
压缩空气热力学特性变化过程如图 7所示，由图可知，第一个充气阶段，压缩空气温度和压力随时间迅速升高，空气压力随时间线性升高，在24 h迅速上升至10 MPa，温度先迅速升高后缓慢升高至415 K。压缩空气的温度和压力在放气过程中迅速降低，随后的运行循环中，空气温度会波动降低，稳定时的温度波动上下限279~314 K，波动范围35 K。
![]()
图 7 压缩空气热力学特性变化过程Figure 7. Variation of thermodynamic characteristics of compressed air3.2 地下水对储气库密封性影响
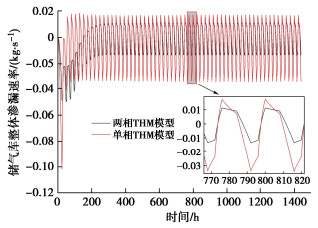
密封性以储气库内气体质量为对象，储气库渗漏率以储气库气体减少为负，增加为正。两种模型储气库60个运行循环整体渗漏速率变化过程如图 8所示，有无地下水两种地质条件下的储气库渗漏速率对运行过程周期性波动变化。由于空气压力的动态变化，初始时衬砌和围岩内渗流压力较低，但是储气库内气体压力迅速升高，因此初始循环时气体渗漏最快。随着渗流压力扩散，衬砌和围岩内渗流压力升高，此时渗漏速率逐步降低，最后形成稳定波动。单相THM模型渗漏速率稳定时波动范围为-0.034~0.0165 kg/s，两相THM模型渗漏速率稳定波动范围为-0.0135~0.011 kg/s。值得注意的是，在放气阶段，气体渗漏为正，即气体在放气阶段由衬砌围岩向储气库内渗流，原因为放气阶段由于气体压力迅速降低3 MPa，衬砌结构内渗流压力的变化存在滞后性，其压力高于储气库内气体压力，此时渗流方向向内。
![]()
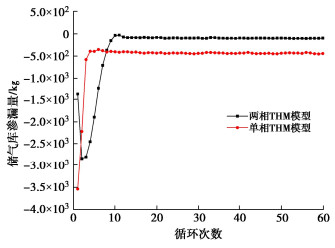
图 8 两种模型储气库整体渗漏速率变化规律Figure 8. Variation of overall leakage rate of two models for gas reservoir储气库每个循环气体渗漏质量变化规律如图 9所示，每个循环气体渗漏质量变化规律随循环过程总体成减小并稳定的趋势。单相THM模型在第4个循环是渗漏质量达到稳定，稳定时每个循环气体质量损失为440 kg，两相THM模型在10个循环时达到稳定，稳定时每个循环气体损失为95 kg。该储气库稳定运行时充气速率47.5 kg/s，充气时间8 h，每个循环充气质量为1.37×106 kg，单相THM模型每个循环气体渗漏质量占充气质量0.032%，两相THM模型每个循环气体渗漏质量占充气质量0.007%。两个模型稳定运行时每个循环气体损失均小于1%，表明当衬砌密封层渗透率为1×10-20 m2，考虑其受力过程产生的应变而导致渗透率变化，该衬砌密封层密封效果满足要求。且地下水存在时，会导致气体质量损失降低78%，地下水可有效辅助密封。
![]()
图 9 储气库每个循环气体渗漏质量随运行过程变化规律Figure 9. Variation of gas leakage quality in each cycle of gas reservoir with operation process3.3 地下水对储气库结构受力特性影响
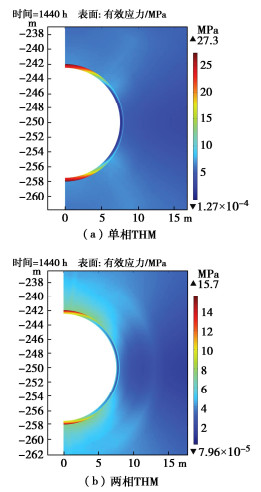
储气库衬砌围岩结构的受力状态决定了储气库的安全稳定性，两种模型在稳定运行过程充气段末衬砌和围岩有效应力分布如图 10所示，由图可知，当衬砌结构强度高于围岩时，衬砌结构受力高于围岩，是主要受力结构，衬砌顶部和底部会出现应力集中现象，单相THM模型充气段末衬砌最大有效应力为27.3 MPa，而两相THM模型衬砌最大有效应力为15.7 MPa。当储气库地层中有地下水作用时，衬砌结构顶部和顶部的集中有效应力会有较大幅度降低，充气段末的最大应力降低幅度为42.5%。
![]()
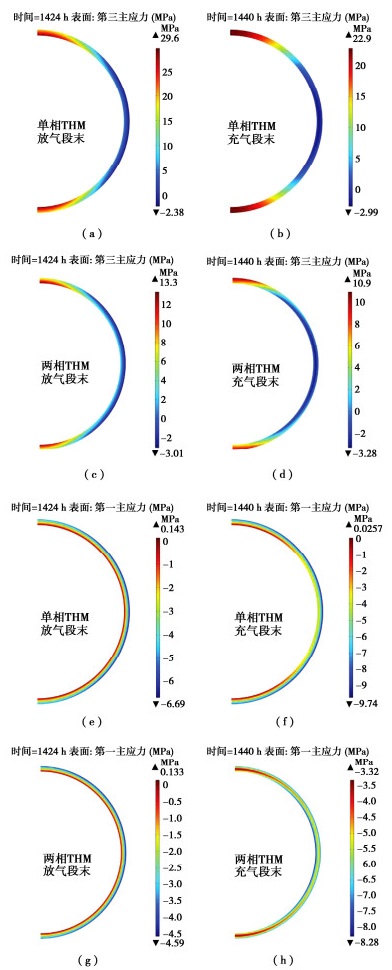
图 10 充气段末衬砌和围岩受力分布云图Figure 10. Stress distribution of lining and surrounding rock at end of charging stage分析衬砌密封层结构的主要受力形态和可能发生的破坏形式，有助于对储气库结构的安全稳定性做出准确评估。此处第三、第一主应力按照岩土力学规定进行划分。储气库衬砌结构第60循环充气和放气段末第三、第一主应力分布如图 11所示，由图 11可知，①放气段末衬砌结构第三主应力高于充气段末，即放气段结构失稳危险程度高于充气段；②衬砌结构在充气和放气阶段第三主应力大范围表现为正，即衬砌结构大范围承受拉应力，拉应力较高位置为顶部和底部，侧壁位置第三主应力为负，表现为压应力；③两相THM模型衬砌结构充放气段第三、第一主应力均小于单相THM模型，即有地下水时，衬砌结构最大拉应力可以降低52%。
![]()
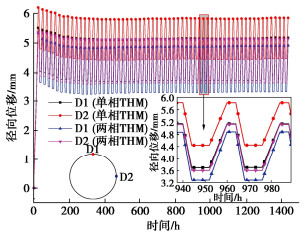
图 11 典型运行阶段末两种模型衬砌第三和第一主应力分布Figure 11. Distribution of first and third principal stresses of lining structures of two models at end of typical operation stage为消除开挖和施工变形位移差异对衬砌结构最终变形位移结果的影响，以运行初期为参照对两种模型衬砌结构典型位置测点位移变化进行研究，其规律如图 12所示。衬砌径向位移随空气压力升高迅速变大，然后随充放气状态起伏波动，稳定运行时径向位移波动范围为1.5 mm。洞室侧壁水平位移大于顶部竖向位移，即运行过程中储气库横向膨胀变形大于纵向，整体变形成椭圆形膨胀。单相THM模型侧壁水平位移和顶部竖向位移分别比两相THM模型大0.8 mm和0.4 mm。
![]()
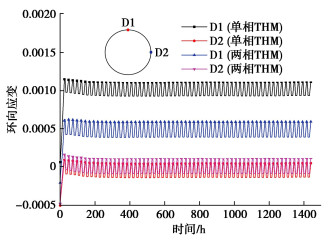
图 12 衬砌测点径向位移变化规律Figure 12. Variation of radial displacement of monitoring points for lining衬砌典型测点环向应变变化规律如图 13所示，衬砌结构顶部应变大于侧壁，该规律与Kim等[29]研究成果相一致。衬砌顶部环向应变为拉应变，侧壁环向应变状态随充放气变化，充气时为拉应变，放气时为压应变。单相THM模型衬砌测点环向应变均大于两相THM模型，单相THM模型衬砌最大环向应变为0.0011，该应变结果与相似工况下的夏才初等[17]的研究成果相类似，而两相THM模型最大为0.0006。可知地下水可有效降低衬砌顶部拉应变。
![]()
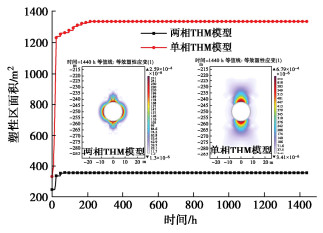
图 13 衬砌测点环向应变变化规律Figure 13. Variation of circumferential strain at different measuring points for lining储气库运行过程中围岩塑性区面积变化和分布规律如图 14所示。储气库围岩塑性区为剪切塑性区，稳定运行时两相THM模型围岩塑性区成环形分布于洞室周围，而单相THM模型围岩塑性区成矩形分布于洞室周围，在洞室顶部和底部向围岩中延伸，最远可达围岩内部20 m。开挖围岩塑性区集中于洞室腰部围岩内，随着运行过程增加，洞室顶部和底部围岩有效应力增加，塑性区逐渐向顶部和底部围岩中发展。初始运行时单相THM模型塑性区面积为332 m2，随后的两个循环中急速增长，之后缓慢增长至第10个循环时达到稳定，稳定时围岩塑性区面积为1337 m2。初始运行时两相THM模型塑性区面积为248 m2，在第3个循环时达到稳定，稳定时塑性区面积为356 m2。地下水可以有效降低运行过程中围岩塑性区分布。根据此项结果，围岩在施工过程中需要进行加固处理，在没有地下水影响时需对洞室顶部、底部深部区域进行加固处理。
![]()
图 14 围岩塑性区面积随时间变化及分布规律Figure 14. Variation and distribution laws of plastic zone area of surrounding rock with time3.4 讨论
储气库THM耦合模型结果和两相THM耦合模型结果对比如表 2所示。相同条件下当有地下水时，储气库渗漏速率从-0.034~0.016 kg/s降低至-0.013~0.011 kg/s，每个循环渗漏百分比从0.035%降低至0.008%，地下水的存在可有效辅助气体密封。
表 2 有无地下水对储气库渗漏和受力特性影响Table 2. Influences of groundwater on leakage and mechanical.characteristics of gas reservoir工况 渗漏速率/(kg·s-1) 渗漏百分比% 衬砌最大有效应力/MPa 衬砌最大第三主应力/MPa 围岩最大有效应力/MPa 衬砌最大拉应变 围岩塑性区面积/m2 无地下水 -0.034 ~ 0.016 0.032 27.3 29.6 7.63 0.0011 1337 有地下水 -0.013 ~ 0.011 0.007 15.7 13.3 7.57 0.0006 356 注：表中应力符号规定为拉正压负，渗漏速率以气体从储气库向外为负 衬砌出现应力集中，当有地下水时，衬砌最大有效应力从27.3 MPa降低至15.7 MPa，最大第三主应力也从29.6 MPa降低至13.3 MPa，最大剪应力从31 MPa降低至17.9 MPa，衬砌最大拉应变降低0.0005。围岩剪应力大小和分布均出现较大范围降低，塑性区面积从1337 m2降低至356 m2。
地下水存在时，衬砌外侧和围岩内孔隙压力增高，有效应力降低，尤其是衬砌结构内，衬砌最大有效应力、最大第三主应力和剪应力均降低1/3。地下水的影响会使围岩塑性区面积也出现了大幅度降低，降低幅度为92%，其原因为有地下水时，洞周围岩内孔压增加，有效应力降低、同时剪应力降低，由于正应力降低导致的抗剪强度也随之降低，但是在本文模型的洞室形状、洞室埋深、地下水位和运行条件下，围岩的剪应力降低幅度高于抗剪强度的降低幅度，因此围岩剪切塑性区分布区域减小。有效应力和塑性区的降低幅度主要由孔隙压力增高幅度决定，孔隙压力的增高幅度主要由埋深与地下水位相对关系控制。由此可知，地下水的存在会大幅度降低衬砌有效应力和减小围岩塑性区面积。
4. 结论
对CAES储气库密封可靠性和安全稳定性的研究是保证CAES电站可靠运行的基础，地下储气库的密封效果和安全稳定性的影响因素众多，耦合过程复杂，同时耦合变量之间高度非线性增加了对储气库安全性和可靠性评价的难度。本文采用热流固耦合理论、两相渗流理论、压缩空气热力学理论对储气库运行过程中涉及到的流体状态变化、空气渗漏、衬砌围岩单相THM和两相THM耦合过程进行了建模。该模型计算了有无地下水两种情况下储气库从开挖至60 d运行过程，主要得出以下3点结论。
（1）在该储气库以本文模型设定方案运行时，衬砌渗透率为1×10-20 m2时，储气库渗漏率低于1%，可满足密封要求。地下水的存在可使储气库每个循环气体损失量降低78%。
（2）该模型储气库运行时衬砌为受力主体，衬砌顶部和底部出现应力集中，且表现为受拉应力作用，因此衬砌顶部和底部需注意配加密筋以满足受力要求。运行时储气库总体成椭圆形膨胀变形，横向变形大于竖向。
（3）地下水存在时可大幅度降低衬砌结构有效应力和围岩塑性区面积。
-
![]()
图 1 结构面样本渐进扩大法示意图
Figure 1. Schematic diagram of progressively magnifying method for joint sample
![]()
图 6 σn=1.2 MPa下系列尺寸结构面剪应力-剪切位移曲线
Figure 6. Shear stress-shear displacement curves of joints with series sizes at σn=1.2 MPa
![]()
图 7 不同充填度下抗剪强度尺寸效应规律
Figure 7. Size effect laws of shear strength under different infill ratios
![]()
图 8 归一化峰值抗剪强度随充填度的变化规律
Figure 8. Variation laws of normalized peak shear strength with infill ratios
![]()
图 11 不同尺寸结构面衰减系数变化趋势
Figure 11. Variation trend of attenuation coefficient of joints with different sizes
表 1 类岩石材料配合比
Table 1 Mix ratios of rock-like materials
水泥 砂 大理
石粉树脂 固化剂 促凝剂 保水剂 37% 24% 30% 6% 1% 1% 1% 
下载: 导出CSV
表 2 系列尺寸充填结构面剪切破坏模式
Table 2 Shear failure modes of infilled joints with series sizes
充填度t/a 结构面尺寸/(mm×mm) 破坏模式 100×200 200×200 300×200 400×200 0.0 
“岩-岩”剪断破坏 0.6 
以“岩-岩”剪损及“岩-土界面”滑动破坏为主 1.0 
1.6 
2.0 
以“岩-土界面”滑动破坏为主 注：其中充填度t/a=1.6时，尺寸为100 mm×200 mm、200 mm×200 mm的结构面破坏模式以“岩-土界面”滑动破坏为主。
下载: 导出CSV
-
[1] JIANG Q, SONG L B, YAN F, et al. Experimental investigation of anisotropic wear damage for natural joints under direct shearing test[J]. International Journal of Geomechanics, 2020, 20(4): 04020015. doi: 10.1061/(ASCE)GM.1943-5622.0001617
[2] ZHOU D, ZHAO Z H, LI B, et al. Permeability evolution of grout infilled fractures subjected to triaxial compression with low confining pressure[J]. Tunnelling and Underground Space Technology, 2020, 104: 103539. doi: 10.1016/j.tust.2020.103539
[3] 祝艳波, 张宇轩, 李文杰, 等. 粗糙度对硅质板岩-泥岩界面强度与变形特性影响试验研究[J]. 岩石力学与工程学报, 2022, 41(7): 1358-1372. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202207006.htm ZHU Yanbo, ZHANG Yuxuan, LI Wenjie, et al. Experimental study on effect of roughness on strength and deformation characteristics of interface between siliceous slate and mudstone[J]. Chinese Journal of Rock Mechanics and Engineering, 2022, 41(7): 1358-1372. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202207006.htm
[4] ZHAO Z H, LIN T, CHEN Y D, et al. Shear behaviors of natural rock fractures infilled with cemented calcite[J]. Computers and Geotechnics, 2022, 141: 104493. doi: 10.1016/j.compgeo.2021.104493
[5] HAN G S, JING H W, JIANG Y J, et al. Effect of cyclic loading on the shear behaviours of both unfilled and infilled rough rock joints under constant normal stiffness conditions[J]. Rock Mechanics and Rock Engineering, 2020, 53(1): 31-57. doi: 10.1007/s00603-019-01866-w
[6] WU D Y, CHEN F, TANG L, et al. Influence of weak interlayer filling state on the failure patterns of natural rock joints[J]. International Journal of Geomechanics, 2022, 22(7): 04022086. doi: 10.1061/(ASCE)GM.1943-5622.0002410
[7] 许万忠, 林杭, 曹日红. 充填粗糙节理直剪数值模拟宏细观分析[J]. 西南交通大学学报, 2018, 53(3): 548-557. https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT201803016.htm XU Wanzhong, LIN Hang, CAO Rihong. Simulation and macro-mesoscopic parameter analysis for direct shear of filled rough joints[J]. Journal of Southwest Jiaotong University, 2018, 53(3): 548-557. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT201803016.htm
[8] LADANYI B, ARCHAMBAULT G. Shear strength and deformability of filled indented joints[C]//Proceedings of International Symposium on Geotechnics of Structurally Complex Formations, Capri, Italy, 1977.
[9] TANG J Z, YANG S Q, ZHAO Y L, et al. Experimental and numerical modeling of the shear behavior of filled rough joints[J]. Computers and Geotechnics, 2020, 121: 103479. doi: 10.1016/j.compgeo.2020.103479
[10] 肖维民, 余欢, 朱占元, 等. 薄层充填岩石节理剪胀特性试验研究[J]. 岩土工程学报, 2020, 42(8): 1499-1508. doi: 10.11779/CJGE202008015 XIAO Weimin, YU Huan, ZHU Zhanyuan, et al. Experimental study on shear dilatancy characteristics of thinly-infilled rock joints[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(8): 1499-1508. (in Chinese) doi: 10.11779/CJGE202008015
[11] 肖维民, 余欢, 李锐, 等. 薄层充填岩石节理抗剪强度特性试验研究[J]. 岩石力学与工程学报, 2019, 38(增刊2): 3420-3428. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2019S2017.htm XIAO Weimin, YU Huan, LI Rui, et al. Experimental research on the shear strength of thinly-infilled rock joints during shearing[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(S2): 3420-3428. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2019S2017.htm
[12] KARAKUS M, LIU Y, ZHANG G C, et al. A new shear strength model incorporating influence of infill materials for rock joints[J]. Geomechanics and Geophysics for Geo-Energy and Geo-Resources, 2016, 2(3): 183-193. doi: 10.1007/s40948-016-0032-4
[13] PAPALIANGAS T, HENCHER S R, LUMSDEN A C, et al. The effect of frictional fill thickness on the shear strength of rock discontinuities[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1993, 30(2): 81-91.
[14] 史玲, 蔡美峰, 赵坚. 充填节理破坏机理及实验[J]. 北京科技大学学报, 2012, 34(3): 253-259. https://www.cnki.com.cn/Article/CJFDTOTAL-BJKD201203003.htm SHI Ling, CAI Meifeng, ZHAO Jian. Fracture mechanism and experiment of infilled rock joints[J]. Journal of University of Science and Technology Beijing, 2012, 34(3): 253-259. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BJKD201203003.htm
[15] ZHAO Y L, LI Y, CHANG L, et al. Shear behaviors of clay-infilled joint with different water contents: experiment and model[J]. Arabian Journal of Geosciences, 2021, 14(17): 1-16.
[16] PHIEN-WEJ N, SHRESTHA U B, RANTUCCI G. Effect of infill thickness on shear behaviour of rock joints[C]// Proceedings of the International Conference on Rock Joints, Loen, 1990: 289-294.
[17] INDRARATNA B, WELIDENIYA H S, BROWN E T. A shear strength model for idealized filled joints under constant normal stiffness[J]. Géotechnique, 2005, 55(3): 215-226. doi: 10.1680/geot.2005.55.3.215
[18] SHRIVASTAVA A K, RAO K S. Physical modeling of shear behavior of infilled rock joints under CNL and CNS boundary conditions[J]. Rock Mechanics and Rock Engineering, 2018, 51(1): 101-118. doi: 10.1007/s00603-017-1318-8
[19] JAHANIAN H, SADAGHIANI M H. Experimental study on the shear strength of sandy clay infilled regular rough rock joints[J]. Rock Mechanics and Rock Engineering, 2015, 48(3): 907-922. doi: 10.1007/s00603-014-0643-4
[20] ZHAO Y L, ZHANG L Y, WANG W J, et al. Experimental study on shear behavior and a revised shear strength model for infilled rock joints[J]. International Journal of Geomechanics, 2020, 20(9): 04020141. doi: 10.1061/(ASCE)GM.1943-5622.0001781
[21] WEI Y, MING M. Investigation on the scale dependence of shear mechanical behavior of rock joints using DEM simulation[J]. Computational Particle Mechanics, 2023, 10: 1613-1627. doi: 10.1007/s40571-023-00577-y
[22] JEFFERY M, HUANG J, FITYUS S, et al. A large-scale application of the stochastic approach for estimating the shear strength of natural rock discontinuities[J]. Rock Mechanics and Rock Engineering, 2023, 56(8): 6061-6078. doi: 10.1007/s00603-023-03393-1
[23] 罗战友, 杜时贵, 黄曼. 岩石结构面峰值摩擦角应力效应试验研究[J]. 岩石力学与工程学报, 2014, 33(6): 1142-1148. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201406007.htm LUO Zhanyou, DU Shigui, HUANG Man. Experimental study of stress effect on peak friction angle of rock structural plane[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(6): 1142-1148. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201406007.htm
[24] BANDIS S C, LUMSDEN A C, BARTON N R. Experimental studies of scale effects on the shear behaviour of rock joints[J]. International Journal of Rock Mechanics and Mining Science and Geomechanics Abstracts, 1981, 18(1): 1-21.
[25] HUANG M, HONG C J, DU S G, et al. Experimental technology for the shear strength of the series-scale rock joint model[J]. Rock Mechanics and Rock Engineering, 2020, 53(12): 5677-5695. doi: 10.1007/s00603-020-02241-w
[26] JOHANSSON F. Influence of scale and matedness on the peak shear strength of fresh, unweathered rock joints[J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 82: 36-47. doi: 10.1016/j.ijrmms.2015.11.010
[27] BAHAADDINI M, HAGAN P C, MITRA R, et al. Scale effect on the shear behaviour of rock joints based on a numerical study[J]. Engineering Geology, 2014, 181: 212-223. doi: 10.1016/j.enggeo.2014.07.018
[28] KANG Y S, HOU C C, LIU B, et al. Influence of water content on the shear strength of rock joints with clay-rich fillings[J]. Rock Mechanics and Rock Engineering, 2023, 56(2): 1437-1449. doi: 10.1007/s00603-022-03158-2
[29] MENG F Z, ZHOU H, WANG Z Q, et al. Influences of shear history and infilling on the mechanical characteristics and acoustic emissions of joints[J]. Rock Mechanics and Rock Engineering, 2017, 50(8): 2039-2057. doi: 10.1007/s00603-017-1207-1
[30] SHE C X, SUN F T. Study of the peak shear strength of a cement-filled hard rock joint[J]. Rock Mechanics and Rock Engineering, 2018, 51(3): 713-728. doi: 10.1007/s00603-017-1358-0
[31] TATONE B, GRASSELLI G. An investigation of discontinuity roughness scale dependency using high- resolution surface measurements[J]. Rock Mechanics and Rock Engineering, 2013, 46(4): 657-681. doi: 10.1007/s00603-012-0294-2
[32] 杜时贵, 吕原君, 罗战友, 等. 岩体结构面抗剪强度尺寸效应联合试验系统及初级应用研究[J]. 岩石力学与工程学报, 2021, 40(7): 1337-1349. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202107002.htm DU Shigui, LÜ Yuanjun, LUO Zhanyou, et al. Combined test system for size effect of rock joint shear strength and its primary application research[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(7): 1337-1349. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202107002.htm
[33] BAN L R, DU W S, QI C Z, et al. Modified 2D roughness parameters for rock joints at two different scales and their correlation with JRC[J]. International Journal of Rock Mechanics and Mining Sciences, 2021, 137: 104549. doi: 10.1016/j.ijrmms.2020.104549
-
期刊类型引用(1)
1. 张国华，王薪锦，相月，潘佳，熊峰，华东杰，唐志成. 压缩空气硬岩储库关键问题研究进展：气密性能、热力过程与稳定性. 岩石力学与工程学报. 2024(11): 2601-2626 . 
百度学术
其他类型引用(0)
-
其他相关附件
计量
- 文章访问数: 549
- HTML全文浏览量: 72
- PDF下载量: 138
- 被引次数: 1
