二阶Stokes波作用下多孔弹性海床动力响应解析解

王哲; 周博豪; 张智卿; 李西斌

doi:10.11779/CJGE20230504

二阶Stokes波作用下多孔弹性海床动力响应解析解 English Version

1.
浙江工业大学岩土工程研究所, 浙江杭州 310014
2.
温州理工学院建筑与能源工程学院, 浙江温州 325035
3.
浙江农林大学风景园林与建筑学院, 浙江杭州 311300

基金项目:

浙江省自然科学基金重点项目 LHZ21E090001

国家自然科学基金项目 52178367

详细信息

作者简介:
王哲(1978—)，男，博士，教授，主要从事岩土工程的教学和科研工作。E-mail: wangzsd@zjut.edu.cn

通讯作者:
李西斌, E-mail: ytulxb@zafu.edu.cn

中图分类号: TU43
计量
- 文章访问数: 572
- HTML全文浏览量: 62
- PDF下载量: 125
出版历程
- 收稿日期: 2023-06-04
- 网络出版日期: 2024-03-24
- 刊出日期: 2024-08-31

Analytical solutions for dynamic response in poroelastic seabed under second-order Stokes waves

1.
Institute of Geotechnical Engineering, Zhejiang University of Technology, Hangzhou 310014, China
2.
College of Architecture and Energy Engineering, Wenzhou University of Technology, Wenzhou 325035, China
3.
School of Landscape Architecture, Zhejiang A & F University, Hangzhou 311300, China

摘要

摘要: 基于二阶Stokes波理论，研究了非线性海洋波作用下多孔弹性海床的动力响应问题。利用Biot固结理论以及Verruijt储存方程，在笛卡尔坐标下建立了海床的控制方程。通过将海洋波函数拓展到复数域，采用严格的数学推导求得了海床动力响应的解析解，并将该解与既有解进行对比验证。最后分析了波浪和海床特征参数对海床有效应力、剪切应力和孔压分布的影响，结果表明波浪和海床的参数对海床动力响应具有显著的影响。其中波浪周期和水深对二阶Stokes波的二阶项有较大影响，渗透系数和剪切模量则分别影响海床动力响应的变化速率和幅值。
- 二阶Stokes波 /
- 海床 /
- 动力响应 /
- 解析解
Abstract: Based on the theory of the second-order Stokes waves, the dynamic response of a poroelastic seabed induced by nonlinear ocean waves is investigated. The governing equations for the seabed are established in Cartesian coordinates using the Biot's general consolidation theory and the Verruijt's storage equation. The analytical solutions for the dynamic response of the seabed are obtained by extending the ocean wave function and the field quantities in the seabed to the complex domain using a rigorous mathematical derivation. The correctness and reliability of the analytical solutions are verified by comparing with the existing solutions. Finally, the effects of the characteristic parameters of the waves and seabed on the vertical effective stress, horizontal effective stress, shear stress and pore pressure distribution of the seabed are analyzed. The results show that the characteristic parameters of the waves and seabed have a significant effect on the dynamic response of the seabed. The wave period and water depth have a significant impact on the second-order term of the nonlinear waves, while the permeability and shear modulus respectively affect the rate of change and amplitude.
- second-order Stokes wave /
- seabed /
- dynamic response /
- analytical solution

HTML全文

0. 引言

在波浪荷载作用下，海床内孔隙水压力增大以及垂直有效应力降低，进而导致海床土体失稳甚至液化^[1]。在人类探索海洋资源的近几十年内，海床的液化对人类在海洋中的作业安全产生了很大的影响^[2]。因此，针对波浪荷载对海床动力响应的研究具有重要的理论意义和工程价值。

自20世纪中叶起，学者们开始分别基于刚性非耦合模型^[3]、Biot流固耦合模型^[4]和多孔介质弹塑性模型^[5]对波浪荷载引起的海床动力响应问题进行了理论研究。其中基于可考虑饱和介质压缩性的Biot三维准静态固结理论^[6]和动力固结理论应用^[7]最为广泛。Yamamoto等^[8]基于Biot准静态固结理论得到了线性波作用下无限厚度海床内孔隙水压力、有效应力和土骨架位移的闭合形式解，为此后的研究奠定了基础。Madsen^[9]在此基础上，引入了Verruijt^[10]提出的考虑海床土体饱和度的储存方程，得到了线性波作用下无限厚度准饱和海床动力响应的解析解，发现海床的动力响应受到海床土体饱和度的影响显著。基于Madsen的研究，Okusa^[11]发现海床土体的参数对无限厚度海床动力响应的影响可以忽略不计。Mei等^[12]采用边界层近似法，即通过将海床分为上下两部分，求解无限厚度海床动力响应的方法求解上半区域海床，并得到下半区域海床的简化解，最终得到波浪荷载作用下有限厚度多孔弹性海床的动力响应的近似解。Hsu等^[13]则得到了波浪荷载作用下有限厚度海床动力响应的解析解，发现当海床厚度趋于无穷大时，有限厚度海床的动力响应与无限厚度海床的解析解结果基本一致。

Zienkiewicz等^[14]基于Biot准静态固结理论和Biot动力固结理论，整理总结得到了适应于饱和土体的准静态理论、部分动态理论和完整动态理论。Ulker等^[15]通过对准静态解、部分动态解和完整动态解的对比分析研究，发现在一定的海床和波浪条件下三者得到的结果基本一致。考虑到准静态理论的推导简单，便于用于实际工程分析，于是学者们在准静态理论的基础上进行了一系列深入的研究工作。海洋中波浪特性往往相当复杂^[16]，而且波浪非线性特性对海床动力响应的研究尚不够深入。Madsen^[9]虽然得到了无限厚度海床动力响应的解答，但是该研究没有考虑海床底部下卧基岩的情况以及波浪非线性的影响。王忠涛等^[17]则通过数值模拟的方法给出了波浪非线性对海床动力响应的影响。郭秀军等^[18]研究基于有限差分法研究了海床的分层对动力响应的影响。Zhou等^[19]和Zhang等^[20]考虑了海床分层的影响得到了二阶Stokes波作用下多层海床的半解析解。周晓智等^[21]研究了驻波作用下海床应力路径特性。但是前述学者的研究均没有考虑波浪参数对海床动力响应的影响，且没有得到二阶Stokes波作用下有限厚度海床动力响应的准静态解析解。

因此本文基于准静态理论求解均质各向同性海床在二阶Stokes波作用下动力响应的解析解，通过与既有解进行对比验证，并结合数值计算分析了波浪和海床土体的参数对海床动力响应的影响规律。

1. 控制方程和边界条件

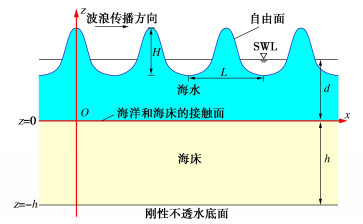
如图 1所示，本文考虑了下卧刚性不透水基岩的多孔弹性海床在二阶Stokes波作用下动力响应问题。其中二阶Stokes波的传播方向为x轴的正方向。与Li等^[1]的研究一致，取海床和海洋的接触面为笛卡尔坐标系的零点，z轴垂直向上时为正值，负值在海床和海洋的接触面以下。此外，图中H和L分别为二阶Stokes波的波高和波长；d为水深；h为海床的厚度。

图 1 波浪和多孔弹性海床之间的动力相互作用

Figure 1. Dynamic interaction between ocean waves and poroelastic seabed

下载: 全尺寸图片幻灯片

1.1 控制方程

基于Biot三维准静态固结理论^[6]与Verruijt储能方程^[10]，多孔弹性海床的控制方程可以表示为

${\sigma _{ij,j}} = 0 \text{，}$

(1)

$- {p_{,i}} = {{{\rho _{\text{f}}}g{{\dot w}_i}} \mathord{\left/ {\vphantom {{{\rho _{\text{f}}}g{{\dot w}_i}} K}} \right. } K} 。$

(2)

式中：下标i和j表示该场量沿x或z方向的分量；下标‘, i’和‘, j’表示该场量对x或z方向的一阶偏导；字母上的‘•’表示该场量对时间t的一阶导数； ${\sigma _{ij}}$ 为总应力张量；p为孔隙水压力； ${\rho _{\text{f}}}$ 为孔隙流体密度；g为重力加速度；K为渗透系数（水力传导系数）。

流体的质量守恒方程为

${\dot u_{i,i}} + {\dot w_{i,i}} = - n\beta \dot p = \partial {\rho _{\text{f}}}/\partial t 。$

(3)

式中：u为土骨架的位移；w为孔隙流体相对土骨架的位移；n为海床土体的孔隙率；β为孔隙流体压缩性系数。当海床土体中含有少量气体时，β可以通过下式计算：

$\beta = 1/{K_{\text{w}}} + (1 - {S_{\text{r}}})/{P_{{\text{w0}}}} 。$

(4)

式中： ${K_{\text{w}}}$ 为孔隙流体的实际体积弹性模量，一般取 ${K_{\text{w}}}$ =2×10⁹ Pa； ${S_{\text{r}}}$ 为海床土体的饱和度； ${P_{{\text{w0}}}}$ 为由水深d确定的绝对压力， ${P_{{\text{w0}}}}$ = ${\rho _{\text{f}}}$ gd。

将式（2）代入式（3），消去w项，可以将控制方程改写为

$K\left( {\frac{{{\partial ^2}p}}{{\partial {x^2}}} + \frac{{{\partial ^2}p}}{{\partial {z^2}}}} \right) - {\gamma _{\text{w}}}n\beta \frac{{\partial p}}{{\partial t}} = {\gamma _{\text{w}}}\frac{\partial }{{\partial t}}\left( {\frac{{\partial {u_x}}}{{\partial x}} + \frac{{\partial {u_z}}}{{\partial z}}} \right) 。$

(5)

式中： ${\gamma _{\text{w}}}$ 为孔隙流体的重度。

根据式（1），采用 ${\sigma^{\prime}_{xx}}$ ， ${\sigma{zz}^{\prime}_}$ 和τ_xz分别表示沿x方向和z方向的有效应力以及剪切应力，那么多孔弹性海床的整体平衡方程可以表示为

$\frac{{\partial {{\sigma^{\prime}}_{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{xz}}}}{{\partial z}} = - \frac{{\partial p}}{{\partial x}} \text{，}$

(6)

$\frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {{\sigma^{\prime}}_{zz}}}}{{\partial z}} = - \frac{{\partial p}}{{\partial z}} 。$

(7)

多孔弹性海床的本构关系可以表示为

$\left.\begin{array}{l}{{\sigma }^{\prime }}_{xx}=-\frac{2(1-\mu )G}{1-2\mu }\left(\frac{\partial {u}_{x}}{\partial x}+\frac{\mu }{1-\mu }\frac{\partial {u}_{z}}{\partial z}\right)\text{ }\text{，}\\ {{\sigma }^{\prime }}_{zz}=-\frac{2(1-\mu )G}{1-2\mu }\left(\frac{\mu }{(1-\mu )}\frac{\partial {u}_{x}}{\partial x}+\frac{\partial {u}_{z}}{\partial z}\right)\text{ }\text{，}\\ {\tau }_{xz}=-G\left(\frac{\partial {u}_{x}}{\partial z}+\frac{\partial {u}_{z}}{\partial x}\right)\text{ }。\end{array}\right\}$

(8)

式中：μ为泊松比；G为剪切模量。

1.2 边界条件

（1）海床表面的边界条件（z=0）

如图 1所示，海床表面的垂直有效应力和剪切应力趋于零，且海洋表面产生波浪运动引起的周期荷载：

${\sigma{zz}^{\prime}_} = {\tau _{xz}} = 0 \text{，} {p_{\text{f}}} = {p_{\text{b}}}(x,t) 。$

(9)

海床表面的波浪压力可以进一步表示为

${p_{\text{b}}}(x,t) = \sum\limits_{m = 1}^2 {{P_m}\cos } (mkx - m\omega t) \text{，}$

(10)

其中

${P_1} = \frac{{{\rho _{\text{f}}}gH}}{{2\cosh (kd)}} \text{，}$

(11)

${P_2} = \frac{3}{4}{\gamma _{\text{w}}}H\left( {\frac{{{\text{π }}H}}{L}} \right)\frac{1}{{\sinh (2kd)}}\left[ {\frac{1}{{{{\sinh }^2}(kd)}} - \frac{1}{3}} \right] 。$

(12)

式中： ${p_{\text{b}}}$ 为海床表面的周期荷载；m=1, 2，P₁和P₂分别为海床表面的一阶和二阶压力；k=2π/L为波数，由波长L确定；ω=2π/T为波的角频率，由周期T确定。

（2）海床底面的边界条件（z=-h）

如图 1所示，假定有限厚度海床的底面为刚性、不透水基岩，底部边界条件可以表示为

${u_x} = {u_z} = 0 \text{，} {{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial z}}} \right. } {\partial z}} = 0 。$

(13)

2. 海床动力响应求解

由于作用在海床表面的波浪荷载呈现周期性变化，因此未知场量同样随着波数k与角频率ω的变化产生周期性变化，可以基于Madsen^[14]求解过程中使用的复变量对该问题进行求解。同时，考虑到二阶Stokes波由不同阶次的波浪组成，因此可以将所有场量改写成由不同阶次求和的复变量形式：

$\left\{ {\begin{array}{*{20}{c}} {{u_x}(x,z,t)} \\ {{u_z}(x,z,t)} \\ {p(x,z,t)} \end{array}} \right\} = \sum\limits_{m = 1}^2 {{Re} \left\{ {\begin{array}{*{20}{c}} {U_x^{\left( m \right)}(z)} \\ {U_z^{\left( m \right)}(z)} \\ {{P^{\left( m \right)}}(z)} \end{array}} \right\}} {{\text{e}}^{{\text{i}}m\left( {kx - \omega t} \right)}} 。$

(14)

式中：i=(-1)^1/2为虚数；Re代表对结果取实部； $U_x^{\left( m \right)}$ 、 $U_z^{\left( m \right)}$ 和 ${P^{\left( m \right)}}$ 为波浪荷载引起的海床动力响应的幅值。值得注意的是，由于将场量拓展到复数域进行求解，因此仅取最后得到结果的实部进行分析。

波浪作用在海床表面的荷载在复数域可以表示为

${p_{\text{b}}}(x,t) = \sum\limits_{m = 1}^2 {{P_m}{{\text{e}}^{{\text{i}}m\left( {kx - \omega t} \right)}}} 。$

(15)

通过将场量表示为复变量形式，式（5），（6）和（8）可以分别改写为

$\frac{{{\partial ^2}{P^{\left( m \right)}}}}{{\partial {z^2}}} - \left( {{m^2}{k^2} - \frac{{{\gamma _{\text{w}}}n\beta }}{K}{\text{i}}m\omega } \right){P^{\left( m \right)}}$

$\begin{array}{*{20}{c}} {}&{}&{}&{} \end{array} = - \frac{{{\text{i}}m\omega {\gamma _{\text{w}}}}}{K}\left( {{\text{i}}mkU_x^{\left( m \right)} + \frac{{\partial U_z^{\left( m \right)}}}{{\partial z}}} \right) \text{，}$

(16)

${P^{\left( m \right)}} = - \left( {{{\sigma^{\prime}}_{xx}} + \frac{1}{{{\text{i}}mk}}\frac{{\partial {\tau _{xz}}}}{{\partial z}}} \right) \text{，}$

(17)

$\left.\begin{array}{l}{{\sigma }^{\prime }}_{xx}=-\frac{2(1-\mu )G}{1-2\mu }\left(\text{i}mk{U}_{x}^{\left(m\right)}+\frac{\mu }{1-\mu }\frac{\partial {U}_{z}^{\left(m\right)}}{\partial z}\right)\text{ }\text{，}\\ {{\sigma }^{\prime }}_{zz}=-\frac{2(1-\mu )G}{1-2\mu }\left(\frac{\mu }{1-\mu }\text{i}mk{U}_{x}^{\left(m\right)}+\frac{\partial {U}_{z}^{\left(m\right)}}{\partial z}\right)\text{ }\text{，}\\ {\tau }_{xz}=-G\left(\frac{\partial {U}_{x}^{\left(m\right)}}{\partial z}+\text{i}mk{U}_{z}^{\left(m\right)}\right)\text{ }。\end{array}\right\}$

(18)

将式（17）代入式（7）和式（16）可以分别得到

$\frac{{\partial {{\sigma^{\prime}}_{zz}}}}{{\partial z}} + {\text{i}}mk{\tau _{xz}} = \frac{{\partial {{\sigma^{\prime}}_{xx}}}}{{\partial z}} + \frac{1}{{{\text{i}}mk}}\frac{{{\partial ^2}{\tau _{xz}}}}{{\partial {z^2}}} \text{，}$

(19)

$\frac{{{\partial ^2}{{\sigma^{\prime}}_{xx}}}}{{\partial {z^2}}} + \frac{1}{{{\text{i}}mk}}\frac{{{\partial ^3}{\tau _{xz}}}}{{\partial {z^3}}} - \left( {{m^2}{k^2} - \frac{{{\gamma _{\text{w}}}n\beta }}{K}{\text{i}}m\omega } \right)\left( {{{\sigma^{\prime}}_{xx}} + \frac{1}{{{\text{i}}mk}}\frac{{\partial {\tau _{xz}}}}{{\partial z}}} \right) \\ \;\;\;\;\;\;\;\;\;\; = \frac{{{\text{i}}m\omega {\gamma _{\text{w}}}}}{K}\left( {{\text{i}}mkU_x^{(m)} + \frac{{\partial U_z^{(m)}}}{{\partial z}}} \right) 。$

(20)

将多孔弹性介质本构关系式（18）代入式（19），可以得到

$\frac{{{\partial ^2}U_z^{(m)}}}{{\partial {z^2}}} - {m^2}{k^2}U_z^{(m)} = \frac{1}{{{\text{i}}mk}}\left( {\frac{{{\partial ^3}U_x^{(m)}}}{{\partial {z^3}}} - {m^2}{k^2}\frac{{\partial U_x^{(m)}}}{{\partial z}}} \right) 。$

(21)

将式（7）代入式（20），可以得到

$\begin{array}{l} \left\{ {\frac{{{\partial ^3}U_z^{\left( m \right)}}}{{\partial {z^3}}} - {m^2}{k^2}\frac{{\partial U_z^{\left( m \right)}}}{{\partial z}} + } \right. \\ \left. {\frac{{{\text{i}}m\omega {\gamma _{\text{w}}}\left[ {n\beta + (1 - 2\mu )/G} \right]}}{K}\frac{{\partial U_z^{\left( m \right)}}}{{\partial z}}} \right\} \\ = - \frac{1}{{{\text{i}}mk}}\left\{ {(1 - 2\mu )\frac{{{\partial ^4}U_x^{\left( m \right)}}}{{\partial {z^4}}} - \left[ {2(1 - \mu ){m^2}{k^2} + (1 - 2\mu ) \cdot } \right.} \right. \\ {\text{ }}\left. {\left( {{m^2}{k^2} - \frac{{{\text{i}}m\omega {\gamma _{\text{w}}}n\beta }}{K}} \right)} \right]\frac{{{\partial ^2}U_x^{\left( m \right)}}}{{\partial {z^2}}} + \\ {m^2}{k^2}\left[ {2(1 - \mu ){m^2}{k^2} - {\text{i}}m\omega {\gamma _{\text{w}}} \cdot } \right. \\ \end{array}$

$\left. {\left. {\frac{{2n\beta (1 - \mu ) + (1 - 2\mu )/G}}{K}} \right]U_x^{\left( m \right)}} \right\} 。$

(22)

将式（21）代入式（22），可以得到

$\begin{array}{l} \frac{{\partial U_z^{\left( m \right)}}}{{\partial z}} = \frac{{2(1 - \mu )K}}{{{m^2}\omega k{\gamma _{\text{w}}}\left[ {n\beta + (1 - 2\mu )/G} \right]}} \times \\ \;\;\;\;\;\;\;\left\{ {\frac{{{\partial ^4}U_x^{\left( m \right)}}}{{\partial {z^4}}} - \left[ {2{m^2}{k^2} - \frac{{{\text{i}}m\omega {\gamma _{\text{w}}}n\beta }}{K}\frac{{(1 - 2\mu )}}{{2(1 - \mu )}}} \right]\frac{{{\partial ^2}U_x^{\left( m \right)}}}{{\partial {z^2}}} + } \right. \end{array} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{m^2}{k^2}({m^2}{k^2} - {\kappa ^2})U_x^{\left( m \right)}\left. \begin{gathered} \\ \\ \end{gathered} \right\} 。$

(23)

式中：

${\kappa ^2} = \frac{{{\text{i}}m\omega {\gamma _{\text{w}}}\left( {n\beta + \frac{{(1 - 2\mu )}}{{2G(1 - \mu )}}} \right)}}{K} 。$

(24)

将式（23）代入式（22），可以得到

$\frac{{{\partial ^6}U_x^{\left( m \right)}}}{{\partial {z^6}}} - {m^2}{k^2}\left( {3 - \frac{{{\kappa ^2}}}{{{m^2}{k^2}}}} \right)\frac{{{\partial ^4}U_x^{\left( m \right)}}}{{\partial {z^4}}} +$

${m^4}{k^4}\left( {3 - 2\frac{{{\kappa ^2}}}{{{m^2}{k^2}}}} \right)\frac{{{\partial ^2}U_x^{\left( m \right)}}}{{\partial {z^2}}} - {m^6}{k^6}\left( {1 - \frac{{{\kappa ^2}}}{{{m^2}{k^2}}}} \right)U_x^{\left( m \right)} = 0 。$

(25)

式（25）为六阶偏微分方程，该方程的解可以假设为

$U_x^{\left( m \right)} = A{{\text{e}}^{\gamma mkz}} 。$

(26)

将所假设的解式（26）代入式（25）中，可以得到

$({\gamma ^2} - 1)({\gamma ^2} - 1)\left( {{\gamma ^2} - 1 + \frac{{{\kappa ^2}}}{{{m^2}{k^2}}}} \right) = 0 。$

(27)

由式（27），可以得到 $U_x^{\left( m \right)}$ 的解析解为

${U}_{x}^{\left(m\right)}=({A}_{1}+{A}_{2}z){\text{e}}^{mkz}+({A}_{3}+{A}_{4}z){\text{e}}^{-mkz}+{A}_{5}{\text{e}}^{{k}_{*}mkz}+{A}_{6}{\text{e}}^{-{k}_{*}mkz}。$

(28)

式中： ${k_*}$ =[1-κ²/(mk)²]。

考虑到后续计算中矩阵求逆的正指数溢出问题，通过将式（28）重构为

$U_x^{\left( m \right)} = ({A_1} + {A_2}z){{\text{e}}^{mkz}} + {A_5}{{\text{e}}^{{k_*}mkz}} + ({A_3} + {A_4}z){{\text{e}}^{ - mk\left( {z + h} \right)}} +$

${A_6}{{\text{e}}^{ - {k_*}mk\left( {z + h} \right)}} 。$

(29)

将式（29）代入式（23），并对z求积分，可以得到 $U_z^{\left( m \right)}$ 的解析解为

$U_z^{\left( m \right)} = - {\text{i}}\left\{ {\left( {{A_1} + {A_2}z - \frac{{1 + 2\delta }}{{mk}}{A_2}} \right){{\text{e}}^{mkz}}{\text{ + }}{k_*}{A_5}{{\text{e}}^{{k_*}mkz}} - } \right.$

$\left. {\left( {{A_3} + {A_4}z + \frac{{1 + 2\delta }}{{mk}}{A_4}} \right){{\text{e}}^{ - mk\left( {z + h} \right)}} - {k_*}{A_6}{{\text{e}}^{ - {k_*}mk\left( {z + h} \right)}}} \right\} 。$

(30)

式中：

$\delta = \frac{{(1 - 2\mu )n\beta }}{{n\beta + {{(1 - 2\mu )} \mathord{\left/ {\vphantom {{(1 - 2\mu )} G}} \right. } G}}} 。$

(31)

同理可得孔隙水压力和有效应力的解析解为

${P^{\left( m \right)}} = 2G{\text{i}}\left\{ {\frac{{(\delta + 2\mu - 1)}}{{1 - 2\mu }}{A_2}{{\text{e}}^{mkz}} + \left[ {\frac{{(1 - \mu )(1 - k_*^2)}}{{1 - 2\mu }}} \right]mk{A_5}{{\text{e}}^{{k_*}mkz}} + } \right. \\ \left. {\frac{{1 - 2\mu - \delta }}{{1 - 2\mu }}{A_4}{{\text{e}}^{ - mk\left( {z + h} \right)}} + \frac{{(1 - \mu )(1 - k_*^2)}}{{1 - 2\mu }}mk{A_6}{{\text{e}}^{ - {k_*}mk\left( {z + h} \right)}}} \right\} \text{，}$

(32)

$\sigma_{x x}^{\prime(m)} = - 2G{\text{i}}\left\{ {mk{A_1}{{\text{e}}^{mkz}} + \frac{{(1 - 2\mu )mkz + 2\mu \delta }}{{1 - 2\mu }}{A_2}{{\text{e}}^{mkz}} + } \right.$

${\text{ }}\frac{{1 - \mu - \mu k_*^2}}{{1 - 2\mu }}mk{A_5}{{\text{e}}^{{k_*}mkz}} + mk{A_3}{{\text{e}}^{ - mk\left( {z + h} \right)}} +$

${\text{ }}\frac{{(1 - 2\mu )mkz - 2\mu \delta }}{{1 - 2\mu }}{A_4}{{\text{e}}^{ - mk\left( {z + h} \right)}} +$

$\left. {\frac{{1 - \mu - \mu k_*^2}}{{1 - 2\mu }}mk{A_6}{{\text{e}}^{ - {k_*}mk\left( {z + h} \right)}}} \right\} \text{，}$

(33)

$\begin{gathered} \sigma_{z z}^{\prime(m)} = 2G{\text{i}}\left\{ {mk{A_1}{{\text{e}}^{mkz}} - \left[ { - mkz + \frac{{2(1 - \mu )}}{{1 - 2\mu }}\delta } \right]{A_2}{{\text{e}}^{mkz}} - } \right. \\ {\text{ }}\frac{{\mu - (1 - \mu )k_*^2}}{{1 - 2\mu }}mk{A_5}{{\text{e}}^{{k_*}mkz}} + mk{A_3}{{\text{e}}^{ - mk\left( {z + h} \right)}} + \\ {\text{ }}\left[ {mkz + \frac{{2\delta (1 - \mu )}}{{1 - 2\mu }}} \right]{A_4}{{\text{e}}^{ - mk\left( {z + h} \right)}} - \\ \end{gathered}$

$\left. {\frac{{\mu - (1 - \mu )k_*^2}}{{1 - 2\mu }}mk{A_6}{{\text{e}}^{ - {k_*}mk\left( {z + h} \right)}}} \right\} \text{，}$

(34)

$\begin{gathered} \tau _{xz}^{\left( m \right)} = 2G\left\{ { - mk{A_1}{{\text{e}}^{mkz}} - (mkz - \delta ){A_2}{{\text{e}}^{mkz}} - {k_*}mk{A_5}{{\text{e}}^{{k_*}mkz}}} \right. + \\ {\text{ }}mk{A_3}{{\text{e}}^{ - mk\left( {z + h} \right)}} + (mkz + \delta ){A_4}{{\text{e}}^{ - mk\left( {z + h} \right)}} + \end{gathered} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left. {{k_*}mk{A_6}{{\text{e}}^{ - {k_*}mk\left( {z + h} \right)}}} \right\} 。$

(35)

式中：未知参数A₁~A₆可以代入边界条件（式（9），（13））确定，如下式所示：

$\left[\begin{array}{c}{A}_{1}\\ {A}_{2}\\ {A}_{3}\\ {A}_{4}\\ {A}_{5}\\ {A}_{6}\end{array}\right]={\left[\begin{array}{cccccc}{B}_{1}& -{B}_{2}& {B}_{1}{B}_{5}& {B}_{2}{B}_{5}& -{B}_{3}{B}_{1}& -{B}_{3}{B}_{1}{B}_{10}\\ -{B}_{1}& \delta & {B}_{1}{B}_{5}& \delta {B}_{5}& -{B}_{4}& {B}_{4}{B}_{10}\\ {B}_{5}& -{B}_{5}h& 1& -h& {B}_{10}& 1\\ {B}_{5}& -{B}_{5}h-{B}_{7}{B}_{5}& -1& h-{B}_{7}& {k}_{*}{B}_{10}& -{k}_{*}\\ 0& {B}_{8}{B}_{5}& 0& {B}_{8}& {B}_{9}{B}_{4}{B}_{10}& -{B}_{9}{B}_{4}\\ 0& 2G\text{i}{B}_{8}& 0& -2G\text{i}{B}_{8}{B}_{5}& 2G\text{i}{B}_{9}{B}_{1}& 2G\text{i}{B}_{9}{B}_{1}{B}_{10}\end{array}\right]}^{-1}\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ {p}_{b}\end{array}\right]。$

(36)

式中：

$\begin{array}{l} {B_1} = mk;{B_2} = \frac{{2\delta (1 - \mu )}}{{1 - 2\mu }};{B_3} = \frac{{\mu - (1 - \mu )k_*^2}}{{1 - 2\mu }};{B_4} = {k_*}mk; \\ {B_5} = {{\text{e}}^{ - mkh}};{B_6} = {{\text{e}}^{mkh}};{B_7} = \frac{{1 + 2\delta }}{{mk}};{B_8} = \frac{{\delta + 2\mu - 1}}{{1 - 2\mu }}; \end{array} \\ \;\;\;\; {B_9} = \frac{{(1 - \mu )(1 - k_*^2)}}{{1 - 2\mu }};{B_{10}} = {{\text{e}}^{ - {k_*}mkh}};{B_{11}} = {{\text{e}}^{{k_*}mkh}} 。$

(37)

3. 二阶Stokes波作用下海床动力响应分析

3.1 与既有解的对比

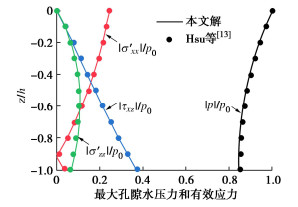
为了对比验证本文得到的二阶Stokes波作用下海床动力响应的解析解，本文分别给出了线性波和二阶Stokes波作用下的对比结果，对比结果中实线代表本文解析解，点代表既有解。首先通过选取与Hsu等^[13]一致的参数：T=15 s，d=70 m，L=324 m，h=25 m，G=10⁷ Pa，n=0.3，μ=1/3以及K=10^-2 m/s，将本文解析解与Hsu等^[13]得到的线性波作用下的解进行对比。由图 2可知本文解析解得到的孔隙水压力和有效应力曲线与Hsu等的曲线完全一致，从而可以证明本文解析解的正确与可靠。

图 2 线性波作用下本文解析解与Hsu等的解之间的对比

Figure 2. Comparison of seabed response between present solution and solution by Hsu et al. under linear waves

下载: 全尺寸图片幻灯片

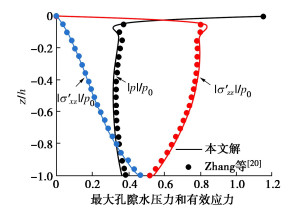
进一步地，将本文解析解与Zhang等^[20]二阶Stokes波作用下的解进行对比如图 3所示。对比中选用的参数与Zhang等一致：T=12 s，H=8 m，d=0.125L，h=24 m，S_r=0.975，n=0.35，μ=0.4，K=10^-4 m/s以及G=5×10⁶ Pa。对比结果表明本文解析解与Zhang等^[20]的解有良好的匹配性，进一步表明了本文解的正确性和可靠性。

图 3 二阶斯托克斯波作用下本文解析解与Zhang等的解之间的对比

Figure 3. Comparison of seabed response between present solution and solution by Zhang et al. under second-order Stokes waves

下载: 全尺寸图片幻灯片

3.2 波浪和海床参数对动力响应的影响

由二阶Stokes波作用在海床表面周期压力的表达式（10）~（12）可知，波浪的周期T、波高H以及水深d对二阶Stokes波的影响较大；而在对海床动力响应的求解过程中可知，海床土体的剪切模量G和渗透系数K同样会对海床的动力响应产生影响。为了探究波浪参数和海床土体参数对海床动力响应的影响，给出了如表 1所示的波浪和海床土体参数并进行算例计算和分析。在下列算例计算和分析中，没有提及的参数的取值均来源于表 1。

表 1 多孔弹性海床和波浪的基本参数

Table 1. Basic poroelastic properties and wave conditions

波浪和海床土参数	数值
波的周期T	10 s
波高H	5 m
水深d	0.125L^*
海床厚度h	20 m
孔隙流体的实际体积弹性模量K_w	2×10⁹ Pa
孔隙流体密度ρ_f	1000 kg/m³
孔隙率n	0.35
泊松比μ	0.33
渗透系数K	10^-4 m/s
剪切模量G	1×10⁷ Pa
海床土饱和度S_r	0.975
^*表中L代表波长。

下载: 导出CSV

| 显示表格

（1）波浪参数的影响

首先对波浪参数对海床动力响应的影响进行研究。图 4是二阶Stokes波作用下波浪周期T对海床动力响应的影响。其中波浪周期T的取值分别为8，9，10，11，12 s。从图 4中可以发现不同的波浪周期T对海床动力响应随深度方向z/h的变化趋势是一致的，还可以从图中发现：在海床相同深度z/h时，最大孔隙水压力|p|随着波浪周期T的增加而增加；最大水平有效应力|σ′_xx|在较浅区域随着波浪周期T的增加而减小，在较深区域则呈现相反的趋势；最大垂直有效应力|σ′_zz|和最大剪切应力|τ_xz|在较浅区域随着波浪周期T的增加而减小，在较深区域则存在转折点。同时还可以看出在相对水深d/L不变的情况下，波浪周期T越小，海床的动力响应受到二阶Stokes波的二阶项的影响越明显。

图 4 二阶Stokes波作用下波浪周期T对海床动力响应的影响

Figure 4. Influences of wave period on dynamic response of seabed under second-order Stokes waves

下载: 全尺寸图片幻灯片

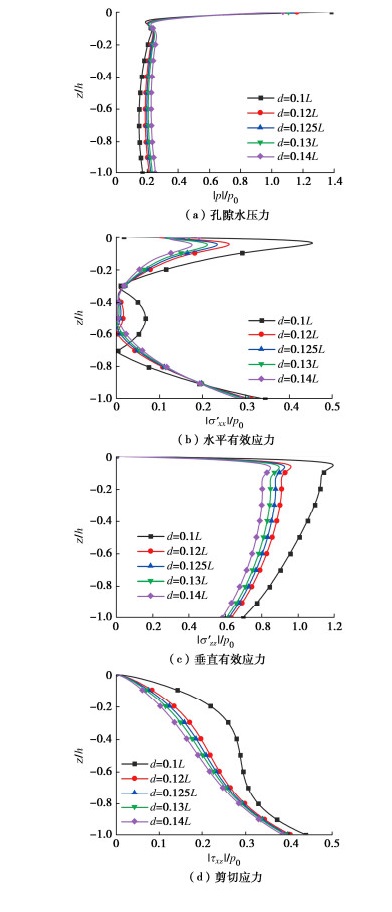
图 5是二阶Stokes波作用下水深d对海床动力响应的影响。Le Méhauté^[22]认为当水深d小于0.1L时，Stokes波不能严格满足自由水面的边界条件，故水深d的取值分别为：0.1L，0.12L，0.125L，0.13L，0.14L。从图 5可以得知水深d对海床的动力响应有明显的影响，同时水深d还对二阶Stokes波的二阶项引起的海床动力响应的大小有相当显著的影响。与波浪周期T的影响类似，海床动力响应随深度方向z/h的变化趋势是一致的。最大孔隙水压力|p|、最大水平有效应力|σ′_xx|、最大垂直有效应力|σ′_zz|和最大剪切应力|τ_xz|随着水深d的增加与波浪周期T增加时均表现出相似的规律。当波浪周期T不变时，随着相对水深d/L较小时（例如d/L=0.1），海床的动力响应受二阶Stokes波二阶项的影响有显著的影响。

图 5 二阶Stokes波作用下水深d对海床动力响应的影响

Figure 5. Influences of water depth on dynamic response of seabed under second-order Stokes waves

下载: 全尺寸图片幻灯片

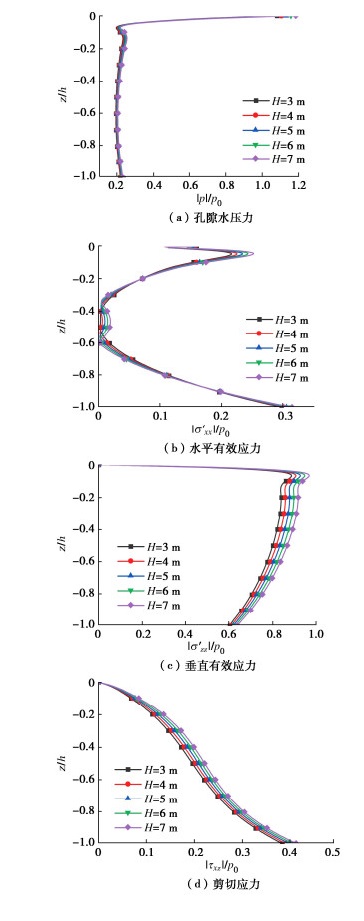
图 6是二阶Stokes波作用下波高H对海床动力响应的影响。其中波高H的取值分别为3，4，5，6，7 m。由图 6可以得知波高H对海床动力响应的影响较小。在海床的相同深度z/h处，最大孔隙水压力|p|、最大垂直有效应|σ′_zz|和最大剪切应力|τ_xz|均随着波高H的增大而增大。同时，波高H对二阶Stokes波二阶项引起的海床动力响应基本没有影响。

图 6 二阶Stokes波作用下波高H对海床动力响应的影响

Figure 6. Influences of seabed thickness on dynamic response of seabed under second-order Stokes waves

下载: 全尺寸图片幻灯片

（2）海床土体参数对海床动力响应的影响

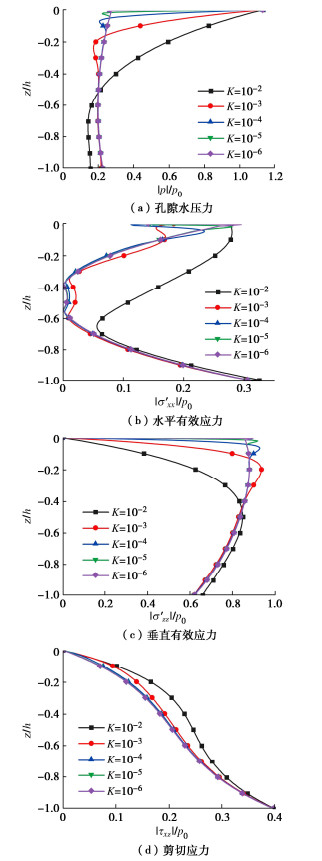
图 7是二阶Stokes波作用下渗透系数K对海床动力响应的影响。其中渗透系数K的取值分别为10^-2，10^-3，10^-4，10^-5，10^-6 m/s。由图 7可得：渗透系数K对海床的动力响应有显著的影响。渗透系数K对海床动力响应的影响体现在沿深度方向z/h的变化率上，随着渗透系数K的减小在深度较浅处的最大孔隙水压力|p|减小速率越快，最大垂直有效应力|σ′_zz|增大速率越快，而在较深区域这些场量的变化速率与渗透系数K的相关性减小。当渗透系数K较大时，最大水平有效应力|σ′_xx|和最大剪切应力|τ_xz|受到的影响较大，渗透系数K较小时对最大剪切应力|τ_xz|基本没有影响，且对最大水平有效应力|σ′_xx|的影响较小。

图 7 二阶Stokes波作用下渗透系数K对海床动力响应的影响

Figure 7. Influences of permeability on dynamic response of seabed under second-order Stokes waves

下载: 全尺寸图片幻灯片

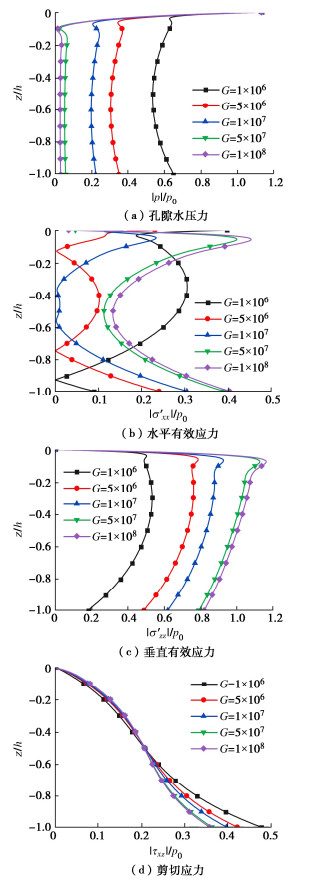
图 8是二阶Stokes波作用下剪切模量G对海床动力响应的影响。其中剪切模量G的取值分别为1×10⁶，5×10⁶，1×10⁷，5×10⁷，1×10⁸ Pa。从图 8中可以得出：剪切模量G对海床的动力响应有显著的影响。在海床的相同深度z/h处，最大孔隙水压力|p|和最大垂直有效应力|σ′_zz|随着剪切模量G的增大而分别减小和增大。而最大剪切应力|τ_xz|在深度z/h大约为0.5处存在一个转折点，在转折点以上的相同深度z/h处随着剪切模量G的增大而增大，在转折点以下则呈现相反的变化趋势，此现象可能是由于竖向和水平向有效应力状态改变引起的，即在z/h=0.5以下部分，水平有效应力出现了快速的增大而竖直有效应力出现了减小，在竖向偏应力状态改变的情况下，剪切应力状态呈现了相反的变化趋势。

图 8 二阶Stokes波作用下剪切模量G对海床动力响应的影响

Figure 8. Influences of shear modulus on dynamic response of seabed under second-order Stokes waves

下载: 全尺寸图片幻灯片

4. 结论

本文研究引入了二阶Stokes波理论模拟波浪荷载，考虑了波浪非线性的影响，最终建立了二阶Stokes波作用下有限厚度海床动力响应的解析解。并将本文得到的解析解与线性波既有解进行了对比，验证了本文解的正确性和可靠性。最后分析了波浪和海床土体参数对海床动力响应的影响。通过本文的研究主要得出以下3点结论。

（1）在相对水深d/L确定，波浪周期T较小时，以及波浪周期T确定，相对水深较小时，海床的动力响应受到二阶Stokes波的二阶项影响均增加。

（2）波浪周期T、水深d和波高H均会对海床的动力响应产生影响，但波高H对二阶Stokes波的二阶项引起的海床动力响应基本没有影响。

（3）海床土体的渗透系数K和剪切模量G均会对海床的动力响应有显著的影响。渗透系数K对海床动力响应的影响表现为沿深度方向的变化速率，而剪切模量G对海床动力响应体现为幅值大小的影响。

图 1 波浪和多孔弹性海床之间的动力相互作用

Figure 1. Dynamic interaction between ocean waves and poroelastic seabed

下载: 全尺寸图片幻灯片

图 2 线性波作用下本文解析解与Hsu等的解之间的对比

Figure 2. Comparison of seabed response between present solution and solution by Hsu et al. under linear waves

下载: 全尺寸图片幻灯片

图 3 二阶斯托克斯波作用下本文解析解与Zhang等的解之间的对比

Figure 3. Comparison of seabed response between present solution and solution by Zhang et al. under second-order Stokes waves

下载: 全尺寸图片幻灯片

图 4 二阶Stokes波作用下波浪周期T对海床动力响应的影响

Figure 4. Influences of wave period on dynamic response of seabed under second-order Stokes waves

下载: 全尺寸图片幻灯片

图 5 二阶Stokes波作用下水深d对海床动力响应的影响

Figure 5. Influences of water depth on dynamic response of seabed under second-order Stokes waves

下载: 全尺寸图片幻灯片

图 6 二阶Stokes波作用下波高H对海床动力响应的影响

Figure 6. Influences of seabed thickness on dynamic response of seabed under second-order Stokes waves

下载: 全尺寸图片幻灯片

图 7 二阶Stokes波作用下渗透系数K对海床动力响应的影响

Figure 7. Influences of permeability on dynamic response of seabed under second-order Stokes waves

下载: 全尺寸图片幻灯片

图 8 二阶Stokes波作用下剪切模量G对海床动力响应的影响

Figure 8. Influences of shear modulus on dynamic response of seabed under second-order Stokes waves

下载: 全尺寸图片幻灯片

表 1 多孔弹性海床和波浪的基本参数

Table 1 Basic poroelastic properties and wave conditions

波浪和海床土参数	数值
波的周期T	10 s
波高H	5 m
水深d	0.125L^*
海床厚度h	20 m
孔隙流体的实际体积弹性模量K_w	2×10⁹ Pa
孔隙流体密度ρ_f	1000 kg/m³
孔隙率n	0.35
泊松比μ	0.33
渗透系数K	10^-4 m/s
剪切模量G	1×10⁷ Pa
海床土饱和度S_r	0.975
^*表中L代表波长。

下载: 导出CSV

参考文献(22)

[1]	LI X B, ZHANG Z Q, PAN E N. Wave-induced dynamic response in a transversely isotropic and multilayered poroelastic seabed[J]. Soil Dynamics and Earthquake Engineering, 2020, 139: 106365. doi: 10.1016/j.soildyn.2020.106365
[2]	JENG D S. Review of liquefaction around marine structures by B mutlu sumer[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2015, 141(5): 07515001. doi: 10.1061/(ASCE)WW.1943-5460.0000296
[3]	PUTNAM J A. Loss of wave energy due to percolation in a permeable sea bottom[J]. Transactions, American Geophysical Union, 1949, 30(3): 349. doi: 10.1029/TR030i003p00349
[4]	BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid: Ⅰ low-frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28(2): 168-178. doi: 10.1121/1.1908239
[5]	SEKIGUCHI H, KITA K, OKAMOTO O. Response of poro-elastoplastic beds to standing waves[J]. Soils and Foundations, 1995, 35(3): 31-42. doi: 10.3208/sandf.35.31
[6]	BIOT M A. General theory of three-dimensional consolidation[J]. Journal of Applied Physics, 1941, 12(2): 155-164. doi: 10.1063/1.1712886
[7]	BIOT M A. Mechanics of deformation and acoustic propagation in porous media[J]. Journal of Applied Physics, 1962, 33(4): 1482-1498. doi: 10.1063/1.1728759
[8]	YAMAMOTO T, KONING H L, SELLMEIJER H, et al. On the response of a poro-elastic bed to water waves[J]. Journal of Fluid Mechanics, 1978, 87(1): 193-206. doi: 10.1017/S0022112078003006
[9]	MADSEN O S. Wave-induced pore pressures and effective stresses in a porous bed[J]. Géotechnique, 1978, 28(4): 377-393. doi: 10.1680/geot.1978.28.4.377
[10]	VERRUIJT A. Elastic storage of aquifers[M]// Flow through Porous Media. DE WIEST R J M. New York: Academic Press, 1969.
[11]	OKUSA S. Wave-induced stresses in unsaturated submarine sediments[J]. Géotechnique, 1985, 35(4): 517-532. doi: 10.1680/geot.1985.35.4.517
[12]	MEI C C, FODA M A. Wave-induced responses in a fluid-filled poro-elastic solid with a free surface: a boundary layer theory[J]. Geophysical Journal International, 1981, 66(3): 597-631. doi: 10.1111/j.1365-246X.1981.tb04892.x
[13]	HSU J R C, JENG D S. Wave-induced soil response in an unsaturated anisotropic seabed of finite thickness[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1994, 18(11): 785-807. doi: 10.1002/nag.1610181104
[14]	ZIENKIEWICZ O C, CHANG C T, BETTESS P. Drained, undrained, consolidating and dynamic behaviour assumptions in soils[J]. Géotechnique, 1980, 30(4): 385-395. doi: 10.1680/geot.1980.30.4.385
[15]	ULKER M B C, RAHMAN M S, JENG D S. Wave-induced response of seabed: various formulations and their applicability[J]. Applied Ocean Research, 2009, 31(1): 12-24. doi: 10.1016/j.apor.2009.03.003
[16]	LAUTON G, PATTIARATCHI C B, LENTINI C A D. Observations of breaking internal tides on the australian north west shelf edge[J]. Frontiers in Marine Science, 2021, 8: 629372. doi: 10.3389/fmars.2021.629372
[17]	王忠涛, 栾茂田, 刘占阁, 等. 浅水区波浪非线性效应对砂质海床动力响应的影响[J]. 海洋工程, 2005, 23(1): 41-46. doi: 10.3969/j.issn.1005-9865.2005.01.007 WANG Zhongtao, LUAN Maotian, LIU Zhange, et al. Studies on the effect of non-linear wave loading in shallow water region on dynamic response of sandy seabed[J]. The Ocean Engineering, 2005, 23(1): 41-46. (in Chinese) doi: 10.3969/j.issn.1005-9865.2005.01.007
[18]	郭秀军, 朱大伟, 孟庆生, 等. 波浪作用下黄河口多层粉质土海床动力响应特征差异性分析[J]. 岩土工程学报, 2012, 34(12): 2270-2276. http://cge.nhri.cn/article/id/14954 GUO Xiujun, ZHU Dawei, MENG Qingsheng, et al. Differences in dynamic response characteristics of multi-layer silty seabed under waves in Yellow River Estuary[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(12): 2270-2276. (in Chinese) http://cge.nhri.cn/article/id/14954
[19]	ZHOU X L, XU B, WANG J H, et al. An analytical solution for wave-induced seabed response in a multi-layered poro-elastic seabed[J]. Ocean Engineering, 2011, 38(1): 119-129. doi: 10.1016/j.oceaneng.2010.10.003
[20]	ZHANG Z Q, ZHOU B H, LI X B, et al. Second-order Stokes wave-induced dynamic response and instantaneous liquefaction in a transversely isotropic and multilayered poroelastic seabed[J]. Frontiers in Marine Science, 2022, 9: 1082337. doi: 10.3389/fmars.2022.1082337
[21]	周晓智, 陈育民, 刘汉龙. 驻波作用下有限厚度海床动应力路径特性研究[J]. 岩土工程学报, 2018, 40(5): 890-899. doi: 10.11779/CJGE201805014 ZHOU Xiaozhi, CHEN Yumin, LIU Hanlong. Study on characteristics of dynamic stress path of finite-thickness seabed under standing waves[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 890-899. (in Chinese) doi: 10.11779/CJGE201805014
[22]	LEMÉHAUTÉ B. An Introduction to Hydrodynamics and Water Waves[M]. New York: Springer-Verlag, 1976.