考虑温度与围压影响的冻结砂土非正交弹塑性本构模型

梁靖宇; 齐吉琳; 张跃东; 路德春; 李昊雯

doi:10.11779/CJGE20230455

考虑温度与围压影响的冻结砂土非正交弹塑性本构模型 English Version

1.
北京建筑大学土木与交通工程学院, 北京 100044
2.
北京工业大学城市与工程安全减灾教育部重点试验室, 北京 100124

基金项目:

国家自然科学基金项目 52108294

国家自然科学基金项目 41972279

国家自然科学基金项目 52025084

北京建筑大学金字塔人才培养工程项目 JDYC20220812

详细信息

作者简介:
梁靖宇(1988—)，男，博士，副研究员，主要从事岩土材料工程特性及其本构理论方面的教学与科研工作。E-mail: liangjy@bucea.edu.cn

通讯作者:
齐吉琳, E-mail: jilinqi@bucea.edu.cn

中图分类号: TU43
计量
- 文章访问数: 439
- HTML全文浏览量: 69
- PDF下载量: 110
出版历程
- 收稿日期: 2023-05-22
- 网络出版日期: 2024-03-24
- 刊出日期: 2024-08-31

Non-orthogonal elastoplastic model for frozen sand incorporating effects of temperature and confining pressure

1.
School of Civil and Transportation Engineering, Beijing University of Civil Engineering and Architecture, Beijing 100044, China
2.
Key Lab of Urban Security and Disaster Engineering, Ministry of Education, Beijing University of Technology, Beijing 100124, China

摘要

摘要: 冻土的受力变形特性受温度与围压的影响显著。为描述温度的影响，通过建立冻土三向拉伸强度与温度的非线性关系，并采用平移变换的方法将其考虑到屈服函数中。为描述围压的影响，通过建立潜在强度衰减因子，并将其引入统一硬化参量中，发展得出了考虑围压影响的硬化参量。最终，基于非正交弹塑性模型框架，在平移变换应力空间内建立了能够考虑温度和围压影响的冻土非正交弹塑性本构模型。模型预测结果与冻结粉砂三轴压缩试验结果的对比表明，所建立模型能够模拟不同温度和围压下冻结砂土应力–应变关系。其不仅能够反映冻土峰值抗剪强度随温度降低而增大的温度效应，还能描述围压增大条件下应力应变曲线由剪胀与软化型逐渐转变为剪缩与硬化型的规律。
- 冻土 /
- 本构模型 /
- 非正交塑性流动法则 /
- 温度效应 /
- 围压效应
Abstract: The mechanical properties of frozen soils are significantly affected by temperature and confining pressure. To characterize the effects of temperature, a nonlinear relationship between the three-dimensional tensile strength and the temperature is established, which is incorporated into the yield function based on the coordinate transformation method. To characterize the effects of confining pressure, a potential strength degradation factor is established, which is used to develop the hardening parameters that effectively account for the effects of the confining pressure. Finally, based on the framework of the non-orthogonal elastoplastic model, a non-orthogonal elastoplastic constitutive model for frozen soils that can consider the effects of temperature and confining pressure is developed in the coordinate transformation space. Comparisons between the model predictions and the triaxial compression test results of the frozen silty sand demonstrate that the developed constitutive model can simulate the stress-strain relationship of frozen silty sand under different temperatures and confining pressures. The developed constitutive model characterizes the temperature effects, i.e., the increase in the peak shear strength with decreasing temperature, and the confining pressure effects, i.e., the transition from shear dilation and softening to shear contraction and hardening as reflected by the stress-strain curve under the increasing confining pressure.
- frozen soil /
- constitutive model /
- non-orthogonal plastic flow rule /
- temperature effect /
- confining pressure effect

HTML全文

0. 引言

冻土是在温度低于冰点条件下土颗粒被孔隙冰所胶结的特殊岩土材料。中国是冻土大国，多年冻土与季节性冻土约占国土面积的21.5%与53.5%^[1-2]。由于国家发展的需要，很多已建或在建的重大工程穿越冻土区^{[1, 3]}。同时，在城市地下工程中，冻结法施工工艺常用于富水以及复杂地质条件下的地层隔水与变形控制。在寒区重大工程与城市冻结法施工工程中，地基与围岩均以冻土作为工程赋存条件的主体。因此，深入认识与合理描述冻土的受力变形行为是寒区工程建设与城市冻结法施工工程所面临的迫切需要。

与融土相比，冻土最大的特点是土颗粒被孔隙冰所胶结，冻土所受外荷载主要由土颗粒与孔隙冰共同承担。因此，影响土颗粒与孔隙冰的因素都会影响冻土的受力变形特性，包括温度、围压、含水率、加载速率以及含盐量等^[4-8]。已有研究表明，这些因素中的温度与围压对冻土工程特性影响最为显著，同时也是研究其它因素影响的基础。随着温度降低，冻土中孔隙冰的黏聚力增强，其抗剪强度呈现出增大趋势，即冻土表现出显著的温度效应^[9-10]。而对某一负温条件下的冻土，围压的增大使冻土中裂缝与孔隙的发展受到限制，并增大了颗粒间的摩擦力，从而提高冻土的抗剪强度^[11]；同时，恒定负温条件下冻土的变形特性试验研究^[12]表明，冻土存在等效前期固结压力，当平均应力低于等效前期固结压力时，冻土表现出软化与剪胀特性，而随着平均应力增大，冻土的软化与剪胀特性减弱；当平均应力条件超过等效前期固结压力时，冻土在剪切荷载作用下主要表现为硬化与剪缩特性，这主要体现了冻土的围压效应。而随着温度的降低，冻土的等效前期固结压力也表现出增大的趋势^[13]。合理考虑温度和围压对冻土变形的显著影响是建立冻土本构模型及描述其它因素影响的基础^{[3, 14-15]}。

已有冻土本构理论方面的研究已经从非线性弹性模型、亚塑性模型、二元介质模型^[16]以及弹塑性模型等方面描述冻土的温度效应与围压效应。其中，弹塑性理论由于物理概念清晰、模型框架逻辑严谨，且有许多已有融土弹塑性模型作为借鉴，在建立冻土模型过程中表现出了明显的优势。研究者们在弹塑性力学框架内进行了不同的尝试，如基于临界状态冻土本构模型^[17]、多屈服面模型^[18]以及超塑性模型^[12]等。建立弹塑性本构模型的核心就是确定塑性应变增量，包括塑性应变增量的方向与大小两个方面。在确定冻土的塑性应变增量方向过程中，为了简化模型，很多研究者采用相关联流动法则^{[17, 19]}，即采用塑性势函数与屈服函数相同的方式。但Lai等^[17]理论研究表明，基于相关联流动法则的本构模型难以合理预测冻土材料的剪胀规律。Yang等^[20]采用非关联流动法则，根据试验规律构造出冻结粉土塑性势函数的方式，使塑性应变增量方向与屈服面之间非正交，所建立模型能够较好地预测试验结果。然而塑性势函数难以直接通过试验结果进行构造，并且可能引入物理意义不明确的参数，从而使建立本构模型的过程变得复杂。对于相关联流动法则和非关联流动法则，一个共同的特点是采用了一阶导数，塑性方向的计算限制在可微函数的正交梯度上，因此，它们也可以称为正交流动法则。Lu等^[21-22]将分数阶微分与协变变换相结合提出了非正交塑性流动法则，其直接基于屈服函数确定与屈服面非正交的塑性应变增量方向，避免了构建塑性势函数的难题。非正交流动法则在描述岩土材料塑性变形的优势越来越明显，已经被用于发展不同岩土材料的弹塑性本构模型^[23-26]中。然而，基于非正交流动法则建立冻土的弹塑性本构模型还需要进一步考虑冻土的特殊性质，尚需进一步深入探索。

在确定塑性应变增量的过程中，除确定其方向外，还需要确定其大小。塑性应变增量的大小一般利用塑性标量因子描述，其通过一致性条件确定。因此，合理的屈服函数与硬化参量至关重要。为了描述冻土的温度效应，研究者通常建立三向拉伸强度^[27]或低温吸力^[19]与温度之间的联系，并将三向拉伸强度或低温吸力引入到屈服函数中，以模拟温度变化对冻土屈服特性的影响。为了描述冻土的围压效应，研究者通常构造相应的硬化参量或采用多个屈服面，以模拟围压条件对冻土变形特性的影响。Lai等^[17]用单屈服面描述冻土的屈服特性，采用塑性功为硬化参量，该硬化参量可以描述冻土的硬化/软化现象，并建立了冻结砂土的弹塑性本构模型。在多屈服面模型中，Sun等^[19]采用屈服面、参考屈服面和统一硬化参量建立了考虑低温吸力的冻土多屈服面本构模型。Lai等^[18]基于广义塑性力学建立了冻土多屈服面本构模型，并构造不同机理的屈服函数与相应的硬化参量描述冻土的硬化/软化、剪缩/剪胀特性。由上述研究可知，温度效应和围压效应的合理描述对冻土本构模型的建立至关重要，如何对其进行合理地考虑是需要持续探索的问题。

本文采用平移变换的方法将冻土的三向拉伸强度 ${\sigma _0}$ 引入屈服函数中，在平移变换应力空间中描述冻土的屈服特性；采用了非正交流动法则与平移变换应力空间中的屈服函数相结合的方式，确定了塑性应变增量方向；通过建立冻土的潜在强度衰减因子，发展了统一硬化参量，用于确定塑性应变增量大小。最终，在平移变换应力空间中确定了冻土的塑性应变增量，并利用所建模型对不同温度和围压下冻结粉砂的三轴剪切试验进行了预测，验证了模型的合理性。

1. 冻土非正交弹塑性本构模型的建立

根据弹塑性理论可知，冻土的总应变增量可以分解为弹性应变增量 ${\text{d}}\varepsilon _{ij}^{\text{e}}$ 与塑性应变增量 ${\text{d}}\varepsilon _{ij}^{\text{p}}$ ，即

${\text{d}}{\varepsilon _{ij}} = {\text{d}}\varepsilon _{ij}^{\text{e}}{\text{ + d}}\varepsilon _{ij}^{\text{p}}。$

(1)

式中： ${\text{d}}\varepsilon _{ij}^{\text{e}}$ 可利用弹性Hooke定律确定； ${\text{d}}\varepsilon _{ij}^{\text{p}}$ 利用塑性理论确定。

1.1 弹性应变增量

为了简单地确定冻土弹性应变增量 ${\text{d}}\varepsilon _{ij}^{\text{e}}$ ，本文采用了与修正剑桥模型相同的确定方法。根据Hooke定律可知， ${\text{d}}\varepsilon _{ij}^{\text{e}}$ 可表达为

${\text{d}}\varepsilon _{ij}^{\text{e}} = \frac{{1 + \nu }}{E}{\text{d}}{\sigma _{ij}} - \frac{\nu }{E}{\text{d}}{\sigma _{kk}}{\delta _{ij}} 。$

(2)

式中： $\nu$ 为泊松比；E为弹性模量。由式（2）可知，弹性体积变形增量 ${\text{d}}\varepsilon _{\text{v}}^{\text{e}}$ 可表示为

${\text{d}}\varepsilon _{\text{v}}^{\text{e}} = \frac{{3(1 - 2\nu )}}{E}{\text{d}}p 。$

(3)

基于e-lnp坐标中的等向压缩线与卸载线，可得弹性体应变增量的表达式：

$\varepsilon _{\text{v}}^{\text{e}} = \frac{\kappa }{{1 + {e_{\text{0}}}}}\ln \frac{p}{{{p_0}}} 。$

(4)

式中：κ为回弹再加载曲线的斜率；e₀为初始孔隙比； ${p_0}$ 为初始平均应力。对式（4）两侧求微分可得

${\text{d}}\varepsilon _{\text{v}}^{\text{e}} = \frac{\kappa }{{1 + {e_{\text{0}}}}}\frac{{{\text{d}}p}}{p} 。$

(5)

对比式（3）和式（5），可得弹性模量E的表达式：

$E{\text{ = }}\frac{{3(1 - 2\nu )(1 + {e_{\text{0}}})}}{\kappa }p 。$

(6)

1.2 塑性应变增量

塑性应变增量 ${\text{d}}\varepsilon _{ij}^{\text{p}}$ 实际上是一个空间矢量，可表示为塑性应变增量大小与方向的乘积。在弹塑性理论框架内， ${\text{d}}\varepsilon _{ij}^{\text{p}}$ 的表达式为

${\text{d}}\varepsilon _{ij}^{\text{p}} = \Lambda \cdot {m_{ij}}。$

(7)

式中：Λ为塑性标量因子，反映了塑性应变增量的大小，可通过一致性条件确定；m_ij为塑性流动方向，用于描述塑性应变增量的方向，在本文中利用非正交塑性流动法则确定。

对于冻结砂土，其受力变形特性受到孔隙冰胶结作用的显著影响，因此，应在屈服方程中考虑三向拉伸强度的影响。这里引入坐标平移变换的方法^[28]，其可以利用平移变换应力空间中的简单屈服函数直接考虑普通应力空间中三向拉伸强度对屈服特性的影响。平移变换应力与普通应力之间的关系可以表示为

${\bar \sigma _{ij}}{\text{ = }}{\sigma _{ij}} + {\sigma _0}{\delta _{ij}}。$

(8)

式中： ${\bar \sigma _{ij}}$ 为平移变换应力空间的应力， ${\sigma _{ij}}$ 为普通应力， ${\sigma _0}$ 为岩土材料的三向拉伸强度。

基于平移变换应力的定义式（8），冻土的屈服函数可以表示为

$f = {\bar q^2} + {\zeta ^2}{M^2}({\bar p^2} - {\bar p_x}\bar p) = 0。$

(9)

式中： $\bar p$ 和 $\bar q$ 为平移变换空间的平均应力和广义剪应力； ${\bar p_x}$ 为等效平均应力，其与硬化参量之间的关系为

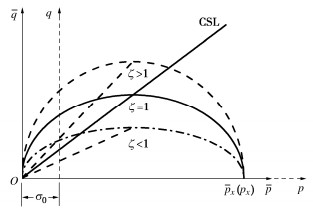
${\bar p_x} = {\bar p_0}\exp \left( {\frac{{1 + {e_0}}}{{\lambda - \kappa }}H} \right) 。$

(10)

式中：H为硬化参量，将由下节给出；λ为e-lnp坐标中的等向压缩线的斜率； ${\bar p_0}$ 为平移变换应力空间内初始等效固结压力。 ${\bar p_x}$ 描述的是屈服面与 $\bar p$ 轴交点处的平均应力，可由屈服面上任一应力点确定，即 ${\bar p_x} = {\bar q^2}/({\zeta ^2}{M^2}\bar p) + \bar p$ ；M为临界状态线的斜率； $\zeta$ 为控制椭圆形屈服面纵轴与横轴比值的参数，如所示。改进的屈服面将会有3种情况：当 $\zeta$ > 1时，临界应力线处于椭圆顶点的下方；当 $\zeta$ < 1时，临界应力线处于椭圆顶点的上方；当 $\zeta$ =1时，临界应力线过椭圆的顶点。

图 1 在不同应力空间的冻土屈服曲线

Figure 1. Yield curves for frozen soils in different stress spaces

下载: 全尺寸图片幻灯片

（1）塑性应变增量的方向

已有研究表明^{[17, 20]}，冻土的塑性应变增量方向与屈服面是非正交的，因此，本文采用了Lu等^[21-22]提出的非正交塑性流动法则直接基于冻土的屈服函数确定塑性流动方向。m_ij可以表示为

${m_{ij}} = \frac{{{\partial ^\mu }f}}{{\partial \bar S_{kl}^\mu }}\frac{{\partial {{\bar S}_{kl}}}}{{\partial {{\bar \sigma }_{ij}}}} 。$

(11)

式中：f为冻土的屈服函数； ${\bar S_{kl}}$ 为构成屈服函数的应力参量，由 ${\bar \sigma _{ij}}$ 构成； ${\partial ^\mu }f/\partial \bar S_{kl}^\mu$ 为屈服函数对 ${\bar S_{kl}}$ 的分数阶微分，μ为微分阶次。本文选用Riemann-Liouville（R-L）型分数阶微分^[24-25]计算，其定义如下：

$_a^{{\text{RL}}}D_x^\mu f(x) = \frac{1}{{\Gamma (n - \mu )}}\frac{{{{\text{d}}^n}}}{{{\text{d}}{x^n}}}\left[ {\int_a^x {{{(x - r)}^{n - \mu - 1}}f(r){\text{d}}r} } \right] 。$

(12)

式中：n为大于分数阶次μ的最小整数，即n = [μ]+1；Γ(z)为gamma函数，其表达式为( $\Gamma (z) = \int {_0^\infty } {e^{ - \tau }}{\tau ^{z - 1}}{\text{d}}\tau$ )。通过协变变换可以将 $(\bar p,\bar q)$ 坐标系中的塑性应变增量方向转化到 ${\bar \sigma _{ij}}$ 坐标系，因此，式（11）可进一步表达为

${m_{ij}} = \frac{{{\partial ^\mu }f}}{{\partial {{\bar p}^\mu }}}\frac{{\partial \bar p}}{{\partial {{\bar \sigma }_{ij}}}} + \frac{{{\partial ^\mu }f}}{{\partial {{\bar q}^\mu }}}\frac{{\partial \bar q}}{{\partial {{\bar \sigma }_{ij}}}} 。$

(13)

基于R-L型分数阶微分定义，求解屈服函数f对 $\bar p$ 和 $\bar q$ 的分数阶微分，并结合 ${\bar p_x} = {\bar q^2}/({\zeta ^2}{M^2}\bar p) + \bar p$ ，求得( $\bar p$ , $\bar q$ )坐标系中的塑性流动方向：

$\left.\begin{array}{l}\frac{{\partial }^{\mu }f}{\partial {\overline{p}}^{\mu }}=\frac{({\mu }^{2}-2\mu ){\overline{q}}^{2}+\mu {\zeta }^{2}{M}^{2}{\overline{p}}^{2}}{\Gamma (3-\mu ){\overline{p}}^{\mu }}\text{ }\text{，}\\ \frac{{\partial }^{\mu }f}{\partial {\overline{q}}^{\mu }}=\frac{(3\mu -{\mu }^{2}){\overline{q}}^{\text{2}-\mu }}{\Gamma (3-\mu )}\text{ }。\end{array}\right\}$

(14)

式（13）中应力参量 $(\bar p,\bar q)$ 和普通应力张量 ${\bar \sigma _{ij}}$ 之间的协变变换系数可表示为

$\left\{\begin{array}{l}\frac{\partial \overline{p}}{\partial {\overline{\sigma }}_{ij}}=\frac{1}{3}{\delta }_{ij}\text{ }\text{，}\\ \frac{\partial \overline{q}}{\partial {\overline{\sigma }}_{ij}}=\frac{3\text{(}{\overline{\sigma }}_{ij}-\overline{p}{\delta }_{ij}\text{)}}{2\overline{q}}\text{ }。\end{array}\right.$

(15)

将式（14）和式（15）代入式（13），即可得到塑性应变增量的方向m_ij的张量表达式为

$\begin{array}{l}{m_{ij}} =& \frac{{({\mu ^2} - 2\mu ){{\bar q}^2} + \mu {\zeta ^2}{M^2}{{\bar p}^2}}}{{3\Gamma (3 - \mu ){{\bar p}^\mu }}}{\delta _{ij}} + \\ & \frac{{{\text{(}}3\mu - {\mu ^2}{\text{)}}{{\bar q}^{{\text{2}} - \mu }}}}{{\Gamma (3 - \mu )}}\frac{{3({{\bar \sigma }_{ij}} - \bar p{\delta _{ij}})}}{{2\bar q}} 。 \end{array}$

(16)

（2）塑性应变增量的大小

确定塑性应变增量的大小不仅需要屈服函数，还需要能合理反映材料特性的硬化参量。本文以单屈服面为基础，参考姚仰平等^[29-30]的研究工作，将其硬化参量扩展用于描述冻土硬化规律，表达式如下：

$H = \int {\frac{{M_{\text{f}}^{\text{4}} - {{\bar \eta }^4}}}{{{M^4} - {{\bar \eta }^4}}}{\text{d}}\varepsilon _{\text{v}}^{\text{p}}} 。$

(17)

式中： $\bar \eta$ 为平移变换应力空间中的应力比，具体表达式为 $\bar \eta = {{\bar q} \mathord{\left/ {\vphantom {{\bar q} {\bar p}}} \right. } {\bar p}}$ ；M_f被定义为冻土的潜在破坏应力比。土的三轴试验结果^{[17, 31]}与CT扫描试验结果^[32-33]表明，冻土剪应变的增大使其材料内部结构与性质发生劣化，冻土的抗剪能力降低。这体现了冻土的潜在应力比M_f随剪应变的发展而逐渐退化衰减的规律。基于此，本文构建了用于描述冻土M_f衰减规律的强度衰减因子ω，表达式为

$\omega = \exp \left[ {\chi {{\left( {\frac{{\varepsilon _{\text{d}}^{\text{p}}}}{{\varepsilon _{{\text{dr}}}^{\text{p}}}}} \right)}^2}} \right]。$

(18)

式中： $\varepsilon _{{\text{dr}}}^{\text{p}}$ 为参考塑性剪应变；χ为反映M_f衰减速度的参数。随着加载的进行，塑性剪应变逐渐增大，M_f逐渐减小直至达到临界应力比M。M_f的这一变化规律可以通过下式进行描述：

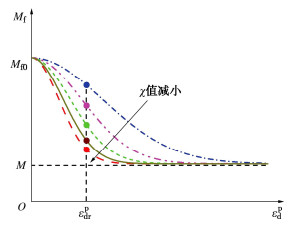
${M_{\text{f}}} = \omega ({M_{{\text{f0}}}} - M) + M。$

(19)

式中：M_f0为冻土的初始潜在应力比。图 2所示为M_f随 $\varepsilon _{\text{d}}^{\text{p}}$ 增大而减小的变化规律。由图 2可知，χ值将影响M_f的衰减速度，χ值越小，M_f衰减速度越大。当 $\varepsilon _{{\text{dr}}}^{\text{p}}$ 和χ确定时，潜在应力比的衰减规律即可确定。

图 2 潜在破坏应力比M_f的演化规律

Figure 2. Evolution of potential strength M_f

下载: 全尺寸图片幻灯片

确定了屈服函数和硬化参量后，即可通过一致性条件确定塑性标量因子。根据一致性条件，对屈服函数式（9）求全微分得

${\text{d}}f = \frac{{\partial f}}{{\partial \bar p}}{\text{d}}\bar p + \frac{{\partial f}}{{\partial \bar q}}{\text{d}}\bar q{\text{ + }}\frac{{\partial f}}{{\partial H}}\frac{{\partial H}}{{\partial \varepsilon _{\text{v}}^{\text{p}}}}{\text{d}}\varepsilon _{\text{v}}^{\text{p}} = 0 。$

(20)

将式（7）代入式（20），可以求得塑性标量因子：

$\Lambda = - \frac{{\frac{{\partial f}}{{\partial \bar p}}{\text{d}}\bar p + \frac{{\partial f}}{{\partial \bar q}}{\text{d}}\bar q}}{{\frac{{\partial f}}{{\partial H}}\frac{{\partial H}}{{\partial \varepsilon _{\text{v}}^{\text{p}}}}{m_{\text{p}}}}}。$

(21)

式中： ${m_{\text{p}}}$ 为塑性体变增量 ${\text{d}}\varepsilon _{\text{v}}^{\text{p}}$ 对应的塑性流动方向，由式（14）确定。式（20）中各项偏导数可根据屈服函数式（9）与式（10）确定，进一步结合 ${\bar p_x} = {\bar q^2}/$ $({\zeta ^2}{M^2}\bar p) + \bar p$ ，可得

$\frac{{\partial f}}{{\partial \bar p}} = \frac{{{\zeta ^2}{M^2}{{\bar p}^2} - {{\bar q}^2}}}{{\bar p}}{\text{ }},{\text{ }}\frac{{\partial f}}{{\partial \bar q}} = 2\bar q \text{，}$

(22)

$\frac{{\partial f}}{{\partial H}}\frac{{\partial H}}{{\partial \varepsilon _{\text{v}}^{\text{p}}}} = - \frac{1}{{{l_{\text{p}}}}}\left[ {{{\bar q}^2} + {\zeta ^2}{M^2}{{\bar p}^2}} \right]\frac{{M_{\text{f}}^{\text{4}} - {{\bar \eta }^4}}}{{{M^4} - {{\bar \eta }^4}}}。$

(23)

将式（22），（23）代入式（21），可得塑性标量因子Λ的表达式：

$\Lambda = {l_{\text{p}}}\frac{{{M^4} - {{\bar \eta }^4}}}{{M_{\text{f}}^4 - {{\bar \eta }^4}}}\frac{{({\zeta ^2}{M^2}{{\bar p}^2} - {{\bar q}^2}){\text{d}}\bar p + 2\bar q\bar p{\text{d}}\bar q}}{{\bar p\left[ {{{\bar q}^2} + {\zeta ^2}{M^2}{{\bar p}^2}} \right]{m_{\text{p}}}}} 。$

(24)

将式（16），（24）代入式（7），即可得出塑性应变增量 ${\text{d}}\varepsilon _{ij}^{\text{p}}$ 的表达式：

$\begin{array}{l} {\text{d}}\varepsilon _{ij}^{\text{p}} = & {l_{\text{p}}}\frac{{{M^4} - {{\bar \eta }^4}}}{{M_{\text{f}}^4 - {{\bar \eta }^4}}}\frac{{({\zeta ^2}{M^2}{{\bar p}^2} - {q^2}){\text{d}}\bar p + 2\bar q\bar p{\text{d}}\bar q}}{{\bar p\left[ {{{\bar q}^2} + {\zeta ^2}{M^2}{{\bar p}^2}} \right]}} \cdot \\ & \left( {\frac{1}{3}{\delta _{ij}} + \frac{{3(3 - \mu ){{\bar q}^{1 - \mu }}{{\bar p}^\mu }({\sigma _{ij}} - \bar p{\delta _{ij}})}}{{2(\mu - 2){{\bar q}^2} + 2{\zeta ^2}{M^2}{{\bar p}^2}}}} \right) 。 \end{array}$

(25)

根据式（1），将式（2）中的弹性应变增量与式（25）中的塑性应变增量相叠加，即可得出冻土非正交弹塑性模型的应力应变关系式。

1.3 模型参数与确定方法

冻结砂土的非正交弹塑性本构模型共有9个参数，其中4个参数（ $\lambda$ ，κ，υ和M）与修正剑桥模型中的参数相同，可通过冻土的等向压缩与回弹试验、三轴剪切试验确定。模型参数还包括 ${\sigma _0}$ ，M_f0， $\varepsilon _{{\text{dr}}}^{\text{p}}$ ，χ，μ，确定方法如下：

冻土三向拉伸强度 ${\sigma _0}$ 与温度直接相关。某一温度条件下的 ${\sigma _0}$ 可根据p-q坐标系中冻土达到临界状态时的抗剪强度试验结果线性拟合得出强度线与p轴交点的坐标。而T=0℃条件下，土样尚未被冻结，因此，假定其抗剪强度为0。基于此，本文引入双曲线函数关系描述 ${\sigma _0}$ 随T变化的规律，其表达式为

${\sigma _0} = \frac{{\left| T \right|}}{{a\left| T \right| + b}}。$

(26)

式中： $\left| T \right|$ 为温度的绝对值；a和b为温度效应系数。

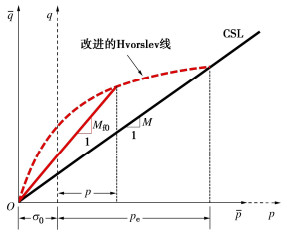
M_f0为平移变换应力空间中的初始潜在应力比，可通过改进Hvorslev线^[29-30]确定，如图 3所示，其具体表达式如下：

${M_{{\text{f0}}}}{\text{ = 6}}\left[ {\sqrt {\frac{{{M^2} \cdot {\text{OCR}}}}{{12(3 - M)}}\left( {1 + \frac{{{M^2} \cdot {\text{OCR}}}}{{12(3 - M)}}} \right)} - \frac{{{M^2} \cdot {\text{OCR}}}}{{12(3 - M)}}} \right] 。$

(27)

图 3 改进Hvorslev面

Figure 3. Improved Hvorslev surface

下载: 全尺寸图片幻灯片

式中：OCR表示冻土的等效超固结比，为平移变换应力空间中的等效前期固结压力 ${\bar p_{\text{e}}}$ 与当前平移变换应力 $\bar p$ 的比值，表达式为

${\text{OCR}} = \frac{{{{\bar p}_{\text{e}}}}}{{\bar p}} = \frac{{{p_{\text{e}}} + {\sigma _0}}}{{p + {\sigma _0}}}。$

(28)

式中：p_e为冻土的等效前期固结压力，在这一平均应力条件下冻土的剪切过程表现出应变硬化特性。通过对试验结果^{[4, 13]}的分析可知，随着温度的降低，冻土的等效前期固结压力p_e逐渐增加，p_e与温度之间的关系可采用线性表达式进行拟合。

$\varepsilon _{{\text{dr}}}^{\text{p}}$ 为参考塑性剪应变，可取应力比达到峰值条件时对应的塑性剪应变。基于对已有试验数据的分析可知， $\varepsilon _{{\text{dr}}}^{\text{p}}$ 受温度影响较小，为了简单起见，可取不同温度条件 $\varepsilon _{{\text{dr}}}^{\text{p}}$ 的平均值用于模型预测。

$\chi$ 为映M_f衰减程度的参数。当 $\varepsilon _{\text{d}}^{\text{p}} = \varepsilon _{{\text{dr}}}^{\text{p}}$ 时，M_f达到M_fr。因此，由式（18），（19）可得

${M_{{\text{fr}}}} = \exp (\chi )({M_{{\text{f0}}}} - M) + M。$

(29)

整理式（29）可得

$\chi = \ln \frac{{{M_{{\text{fr}}}} - M}}{{{M_{{\text{f0}}}} - M}} 。$

(30)

根据式（30）可知，χ实际上反映了M， ${M_{{\text{fr}}}}$ 与 ${M_{{\text{f0}}}}$ 之间的相对大小关系。其中， ${M_{{\text{fr}}}}$ 为与 $\varepsilon _{{\text{dr}}}^{\text{p}}$ 对应的应力比，可根据等效超固结比最大的试验结果进行确定。

分数阶次μ实际上是与椭圆屈服面纵横轴比 $\zeta$ 一一相关的。当应力比达到相变应力比时，即 $\bar \eta$ =M时，冻土达到相变状态，此时，剪胀比d=0。根据塑性应变增量方向表达式（16）可得冻土的剪胀方程：

$d = \frac{{{m_p}}}{{{m_q}}} = \frac{{({\mu ^2} - 2\mu ){{\bar \eta }^2} + \mu {\zeta ^2}{M^2}}}{{(3\mu - {\mu ^2}){{\bar \eta }^{{\text{2}} - \mu }}}} 。$

(31)

将 $\bar \eta$ =M时d=0的条件代入上式，可得

$\mu = 2 - {\zeta ^2}。$

(32)

基于文献[]可知， $\zeta$ 可以通过NCL与CSL之间的距离ΔΠ确定，具体表达式为

$\zeta = {1 \mathord{\left/ {\vphantom {1 {\sqrt {\exp \left( {\frac{{\Delta \Pi }}{{\lambda - \kappa }}} \right) - 1} }}} \right. } {\sqrt {\exp \left( {\frac{{\Delta \Pi }}{{\lambda - \kappa }}} \right) - 1} }}。$

(33)

在模型预测过程中如无法得到NCL与CSL之间的距离，也可基于某一条件下的试验结果采用试错法进行确定，用于模拟其它条件下的试验结果。

2. 模型特性分析

本节以 ${\sigma _3}$ 为常数的三轴压缩应力路径为例，从屈服面的演化规律和M_f与 $\bar \eta$ 的相对大小的角度分析模型在模拟硬化/软化特性方面的能力，通过塑性流动方向的变化和剪胀曲线的角度分析模型的描述剪缩/剪胀特性的能力。

2.1 硬化/软化特性

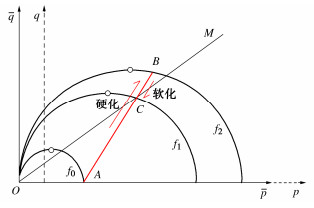
常规三轴压缩应力路径下屈服面的演化过程如图 4所示。点A为冻土的初始应力状态点，即初始屈服面f₀与p轴的交点。随着塑性剪应变 $\varepsilon _{\text{d}}^{\text{p}}$ 的增大，应力状态从A点逐渐变化到峰值应力点B，屈服面从f₀逐渐增大为f₂，在此过程中，剪应力随塑性剪应变的增加而持续增大，冻土主要表现为应变硬化。随着 $\varepsilon _{\text{d}}^{\text{p}}$ 进一步增大，应力状态将从B点逐渐变化到临界状态点C，屈服面从f₂逐渐减小为f₁，剪应力随塑性剪应变的增加而减小，冻土主要表现为应变软化的特征。

图 4 常规三轴压缩应力路径下屈服面的演化

Figure 4. Evolution of yield surface under triaxial compression stress path

下载: 全尺寸图片幻灯片

反映冻土硬化/软化特性的屈服面演化规律实际上受硬化参量变化规律的控制。而根据式（17）可知，硬化参量H中的潜在应力比M_f是影响描述冻土硬化/软化规律的核心要素，其反映了冻土在当前应力和温度条件下所具有的抵抗破坏的潜在能力。由式（18），（19）可知，M_f随着塑性剪应变的增大而减小，如图 5（a）所示，而在加载过程中，M_f与 $\bar \eta$ 的相对大小关系如所示。在初始状态，塑性剪应变 $\varepsilon _{\text{d}}^{\text{p}}$ = 0，此时，应力比 $\bar \eta$ = 0，潜在应力比 ${M_{\text{f}}}$ = ${M_{{\text{f0}}}}$ ，对应于中的A点；随着加载的进行， $\varepsilon _{\text{d}}^{\text{p}}$ 增大，此时， ${M_{\text{f}}}$ 逐渐减小，而 $\bar \eta$ 逐渐增大，此时， $\bar \eta$ < ${M_{\text{f}}}$ ，冻土处于应变硬化阶段，直至 $\bar \eta$ 增大到了与 ${M_{\text{f}}}$ 相等的峰值应力状态，如图 5所示，这一加载过程对应于中的应力路径AB段；随着 $\varepsilon _{\text{d}}^{\text{p}}$ 的进一步增大， ${M_{\text{f}}}$ 进一步减小， $\bar \eta$ 开始由增大转变为减小，此时， $\bar \eta$ > ${M_{\text{f}}}$ ，冻土处于应变软化阶段，直至 $\bar \eta$ 与 ${M_{\text{f}}}$ 同时趋近于M，最终达到临界状态，如图 5所示，这一过程对应于图 4中的应力路径BC段。

图 5 M_f与η的演化规律

Figure 5. Evolution of M_f and

$\bar \eta$

下载: 全尺寸图片幻灯片

2.2 剪缩/剪胀特性

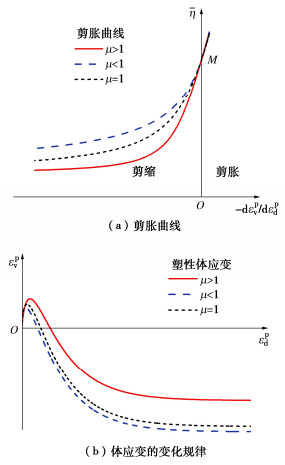
土的剪缩/剪胀性是土的基本特性之一^[29]，同时也是建立本构模型过程中必须要考虑的基本问题。剪缩/剪胀性通常利用剪胀比d的变化规律进行描述。而剪胀比d是塑性体应变与塑性剪应变之间比例 ${\text{d}}\varepsilon _{\text{v}}^{\text{p}}{\text{/d}}\varepsilon _{\text{d}}^{\text{p}}$ ，实际上反映的是塑性应变增量的方向。因此，土的剪缩/剪胀性的核心是塑性应变增量方向在加载过程中的变化规律。

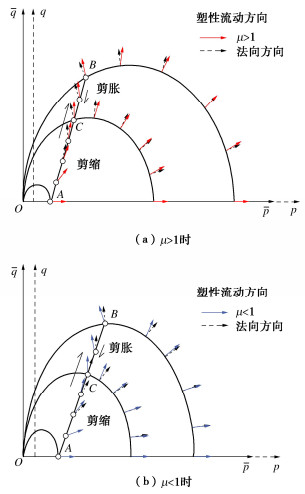
由式（16）可知，非正交塑性流动方向受分数阶次μ控制。而根据式（32）可知，μ的取值与ζ有直接关系μ=2–ζ²。当ζ=1时，μ=1，此时，屈服函数退化为MCC模型的椭圆屈服函数，而塑性应变增量方向退化为椭圆屈服面的法线方向。而在ζ≠1的条件下，可得以下两种情况：（a）μ > 1，ζ < 1；（b）μ < 1，ζ > 1。这里同样以 ${\sigma _3}$ 为常数的常规压缩应力路径为例对两种不同情况下的塑性应变增量方向进行分析，如图 6所示。情况（a）与情况（b）的塑性应变增量方向分别由中的红色箭头与中的蓝色箭头表示。对于 $\bar \eta$ =0的初始状态A点， ${\text{d}}\varepsilon _{\text{d}}^{\text{p}}$ =0，塑性应变增量方向与 $\bar p$ 轴正轴方向一致；随 $\bar \eta$ 从0增大到M，塑性应变增量方向由与 $\bar p$ 轴一致的水平方向逐渐变化到竖直向上，冻土主要体现为剪缩特性；对于 $\bar \eta$ 达到M时的C点， ${\text{d}}\varepsilon _{\text{v}}^{\text{p}}$ =0，塑性应变增量方向竖直向上，为剪缩/剪胀的相变状态点；随着 $\bar \eta$ 进一步增大，塑性应变增量方向从竖直方向逐渐向 $\bar p$ 轴负轴方向偏转，此时，冻土主要表现为剪胀特性；当η达到与M_f相等时，应力状态达到峰值状态点B；随着加载的进行， $\bar \eta$ 与M_f同时减小，并在较大应变条件下趋于临界状态点C，此时， $\bar \eta$ =M，塑性应变增量竖直向上。如图 6所示，情况（a）与情况（b）的塑性应变增量方向变化规律基本一致，都表现为有水平向右转向竖直向上，并偏向左侧后再偏转回竖直向上，从而体现出了剪缩/剪胀以及相变与临界状态的特征。同时，由图 6可知，在μ > 1与μ < 1两种情况下，对应的临界应力点C都不在屈服函数的顶点上，而是分别处于屈服函数顶点左侧与右侧。

图 6 塑性流动方向的演化

Figure 6. Evolution of plastic flow direction

下载: 全尺寸图片幻灯片

根据以上分析可知μ=1时，塑性应变增量方向退化为椭圆屈服面的法线方向，对应的剪胀曲线如图 7（a）中的黑色短划线所示。而对于μ > 1和μ < 1的情况，剪胀曲线在分别表示为红色实线和蓝色虚线。可以看出在 $\bar \eta$ < M时剪胀曲线差别明显，μ > 1和μ < 1条件下的剪胀曲线分别低于和高于μ=1条件下的剪胀曲线，反映了冻土不同的剪缩特性；而在M < $\bar \eta$ < M_f时，剪胀曲线差异较小，反映了这一阶段基本一致的冻土剪胀规律。相应地，对应μ不同的3种情况，冻土在剪切过程中塑性体应变随塑性剪应变变化的规律如图 7（b）所示。随着塑性剪应变的增大，塑性体应变先增大，后逐渐减小，直至达到某一负值。这一变化过程反映了冻土在剪切过程中的先体缩后体胀直至达到临界状态的特性。

图 7 剪切过程中的体胀规律

Figure 7. Variation rules of volume during shearing

下载: 全尺寸图片幻灯片

3. 模型验证

为了评估冻土非正交弹塑性模型在描述冻土受力变形规律方面的性能，本文采用Xu等^[4]所得不同温度（T=-2℃，-4℃，-6℃）下冻结脱盐粉砂三轴剪切试验结果对所建模型进行验证，脱盐粉砂的干密度为ρ_d=1.90 g/cm³，其土粒相对质量密度取为G_s=2.70时，即可得冻土的初始孔隙比e₀=0.420。试验过程中采用位移控制的轴向加载模式，所采用的围压条件分别为0.3，0.5，1.0，2.0，3.0 MPa。

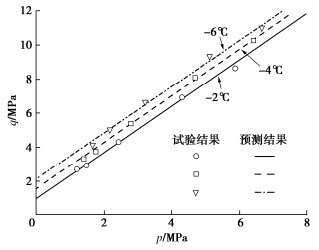
通过将3种不同温度条件下轴向应变达到20%时的冻土剪应力进行整理，可得如图 8中所示冻土抗剪强度的试验结果。基于对结果分析可知，在不同温度条件下冻土抗剪强度线的斜率变化不大，而截距显著不同。因此，本文将不同温度条件下强度线的斜率的平均值M = 1.35用作预测参数，对应可得3种温度下强度线与p轴交点的截距坐标，即 ${\sigma _0}$ =0.69，1.12，1.55。对应强度线与试验结果的对比，如图 8所示。

图 8 不同温度下冻土抗剪强度线

Figure 8. Shear strength lines for frozen soils at different temperatures

下载: 全尺寸图片幻灯片

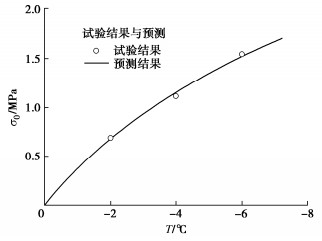
在利用试验结果确定不同温度下的 ${\sigma _0}$ 后，本文利用式（26）对不同温度下的 ${\sigma _0}$ 进行拟合，得到a=0.246和b=2.467。不同温度下的 ${\sigma _0}$ 与预测曲线之间的对比关系如所示，可以看出，预测曲线与不同温度条件下的 ${\sigma _0}$ 吻合较好。

图 9 冻土三向拉伸强度和温度的拟合曲线

Figure 9. Fitting curve of three-dimensional tensile strength and temperature of frozen soils

下载: 全尺寸图片幻灯片

根据冻土的三轴剪切试验结果与不同温度条件下的应变软化变化趋势，本文采用冻土的等效前期固结压力表达式为p_e=4+0.5|T| MPa。根据试验条件可知， ${\sigma _3}$ =0.3 MPa对应的等效超固结比最大，因此，可根据试验结果确定三级温度条件下的M_fr=2.034，1.89，1.86，并据此计算得出χ=−0.2704，−0.4371，−0.4669。为了简单起见，本文取平均值χ=−0.392用于模型预测。除温度相关的 ${\sigma _0}$ 与p_e外，模型预测所采用的与温度无关的参数如所示。鉴于缺少等效超固结度为1时的试验数据，这里采用 ${\sigma _3}$ =0.3 MPa条件下的试验结果拟合得 $\zeta$ =0.7，并根据式（32）求得μ=1.51。

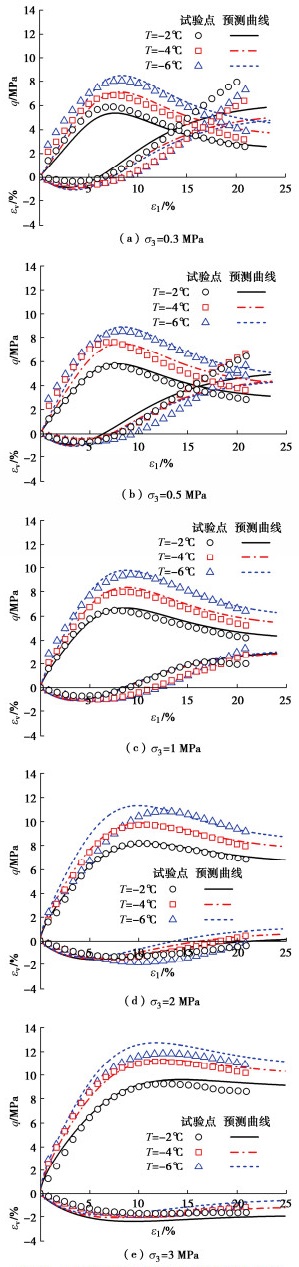
表 1 冻土的模型参数

Table 1. Model parameters of frozen soils

λ	κ	υ	M	$\varepsilon _{{\text{dr}}}^{\text{p}}$	χ	μ
0.042	0.004	0.3	1.35	0.07	-0.392	1.51

下载: 导出CSV

| 显示表格

在不同围压条件（0.3，0.5，1.0，2.0，3.0 MPa）下，3种不同温度条件（T=-2℃，-4℃，-6℃）的冻土试验结果与模型预测结果的对比如图 10所示。由图 10可知，对于某一给定围压条件下的冻土，在3种温度条件下的试验结果均表现出显著的先应变硬化后应变软化以及先体缩后体胀的特征；随着温度的降低，应力应变关系整体变化趋势基本一致，但峰值抗剪强度显著增大，体缩增大不显著。通过模型预测结果与试验结果的对比可以看出，所建立冻土模型可以较好地描述冻土在不同温度条件下的变形特征与抗剪强度的温度相关性。

图 10 冻结粉砂试验结果与模型预测对比

Figure 10. Comparison of test results and model predictions for frozen soils

下载: 全尺寸图片幻灯片

随着 ${\sigma _3}$ 的增大，如~所示，冻土的受力变形特征除表现出抗剪强度增大外，还表现出了应变硬化/软化与剪缩/剪胀特征的逐渐减弱，逐渐转变为应变硬化与体缩的特征；直至 ${\sigma _3}$ =3 MPa时，冻土的应变软化与剪胀的趋势已不再显著。可以看出，冻土变形特征随围压增大而表现出了明显的类超固结性。通过对比可以看出，冻土的类超固结性可以通过所建立的冻土非正交弹塑性模型进行描述。

模型预测结果与试验结果的对比虽然整体上吻合度较好，但对于 ${\sigma _3}$ =2.0 MPa、T=-6℃（）和 ${\sigma _3}$ =3.0 MPa、T=-6℃（图 10（e））两种条件下的试验结果，模型预测精度降低。基于试验结果可以看出，这两种条件下的峰值抗剪强度增大趋势不显著，且加载初期刚度较小，甚至低于T=-4℃的刚度。这一特征可能主要是由于高围压情况下冻土的压融导致，也可能是由于试验结果的离散性造成，鉴于试验结果有限，尚无法确定。本文所建立模型尚没有考虑冻土的压融特征，有待进一步的发展完善。

4. 结论

本文基于非正交弹塑本构模型框架，建立了冻土的非正交弹塑性本构模型，用于描述冻土在剪切荷载作用下的温度相关性与围压相关性，并利用不同温度与不同围压条件下冻土的常规三轴剪切试验结果对模型的性能进行了验证，主要得到以下3点结论。

（1）采用双曲函数描述冻土的三向拉伸强度，通过平移变换的方法将其引入到屈服函数中，从而使本构模型在平移变换应力空间内可以考虑三向拉伸强度的影响。

（2）将基于R-L型分数阶微分的非正交流动法则应用于平移变换应力空间中的屈服函数，从而得出了与屈服曲线非正交的塑性应变增量方向。建立了冻土潜在强度衰减因子，并引入到统一硬化参量中，发展得出考虑温度和围压影响的冻土硬化参量，确定了塑性应变增量的大小。

（3）利用所建立的冻土非正交弹塑性模型对不同温度与围压条件下的冻结砂土常规三轴剪切试验结果进行预测，对比结果表明本文所建立的冻土非正交弹塑性本构模型能够合理描述冻土受力变形规律中表现出的温度效应与围压效应。

图 1 在不同应力空间的冻土屈服曲线

Figure 1. Yield curves for frozen soils in different stress spaces

下载: 全尺寸图片幻灯片

图 2 潜在破坏应力比M_f的演化规律

Figure 2. Evolution of potential strength M_f

下载: 全尺寸图片幻灯片

图 3 改进Hvorslev面

Figure 3. Improved Hvorslev surface

下载: 全尺寸图片幻灯片

图 4 常规三轴压缩应力路径下屈服面的演化

Figure 4. Evolution of yield surface under triaxial compression stress path

下载: 全尺寸图片幻灯片

图 5 M_f与η的演化规律

Figure 5. Evolution of M_f and $\bar \eta$

下载: 全尺寸图片幻灯片

图 6 塑性流动方向的演化

Figure 6. Evolution of plastic flow direction

下载: 全尺寸图片幻灯片

图 7 剪切过程中的体胀规律

Figure 7. Variation rules of volume during shearing

下载: 全尺寸图片幻灯片

图 8 不同温度下冻土抗剪强度线

Figure 8. Shear strength lines for frozen soils at different temperatures

下载: 全尺寸图片幻灯片

图 9 冻土三向拉伸强度和温度的拟合曲线

Figure 9. Fitting curve of three-dimensional tensile strength and temperature of frozen soils

下载: 全尺寸图片幻灯片

图 10 冻结粉砂试验结果与模型预测对比

Figure 10. Comparison of test results and model predictions for frozen soils

下载: 全尺寸图片幻灯片

表 1 冻土的模型参数

Table 1 Model parameters of frozen soils

λ κ υ M $\varepsilon _{{\text{dr}}}^{\text{p}}$ χ μ

0.042 0.004 0.3 1.35 0.07 -0.392 1.51

下载: 导出CSV

参考文献(33)

[1]	LAI Y M, XU X T, DONG Y H, et al. Present situation and prospect of mechanical research on frozen soils in China[J]. Cold Regions Science and Technology, 2013, 87: 6-18. doi: 10.1016/j.coldregions.2012.12.001
[2]	马巍, 王大雁. 中国冻土力学研究50a回顾与展望[J]. 岩土工程学报, 2012, 34(4): 625-640. http://cge.nhri.cn/cn/article/id/14543 MA Wei, WANG Dayan. Studies on frozen soil mechanics in China in past 50 years and their prospect[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(4): 625-640. (in Chinese) http://cge.nhri.cn/cn/article/id/14543
[3]	ZHAO Y H, ZHANG M Y, GAO J. Research progress of constitutive models of frozen soils: a review[J]. Cold Regions Science and Technology, 2023, 206: 103720. doi: 10.1016/j.coldregions.2022.103720
[4]	XU X T, WANG Y B, BAI R Q, et al. Comparative studies on mechanical behavior of frozen natural saline silty sand and frozen desalted silty sand[J]. Cold Regions Science and Technology, 2016, 132: 81-88. doi: 10.1016/j.coldregions.2016.09.015
[5]	KIM S Y, KIM Y, LEE J S. Effects of frozen water content and silt fraction on unconfined compressive behavior of fill materials[J]. Construction and Building Materials, 2021, 266: 120912. doi: 10.1016/j.conbuildmat.2020.120912
[6]	NIU Y Q, WANG X, LIAO M K, et al. Strength criterion for frozen silty clay considering the effect of initial water content[J]. Cold Regions Science and Technology, 2022, 196: 103521. doi: 10.1016/j.coldregions.2022.103521
[7]	孙晓宇, 齐吉琳, 尹振宇. 冻结饱和标准砂压缩性试验研究[J]. 岩土工程学报, 2018, 40(9): 1723-1728. doi: 10.11779/CJGE201809020 SUN Xiaoyu, QI Jilin, YIN Zhenyu. Experimental study on compressibility of frozen saturated ISO standard sand[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(9): 1723-1728. (in Chinese) doi: 10.11779/CJGE201809020
[8]	高娟, 赖远明, 常丹, 等. 考虑加载速率影响的冻结含盐砂土强度准则研究[J]. 岩土工程学报, 2019, 41(1): 104-110. doi: 10.11779/CJGE201901011 GAO Juan, LAI Yuanming, CHANG Dan, et al. Strength criterion for frozen saline sand considering effects of loading rates[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(1): 104-110. (in Chinese) doi: 10.11779/CJGE201901011
[9]	LI X, YAN Y, JI S Y. Mechanical properties of frozen ballast aggregates with different ice contents and temperatures[J]. Construction and Building Materials, 2022, 317: 125893. doi: 10.1016/j.conbuildmat.2021.125893
[10]	ZHANG D, LIU E L, LIU X Y, et al. A new strength criterion for frozen soils considering the influence of temperature and coarse-grained contents[J]. Cold Regions Science and Technology, 2017, 143: 1-12. doi: 10.1016/j.coldregions.2017.08.006
[11]	LUO F, LIU E L, ZHU Z Y. A strength criterion for frozen moraine soils[J]. Cold Regions Science and Technology, 2019, 164: 102786. doi: 10.1016/j.coldregions.2019.102786
[12]	LAI Y M, LIAO M K, HU K. A constitutive model of frozen saline sandy soil based on energy dissipation theory[J]. International Journal of Plasticity, 2016, 78: 84-113. doi: 10.1016/j.ijplas.2015.10.008
[13]	QI J L, HU W, MA W. Experimental study of a pseudo-preconsolidation pressure in frozen soils[J]. Cold Regions Science and Technology, 2010, 60(3): 230-233. doi: 10.1016/j.coldregions.2009.10.008
[14]	CHANG D, LAI Y M, YU F. An elastoplastic constitutive model for frozen saline coarse sandy soil undergoing particle breakage[J]. Acta Geotechnica, 2019, 14(6): 1757-1783. doi: 10.1007/s11440-019-00775-0
[15]	YAO X L, XU G F, ZHANG M Y, et al. A frozen soil rate dependent model with time related parabolic strength envelope[J]. Cold Regions Science and Technology, 2019, 159: 40-46. doi: 10.1016/j.coldregions.2018.12.006
[16]	ZHANG D, LIU E L. Binary-medium-based constitutive model of frozen soils subjected to triaxial loading[J]. Results in Physics, 2019, 12: 1999-2008. doi: 10.1016/j.rinp.2019.02.029
[17]	LAI Y M, JIN L, CHANG X X. Yield criterion and elasto-plastic damage constitutive model for frozen sandy soil[J]. International Journal of Plasticity, 2009, 25(6): 1177-1205. doi: 10.1016/j.ijplas.2008.06.010
[18]	LAI Y M, YANG Y G, CHANG X X, et al. Strength criterion and elastoplastic constitutive model of frozen silt in generalized plastic mechanics[J]. International Journal of Plasticity, 2010, 26(10): 1461-1484. doi: 10.1016/j.ijplas.2010.01.007
[19]	SUN K, ZHOU A N. A multisurface elastoplastic model for frozen soil[J]. Acta Geotechnica, 2021, 16(11): 3401-3424. doi: 10.1007/s11440-021-01391-7
[20]	YANG Y G, LAI Y M, DONG Y H, et al. The strength criterion and elastoplastic constitutive model of frozen soil under high confining pressures[J]. Cold Regions Science and Technology, 2010, 60(2): 154-160. doi: 10.1016/j.coldregions.2009.09.001
[21]	LU D C, LIANG J Y, DU X L, et al. Fractional elastoplastic constitutive model for soils based on a novel 3D fractional plastic flow rule[J]. Computers and Geotechnics, 2019, 105: 277-290. doi: 10.1016/j.compgeo.2018.10.004
[22]	LU D C, ZHOU X, DU X L, et al. A 3D fractional elastoplastic constitutive model for concrete material[J]. International Journal of Solids and Structures, 2019, 165: 160-175. doi: 10.1016/j.ijsolstr.2019.02.004
[23]	LI H C, TONG C X, CHANG X, et al. Constitutive modelling of temperature-dependent behaviour of soft rocks with fractional-order flow rule[J]. Applied Sciences, 2022, 12(8): 3875. doi: 10.3390/app12083875
[24]	LIANG J Y, LU D C, DU X L, et al. Non-orthogonal elastoplastic constitutive model for sand with dilatancy[J]. Computers and Geotechnics, 2020, 118: 103329. doi: 10.1016/j.compgeo.2019.103329
[25]	LIANG J Y, LU D C, ZHOU X, et al. Non-orthogonal elastoplastic constitutive model with the critical state for clay[J]. Computers and Geotechnics, 2019, 116: 103200. doi: 10.1016/j.compgeo.2019.103200
[26]	QU P F, ZHU Q Z, ZHAO L Y, et al. A micromechanics-based fractional frictional damage model for quasi-brittle rocks[J]. Computers and Geotechnics, 2021, 139: 104391. doi: 10.1016/j.compgeo.2021.104391
[27]	SUN K, TANG L, ZHOU A N, et al. An elastoplastic damage constitutive model for frozen soil based on the super/subloading yield surfaces[J]. Computers and Geotechnics, 2020, 128: 103842. doi: 10.1016/j.compgeo.2020.103842
[28]	姚仰平, 路德春, 周安楠. 岩土类材料的变换应力空间及其应用[J]. 岩土工程学报, 2005, 27(1): 24-29. doi: 10.3321/j.issn:1000-4548.2005.01.003 YAO Yangping, LU Dechun, ZHOU Annan. Transformed stress space for geomaterials and its application[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 24-29. (in Chinese) doi: 10.3321/j.issn:1000-4548.2005.01.003
[29]	姚仰平. UH模型系列研究[J]. 岩土工程学报, 2015, 37(2): 193-217. doi: 10.11779/CJGE201502001 YAO Yangping. Advanced UH models for soils[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(2): 193-217. (in Chinese) doi: 10.11779/CJGE201502001
[30]	YAO Y P, GAO Z W, ZHAO J D, et al. Modified UH model: constitutive modeling of overconsolidated clays based on a parabolic hvorslev envelope[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(7): 860-868. doi: 10.1061/(ASCE)GT.1943-5606.0000649
[31]	高娟, 赖远明. 冻结盐渍土三轴剪切试验过程中的损伤及压融分析[J]. 岩土工程学报, 2018, 40(4): 707-715. doi: 10.11779/CJGE201804015 GAO Juan, LAI Yuanming. Damage and pressure melting analysis of frozen saline soilsinprocess of triaxial compression tests[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(4): 707-715. (in Chinese) doi: 10.11779/CJGE201804015
[32]	孙星亮, 汪稔, 胡明鉴. 冻土三轴剪切过程中细观损伤演化CT动态试验[J]. 岩土力学, 2005, 26(8): 1298-1302, 1311. doi: 10.3969/j.issn.1000-7598.2005.08.022 SUN Xingliang, WANG Ren, HU Mingjian. A CT-timely experimental study on meso-scopic structural damage development of frozen soil under triaxial shearing[J]. Rock and Soil Mechanics, 2005, 26(8): 1298-1302, 1311. (in Chinese) doi: 10.3969/j.issn.1000-7598.2005.08.022
[33]	赵淑萍, 马巍, 郑剑锋, 等. 基于CT单向压缩试验的冻结重塑兰州黄土损伤耗散势研究[J]. 岩土工程学报, 2012, 34(11): 2019-2025. http://cge.nhri.cn/cn/article/id/14883 ZHAO Shuping, MA Wei, ZHENG Jianfeng, et al. Damage dissipation potential of frozen remolded Lanzhou loess based on CT uniaxial compression test results[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(11): 2019-2025. (in Chinese) http://cge.nhri.cn/cn/article/id/14883