0.   引言

在国内外越江海软土隧道建设中，几乎均采用了泥水盾构法，如东京湾海底隧道、上海长江隧道、狮子洋高铁隧道等等^[1]。泥水盾构在掘进过程中主要通过开挖舱中带压力的泥水支撑开挖面前方的水土压力。压力设定过高，极易发生泥水劈裂地层，该现象曾多次发生于国内外的盾构隧道工程^[1-3]。泥水劈裂后，若控制不当，任其伸展至地表喷发，最终会导致盾构隧道发生冒顶、海水倒灌^[4-5]等事故。

泥水劈裂是泥水盾构开挖面失稳的特殊现象，其失稳压力比盾构开挖面的“被动失稳”压力要小得多^[2]。由于盾构泥水劈裂受复杂的边界条件的影响，加之裂缝观测手段有限，很难在现场捕捉到盾构泥水劈裂现象。通过调研分析，目前对于泥水劈裂的研究主要采用常重力模型试验、数值模拟与理论分析等手段，对于离心试验方面的研究几乎空白^[4-5]。离心试验可以通过提供一个等效的高倍重力加速度有效还原真实的应力场，近年来，已被广泛地应用于隧道工程领域，可为盾构泥水劈裂问题提供一个可行的研究手段。

然而，泥水劈裂涉及到土体-泥水-隧道等多方面的影响，尤其多种流体的存在使得模型试验中量纲分析，试验参数缩放和数据解释更加复杂化。Goodings^[6]曾推导了离心试验中土石坝渗流和漫顶时流体运动的相似比例。Cargill等^[7]基于白金汉第二定理，推导了土石坝中瞬变流现象离心模型试验的相似关系，研究结果发现，土体饱和度对于试验中的相似关系协调具有重要影响，因为饱和度的改变直接影响土体渗透性。De Pater等^[8]推导了水力劈裂裂缝扩展物理模型试验的相似比例，其中涉及到弹性变形、流体摩擦、裂纹扩展以及流体泄露等多方面的参数，并通过水泥块劈裂试验进行验证。朱维新^[9]推导了模拟土石坝变形裂缝的相似理论，理论上证明了用离心模型预测土石坝变形裂缝与稳定现象的正确性。Bunger等^[10]通过自主设的计水力压裂试验给出了与流体黏度相关的不变量取不同值的试验结果。上述针对水力劈裂离心模型试验的相似性分析可提供一定的借鉴，但试验中仅涉及到一种流体，而针对多种流体共同作用下的相似关系，目前既有研究大多针对“重力驱动”条件下的流体运动。Culligan等^[11]对模拟多孔介质中的非水相液体（non-aqueous phase liquid, NAPL）流动的相似关系进行了研究，结果显示为了模拟裂缝中流体的侵入，物体重力与毛细力的比值必须正确，因此裂缝开度不会进行缩放。Hensley等^[12]也针对多孔介质中污染物迁移问题，推导了控制离心机模型与其相应原型之间关系的相似比例定律。宋东日等^[13]基于两相流无量纲参数的基础上，建立了泥石流土工离心模型试验的分层次相似性设计体系。Antoniou等^[14]基于无量纲数建立了钢筋混凝土开裂模型试验的相似准则，所提出的标度规律使得新型隧道衬砌模型试验材料的设计具有通用性。上述研究可为盾构泥水劈裂模型试验相似性分析提供一定参考，但土工离心机模拟盾构泥水劈裂现象涉及隧道、土体、泥浆等多相耦合，许多试验研究低估了黏度的作用，甚至忽略了试验中的黏度效应^[15-16]。此外，试验中的裂缝尺度和现场的原位尺度有很大的不同，其比例不能简单地按照相似比例进行缩放，需根据实际问题进行具体分析。

土工离心机模拟盾构泥水劈裂的动态过程涉及黏滞力，外界压力、重力等多种力的复杂耦合作用，合理的相似比例关系是模型试验成功的关键前提。本文在分析盾构泥水劈裂基本物理过程的基础上，基于无量纲数和量纲分析探讨盾构泥水劈裂离心模型试验物理量的相似关系，为采用离心模型试验手段研究盾构泥水劈裂问题奠定理论基础。

1.   泥水劈裂离心模型试验相似性分析

1.1   离心试验的优势

目前针对盾构泥水劈裂试验研究主要集中在三轴劈裂试验和常重力模型试验^[17]。其中三轴劈裂试验主要通过对不同围压条件下的中空圆柱体内部施加压力来探究土体劈裂破坏的压力。然而，这种单元应力试验与盾构开挖面前方土体实际的应力状态及边界条件有着较大的差别，而且试样的应力及渗流场较为复杂，试验中各项因素的轻重之分与相互关系难以区分。因此利用三轴试验模拟盾构开挖面泥水劈裂的发生条件和伸展过程具有较大难度，其相关成果较难应用于实际的盾构工程。对于在传统的lg重力场中进行的小规模模型试验通常无法揭示原型应力水平可能存在的一些重要现象，尤其对于岩土体材料，其力学响应取决于土体内的有效应力水平。离心模型试验通过提供一个等效的高倍重力加速度场，可以在小比尺模型中提供真实的土体应力状态。对于盾构开挖面泥水劈裂问题，采用离心模型试验手段进行研究有以下几个方面的优势：

（1）可以还原真实的应力场。盾构开挖面泥水压力的大小是驱动泥水裂缝向地表伸展的重要影响因素，其与地应力的相对关系直接决定裂缝尖端的伸展情况。1g试验无法提供原位级别的应力大小，而离心试验通过高倍重力实现原位应力，可以有效还原真实的泥水劈裂启裂、伸展及喷发现象。

（2）可以有效保证试验土体与泥水材料的相似性。一般1g模型试验中土体试样的参数很难与实际完全相似，尤其对于强度与渗透性等特性参数很难通过制样的控制来保证其相似性^[4]，而盾构泥水劈裂模型试验中，还涉及到泥水的作用，其密度、黏度等参数是泥水伸展的重要影响因素，1g模型试验很难同时保证泥水参数和土体参数的相似性，这也给1g模型试验带来一定误差。而离心试验中，一般土体均采用原状土，通过合理的相似性分析与推导，可以有效保证试验中材料、模型尺寸、时间等多方面涉及参数的相似性。

（3）可以有效保证黏土的固结度。黏性土的强度性状相对于非黏性土更为复杂，不仅随剪切条件不同而不同，而且还受土体的固结排水条件、应力历史、土的各向异性等因素的影响。Andersen等^[18]的研究显示，黏土固结度对土体劈裂压力的大小有重要影响。在1g模型试验中为了加快黏土试样的固结，往往会施加远大于试验中产生应力大小的预应力，这使得试验中的黏土试样往往都是超固结土。而离心试验中的固结时间不仅远比实际固结时间要短得多，并且通过设置固结加速度与试验加速度的相对大小或者不同的固结时间等，可以得到欠固结、正常固结以及超固结等不同固结程度的黏土试样。

1.2   盾构泥水劈裂基本力学物理过程

对于泥水劈裂的离心模型试验相似性分析，首先需要理解原型中盾构泥水劈裂现象的物理与力学作用过程，明确试验中涉及的物理力学参数，并通过适当地简化突出研究问题的主要矛盾。

泥水盾构在掘进过程中主要依靠开挖舱中带压力的泥水平衡前方的水土压力。泥水劈裂的物理过程主要包括启裂、伸展以及喷发过程^[1]。首先在开挖舱内的泥水主要受自身重力和外界压力的作用。随着气压的增加，开挖面前方的泥水压力也逐渐增加，泥水在压力驱动下，在开挖面会形成扩张及渗透趋势，对于渗透性低的土体，主要以扩张趋势为主并对土体产生挤密作用；而对于渗透性高的土体则两种趋势并存，其作用相对大小与土体渗透性大小有关。由于泥水介质为液体，随着压力的进一步增加，当开挖面前方土体达到其临界应力条件时，土体会被泥水劈裂破坏而不是发生被动破坏的楔形体破坏形式，其破坏的启裂压力也会比被动破坏的压力要小得多^[2]。此外，由于开挖面前方土体的不均匀性，可能会存在多个局部启裂裂缝。但根据前人的研究显示，开挖面土体的不均性并不影响水力劈裂的发展和其路径^[19]。一般土体启裂后，裂缝会沿着垂直于最小主应力的方向伸展^[4]。由于泥水具有一定黏度，在伸展过程中不仅受到重力、地层抗力、气压等力的作用，同时也会受到黏滞力，摩擦力等力的作用。而且，裂缝表面流体的压力也会引起周边土体的变形与渗透作用，产生局部固结效应，各种力的相互作用在具有不同强度以及渗透特性的土体中可能会导致复杂的泥水流动现象。最终，在压力的持续作用下，裂缝会沿着垂直于最小主应力方向伸展并贯通至地表，导致泥水喷发。

综上所述，泥水劈裂是一个非常复杂的过程，其物理过程包含多种相互作用力，目前没有明确的物理数学模型描述这种复杂的耦合关系。但想要在试验条件下还原真实的盾构泥水劈裂现象，就需要保证各作用力及其相对关系在试验与原型中的相似性。Lee等^[15]研究指出，土工离心机试验可以通过考虑适当的无量纲数来表征试验要模拟的过程。因此本文基于以上分析，通过考虑泥水劈裂现象中涉及的关键无量纲数，明确盾构泥水劈裂离心模型试验需要满足的相似性条件。

1.3   基于无量纲数的相似性考虑

无量纲数一般指两个具有相同量纲的物理量的比值，研究显示，要保证两个系统的相似性，那么这两个系统涉及的无量纲数要相等^[20]。基于上文对泥水劈裂基本物理过程的分析，抓住主要变量，通过考虑以下4个无量纲数来分析盾构开挖面泥水劈裂离心模型试验的相似性。

（1）流体压力与惯性力比值

岩土体中裂缝均会沿着垂直于最小主应力的方向伸展，因此泥水在开挖面处压力作用下启裂后一般都会向地表伸展，伸展过程泥水受到外压力的同时也受到自身重力的影响。因此，考虑流体压力与惯性力的比值如下^[20]：

式中：P为泥水压力；$\rho$为泥水密度；u为泥水伸展速度。

该比值即为流体力学中的欧拉数，该无量纲数不仅表示了流体的压力与惯性力之比，同时在不可压缩流动中，欧拉数也表示了流体的加减速程度。保证模型与原型中流体压力与惯性力比值的相等，可以有效还原模型中泥水在压力与重力相互作用下的流动现象。

（2）流体惯性力与黏性力比值

由于泥水为带有黏度的流体，其在伸展过程中不仅受到重力的阻力作用，同时也会受到黏滞阻力，这种黏性力与惯性力的相对大小在原型和离心试验中也应该保持一致。流体惯性力与黏性力的比值本质就是雷诺数，被广泛地用于描述流体流动中紊动程度的无量纲数，计算如下^[20]：

式中：$\mu$为泥水的动力黏度；e为裂缝开度。

保证模型与原型中流体惯性力与黏性力比值的相等，可以有效还原模型中泥水伸展过程中泥水重力与黏滞力之间的相互作用。

（3）裂缝渗流与孔隙渗流速度比值

岩土体属于多孔非均匀介质，其渗流作用同时发生在基质孔隙和裂缝中，通常基质的水力传导能力低于裂缝的水力传导能力。基质中流体的流动主要受粒径孔隙大小与排列的影响，而裂缝中流体的流动主要取决于裂缝尺寸与应力条件等因素的影响。泥水劈裂过程中，岩土体在带压力的泥水作用下会产生局部固结和强化效应，这种固结效应取决于劈裂伸展速度、裂缝开度以及土体的固结系数。本文基于Finnie等^[21]的研究，引入归一化速度，将这些影响因素可归结为一个无量纲数如下所示：

式中：${c_{\text{v}}}$为土体固结系数。

为保证试验和原型中劈裂现象产生局部固结效应的相似性，两者的归一化速度应该相等。

（4）流体流动与孔压消散时间比值

一般离心机中典型的应变速率要比原型的快1000倍到10000倍^[9]，由于模型与原型加荷速率的差异，离心试验中可能会存在多种相似比例的时间尺度。泥水启裂后裂缝一方面会沿着垂直于最小主应力的方向伸展，另一方面泥水在压力的持续作用下也会有渗透进土体的趋势，这种渗透作用和泥水黏度、裂缝尺寸、土体渗透性及强度等因素有关，为量化泥水在压力作用下沿裂缝流动时间与渗透作用时间的相对长短，考虑泥水流动作用与渗透作用时间比如下^[20]：

式中：L为裂缝长度；A为裂缝横截面面积；$\kappa$为土体渗透率；E为土体弹性模量。

保证模型与原型中泥水流动时间与渗透作用时间比值的相等，可以有效还原模型中泥水流动作用与渗透作用的相对关系。

2.   Butterfield量纲分析法

一般相似性关系有两种分析方法：控制方程分析和量纲分析。控制方程分析主要思想是通过对原理性控制方程进行相似变换，得到具有相同函数形式的无量纲方程，从而建立试验模型与实际系统之间的相似关系。由于目前没有明确的物理数学模型描述泥水劈裂过程中复杂的耦合关系，本文考虑通过量纲分析建立相似性准则。量纲分析方法是在维度同质性的原理上建立的，维度同质性简单来说就是任何物理方程的左边与右边必须具有相同的维度。由Buckingham^[22]提出并建立了$\pi$定理，该定理指出，涉及n₂个基本物理维度的n₁个变量之间的任何物理有效关系（例如，质量、长度和时间）都可以简化为n₁−n₂个无量纲变量之间的关系。用无因次变量来表达物理关系具有深刻的理论意义，因为大自然的运行独立于人类的发明，包括我们对质量、长度和时间的定义。因此，任何有效的物理原理都可以用一种不依赖于这些定义的无量纲数学形式来表示。无量纲$\pi$组对于试验设计也有很大的实际意义，因为它们可以作为缩放参数，指导扩大、缩小或简化试验的策略。通过分离n₁-n₂维的无量纲Π组的影响，而不是n₁维变量的影响，研究人员可以缩小他们的试验目标。此外，当试验相对于自然现象缩小时，通过保持$\pi$组的值不变，试验者可以创建一个自然原型的有效比例模型。

2.1   系统关键参量

本试验针对盾构泥水劈裂现象展开研究，研究范畴涉及隧道、土体、泥水的相互作用。不同于单一物质，试验中很难保证所有的参数都满足相似性，只能在关键影响参数做到满足相似原理。基于上述对泥水劈裂基本物理过程的分析，根据Butterfield量纲分析法^[23-24]，首先将离心试验中泥水劈裂作用过程中涉及的关键参量列出如下：

（1）隧道：覆土厚度H、隧道直径D；

（2）土体：不排水抗剪强度${c_{\text{u}}}$，内摩擦角φ，密度${\rho _{\text{c}}}$，土体固结系数${c_{\text{v}}}$，弹性模量E，渗透率$\kappa$，泊松比$\nu$，粒径d；

（3）泥水：流体密度${\rho _{\text{s}}}$，流体黏度μ，泥水压力P_s，泥水流量q，裂缝宽度w，长度L以及开度e，泥水伸展速度u；

（4）环境：重力加速度g，时间t。

取质量M、长度L、时间T作为3个基本量纲，各参数量纲形式如表 1所示。

表  1  离心模型试验参数相似关系

Table  1.  Similarity relationship of centrifuge modelling parameters

物理量	量纲	相似比
重力加速度(m·s-2)	LT-2	1∶N
隧道直径(m)	L	1∶N
隧道埋深(m)	L	1∶N
土体密度(kg·m-3)	ML-3	1∶1
土体粒径(mm)	L	1∶1
弹性模量(MPa)	ML-1T-2	1∶1
不排水抗剪强度(kPa)	ML-1T-2	1∶1
渗透率(m2)	L2	1∶1
固结系数(m2·a-1)	L2 T-1	1∶1
内摩擦角	1	1∶1
泊松比	1	1∶1
泥水压力(kPa)	ML-1T-2	1∶1
泥水密度(kg·m-3)	ML-3	1∶1
泥水黏度(Pa·s)	ML-1T-1	1∶1
裂缝长度(mm)	L	1∶N
裂缝宽度(mm)	L	1∶N
裂缝开度(mm)	L	1∶1
流量(m3·s-1)	L3T-1	1∶N
流速(m·s-1)	ML-1	1∶1
时间（劈裂）(s)	T	1∶N
时间（固结）(s)	T	1∶N2

下载: 导出CSV 

| 显示表格

2.2   无量纲项的导出

盾构泥水劈裂作用过程涉及20个物理量，将所有物理量生成变量集合V为

根据Buckingham定理，取流体密度、伸展速度、长度为独立基本物理量，需要指出的是，本研究中长度涉及到宏观和微观两个尺度，因此最终可以生成16组无量纲项如下：

上述导出的16组无量纲项控制着离心试验中泥水劈裂的启裂，伸展以及喷发全过程的相似性。现分别从尺寸、材料、无量纲数、时间等方面分析并建立盾构泥水劈裂离心试验的相似准则。

3.   “隧道-土-泥水”系统相似性建立

3.1   尺寸

从物理上讲，对于多孔介质来说，至少存在两种长度尺度：微观长度尺度（如粒度）和宏观长度尺度（如样本大小）^[25]。以往研究显示，一旦流体进入裂缝，相似性将取决于流动机制本身^[16]。因此，在考虑裂缝流体流动时，对于裂缝长度与宽度，边界长度等一般认为是宏观尺寸，其相似比例一般为1∶N；而土体粒径、裂缝开度等均为微观尺寸，其相似比例一般为1∶1^{[11, 26]}。

（1）宏观尺寸

无量纲项中的$H/L,D/L,w/L$为反应宏观尺寸的无量纲数。在设计离心模型试验时，模型宏观大小一般均按照设计加速度N进行缩放，因此，无量纲项${\pi _1},{\pi _2},{\pi _{14}}$在原型与离心模型试验中相等恒成立。

（2）微观尺寸

$d/e$为反应微观尺寸的无量纲数，该无量纲项在以往的离心模型试验相似关系设计中为$d/L$，由于离心模型试验中的粒径尺寸效应不可避免，$d/L$并不满足无量纲数相等的相似要求，但当$d/L$在一定范围内时，可以忽略粒径尺寸效应带来的误差^{[9, 16]}（本试验模型土颗粒粒径与结构尺寸之比在可以忽略粒径尺寸效应带来误差的范围内）。而在本试验中，对于泥水劈裂产生的裂缝而言，裂缝开度属于微观尺寸，因此，本文将该无量纲项考虑为土体粒径与裂缝开度的比值。若要保证该无量纲项${\pi _{10}}$相等，就意味着泥水劈裂引发裂缝的开度在模型与原型中应该基本一致，或者说至少应该处于同一量级范围内。

3.2   材料

（1）黏土

一般离心试验中采用与原型相同的土体材料，因此无量纲项${\pi _4},{\pi _9}$在模型与原型中相等恒成立。此外，渗透率$\kappa$反应了土体排水特性，与土体孔隙、形状及排列有关，是土体渗透性的内在指标，其在模型与原型中也相等，因此无量纲项${\pi _8}$相等也成立。

（2）泥水

还原真实的流体环境是在离心模型试验中实现盾构泥水劈裂现象还原的关键，对于试验的真实性与可靠性具有重要意义。还原真实的流体环境不仅仅是对原型水条件的复制，对于盾构泥水劈裂问题而言，在控制各流体在模型与其相应原型之间比例关系的同时还需控制流体环境中各流体之间的相对比例关系。

本试验中采用原型土体，要保证无量纲项${\pi _5}$的成立，意味着试验中的泥水密度也要与实际中的泥水密度相等。而对于泥水黏度的相似比例还需进一步通过泥水劈裂现象中涉及到的无量数进行确定。

3.3   无量纲数

（1）欧拉数（Euler number）

无量纲项${\pi _{12}}$即为欧拉数，考虑泥水压力与惯性力的作用关系。前面提到试验中的泥水密度应与实际中的泥水密度相等，因此，要保证欧拉数的相等，泥水劈裂后的伸展速度在模型与原型中也应该相等。

（2）雷诺数（Reynolds number）

无量纲项${\pi _{11}}$即为雷诺数，考虑泥水惯性力与黏性力的作用关系。前面分析推导得到泥水伸展速度的相似比例为1∶1，若要保证雷诺数的相等，则泥水黏度的相似比例也应该为1∶1。

（3）归一化速度（Normalized velocity）

无量纲项${\pi _6}$即为归一化速度，考虑泥水劈裂作用下土体的固结效应，试验中采用原状土，因此固结系数相似比例为1∶1，根据前面的分析，裂缝开度和伸展速度相似比例也均为1∶1，因此模型归一化速度与原型归一化速度相等成立。

（4）归一化时间（Normalized time）

归一化时间考虑裂缝流动时间与孔压消散时间的相对关系，由无量纲项${\pi _7},{\pi _8},{\pi _{11}},{\pi _{14}}$共同决定，前面分析了${\pi _8},{\pi _{11}},{\pi _{14}}$的成立，无量纲项${\pi _7}$与${\pi _{12}}$性质相似，根据欧拉数的分析，${\pi _7}$在泥水劈裂伸展速相似比例为1∶1的前提下是成立的。

3.4   时间

（1）固结时间

试验中采用原型土体，模型与原型中试样的渗透率相等，然而土体渗透系数不仅受土体固有特性的影响，同时也受渗流流体特性的影响。试验中试样通过水搅拌后固结，土体渗透系数计算公式如下：

式中：${\rho _{\text{w}}}$与${\mu _{\text{w}}}$为水的密度与黏度。

通过上式可知模型中的渗透系数是原型的N倍，由于原型中的宏观尺寸是模型的N倍，因此土体固结过程要比原型快n²倍，固结时间比例应为1∶N²。

（2）泥水劈裂作用时间

无量纲项${\pi _{16}}$涉及泥水劈裂的作用时间，根据前面的分析，伸展距离与速度相似比例分别为1∶N和1∶1，因此泥水劈裂作用时间相似比例为1∶N。由此可知，本离心试验中土体固结时间比尺是泥水劈裂作用时间比尺的N倍。

通过以上相似性分析，最终确定盾构泥水劈裂离心试验参数相似关系如表 1所示。

4.   试验验证

通过上述分析，理论上建立了盾构开挖面泥水劈裂离心模型试验的相似准则：即模型中土体与泥水各特性参数均与原型保持一致，通过开展软黏土地层盾构开挖面泥水劈裂的离心模型试验，验证本文提出的相似性准则。

4.1   试验装置

本次离心模型试验依托新加坡国立大学土工离心机。吊篮空间为0.75 m（长）×0.7 m（宽）×1.2 m（高），离心机半径（轴线到箱底半径）为5 m，有效容量40 g·t。重力水平增加时测试的复杂性和离心机尺寸限制的小型化要求使得本试验设备的设计和加工非常具有挑战性。

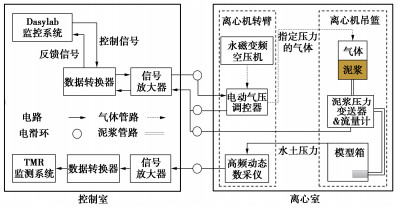
试验设计原理框架如图 1所示，主要包括控制室和离心室的装置设计。其中控制室里主要包括Dasylab监控系统和TMR监测系统，前者主要进行泥水压力与流量的监测以及气压的监测与控制；后者主要负责模型箱中水土压力的监测。离心室里主要包括离心机转臂上的气压系统和高频动态数采仪以及离心机吊篮里的泥水系统和模型箱装置。试验过程中，离心室里通过泥水压力变送器、流量计以及高频动态数采仪监测到的信号通过电滑环传输到控制室，并通过信号放大器和数据转换器将信号转换至监测与监控系统。根据接收到的反馈信号，通过Dasylab监控系统发送气压控制信号，经由同样的传输线路发送至离心机转臂上的气压调控器，进而控制泥水压力。

图  1  试验设计原理框架图

Figure  1.  Schematic diagram of experimental design principle

下载: 全尺寸图片 幻灯片

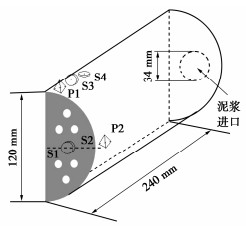
试验设计离心加速度为100g，模型隧道的直径为120 mm，几何相似比为100。考虑模型试验的对称性，设计模型盾构机为封闭半圆形刚性装置紧贴土箱侧面布设，该侧面配有高强度、高透明度的有机玻璃窗，试验时可通过高清运动相机进行图像采集。隧道模型前方为可拆卸开挖面钢板，开口率约为15%，隧道后方有一个直径约为34 mm的开口连通泥水管。试验中水土压力采用TMR微型土压计，通过TML高频动态数采仪进行实时监测，监测频率最高可达1000 Hz，离心室各装置布设如图 2所示。

图  2  离心室装置布设图

Figure  2.  Layout of devices in centrifugal chamber

下载: 全尺寸图片 幻灯片

4.2   材料与监测方案

试验采用马来西亚高岭黏土，与水按照1∶1.2的比例真空混合搅拌约6 h，而后以100g的离心加速度固结约10 h制成，材料参数如表 2所示。

表  2  马来西亚高岭黏土力学参数表

Table  2.  Mechanical parameters of Malaysia kaolin clay

材料	液限/ %	塑限/ %	相对质量密度	内摩擦 角/(°)	固结 系数	渗透 系数
马来西亚高岭黏土	80	40	2.65	24	40 m2/a	2×10-8 m/s

下载: 导出CSV 

| 显示表格

泥水通过小离心机进行配比试验，调配得到钠基膨润土和水配比为8∶100时可以保证泥水在高离心加速度下不发生离析。试验监测方案如图 3所示，水土压力传感器均沿着模型隧道表面布设，其中S2位于开挖面中心高度处的背面，因此S2主要监测开挖面处的泥水压力而S1主要监测开挖面前方的水土压力。

图  3  水土压力布设方案

Figure  3.  Layout of pressure sensors

下载: 全尺寸图片 幻灯片

4.3   结果分析

试验中通过高清运动相机对模型箱的实时录制，观测到泥水从开始启裂出现裂缝到喷发至地表大概用时3~4 s的时间，伸展速度约为0.03~0.04 m/s，与Yuan等开展的1g模型试验（0.026 m/s）以及刘学彦等开展的现场泥水劈裂试验（0.034 m/s）^[27]中测得的泥水伸展速度基本一致。泥水劈裂后裂缝形态如图 4所示，结束后对裂缝形态进行测量得到裂隙开度约为1~3 mm，考虑试验后裂缝有一定的收缩，实际劈裂过程中裂缝的开度应该在2~4 mm左右，与前人观测到的裂缝宽度基本一致。若将离心试验测量得到的裂缝开度进行N倍缩放，意味着原型中的裂缝开度将达到0.2~0.4 m，这在实际中显然是不存在的，因此进一步验证了本文建立相似关系的合理性。

图  4  泥水劈裂裂缝形态

Figure  4.  Morphology of slurry fracturing cracks

下载: 全尺寸图片 幻灯片

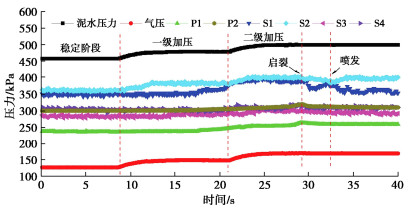
试验过程中监测的泥水压力、气压以及隧道附近的水土压力如图 5所示。随着泥水压力的逐级增加，开挖面背面处S1监测到的压力与泥水压力基本保持一致。而开挖面正面处S2监测到的侧向土应力虽然也逐渐增加，但没有呈现与S1类似逐级增加的模式。拱顶处的土应力随着泥水压力的增加存在一定滞后性，前期只是小幅度增加，在启裂前突增，并在启裂时达到峰值，而后随着劈裂的伸展急剧减小，并在喷发后逐渐保持稳定。其中竖向土压力与侧向土压力在泥水劈裂过程中趋于相等，可能是由于启裂后，拱顶附近已经形成泥水通路，竖向土压力计与横向土压力计监测到的压力实际上均为泥水的压力。

图  5  试验中水土压力的变化

Figure  5.  Variation of soil and pore pressures during tests

下载: 全尺寸图片 幻灯片

开挖面附近的孔隙水压力随着泥水压力的逐级增加而呈现非线性增加趋势，并且存在一定滞后性。其中拱顶处的孔压增幅比开挖面中心高度处的孔压增幅更大，并且在泥水压力加压过程存在小幅骤降，说明此时开挖面附近已经出现一些小裂纹的启裂，但泥水压力还不足以支撑泥水进一步伸展。当泥水劈裂快要发生时，孔隙水压力的增速也突然增大，并在启裂时达到峰值，而后随着劈裂的伸展逐渐减小并在喷发后趋于稳定。

试验中土体启裂时开挖面中心处的泥水压力约为400 kPa，试验过程监测到水土压力随泥水压力的变化包括启裂时的骤降与以往研究均基本一致^{[2, 5, 26]}，说明本文建立的相似准则能够有效还原盾构泥水劈裂中的应力场。此外，流量在启裂时从稳定状态突增，变化规律也与前人研究保持一致^[27]。限于本文篇幅，针对试验结果的深入分析将在后续研究中进一步开展。

5.   结论

（1）阐明了盾构开挖面泥水劈裂启裂-伸展-喷发的基本物理全过程，提出了基于欧拉数、雷诺数、归一化速度与归一化时间等无量纲数相等的相似性推导方法。

（2）基于Butterfield量纲分析法建立了应用于土工离心机模拟盾构泥水劈裂的“隧道-土-泥水”系统相似性试验设计体系，分别从尺寸、材料、无量纲数、时间等多方面保证了模型系统与原型系统的相似性。

（3）盾构泥水劈裂离心模型试验中，材料关键物理力学参数如密度、泥水黏度、土体不排水抗剪强度等相似比例均为1∶1。泥水劈裂宽度、长度等参数为宏观尺寸，相似比为1∶N，而裂缝开度，粒径等参数为微观尺寸，相似比为1∶1。

（4）通过开展盾构泥水劈裂离心模型试验，，验证了本文建立的相似性准则，为相关泥水劈裂物理模拟的相似性分析提供一定参考。