砂土地基中螺旋锚上拔承载特性试验与理论研究

胡伟; 林天宇; 林志; 冯世进; IVANPuig Damians

doi:10.11779/CJGE20230394

砂土地基中螺旋锚上拔承载特性试验与理论研究 English Version

1.
岩土工程稳定控制与健康监测湖南省重点实验室, 湖南湘潭 411201
2.
福建省高速公路融通投资有限公司, 福建福州 350005
3.
同济大学地下建筑与工程系, 上海 200092
4.
Department of Civil and Environmental Engineering (DECA), School of Civil Engineering, Universitat Politècnica de Catalunya-BarcelonaTech (UPC), Jordi Girona 1-3, 08034 Barcelona

基金项目:

国家自然科学基金项目 52178332

详细信息

作者简介:
胡伟(1982—)，男，博士，教授，博士生导师，主要从事地基与基础工程方面的教学与研究工作。E-mail: yilukuangben1982@163.com

中图分类号: TU441
计量
- 文章访问数: 585
- HTML全文浏览量: 94
- PDF下载量: 127
出版历程
- 收稿日期: 2023-05-04
- 网络出版日期: 2023-11-29
- 刊出日期: 2024-07-31

Experimental and theoretical studies on modeling of uplift bearing characteristics of screw anchors in sandy soil foundation

1.
Hunan Province Key Laboratory of Geotechnical Engineering Stability Control and Health Monitoring, Xiangtan 411201, China
2.
Fujian Expressway Rongtong Investment Co., Ltd., Fuzhou 350005, China
3.
Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
4.
Department of Civil and Environmental Engineering (DECA), School of Civil Engineering, Universitat Politècnica de Catalunya-BarcelonaTech (UPC), Jordi Girona 1-3, 08034 Barcelona, Spain

摘要

摘要: 目前多锚片螺旋锚上拔承载的理论研究需人为引入临界埋深比和临界间距比的概念，这将一个连续演化问题割裂成多种特殊工况，但两个临界值的取值标准又存在不统一的问题，导致理论的工程应用存在风险。基于模型试验并结合数字照相测量技术开展砂土地基中螺旋锚上拔承载特性研究，主要得到以下结论：①单、双锚片螺旋锚上拔荷载位移曲线的变化均可分为增长区间和震荡下降区间两个阶段，埋深比越大，荷载峰值越高，但随之增强的土拱效应也导致曲线震荡幅度越显著。②抗拔承载力突破因子N_γ随埋深比的变化曲线存在峰值特征，先快速增大后缓慢减小；下层锚承载力发挥系数η随间距比的增大呈先快后缓的增加趋势。③多锚片螺旋锚的各层锚片对应的破坏滑动面均可用随埋深比增大长短轴比逐渐减小的椭圆来刻画，首层锚滑动面与同埋深下单锚片滑动面形态一致，下层锚滑动面的椭圆长短轴之比受到间距比变化的影响可分为3个阶段。④多锚片螺旋锚的首层锚和下层锚各自有3种滑动面工况，对应3种力学模型，这取决于埋深比和间距比，螺旋锚总的上拔承载力学模型由它们组合而成。⑤推导建立了多锚片螺旋锚上拔承载力计算方法，该方法可以考虑任意锚片数量、埋深比和间距比，并通过对4个松砂和中密砂地基中试验案例的计算验证了该方法的有效性。
- 螺旋锚 /
- 埋深比 /
- 间距比 /
- 抗拔承载力 /
- 承载力发挥系数 /
- 滑动面
Abstract: At present, it is necessary to introduce the concepts of the critical burial depth ratio and critical spacing ratio artificially into the theoretical researches on the uplift bearing of screw anchors with multiple blades, which divides a continuous evolution problem into two special working conditions. However, the criteria of the two critical values are inconsistent, leading to risks in the engineering application of the theory. Based on model tests and combined with the digital photographic measurement technology, the studies on the uplift bearing characteristics of screw anchors in sandy soil foundation are made, and the main conclusions are drawn as follows: (1) The variation of the uplift load displacement curves of the screw anchors with single and double blades can be divided into two stages, growth interval and oscillation decline interval. The larger the burial depth ratio, the higher the peak load, but then the enhanced soil arching effects also lead to the more significant oscillation amplitude of the curve. (2) The curve of the breakout factor N_γ with the burial depth ratio has a peak characteristic, which increases rapidly first and then decreases slowly. The bearing capacity playing coefficient η of lower blade increases rapidly and then increases slowly with the increase of spacing ratio. (3) The failure sliding surface corresponding to each layer of the screw anchor with multi-blades can be characterized by an ellipse with the decreasing axis ratio as the depth ratio increases. and the sliding surface shape of the first blade is consistent with that of the single blade with the same burial depth. The axis ratio of the ellipse of the sliding surface of the lower anchor can be divided into three stages under the influences of spacing ratio. (4) There are three sliding surface conditions of the first-layer anchor and the lower-layer anchors, respectively, corresponding to three mechanical models, which depend on the buried depth ratio and the spacing ratio. The overall mechanical model for the screw anchors is composed of them. (5) A method for calculating the uplifting capacity of the screw anchors with multiple anchor plates is developed to consider any number of anchor blades, buried depth ratio and spacing ratio. The effectiveness of the proposed method is verified by the calculation of four test cases in loose sand and medium-dense sand foundation.
- screw anchor /
- burial depth ratio /
- spacing ratio /
- uplift bearing capacity /
- playing coefficient of bearing capacity /
- sliding surface

HTML全文

0. 引言

螺旋锚是一种具有良好抗拔承载性能的基础型式，且具有施工便捷、适应性强和经济环保等优点，当前正在被大量应用于建筑、电力、交通、水利等多个领域的工程实践中^[1]。螺旋锚一般采用机械方式施加扭矩旋入土中，工程中为了降低螺旋锚的旋入难度或获得更大的承载能力，通常采用多锚片方案^[2]。

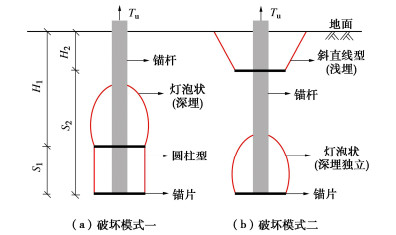
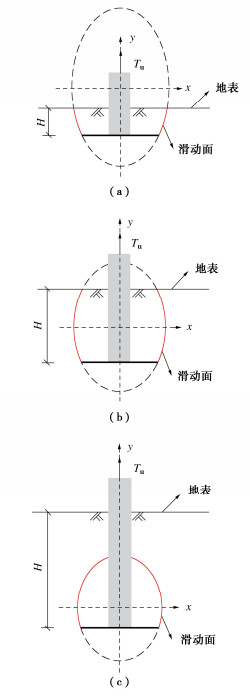
螺旋锚的上拔承载能力主要由锚片提供，上拔时螺旋锚的荷载传递机制是从首层锚开始，自上而下，逐步逐层往下层锚传递的，直至所有锚片都达到承载能力极限状态^[3]。既有研究表明：螺旋锚各锚片的承载特性与其所处位置（首层锚还是下层锚）、埋深和锚片间距有关，且上层锚不受下层锚的影响，但却对下层锚产生影响，故间距只影响下层锚^[4-5]。对于首层锚，其承载特性只与其埋深有关，随着埋深的增大，破坏时相应的滑动面将出现两种截然不同的形态，即浅埋时延伸至地表的直线或曲线型^[6]和深埋时局限于土体内部的“灯泡状”型^[7]。对此，研究中一般引入临界埋深比的概念首先区分浅埋深埋类型，而后分别构建承载力学模型^[8-9]。姚琛等^[10]总结了既有成果提出的临界埋深比取值标准，发现各标准间差异十分显著，尚无统一认识，并分析了这可能给工程带来的安全风险。下层锚的承载特性不仅与其埋深有关，还很大程度上受其与上一层锚片的间距影响^[11]。若该间距足够小，拉拔时只有上下层锚间的土层会对下层锚产生阻力作用，下层锚冲切该土层，最终沿着上下层锚的边缘形成贯通性的圆柱形滑动面^[12]，下层锚的承载力不能充分发挥。若该间距足够大，上层锚对下层锚的影响则可以忽略，下层锚可视为独立承载，承载特性只取决于其埋深^[13]。为了区分下层锚的这两种破坏模式，研究中又引入了临界间距比的概念，表 1中对该值进行了统计。不难看出，和临界埋深比取值一样，临界间距比各取值标准间差异同样也十分显著。上述分析可知，基于当前的研究成果开展多锚片螺旋锚承载性能理论分析需先引入临界埋深比和临界间距比两个参数先划定每个锚片的承载破坏类型。以双锚片螺旋锚为例，其首层锚存在浅埋和深埋两种工况，下层锚也存在独立承载量破坏和非独立圆柱形剪切面破坏两种工况，其中独立承载又需进一步区分浅埋和深埋类型，组合之后整个螺旋锚的承载力学模型共有5种。图 1给出了其中两种，图 1（a）是上层锚深埋呈灯泡状破坏，下层锚圆柱剪切破坏；图 1（b）是上层锚浅埋呈斜直线型破坏，下层锚深埋独立承载破坏。这样看来，相较于单锚片螺旋锚，双锚片螺旋锚承载性状的力学表征难度显著增大，其他多锚片情况则更加复杂。加上临界埋深比和间距比取值标准尚未有统一认识，其叠加效应将进一步降低表征的准确性，于工程实践是极为不利的。产生这种后果的根本原因是对螺旋锚上拔破坏滑动面随埋深、间距连续演化的本质特征认识和表征不充分，人为引入临界值进行割裂所致。Ghaly等^[14]、朱长歧等^[15]均在试验中发现并指出，随着埋深比的增加，滑动面由浅埋型向深埋型渐近转化，其间并没有明显的界限。

表 1 不同临界间距比取值标准

Table 1. Different standards of critical spacing ratio

标准来源	临界间距比（S/D）	土体类别
Tsuha等^[4]	3	砂土
Tappenden等^[12]	2	天然土
Merifield ^[13]	1.58	黏性土
Stanier等^[16]	3	软黏土
姚敬宇^[17]	2	密砂
郝冬雪等^[18]	1.5	中密砂

下载: 导出CSV

| 显示表格

图 1 典型双锚片螺旋锚竖向拉拔破坏模式

Figure 1. Typical uplift failure modes of screw anchors with double blades

下载: 全尺寸图片幻灯片

可见，多锚片螺旋锚上拔承载性状的理论研究需重新审视以往引入临界埋深比和间距比的思路，而从连续演化的视角来看待和表征滑动面随埋深和间距的变化。为此，本文在砂土地基中开展单、双锚片螺旋锚的模型试验，研究承载性能的变化规律；基于数字照相测量技术对下层锚周土体的滑动面进行提取，开展特征分析和理论表征；最后针对多锚片螺旋锚力学模型的构建和承载力计算提出新的分析思路和方法。

1. 模型试验简介

1.1 试验装置

本文采用的可视化半模试验装置包括试验砂箱、加载系统、数据采集系统均同文献[19]。试验用模型螺旋锚的制作则综合考量模型箱尺寸、锚片间距以及工程中螺旋锚的规格，并基于相似比例进行设计。常用螺旋锚通常由锚头（导程）、锚杆和螺旋叶片三部分组成，相应参数主要有锚杆直径、锚片直径、锚片间距、螺距和厚度。锚头主要作用是便于旋入，对承载性能基本没有影响，故模型制作时不予考虑。郝冬雪等^[18]通过小比尺模型试验证明了平板圆锚上拔承载性能与等直径螺旋锚差异很小，可以忽略。考虑到模型加工和安装的难度，采用平板圆锚替代螺旋锚开展试验。结合市面上螺旋锚锚片与锚杆直径比的常用规格（2.5~3.4），本次平板圆锚模型锚片采用直径D=5 cm，厚度t=2 mm的半圆形钢片，杆径d设计为1.7 cm，锚片与锚杆直径比为2.94，如图 2所示。

图 2 平板圆锚模型

Figure 2. Model for circular flat anchor

下载: 全尺寸图片幻灯片

1.2 试验用砂及试验工况

试验用砂同文献[19]，由标准砂和彩色石英砂混合而成，其物理力学指标如表 2所示，彩砂物理力学性质指标如表 2所示。表 2中，φ为试验用砂的内摩擦角；γ为土体重度；ρ_dmin为最小干密度；ρ_dmax为最大干密度；D_r为相对密实度；C_u为不均匀系数；C_c为曲率系数。砂土地基填筑方式和锚板安装方法均与文献[19]中保持一致。本次试验以锚片埋深比和间距比为变量设计试验工况，如表 3所示。锚片螺旋锚设计12种埋深比，双锚片螺旋锚设计5种首层锚埋深比和6种间距比，共计42种试验工况。为确保试验数据合理有效，正式试验前先选取代表性工况进行预试验，待确认试验可靠性后对每个工况开展两次平行试验，若两次试验结果有明显差异则增加试验次数。

表 2 试验用砂物理力学指标

Table 2. Physical and mechanical indexes of test sand

D_r	C_u	C_c	φ/(°)	ρ_dmin/ (g·cm^-3)	ρ_dmax/ (g·cm^-3)	γ/(kN·m^-3)
0.57	2.5	1.1	33.1	1.616	1.766	16.56

下载: 导出CSV

| 显示表格

表 3 试验工况

Table 3. Test conditions

锚片数	首层锚埋深比H/D	锚片间距比S/D
1	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	0
2	1, 2, 4, 6, 8	1.0, 1.5, 2.0, 3.0, 4.5, 6.0

下载: 导出CSV

| 显示表格

1.3 试验方法

砂样制备采用落雨法结合分层法进行，分层厚度为5 cm。当砂面高度到达锚板预设高度后，将平板锚模型轻置于砂面上，使其对称面紧贴于试验箱前玻璃板内侧并保持竖直，继续填筑砂土至达到预设埋置深度为止。加载过程采用位移控制，单调加载速率为0.01 mm/s，当上拔位移量累计达到10 cm后，结束加载。试验过程中，数码相机固定在有机玻璃试验箱正前方1.5 m处，调节相机镜头轴线和锚片处在同一个高度，设置相机定时拍间隔为5 s/张。

2. 螺旋锚上拔承载特性规律分析

2.1 单锚片试验结果分析

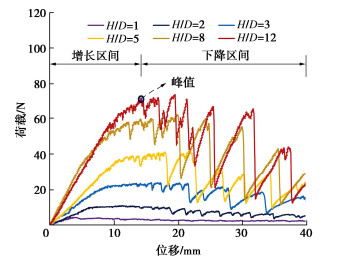
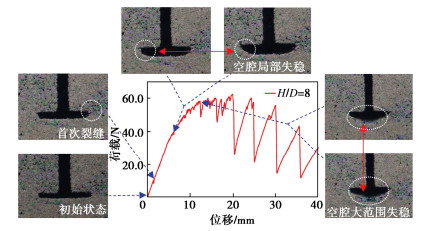
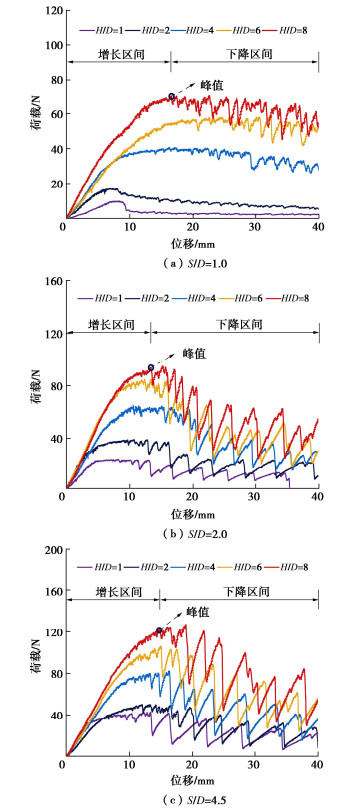
试验结果表明：埋深比越大，临近埋深比的荷载-位移曲线间的差异越小，故为避免曲线重叠显示不清，取代表性埋深比（H/D=1，2，3，5，8，12）绘制单锚片螺旋锚上拔荷载位移曲线。另外，虽然试验设置极限拉拔位移为100 mm，但从曲线结果来看，40 mm位移所对应的曲线段已可以反映出整个曲线的主要特征，故为提高作图效果，设置图中最大位移为40 mm。如图 3所示，所有埋深比下的曲线均存在峰值特征，且以峰值点为界限曲线可分为两个阶段，即增长区间和震荡下降区间。具体表现为：初始时，荷载随位移的增加快速线性增大；至一定位移值后，荷载增长速率开始减小，曲线趋缓并伴随小幅震荡，且很快达到峰值；峰值之后进入第二阶段，荷载减小，曲线出现大幅震荡，且埋深比越大，曲线震荡幅度越大，与峰值承载力相比，最终位移对应承载力的降幅也越大。曲线出现震荡的主要原因在于拉拔后，锚片下方会逐渐形成空腔，该空腔的大小和稳定性会随着拉拔不断发生变化。图 4给出了拉拔过程中空腔变化与荷载位移曲线的对应关系（以H/D=8为例），两者间的相关性显著。在拉拔之初，空腔即开始形成，在较小位移时，最先在锚板两端土体出现肉眼可见裂缝，荷载位移曲线相应出现单个波动，但此时土拱效应还未失效，土颗粒没有流泻。随着位移继续发生，空腔增大，裂缝进一步扩展，至一定时刻，空腔两端处因土拱效应局部失效而发生小范围失稳，少量土颗粒脱落流泻至空腔，从而导致上部土体应力一定幅度释放，荷载将有所降低。因土颗粒的脱落过程是不断发生的，则荷载位移曲线即相应发生连续的小幅震荡。位移继续增大至一定数值，土拱效应将首次出现大范围失效，空腔大规模坍塌，导致上部土体应力大幅释放，荷载骤然降低，对应荷载位移曲线第一次出现大幅跌落。随着拉拔继续进行，锚片又重新压密上方土体，土压力增大，荷载再次升高，空腔则在新的土拱效应下可维持暂时的整体稳定，局部失稳则持续进行，荷载位移曲线小幅震荡，但由于此时锚周土体的累积位移变形量已很大，进一步抵抗变形的能力很弱，导致空腔越发容易大范围失稳，并在之后的拉拔过程中反复发生，第二阶段曲线即表现为大幅震荡。埋深比越大，砂土所受的约束程度越强，砂土从锚片边缘流泻后造成土中应力释放的幅度越大，拉力降幅也就越大。郝冬雪等^[18]、Rowe等^[20]的试验研究中也曾观测到这种空腔形成变化与荷载位移曲线变化的现象。

图 3 代表性荷载-位移曲线

Figure 3. Representative load-displacement curves

下载: 全尺寸图片幻灯片

图 4 空腔变化与荷载位移曲线对应关系

Figure 4. Relationship between cavity change and load-displacement curve (H/D=8)

下载: 全尺寸图片幻灯片

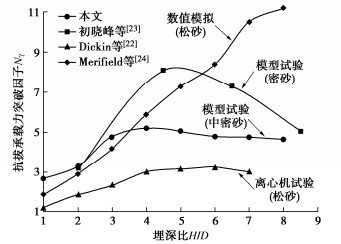
根据Bradshaw等^[21]的研究，在1g模型试验中，通过缩放土体的本构行为和以无量纲化形式表达承载力可以将尺寸效应减小到最低，定义无量纲抗拔承载力突破因子N_γ= T_u/γAH，其中T_u为抗拔极限承载力，γ为砂土有效重度，A为锚片面积，H为螺旋锚锚片埋置深度。抗拔承载力突破因子N_γ随埋深比的变化规律如图 5所示，N_γ先随着埋深比的增长而快速增加，在H/D=4左右时达到峰值，然后有较小程度的下降。曲线呈现的峰值特征与Dickin等^[22]进行的离心机试验结果相似，但后者的曲线在H/D=6左右时才达到峰值。初晓锋等^[23]在密砂中的模型试验结果呈现出更为显著的峰值特征，峰值在埋深比为5左右，而在其前后承载力突破因子都随埋深比快速变化。值得注意的是许多其他研究结果却并非如此。如Rowe等^[20]和Ilamparuthi等^[9]的试验结果呈现双曲线特征；Merifield等^[24]的数值模拟结果以及Liu等^[25]和Cerfontaine等^[26]的统计结果都显示N_γ随着埋深比的增长而增加，且增长速率在研究范围内未见减缓趋势，这与郝冬雪等^[18]试验结果不符；Choudhary等^[27]的数值模拟曲线则同时具有这两个特点，当土壤的内摩擦角小于40°时表现为双曲线；否则，曲线增长呈加速趋势。由此可见，数值模拟、模型试验和离心机试验的结果尚存在较大差异，目前对抗拔承载力突破因子N_γ随埋深比的变化规律仍未达成共识，但相比模型试验和数值模拟而言，离心机试验应更具有说服力，而最终还需要通过原型试验来检验其准确性。

图 5 N_γ随埋深比变化规律

Figure 5. Variation of N_γ with burial depth ratio

下载: 全尺寸图片幻灯片

2.2 双锚片试验结果分析

双锚片螺旋锚代表性上拔荷载-位移曲线（S/D为1.0，2.0，4.5）分别如图 6所示。与单锚片曲线相似，双锚片螺旋锚荷载-位移曲线同样表现出两阶段性和震荡性。间距比一定时，首层锚埋深越大，荷载峰值越大，即极限承载力随埋深的增大而增加。而首层锚埋深比一定时，随着锚片间距比增大，极限承载力同样增加且曲线震荡幅度加大。曲线震荡幅度增大的原因主要是由于埋深比越大，土体的受约束程度越强，土拱效应也越显著，这样当土拱效应失效，空腔发生失稳时，荷载的下降幅度也就越大。对于多锚片螺旋锚而言，其承载机制不仅涉及锚-土相互作用，还存在锚-锚相互作用。由于锚片的承载能力主要来自其上部土体的抗力，因而锚-锚相互作用主要是指上层锚对下层锚的影响，而下层锚对上层锚的影响相对较小。为理清这种相互作用机制，对双锚片螺旋锚下层锚和同等埋深情况下单锚片的承载力发挥情况进行对比。定义下层锚的承载力发挥系数η等于双锚片螺旋锚极限承载力T_u与其首层锚同埋深的单锚片螺旋锚极限承载力T₁的差值与下层锚同埋深的单锚片螺旋锚极限承载力T₂的比值：

$\eta = \frac{{{T_{\text{u}}} - {T_1}}}{{{T_2}}} \times 100{\text{% }}。$

(1)

图 6 荷载-位移曲线

Figure 6. Load-displacement curves

下载: 全尺寸图片幻灯片

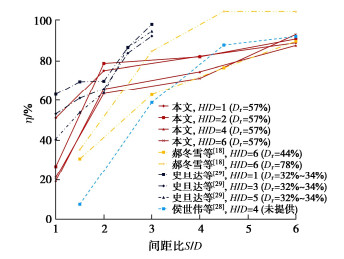
双锚片螺旋锚下层锚承载力发挥系数随锚间距的变化如所示。总体上，不同埋深比下下层锚承载力发挥系数随间距比的变化规律较为一致，即 $\eta$ 随间距比的增大非线性增长，速率先快后缓。间距比相同的情况下，埋深比越小，承载力发挥系数一般越大。S/D=1时，除H/D=1外，其他工况下的发挥系数都较小，在19.2%~26.5%；当S/D增加到2时，发挥系数显著增大至63.3%~74.9%，随后增速减缓，至埋深比H/D=6时，发挥系数保持在90%左右。下层锚的承载力发挥系数始终是小于1的，本次试验的最大值约为92.9%，这与上层锚的承载力发挥减小下层锚上部土层的应力有关。类似成果在其他人的研究中也有体现，侯世伟等^[28]、郝冬雪等^[18]（中密砂D_r=44%）的试验在小间距比1.5时η分别为7.6%和30.7%，小于本次试验，尤其是前者；间距比大于4后，则在58.8%~91.8%变化，与本次试验结果接近。史旦达等^[29]的结果规律则刚好相反，间距比为1~2时，η在40.7%~63.8%变化，与本文结果较相近，但该阶段增长速率要小于本文；当间距比为3时，发挥系数最大值已达到97.8%，远高于本文与其他试验结果。郝冬雪等^[18]（密砂D_r=78%）的试验在小间距比时发挥系数和本文较为接近，但大间距比时发挥系数已大于1，理论上应是不可能的，可能是试验误差所致。总的来说，本文结果介于其他结果之间，代表性较好。

图 7 发挥系数η随间距比变化

Figure 7. Variation of η with spacing ratio

下载: 全尺寸图片幻灯片

3. 锚周土体变形破坏分析

锚片上拔至极限承载的过程即对应锚周土体变形累积至到滑动面形成扩展延伸直至破坏的全过程，因而开展锚周土体的变形破坏分析是理清螺旋锚上拔承载机制的前提。

3.1 锚周土体滑动面形成延伸力学分析

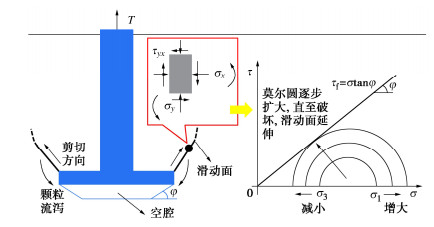
锚周土体滑动面形成与空腔变化相关力学分析如所示。锚片上拔时，其正上方土体最先受到竖向挤压，锚片外侧土体则受正上方土体的侧向挤压作用，导致其土体单元水平应力 ${\sigma _x}$ 增大；当锚片下方空腔由于土拱效应失效而发生坍塌时，土颗粒从锚片边缘流入空腔，使得锚片边缘外侧土体单元的竖向应力 ${\sigma _y}$ 减小。在两者的共同变化下，土体单元的应力莫尔圆将逐步扩大，直至达到极限状态，土体单元发生破坏，滑动面形成并在接下来的拉拔过程中逐步扩展延伸。

图 8 空腔变化与滑动面形成的相关力学机制

Figure 8. Mechanical mechanism of cavity variation and sliding surface formation

下载: 全尺寸图片幻灯片

3.2 首层锚锚周土体滑动面形态分析

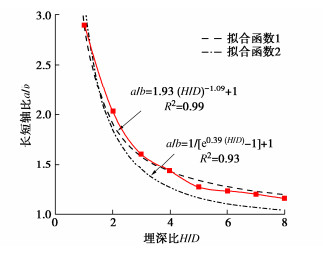
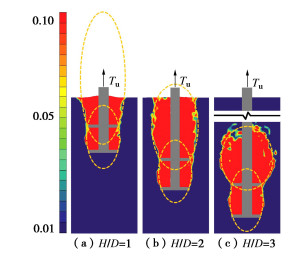
应用Photoinfor和Postviewer数字图像分析软件对试验过程中拍摄的锚周土体图像进行处理，获得极限拉拔时锚周土体的最大剪应变场云图。由于极限拉拔时，锚周土体的变形梯度很大，若全域显示变形区间将无法精准识别滑动面。本文根据典型岩土工程破坏所对应的应变量级，设置应变显示区间为0.01和0.1，认为γ_max≥0.1后土体进入了工程破坏的应变范畴^[32]，视这一剪应变值的边界为滑动面，据此分析埋深比和间距比对锚周土体滑动面形态的影响。单锚片螺旋锚锚周土体滑动面随埋深比的变化如图 9所示。埋深比等于1时，滑动面近似呈直线并能延伸至地表；埋深比等于2时，滑动面上部内倾，存在闭合的趋势，但仍能延伸至地表；埋深比等于4时，滑动面已闭合，整体位于土体内部。此外，还可以发现，不论埋深比大小，滑动面都可用一椭圆的部分圆周来近似刻画。当埋深比很小时，该椭圆具有很大的长短轴比，其圆周曲率很小，可近似表征直线型的滑动面；埋深比增大，椭圆长短轴比减小，圆周曲率增大，地表位于椭圆短轴以上，可近似表征内倾曲线型的滑动面；埋深比进一步增大，椭圆长短轴比则进一步减小，当地表位于椭圆顶点以上，椭圆则全部在土体内部，可近似表征局限于土体内部的灯泡状滑动面；埋深比继续增大，椭圆长短轴比则继续减小，椭圆高度也继续减小，可表征滑动面进一步收缩的特征。基于上述发现，提取不同埋深比下刻画滑动面椭圆的长短轴长度分别为a和b，计算其比值a/b，绘制该比值随埋深比的变化如图 10所示。可见，随着埋深比的增加，a/b逐渐减小，且速率先快后慢，存在渐近值。分别用胡伟等^[30]和杨枭等^[31]提出的函数（2）和（3）进行拟合，均有较好的效果，前者稍优于后者。

$\frac{a}{b} = l \cdot {(H/D)^m} + 1 \text{，}$

(2)

$\frac{a}{b} = \frac{1}{{{{\text{e}}^{n\left( {H/D} \right)}} - 1}} + 1。$

(3)

图 9 单锚片滑动面随埋深比变化

Figure 9. Variation of sliding surface with burial depth ratio of single blade

下载: 全尺寸图片幻灯片

图 10 a/b随埋深比变化规律

Figure 10. Variation of a/b with burial depth ratio

下载: 全尺寸图片幻灯片

对于双锚片螺旋锚，以间距比1为例，其首层锚锚周土体滑动面随埋深比变化如图 11所示。随着埋深比的增大，其滑动面形态同样经历了上述3个变化阶段。进一步对比图 9可发现，对于埋深比相同的单锚片螺旋锚和双锚片螺旋锚的首层锚，其滑动面形态是基本相同的，可用同一个椭圆来进行刻画。这也就意味着下层锚的存在对上层锚锚周土体的滑动面形态几乎不产生影响。因此，在对多锚片螺旋锚首层锚锚周土体滑动面进行理论表征时，可以不考虑下层锚的影响。既有研究中虽然也采用忽略下层锚影响的做法，但一直未提供相应的依据，本次试验对此予以了证实。

图 11 双锚片滑动面随埋深比变化（S/D=1）

Figure 11. Variation of sliding surface with burial depth ratio of double blades (S/D=1)

下载: 全尺寸图片幻灯片

3.3 下层锚锚周土体滑动面形态分析

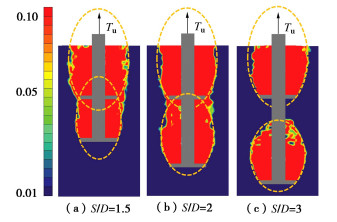
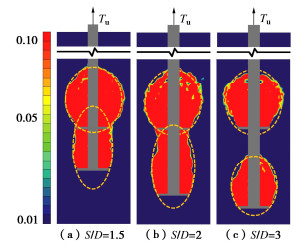
以埋深比2，6为例，双锚片螺旋锚锚周滑动面的变化如图 12，13所示。不同间距比，但首层锚埋深比相同时，用于刻画首层锚滑动面的椭圆大小是相等的，这也进一步证实了前面所述下层锚对上层锚对应滑动面形态的影响可忽略的观点。对于下层锚，间距比较小时（S/D=1.5），在不同埋深比下，下层锚锚周土体滑动面均从下层锚边缘曲线延伸至上层锚的两端，呈现出对称且两侧中心处稍有外扩的特征；间距比S/D增大到2后，下层锚对应的滑动面仍能延伸至上层锚底部，但交点位于锚片端点与中心点之间，且两侧中心处外扩特征更加显著；当间距比S/D增大至3，下层锚相应的滑动面已不再延伸至首层锚，而是整体局限于两层锚片之间，表明此时上层锚对下层锚的影响已大幅减小，下层锚开始表现出独立承载的特征。对于下层锚滑动面的这一变化规律，发现同样可以用一长短轴比随间距比连续变化的椭圆来进行刻画。当间距比较小时，上层锚、下层锚均为椭圆的一条弦，对应滑动面从下层锚两端曲线延伸至上层锚的两端；间距比增大到一定程度，椭圆长短轴比减小，但下层锚始终是椭圆的一条弦，椭圆仍能延伸至上层锚，与上层锚相交于上层锚中间某点；间距比继续增大，椭圆不再与上层锚相交，对应下层锚表现出的独立承载特征，此时下层锚可视为单锚，可用单锚的滑动面特征和相应椭圆来对其锚周土体滑动面进行刻画，这也意味着当间距比继续增大后，下层锚对应的滑动面将不再受其影响，而仅与其埋深比有关。

图 12 滑动面随间距比变化（H/D=2）

Figure 12. Variation of sliding surface with spacing ratio(H/D=2)

下载: 全尺寸图片幻灯片

图 13 滑动面随间距比变化（H/D=6）

Figure 13. Variation of sliding surface with spacing ratio(H/D=6)

下载: 全尺寸图片幻灯片

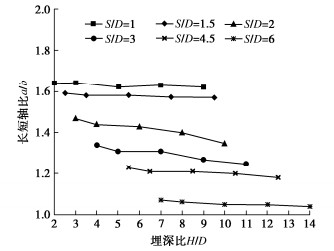
提取刻画下层锚滑动面椭圆长短轴a和b的长度，计算其比值，绘制相同间距比下该比值随下层锚埋深比的曲线如图 14所示。由图 14可知，埋深比越大，该比值越小；不同间距比下该比值随埋深比的变化可分为3个阶段。第一阶段，当间距比较小时（S/D=1，1.5），该比值仅与间距比有关，而几乎不受下层锚埋深比影响；第二阶段，当间距比S/D=2，3时，随着埋深比的增加，该比值有明显的减小趋势；而当S/D=4.5时，比值的变化又变得不太明显，至S/D=6时，该比值已几乎不再随埋深比变化，显然已进入了第三阶段。再者，还可以发现，比值在S/D=1到1.5的差异要显著小于在S/D=1.5~2的差异，这说明长短轴比的变化在这两个阶段间是有所不同的，这在计算中需予以体现。

图 14 a/b随埋深比的变化规律

Figure 14. Variation of a/b with burial depth ratio

下载: 全尺寸图片幻灯片

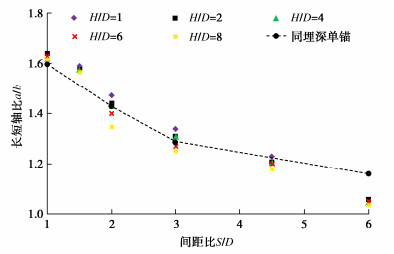
图 15给出了不同首层锚埋深比时，下层锚滑动面椭圆长短轴比a/b随间距比的变化。随着间距比的增大，下层锚的埋深增加，a/b值逐渐减小，速率先快后缓，这与单锚的滑动面椭圆收缩变化是一致的。再者，取首层锚埋深比为2，不同间距比下的下层锚a/b与具有相同埋深比（下层锚的）单锚的a/b进行对比，如图所示。除当间距比为6，下层锚埋深比为8时，两者有一定的差异，前者要比后者小约10%，其他工况时，两者大致相当，这说明下层锚的滑动面椭圆可使用具有相同埋深比单锚的椭圆来替代，误差较小。

图 15 下层锚和相同埋深比单锚的a/b对比

Figure 15. Comparison of a/b between lower anchor and single anchor with same burial depth ratio

下载: 全尺寸图片幻灯片

4. 多锚片力学模型构建思路分析

构建多锚片螺旋锚力学模型需首先理清每层锚片对应滑动面的变化规律，而后再进行组合。现以双锚片螺旋锚为例，提出多锚片螺旋锚力学模型构建思路及全过程如下。根据第3节的分析，每层锚片的滑动面均用一椭圆的部分圆周进行刻画，但对于不同锚片，影响该椭圆长短轴比的因素有所不同。对于首层锚，椭圆大小仅取决于首层锚埋深比，并通过椭圆与地面的位置来反映滑动面随埋深比的连续演化；而对于下层锚，其首先作为一个独立存在的锚片个体，承载特性受到其自身埋深比的影响，相应的滑动面椭圆与单锚相同；而后通过判断该椭圆与上层锚的位置关系来进一步反映间距比对下层锚滑动面的影响。由此，在一定间距比范围内，椭圆大小同时受间距比和自身埋深比的影响，而超出该范围后，则仅取决于后者。基于上述思路，构建力学模型的全过程如下。

（1）对于首层锚。当刻画椭圆长短轴比很大，椭圆短轴高于地面时，滑动面为介于锚片与地表之间的椭圆圆弧部分，对应可延伸至地表的近似直线型滑动面，如图 16（a）所示的第一种形态；埋深增加，椭圆长、短轴长度减小，比值也减小，当地表介于椭圆短轴和椭圆顶点之间时，滑动面表现为第二种形态，如图 16（b）所示，滑动面仍为介于锚片与地表之间的椭圆圆弧部分，但滑动面已越过椭圆短轴，具有内倾特征；埋深进一步增大，椭圆长、短轴长度和比值继续减小，当地表位于椭圆顶点之上，椭圆全部在土体内部，滑动面为锚片以上的椭圆圆弧部分，如图 16（c）所示；若埋深比继续增大，椭圆维持第三种形态，但进一步向锚片附近收缩，滑动面趋近于圆形圆弧。

图 16 首层锚滑动面3种形态

Figure 16. Three types of sliding surfaces of first anchor blade

下载: 全尺寸图片幻灯片

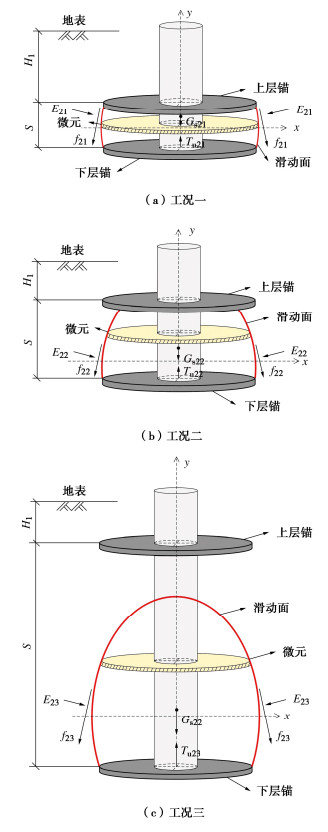
（2）对于下层锚。首先将其视为单锚，根据其自身埋深比按第一步确定刻画其滑动面的初始椭圆，而后根据该椭圆与上层锚的关系分3种情况区分其演化形态。第一种，当上层锚与下层锚的滑动面椭圆没有交点，即上层锚在该椭圆内部，这种情况下，下层锚的滑动面椭圆需重新定义。如图 17（a）所示，此时下层锚和上层锚将是新椭圆的两条弦，下层锚滑动面则是该椭圆介于两锚之间的部分圆弧，用于刻画间距比很小时，滑动面从下层锚边缘曲线延伸至上层锚的两端，且表现出两侧中心处稍有外扩的特征。第二种，锚片间距增大，当上层锚与下层锚的滑动面椭圆相交，即下层锚的滑动面被上层锚截断，如图 17（b）所示。此时该椭圆即为下层锚的滑动面椭圆，下层锚滑动面为该椭圆在下层锚和上层锚之间的椭圆圆弧部分，用以刻画间距比增大后，下层锚滑动面能延伸至上层锚底部，但交点位于上层锚端点与中心点之间的形态；当间距比进一步增大，当上层锚与下层锚的滑动面椭圆不相交，下层锚滑动面整体位于上层锚以下，如图 17（c）所示。此时该椭圆即为下层锚的滑动面椭圆，下层锚滑动面为下层锚以上的全部椭圆圆弧部分，用以刻画间距比大到一定数值后，下层锚滑动面不再延伸至上层锚，而是整体局限于两层锚片之间，下层锚开始表现出独立承载特征。

图 17 下层锚滑动面3种形态

Figure 17. Three types of sliding surfaces of lower anchor blade

下载: 全尺寸图片幻灯片

（3）滑动面形态组合。将第一步和第二部判断出每层锚片的滑动面形态进行组合，对于双锚片螺旋锚，上下层锚滑动面各有3种形态，组合之后则有9种工况，如表 4所示。在此基础上，选择隔离体，开展力学极限分析，则可以推导建立双锚片螺旋锚的上拔承载力计算方法。

表 4 双锚片螺旋锚滑动面组合形态

Table 4. Combined forms of sliding surface of screw anchors with double blades

工况	1	2	3	4	5	6	7	8	9
首层滑动面	①	②	③	①	②	③	①	②	③
下层滑动面	Ⅰ	Ⅰ	Ⅰ	Ⅱ	Ⅱ	Ⅱ	Ⅲ	Ⅲ	Ⅲ

下载: 导出CSV

| 显示表格

5. 螺旋锚上拔承载力计算方法推导

据上文分析，多锚片螺旋锚承载力学模型是由首层锚和下层锚各自的力学模型组合而成，各层锚的力学模型均可以椭圆函数表达的滑动面为基础考虑埋深比和与上层锚的间距比来构建。对于首层锚，可视为单锚。杨枭等^[31]基于椭圆型滑动面针对砂土中条形锚板构建了统一力学分析模型，并推导建立了条形锚板上拔承载力计算方法。对于单锚片或多锚片螺旋锚的首层锚而言，可在其结果的基础上考虑圆形锚的轴对称特性在[0，2π]进行积分即可，这部分计算公式将在完成下层锚的理论推导后直接给出。现重点针对下层锚开展理论分析。

下层锚竖向平面内的初始椭圆函数为

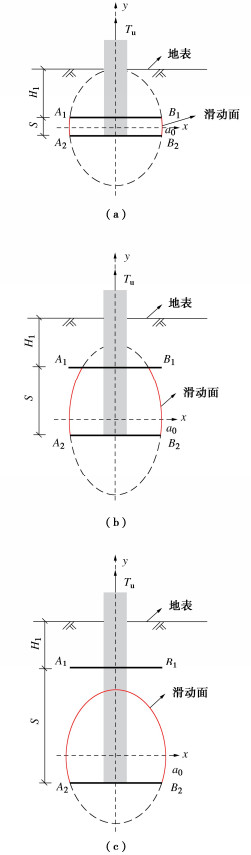
${y^2}/{a_2}^2 + {x^2}/{b_2}^2 = 1 。$

(4)

式中：a₂为椭圆长半轴长度；b₂为椭圆短半轴长度，k=a₂/b₂的比值表达式可选式（2）或（3）。以下层锚滑动面椭圆短轴、长轴所在位置分别建立x轴、y轴，如图 18所示。图中首层锚埋深为H₁，两端点分别为A₁、B₁；下层锚埋深为H₂，锚片间距为S，则H₂= H₁+S，两端点坐标分别为A₂（-D/2， ${y_{{A_{\text{2}}}}}$ ）、B₂（D/2， ${y_{{B_{\text{2}}}}}$ ），滑动面的初始角为 ${\alpha _0}$ 。

图 18 隔离体受力分析

Figure 18. Force analysis of isolators

下载: 全尺寸图片幻灯片

据B₂点横坐标D/2和该处滑动面初始角 ${\alpha _0}$ ^[10]有

$y'{|_{x = \frac{D}{2}}} = \frac{{{a_2}(D/2)}}{{{b_2}^2\sqrt {1 - \frac{{{{(D/2)}^2}}}{{{b_2}^2}}} }} = \tan {\alpha _0}。$

(5)

将k代入式（5）得

${a_2} = Dk/2\sqrt {{k^2}/{{\tan }^2}({\alpha _0}) + 1} {\text{ }}\text{，}$

(6)

${b_2} = D/2\sqrt {{k^2}/{{\tan }^2}({\alpha _0}) + 1} {\text{ }}。$

(7)

将a₂，b₂值代入（4）得

${y_{{B_{\text{2}}}}} = - D{k^2}/2\tan {\alpha _0}。$

(8)

即下层锚竖向平面内的初始椭圆函数是锚片直径D、埋深比H₂、与上层锚的间距S和初始角α₀的函数。

对于下层锚的第一种工况，上层锚在下层锚初始椭球滑动面的内部，两者不相交，则有间距比S＜2| ${y_{{B_{\text{2}}}}}$ |。此时，下层锚竖向平面内的滑动面将不再是初始椭圆的形态，而是由下层锚端部延伸至上层锚端部，滑动面椭圆需重新定义。新定义的椭圆满足下层锚和上层锚所在竖向平面内的线段是关于椭圆短轴对称的两条弦，下层锚滑动面则是该椭圆介于两锚之间的部分圆弧面，此时有B₂坐标为（D/2，-S/2），代入式（4）得下层锚竖向平面内的滑动面椭圆函数：

$\frac{{{S^2}}}{{4{a_2}^2}} + \frac{{{D^2}}}{{4{b_2}^2}} = 1 \text{，}$

(9)

${a_2}{\text{ = }}\frac{1}{2}\sqrt {{S^2} + SD\tan {\alpha _0}} \text{，}$

(10)

${b}_{\text{2}}\text{=}\sqrt{（SD+{D}^{2}\mathrm{tan}{\alpha }_{0}）/4\mathrm{tan}{\alpha }_{0}} 。$

(11)

取滑动面、上、下层锚所围成的空间体为隔离体，开展受力分析如图 18（a）所示。在纵坐标y处取厚度为dy的圆柱形微元体，作用在圆弧形滑动面微元上的正应力微元dE₂₁、切应力微元df₂₁分别计算如下：

${\text{d}}{E_{21}} = \frac{{2{\rm{\mathsf{π}}}{b_2}}}{{\sin \alpha }}\sqrt {1 - \frac{{{y^2}}}{{{a_2}^2}}} \gamma K\left( {{H_1} + \frac{S}{2} - y} \right){\text{d}}y \text{，}$

(12)

${\text{d}}{f_{21}} = {\text{d}}{E_{21}}\tan \varphi 。$

(13)

式中： $\gamma$ 为砂土重度；φ为内摩擦角；K为该微元上的土压力系数； $\alpha$ 为微元处滑动面竖直面内的切线与水平方向的夹角，

$\tan \alpha = y' = {a_2}x/(b{{}_2^2}\sqrt {1 - {x^2}/{b_2}^2} )。$

(14)

将应力微元函数在[0，2π]上积分可得滑动面上所受正应力合力和摩擦力合力的竖向分量E₂₁、f₂₁以及隔离体内土体重量G_s21分别为

${E_{21}} = 2{\rm{\mathsf{π}}}{b_2}\gamma \left[ {\int_0^{\frac{S}{2}} {\sqrt {1 - \frac{{{y^2}}}{{{a_2}^2}}} {K_{\text{2}}}\left( {{H_1} + \frac{S}{2} - y} \right)\left( {\frac{{{b_2}y}}{{{a_2}\sqrt {{a_2}^2 - {y^2}} }}} \right)} } \right. \cdot \\{\text{d}}y - \left. {\int_{ - \frac{S}{2}}^0 {\sqrt {1 - \frac{{{y^2}}}{{{a_2}^2}}} {K_{\text{1}}}\left( {{H_1} + \frac{S}{2} - y} \right)\left( {\frac{{{b_2}y}}{{{a_2}\sqrt {{a_2}^2 - {y^2}} }}} \right){\text{d}}y} } \right] \text{，}$

(15)

${f_{21}} = 2{\rm{\mathsf{π}}}{b_2}\gamma \tan \varphi \left[ {\int_{ - \frac{S}{2}}^0 {\sqrt {1 - \frac{{{y^2}}}{{{a_2}^2}}} {K_{\text{1}}}\left( {{H_1} + \frac{S}{2} - y} \right){\text{d}}y + } } \right.$

$\left. {\int_0^{\frac{S}{2}} {\sqrt {1 - \frac{{{y^2}}}{{{a_2}^2}}} {K_{\text{2}}}\left( {{H_1} + \frac{S}{2} - y} \right){\text{d}}y} } \right]。$

(16)

需注意的是，由于椭圆短轴上下滑动面上作用应力方向不同，应分开计算。

${G_{{\text{s21}}}} = {\rm{\mathsf{π}}}\gamma \left[ {\int_{ - \frac{S}{2}}^{\frac{S}{2}} {({b_2}\sqrt {1 - \frac{{{y^2}}}{{{a_2}^2}}} } {)^2}{\text{d}}y - {{(\frac{d}{2})}^2}S} \right]。$

(17)

对于下层锚的第二种工况，此时上层锚与下层锚的滑动面椭圆相交，下层锚的滑动面被上层锚截断。该工况的极限状态是下层锚滑动面椭圆在其顶点与上层锚相切，此时有S=| ${y_{{B_{\text{2}}}}}$ |+a₂。综合可得第二工况对应的间距比应满足2| ${y_{{B_{\text{2}}}}}$ |≤S≤| ${y_{{B_{\text{2}}}}}$ |+a₂。此时式（4）即为下层锚滑动面的初始椭圆函数，长、短轴分别由式（6），（7）确定。下层锚滑动面为该椭圆对应的椭球夹在下层锚和上层锚之间的圆弧面。该工况下隔离体的力学分析如图 18（b）所示，参考第一种工况的理论推导，可得该工况下滑动面所受的正应力合力和摩擦力合力的竖向分量E₂₂、f₂₂以及隔离体内土体重量G_s22计算公式如下：

${E_2}_{\text{2}} = 2{\rm{\mathsf{π}}}{b_2}\gamma \left[ {\int_0^{{y_{{{\text{B}}_2}}} + s} {\sqrt {1 - \frac{{{y^2}}}{{a_2^2}}} {K_{\text{2}}}\left( {{H_2} + {y_{{{\text{B}}_2}}} - y} \right)\left( {\frac{{{b_2}y}}{{{a_2}\sqrt {a_2^2 - {y^2}} }}} \right) \cdot } } \right. \\ {\text{d}}y - \left. {\int_{{y_{{{\text{B}}_2}}}}^0 {\sqrt {1 - \frac{{{y^2}}}{{a_2^2}}} {K_{\text{1}}}({H_2} + {y_{{B_2}}} - y)\left( {\frac{{{b_2}y}}{{{a_2}\sqrt {a_2^2 - {y^2}} }}} \right){\text{d}}y} } \right] \text{，}$

(18)

${f_{22}} = 2{\rm{\mathsf{π}}}{b_2}\gamma \tan \varphi \left[ {\int_{{y_{{B_2}}}}^0 {\sqrt {1 - \frac{{{y^2}}}{{{a_2}^2}}} {K_{\text{1}}}({H_2} + {y_{{B_2}}} - y){\text{d}}y + } } \right.$

$\left. {\int_0^{{y_{{B_2}}} + S} {\sqrt {1 - \frac{{{y^2}}}{{{a_2}^2}}} {K_{\text{2}}}({H_2} + {y_{{B_2}}} - y){\text{d}}y} } \right]\text{，}$

(19)

${G_{{\text{s22}}}} = {\rm{\mathsf{π}}}\gamma \left[ {\int_{{y_{{B_2}}}}^{{y_{{B_2}}} + S} {\left( {{b_2}\sqrt {1 - \frac{{{y^2}}}{{a_2^2}}} } \right)} {)^2}{\text{d}}y - {{\left( {\frac{d}{2}} \right)}^2}S} \right]。$

(20)

对于下层锚的第三种工况，下层锚滑动面椭圆与上层锚不相交，上层锚在椭圆顶点之上，即有 $\left| {{y_{{B_2}}}} \right|$ +a＜S。此时下层锚承载不受上层锚影响，表现出独立承载特性，初始椭圆长、短轴同样分别由式（6）和（7）确定，下层锚滑动面为该椭圆对应的椭球在下层锚以上的全部圆弧面。该工况下隔离体的力学分析如图 18（c）工况三所示，参考第二种工况的理论推导，可得该工况下滑动面所受的正应力合力和摩擦力合力的竖向分量E₂₃、f₂₃以及隔离体内土体重量G_s23计算公式如下：

${E_{23}} = 2{\rm{\mathsf{π}}}{b_2}\gamma \left[ {\int_0^{{a_2}} {\sqrt {1 - \frac{{{y^2}}}{{a_2^2}}} {K_{\text{2}}}({H_2} + {y_{{B_2}}} - y)\left( {\frac{{by}}{{{a_2}\sqrt {a_2^2 - {y^2}} }}} \right) \cdot } } \right. \\{\text{d}}y\left. { - \int_{{y_{{B_2}}}}^0 {\sqrt {1 - \frac{{{y^2}}}{{a_2^2}}} {K_{\text{1}}}\left( {{H_2} + {y_{{B_2}}} - y} \right)\left( {\frac{{by}}{{{a_2}\sqrt {a_2^2 - {y^2}} }}} \right){\text{d}}y} } \right] \text{，}$

(21)

${f_{23}} = 2{\rm{\mathsf{π}}}{b_2}\gamma \tan \varphi \left[ {\int_{{y_{{B_2}}}}^0 {\sqrt {1 - \frac{{{y^2}}}{{a_2^2}}} {K_{\text{1}}}({H_2} + {y_{{B_2}}} - y){\text{d}}y} } \right. +$

$\left. {\int_0^{{a_2}} {\sqrt {1 - \frac{{{y^2}}}{{a_2^2}}} {K_{\text{2}}}({H_2} + {y_{{B_2}}} - y){\text{d}}y} } \right] \text{，}$

(22)

${G_{{\text{s23}}}} = {\rm{\mathsf{π}}}\gamma \left[ {{{\int_{{y_{{B_2}}}}^{{a_2}} {\left( {{b_2}\sqrt {1 - \frac{{{y^2}}}{{a_2^2}}} } \right)} }^2}\gamma {\text{d}}y - {{\left( {\frac{d}{2}} \right)}^2}S} \right]。$

(23)

式（15）~（23）中土压力系数K₁、K₂的计算沿用杨枭等^[31]所建议的方法：

${K_{\text{1}}} = {K_{\text{0}}} - \frac{{{K_{\text{0}}} - {K_{\text{a}}}}}{{{y_{{B_2}}}}}y \text{，}$

(24)

${K_{\text{2}}} = \frac{{{K_{\text{p}}}\tan (2\varphi /3) - {K_{\text{0}}}}}{{{a_2}}}y + {K_{\text{0}}}。$

(25)

式中：主动土压力系数K_a=tan²(45°-φ/2)；静止土压力系数K₀=1-sinφ；被动土压力系数K_p=tan²(45°+φ/2)。

对于首层锚，其表现与单锚相同，以下在杨枭等^[31]针对二维问题推导建立的方法基础上，通过在[0，2π]角度范围上积分可得3种工况下各力学分量的计算结果。第一种工况，地面低于椭圆短轴，即H₁＜| ${y_{{B_1}}}$ |，该工况下首层锚滑动面上所受的正应力合力和摩擦力合力的竖向分量E₁₁、f₁₁以及隔离体内土体重量G_s11计算公式如下：

${E_{{\text{11}}}} = - \int_{{y_{{B_1}}}}^{{y_{{B_1}}} + {H_1}} {2{\rm{\mathsf{π}}}{b_1}\sqrt {1 - \frac{{{y^2}}}{{a_1^2}}} \gamma {K_{\text{1}}}({H_1} - y + {y_{{B_1}}}) \cdot }$

$\left( {\frac{{{b_1}y}}{{{a_1}\sqrt {a_1^2 - {y^2}} }}} \right){\text{d}}y\text{，}$

(26)

${f_{{\text{11}}}} = 2{\rm{\mathsf{π}}}{b_1}\gamma \tan \varphi \int_{{y_B}_{_1}}^{{y_B}_{_1} + {H_1}} {\sqrt {1 - \frac{{{y^2}}}{{a_1^2}}} {K_{\text{1}}}({H_1} - y + {y_{{B_1}}}){\text{d}}y} \text{，}$

(27)

${G_{{\text{s}}11}} = {\rm{\mathsf{π}}}\gamma \left[ {{{\int_{{y_B}_{_1}}^{{y_B}_{_1} + {H_1}} {\left( {{b_1}\sqrt {1 - \frac{{{y^2}}}{{a_1^2}}} } \right)} }^2}{\text{d}}y - {{\left( {\frac{d}{2}} \right)}^2}H} \right] 。$

(28)

式中：a₁，b₁， ${y_B}_{_1}$ 同样分别使用式（6）~（8）按照首层锚的埋深比进行计算。

第二种工况，地面介于首层锚滑动面椭圆的短轴和椭圆顶点之间，即0≤H≤a₁。该工况下首层锚滑动面上所受的正应力合力和摩擦力合力的竖向分量E₁₂、f₁₂以及隔离体内土体重量G_s12计算公式如下：

${E_{12}} = 2{\rm{\mathsf{π}}}b\gamma \left[ {\int_0^{{y_{{B_1}}} + {H_1}} {\sqrt {1 - \frac{{{y^2}}}{{a_1^2}}} {K_{\text{2}}}({H_1} - y + {y_{{B_1}}})\left( {\frac{{{b_1}y}}{{{a_1}\sqrt {a_1^2 - {y^2}} }}} \right) \cdot } } \right.\\ \left. {{\text{d}}y - \int_{{y_{{B_1}}}}^0 {\sqrt {1 - \frac{{{y^2}}}{{a_1^2}}} {K_{\text{1}}}({H_1} - y + {y_{{B_1}}})\left( {\frac{{{b_1}y}}{{{a_1}\sqrt {a_1^2 - {y^2}} }}} \right){\text{d}}y} } \right]\text{，}$

(29)

${f_{{\text{12}}}} = 2{\rm{\mathsf{π}}}b\gamma \tan \varphi \left[ {\int_{{y_{{B_1}}}}^0 {\sqrt {1 - \frac{{{y^2}}}{{a_1^2}}} {K_{\text{1}}}({H_1} - y + {y_{{B_1}}}){\text{d}}y} + } \right.$

$\left. {\int_0^{{y_{{B_1}}} + {H_1}} {\sqrt {1 - \frac{{{y^2}}}{{a_1^2}}} {K_{\text{2}}}({H_1} - y + {y_{{B_1}}}){\text{d}}y} } \right]\text{，}$

(30)

${G_{{\text{s12}}}} = {\rm{\mathsf{π}}}\gamma \left[ {{{\int_{{y_{{B_1}}}}^{{y_{{B_1}}} + {H_1}} {\left( {{b_1}\sqrt {1 - \frac{{{y^2}}}{{a_1^2}}} } \right)} }^2}{\text{d}}y - {{\left( {\frac{d}{2}} \right)}^2}H} \right]。$

(31)

第三种工况，地面在首层锚滑动面椭圆顶点以上，即a₁ < H。该工况下首层锚滑动面上所受的正应力合力和摩擦力合力的竖向分量E₁₃，f₁₃以及隔离体内土体重量G_s13计算公式分别同下层锚独立承载工况的公式（21）~（23），只需将里面的a₂，b₂， ${y_{{B_2}}}$ ，H₂替换为a₁，b₁， ${y_{{B_1}}}$ ，H₁即可。式（26）~（31）中土压力系数K₁，K₂的计算也需做相应替换。

至此，得到了多锚片螺旋锚首层锚和下层锚各工况下力学分量的计算表达式，即可根据整体的竖向力的极限平衡条件得螺旋锚的极限上拔承载力计算表达式为

${T_{\text{u}}} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^3 {{E_{ij}} + {f_{ij}} + {G_{{\text{s}}ij}} + {G_{\text{M}}}} } 。$

(32)

式中：下角标i表示第i层锚片，i=1时代表首层锚；j代表工况，每层锚片均存在3种工况；G_M为螺旋锚的自重。

6. 对比验证

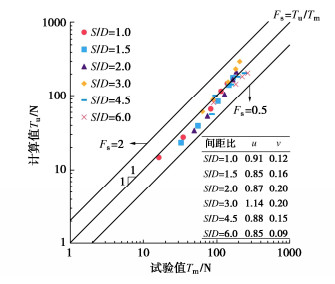
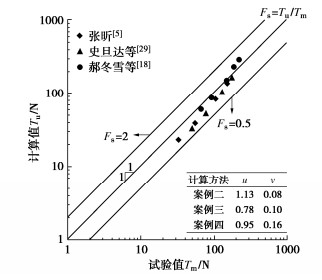
为验证本文所推导建立的多锚片螺旋锚上拔承载力计算方法，以下选用4个试验案例开展对比分析。试验案例包括本文试验（案例一）、案例二（张昕^[5]）、案例三（史旦达等^[29]）、案例四（郝冬雪等^[18]），各案例试验参数如表 5所示。4组试验所用砂土内摩擦角φ为30°~33.1°，相对密实度D_r为27%~57%，属于松砂、中密砂范畴。各试验案例工况实测上拔承载力为T_m，本文方法计算值为T_u，定义F_s=T_u/T_m。以每个案例F_s的平均值u和标准偏差v作为评价计算效果的指标。本次计算选取式（3）作为k的表达式，式中 m对于松砂、中密砂分别取0.01，0.02；式（5）中α₀对于松砂、中密砂分别取π/2-φ/2，π/2-3φ/4^[10]。本文试验和其他3个试验案例的计算对比结果分别如图 19，20所示。

表 5 试验案例基本情况

Table 5. Basic information of experimental cases

案例	内摩擦角φ/(°)	重度γ/(kN·m^-3)	相对密实度D_r/%	直径D/mm	埋深比(H/D)	间距比(S/D)
一	33.1	15.56	57	50	1/2/4/6/8	1.0/1.5/2.0/3.0/4.5/6.0
二	30.0	14.44	23~32	50	4/5	1.5/2.0
三	31.0	13.82	33~42	50	5	0/1.0/1.5/2.0
四	32.0	19.00	44	20	6	0/1.5/3.0/4.5/6.0

下载: 导出CSV

| 显示表格

图 19 本文试验值与计算值对比

Figure 19. Comparison between calculated and measured values

下载: 全尺寸图片幻灯片

图 20 试验值与计算值对比

Figure 20. Comparison between calculated and measured values

下载: 全尺寸图片幻灯片

由图 19可知，对于本次试验，计算值和试验值总体上吻合较好，数据点分布在1∶1线两侧。相对而言，承载力较大的数据点更接近于1∶1线，这可能与承载力小时，试验误差会更加凸显有关。F_s均值u=0.92，整体偏小，平均误差约为8%，标准偏差v=0.15。具体来看，除埋深比H/D等于3时，F_s=1.14，计算值较实验室偏大以外，其余埋深比下，F_s均小于1，为0.85~0.91，计算值偏小。同时，大埋深比时，标准偏差v较小，这也是由于大埋深比对应大的承载力，试验误差造成的偏差降低所致。

由图 20可知，对于案例二，当埋深比H/D=4，间距比S/D分别为1.5和2.5时，对应F_s分别为1.06，1.10；H/D=5，S/D等于1.5和2.5时的F_s分别为1.26，1.09，最大误差26%，均值u=1.13，计算值偏大，平均误差约为13%，v=0.08，稳定性较好。案例三中，埋深比为5，间距比分别为0，1，1.5，2，F_s分别为0.95，0.75，0.71，0.71，比值均值u=0.78，计算值偏小，v=0.10，稳定性较好。案例四中，H/D=6，S/D=0，1.5，3.0，4.5，6.0时，F_s分别为0.93，0.88，0.75，0.96，1.24，比值均值u=0.95，v=0.16；除S/D=6.0外，其他工况时计算值都偏小，S/D=4.5时计算效果最好，误差仅为4%。3个案例中计算效果最好的是案例四，案例二次之，案例三效果稍差。所有F_s数据点的比值均值u=0.95，v=0.18，这说明本文方法对这3个试验案例的计算效果总体是较好的。

7. 结论

本文基于室内模型试验开展了砂土中多锚片螺旋锚竖向拉拔承载特性研究，采用数字照相测量技术提取分析了破坏滑动面特征，继而提出了多锚片螺旋锚上拔承载力学模型的构建思路，得到以下5点结论。

（1）单锚片和双锚片螺旋锚的拉拔荷载位移曲线均可分为增长区间和震荡下降区间两个阶段。埋深比越大，荷载峰值越高，曲线震荡幅度也越大。曲线震荡的原因是由拉拔后锚片下方逐渐形成的空腔和土体的土拱效应共同作用所致。

（2）单锚片螺旋锚的抗拔承载力因子N_γ随着埋深比的增加呈现先快速增大后缓慢下降的趋势，具有峰值；下层锚承载力发挥系数η随间距比的增大呈非线性增长，速率先快后缓。间距比相同的情况下，埋深比越小，承载力发挥系数一般越大。

（3）埋深比相同的单锚片螺旋锚和双锚片螺旋锚的首层锚，其滑动面形态基本相同，可用同一个随埋深比增大长短轴比逐渐减小的椭圆来连续刻画；双锚片螺旋锚下层锚的滑动面同样可用一椭圆来进行表征，埋深比越大，该椭圆长短轴比值越小，其变化规律按间距比的不同可分为3个阶段。

（4）多锚片螺旋锚的首层锚和下层锚各自有3种滑动面工况，各工况间有明确的界定条件，这取决于埋深比和间距比；对于双锚片螺旋锚而言，上、下层锚滑动面各有3种形态，组合之后则有9种工况；每个滑动面工况对应一种力学模型，螺旋锚总的上拔承载力学模型则由它们组合而成。

（5）通过对每层锚的每种工况分析构建力学模型，推导建立了多锚片螺旋锚上拔承载力计算方法，该方法可以考虑任意锚片数量、埋深比和间距比；本文通过对4个松砂和中密砂地基中试验案例的计算验证了该方法的有效性。

图 1 典型双锚片螺旋锚竖向拉拔破坏模式

Figure 1. Typical uplift failure modes of screw anchors with double blades

下载: 全尺寸图片幻灯片

图 2 平板圆锚模型

Figure 2. Model for circular flat anchor

下载: 全尺寸图片幻灯片

图 3 代表性荷载-位移曲线

Figure 3. Representative load-displacement curves

下载: 全尺寸图片幻灯片

图 4 空腔变化与荷载位移曲线对应关系

Figure 4. Relationship between cavity change and load-displacement curve (H/D=8)

下载: 全尺寸图片幻灯片

图 5 N_γ随埋深比变化规律

Figure 5. Variation of N_γ with burial depth ratio

下载: 全尺寸图片幻灯片

图 6 荷载-位移曲线

Figure 6. Load-displacement curves

下载: 全尺寸图片幻灯片

图 7 发挥系数η随间距比变化

Figure 7. Variation of η with spacing ratio

下载: 全尺寸图片幻灯片

图 8 空腔变化与滑动面形成的相关力学机制

Figure 8. Mechanical mechanism of cavity variation and sliding surface formation

下载: 全尺寸图片幻灯片

图 9 单锚片滑动面随埋深比变化

Figure 9. Variation of sliding surface with burial depth ratio of single blade

下载: 全尺寸图片幻灯片

图 10 a/b随埋深比变化规律

Figure 10. Variation of a/b with burial depth ratio

下载: 全尺寸图片幻灯片

图 11 双锚片滑动面随埋深比变化（S/D=1）

Figure 11. Variation of sliding surface with burial depth ratio of double blades (S/D=1)

下载: 全尺寸图片幻灯片

图 12 滑动面随间距比变化（H/D=2）

Figure 12. Variation of sliding surface with spacing ratio(H/D=2)

下载: 全尺寸图片幻灯片

图 13 滑动面随间距比变化（H/D=6）

Figure 13. Variation of sliding surface with spacing ratio(H/D=6)

下载: 全尺寸图片幻灯片

图 14 a/b随埋深比的变化规律

Figure 14. Variation of a/b with burial depth ratio

下载: 全尺寸图片幻灯片

图 15 下层锚和相同埋深比单锚的a/b对比

Figure 15. Comparison of a/b between lower anchor and single anchor with same burial depth ratio

下载: 全尺寸图片幻灯片

图 16 首层锚滑动面3种形态

Figure 16. Three types of sliding surfaces of first anchor blade

下载: 全尺寸图片幻灯片

图 17 下层锚滑动面3种形态

Figure 17. Three types of sliding surfaces of lower anchor blade

下载: 全尺寸图片幻灯片

图 18 隔离体受力分析

Figure 18. Force analysis of isolators

下载: 全尺寸图片幻灯片

图 19 本文试验值与计算值对比

Figure 19. Comparison between calculated and measured values

下载: 全尺寸图片幻灯片

图 20 试验值与计算值对比

Figure 20. Comparison between calculated and measured values

下载: 全尺寸图片幻灯片

表 1 不同临界间距比取值标准

Table 1 Different standards of critical spacing ratio

标准来源	临界间距比（S/D）	土体类别
Tsuha等^[4]	3	砂土
Tappenden等^[12]	2	天然土
Merifield ^[13]	1.58	黏性土
Stanier等^[16]	3	软黏土
姚敬宇^[17]	2	密砂
郝冬雪等^[18]	1.5	中密砂

下载: 导出CSV

表 2 试验用砂物理力学指标

Table 2 Physical and mechanical indexes of test sand

D_r	C_u	C_c	φ/(°)	ρ_dmin/ (g·cm^-3)	ρ_dmax/ (g·cm^-3)	γ/(kN·m^-3)
0.57	2.5	1.1	33.1	1.616	1.766	16.56

下载: 导出CSV

表 3 试验工况

Table 3 Test conditions

锚片数	首层锚埋深比H/D	锚片间距比S/D
1	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	0
2	1, 2, 4, 6, 8	1.0, 1.5, 2.0, 3.0, 4.5, 6.0

下载: 导出CSV

表 4 双锚片螺旋锚滑动面组合形态

Table 4 Combined forms of sliding surface of screw anchors with double blades

工况	1	2	3	4	5	6	7	8	9
首层滑动面	①	②	③	①	②	③	①	②	③
下层滑动面	Ⅰ	Ⅰ	Ⅰ	Ⅱ	Ⅱ	Ⅱ	Ⅲ	Ⅲ	Ⅲ

下载: 导出CSV

表 5 试验案例基本情况

Table 5 Basic information of experimental cases

案例	内摩擦角φ/(°)	重度γ/(kN·m^-3)	相对密实度D_r/%	直径D/mm	埋深比(H/D)	间距比(S/D)
一	33.1	15.56	57	50	1/2/4/6/8	1.0/1.5/2.0/3.0/4.5/6.0
二	30.0	14.44	23~32	50	4/5	1.5/2.0
三	31.0	13.82	33~42	50	5	0/1.0/1.5/2.0
四	32.0	19.00	44	20	6	0/1.5/3.0/4.5/6.0

下载: 导出CSV

参考文献(32)

[1]	汪滨. 螺旋锚技术及其在工程中的应用[M]. 北京: 中国水利水电出版社, 2005. WANG Bin. Screw Anchor Technique and its Application in Engineering[M]. Beijing: China Water & Power Press, 2005. (in Chinese)
[2]	曹广礼, 崔维钧. 输电线路铁塔基础锚具的研究[J]. 电力建设, 1992(4): 60-70. https://www.cnki.com.cn/Article/CJFDTOTAL-DLJS199204019.htm CAO Guangli, CUI Weijun. Study of tower foundation anchorage for transmission lines[J]. Electric Power Construction, 1992(4): 60-70. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DLJS199204019.htm
[3]	董天文, 梁力, 王明恕, 等. 极限荷载条件下螺旋桩的螺距设计与承载力计算[J]. 岩土工程学报, 2006, 28(11): 2031-2034. http://cge.nhri.cn/cn/article/id/12231 DONG Tianwen, LIANG Li, WANG Ming-shu, et al. Pitch of screws and bearing capacity of screw piles under ultimate load[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(11): 2031-2034. (in Chinese) http://cge.nhri.cn/cn/article/id/12231
[4]	TSUHA C H C, AOKI N, RAULT G, et al. Evaluation of the efficiencies of helical anchor plates in sand by centrifuge model tests[J]. Canadian Geotechnical Journal, 2012, 49(9): 1102-1114. doi: 10.1139/t2012-064
[5]	张昕. 螺旋锚锚周土体变形试验与抗拔承载力计算模型研究[D]. 郑州: 郑州大学, 2014. ZHANG Xin. Experimental Analysis of Soil Deformation Around Uplifting Screw Anchors and Theoretical Research of Uplifting Capacity Models[D]. Zhengzhou: Zhengzhou University, 2014. (in Chinese)
[6]	MURRAY E J, GEDDES J D. Uplift of anchor plates in sard[J]. Journal of Geotechnical Engineering, 1987, 113(3): 202-215. doi: 10.1061/(ASCE)0733-9410(1987)113:3(202)
[7]	朱鸿鹄, 高宇新, 李元海, 等. 土工格栅加筋砂土中水平锚板抗拔特性试验研究[J]. 岩土力学, 2022, 43(5): 1207-1214. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202205006.htm ZHU Honghu, GAO Yuxin, LI Yuanhai, et al. Experimental study of pullout behavior of horizontal anchor plates in geogrid reinforced sand[J]. Rock and Soil Mechanics, 2022, 43(5): 1207-1214. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202205006.htm
[8]	董天文, 梁力, 黄连壮, 等. 螺旋桩基础抗拔试验研究[J]. 岩土力学, 2009, 30(1): 186-190. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200901043.htm DONG Tianwen, LIANG Li, HUANG Lianzhuang, et al. Pullout test of screw pile foundation[J]. Rock and Soil Mechanics, 2009, 30(1): 186-190. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200901043.htm
[9]	ILAMPARUTHI K, DICKIN E A, MUTHUKRISNAIAH K. Experimental investigation of the uplift behavior of circular plate anchors embedded in sand[J]. Canadian Geotechnical Journal, 2002, 39(3): 648-664. doi: 10.1139/t02-005
[10]	姚琛, 胡伟, 孟建伟, 等. 砂土中水平条形锚板竖向拉拔承载力统一计算方法研究[J]. 工程力学, 2021, 38(5): 209-218. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202105020.htm YAO Chen, HU Wei, MENG Jianwei, et al. Unified method for calculation of vertical pulling capacity of horizontal strip anchor plate in sand[J]. Engineering Mechanics, 2021, 38(5): 209-218. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202105020.htm
[11]	RAO S N, PRASAD Y, SHETTYB M D. The behaviour of model screw piles in cohesive soils[J]. Soils and Foundations, 2008, 31(2): 35-50.
[12]	TAPPENDEN K, SEGO D, ROBERTSON P. Load transfer behavior of full-scale instrumented screw anchors[C]// International Foundation Congress & Equipment Expo. 2009.
[13]	MERIFIELD R S. Ultimate uplift capacity of multiplate helical type anchors in clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(7): 704-716.
[14]	GHALY A, HANNA A. Stresses and strains around helical screw anchors in sand[J]. Soils and Foundations, 1992, 32(4): 27-42.
[15]	朱长歧, 初晓锋. 钙质砂中锚定板的极限抗拔力计算[J]. 岩土力学, 2003, 24(增刊2): 153-158. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2003S2034.htm ZHU Changqi, CHU Xiaofeng. Calculation of ultimate extraction resistence of anchoring plates in calcaress sands[J]. Rock and Soil Mechanics, 2003, 24(S2): 153-158. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2003S2034.htm
[16]	STANIER S A, BLACK J A, HIRD C C. Modelling helical screw piles in soft clay and design implications[J]. Geotechnical Engineering, 2014, 167(5): 447-460.
[17]	姚敬宇. 砂土中多节螺旋锚抗拔承载特性及锚土变形模型试验研究[D]. 郑州: 华北水利水电大学, 2017. YAO Jingyu. Experimental Study on Uplift Capacity and Soil Deformation Around Multiplate Helical Type Anchors in Sand[D]. Zhengzhou: North China University of Water Resources and Electric Power, 2017. (in Chinese)
[18]	郝冬雪, 陈榕, 符胜男. 砂土中螺旋锚上拔承载特性模型试验研究[J]. 岩土工程学报, 2015, 37(1): 126-132. doi: 10.11779/CJGE201501015 HAO Dongxue, CHEN Rong, FU Shengnan. Experimental study on uplift capacity of multi-helix anchors in sand[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(1): 126-132. (in Chinese) doi: 10.11779/CJGE201501015
[19]	林志, 胡伟, 赵璞, 等. 砂土中平板圆锚倾斜拉拔承载特性模型试验研究[J]. 岩土力学, 2021, 42(11): 3059-3068, 3168. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202111016.htm LIN Zhi, HU Wei, ZHAO Pu, et al. Experimental study on the uplift behavior of circular anchor plate inclined drawing in sand[J]. Rock and Soil Mechanics, 2021, 42(11): 3059-3068, 3168. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202111016.htm
[20]	ROWE R K, DAVIS E H. The behaviour of anchor plates in sand[J]. Géotechnique, 1982, 32(1): 25-41.
[21]	BRADSHAW A S, GERKUS H, FANNING J, et al. Scaling considerations for 1-g model horizontal plate anchor tests in sand[J]. Geotechnical Testing Journal, 2016, 39(6): 1-9.
[22]	DICKIN E A, LAMAN M. Uplift response of strip anchors in cohesionless soil[J]. Advances in Engineering Software, 2006, 38(8): 618-625.
[23]	初晓锋, 李志刚, 汪稔, 等. 钙质砂中锚定物锚固性能的试验研究[J]. 岩土力学, 2002, 23(3): 368-371. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200203028.htm CHU Xiaofeng, LI Zhigang, WANG Ren, et al. The test research of anchor's uplift behavior in calcareous sand[J]. Rock and Soil Mechanics, 2002, 23(3): 368-371. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200203028.htm
[24]	MERIFIELD R S, LYAMIN A V, SLOAN S W. Three- dimensional lower-bound solutions for the stability of plate anchors in sand[J]. Géotechnique, 2006, 56(2): 123-132.
[25]	LIU J Y, LIU M L, ZHU Z D. Sand deformation around an uplift plate anchor[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(6): 728-737.
[26]	CERFONTAINE B, KNAPPETT J A, BROWN M J, et al. Effect of soil deformability on the failure mechanism of shallow plate or screw anchors in sand[J]. Computers and Geotechnics, 2019, 109: 34-45.
[27]	CHOUDHARY A. Pullout Behaviour of Strip Anchor in Soil Using FLAC2D[C]// Indian Geotechnical Conference 2017. Hyderabad, 2017.
[28]	侯世伟, 高广亮, 张皓, 等. 螺旋锚复合基础对村镇生土建筑抗震性能影响研究[J]. 防灾减灾工程学报, 2023, 43(4): 778-786, 796. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK202304016.htm HOU Shiwei, GAO Guangliang, ZHANG Hao, et al. Influence of screw anchor composite foundation on seismic performance of rural raw soil buildings[J]. Journal of Disaster Prevention and Mitigation Engineering, 2023, 43(4): 778-786, 796. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK202304016.htm
[29]	史旦达, 俞快, 毛逸瑶, 等. 松砂中双叶片螺旋锚上拔承载及土体变形特性试验研究[J]. 岩土力学, 2022, 43(11): 3059-3072, 3082. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202211013.htm (SHI Danda, YU Kuai, MAO Yiyao, et al. Experimental study on the uplift behavior and soil deformation characteristics of the double-blade screw anchor in loose sand[J]. Rock and Soil Mechanics, 2022, 43(11): 3059-3072, 3082. (in Chinese https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202211013.htm
[30]	胡伟, 张翰林, 孟建伟, 等. 砂土中倾斜条形锚板法向拉拔承载特性研究[J]. 岩土工程学报, 2023, 45(7): 1451-1460. doi: 10.11779/CJGE20220474 HU Wei, ZHANG Hanlin, MENG Jianwei, et al. Research on normal pullout bearing characteristics of inclined strip anchor plate in sand[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(7): 1451-1460. (in Chinese) doi: 10.11779/CJGE20220474
[31]	杨枭, 胡伟, 孟建伟, 等. 基于椭圆型滑动面的砂土中条形锚板上拔承载力计算方法[J]. 海洋工程, 2023, 41(3): 177-184. https://www.cnki.com.cn/Article/CJFDTOTAL-HYGC202303017.htm YANG Xiao, HU Wei, MENG Jianwei, et al. Calculation method of uplift bearing capacity of strip anchor plate in sand based on elliptical sliding surface[J]. The Ocean Engineering, 2023, 41(3): 177-184. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HYGC202303017.htm
[32]	顾晓强, 吴瑞拓, 梁发云, 等. 上海土体小应变硬化模型整套参数取值方法及工程验证[J]. 岩土力学, 2021, 42(3): 833-845. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202103026.htm GU Xiaoqiang, WU Ruituo, LIANG Fayun, et al. On HSS model parameters for Shanghai soils with engineering verification[J]. Rock and Soil Mechanics, 2021, 42(3): 833-845. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202103026.htm