Analytical solutions for performance of existing shield tunnel subjected to overlying excavation under anti-uplift portal frame
-
摘要: 上方开挖卸载导致既有盾构隧道结构产生上浮，易引发结构渗漏水、开裂等病害。竖井开挖联合门式框架技术是限制上方开挖引起既有隧道上浮的一种有效控制措施，但是目前仍缺少相应的理论方法用于指导门式抗浮框架的设计。为此，提出了既有隧道结构响应的解析解，可以实现竖井和基坑开挖阶段既有隧道结构纵向和横截面变形计算，并给出了相关的计算流程。通过与工程实例和三维数值模拟结果进行对比，验证了解析解的可靠性。通过典型算例计算和参数敏感性分析讨论了门式抗浮框架的作用机理以及既有隧道埋深和竖井开挖尺寸等因素的影响规律。结果表明：门式抗浮框架在基坑开挖阶段可以有效控制上方开挖引起的既有隧道变形，控制效果与既有隧道上方剩余覆土厚度密切相关，剩余覆土越小控制效果越明显；门式抗浮框架的作用效果主要取决于抗浮板与土体之间的作用力，抗拔桩与土体的作用力对既有隧道变形影响较小。
-
关键词:
- 既有隧道 /
- 门式抗浮框架 /
- 解析解 /
- 竖井开挖 /
- Timoshenko梁
Abstract: The heave of the existing shield tunnels will be induced due to the above excavation, and then structural damages, including leakage and cracking, easily happen. The combination of the shaft excavation and anti-uplift portal frame is an effective technique to limit the heave of the existing tunnels, while the theoretical method is absent presently for the design of the anti-portal frame. Thus, the analytical solutions for the performance of the existing tunnels are proposed for both the longitudinal and cross-section deformations of the existing tunnels during the shaft excavation and foundation pit excavation, respectively. The flow chart is also provided. The results predicted by the analytical solutions are in good agreement with those of the field measurement and 3D numerical simulation, which proves the reliability of the analytical solutions. The mechanism of the anti-uplift portal frame is carefully investigated, and the sensitivity analysis of the buried depth of the existing tunnels and the excavation size of the shaft is performed. The results show that the anti-uplift portal frame can effectively control the deformation of the existing tunnels caused by the above excavation, strongly depending on the thickness of the soil above the existing tunnels. The efficiency of the anti-uplift portal frame is stronger with the decrease of the thickness of the soil above the existing tunnels. The effects of the anti-uplift portal frame mainly depends on the force between the anti-floating slab and the soil, and the uplift pile shows a minor influence on the deformation of the existing tunnels. -
0. 引言
中国城市地下工程建设呈现出“深、大、近、杂”的特点和趋势。地铁盾构隧道通常是由预制管片拼接而成，管片之间通过螺栓进行连接，隧道结构纵向整体刚度较小，抵抗变形能力差。城市地下空间开发与运营地铁隧道保护之间的矛盾日益突出。魏纲[1]收集了国内14个隧道上方基坑开挖实例，发现64%的隧道上浮量超过报警值（10 mm）。上浮开挖过程中不可避免地对基坑坑底土体造成卸荷扰动，使既有盾构隧道结构产生附加荷载，易引发管片错台、开裂、渗漏水等病害[2-4]，影响隧道正常运营和行车舒适性。
近年来，国内外研究学者针对上方基坑开挖影响下既有盾构隧道响应问题开展了较为深入的研究。两阶段法是目前普遍采用的解析方法[5-8]，该方法概念清晰、计算简便、易于应用。解析方法计算结果的可靠性主要取决于开挖引起的隧道上附加荷载计算和隧道-土体之间的相互作用模型的选取。陈郁等[9]利用Mindlin弹性半空间理论计算开挖引起的隧道位置处土体附加荷载，进而根据分层总和法求解隧道变形。隧道纵向结构分析通常基于弹性地基梁理论展开，其中Winkler模型是目前常用的地基模型。当既有盾构隧道受基坑开挖影响较为明显时，需要采用不同的控制措施减小既有隧道变形，但是上述理论和模型试验主要适用于简单工况条件，难以反映各类控制措施的影响。
针对基坑开挖下卧隧道变形控制技术，也有部分学者进行了研究。如Huang等[10]采用数值模拟的手段，探讨了开挖周期、土体性质等因素的影响规律，并与实测数据进行了对比。黄宏伟等[11]以上海外滩通道为例，对比分析了土体加固、坑底堆载以及加固和堆载共同作用3种隧道保护措施的实施效果。谢雄耀等[12]通过有限元模拟发现MJS工法加固坑内外土体对控制隧道变形具有良好的效果。当基坑开挖深度较大、范围广且隧道距离坑底近的情况，通常采用分块开挖、土体加固等措施仍不能有效控制隧道变形。近些年提出的竖井开挖联合门式框架技术成为限制上方开挖引起既有隧道上浮的一种有效控制措施。该方法在深圳市双界河路市政工程和桂庙路快速化路改造工程均有应用，实施效果较好，可以有效地限制隧道上浮变形[13-14]。吴怀娜等[15]针对竖井开挖联合门式框架技术开展了数值模拟研究，探究门式抗浮框架与地层相互作用机制及抗浮效果。
目前针对门式框架技术的研究多集中在数值模拟或实测数据分析方面，缺少相应的理论方法研究。实际工程中门式抗浮框架相关设计参数也多为根据工程经验确定。本文基于竖井开挖联合门式抗浮框架的施工工法，提出了考虑门式抗浮框架的隧道纵向和横截面变形理论计算方法，并分别与现场实测和数值模拟结果进行对比，验证了理论计算方法的有效性。在此基础上，分析了门式抗浮框架的作用机理并开展了主要设计参数敏感性分析。本文研究成果可为门式抗浮框架的工程设计提供理论指导。
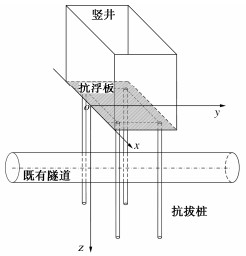
1. 门式抗浮框架介绍
门式抗浮框架主要是由抗浮板和抗拔桩组成，抗浮板和抗拔桩通过刚性连接形成抗浮体系。为了减小门式抗浮框架施工过程中下卧隧道的上浮变形，通常采用竖井开挖的方式逐步施作抗浮板。如图 1所示，首先在隧道两侧施工抗拔桩，然后开挖一期竖井，竖井开挖到底后尽快浇筑抗浮板，待抗浮板具有一定强度后再进行二期竖井的开挖，这样逐期施工直至隧道上方抗浮板全部施作完成。隧道上方形成完成的门式框架后，可采用分层、分段的方式进行隧道上方大面积基坑开挖卸载。
![]()
图 1 竖井开挖联合门式抗浮框架三维示意图Figure 1. Illustration of combination of shaft excavation and anti-uplift portal frame2. 考虑门式抗浮框架作用的土体变形解析解
两阶段法是目前求解隧道-土体相互作用的一种最为常用的分析方法。本文同样也采用两阶段法的计算思想，求解门式抗浮框架作用下竖井和基坑开挖引起的既有隧道响应。
不考虑既有隧道的影响，对于基坑底部任意点处土体竖向位移ws可以表示为
ws=wsu+wsp+wss。 (1) 式中：wsu为上方开挖卸载引起的土体竖向位移；wsp为抗拔桩-土体相互作用力引起的土体竖向位移；wss为抗浮板作用力引起的土体竖向位移。显然，当采用式（1）计算一期竖井开挖期间土体的竖向位移时，抗浮板并未发挥作用，此时可取wss=0。
2.1 开挖引起的下卧土体竖向变形计算
上方开挖卸载引起的土体竖向位移wsu可采用分层总和法进行计算：
wsu=j∑i=1ΔσriEHi。 (2) 式中：Δσri为土体分层平均竖向卸载应力，可采用Mindlin解进行计算[9]；E为土体弹性模量，计算中取土体的回弹模量；Hi为土体分层厚度；j为土体分层数。
2.2 抗拔桩-土体相互作用
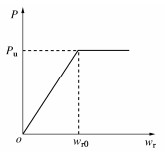
在分析抗拔桩-土体相互作用时，本文提出以下3个假设条件：①抗拔桩为刚体，本身不发生变形；②抗拔桩为摩擦型桩，抗拔桩的内力完全由桩侧摩阻力提供；③桩-土相互作用模式为理想弹塑性模型，如图 2所示。
桩土作用力P可按下式计算：
P={Pu (wr⩾ (3) 式中：Pu为极限桩土作用力，Pu= k{w_{{\text{r0}}}} ； {w_{\text{r}}} 为桩土相对位移； {w_{{\text{r0}}}} 为极限桩土相对位移；k为桩土界面的剪切刚度，宜根据单桩抗拔试验进行确定。如图 2所示，在弹性阶段，假设桩土作用力与桩土相对位移成正比；在塑性阶段，桩土作用力达到极限值，不再随桩土相对位移增加。
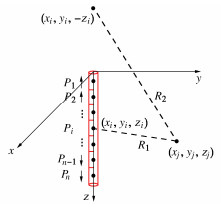
将抗拔桩沿桩身方向离散为n个桩单元，每个桩单元上的桩土相互作用力作用简化为集中力，集中力作用在桩单元的中心，如图 3所示。桩单元作用力Pi在（xj, yj, zj）处产生的土体竖向位移 {w_{{\text{sp}}i}} 可以表示为
{w_{{\text{sp}}i}} = {I_i}{P_i} 。 (4) 式中： {I_i} 为作用在（xi, yi, zi）处的单位点荷载在（xj, yj, zj）处产生的土体竖向位移，可通过Mindlin解进行计算：
\begin{array}{c} {I_i} = \frac{{{P_i}(1 + \mu )}}{{8\pi E(1 - \mu )}}\left[ {\frac{{3 - 4\mu }}{{{R_1}}} + \frac{{8{{(1 - \mu )}^2} - (3 - 4\mu )}}{{{R_2}}}} \right.{\text{ + }}\frac{{{{({z_j} - {z_i})}^2}}}{{R_1^3}} + \\ \left. {\frac{{(3 - 4\mu ){{({z_j} + {z_i})}^2} - 2{z_i}{z_j}}}{{R_2^3}} + \frac{{6{z_i}{z_j}{{({z_j} + {z_i})}^2}}}{{R_2^5}}} \right] 。 \end{array} (5) 式中：μ为土体泊松比；R1和R2为与桩土相对位置有关的系数，
{R_1} = \sqrt {{{({x_i} - {x_j})}^2} + {{({y_i} - {y_j})}^2} + {{({z_i} - {z_j})}^2}} \text{，} (6) {R_2} = \sqrt {{{({x_i} - {x_j})}^2} + {{({y_i} - {y_j})}^2} + {{({z_i} + {z_j})}^2}} 。 (7) 单根抗拔桩全部n个桩单元在（xi, yi, zi）处产生的土体竖向位移可以表示为
{w_{{\text{sp}}}} = \sum\limits_{i = 1}^n {{I_i}{P_i}} 。 (8) 根据式（8）可以计算不同位置处抗拔桩引起的土体竖向位移，并进行累加即可获得所有抗拔桩共同作用引起的土体竖向位移。计算过程中可以近视认为同一竖井下方各抗拔桩受力情况相同。
2.3 抗拔桩-抗浮板相互作用
不考虑抗拔桩自重条件下，抗拔桩桩顶轴力P0可以表示为
{P_0}{\text{ = }}\sum\limits_{i = 1}^n {{P_i}} 。 (9) 显然，当一期竖井开挖到底或抗拔桩与抗浮板没有作用力时，抗拔桩桩顶轴力为0，即P0=0。
假设抗浮板与土体之间作用力 {q_{\text{s}}} 为均布分布，则
{q_{\text{s}}} = \frac{{{P_0}m}}{A} 。 (10) 式中：A为抗浮板面积；m为抗拔桩数量。需要说明的是，抗拔桩对抗浮板的作用力集中在抗浮板的两端，当抗浮板刚度相对较大时，可以近视认为抗浮板与土体之间作用力均布分布；当抗浮板刚度相对较小时，需要考虑抗浮板产生一定的挠度变形后引起的作用力分布不均匀的情况，此时可以将抗浮板与土体相互作用简化为Winkler地基上的欧拉-伯努利梁，进而计算抗浮板与土体之间的作用力。抗浮板作用力引起的土体竖向位移 {w_{{\text{ss}}}} 可以按照计算开挖引起的下卧土体竖向变形计算方法，通过Mindlin解获得土体的竖向附加荷载，进而通过分层总和法进行计算。
2.4 平衡方程
取任意抗拔桩桩周土体进行分析，抗拔桩桩周土体任意点的竖向位移可以表示为
{w_{\text{s}}} = {w_{\text{p}}} + {w_{\text{r}}} 。 (11) 式中： {w_{\text{p}}} 为抗拔桩的竖向位移。
联立式（1），（11），可以得到
{w_{{\text{su}}}} + {w_{{\text{sp}}}} + {w_{{\text{ss}}}}{\text{ = }}{w_{\text{p}}} + {w_{\text{r}}} 。 (12) 将式（8）代入式（12）中，可以得到
{w_{{\text{su}}}} + \sum\limits_{i = 1}^n {{I_{ij}}k} {w_{\text{r}}}{\text{ + }}{w_{{\text{ss}}}} = {w_{\text{p}}} + {w_{\text{r}}} 。 (13) 因此，桩土相对位移可以表示为
{w_{\text{r}}} = {\left( {1 - \sum\limits_{i = 1}^n {{I_i}k} } \right)^{ - 1}}({w_{{\text{su}}}} - {w_{\text{p}}} - {w_{{\text{ss}}}}) 。 (14) 对于抗浮板没有发挥作用的情况，式（14）可以表示为
{w_{\text{r}}} = {\left( {1 - \sum\limits_{i = 1}^n {{I_i}k} } \right)^{ - 1}}({w_{{\text{su}}}} - {w_{\text{p}}}) 。 (15) 3. 既有隧道结构变形解析解
上方开挖会导致既有隧道在纵向上发生不均匀上浮变形，同时隧道横截面的收敛变形也会发生变化。因此，本文分别针对开挖引起的既有隧道纵向和横截面变形提出了计算方法。
3.1 纵向隧道-地层相互作用模型
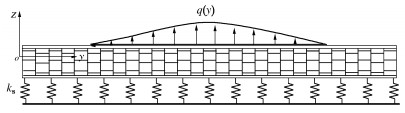
针对隧道纵向变形的分析，可以将隧道视为一维梁结构。已有的研究常将隧道视为欧拉-伯努利梁，认为隧道只发生弯曲变形，忽略了剪切变形，会导致在一定程度上低估隧道的变形量[16]。本文采用铁木辛科梁模型表示盾构隧道，可以同时考虑盾构隧道的弯曲和剪切变形[16-17]。本文采用位于Winkler地基上的一维均匀铁木辛科梁描述盾构隧道-土体相互作用，如图 4所示。根据该地基模型，可以得到如下控制方程：
\begin{array}{c} \frac{{{{\text{d}}^4}\omega (y)}}{{{\text{d}}{y^4}}} - \frac{{{k_{\text{s}}}}}{{{{(\kappa GA)}_{{\text{eq}}}}}}\frac{{{{\text{d}}^2}\omega (y)}}{{{\text{d}}{y^2}}} + \frac{{{k_{\text{s}}}}}{{{{(EI)}_{{\text{eq}}}}}}\omega (y) \\ = \frac{1}{{{{(EI)}_{{\text{eq}}}}}}q(y) - \frac{1}{{{{(\kappa GA)}_{{\text{eq}}}}}}\frac{{{{\text{d}}^2}q(y)}}{{{\text{d}}{y^2}}}。 \end{array} (16) ![]()
图 4 Winkler地基上的铁木辛柯梁模型示意图Figure 4. Illustration of Timoshenko beam lying on Winkler foundation式中：ω为既有隧道竖向变形；q为作用在既有隧道上的竖向附加荷载；ks为Winkler地基的地基反力系数；(EI)eq和(κGA)eq分别为既有隧道的等效弯曲刚度和等效剪切刚度。
采用Winkler地基上铁木辛科梁理论分析既有隧道变形，其关键在于确定作用在既有隧道的附加荷载q。根据式（1）可以计算得到既有隧道所在位置的自由场土体竖向变形，q可以表示为
q = {k_{\text{s}}}{w_{\text{s}}} 。 (17) Vesic[18]基于集中力作用的无限长梁的响应推导了地基反力系数 {k_{\text{s}}} ，计算表达式为
{k_{\text{s}}} = \frac{{0.65E}}{{D(1 - {\mu ^2})}}\sqrt[{12}]{{\frac{{E{D^4}}}{{{{(EI)}_{eq}}}}}} \text{，} (18) 式中，D为既有隧道外径。
盾构隧道的等效抗弯刚度可表示为[19]
{(EI)_{{\text{eq}}}} = {E_{\text{s}}}{I_{\text{s}}}\frac{{{K_{\text{f}}}{l_{\text{s}}}}}{{{K_{\text{f}}}({l_{\text{s}}} - \lambda {l_{\text{b}}})}}。 (19) 式中：Es为隧道管片的弹性模量；Is为隧道横截面的惯性矩；Kf为弯曲刚度折减系数；ls和lb分别为管片环的宽度和螺栓的长度；\lambda {l_{\text{b}}}为螺栓的影响长度。
基于Liao等[20]的研究结果，Wu等[16]提出了一种盾构隧道等效剪切刚度的计算方法，计算表达式为
{(\kappa GA)_{{\text{eq}}}} = \xi {l_{\text{s}}}{\left( {\frac{{{l_{\text{b}}}}}{{n{\kappa _{\text{b}}}{G_{\text{b}}}{A_{\text{s}}}}} + \frac{{{l_{\text{s}}} - {l_{\text{b}}}}}{{{\kappa _{\text{s}}}{G_{\text{s}}}{A_{\text{s}}}}}} \right)^{ - 1}}。 (20) 式中：n为纵向螺栓个数；{\kappa _{\text{b}}}和{\kappa _{\text{s}}}分别为螺栓和管片的铁木辛科剪切系数；{G_{\text{b}}}和{G_{\text{s}}}分别为螺栓和管片的剪切模量；Ab和As分别为螺栓和管片的横截面积；ξ为修正系数。
3.2 横截面隧道-地层相互作用模型
采用多铰圆环模型计算隧道横截面的变形和内力[21]。盾构隧道在施工完成后，盾构管片同时承受土压力和水压力的作用。
{p_1} 为隧道拱顶竖向荷载，满足
{p_1} = {p_0} + {q_1} + {q_2} 。 (21) 式中： {p_0} 为地面荷载； {q_1} 为隧道拱顶土体竖向压力； {q_2} 为隧道拱肩范围内的土体竖向压力，满足
{q_{\text{2}}} = {\text{(1}} - {\rm{ \mathsf{ π} }}/4{\text{)}}r\gamma 。 (22) 式中：r为隧道半径，γ为隧道拱肩范围内的土体平均重度。
{p_2} 为隧道拱底竖向荷载，满足
{p_{\text{2}}} = {p_{\text{1}}} + {\rm{ \mathsf{ π} }}t{\gamma _{\text{c}}} \text{，} (23) 式中，t和 {\gamma _{\text{c}}} 分别为管片的厚度和重度。
{p_3} 为隧道拱顶水平荷载，满足
{p_{\text{3}}} = ({p_0} + {q_1}){\tan ^2}\left( {\frac{{\rm{ \mathsf{ π} }}}{4} - \frac{\varphi }{2}} \right) - 2c\tan \left( {\frac{{\rm{ \mathsf{ π} }}}{4} - \frac{\varphi }{2}} \right) \text{，} (24) 式中，c和φ分别为土体的黏聚力和内摩擦角。
{p_4} 为隧道深部范围内的水平荷载增量，满足
{p_{\text{4}}} = {\text{2}}r\gamma {\tan ^2}\left( {\frac{{\rm{ \mathsf{ π} }}}{4} - \frac{\varphi }{2}} \right) 。 (25) {p_5} 为隧道管片的平均自重，
{p_{\text{5}}} = {\gamma _{\text{c}}}t 。 (26) {p_6} 为盾构管片两侧的土体抗力，
{p_{\text{6}}} = {p_{\text{h}}}(1 - {\cos ^2}\varphi )\;\;\;{{\rm{ \mathsf{ π} }}\text{/4}} \leqslant \phi \leqslant \;3{{\rm{ \mathsf{ π} }}\text{/4}} \text{，} (27) {p_{\text{h}}} = {k_{\text{s}}}{\mathit{\Delta } _{\text{h}}} 。 (28) 式中： {p_{\text{h}}} 为隧道拱腰处的土体抗力； {\mathit{\Delta } _{\text{h}}} 为隧道拱腰处的水平变形。
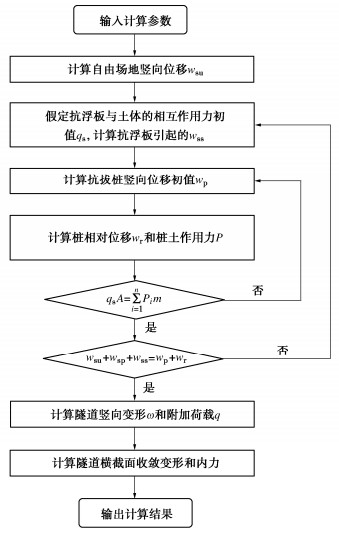
既有隧道上方开挖时，隧道周边土体在竖向方向的应力释放较为明显，而水平方向的应力释放相对较小。因此，基于上述荷载分布模式，计算上方开挖引起的既有隧道横向变形和内力分布时，仅考虑上方开挖引起的隧道拱顶竖向荷载q1的变化量Δq1。Δq1可以根据既有隧道拱顶所在位置的自由场土体竖向变形，按照式（17）进行计算。通过计算荷载变化前后隧道的收敛变形和内力，获得上方开挖作用下既有隧道水平和竖向收敛变化量以及相应的内力。基于上述计算模型和理论公式，图 5给出了既有隧道响应解析解的详细计算流程。
![]()
图 5 既有隧道变形计算流程图Figure 5. Flow chart for calculation of deformation of existing tunnel4. 模型验证
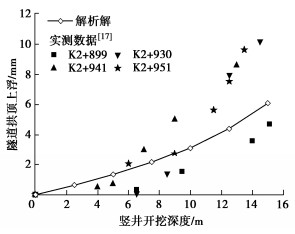
为了验证本文解析解的有效性，采用桂庙快速化改造工程[14]，该工程与深圳地铁11号线长距离共线，采用明挖法进行施工。为了减小开挖引起的既有地铁隧道变形，在工程部分区段采用门式抗浮框架联合竖井开挖的控制措施。选取里程段K2+898—K2+957的隧道变形监测数据进行对比，该里程段竖井开挖到底后隧道上方剩余覆土约为6.2 m，隧道所处地层为砾质黏性土。简化后的竖井开挖尺寸为7.2 m×15 m（长×宽），开挖深度为15 m。抗拔桩沿隧道两侧等间距布置，每个竖井下包括4根抗拔桩，抗拔桩直径为1 m，桩长18 m，与隧道结构水平净距为2.5 m。盾构隧道管片采用采用C50混凝土，管片外径为6.7 m，厚度为0.35 m。竖井采用分期和隔二挖一的开挖方式，本文选取一期竖井开挖期间隧道的变形监测数据进行对比，因此可以近似不考虑竖井之间的相互影响。
图 6比较了竖井开挖期间隧道拱顶上浮量的解析解和实测值。理论模型计算中选取隧道等效抗弯刚度为2.26×108 kN·m2，等效剪切刚度为5.14×106 kN，地基反力系数为3.25×104 kN/m2。已有研究表明，上方卸载导致隧道横截面表现为水平压缩和竖向伸长，因此，隧道拱顶上浮由两部分组成：隧道拱顶的上浮和隧道横截面竖向收敛变形。采用理论模型计算隧道拱顶上浮时，首先采用纵向隧道-地层相互作用模型计算隧道拱底上浮，然后采用横截面隧道-地层相互作用模型计算隧道竖向收敛变形，最后将两个变形量叠加获得隧道拱顶上浮。从图 6可以看出，随着竖井开挖深度的增加，隧道拱顶的上浮也在逐渐地增大，并且增大的幅度也在逐渐增大。通过解析解与实测结果进行对比，发现本文理论模型能够较好地反映竖井开挖期间隧道的上浮变形规律。此外，还可以发现竖井开挖引起的隧道上浮变形不可忽视，实测结果显示该阶段隧道最大上浮变形可能会超过10 mm，同时相邻竖井开挖期间隧道上浮可能会进一步发展，因此根据隧道上浮变形，在进行下一期竖井开挖前对已开挖竖井进行回填，待完成所有抗浮结构后再进行开挖。
![]()
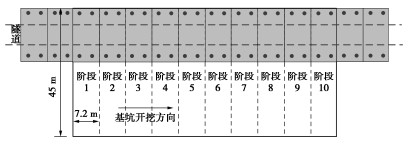
图 6 竖井开挖期间隧道拱顶上浮量解析解和实测值比较Figure 6. Comparison between analytical and measured heaves of tunnel crown caused by shaft excavation吴怀娜等[15]为了进一步探究门式抗浮框架建成后基坑开挖过程中门式抗浮框架的作用机理，依托桂庙快速化改造工程开展了三维数值模拟。如图 7所示，基坑沿隧道纵向分段开挖，分段长度与竖井长度保持一致（7.2 m），共分为10段，从左至右依次开挖，基坑开挖宽度为45 m。
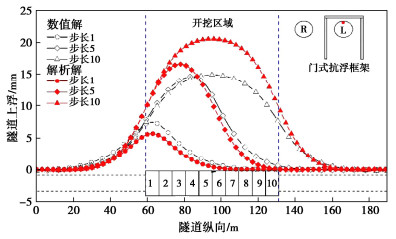
图 8比较了分别采用理论模型和数值模拟获得的不同基坑开挖阶段下沿纵向隧道拱顶上浮曲线。可以看出，随着开挖的逐步进行，在叠加效应影响下最大隧道拱顶上浮逐渐增大，并且最大上浮的位置基本位于基坑开挖的中心位置处。数值模拟计算结果显示，当基坑开挖到阶段5时，最大隧道拱顶上浮基本保持不变，但是解析解仍略有增大，这主要是由于两种方法中关于土体本构模型的选取有关。整体上对比解析解与数值模拟结果可以发现，本文理论模型能够用于考虑门式抗浮框架作用的上方基坑开挖导致的隧道上浮变形计算。
![]()
图 8 基坑开挖导致的隧道拱顶上浮量解析解和数值解比较Figure 8. Comparison between analytical and numerical heaves of tunnel crown caused by excavation5. 门式抗浮框架机理分析
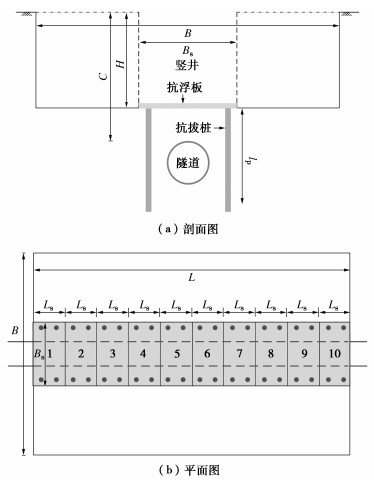
为了探究不同开挖条件下门式抗浮框架的作用机理，本文选取一个理想化的计算模型，模型中门式抗浮框架和基坑开挖布置如图 9所示。门式抗浮框架：抗拔桩桩长为20 m，抗拔桩桩径为1 m，抗拔桩间距为3 m。竖井：宽度Bs为12 m，长度Ls为6 m，深度H为10 m，基坑长度为60 m，宽度B为36 m。其他参数见表 1。门式抗浮框架主要在基坑开挖阶段发挥作用，因此本文假设模型主要探究基坑开挖阶段的隧道变形规律和门式抗浮框架的作用机理。在计算模型中，抗浮板施作完成后进行竖井回填至原始标高，并且认为回填后隧道变形完全恢复，此时抗拔桩和抗浮板无相互作用力。基坑开挖阶段抗浮板与土体作用力假设为均布力。
![]()
图 9 门式抗浮框架和基坑开挖布置示意图Figure 9. Illustration of anti-uplift portal frame and excavation表 1 门式抗浮框架计算模型参数Table 1. Parameters of model for anti-uplift portal frame既有隧道 地层 埋深C/m 外径/m 等效抗弯刚度/(kN·m-2) 等效剪切刚度/kN E/kPa \gamma /(kN·m-3) \nu c/kPa φ/(°) wr0/m k/(kN·m-1) 15 6.2 2.26×108 5.14×106 5×104 18 0.3 23 23.5 0.01 130 注：wr0为极限桩土相对位移，k为桩土界面的剪切刚度。 5.1 既有隧道变形
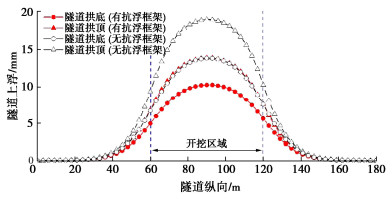
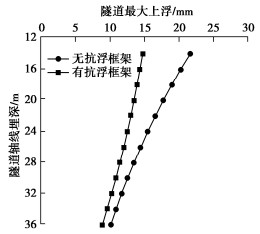
图 10给出了在有无门式抗浮框架下基坑开挖引起的隧道拱顶和拱底纵向上浮变形分布曲线。隧道拱顶和拱底最大上浮变形均出现在基坑中心的位置处，纵向距基坑边界20 m处隧道上浮变形趋近于0，表明基坑开挖对纵向隧道的影响范围约为2倍的开挖深度。计算结果显示，无门式抗浮框架时隧道拱顶和拱底最大上浮变形分别为19.0，13.8 mm，在门式抗浮框架作用下隧道拱顶和拱底最大上浮变形分别减小至13.9，10.2 mm，减小率分别为26.8%和26.1%。可以看出，门式抗浮框架可以在一定程度减小基坑开挖期间隧道的上浮变形。此外，还可以发现隧道拱顶上浮明显大于隧道拱底上浮，说明基坑开挖隧道在横截面上也会发生明显的变形。
![]()
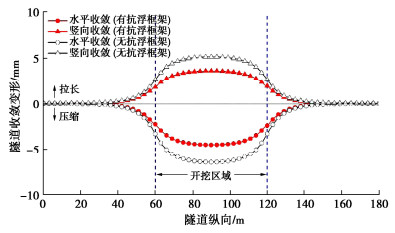
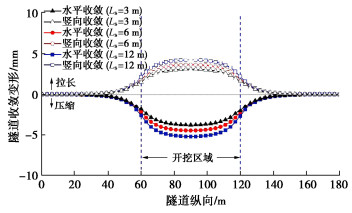
图 10 有无门式抗浮框架隧道上浮变形的比较Figure 10. Comparison of tunnel heaves with and without anti-uplift portal frame图 11给出了在有无门式抗浮框架下基坑开挖引起的沿纵向隧道横截面收敛变形分布曲线。基坑开挖后隧道横截面表现为水平向压缩，在竖向上拉长，表明隧道横截面从开挖前的横椭圆形式逐渐减弱。与开挖前的收敛变形相比较（水平收敛8.0 mm，竖向收敛-6.4 mm），开挖后隧道横截面形态仍未完全恢复成真圆形式。隧道最大收敛变形均出现在基坑中心的位置处，这与隧道上浮变形分布形式保持一致。计算结果显示，无门式抗浮框架时基坑开挖引起的隧道最大水平和竖向收敛变形分别为-6.5，5.1 mm，在门式抗浮框架作用下隧道最大水平和竖向收敛变形分别减小至-4.5，3.6 mm，减小率分别为30.1%和29.4%。可以看出，门式抗浮框架也会在一定程度减小基坑开挖期间隧道横截面收敛变形的变化量。
![]()
图 11 有无抗浮框架隧道收敛变形的比较Figure 11. Comparison of tunnel convergences with and without anti-uplift portal frame5.2 抗拔桩和抗浮板
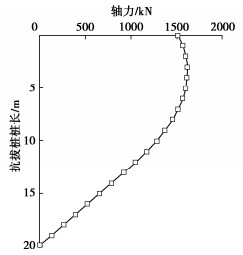
图 12给出了基坑开挖完成后抗拔桩的轴力分布图。基坑开挖会引起坑底土体和门式抗浮框架产生一定的上浮变形，由于桩土相互作用的影响，桩身会产生轴力并表现为受拉状态。如图 12中曲线所示，在曲线拐点处桩身轴力达到最大值1619 kN，拐点以下抗拔桩受到负摩阻力，拐点以上为正摩阻力。在桩顶处抗拔桩轴力为1522 kN，该轴力提供了抗浮板与土体的作用力，根据式（10）可以获得抗浮板与土体的作用力为85 kPa。可以发现，抗拔桩的受力情况会直接影响门式抗浮框架的作用效果，因此，在进行门式抗浮框架设计时，抗拔桩作用效果的计算分析是关键。
![]()
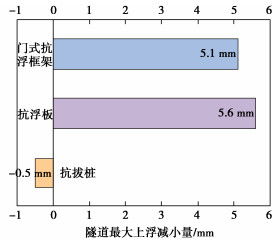
图 12 基坑开挖后抗拔桩的轴力分布Figure 12. Distribution of axial force of uplift pile after excavation从式（1）中可以看出，抗拔桩-土体作用力和抗浮板-土体作用力都会对既有隧道的变形产生影响。为了探究两者的影响程度，以隧道最大拱顶上浮变形为参考，图 13比较了抗拔桩和抗浮板对隧道上浮变形的作用效果。可以看出，抗浮板与土体的作用力引起的隧道最大上浮减小量为5.6 mm，而抗拔桩与土体的作用力导致隧道最大上浮量增加0.5 mm。因此，抗浮板表现出限制隧道上浮的作用，而抗拔桩的作用效果相反，并且抗浮板对隧道上浮的作用效果明显高于抗拔桩。
![]()
图 13 门式抗浮框架中抗浮板和抗拔桩的抗浮效果比较Figure 13. Comparison of anti-floating effects of anti-floating slab and uplift pile in anti-uplift portal frame6. 参数敏感性分析
本节采用图 9所示计算模型，分别探究不同既有隧道埋深、竖井开挖尺寸和抗拔桩桩长条件下门式抗浮框架对既有隧道变形的限制作用。
6.1 既有隧道埋深的影响
图 14给出了有无门式抗浮框架的隧道最大上浮变形与既有隧道埋深的变化关系。可以看出，随着既有隧道埋深的增加，最大上浮变形逐渐减小，并呈现出近似线性递减的趋势。在既有隧道越靠近基坑坑底的位置，门式抗浮框架对应的隧道最大上浮越小于无门式抗浮框架的情况，并且它们的差值会随着隧道埋深的增加而逐渐减小，这说明门式抗浮框架对隧道上浮变形的限制作用在逐渐减弱。因此，门式抗浮框架对于隧道剩余覆土较小时的控制效果更好。
![]()
图 14 不同既有隧道埋深下隧道最大上浮变化Figure 14. Variation of maximum tunnel heave under different buried depths of existing tunnel6.2 竖井开挖尺寸的影响
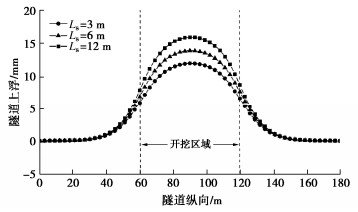
图 15，16分别给出了不同竖井长度条件下沿纵向隧道拱顶上浮和横截面收敛变形分布曲线。计算中，分别取竖井开挖长度为3，6，12 m，每个竖井下方的抗浮板仍保持4根抗拔桩与之连接。从图 15中可以看出，随着竖井开挖长度的增加，隧道最大上浮变形也逐渐增大，当竖井开挖长度从3 m增加到12 m时，隧道拱顶最大上浮从11.9 mm增加到15.9 mm。同样的，隧道横截面的收敛变形也会随着竖井开挖长度的增加而增大。分析抗浮板与土体的作用力可以发现，竖井开挖长度为3，6，12 m时分别对应的抗浮板与土体的作用力为53，85，116 kPa。这也进一步说明了竖井开挖尺寸对门式抗浮框架作用效果的影响，主要取决于抗浮板与土体之间的作用力。
![]()
图 15 不同竖井开挖尺寸下隧道上浮变化Figure 15. Variation of tunnel heave under different sizes of shaft![]()
图 16 不同竖井开挖尺寸下隧道收敛变形变化Figure 16. Variation of tunnel convergence under different sizes of shaft6.3 抗拔桩桩长的影响
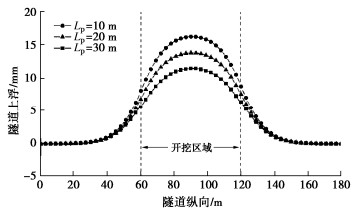
图 17给出了不同抗拔桩桩长条件下沿纵向隧道拱顶上浮变形分布曲线。从图 17可以发现，随着抗拔桩桩长的增加，隧道上浮量逐渐减小，这也说明门式抗浮框架的控制效果逐渐增强。究其原因有两个方面：①抗拔桩能够提供的抗浮板与土体的极限作用力增大；②抗拔桩可以将开挖引起的竖向卸载应力传递到更深的土体中。
![]()
图 17 不同抗拔桩桩长下隧道上浮变化Figure 17. Variation of heave of existing tunnel under different lengths of up-lift pile7. 结论
本文针对上方开挖引起的既有隧道变形规律开展研究，考虑了门式抗浮框架对隧道变形的限制作用，得到以下4点结论。
（1）提出的考虑门式抗浮框架的既有隧道变形计算方法，不仅能反映抗拔桩和抗浮板对地层变形的影响，还考虑了竖井分期和基坑分段开挖等因素的影响。
（2）通过与工程实例和三维数值模拟进行对比，分别验证了本文的理论分析模型在计算竖井开挖阶段和基坑开挖阶段既有隧道的上浮变形的准确性。此外，本文的理论分析方法可以用于上方开挖卸载引起的隧道纵向和横截面变形计算。
（3）门式抗浮框架在基坑开挖阶段可以在一定程度上控制上方开挖引起的隧道变形，其中抗浮板对隧道上浮的限制作用明显高于抗浮板。上方基坑开挖引起的既有隧道拱顶上浮变形大于拱底上浮，主要是由于隧道横截面收敛变形引起的，开挖后隧道横截面形态仍未完全恢复成真圆形式。
（4）门式抗浮框架控制效果与隧道上方剩余覆土厚度和竖井开挖尺寸密切相关，剩余覆土越小控制效果越明显；随着竖井开挖尺寸长度的增加，抗浮板与土体之间的作用力减小，导致控制效果减弱。
-
![]()
图 1 竖井开挖联合门式抗浮框架三维示意图
Figure 1. Illustration of combination of shaft excavation and anti-uplift portal frame
![]()
图 4 Winkler地基上的铁木辛柯梁模型示意图
Figure 4. Illustration of Timoshenko beam lying on Winkler foundation
![]()
图 5 既有隧道变形计算流程图
Figure 5. Flow chart for calculation of deformation of existing tunnel
![]()
图 6 竖井开挖期间隧道拱顶上浮量解析解和实测值比较
Figure 6. Comparison between analytical and measured heaves of tunnel crown caused by shaft excavation
![]()
图 8 基坑开挖导致的隧道拱顶上浮量解析解和数值解比较
Figure 8. Comparison between analytical and numerical heaves of tunnel crown caused by excavation
![]()
图 9 门式抗浮框架和基坑开挖布置示意图
Figure 9. Illustration of anti-uplift portal frame and excavation
![]()
图 10 有无门式抗浮框架隧道上浮变形的比较
Figure 10. Comparison of tunnel heaves with and without anti-uplift portal frame
![]()
图 11 有无抗浮框架隧道收敛变形的比较
Figure 11. Comparison of tunnel convergences with and without anti-uplift portal frame
![]()
图 12 基坑开挖后抗拔桩的轴力分布
Figure 12. Distribution of axial force of uplift pile after excavation
![]()
图 13 门式抗浮框架中抗浮板和抗拔桩的抗浮效果比较
Figure 13. Comparison of anti-floating effects of anti-floating slab and uplift pile in anti-uplift portal frame
![]()
图 14 不同既有隧道埋深下隧道最大上浮变化
Figure 14. Variation of maximum tunnel heave under different buried depths of existing tunnel
![]()
图 15 不同竖井开挖尺寸下隧道上浮变化
Figure 15. Variation of tunnel heave under different sizes of shaft
![]()
图 16 不同竖井开挖尺寸下隧道收敛变形变化
Figure 16. Variation of tunnel convergence under different sizes of shaft
![]()
图 17 不同抗拔桩桩长下隧道上浮变化
Figure 17. Variation of heave of existing tunnel under different lengths of up-lift pile
表 1 门式抗浮框架计算模型参数
Table 1 Parameters of model for anti-uplift portal frame
既有隧道 地层 埋深C/m 外径/m 等效抗弯刚度/(kN·m-2) 等效剪切刚度/kN E/kPa /(kN·m-3) c/kPa φ/(°) wr0/m k/(kN·m-1) 15 6.2 2.26×108 5.14×106 5×104 18 0.3 23 23.5 0.01 130 注：wr0为极限桩土相对位移，k为桩土界面的剪切刚度。 
下载: 导出CSV
-
[1] 魏纲. 基坑开挖对下方既有盾构隧道影响的实测与分析[J]. 岩土力学, 2013, 34(5): 1421-1428. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201305029.htm WEI Gang. Measurement and analysis of impact of foundation pit excavation on below existed shield tunnels[J]. Rock and Soil Mechanics, 2013, 34(5): 1421-1428. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201305029.htm
[2] MENG F Y, CHEN R P, XU Y, et al. Contributions to responses of existing tunnel subjected to nearby excavation: a review[J]. Tunnelling and Underground Space Technology, 2022, 119: 104195. doi: 10.1016/j.tust.2021.104195
[3] 郑刚, 杜一鸣, 刁钰, 等. 基坑开挖引起邻近既有隧道变形的影响区研究[J]. 岩土工程学报, 2016, 38(4): 599-612. doi: 10.11779/CJGE201604003 ZHENG Gang, DU Yiming, DIAO Yu, et al. Influenced zones for deformation of existing tunnels adjacent to excavations[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(4): 599-612. (in Chinese) doi: 10.11779/CJGE201604003
[4] 徐中华, 宗露丹, 沈健, 等. 邻近地铁隧道的软土深基坑变形实测分析[J]. 岩土工程学报, 2019, 41(增刊1): 41-44. doi: 10.11779/CJGE2019S1011 XU Zhonghua, ZONG Ludan, SHEN Jian, et al. Deformation of a deep excavation adjacent to metro tunnels in soft soils[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S1): 41-44. (in Chinese) doi: 10.11779/CJGE2019S1011
[5] 黄茂松, 李豪, 俞剑, 等. 上方基坑开挖引起下卧隧道纵向变形分析方法[J]. 岩土工程学报, 2023, 45(11): 2209-2216. doi: 10.11779/CJGE20220780 HUANG Maosong, LI Hao, YU Jian, et al. Approach on longitudinal deformation of underlying tunnel due to pit excavation above[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(11): 2209-2216. (in Chinese) doi: 10.11779/CJGE20220780
[6] 张治国, 张孟喜. 软土城区土压平衡盾构上下交叠穿越地铁隧道的变形预测及施工控制[J]. 岩石力学与工程学报, 2013, 32(增刊2): 3428-3440. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S2057.htm ZHANG Zhiguo, ZHANG Mengxi. Deformation prediction of subway tunnel induced by EPB shield in soft clay during above and down overlapped traversing process and its construction control[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 3428-3440. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S2057.htm
[7] ZHANG D M, HUANG Z K, LI Z L, et al. Analytical solution for the response of an existing tunnel to a new tunnel excavation underneath[J]. Computers and Geotechnics, 2019, 108(5): 197-211.
[8] CHENG H Z, CHEN R P, WU H N, et al. General solutions for the longitudinal deformation of shield tunnels with multiple discontinuities in strata[J]. Tunnelling and Underground Space Technology, 2021, 107: 103652. doi: 10.1016/j.tust.2020.103652
[9] 陈郁, 李永盛. 基坑开挖卸荷引起下卧隧道隆起的计算方法[J]. 地下空间与工程学报, 2005(1): 91-94. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE20050100J.htm CHEN Yu, LI Yongsheng. Calculation of tunnel heaving due to unloading of pit excavation[J]. Chinese Journal of Underground Space and Engineering, 2005(1): 91-94. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BASE20050100J.htm
[10] HUANG A J, WANG D Y, WANG Z X. Rebound effects of running tunnels underneath an excavation. Tunnelling and Underground Space Technology, 2006, 21(3/4): 399.
[11] 黄宏伟, 黄栩HELMUT S F. 基坑开挖对下卧运营盾构隧道影响的数值模拟研究[J]. 土木工程学报, 2012, 45(3): 182-189. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201203024.htm HUAUG Hongwei, HUAUG Xu, HELMUT S F. Numerical analysis of the influence of deep excavation on underneath existing road tunnel[J]. China Civil Engineering Journal, 2012, 45(3): 182-189. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201203024.htm
[12] 谢雄耀, 郁宏杰, 王庆国, 等. 基坑开挖引起下卧既有电力隧道变形的控制技术研究[J]. 岩土工程学报, 2013, 36(1): 88-97. doi: 10.11779/CJGE201401007 XIE Xiongyao, YU Hongjie, WANG Qingguo, et al. Deformation control of operating tunnels induced by deep excavation of overlying metro[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(1): 88-97. (in Chinese) doi: 10.11779/CJGE201401007
[13] 郭劲睿. 近距离基坑开挖对下卧地铁隧道位移影响分析及位移控制措施研究[D]. 广州: 广州大学, 2018. GUO Jinrui. Analysis of the Influence of Short-distance of Foundation Pit Excavation on the Displacement of the Underlying Subway Tunnel and Research on Displacement Control Measures[D]. Guangzhou: Guangzhou University, 2018. (in Chinese)
[14] 蓝淦洲. 基于门式抗浮框架的基坑开挖下卧隧道变形控制研究[D]. 长沙: 湖南大学, 2021. LAN Ganzhou. Study on Deformation Control of Underlying Tunnel in Foundation Pit Excavation Based on Portal Anti-Floating Frame[D]. Changsha: Hunan University, 2021. (in Chinese)
[15] 吴怀娜, 冯东林, 刘源, 等. 基于门式抗浮框架的基坑开挖下卧隧道变形控制[J]. 上海交通大学学报, 2022, 56(9): 1227-1237. https://www.cnki.com.cn/Article/CJFDTOTAL-SHJT202209013.htm WU Huaina, FENG Donglin, LIU Yuan. Anti-uplift portal frame in control of underlying tunnel deformation induced by foundation pit excavation[J]. Journal of Shanghai Jiao Tong University, 2022, 56(9): 1227-1237. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SHJT202209013.htm
[16] WU H N, SHEN S L, LIAO S M, et al. Longitudinal structural modelling of shield tunnels considering shearing dislocation between segmental rings[J]. Tunnelling and Underground Space Technology, 2015, 50: 317-323. doi: 10.1016/j.tust.2015.08.001
[17] CHENG H Z, CHEN R P, WU H N, et al. A simplified method for estimating the longitudinal and circumferential behaviors of the shield-driven tunnel adjacent to a braced excavation[J]. Computers and Geotechnics, 2020, 123: 103595. doi: 10.1016/j.compgeo.2020.103595
[18] VESIC A S. Bending of beams resting on isotropic elastic solid[J]. Journal of the Engineering Mechanics Division, ASCE, 1961, 87(2): 35-53. doi: 10.1061/JMCEA3.0000212
[19] SHIBA Y, KAWASHIMA K, OBINATA N, et al. Evaluation method of longitudinal stiffness of shield tunnel linings for application to seismic response analysis[J]. Proceedings of the Japan Society of Civil Engineers, 1988, 398: 319-327. (in Japanese)
[20] LIAO S M, PENG F L, SHEN S L. Analysis of shearing effect on tunnel induced by load transfer along longitudinal direction[J]. Tunnelling and Underground Space Technology, 2008, 23(4): 421-430. doi: 10.1016/j.tust.2007.07.001
[21] LEE K M, HOU X Y, GE X W, et al. An analytical solution for a jointed shield-driven tunnel lining[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(4): 365-390. doi: 10.1002/nag.134
-
期刊类型引用(3)
1. 汤立峰. 基坑小净距上跨盾构隧道扰动变形分析及加固方案研究. 甘肃科学学报. 2025(01): 76-84 . 
百度学术
2. 杨潇. 淤泥质地层基坑开挖卸荷对下卧区间隧道变形扰动分析. 黑龙江交通科技. 2024(10): 120-124 . 百度学术
3. 甘波. 上跨既有盾构隧道深基坑围护设计及快速施工技术研究. 建筑施工. 2024(12): 2101-2104+2109 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 383
- HTML全文浏览量: 64
- PDF下载量: 85
- 被引次数: 3
