深切V型峡谷物理驱动人工智能波动模拟

栾绍凯; 陈苏; 丁毅; 金立国; 王巨科; 李小军

doi:10.11779/CJGE20230263

深切V型峡谷物理驱动人工智能波动模拟 English Version

栾绍凯^1,,
陈苏^1, ,,
丁毅¹,
金立国²,
王巨科²,
李小军^{1, 2}

1.
北京工业大学城市与工程安全减灾教育部重点实验室, 北京 100124
2.
中国地震局地球物理研究所, 北京 100081

基金项目:

国家自然科学基金重大项目 52192675

国家自然科学基金项目 51878626

国家自然科学基金项目 U1839202

详细信息

作者简介:
栾绍凯(1999—)，男，硕士研究生，主要从事物理驱动工程波动模拟方向的研究工作。E-mail: luanshaokaipsg@163.com

通讯作者:
陈苏, E-mail: chensuchina@126.com

中图分类号: TU435;P315
计量
- 文章访问数: 349
- HTML全文浏览量: 50
- PDF下载量: 74
出版历程
- 收稿日期: 2023-03-26
- 网络出版日期: 2024-06-04
- 刊出日期: 2024-05-31

Wave simulation of symmetric V-shaped canyon based on physics-informed deep learning method

LUAN Shaokai^1,,
CHEN Su^1, ,,
DING Yi¹,
JIN Liguo²,
WANG Juke²,
LI Xiaojun^{1, 2}

1.
Key Laboratory of Urban Security and Disaster Engineering of the Ministry of Education, Beijing University of Technology, Beijing 100124, China
2.
Institute of Geophysics, China Earthquake Administration, Beijing 100081, China

摘要

摘要: 高山峡谷区场地地震效应是地震工程领域研究热点。V形峡谷引起的圆柱形SH波散射和衍射波函数的级数解已较为成熟，并为众多河谷区重大工程提供了合理、科学的地震动输入。采用物理驱动深度学习方法结合与解析结果的对比分析，近一步明确了V型河谷地形地震反应特性及复杂波场空间分布。此方法主要关注稀疏样本及可诠释性人工智能，结合强形式自动微分和软约束边界条件嵌入，建立深度神经网络实现半无限域地震传播模型。采用时间域分解策略，实现不同给定波场工况下V型河谷高精度预测。通过与解析解对比，评估了所提出的物理驱动人工智能方法的精度和效率。结果表明，物理驱动人工智能方法可应用于地形效应分析，柱面SH波在V型峡谷底端发生显著衰减与振荡，边缘区呈现放大效应。
- 物理驱动深度学习 /
- 河谷地震 /
- 波动模拟 /
- 科学人工智能
Abstract: The seismic effects of alpine and canyon sites are a research hotspot in the field of earthquake engineering. The series solution of the two-dimensional scattering and diffraction wave functions of cylindrical SH waves caused by V-shaped canyons is relatively mature and provides reasonable and scientific ground motion input for many major projects in river valleys. In this study, the physics-informed deep learning method combined with the comparative analysis of the analytical results is used to further clarify the seismic response characteristics and complex wave field spatial distribution of the V-shaped river valley. The method mainly focuses on sparse samples and interpretable artificial intelligence, and establishes a deep neural network to realize the semi-infinite seismic propagation model by combining the strong formal automatic differentiation with the soft constraint boundary condition embedding, and realizes high-precision prediction of V-shaped river valleys under different given wave field conditions by adopting the time domain decomposition strategy. By comparing with the analytical solution, the accuracy and efficiency of the proposed physics-driven artificial intelligence method are evaluated. The results show that the physics-driven artificial intelligence method can be applied to the analysis of terrain effects, and the cylindrical SH waves are significantly attenuated at the bottom of the V-shaped canyon, and the edge area shows an amplification effect.
- physics-informed deep learning /
- river valley earthquake /
- wave simulation /
- AI for science

HTML全文

0. 引言

地表局部地形对地震波的传播有显著影响，当地震波遇到高山、峡谷等，会产生散射波、入射波和反射波等复杂波场，并引起地面运动的放大或衰减，称为地形效应。目前针对地形效应已有了相应的研究（表 1），主要包含了数值模拟和解析分析两种。解析主要运用的是波函数展开法，Wong等^[1]提出了半圆形峡谷对地震SH波散射的波函数级数解，随后众多学者提出了多种圆弧形峡谷的解析解^[2-6]，Gao等^[7]提出了通过坐标变换求解V形对称峡谷引起的圆柱形SH波二维散射和衍射波函数的级数解。数值方法包含了有限差分法^[8]，谱元法等^[9]等，数值方法可实现复杂地形地震波传播模拟，具备边界和复杂几何处理的灵活性，但在计算精度方面往往需要解析解的校准。

表 1 复杂地形效应近场波动模拟研究现状

Table 1. Researches on near-field fluctuation problems

模拟方法	应用场景	时间	文献
解析法	平面SH波在半圆柱型峡谷的散射	1972年	[1]
	平面SH波在半圆柱型冲击峡谷的散射	1971年	[2]
	平面SH波在半椭圆形冲击峡谷的散射	1974年	[3]
	平面SH波在圆弧形峡谷的散射	2009年	[4]
	平面SH波在截断峡谷的散射	2009年	[5]
	U型峡谷引起的地形放大对地震波的影响	2012年	[6]
	柱面SH波在对称V型峡谷的反射和散射	2013年	[7]
有限差分法	极坐标尺度不规则地形FEM方法	2021年	[8]
谱元法	入射平面SV波作用下梯田形山丘的表面运动	2017年	[9]
PINN	近场波动数值模拟	2022年	[30]

下载: 导出CSV

| 显示表格

近场波动在数学上可归结为偏微分方程的初值、边值问题，偏微分方程的数值离散化在模拟多物理场问题方面取得了很大的进展，但通过使用经典的分析或计算工具来建模和预测非线性多尺度系统的演化较困难，面对复杂网络剖分、参数化偏微分方程控制的高维问题等。

近年来的研究发现，物理信息神经网络（PINN）可以用于对控制物理系统的偏微分方程进行建模，通过嵌入物理信息解决了传统神经网络算法对于求解方面的局限性，例如高度依赖数据驱动，缺乏物理可解释性、易陷入过拟合以及可获取数据的稀疏性等。PINN方法仅依赖于少量甚至零标记的数据集，并实现数据稀缺、物理约束的学习。嵌入物理公式为可训练参数提供约束，缓解过拟合问题，减少对大型训练数据集的需求，从而提高训练模型的鲁棒性，以实现可靠的预测。Raissi等^[10]利用深度学习神经网络（DNN）的强表达性，开发了通用PINN框架，解决了涉及小数据集甚至没有任何标记数据的非线性偏微分方程系统的正逆问题。最近几年PINN方法在地球物理学^[11-13]、固体力学^[14-16]、流体动力学^[17-20]、热传导^[21-22]等方面有了相应的研究。众多学者针对不同的偏微分方程，让PINN方法更好地适应不同的物理问题^[23-29]。也有了少数利用物理信息神经网络求解波动方程的工作，Rao等^[19]通过DNN复合方案以硬嵌入的方式强制满足初值、边值条件，在截断域的波传播问题上进行了模拟。陈苏等^[30]结合了数值模拟原理和物理驱动深度学习建立了波动模拟方法，提出了可以提高网络训练效率的迁移学习方法。

在前人研究的基础上，提出通过物理信息神经网络模拟圆柱形SH波在不规则地形下的散射和衍射方法。通过新的参数加载代理建模策略，在给定初始时刻稀疏地震位移波场，模拟地震波在半无限域的传播，通过对比解析解和PINN预测解来评估所提出的规则地形下PINN模型的性能。通过PINN模型模拟不规则地形下圆柱形SH波的二维散射和衍射，证明该方法具有良好的泛化性。

1. 物理驱动深度学习原理

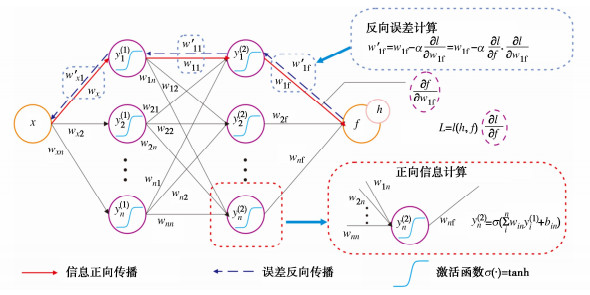
深度学习神经网络（DNN）具备出色的计算表达能力，在图像识别和自然语言处理等领域获得了较多应用。前馈全连接神经网络可以假设为输入层、多个隐藏层和输出层的堆栈。相邻两层之间的连接，例如从第i−1层到第i层，可用张量的形式简单表示为

$\boldsymbol{Y}_i=\alpha\left(\boldsymbol{W}_i \boldsymbol{Y}_{i-1}+\boldsymbol{b}_i\right) \quad(1 \leqslant i \leqslant n+1) 。$

(1)

式中：n为隐层总数；σ(·)为按元素作用的激活函数； ${\boldsymbol{Y}_0}$ 和 ${\boldsymbol{Y}_{n + 1}}$ 分别为输入张量和输出张量； ${\boldsymbol{W}_i}$ ， ${\boldsymbol{b}_i}$ 为第i层的可训练权重矩阵和偏置向量。DNN作为弹性动力学问题的参数化近似解，其中时空位置X = (x, t)为自变量。通过最优逼近物理系统理论解，获取训练参数，需设计嵌入物理定律的损失函数作为训练目标，网络训练中需评估物理场对时空变量的偏导数，Tensorflow和Pytorch框架中可完成自动微分功能。以前馈神经网络为例，网络以变量x为输入，在式（1）中定义的非线性变换后输出f，表示第i个隐藏层中第j个神经元的输出。由于输出f可以表示为x的嵌套函数，应用链式法则，可以计算每一层之间的梯度关系，通过构建损失函数和误差的反向传播，每训练一步后更新权重和偏置，如图 1所示，权重和偏置的更新计算为

图 1 DNN网络自动微分简图

Figure 1. Automatic differential diagram of DNN network

下载: 全尺寸图片幻灯片

$\omega_{1 \mathrm{f}}^{\prime}=\omega_{1 \mathrm{f}}-\alpha \frac{\partial l}{\partial \omega_{1 \mathrm{f}}} ,$

(2)

$\frac{\partial l}{\partial \omega_{\mathrm{1f}}}=\frac{\partial l}{\partial f} \cdot \frac{\partial f}{\partial \omega_{\mathrm{1f}}},$

(3)

$f=\sigma\left(\sum_i^n \omega_{i \mathrm{f}} y_i^{(2)}+b_i\right),$

(4)

$\frac{\partial f}{\partial \omega_{1 \mathrm{f}}}=\sigma y_1^{(2)}。$

(5)

式中： $\alpha$ 为DNN网络的学习率；l为期望值h与网络输出值f构建的损失函数。

损失函数L可以求得 $\tfrac{{\partial l}}{{\partial f}}$ 的值，式（4）中节点 $y_1^{(2)}$ 与输出f之间关系可以求得 $\tfrac{{\partial f}}{{\partial {\omega _\text{1f}}}}$ ，再通过式（2），（3）求得更新后的权重 ${\omega '_\text{1f}}$ 。偏置 ${b'_\text{1f}}$ 的计算同理，网络参数更新过后采用梯度下降最快的策略，使得损失函数L减小到0，最终输出值f与期望值h以及两者的导数实现强形式的相等，如图 1所示。

从函数逼近论角度，具有单一隐藏层的神经网络可精确逼近任何线性或非线性连续函数，因此可以将神经网络作为非线性函数逼近器。Rassi等^[10]通过训练全连接神经网络来逼近偏微分方程的解，用神经网络逼近方程的各阶偏导数，实现将PDE残差以及初、边值条件作为正则项加入损失函数中。

以一维杆件中波的传播为例，介绍物理驱动深度学习方法求解偏微分方程的可行性。杆件长10 m，在杆左端施加Ricker子波，波速为1 m/s。一维标量波动方程形式为

$\frac{{{\partial ^2}u}}{{{\partial ^2}t}} - c\frac{{{\partial ^2}u}}{{{\partial ^2}x}} = 0{\text{ }}\left( {x \in [0, 10], t \in [0, 20]} \right),$

(6)

Ricker子波公式 $:$

$u_{\mathrm{r}}=\left[\frac{2 \pi^2\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}}。$

(7)

Ricker子波从x=0处输入，所以在x=0处的边界条件可以表示为

$u(0, t)=\left[\frac{2 \pi^2\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}}。$

(8)

式中：c为波速， ${t_\text{s}}$ 为Ricker波的半周期，根据波动传播理论，得到

$u=f\left(t+\frac{x}{c}\right)=\left[\frac{2 \pi^2\left(t-t_\text{s}\right)^2}{t_\text{s}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_\text{s}\right)^2}{t_\text{s}^2}}。$

(9)

化简后易得上述波动方程解析解：

$u(x, t)=\left[\frac{2 \pi^2\left(t-t_{\mathrm{s}}-\frac{x}{c}\right)^2}{t_{\mathrm{s}}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_{\mathrm{s}}-\frac{x}{c}\right)^2}{t_{\mathrm{s}}^2}}。$

(10)

此案例满足如下形式的偏微分方程：

$\left. \begin{array}{l}\begin{gathered} \boldsymbol{D}(u(x, t) ; \lambda)=f(x, t) \quad(x \in \varOmega, t \in[0, T]), \\ u(x, t)=\boldsymbol{B}_D(t) \quad\left(x \in \partial \varOmega_D, t \in[0, T]\right), \\ \nabla u(x, t)=\boldsymbol{B}_N(t) \quad\left(x \in \partial \varOmega_N, t \in[0, T]\right), \\ u(0, t)=\boldsymbol{B}_0(t) \quad(t \in[0, T]), \\ u(x, 0)=\boldsymbol{J}_0(x) \quad(x \in \varOmega) 。 \end{gathered}\end{array} \right\}$

(11)

式中： $u(x, t)$ 为偏微分方法的解； $\boldsymbol{D}( \cdot )$ 为带参数 $\lambda$ 的微分算子；x为域 $\varOmega \in {R^d}$ 中的空间变量， $d = 1, 2, \ldots n$ ；域边界 $\partial \varOmega$ 由Dirichlet边界 $\partial {\varOmega _D}$ 和Neumann边界 $\partial {\varOmega _N}$ 组成； $t \in [0, T]$ 为时间变量； ${\boldsymbol{B}_D}(t), {\boldsymbol{B}_N}(t)$ 分别为偏微分方程的初边值问题中的Dirichlet、Neumann边界条件函数； ${\boldsymbol{B}_0}(t)$ 为在x=0处的边界条件函数； ${\boldsymbol{J}_0}(x)$ 为初始条件函数。

对于这些初、边值函数，通过设计损失函数 $\sum (\theta )$ 架构并训练神经网络：

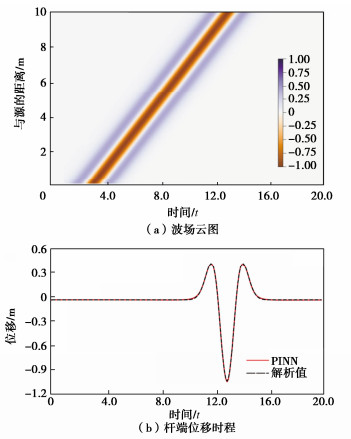
$\sum (\theta ) = {\sum _{\text{p}}}(\theta ) + {\sum _{{\text{bc}}}}(\theta ) + {\sum _{{\text{ic}}}}(\theta ) ,$

(12)

$\left. \begin{array}{l}\begin{aligned} \sum\nolimits_{\mathrm{bc}}(\theta)= & \frac{1}{N_{\mathrm{d}}} \sum\nolimits_i^{N_{\mathrm{p}}}\left\|\nabla \boldsymbol{N} \boldsymbol{N}\left(x_i, t_i ; \theta\right)-\boldsymbol{B}_D(t)\right\|_{\partial \varOmega_D \times[0, T]}^2+ \\ & \frac{1}{N_{\mathrm{n}}} \sum\nolimits_i^{N_{\mathrm{n}}}\left\|\nabla \boldsymbol{N} \boldsymbol{N}\left(x_i, t_i ; \theta\right)-\boldsymbol{B}_N(t)\right\|_{\partial \varOmega_N \times[0, T]}^2, \\ \sum\nolimits_{\mathrm{ic}}(\theta)= & \frac{1}{N_{\mathrm{ic}}} \sum\nolimits_i^{N_{\mathrm{ic}}}\left(\left\|\nabla \boldsymbol{N} \boldsymbol{N}\left(x_i, 0 ; \theta\right)-\boldsymbol{J}_0(t)\right\|_{\varOmega \times\{t=0\}}^2+\right. \\ & \left.\left\|\nabla \boldsymbol{N} \boldsymbol{N}_t\left(x_i, 0 ; \theta\right)-\boldsymbol{J}_1(t)\right\|_{\varOmega \times\{t=0\}}^2\right), \\ \sum\nolimits_{\mathrm{p}}(\theta)= & \frac{1}{N_{\mathrm{p}}} \sum\nolimits_i^{N_{\mathrm{p}}}\left(\left\|\boldsymbol{D}\left(\boldsymbol{N} \boldsymbol{N}\left(x_i, t_i ; \theta\right) ; \lambda\right)-f\left(x_i\right)\right\|_{\varOmega \times[0, T]}^2\right.。 \end{aligned}\end{array} \right\}$

(13)

使用Sobol序列算法分别生成PDE残差损失项、初始条件损失项的时空采样点。采用8个隐藏层、每层20个神经元的全连接神经网络，使用Adam优化器训练40000步，波场云图及PINN的预测解与解析解对比如图 2所示，PINN预测值与解析解之间的绝对误差最大值为0.007 m，表明经过训练的神经网络已具备较强逼近波动方程真解的能力。

图 2 波场云图及PINN预测与解析对比图

Figure 2. Comparison of wavefield clouds and PINN prediction and resolution

下载: 全尺寸图片幻灯片

2. 物理驱动人工智能波动模拟方法

2.1 方法介绍

以SH波在平面内和地表及峡谷处的散射反射为例，二维波动方程为

$\frac{{{\partial ^2}u}}{{{\partial ^2}t}} - c\left( {\frac{{{\partial ^2}u}}{{{\partial ^2}x}} + \frac{{{\partial ^2}u}}{{{\partial ^2}z}}} \right) = f。$

(14)

式中： $u(x, z, t)$ 为出平面波动位移；c为介质物理波速； $f(x, z, t)$ 为外荷载，令 $f \equiv 0$ ，并通过给定初始波场等效施加外力。

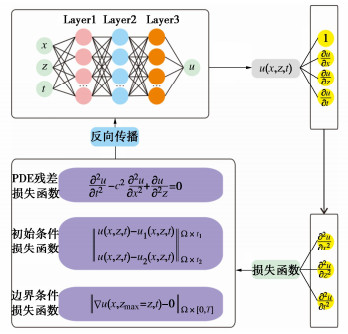
根据陈苏等^[30]提出的二维波动方程PINN求解框架，指定时空坐标 $X = (x, z, t)$ 的3个分量为网络的输入值，位移场 $Y = u(x, z, t)$ 为网络的输出值，通过Pytorch的自动微分功能，得到位移对于各分量的微分值，即 $\tfrac{{{\partial ^2}u}}{{{\partial ^2}t}}, \tfrac{{{\partial ^2}u}}{{{\partial ^2}x}}, \tfrac{{{\partial ^2}u}}{{{\partial ^2}z}}$ ，并构建损失函数。

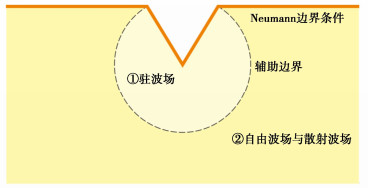
Gao等^[7]提出了对称V形峡谷引起的柱面SH波二维散射和衍射的波函数级数解。峡谷模型如所示，采用半径为a（峡谷壁长度）的圆弧作为辅助边界，将整个空间分成两个子区域。子区域①中为驻波波场，子区域②中包含没有牵引边界的自由波场和因为峡谷存在而产生的散射波场。要求波源的位置位于子区域②中，通过波函数展开法和坐标变换得到了此模型下二维圆柱SH波的反射结果，即半平面内的位移场 ${Y_\text{reli}} = {u_\text{reli}}(x, z, t)$ 。本文采用解析计算得到的 ${t_1}, {t_2}$ 时刻的两个早期位移场作为初始条件，通过两帧波场快照 ${\boldsymbol{u}_1}, {\boldsymbol{u}_2}$ 约束震源的位置、形状和SH波的传播方向。垂直地表的应力为零的边界条件可通过损失函数中的Neumann边界条件 $\nabla u(x, z = {z_\text{top}}, t) = 0$ 表示。

图 3 对称V型峡谷模型示意图

Figure 3. Schematic diagram of a symmetrical V-shaped canyon model

下载: 全尺寸图片幻灯片

$\boldsymbol{L}(\theta)=\lambda_1 \boldsymbol{L}_{\mathrm{p}}(\theta)+\lambda_2 \boldsymbol{L}_{\mathrm{bc}}(\theta)+\lambda_3 \boldsymbol{L}_{\mathrm{ic}}(\theta) ,$

(15)

$\left. \begin{array}{l}\boldsymbol{L}_{\text{p}}(\theta )=\frac{1}{{N}_{\text{p}}}{\displaystyle {\sum }_{i}^{{N}_{\text{p}}}}\Vert \frac{{\partial }^{2}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})}{\partial {t}_{i}^{2}}-{c}_{i}^{2}(\frac{{\partial }^{2}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})}{\partial {x}_{i}^{2}}+\\ {\text{ }\frac{{\partial }^{2}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})}{\partial {z}_{i}^{2}})\Vert }_{\varOmega \times [0, T]}^{2}, \\ \boldsymbol{L}_{\text{ic}}(\theta )=\frac{1}{{N}_{\text{ic1}}}{\displaystyle {\sum }_{i}^{{N}_{\text{ic}1}}}\Vert {\Vert \stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})-{U}_\text{rel1}({x}_{i}, {z}_{i}, {t}_{i})\Vert }_{\varOmega \times \{t={t}_{1}\}}^{2}+\\ {\text{ }\frac{1}{{N}_{\text{ic2}}}{\displaystyle {\sum }_{i}^{{N}_{\text{ic2}}}}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})-{U}_\text{rel2}({x}_{i}, {z}_{i}, {t}_{i})\Vert }_{\varOmega \times \{t={t}_{2}\}}^{2}, \\ \boldsymbol{L}_{\text{bc}}(\theta )=\frac{1}{{N}_{\text{bc}}}{\displaystyle {\sum }_{i}^{{N}_{\text{bc}}}{\Vert \nabla \stackrel{⌢}{u}({x}_{i}, {z}_{i}={z}_\text{top}, {t}_{i})\Vert }_{\varOmega \times [0, T]}^{2}。}\end{array} \right\}$

(16)

式中： $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}$ 为PINN逼近的偏微分方程的解， $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} (x, z, t) =$ $\boldsymbol{NN}(x, z, t;\theta )$ 。

根据式（15），（16），在半无限区域的二维波动问题中，损失函数由PDE残差损失项、初始条件损失项和边界条件损失项组成，其中 ${\lambda _1}$ ， ${\lambda _2}$ ， ${\lambda _3}$ 为损失分配系数。求解二维波动方程的物理信息神经网络架构如图 4所示。选择Tanh激活函数作为神经网络的非线性激活函数，以确保网络非零二阶导数存在，并实现高效收敛。采用Adam和L-BFGS共同作用的优化策略。其中Adam优化算法可实现全域快速收敛，接L-BFGS优化获得高精度解。使用Xavier初始化对神经网络中的可训练参数进行初始化。

图 4 物理驱动神经网络架构图

Figure 4. Diagram of PINN architecture

下载: 全尺寸图片幻灯片

2.2 方法验证

半无限均匀介质内的SH波动模型如图所示，模型区域为宽1500 m，深1500 m，峡谷深度d=50 m，峡谷宽度b=150 m。介质物理波速c=3000 m/s，输入波位移时程采用主频为10 Hz的Ricker源时间函数，源位置处于模型中心x = 750 m， z = -750 m。

使用解析计算得到的 ${t_1} = 0.05{\text{ s}}$ ， ${t_2} = 0.1{\text{ s}}$ 的位移场作为初始条件参与训练，其余时刻的结果与PINN的计算结果进行对比验证。解析计算中时间步长为0.01 s，计算总时长为1 s。训练前根据模型的几何数据，定义顶部边界为宽150 m，深50 m的对称V型峡谷，在此边界上添加应力为0的Neumann边界条件。采用Sobol序列算法在整个域中生成用于计算PDE残差损失项的采样点和初始条件采样点。在V型峡谷处的采样点布设做局部加密，在顶部两侧水平边界布设200个采样点，在V型边界布设1000个采样点，删除峡谷上部PDE残差损失项采样点，调整后采样点数 ${N_{\text{p}}} = 9954$ ， ${N_{{\text{ic1}}}} = 500$ ， ${N_{{\text{ic2}}}} = 500$ ， ${N_{{\text{top}}}} = 1400$ 。设置4个隐藏层，每层30个神经元的全连接神经网络。

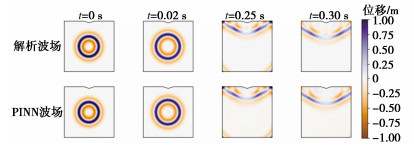
根据时间域分解策略，首先对模型采取预训练（热启动），波场时刻从 ${t_1} = 0.05{\text{ s}}$ 开始算起，预测总时间 $T = 0.1{\text{ s}}$ ，根据经验设置损失分配系数 ${\lambda _1} = {10^{ - 5}}$ ， ${\lambda _2} = 1$ ， ${\lambda _3} = {10^{ - 1}}$ 。调用学习率为6×10^-3的Adam优化器训练20000步，再使用L-BFGS优化器训练200000步。损失分配系数的神经网络会根据初始条件项损失项、边界条件损失项、PDE残差损失项的顺序进行训练，预训练时的SH波还未传播到顶部边界，能够观测到PINN方法很好地预测了柱面SH波的传播过程。保存预训练后的网络结构进行二次训练，调整损失分配系数 ${\lambda _1} = {10^{ - 3}}$ ， ${\lambda _2} = 1$ ， ${\lambda _3} = {10^{ - 1}}$ ，预测总时间 $T =$ $0.3{\text{ s}}$ 。调用L-BFGS优化器训练100000步，进一步优化PDE残差损失项，训练完成后保存网络结构进行最终训练，损失分配系数不变，设置预测总时间T=0.6 s，调用L-BFGS优化器训练200000步。训练完成后，可对任意分辨率下任意时空点的波动方程解及解的各阶偏导进行预测，图 5给出了4个时刻的PINN模拟波场和解析波场的对比。

图 5 半无限空间波动问题: PINN与解析波场快照对比

Figure 5. Semi-infinite space fluctuation problem: PINN vs. analytical wave snapshot

下载: 全尺寸图片幻灯片

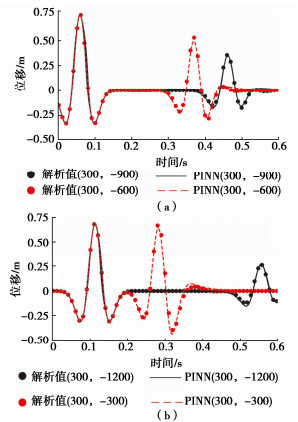
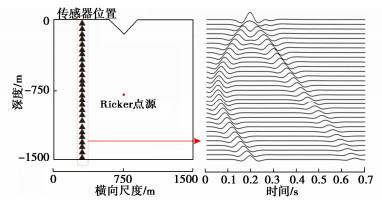
由于此模型的波源位于中心位置，所以可在 $x = 300$ 外布设传感器，观测入射波、反射波和散射波经过的过程，验证PINN在预测柱面SH波在半无限空间内传播和反射特性，给出x坐标同为300 m，z坐标关于 $z = - 750$ 对称点位的时程数据，其中z坐标600 m与z坐标900 m是相对于 $z = - 750$ 的对称坐标，由于t=0 s时刻区域内已存在点源散发出的波场，在0~0.6 s时刻内，在坐标 $z = - 600$ 处和 $z = - 900$ 处有入射波和反射波经过，可以看出PINN方法在此模型下的入射波传播和边界反射的预测值与解析真值基本一致。同时z坐标-300 m与z坐标-1200 m是相对于 $z = - 750$ 的对称坐标，在0~0.6 s时刻内，坐标 $z = - 300$ 处和 $z = - 1200$ 处除入射波和反射波外，还有因峡谷而产生的散射波，可以看出PINN方法在预测柱面SH波在峡谷出的散射值与解析真值基本一致。在 $x = 300$ 布设的位移传感器和预测位移时程结果图 7所示。

图 6 对称位置PINN与解析波场时程对比

Figure 6. Comparison of time histories of symmetrical position PINN and analytical wave field

下载: 全尺寸图片幻灯片

图 7 PINN模拟时程图（x=300）

Figure 7. Time histories of PINN analog (x=300)

下载: 全尺寸图片幻灯片

3. 不同工况深切峡谷波动模拟

为保证PINN方法在处理对称V型峡谷波动模拟问题的有效性，考虑不同波速、不同主频的Ricker波在V型半无限空间内的波动问题。模型区域为宽1500 m，高1500 m，峡谷深度d=50 m，峡谷宽度b=150 m，输入波位移时程采用Ricker源时间函数，源位置处于模型中心x = 750 m，z = -750 m。

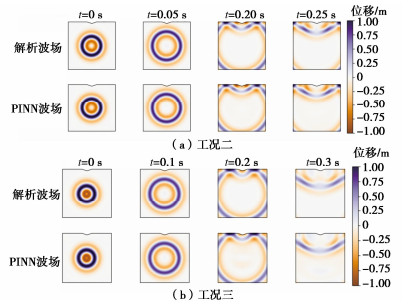
本文所有工况的模型参数和训练参数如表 2所示，工况二和工况三的预测结果与解析值的对比云图如图 8所示，由此可见PINN方法在对称V型峡谷的地形下，能够较好地预测不同频率不同波速下柱面SH波的反射和散射。

表 2 不同工况PINN模型参数

Table 2. Parameters of PINN model under different working conditions

参数	工况一（图 5）		工况二（图 8(a)）	工况三（图 8(b)）
主频 $\omega {\text{/Hz}}$		10	8	5
波速 $c{\text{/}}$ ${\text{(m}} \cdot {{\text{s}}^{ - 1}}{\text{)}}$		3000	3000	2000
第一帧快照时间 ${t_0}{\text{/s}}$		0.20	0.15	0.30
第二帧快照时间 ${t_1}{\text{/s}}$		0.22	0.20	0.40
传播时间 $T{\text{/s}}$		0.60	0.65	1.00
采样点	${N_{\text{p}}} = 9954$ ， ${N_{{\text{ic1}}}} = 500$ ， ${N_{{\text{ic2}}}} = 500$ ， ${N_{{\text{top}}}} = 1400$
预训练损失分配系数	${\lambda _1} = {10^{ - 5}}$ , ${\lambda _2} = 1$ , ${\lambda _3} = {10^{ - 1}}$
后续损失分配系数	${\lambda _1} = {10^{ - 3}}$ , ${\lambda _2} = 1$ , ${\lambda _3} = {10^{ - 1}}$
优化策略	Adam20000步+ LBFGS500000步		Adam20000步+ LBFGS300000步	Adam20000步+ LBFGS300000步

下载: 导出CSV

| 显示表格

图 8 PINN预测与解析真值云图对比

Figure 8. Comparison of PINN prediction and ground truth under condition 3

下载: 全尺寸图片幻灯片

对比不同工况下的预测精度，定义在某一点PINN与解析波场之间的相对 ${L_2}$ 范数误差为

$\varepsilon (\boldsymbol{u}) = \frac{{\sqrt {\sum\nolimits_{i = 1}^N {{{\left\| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ({x_0}, {z_0}, {t_i}) - {u_\text{ref}}({x_0}, {z_0}, {t_i})} \right\|}^2}} } }}{{\sqrt {\sum\nolimits_{i = 1}^N {{{\left\| {{u_\text{ref}}({x_0}, {z_0}, {t_i})} \right\|}^2}} } }}。$

(17)

式中： ${x_0}$ ， ${z_0}$ 为采样点的坐标位置； $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ({x_0}, {z_0}, {t_i})$ 为PINN方法预测得到的该采样点的位移时程； ${u_{ref}}({x_0}, {z_0}, {t_i})$ 为相同位置的解析位移时程；N为计算点数。

给出3种工况预测模型在 $x = 300$ 不同位置的相对范数误差。在x相同时，相对 ${L_2}$ 范数误差与纵坐标z有关，越靠近地表，由于散射波和衍射波的叠加，相对 ${L_2}$ 范数误差会增大，但都保持在0.03以内。表明PINN方法处理对称V型峡谷反射波和散射波的有效性，可实现复杂地形模拟分析。分别给出不同频率下PINN预测的峡谷地表及附近各位置峰值位移分布。由可知：不同SH波（5，8，10 Hz）条件下，V型峡谷地形效应总体上呈现出“M”型分布，中心V型峡谷底端及邻区SH波发生衰减与振荡，在谷肩及地表SH波放大，峡谷边缘出现了显著放大。3种工况下地表处最大峰值位移的相对 ${L_2}$ 误差范数分别为0.0009，0.0006，0.001，由此可见PINN方法在预测低频SH波峡谷处地形效应时更为准确。

图 9 不同工况相对

${L_2}$ 范数误差（x=300）

Figure 9. Relative norm errors under different working conditions (x=300)

下载: 全尺寸图片幻灯片

图 10 地表峰值位移对比

Figure 10. Comparison of peak displacements on surface

下载: 全尺寸图片幻灯片

4. 结论

通过物理信息驱动神经网络（PINN）的自动微分功能求解了二维波动方程，并计算了柱面SH波在对称V型峡谷下的反射和散射。通过与解析值的对比，验证了PINN方法在求解波动问题上的精度。得到3点结论。

（1）物理驱动深度学习（PINN）方法可通过稀疏初始波场数据，模拟柱面SH波在对称V型峡谷下的反射和散射，具备“无网格、强耦合”等特性，可适应不同地形与波源。

（2）对比不同工况的训练结果，发现越靠近地表位置，波场叠加越复杂，相对 ${L_2}$ 误差范数也会越大。且同一模型下，相对 ${L_2}$ 范数误差与柱面SH波的主频关系不大。

（3）对比不同工况下解析与PINN预测的地表峰值位移大小关系，柱面SH波在V型峡谷底端发生衰减现象，在其他位置发生放大现象。其中在V型峡谷边缘处放大现象最明显，且PINN方法在预测低频SH波在峡谷处地形效应时更为准确。

致谢: 本文解析方法得到了安徽建筑大学张宁教授及河海大学博士研究生张煜的大力协助，特此致谢。

图 1 DNN网络自动微分简图

Figure 1. Automatic differential diagram of DNN network

下载: 全尺寸图片幻灯片

图 2 波场云图及PINN预测与解析对比图

Figure 2. Comparison of wavefield clouds and PINN prediction and resolution

下载: 全尺寸图片幻灯片

图 3 对称V型峡谷模型示意图

Figure 3. Schematic diagram of a symmetrical V-shaped canyon model

下载: 全尺寸图片幻灯片

图 4 物理驱动神经网络架构图

Figure 4. Diagram of PINN architecture

下载: 全尺寸图片幻灯片

图 5 半无限空间波动问题: PINN与解析波场快照对比

Figure 5. Semi-infinite space fluctuation problem: PINN vs. analytical wave snapshot

下载: 全尺寸图片幻灯片

图 6 对称位置PINN与解析波场时程对比

Figure 6. Comparison of time histories of symmetrical position PINN and analytical wave field

下载: 全尺寸图片幻灯片

图 7 PINN模拟时程图（x=300）

Figure 7. Time histories of PINN analog (x=300)

下载: 全尺寸图片幻灯片

图 8 PINN预测与解析真值云图对比

Figure 8. Comparison of PINN prediction and ground truth under condition 3

下载: 全尺寸图片幻灯片

不同工况相对 ${L_2}$ 范数误差（x=300）

Figure 9. Relative norm errors under different working conditions (x=300)

下载: 全尺寸图片幻灯片

图 10 地表峰值位移对比

Figure 10. Comparison of peak displacements on surface

下载: 全尺寸图片幻灯片

表 1 复杂地形效应近场波动模拟研究现状

Table 1 Researches on near-field fluctuation problems

模拟方法	应用场景	时间	文献
解析法	平面SH波在半圆柱型峡谷的散射	1972年	[1]
	平面SH波在半圆柱型冲击峡谷的散射	1971年	[2]
	平面SH波在半椭圆形冲击峡谷的散射	1974年	[3]
	平面SH波在圆弧形峡谷的散射	2009年	[4]
	平面SH波在截断峡谷的散射	2009年	[5]
	U型峡谷引起的地形放大对地震波的影响	2012年	[6]
	柱面SH波在对称V型峡谷的反射和散射	2013年	[7]
有限差分法	极坐标尺度不规则地形FEM方法	2021年	[8]
谱元法	入射平面SV波作用下梯田形山丘的表面运动	2017年	[9]
PINN	近场波动数值模拟	2022年	[30]

下载: 导出CSV

表 2 不同工况PINN模型参数

Table 2 Parameters of PINN model under different working conditions

参数	工况一（图 5）		工况二（图 8(a)）	工况三（图 8(b)）
主频 $\omega {\text{/Hz}}$		10	8	5
波速 $c{\text{/}}$ ${\text{(m}} \cdot {{\text{s}}^{ - 1}}{\text{)}}$		3000	3000	2000
第一帧快照时间 ${t_0}{\text{/s}}$		0.20	0.15	0.30
第二帧快照时间 ${t_1}{\text{/s}}$		0.22	0.20	0.40
传播时间 $T{\text{/s}}$		0.60	0.65	1.00
采样点	${N_{\text{p}}} = 9954$ ， ${N_{{\text{ic1}}}} = 500$ ， ${N_{{\text{ic2}}}} = 500$ ， ${N_{{\text{top}}}} = 1400$
预训练损失分配系数	${\lambda _1} = {10^{ - 5}}$ , ${\lambda _2} = 1$ , ${\lambda _3} = {10^{ - 1}}$
后续损失分配系数	${\lambda _1} = {10^{ - 3}}$ , ${\lambda _2} = 1$ , ${\lambda _3} = {10^{ - 1}}$
优化策略	Adam20000步+ LBFGS500000步		Adam20000步+ LBFGS300000步	Adam20000步+ LBFGS300000步

下载: 导出CSV

参考文献(30)

[1]	WONG H L, TRIFUNAC M D. Scattering of plane sh waves by a semi-elliptical canyon[J]. Earthquake Engineering & Structural Dynamics, 1974, 3(2): 157-169.
[2]	TRIFUNAC M D. Surface motion of a semi-cylindrical alluvial valley for incident plane SH waves[J]. Bulletin of the Seismological Society of America, 1971, 61(6): 1755-1770. doi: 10.1785/BSSA0610061755
[3]	WONG H L, TRIFUNAC M D. Surface motion of a semi-elliptical alluvial valley for incident plane SH waves[J]. Bulletin of the Seismological Society of America, 1974, 64(5): 1389-1408. doi: 10.1785/BSSA0640051389
[4]	YUAN X M, LIAO Z P. Scattering of plane SH waves by a cylindrical canyon of circular-arc cross-section[J]. Soil Dynamics and Earthquake Engineering, 1994, 13(6): 407-412. doi: 10.1016/0267-7261(94)90011-6
[5]	TSAUR D H, CHANG K H. Scattering of SH waves by truncated semicircular canyon[J]. Journal of Engineering Mechanics, 2009, 135(8): 862-870. doi: 10.1061/(ASCE)0733-9399(2009)135:8(862)
[6]	GAO Y, ZHANG N, LI D, et al. Effects of topographic amplification induced by a U-shaped canyon on seismic waves[J]. Bulletin of the Seismological Society of America, 2012, 102(4): 1748-1763. doi: 10.1785/0120110306
[7]	GAO Y F, ZHANG N. Scattering of cylindrical SH waves induced by a symmetrical V-shaped canyon: near-source topographic effects[J]. Geophysical Journal International, 2013, 193(2): 874-885. doi: 10.1093/gji/ggs119
[8]	XU J X, ZHANG W, CHEN X F. An optimized finite difference method based on a polar coordinate system for regional-scale irregular topography[J]. Earthquake Science, 2021, 34(4): 334-343. doi: 10.29382/eqs-2021-0022
[9]	KONG X, LI H. Surface motion evaluation of terrace-shaped hill subjected to incident plane SV wave using spectral element method[C]// 16 th World Conference on Earthquake Engineering. Chile, 2017.
[10]	RAISSI M, PERDIKARIS P, KARNIADAKIS G E. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378: 686-707. doi: 10.1016/j.jcp.2018.10.045
[11]	SMITH J D, AZIZZADENESHELI K, ROSS Z E. EikoNet: solving the eikonal equation with deep neural networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(12): 10685-10696. doi: 10.1109/TGRS.2020.3039165
[12]	MOSELEY B, MARKHAM A, NISSEN-MEYER T. Solving the wave equation with physics-informed deep learning[EB/OL]. https://arxiv.org/abs/2006.11894.pdf. 2020.
[13]	RASHT-BEHESHT M, HUBER C, SHUKLA K, et al. Physics-informed neural networks (PINNs) for wave propagation and full waveform inversions[J]. Journal of Geophysical Research: Solid Earth, 2022, 127(5): e2021JB023120. doi: 10.1029/2021JB023120
[14]	SHUKLA K, LEONI P C, BLACKSHIRE J, et al. Physics-informed neural network for ultrasound nondestructive quantification of surface breaking cracks[J]. Journal of Nondestructive Evaluation, 2020, 39(3): 1-20.
[15]	唐明健, 唐和生. 基于物理信息的深度学习求解矩形薄板力学正反问题[J]. 计算力学学报, 2022, 39(1): 120-128. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG202201018.htm TANG Mingjian, TANG Hesheng. A physics-informed deep learning method for solving forward and inverse mechanics problems of thin rectangular plates[J]. Chinese Journal of Computational Mechanics, 2022, 39(1): 120-128. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG202201018.htm
[16]	HAGHIGHAT E, RAISSI M, MOURE A, et al. A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 379: 113741. doi: 10.1016/j.cma.2021.113741
[17]	SUN L N, GAO H, PAN S W, et al. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 361: 112732. doi: 10.1016/j.cma.2019.112732
[18]	GUO H W, ZHUANG X Y, LIANG D, et al. Stochastic groundwater flow analysis in heterogeneous aquifer with modified neural architecture search (NAS) based physics-informed neural networks using transfer learning[EB/OL]. https://arxiv.org/abs/2010.12344.pdf. 2020.
[19]	RAO C P, SUN H, LIU Y. Physics-informed deep learning for incompressible laminar flows[J]. Theoretical and Applied Mechanics Letters, 2020, 10(3): 207-212. doi: 10.1016/j.taml.2020.01.039
[20]	JIN X W, CAI S Z, LI H, et al. NSFnets (Navier-Stokes flow nets): physics-informed neural networks for the incompressible Navier-Stokes equations[J]. Journal of Computational Physics, 2021, 426: 109951. doi: 10.1016/j.jcp.2020.109951
[21]	陆至彬, 瞿景辉, 刘桦, 等. 基于物理信息神经网络的传热过程物理场代理模型的构建[J]. 化工学报, 2021, 72(3): 1496-1503. https://www.cnki.com.cn/Article/CJFDTOTAL-HGSZ202103031.htm LU Zhibin, QU Jinghui, LIU Hua, et al. Surrogate modeling for physical fields of heat transfer processes based on physics-informed neural network[J]. CIESC Journal, 2021, 72(3): 1496-1503. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HGSZ202103031.htm
[22]	赵暾, 周宇, 程艳青, 等. 基于内嵌物理机理神经网络的热传导方程的正问题及逆问题求解[J]. 空气动力学学报, 2021, 39(5): 19-26. https://www.cnki.com.cn/Article/CJFDTOTAL-KQDX202105003.htm ZHAO Tun, ZHOU Yu, CHENG Yanqing, et al. Solving forward and inverse problems of the heat conduction equation using physics-informed neural networks[J]. Acta Aerodynamica Sinica, 2021, 39(5): 19-26. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KQDX202105003.htm
[23]	KARNIADAKIS G E, KEVREKIDIS I G, LU L, et al. Physics-informed machine learning[J]. Nature Reviews Physics, 2021, 3(6): 422-440. doi: 10.1038/s42254-021-00314-5
[24]	LU L, JIN P, KARNIADAKIS G E. Deeponet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators[EB/OL]. https://arxiv.org/abs/1910.03193.pdf. 2019.
[25]	BELBUTE-PERES F A, CHEN Y, SHA F. HyperPINN: Learning parameterized differential equations with physics-informed hypernetworks[EB/OL]. https://arxiv.org/bs/111.01008.pdf. 2021.
[26]	LEUNG W T, LIN G, ZHANG Z C. NH-PINN: neural homogenization-based physics-informed neural network for multiscale problems[J]. Journal of Computational Physics, 2022, 470: 111539. doi: 10.1016/j.jcp.2022.111539
[27]	BRUNTON S L, PROCTOR J L, KUTZ J N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems[J]. Proceedings of the National Academy of Sciences of the United States of America, 2016, 113(15): 3932-3937.
[28]	GAO H, SUN L N, WANG J X. PhyGeoNet: physics-informed geometry-adaptive convolutional neural networks for solving parameterized steady-state PDEs on irregular domain[J]. Journal of Computational Physics, 2021, 428: 110079. doi: 10.1016/j.jcp.2020.110079
[29]	MOSELEY B, MARKHAM A, NISSEN-MEYER T. Finite Basis Physics-Informed Neural Networks (FBPINNs): a scalable domain decomposition approach for solving differential equations[J]. Advances in Computational Mathematics, 2023, 49(4): 62. doi: 10.1007/s10444-023-10065-9
[30]	陈苏, 丁毅, 孙浩, 等. 物理驱动深度学习波动数值模拟方法及应用[J]. 力学学报, 2023, 55(1): 272-282. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202301022.htm CHEN Su, DING Yi, SUN Hao, et al. Methods and applications of physical information deep learning in wave numerical simulation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2023, 55(1): 272-282. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202301022.htm

施引文献(1)

期刊类型引用(1)

李建彪，邬叶飞，马思伟，孙昌利，邵康. 土体侧移作用下螺旋钢桩被动承载机理分析. 路基工程. 2024(05): 32-38 .

百度学术

其他类型引用(0)

资源附件(1)

其他相关附件
- PDF格式
  13-202406-G23-0263⼀⽂审稿意⻅与作者答复点击下载(411KB)

图(10) / 表(2)

计量

文章访问数: 349
HTML全文浏览量: 50
PDF下载量: 74
被引次数: 1

0. 引言
1. 物理驱动深度学习原理
2. 物理驱动人工智能波动模拟方法
2.1 方法介绍
2.2 方法验证
3. 不同工况深切峡谷波动模拟
4. 结论

深切V型峡谷物理驱动人工智能波动模拟 English Version

作者简介: 栾绍凯(1999—)，男，硕士研究生，主要从事物理驱动工程波动模拟方向的研究工作。E-mail: luanshaokaipsg@163.com

通讯作者: 陈苏, E-mail: chensuchina@126.com

计量

出版历程