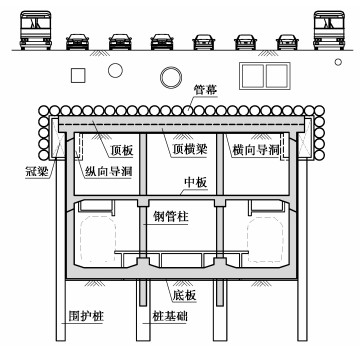
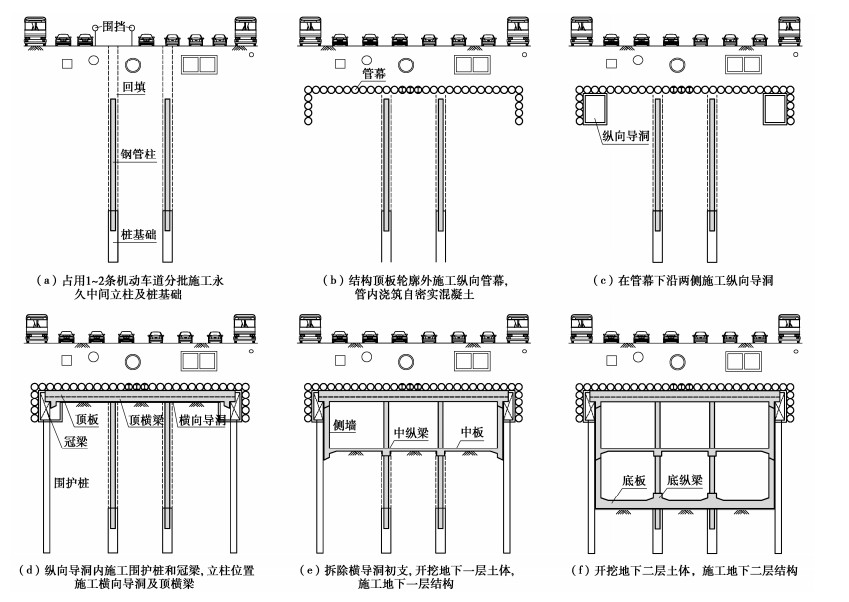
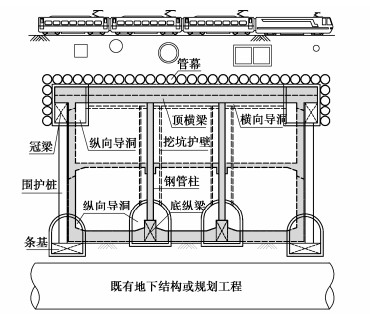
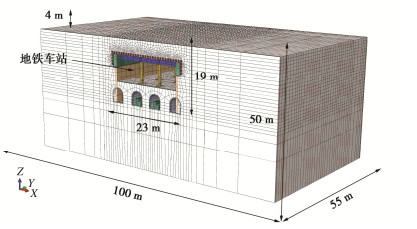
A new underground excavation method based on large rigidity support system
-
摘要: 传统暗挖技术存在施工风险大、施工效率低、对周边环境影响大、工程投资大等问题,很难适用于软弱地层或复杂环境下大型地下结构暗挖施工。为解决以上问题,提出一种基于大刚度支护体系的新型暗挖技术。新型暗挖技术利用纵向管幕、顶横梁和中间立柱构筑大刚度支护体系,支护体系各构件通过非开挖方式或者在管幕保护下利用小空间构筑,保证施工安全的同时,防止地层出现较大应力释放,支护体系构筑完成后即可进行大面积暗挖施工。新型暗挖技术工序简单、施工效率高、风险低、对周边环境影响小、工程投资小。数值分析和工程实例验证了新型暗挖技术的可行性和实用性,新技术为大型地下结构暗挖技术提供了新的思路。Abstract: The traditional underground excavation method has problems such as high risk, low efficiency, great impact on the surrounding environments and large investment. It is difficult to construct large underground structures in soft strata or complex environments. In order to solve these problems, a new underground excavation method based on the large rigidity support system is proposed. The pipe roof, horizontal beam and vertical column are used to construct a large rigidity support system, and each component is constructed by using the non-excavation method or constructed in a small space under the protection of pipe roof, which ensures the construction safety and prevents the stress release of the stratum. After the support system is constructed, bulk excavation can be carried out. The new underground excavation method has the advantages of simple process, high efficiency, low risk, small impact on the surrounding environments and small investment. Numerical analysis and engineering examples verify the feasibility and practicability of the new method, which provides a new idea for the construction of large underground structures.
-
0. 引言
高温冻土是指由土颗粒基质、冰晶、未冻水和气体组成的温度介于-1.5℃~0℃的土体,通常表现出温度敏感性突出、力学性能低劣等特性,工程中极易引发建构筑物冻土地基产生非均匀沉降变形,甚至会导致上部结构开裂和破坏,严重威胁冻土工程安全设计与施工[1]。因此,研究高温冻土本构模型具有重要工程意义,可为预测高温冻土地层变形特性从而避免工程灾害的发生提供重要手段。
朱元林等[2]利用大量单轴压缩试验得出冻土应力-应变关系,结合曲线拟合与塑弹性理论建立了单轴压缩本构模型。苗天德等[3]从微观视角出发,定义了压缩过程中的损伤因子,获得了冻土蠕变损伤本构关系。随后,诸多学者基于损伤力学理论,从细微观角度建立了冻土单轴唯像本构模型[4]、细观损伤本构模型[5]、宏细观本构模型[6]、宏微观黏弹塑性本构模型[7]。冻土体常在低围压条件下呈现出应变软化的变形特征,通过CT技术识别冻土内部变形过程中的损伤变量,可以描述冻土体蠕变过程中的损伤特征[8-9]。对不同温度不同应变率下的冻土试件进行冲击压缩试验,可构建动荷载条件下的冻土本构关系[10-11]。将加载-破坏屈服面及统一硬化参数整合,可建立冻土多相多面本构模型[12]。空心圆柱仪试验可以科学量化不同应力水平条件下的冻土变形特征,为复杂应力条件下的本构关系构建提供了重要参考[13]。
对于常规低温冻结,上述研究成果得到的本构模型基本能表征冻土不同应力状态下的力学状态[14-15]。然而对于近相变区的高温冻土,冻结过程中冻结锋面、冰分凝锋面、冻结缘厚度随时间动态变化[16-17]。当高温冻土未冻水含量相对较高时,内部的孔隙水压力增加较大使得作用在土骨架上的有效应力降低,表现出剪胀、应变软化特征;当高温冻土未冻水含量相对较低时,内部的孔隙水压力增加值小于总应力增加值,表现出剪缩、应变硬化特征,因此高温冻土同时存在剪缩、剪胀、硬化和软化特性[18-19]。针对高温冻土,Liao等[20]从强度随机分布出发,建立了可以反映冻土力学性质较强离散性的随机损伤本构模型,但将其作为弹性体的损伤本构模型研究存在一定的缺陷。Lai等[21]从概率论与数理统计的视角出发,定义了材料截面内部的损失变量,提出了高温冻土损伤统计本构模型,但该模型难以对高低围压三轴应力路径下的高温冻土应力应变行为进行统一描述。
本文考虑黏聚力及内摩擦角的影响,以整体变形εv-lnp曲线对冻土试样变形特征进行表征,建立了能够有效反映高温冻土剪缩、剪胀、硬化和软化特性的本构模型。该模型采用应力路径相关因子对等向固结路径条件下屈服面硬化参数进行修正,获得与应力路径无关的当前屈服面硬化参数,结合临界状态参数推导得到了能够体现高温冻土固有临界特性的参考屈服面硬化参数。自编程序计算了不同围压条件下高温冻土应力应变关系,利用试验数据对本文所构建的双屈服面统一本构模型进行了验证。
1. 本构模型建立
1.1 屈服函数
英国剑桥大学Roscoe等[22]从能量方程推导出应力比与应变增量比的关系,结合正交法则、相关联流动法则及等向固结试验确定塑性应力应变关系,于1963年提出了原始剑桥模型。鉴于原始剑桥模型获得的屈服函数在p - q坐标系中与p轴不正交,Roscoe等[23]于1968年提出了塑性势函数(屈服函数)与p轴正交的修正剑桥模型,定义了应力空间内g(p,q)和(dεpv,dεpd)的正交条件,表示为
dpdεpv+dqdεpd=0。 (1) 荷载作用下塑性变形所消耗的功为
dWp=pdεpv+qdεpd。 (2) 考虑到材料破坏时,也即临界状态下有
qf=M(p+pr)(dεpv=0)。 (3) 式中:M =6sinφ/(3−sinφ);pr=ccotφ,c,φ分别为土的黏聚力和内摩擦角。
将式(3)代入式(2)可得
dWp=(p+pr)dεpv+q dεpd=M(p+pr)dεpd=(p+pr)√(dεpv)2+(M dεpd)2。 (4) 整理式(4)可得
dεpvdεpd=M2(p+pr)2−q22(p+pr)q。 (5) 求解方程(5)可得塑性势函数为
g=q2+M2(p+pr)2−C(p+pr)=0。 (6) 式中:C为积分常数,C取不同的值可得到不同的塑性势函数。
本文得到考虑高温冻土黏聚力及内摩擦角的修正剑桥模型塑性势面如图 1所示。
采用相关流动法则,当广义剪应力q=0时,令平均正应力p=px,积分常数C=M2(px+pr),高温冻土屈服函数可进一步表示为
f=q2+M2p(p+pr)−M2px(p+pr)=0。 (7) 变换式(7),并对两边取自然对数可得
ln[1+q2M2p(p+pr)]=lnpx−lnp。 (8) 1.2 屈服面参量及其修正
将高温冻土的等向固结试验(σ1=σ2=σ3)结果绘制在εv - lnp坐标系中,如图 2所示,回弹再加载曲线的斜率为κ,记等向固结曲线NCL为
εv=φlnp。 (9) 对式(9)进行微分可得
dεv=φ′(lnp)dlnp。 (10) 弹性体积应变变化量为
dεev=κdlnp。 (11) 综合式(10),(11),得到塑性体积应变变化量为
dεpv=dεv−dεev=(φ′lnp−κ)dlnp。 (12) 对式(12)进行变换并积分得到
∫dεpvφ′(lnp)−κ=lnpx−lnp0。 (13) 式中:p0为与初始体积应变εv0相对应的当前屈服面上的球应力,其决定了初始当前屈服面与p轴的交点,其数值的确定在模型参数确定方法中详细介绍。
将式(13)代入式(8)得到屈服面函数为
f=lnpp0+ln(1+q2M2p(p+pr))−∫dεpvφ′(lnp)−κ=0。 (14) 根据式(14),高温冻土屈服面硬化参量可定义为
H=∫dεpvφ′(lnp)−κ。 (15) 为了使所要构建的高温冻土本构模型能够反映常压下的软化剪胀特性及塑性体积应变由剪缩阶段发展至剪胀阶段的特征状态分界线,模型中的硬化参量须包含能够有效反映特征状态的参数。根据姚仰平等[24]提出的应力路径相关因子的方法,将应力路径相关因子设为
R(η)=M4fM4M4−η4M4f−η4。 (16) 依据式(16)表征的应力路径相关因子,屈服面硬化参量修正为
H=∫1R(η)dεpvφ′(lnp)−κ=∫M4(M4f−η4)M4f(M4−η4)dεpvφ′(lnp)−κ。 (17) 由此得到修正后的高温冻土当前屈服面函数:
f=lnpp0+ln(1+q2M2p(p+pr))−∫M4(M4f−η4)M4f(M4−η4)dϵpvϕ′(lnp)−κ。 (18) 临界状态线在q - p空间中表示为一条不可逾越的应力比直线状态,在εv - lnp空间中表示为一个稳定的非线性状态。通过三轴压缩试验可获得不同围压条件下由剪切开始至临界状态整个应力路径过程中冻土材料体积应变改变量与球应力p的关系,对达到临界状态时的球应力p取自然对数并统计与其相对应的体积应变可获得εv - lnp空间中的CSL曲线,如图 3所示,记临界状态曲线CSL为
εv=ψ(lnˉp)。 (19) 可以看出,图 3中的高温冻土临界状态线与图 2中的等向压缩曲线形式相同,因此对其硬化参量的推导同式(13),可以得到
∫dεpvψ′(lnˉp)−κ=lnˉpx−lnˉp0。 (20) 式中:ˉp0为与初始体积应变εv0相对应的参考屈服面上的球应力,其决定了初始参考屈服面与p轴的交点,其数值的确定在模型参数确定方法中详细介绍。
根据式(20)以及屈服函数式(8)便可推导得出参考屈服面函数为
f=lnˉpˉp0+ln[1+ˉq2M2ˉp(ˉp+pr)]−∫dεpvψ′(lnˉp)−κ=0。 (21) 参考屈服面硬化参量为
ˉH=∫dεpvψ′lnˉp−κ。 (22) 1.3 弹性应变增量
对于高温冻土本构模型的弹性部分,根据各向同性的假设,弹性应变增量可用张量表示为
dεeij=1+νEdσij−νEdσkkδij。 (23) 式中:E为弹性模量;ν为泊松比。
根据标记法规则,dσkk=dσ11+dσ22+dσ33,因此高温冻土体积应变与剪切应变增量形式为
dεev=3(1−2ν)Edp,dεed=2(1+ν)3Edq。 (24) 将体积变形模型与剪切变形模量作为其计算参数,通过高温冻土等向固结试验(σ1=σ2=σ3),将结果绘制在εv - lnp坐标系中,得到加载后回弹再加载曲线斜率κ,则弹性体积应变增量公式为
dεev=κdlnp=κpdp。 (25) 对比式(24),(25)的数学表达计算式,模量K与模量G可进一步表示为
K=dpdεev=E3(1−2ν)=pκ, (26) G=dq3dεed=E2(1+ν)=3(1−2ν)2(1+ν)K。 (27) 1.4 塑性应变增量
高温冻土在复杂应力状态下发生变形时,总应变可表示为
dεij=dεeij+dεpij。 (28) 应力应变关系为
dσij=Ceijkldεekl=Ceijkl(dεkl−dεpkl)=Cepijkldεkl。 (29) 式中:Ceijkl为弹性张量;Cepijkl为弹塑性张量。
由广义胡克定律可知弹性张量Cepijkl的具体表达式为
Ceijkl=(K−23G)δijδkl+G(δikδjl+δilδjk) 。 (30) 塑性应变增量由塑性位势理论确定, 因此存在如下数学关系:
dεpij=dλ∂g∂σij。 (31) 式中:dλ为塑性标量因子。
将屈服函数f简记为
f(σij,H(εpij))=0。 (32) 对式(32)微分可得
df=∂f∂σijdσij+∂f∂H∂H∂εpijdεpij=0。 (33) 将式(29),(31)代入式(33),并整理可得塑性标量因子dλ的具体表达式为
dλ=∂f∂σijCeijkldεkl−∂f∂H∂H∂εpij∂g∂σij+∂f∂σijCeijkl∂g∂σkl。 (34) 将式(31),(34)代入式(29),并整理可得弹塑性张量Cepijkl的具体表达式为
Cepijkl=Ceijkl−Ceijmn∂g∂σmn∂f∂σstCestklA+∂f∂σijCeijkl∂g∂σkl。 (35) 式中:A=−∂f∂H∂H∂εpij∂g∂σij。
1.5 应力应变关系
采用相关流动法则,只需对屈服函数f进行微分求导,根据复合函数求导法则有
∂f∂σ=∂f∂I1∂I1∂σ+∂f∂√J2∂√J2∂σ+∂f∂θ∂θ∂σ。 (36) 式中:I1为第一主应力不变量;J2为第二偏应力不变量;θ为Lode角。
∂θ∂σ=√32sin3θ[1(J2)3/322∂J3∂σ−3J3(J2)2∂√J2∂σ]。 (37) 将式(37)代入式(36),整理可得
∂f∂σ=∂f∂I1∂I1∂σ+[∂f∂√J2+∂f∂θcot3θ√J2]∂√J2∂σ+∂f∂θ√32sin3θ.1(J2)3/2∂J3∂σ。 (38) 考虑高温冻土当前屈服面函数形式的计算公式(14),(15),根据复合函数求导法则有
∂f∂I1=√32sin3θ1(J2)3/2−2q2M(θ)3p(p+pr)+M(θ)q2.∂M(θ)∂θ。 (39) 由屈服函数中临界应力比M(θ)定义有
M(θ)=M(θ=0∘)[2α41+α4−(1−α4)cos3θ]14,α=M(θ=60∘)M(θ=0∘)=3−sinφ3+sinφ。} (40) 对式(40)微分得
∂M(θ)∂θ=[2α41+α4−(1−α4)cos3θ]543(α4−1)8α4sin3θ⋅M(θ=0∘)。 (41) 将式(40),(41)代入式(38)即可求得屈服函数f任一应力分量的一阶导数值。
根据式(16),(17)可得
∂f∂H∂H∂εpij∂g∂σij=−M(θ)4(M(θ)4f−η4)M(θ)4f(M(θ)4−η4)1φ′(lnp)−κ.∂εpv∂εpij∂g∂σij。 (42) 因为εpv=εp11+εp22+εp33,所以存在
[∂εpv∂εpij]=[111000]。 (43) 将式(43)代入式(42),整理可得
A=M(θ)4(M(θ)4f−η4)M(θ)4f(M(θ)4−η4)1ϕ′(lnp)−κ(∂g∂σ11+∂g∂σ22+∂g∂σ33)。 (44) 将式(30),(44)代入式(35)即可求得弹塑性张量Cepijkl的具体表达式。
1.6 模型参数及确定方法
根据高温冻土强度包线(直线)可确定内摩擦角φ和黏聚力c;泊松比ν可通过−Δεr/Δεz获得;对于等向固结试验εv-lnp空间中回弹线斜率κ可通过加载后回弹再加载试验确定;εv0为压缩固结完成开始剪切所对应的体积应变;伏斯列夫面(Hvorslev)斜率Mh是q - p空间中不排水强度包线的斜率,通过冻土等向固结试验(σ1=σ2=σ3),将结果绘制在εv - p坐标系中,便可获得等向固结曲线NCL,与初始体积应变εv0对应的即为p0。通过多组不同压力等级下的三轴压缩试验,获得不同压力条件下的冻土临界体积应变与临界状态时球应力p的关系,将结果绘制于εv - p空间中,获得其临界状态曲线CSL,与初始体积应变εv0对应的即为ˉp0。
2. 模型特性分析
2.1 固结参数与潜在强度
由式(21)推导可得参考应力点的球应力ˉp为
ˉp=ˉp0(M2M2+ηη′)exp(∫dεpvψ′(lnˉp)−κ)。 (45) 式中:η=q/(p+pr)=ˉq/(ˉp+pr),η′=ˉq/ˉp。
依据平面解析几何中直线与椭圆的基本关系,结合方程式(21)及η,可求得η′的具体表达式为
η′=(M2+η2)ηprM2ˉp0exp(∫dεpvψ′(lnˉp)−κ)−η2pr+η。 (46) 参照超固结土概念,定义高温冻土固结参数R为参考应力点的球应力ˉp+pr与当前应力点的球应力p+pr的比值,即
R=ˉp+prp+pr。 (47) 综合式(45),(46)可得高温冻土固结参数R的具体表达式为
R=1p+pr{ˉp0(M2M2+ηη′)exp[∫dεpvψ′(lnˉp)−κ]+pr}。 (48) 将高温冻土当前屈服面、参考屈服面、伏斯列夫面(Hvorslev)、临界状态线CSL绘制于同一坐标系(p-q)中,如图 4所示。对于特定的应力状态点(p,q),潜在强度Mf与其相对应,并由参考应力点(ˉp,ˉq)与冻土材料伏斯列夫面(Hvorslev)斜率共同决定,剪应力qf可表示为
qf=M(ˉp+pr)−Mh(ˉp−p), (49) Mf=M(ˉp+pr)−Mh(ˉp−p)p+pr=M+(R−1)(M−Mh)。 (50) 图 5表明了高温冻土固结参数R、潜在强度Mf与硬化参数H之间的相互关系,由于不同的固结程度的高温冻土具有不同的潜在强度,所以固结参数R决定潜在强度Mf的大小;式(17)的硬化参数H中包含了潜在强度Mf,故Mf的变化直接影响硬化参数H;高温冻土在复杂应力作用下的硬化参数H决定着当前屈服面与参考屈服面状态及表达式,进而间接影响固结参数R。
2.2 模型演化分析
微分当前屈服面硬化参量式(15)及参考屈服面硬化参量式(22)可得
dH=M4(M4f−η4)M4f(M4−η4)dεpvφ′(lnp)−κ, (51) dˉH=dεpvψ′(lnp)−κ。 (52) 对式(51),(52)进行整个应力路径中的分析,可得表 1所示的变化规律。
表 1 模型状态演化过程Table 1. Evolution process of model states状态阶段 应力比η、特征状态应力比M及潜在强度Mf间关系 塑性体变增量dεpv、屈服面硬化参量增量增量dH、d¯H 初始状态 0=η<M<Mf dεpv>0,dH>0,dˉH>0 剪缩、硬化阶段 0<η<M<Mf dεpv>0,dH>0,dˉH>0 特征状态 0<η=M<Mf dεpv=0,dH>0,dˉH=0 剪胀、硬化阶段 0<M<η<Mf dεpv<0,dH>0,dˉH<0 峰值应力状态 0<M<η=Mf dεpv<0,dH=0,dˉH<0 第一剪胀软化阶段 0<M<Mf<η dεpv<0,dH<0,dˉH<0 第二剪胀软化阶段 0<M=Mf<η dεpv<0,dH<0,dˉH<0 临界状态 0<M=Mf=η dεpv=0,dH=0,dˉH=0 由此可见,建立在潜在强度Mf、特征状态应力比M和应力比η有关的硬化参数H的基础上,本文模型能够有效反映高温冻土的剪缩、剪胀、硬化和软化特性。
3. 模型试验验证
3.1 模型的试验验证Ⅰ
Ma等[17]对兰州某地饱和冻结粉土进行了一系列三轴剪切室内试验,粉土干密度为1.75 g/cm3,三轴试验MTS810围压设定分别为1.0,2.0,6.0 MPa,高温冻结温度为-1.5℃;试验过程分为等向加载阶段和轴向应力加载阶段,围压约束的加载在5 min内完成,轴向应力以1.108 mm/min的速度加载,以试样轴向应变达到15%时作为试样破坏条件;本文所建模型需要6个参数和2条试验曲线,根据文献[17,19]及参数拟合:c=112.3 kPa,φ=25.8℃,ν=0.32,κ=-8.8×10-7,εv0=1.72×10-2,Mh=1.17,等向固结曲线曲线εv= 2.18×10−6⋅exp(0.726lnp),临界状态曲线曲线εv= 1.83×10−5⋅exp(0.687lnp),
图 6(a)为-1.5℃条件下高温冻结粉土偏应力与轴向应变的模型预测结果与试验数据对比,可以看出,本文模型对1.0,2.0,6.0 MPa围压条件下剪切行为的预测结果与试验数据吻合度较高。在1.0 MPa围压条件下,高温冻结粉土偏应力一直增加(硬化),在6.0 MPa围压条件下,高温冻结粉土偏应力先增加后减小(软化);在相同围压下,应力应变曲线主要呈三阶段变化,在初始阶段曲线呈线性变化,随着轴向应变的增加,曲线逐渐过渡到弹塑性阶段,此时试样内部以不可恢复的塑性变形为主。对于应变硬化的情况,应力逐渐到达最大值,曲线斜率近视趋近于零;对于应变软化的情况,当偏应力超过一定值时,曲线斜率由正转为负值,这是由于高温冻土特有的压融现象使得未冻水含量增加,试样内部超静孔隙水压力增加,颗粒之间的有效应力降低,剪切破坏极易发生。图 6(b)为-1.5℃条件下体积应变与轴向应变的模型预测结果与试验数据对比,可以看出,本文模型对1.0,2.0,6.0 MPa围压条件下体变行为的预测结果与试验数据吻合度较好。在围压较低时,试样因侧向变形受到的约束力较小而表现为稳定的剪缩特征;在围压较高时,试样因内部冰晶结构微裂隙及孔隙损伤开裂破坏而表现为特定的剪胀特征。综合图 6(a)和图 6(b)的试验数据和预测曲线,可以得出,-1.5℃条件下的高温冻结粉土在低围压条件下总体表现出剪缩硬化特性,在高围压条件下总体表现出剪胀软化特性,本文所建模型可以有效反映-1.5℃条件下的高温冻土剪缩、剪胀、硬化和软化特性。
3.2 模型的试验验证Ⅱ
宋丙堂等[18]对兰州市安宁区某地冻结粉土进行了一系列三轴压缩加卸载试验,粉土干密度为1.70 g/cm3,液限和塑限分别为27.6%,19.4%,初始含水率为1.36%;饱和冻结处理后,试验含水率为22.28%,重度为0.017 kN/m3,孔隙比为0.73;MTS810三轴试验围压设定为0.3~6.0 MPa(共8组),高温冻结温度为-1.0℃;试验过程分为等向加载阶段和轴向应力加载阶段,围压约束的加载在5 min内完成,轴向应力以1.108 mm/min的速度加载,以试样轴向应变达到20%时作为试样破坏条件;当高温冻土轴向应变εa=3%时,卸载偏差应力到零,然后将轴向应变加载到5.75%,再进行第二次卸载,应变的加卸载增量步取2.75%,本文所建模型需要6个参数和2条试验曲线,根据文献[18,19]及参数拟合确定参数:c=89.3 kPa,φ=23.4℃,ν=0.35,κ=-8.6×10-7,εv0= 2.14× 10-2,Mh=1.09,等向固结曲线εv=2.23×10−6⋅ exp(0.689lnp),临界状态曲线εv=1.76×10−5⋅exp (0.734lnp),
从图 7(a)可以看出,本文模型对1.4,2.0,4.0,6.0 MPa围压条件下剪切行为的预测结果与试验数据吻合度较好。在1.4,2.0 MPa围压条件下,高温冻结粉土偏应力一直增加(硬化),在4.0,6.0 MPa围压条件下,高温冻结粉土偏应力先增加后减小(软化);在同一围压条件下,初始阶段曲线呈线性变化,试样内部以可恢复的弹性变形为主;随着轴向应变的增加,曲线逐渐过渡到弹塑性阶段,此时试样内部以不可恢复的塑性变形为主。对于应变硬化的情况,应力逐渐增加到最大值,曲线斜率近视趋近于零,可认为该强度即为-1.0℃的高温冻结粉土在该围压条件下的极限强度;对于应变软化的情况,当偏应力超过一定值时,曲线斜率由正转为负值,这是由于高温冻土中形成的不稳定冰晶在一定压力条件下发生破坏,试样内孔隙水压力增加,颗粒之间的有效应力降低,进而发生剪切破坏,强度降低。从图 7(b)可以看出,本文模型对体变行为的预测结果与试验数据吻合度较高。在1.4,2.0 MPa较低围压时,试样因侧向变形受到的约束力较小而表现为稳定的剪缩特征;在4.0,6.0 MPa较高围压时,试样在初始阶段因内部冰晶结构微裂隙及孔隙损伤开裂破坏而表现为特定的剪胀特征,随着轴向应变的增加,试样逐渐表现为稳定的剪缩特征。综合图 7(a),(b)可以得出,-1.0℃条件下的高温冻结粉土在低围压条件下总体表现出剪缩硬化特性,在高围压条件下总体表现出剪胀软化特性,本文所建模型可以有效反映-1.0℃条件下的高温冻土剪缩、剪胀、硬化和软化特性。
4. 结论
(1)与传统模型中使用的e - lnp变形特征曲线相比,以εv - lnp曲线对高温冻土试样变形进行描述后,NCL和CSL曲线表达简便,有利于双屈服面函数形式的简化表征及模型参数的方便获取。
(2)由当前屈服面与参考屈服面间的关系重新定义了能够反映高温冻土应力状态的固结参数及潜在强度,得到的双屈服面统一本构模型能够有效反映高温冻土的剪缩、剪胀、硬化和软化特性。
(3)本模型在经典修正剑桥模型基础上引入的新参数较少,可以通过常规三轴试验、等向固结试验、回弹再加载试验等基本土工试验获取,模型应用简便,试验结果验证了所建模型的合理性。
-
表 1 土层力学参数
Table 1 Mechanical parameters of soils
土层 重度γ/
(kN·m-3)泊松比
ν弹性模量
Ε/MPa黏聚力
c/kPa摩擦角
φ/(°)侧压力系数K0 填土 20 0.30 10 10 10 0.43 砂层 20 0.29 50 2 33 0.34 表 2 支护体系结构材料参数
Table 2 Mechanical parameters of structures
名称 重度
γ/(kN·m-3)泊松比
ν弹性模量Ε/GPa 钢筋混凝土结构 25 0.2 28 管幕、钢管柱 78.5 0.2 200 -
[1] 龚胜. 中洞法施工技术[J]. 岩土工程学报, 2006, 28(增刊1): 1772-1775. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2006S1104.htm GONG Sheng. Middle hole construction method[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(S1): 1772-1775. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2006S1104.htm
[2] 惠丽萍, 崔志杰. PBA工法——一种新的大型地下空间暗挖施工方法[C]// 中国土木工程学会快速轨道交通委员会学术交流会地下铁道专业委员会学术交流会, 北京, 2001. HUI Liping, CUI Zhijie. PBA-a new subsurface excavation construction for large underground space[C]// Academic Exchange Meeting of Fast Rail Transit Committee China Civil Engineering Society, Beijing, 2001. (in Chinese)
[3] 夏才初, 阙程柯, 刘胜. 顶进箱涵全断面置换管幕工法中钢管幕内力研究及实例分析[J]. 岩土力学, 2011, 32(12): 3555-3560. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201112003.htm XIA Caichu, QUE Chengke, LIU Sheng. Study of internal forces and case study of pipe-roof for box culvert jacking and replacement full face pipe-roof method[J]. Rock and Soil Mechanics, 2011, 32(12): 3555-3560. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201112003.htm
[4] 谭忠盛, 马栋, 孙晓静, 等. 不停航机场跑道下大断面隧道施工技术[J]. 土木工程学报, 2015, 48(增刊1): 378-382. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2015S1067.htm TAN Zhongsheng, MA Dong, SUN Xiaojing, et al. Construction technology of large span tunnel under the non-stop flight runway[J]. China Civil Engineering Journal, 2015, 48(S1): 378-382. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2015S1067.htm
[5] 姚大钧, 吴志宏, 张郁慧. 软弱黏土中管幕工法之设计与分析[J]. 岩石力学与工程学报, 2004, 23(增刊2): 4999-5005. YAO Dajun, WU Zhihong, ZHANG Yuhui. Design and analysis of pipe roofing method in soft clay[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(增S2): 4999-5005. (in Chinese)
[6] 余晶, 程勇, 贾瑞华. 港珠澳大桥珠海连接线拱北隧道方案论证[J]. 现代隧道技术, 2012, 49(1): 119-125, 131. https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD201201023.htm YU jing, CHENG Yong, JIA Ruihua. Option demonstration for the Gongbei tunnel at the zhuhai link of the hong kong-zhuhai-macau bridge[J]. Modern Tunnelling Technology, 2012, 49(1): 119-125, 131. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD201201023.htm
[7] 黎永索, 阳军生, 张可能, 等. 弧形密排大直径管群顶管地表沉降分析[J]. 中南大学学报(自然科学版), 2013, 44(11): 4687-4693. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201311046.htm LI Yongsuo, YANG Junsheng, ZHANG Keneng, et al. Surface subsidence caused by construction of large diameter curved jacking-pipes in pipe-roof pre-construction method[J]. Journal of Central South University (Science and Technology), 2013, 44(11): 4687-4693. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201311046.htm
[8] 关永平, 贾鹏蛟, 赵文, 等. 基于ABAQUS的STS管幕结构受力性能数值分析[J]. 建筑结构, 2016, 46(增刊2): 569-573. https://www.cnki.com.cn/Article/CJFDTOTAL-JCJG2016S2122.htm GUAN Yongping, JIA Pengjiao, ZHAO Wen, et al. Numerical analysis of mechanical behavior of steel tube slab structure based on ABAQUS[J]. Building Structure, 2016, 46(S2): 569-573. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JCJG2016S2122.htm
[9] 冯建霖. 下穿机场跑道大断面隧道施工对策及地层变形规律研究[J]. 隧道建设, 2015, 35(5): 473-477. https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201505025.htm FENG Jianlin. Study on construction countermeasures for and ground deformation rule of construction of large cross-section tunnel crossing underneath existing airport runway[J]. Tunnel Construction, 2015, 35(5): 473-477. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSSD201505025.htm
[10] 山村学, 高橋幸久, 近藤達也. 車両基地直下の長距離パイプルーフの施工[J]. トンネル工学報告集, 2006, 16: 499-506. HIGERU Fujimoto, YUICHI Fujita, SHINJO Sato. Under a vehicle base, we used a pipe roof method and constructed a road tunnel[J]. Collection of Tunnel Engineering Reports, 2006, 16: 499-506. (in Japanese)
[11] 罗富荣, 汪玉华, 郝志宏. 地铁车站洞桩法设计与施工关键技术[M]. 北京: 中国铁道出版社, 2015. LUO Furong, WANG Yuhua, HAO Zhihong. Key Technology of Design And Construction of Subway Station Hole Pile Method[M]. Beijing: China Railway Publishing House, 2015. (in Chinese)




 下载:
下载: