多层非均质边坡降雨入渗分析的改进Green-Ampt模型

蒋水华; 刘贤; 黄劲松; 周创兵

doi:10.11779/CJGE20230205

多层非均质边坡降雨入渗分析的改进Green-Ampt模型 English Version

蒋水华^1,,
刘贤^{1, 2, ,},
黄劲松¹,
周创兵¹

1.
南昌大学工程建设学院, 江西南昌 330031
2.
中山大学土木工程学院, 广东珠海 519082

基金项目:

国家自然科学基金优秀青年基金项目 52222905

国家自然科学基金项目 5217910342272326

江西省自然科学基金项目 20232ACB204031

江西省自然科学基金项目 20224ACB204019

详细信息

作者简介:
蒋水华(1987—)，男，江西九江人，教授，博士生导师，主要从事水工岩土工程可靠度和灾害风险防控方面的研究工作。E-mail: sjiangaa@ncu.edu.cn

通讯作者:
刘贤, E-mail: liux597@mail2.sysu.edu.cn

中图分类号: TU47
计量
- 文章访问数: 570
- HTML全文浏览量: 116
- PDF下载量: 181
出版历程
- 收稿日期: 2023-03-07
- 网络出版日期: 2023-07-05
- 刊出日期: 2024-05-31

An improved Green-Ampt model for rainfall infiltration analysis of multi-layered heterogeneous soil slopes

1.
School of Infrastructure Engineering, Nanchang University, Nanchang 330031, China
2.
School of Civil Engineering, Sun Yat-Sen University, Zhuhai 519082, China

摘要

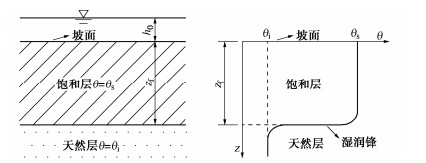
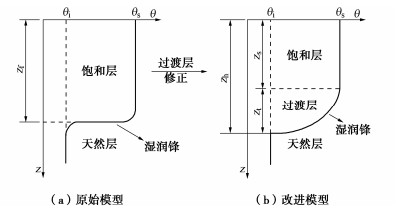
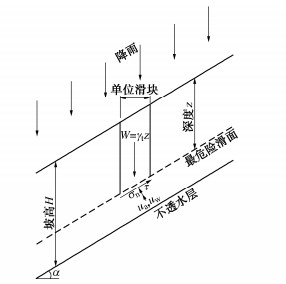
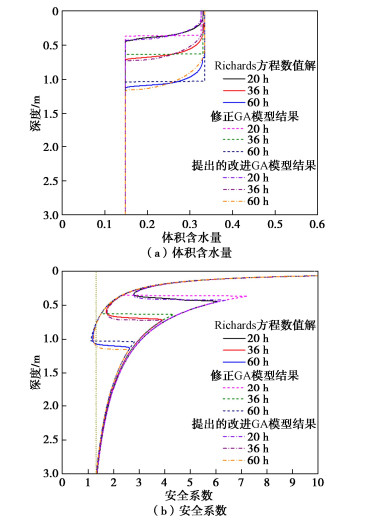
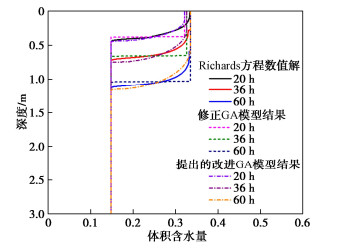
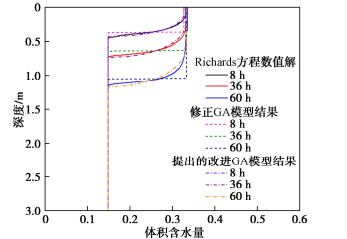
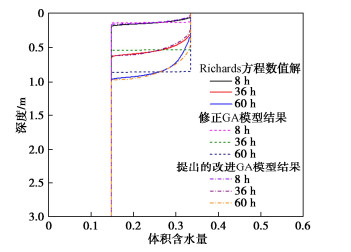
摘要: 边坡降雨入渗分析对于降雨型滑坡加固设计、治理和风险防控至关重要。经典的Green-Ampt模型参数虽然具有明确的物理意义，计算便捷，但是忽略了入渗区客观存在的过渡层，并且不能有效分析考虑土体渗透系数空间变异性的多层非均质边坡降雨入渗问题。为此，提出了一种适用于多层非均质边坡降雨入渗分析的改进Green-Ampt模型，考虑了降雨入渗的椭圆形过渡层，推导了不同降雨历时下边坡含水率分布情况。同时，以无限长边坡模型为例，通过4种常见的边坡工况验证了该模型的有效性，并进行了降雨入渗条件下非均质边坡稳定性分析。结果表明：对于设定的4种工况，提出的改进Green-Ampt模型计算的边坡体积含水量分布、安全系数和滑动面深度与Richards方程数值解吻合，而基于修正Green-Ampt模型计算的边坡体积含水量和滑动面分布存在偏差，边坡安全系数偏小。此外，基于提出的改进Green-Ampt模型能够准确识别最危险滑动面位置。研究成果可为多层非均质边坡降雨入渗分析及降雨型滑坡加固设计及风险防控提供理论参考。
- 非均质边坡 /
- 降雨入渗 /
- 稳定性分析 /
- 改进Green-Ampt模型 /
- 空间变异性
Abstract: The rainfall infiltration analysis of slopes is of a great significance to the reinforcement design, mitigation and risk mitigation of rainfall-induced landslides. The classical Green-Ampt model, whose parameters have clear physical meanings and which is easy to implement, ignores the fact that a transition layer objectively exists in infiltration zone. It cannot effectively analyze the rainfall infiltration process of multi-layered heterogeneous slopes considering the spatial variability of hydraulic conductivity. To this end, an improved Green-Ampt model is proposed for the rainfall infiltration analysis of multi-layered heterogeneous slopes, and it considers the elliptical transition layer of rainfall infiltration and evaluates the water content distributions under different rainfall durations. Additionally, an infinite slope model is taken as an example to validate the effectiveness of the proposed improved Green-Ampt model through four common slope scenarios. The corresponding slope stability analyses under rainfall infiltration are also conducted. The results indicate that the distributions of volumetric water content and the factors of safety evaluated using the proposed model are well consistent with the numerical results of Richards' equation for these four slope cases. In contrast, the modified Green-Ampt model produces the biased distributions of volumetric water content and smaller factors of safety. In addition, the location of the critical slip surface of the slope can be accurately identified using the proposed improved Green-Ampt model. The research outcome provides theoretical references for the rainfall infiltration analysis of multi-layered heterogeneous soil slopes and the reinforcement design and risk control of rainfall-induced landslides.
- heterogeneous slope /
- rainfall infiltration /
- stability analysis /
- improved Green-Ampt model /
- spatial variability

HTML全文

0. 引言

地表局部地形对地震波的传播有显著影响，当地震波遇到高山、峡谷等，会产生散射波、入射波和反射波等复杂波场，并引起地面运动的放大或衰减，称为地形效应。目前针对地形效应已有了相应的研究（表 1），主要包含了数值模拟和解析分析两种。解析主要运用的是波函数展开法，Wong等^[1]提出了半圆形峡谷对地震SH波散射的波函数级数解，随后众多学者提出了多种圆弧形峡谷的解析解^[2-6]，Gao等^[7]提出了通过坐标变换求解V形对称峡谷引起的圆柱形SH波二维散射和衍射波函数的级数解。数值方法包含了有限差分法^[8]，谱元法等^[9]等，数值方法可实现复杂地形地震波传播模拟，具备边界和复杂几何处理的灵活性，但在计算精度方面往往需要解析解的校准。

表 1 复杂地形效应近场波动模拟研究现状

Table 1. Researches on near-field fluctuation problems

模拟方法	应用场景	时间	文献
解析法	平面SH波在半圆柱型峡谷的散射	1972年	[1]
	平面SH波在半圆柱型冲击峡谷的散射	1971年	[2]
	平面SH波在半椭圆形冲击峡谷的散射	1974年	[3]
	平面SH波在圆弧形峡谷的散射	2009年	[4]
	平面SH波在截断峡谷的散射	2009年	[5]
	U型峡谷引起的地形放大对地震波的影响	2012年	[6]
	柱面SH波在对称V型峡谷的反射和散射	2013年	[7]
有限差分法	极坐标尺度不规则地形FEM方法	2021年	[8]
谱元法	入射平面SV波作用下梯田形山丘的表面运动	2017年	[9]
PINN	近场波动数值模拟	2022年	[30]

下载: 导出CSV

| 显示表格

近场波动在数学上可归结为偏微分方程的初值、边值问题，偏微分方程的数值离散化在模拟多物理场问题方面取得了很大的进展，但通过使用经典的分析或计算工具来建模和预测非线性多尺度系统的演化较困难，面对复杂网络剖分、参数化偏微分方程控制的高维问题等。

近年来的研究发现，物理信息神经网络（PINN）可以用于对控制物理系统的偏微分方程进行建模，通过嵌入物理信息解决了传统神经网络算法对于求解方面的局限性，例如高度依赖数据驱动，缺乏物理可解释性、易陷入过拟合以及可获取数据的稀疏性等。PINN方法仅依赖于少量甚至零标记的数据集，并实现数据稀缺、物理约束的学习。嵌入物理公式为可训练参数提供约束，缓解过拟合问题，减少对大型训练数据集的需求，从而提高训练模型的鲁棒性，以实现可靠的预测。Raissi等^[10]利用深度学习神经网络（DNN）的强表达性，开发了通用PINN框架，解决了涉及小数据集甚至没有任何标记数据的非线性偏微分方程系统的正逆问题。最近几年PINN方法在地球物理学^[11-13]、固体力学^[14-16]、流体动力学^[17-20]、热传导^[21-22]等方面有了相应的研究。众多学者针对不同的偏微分方程，让PINN方法更好地适应不同的物理问题^[23-29]。也有了少数利用物理信息神经网络求解波动方程的工作，Rao等^[19]通过DNN复合方案以硬嵌入的方式强制满足初值、边值条件，在截断域的波传播问题上进行了模拟。陈苏等^[30]结合了数值模拟原理和物理驱动深度学习建立了波动模拟方法，提出了可以提高网络训练效率的迁移学习方法。

在前人研究的基础上，提出通过物理信息神经网络模拟圆柱形SH波在不规则地形下的散射和衍射方法。通过新的参数加载代理建模策略，在给定初始时刻稀疏地震位移波场，模拟地震波在半无限域的传播，通过对比解析解和PINN预测解来评估所提出的规则地形下PINN模型的性能。通过PINN模型模拟不规则地形下圆柱形SH波的二维散射和衍射，证明该方法具有良好的泛化性。

1. 物理驱动深度学习原理

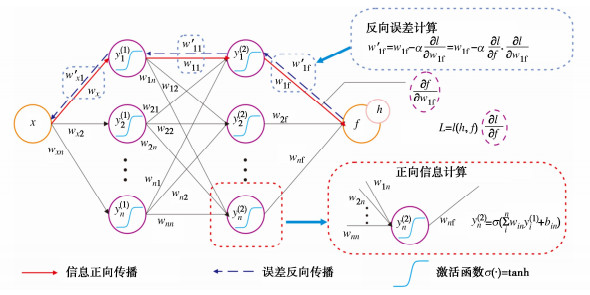
深度学习神经网络（DNN）具备出色的计算表达能力，在图像识别和自然语言处理等领域获得了较多应用。前馈全连接神经网络可以假设为输入层、多个隐藏层和输出层的堆栈。相邻两层之间的连接，例如从第i−1层到第i层，可用张量的形式简单表示为

$\boldsymbol{Y}_i=\alpha\left(\boldsymbol{W}_i \boldsymbol{Y}_{i-1}+\boldsymbol{b}_i\right) \quad(1 \leqslant i \leqslant n+1) 。$

(1)

式中：n为隐层总数；σ(·)为按元素作用的激活函数； ${\boldsymbol{Y}_0}$ 和 ${\boldsymbol{Y}_{n + 1}}$ 分别为输入张量和输出张量； ${\boldsymbol{W}_i}$ ， ${\boldsymbol{b}_i}$ 为第i层的可训练权重矩阵和偏置向量。DNN作为弹性动力学问题的参数化近似解，其中时空位置X = (x, t)为自变量。通过最优逼近物理系统理论解，获取训练参数，需设计嵌入物理定律的损失函数作为训练目标，网络训练中需评估物理场对时空变量的偏导数，Tensorflow和Pytorch框架中可完成自动微分功能。以前馈神经网络为例，网络以变量x为输入，在式（1）中定义的非线性变换后输出f，表示第i个隐藏层中第j个神经元的输出。由于输出f可以表示为x的嵌套函数，应用链式法则，可以计算每一层之间的梯度关系，通过构建损失函数和误差的反向传播，每训练一步后更新权重和偏置，如图 1所示，权重和偏置的更新计算为

图 1 DNN网络自动微分简图

Figure 1. Automatic differential diagram of DNN network

下载: 全尺寸图片幻灯片

$\omega_{1 \mathrm{f}}^{\prime}=\omega_{1 \mathrm{f}}-\alpha \frac{\partial l}{\partial \omega_{1 \mathrm{f}}} ,$

(2)

$\frac{\partial l}{\partial \omega_{\mathrm{1f}}}=\frac{\partial l}{\partial f} \cdot \frac{\partial f}{\partial \omega_{\mathrm{1f}}},$

(3)

$f=\sigma\left(\sum_i^n \omega_{i \mathrm{f}} y_i^{(2)}+b_i\right),$

(4)

$\frac{\partial f}{\partial \omega_{1 \mathrm{f}}}=\sigma y_1^{(2)}。$

(5)

式中： $\alpha$ 为DNN网络的学习率；l为期望值h与网络输出值f构建的损失函数。

损失函数L可以求得 $\tfrac{{\partial l}}{{\partial f}}$ 的值，式（4）中节点 $y_1^{(2)}$ 与输出f之间关系可以求得 $\tfrac{{\partial f}}{{\partial {\omega _\text{1f}}}}$ ，再通过式（2），（3）求得更新后的权重 ${\omega '_\text{1f}}$ 。偏置 ${b'_\text{1f}}$ 的计算同理，网络参数更新过后采用梯度下降最快的策略，使得损失函数L减小到0，最终输出值f与期望值h以及两者的导数实现强形式的相等，如图 1所示。

从函数逼近论角度，具有单一隐藏层的神经网络可精确逼近任何线性或非线性连续函数，因此可以将神经网络作为非线性函数逼近器。Rassi等^[10]通过训练全连接神经网络来逼近偏微分方程的解，用神经网络逼近方程的各阶偏导数，实现将PDE残差以及初、边值条件作为正则项加入损失函数中。

以一维杆件中波的传播为例，介绍物理驱动深度学习方法求解偏微分方程的可行性。杆件长10 m，在杆左端施加Ricker子波，波速为1 m/s。一维标量波动方程形式为

$\frac{{{\partial ^2}u}}{{{\partial ^2}t}} - c\frac{{{\partial ^2}u}}{{{\partial ^2}x}} = 0{\text{ }}\left( {x \in [0, 10], t \in [0, 20]} \right),$

(6)

Ricker子波公式 $:$

$u_{\mathrm{r}}=\left[\frac{2 \pi^2\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}}。$

(7)

Ricker子波从x=0处输入，所以在x=0处的边界条件可以表示为

$u(0, t)=\left[\frac{2 \pi^2\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}}。$

(8)

式中：c为波速， ${t_\text{s}}$ 为Ricker波的半周期，根据波动传播理论，得到

$u=f\left(t+\frac{x}{c}\right)=\left[\frac{2 \pi^2\left(t-t_\text{s}\right)^2}{t_\text{s}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_\text{s}\right)^2}{t_\text{s}^2}}。$

(9)

化简后易得上述波动方程解析解：

$u(x, t)=\left[\frac{2 \pi^2\left(t-t_{\mathrm{s}}-\frac{x}{c}\right)^2}{t_{\mathrm{s}}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_{\mathrm{s}}-\frac{x}{c}\right)^2}{t_{\mathrm{s}}^2}}。$

(10)

此案例满足如下形式的偏微分方程：

$\left. \begin{array}{l}\begin{gathered} \boldsymbol{D}(u(x, t) ; \lambda)=f(x, t) \quad(x \in \varOmega, t \in[0, T]), \\ u(x, t)=\boldsymbol{B}_D(t) \quad\left(x \in \partial \varOmega_D, t \in[0, T]\right), \\ \nabla u(x, t)=\boldsymbol{B}_N(t) \quad\left(x \in \partial \varOmega_N, t \in[0, T]\right), \\ u(0, t)=\boldsymbol{B}_0(t) \quad(t \in[0, T]), \\ u(x, 0)=\boldsymbol{J}_0(x) \quad(x \in \varOmega) 。 \end{gathered}\end{array} \right\}$

(11)

式中： $u(x, t)$ 为偏微分方法的解； $\boldsymbol{D}( \cdot )$ 为带参数 $\lambda$ 的微分算子；x为域 $\varOmega \in {R^d}$ 中的空间变量， $d = 1, 2, \ldots n$ ；域边界 $\partial \varOmega$ 由Dirichlet边界 $\partial {\varOmega _D}$ 和Neumann边界 $\partial {\varOmega _N}$ 组成； $t \in [0, T]$ 为时间变量； ${\boldsymbol{B}_D}(t), {\boldsymbol{B}_N}(t)$ 分别为偏微分方程的初边值问题中的Dirichlet、Neumann边界条件函数； ${\boldsymbol{B}_0}(t)$ 为在x=0处的边界条件函数； ${\boldsymbol{J}_0}(x)$ 为初始条件函数。

对于这些初、边值函数，通过设计损失函数 $\sum (\theta )$ 架构并训练神经网络：

$\sum (\theta ) = {\sum _{\text{p}}}(\theta ) + {\sum _{{\text{bc}}}}(\theta ) + {\sum _{{\text{ic}}}}(\theta ) ,$

(12)

$\left. \begin{array}{l}\begin{aligned} \sum\nolimits_{\mathrm{bc}}(\theta)= & \frac{1}{N_{\mathrm{d}}} \sum\nolimits_i^{N_{\mathrm{p}}}\left\|\nabla \boldsymbol{N} \boldsymbol{N}\left(x_i, t_i ; \theta\right)-\boldsymbol{B}_D(t)\right\|_{\partial \varOmega_D \times[0, T]}^2+ \\ & \frac{1}{N_{\mathrm{n}}} \sum\nolimits_i^{N_{\mathrm{n}}}\left\|\nabla \boldsymbol{N} \boldsymbol{N}\left(x_i, t_i ; \theta\right)-\boldsymbol{B}_N(t)\right\|_{\partial \varOmega_N \times[0, T]}^2, \\ \sum\nolimits_{\mathrm{ic}}(\theta)= & \frac{1}{N_{\mathrm{ic}}} \sum\nolimits_i^{N_{\mathrm{ic}}}\left(\left\|\nabla \boldsymbol{N} \boldsymbol{N}\left(x_i, 0 ; \theta\right)-\boldsymbol{J}_0(t)\right\|_{\varOmega \times\{t=0\}}^2+\right. \\ & \left.\left\|\nabla \boldsymbol{N} \boldsymbol{N}_t\left(x_i, 0 ; \theta\right)-\boldsymbol{J}_1(t)\right\|_{\varOmega \times\{t=0\}}^2\right), \\ \sum\nolimits_{\mathrm{p}}(\theta)= & \frac{1}{N_{\mathrm{p}}} \sum\nolimits_i^{N_{\mathrm{p}}}\left(\left\|\boldsymbol{D}\left(\boldsymbol{N} \boldsymbol{N}\left(x_i, t_i ; \theta\right) ; \lambda\right)-f\left(x_i\right)\right\|_{\varOmega \times[0, T]}^2\right.。 \end{aligned}\end{array} \right\}$

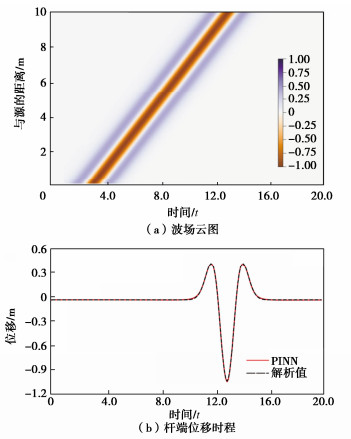
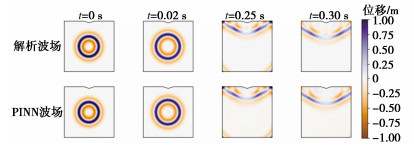
(13)

使用Sobol序列算法分别生成PDE残差损失项、初始条件损失项的时空采样点。采用8个隐藏层、每层20个神经元的全连接神经网络，使用Adam优化器训练40000步，波场云图及PINN的预测解与解析解对比如图 2所示，PINN预测值与解析解之间的绝对误差最大值为0.007 m，表明经过训练的神经网络已具备较强逼近波动方程真解的能力。

图 2 波场云图及PINN预测与解析对比图

Figure 2. Comparison of wavefield clouds and PINN prediction and resolution

下载: 全尺寸图片幻灯片

2. 物理驱动人工智能波动模拟方法

2.1 方法介绍

以SH波在平面内和地表及峡谷处的散射反射为例，二维波动方程为

$\frac{{{\partial ^2}u}}{{{\partial ^2}t}} - c\left( {\frac{{{\partial ^2}u}}{{{\partial ^2}x}} + \frac{{{\partial ^2}u}}{{{\partial ^2}z}}} \right) = f。$

(14)

式中： $u(x, z, t)$ 为出平面波动位移；c为介质物理波速； $f(x, z, t)$ 为外荷载，令 $f \equiv 0$ ，并通过给定初始波场等效施加外力。

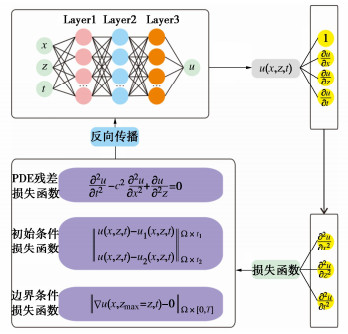
根据陈苏等^[30]提出的二维波动方程PINN求解框架，指定时空坐标 $X = (x, z, t)$ 的3个分量为网络的输入值，位移场 $Y = u(x, z, t)$ 为网络的输出值，通过Pytorch的自动微分功能，得到位移对于各分量的微分值，即 $\tfrac{{{\partial ^2}u}}{{{\partial ^2}t}}, \tfrac{{{\partial ^2}u}}{{{\partial ^2}x}}, \tfrac{{{\partial ^2}u}}{{{\partial ^2}z}}$ ，并构建损失函数。

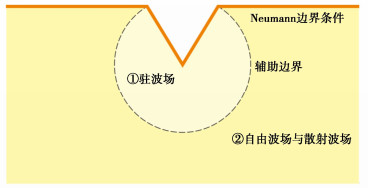
Gao等^[7]提出了对称V形峡谷引起的柱面SH波二维散射和衍射的波函数级数解。峡谷模型如所示，采用半径为a（峡谷壁长度）的圆弧作为辅助边界，将整个空间分成两个子区域。子区域①中为驻波波场，子区域②中包含没有牵引边界的自由波场和因为峡谷存在而产生的散射波场。要求波源的位置位于子区域②中，通过波函数展开法和坐标变换得到了此模型下二维圆柱SH波的反射结果，即半平面内的位移场 ${Y_\text{reli}} = {u_\text{reli}}(x, z, t)$ 。本文采用解析计算得到的 ${t_1}, {t_2}$ 时刻的两个早期位移场作为初始条件，通过两帧波场快照 ${\boldsymbol{u}_1}, {\boldsymbol{u}_2}$ 约束震源的位置、形状和SH波的传播方向。垂直地表的应力为零的边界条件可通过损失函数中的Neumann边界条件 $\nabla u(x, z = {z_\text{top}}, t) = 0$ 表示。

图 3 对称V型峡谷模型示意图

Figure 3. Schematic diagram of a symmetrical V-shaped canyon model

下载: 全尺寸图片幻灯片

$\boldsymbol{L}(\theta)=\lambda_1 \boldsymbol{L}_{\mathrm{p}}(\theta)+\lambda_2 \boldsymbol{L}_{\mathrm{bc}}(\theta)+\lambda_3 \boldsymbol{L}_{\mathrm{ic}}(\theta) ,$

(15)

$\left. \begin{array}{l}\boldsymbol{L}_{\text{p}}(\theta )=\frac{1}{{N}_{\text{p}}}{\displaystyle {\sum }_{i}^{{N}_{\text{p}}}}\Vert \frac{{\partial }^{2}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})}{\partial {t}_{i}^{2}}-{c}_{i}^{2}(\frac{{\partial }^{2}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})}{\partial {x}_{i}^{2}}+\\ {\text{ }\frac{{\partial }^{2}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})}{\partial {z}_{i}^{2}})\Vert }_{\varOmega \times [0, T]}^{2}, \\ \boldsymbol{L}_{\text{ic}}(\theta )=\frac{1}{{N}_{\text{ic1}}}{\displaystyle {\sum }_{i}^{{N}_{\text{ic}1}}}\Vert {\Vert \stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})-{U}_\text{rel1}({x}_{i}, {z}_{i}, {t}_{i})\Vert }_{\varOmega \times \{t={t}_{1}\}}^{2}+\\ {\text{ }\frac{1}{{N}_{\text{ic2}}}{\displaystyle {\sum }_{i}^{{N}_{\text{ic2}}}}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})-{U}_\text{rel2}({x}_{i}, {z}_{i}, {t}_{i})\Vert }_{\varOmega \times \{t={t}_{2}\}}^{2}, \\ \boldsymbol{L}_{\text{bc}}(\theta )=\frac{1}{{N}_{\text{bc}}}{\displaystyle {\sum }_{i}^{{N}_{\text{bc}}}{\Vert \nabla \stackrel{⌢}{u}({x}_{i}, {z}_{i}={z}_\text{top}, {t}_{i})\Vert }_{\varOmega \times [0, T]}^{2}。}\end{array} \right\}$

(16)

式中： $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}$ 为PINN逼近的偏微分方程的解， $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} (x, z, t) =$ $\boldsymbol{NN}(x, z, t;\theta )$ 。

根据式（15），（16），在半无限区域的二维波动问题中，损失函数由PDE残差损失项、初始条件损失项和边界条件损失项组成，其中 ${\lambda _1}$ ， ${\lambda _2}$ ， ${\lambda _3}$ 为损失分配系数。求解二维波动方程的物理信息神经网络架构如图 4所示。选择Tanh激活函数作为神经网络的非线性激活函数，以确保网络非零二阶导数存在，并实现高效收敛。采用Adam和L-BFGS共同作用的优化策略。其中Adam优化算法可实现全域快速收敛，接L-BFGS优化获得高精度解。使用Xavier初始化对神经网络中的可训练参数进行初始化。

图 4 物理驱动神经网络架构图

Figure 4. Diagram of PINN architecture

下载: 全尺寸图片幻灯片

2.2 方法验证

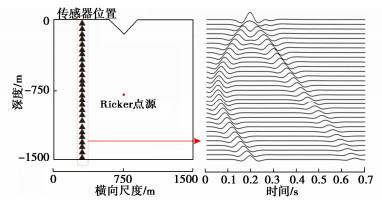
半无限均匀介质内的SH波动模型如图所示，模型区域为宽1500 m，深1500 m，峡谷深度d=50 m，峡谷宽度b=150 m。介质物理波速c=3000 m/s，输入波位移时程采用主频为10 Hz的Ricker源时间函数，源位置处于模型中心x = 750 m， z = -750 m。

使用解析计算得到的 ${t_1} = 0.05{\text{ s}}$ ， ${t_2} = 0.1{\text{ s}}$ 的位移场作为初始条件参与训练，其余时刻的结果与PINN的计算结果进行对比验证。解析计算中时间步长为0.01 s，计算总时长为1 s。训练前根据模型的几何数据，定义顶部边界为宽150 m，深50 m的对称V型峡谷，在此边界上添加应力为0的Neumann边界条件。采用Sobol序列算法在整个域中生成用于计算PDE残差损失项的采样点和初始条件采样点。在V型峡谷处的采样点布设做局部加密，在顶部两侧水平边界布设200个采样点，在V型边界布设1000个采样点，删除峡谷上部PDE残差损失项采样点，调整后采样点数 ${N_{\text{p}}} = 9954$ ， ${N_{{\text{ic1}}}} = 500$ ， ${N_{{\text{ic2}}}} = 500$ ， ${N_{{\text{top}}}} = 1400$ 。设置4个隐藏层，每层30个神经元的全连接神经网络。

根据时间域分解策略，首先对模型采取预训练（热启动），波场时刻从 ${t_1} = 0.05{\text{ s}}$ 开始算起，预测总时间 $T = 0.1{\text{ s}}$ ，根据经验设置损失分配系数 ${\lambda _1} = {10^{ - 5}}$ ， ${\lambda _2} = 1$ ， ${\lambda _3} = {10^{ - 1}}$ 。调用学习率为6×10^-3的Adam优化器训练20000步，再使用L-BFGS优化器训练200000步。损失分配系数的神经网络会根据初始条件项损失项、边界条件损失项、PDE残差损失项的顺序进行训练，预训练时的SH波还未传播到顶部边界，能够观测到PINN方法很好地预测了柱面SH波的传播过程。保存预训练后的网络结构进行二次训练，调整损失分配系数 ${\lambda _1} = {10^{ - 3}}$ ， ${\lambda _2} = 1$ ， ${\lambda _3} = {10^{ - 1}}$ ，预测总时间 $T =$ $0.3{\text{ s}}$ 。调用L-BFGS优化器训练100000步，进一步优化PDE残差损失项，训练完成后保存网络结构进行最终训练，损失分配系数不变，设置预测总时间T=0.6 s，调用L-BFGS优化器训练200000步。训练完成后，可对任意分辨率下任意时空点的波动方程解及解的各阶偏导进行预测，图 5给出了4个时刻的PINN模拟波场和解析波场的对比。

图 5 半无限空间波动问题: PINN与解析波场快照对比

Figure 5. Semi-infinite space fluctuation problem: PINN vs. analytical wave snapshot

下载: 全尺寸图片幻灯片

由于此模型的波源位于中心位置，所以可在 $x = 300$ 外布设传感器，观测入射波、反射波和散射波经过的过程，验证PINN在预测柱面SH波在半无限空间内传播和反射特性，给出x坐标同为300 m，z坐标关于 $z = - 750$ 对称点位的时程数据，其中z坐标600 m与z坐标900 m是相对于 $z = - 750$ 的对称坐标，由于t=0 s时刻区域内已存在点源散发出的波场，在0~0.6 s时刻内，在坐标 $z = - 600$ 处和 $z = - 900$ 处有入射波和反射波经过，可以看出PINN方法在此模型下的入射波传播和边界反射的预测值与解析真值基本一致。同时z坐标-300 m与z坐标-1200 m是相对于 $z = - 750$ 的对称坐标，在0~0.6 s时刻内，坐标 $z = - 300$ 处和 $z = - 1200$ 处除入射波和反射波外，还有因峡谷而产生的散射波，可以看出PINN方法在预测柱面SH波在峡谷出的散射值与解析真值基本一致。在 $x = 300$ 布设的位移传感器和预测位移时程结果图 7所示。

图 6 对称位置PINN与解析波场时程对比

Figure 6. Comparison of time histories of symmetrical position PINN and analytical wave field

下载: 全尺寸图片幻灯片

图 7 PINN模拟时程图（x=300）

Figure 7. Time histories of PINN analog (x=300)

下载: 全尺寸图片幻灯片

3. 不同工况深切峡谷波动模拟

为保证PINN方法在处理对称V型峡谷波动模拟问题的有效性，考虑不同波速、不同主频的Ricker波在V型半无限空间内的波动问题。模型区域为宽1500 m，高1500 m，峡谷深度d=50 m，峡谷宽度b=150 m，输入波位移时程采用Ricker源时间函数，源位置处于模型中心x = 750 m，z = -750 m。

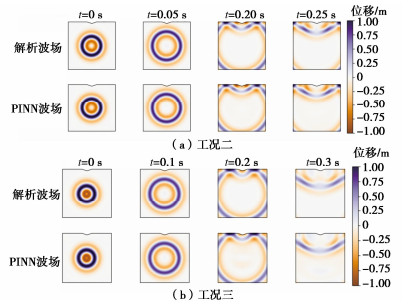
本文所有工况的模型参数和训练参数如表 2所示，工况二和工况三的预测结果与解析值的对比云图如图 8所示，由此可见PINN方法在对称V型峡谷的地形下，能够较好地预测不同频率不同波速下柱面SH波的反射和散射。

表 2 不同工况PINN模型参数

Table 2. Parameters of PINN model under different working conditions

参数	工况一（图 5）		工况二（图 8(a)）	工况三（图 8(b)）
主频 $\omega {\text{/Hz}}$		10	8	5
波速 $c{\text{/}}$ ${\text{(m}} \cdot {{\text{s}}^{ - 1}}{\text{)}}$		3000	3000	2000
第一帧快照时间 ${t_0}{\text{/s}}$		0.20	0.15	0.30
第二帧快照时间 ${t_1}{\text{/s}}$		0.22	0.20	0.40
传播时间 $T{\text{/s}}$		0.60	0.65	1.00
采样点	${N_{\text{p}}} = 9954$ ， ${N_{{\text{ic1}}}} = 500$ ， ${N_{{\text{ic2}}}} = 500$ ， ${N_{{\text{top}}}} = 1400$
预训练损失分配系数	${\lambda _1} = {10^{ - 5}}$ , ${\lambda _2} = 1$ , ${\lambda _3} = {10^{ - 1}}$
后续损失分配系数	${\lambda _1} = {10^{ - 3}}$ , ${\lambda _2} = 1$ , ${\lambda _3} = {10^{ - 1}}$
优化策略	Adam20000步+ LBFGS500000步		Adam20000步+ LBFGS300000步	Adam20000步+ LBFGS300000步

下载: 导出CSV

| 显示表格

图 8 PINN预测与解析真值云图对比

Figure 8. Comparison of PINN prediction and ground truth under condition 3

下载: 全尺寸图片幻灯片

对比不同工况下的预测精度，定义在某一点PINN与解析波场之间的相对 ${L_2}$ 范数误差为

$\varepsilon (\boldsymbol{u}) = \frac{{\sqrt {\sum\nolimits_{i = 1}^N {{{\left\| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ({x_0}, {z_0}, {t_i}) - {u_\text{ref}}({x_0}, {z_0}, {t_i})} \right\|}^2}} } }}{{\sqrt {\sum\nolimits_{i = 1}^N {{{\left\| {{u_\text{ref}}({x_0}, {z_0}, {t_i})} \right\|}^2}} } }}。$

(17)

式中： ${x_0}$ ， ${z_0}$ 为采样点的坐标位置； $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ({x_0}, {z_0}, {t_i})$ 为PINN方法预测得到的该采样点的位移时程； ${u_{ref}}({x_0}, {z_0}, {t_i})$ 为相同位置的解析位移时程；N为计算点数。

给出3种工况预测模型在 $x = 300$ 不同位置的相对范数误差。在x相同时，相对 ${L_2}$ 范数误差与纵坐标z有关，越靠近地表，由于散射波和衍射波的叠加，相对 ${L_2}$ 范数误差会增大，但都保持在0.03以内。表明PINN方法处理对称V型峡谷反射波和散射波的有效性，可实现复杂地形模拟分析。分别给出不同频率下PINN预测的峡谷地表及附近各位置峰值位移分布。由可知：不同SH波（5，8，10 Hz）条件下，V型峡谷地形效应总体上呈现出“M”型分布，中心V型峡谷底端及邻区SH波发生衰减与振荡，在谷肩及地表SH波放大，峡谷边缘出现了显著放大。3种工况下地表处最大峰值位移的相对 ${L_2}$ 误差范数分别为0.0009，0.0006，0.001，由此可见PINN方法在预测低频SH波峡谷处地形效应时更为准确。

图 9 不同工况相对

${L_2}$ 范数误差（x=300）

Figure 9. Relative norm errors under different working conditions (x=300)

下载: 全尺寸图片幻灯片

图 10 地表峰值位移对比

Figure 10. Comparison of peak displacements on surface

下载: 全尺寸图片幻灯片

4. 结论

通过物理信息驱动神经网络（PINN）的自动微分功能求解了二维波动方程，并计算了柱面SH波在对称V型峡谷下的反射和散射。通过与解析值的对比，验证了PINN方法在求解波动问题上的精度。得到3点结论。

（1）物理驱动深度学习（PINN）方法可通过稀疏初始波场数据，模拟柱面SH波在对称V型峡谷下的反射和散射，具备“无网格、强耦合”等特性，可适应不同地形与波源。

（2）对比不同工况的训练结果，发现越靠近地表位置，波场叠加越复杂，相对 ${L_2}$ 误差范数也会越大。且同一模型下，相对 ${L_2}$ 范数误差与柱面SH波的主频关系不大。

（3）对比不同工况下解析与PINN预测的地表峰值位移大小关系，柱面SH波在V型峡谷底端发生衰减现象，在其他位置发生放大现象。其中在V型峡谷边缘处放大现象最明显，且PINN方法在预测低频SH波在峡谷处地形效应时更为准确。

图 1 经典GA入渗模型的含水率分布

Figure 1. Distribution of water content of classic Green-Ampt model

下载: 全尺寸图片幻灯片

图 2 改进的GA入渗模型的含水量分布

Figure 2. Distribution of water content of improved Green-Ampt model

下载: 全尺寸图片幻灯片

图 3 无限长边坡计算模型

Figure 3. Diagram of an infinite slope model

下载: 全尺寸图片幻灯片

图 4 不同降雨历时下边坡体积含水量和安全系数分布的比较（工况1）

Figure 4. Comparison of distribution of water content and factors of safety of slope under different rainfall durations (Scenario Ⅰ)

下载: 全尺寸图片幻灯片

图 5 不同降雨历时下边坡体积含水量分布的比较（工况2）

Figure 5. Comparison of distribution of water content of slope under different rainfall durations (Scenario Ⅱ)

下载: 全尺寸图片幻灯片

图 6 不同降雨历时下边坡体积含水量分布的比较（工况3）

Figure 6. Comparison of distribution of water content of slope under different rainfall durations (Scenario Ⅲ)

下载: 全尺寸图片幻灯片

图 7 饱和渗透系数随机场一次典型实现分布图

Figure 7. Typical realization of random filed of hydraulic conductivity

下载: 全尺寸图片幻灯片

图 8 工况4不同降雨历时下边坡体积含水量分布比较

Figure 8. Comparison of distribution of water content of slope under different rainfall durations (Scenario Ⅳ)

下载: 全尺寸图片幻灯片

图 9 不同工况下边坡体积含水量分布的比较

Figure 9. Comparison of distribution of water content of slope for different scenarios

下载: 全尺寸图片幻灯片

表 1 土体物理力学参数取值

Table 1 Values of physical parameters of soil

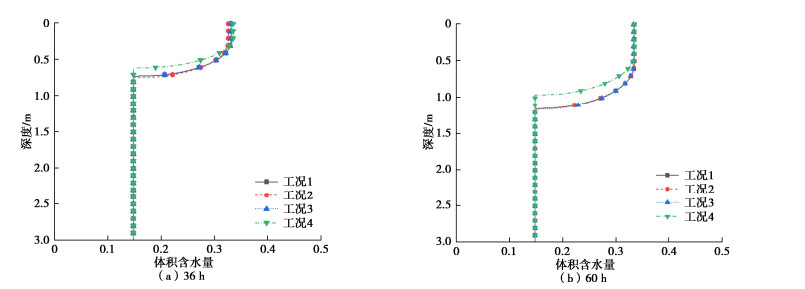
计算参数	取值	计算参数	取值
饱和渗透系数k_s/(mm·h^-1)	3	有效黏聚力 $c'$ /kPa	5
有效内摩擦角 $\varphi '$ /(°)	28	进气值ψ_b/kPa	2.752
土体干重度γ /(kN·m^-3)	16.217	湿润锋处土体概化基质吸力S_f /mm	424.3
饱和含水量 ${\theta _{\rm{s}}}$	0.335	残余含水量 ${\theta _{\rm{r}}}$	0.068
初始含水量 ${\theta _{\rm{i}}}$	0.148	土体孔隙分布特征参数λ	0.319

下载: 导出CSV

表 2 边坡安全系数和最危险滑动面深度的比较（工况1）

Table 2 Comparison of factors of safety and depths of critical slip surface of slope (Scenario Ⅰ)

类别	降雨历时/h	Richards方程数值解	修正GA模型	提出的改进GA模型
入渗区安全系数	20	2.79	2.35	2.78
	36	1.72	1.53	1.74
	60	1.19	1.10	1.22
整个边坡安全系数	20	1.36	1.36	1.36
	36	1.34	1.34	1.34
	60	1.19	1.10	1.22
最危险滑动面深度	20	3.00 m	3.00 m	3.00 m
	36	3.00 m	3.00 m	3.00 m
	60	0.99 m	1.03 m	0.99 m

下载: 导出CSV

表 3 边坡安全系数和最危险滑动面深度的比较（工况2）

Table 3 Comparison of factors of safety and depths of critical slip surface of slope (Scenario Ⅱ)

类别	降雨历时/h	Richards方程数值解	修正GA模型	提出的改进GA模型
入渗区安全系数	20	2.83	2.39	2.81
	36	1.71	1.55	1.76
	60	1.19	1.10	1.22
整个边坡安全系数	20	1.36	1.36	1.36
	36	1.34	1.34	1.34
	60	1.19	1.10	1.22
最危险滑动面深度	20	3.00 m	3.00 m	3.00 m
	36	3.00 m	3.00 m	3.00 m
	60	0.98 m	1.03 m	0.99 m

下载: 导出CSV

表 4 边坡安全系数和最危险滑动面深度的比较（工况3）

Table 4 Comparison of factors of safety and depths of critical slip surface of slope (Scenario Ⅲ)

类别	降雨历时/h	Richards方程数值解	修正GA模型	提出的改进GA模型
入渗区安全系数	20	2.79	2.35	2.78
	36	1.72	1.53	1.74
	60	1.19	1.10	1.22
整个边坡安全系数	20	1.36	1.36	1.36
	36	1.34	1.34	1.34
	60	1.19	1.10	1.22
最危险滑动面深度	20	3.00 m	3.00 m	3.00 m
	36	3.00 m	3.00 m	3.00 m
	60	1.01 m	1.04 m	1.00 m

下载: 导出CSV

表 5 边坡安全系数和最危险滑动面深度的比较（工况4）

Table 5 Comparison of factors of safety and depths of critical slip surface of slope (Scenario Ⅳ)

类别	降雨历时/ h	Richards方程数值解	修正GA模型	提出的改进GA模型
入渗区安全系数	8	6.58	5.62	6.43
	36	1.95	1.72	1.98
	60	1.40	1.24	1.39
整个边坡安全系数	8	1.37	1.37	1.37
	36	1.35	1.35	1.35
	60	1.33	1.24	1.33
最危险滑动面深度	20	3.00 m	3.00 m	3.00 m
	36	3.00 m	3.00 m	3.00 m
	60 h	3.00 m	0.85 m	3.00 m

下载: 导出CSV

参考文献(27)

[1]	FROUDE M J, PETLEY D N. Global fatal landslide occurrence from 2004 to 2016[J]. Natural Hazards and Earth System Sciences, 2018, 18(8): 2161-2181. doi: 10.5194/nhess-18-2161-2018
[2]	雷志栋, 杨诗秀, 谢森传. 土壤水动力学[M]. 北京: 清华大学出版社, 1988. LEI Zhidong, YANG Shixiu, XIE Senchuan. Soil Water Dynamics[M]. Beijing: Tsinghua University Press, 1988. (in Chinese)
[3]	CHEN L, YOUNG M H. Green‐Ampt infiltration model for sloping surfaces[J]. Water Resources Research, 2006, 42(7): W07420.
[4]	张杰, 韩同春, 豆红强, 等. 探讨考虑气阻作用下分层假定的雨水入渗计算分析模型[J]. 岩土工程学报, 2013, 35(12): 2219-2225. http://www.cgejournal.com/cn/article/id/15599 ZHANG Jie, HAN Tongchun, DOU Hongqiang, et al. Analysis model for rainwater infiltration considering gas resistance under stratified assumption[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(12): 2219-2225. (in Chinese) http://www.cgejournal.com/cn/article/id/15599
[5]	ZHANG J, HUANG H W, ZHANG L M, et al. Probabilistic prediction of rainfall-induced slope failure using a mechanics-based model[J]. Engineering Geology, 2014, 168: 129-140. doi: 10.1016/j.enggeo.2013.11.005
[6]	DOU H Q, HAN T C, GONG X N, et al. Probabilistic slope stability analysis considering the variability of hydraulic conductivity under rainfall infiltration-redistribution conditions[J]. Engineering Geology, 2014, 183: 1-13. doi: 10.1016/j.enggeo.2014.09.005
[7]	潘永亮, 简文星, 李林均, 等. 基于改进Green-Ampt模型的花岗岩残积土边坡降雨入渗规律研究[J]. 岩土力学, 2020, 41(8): 2685-2692. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202008020.htm PAN Yongliang, JIAN Wenxing, LI Linjun, et al. A study on the rainfall infiltration of granite residual soil slope with an improved Green-Ampt model[J]. Rock and Soil Mechanics, 2020, 41(8): 2685-2692. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202008020.htm
[8]	蒋水华, 刘贤, 黄发明, 等. 考虑多参数空间变异性的降雨入渗边坡失稳机理及可靠度分析[J]. 岩土工程学报, 2020, 42(5): 900-907. doi: 10.11779/CJGE202005012 JIANG Shuihua, LIU Xian, HUANG Faming, et al. Failure mechanism and reliability analysis of soil slopes under rainfall infiltration considering spatial variability of multiple soil parameters[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(5): 900-907. (in Chinese) doi: 10.11779/CJGE202005012
[9]	王文焰, 汪志荣, 王全九, 等. 黄土中Green-Ampt入渗模型的改进与验证[J]. 水利学报, 2003, 34(5): 30-34. doi: 10.3321/j.issn:0559-9350.2003.05.005 WANG Wenyan, WANG Zhirong, WANG Quanjiu, et al. Improvement and evaluation of the Green-Ampt model in loess soil[J]. Journal of Hydraulic Engineering, 2003, 34(5): 30-34. (in Chinese) doi: 10.3321/j.issn:0559-9350.2003.05.005
[10]	彭振阳, 黄介生, 伍靖伟, 等. 基于分层假设的Green-Ampt模型改进[J]. 水科学进展, 2012, 23(1): 59-66. https://www.cnki.com.cn/Article/CJFDTOTAL-SKXJ201201008.htm PENG Zhenyang, HUANG Jiesheng, WU Jingwei, et al. Modification of Green-Ampt model based on the stratification hypothesis[J]. Advances in Water Science, 2012, 23(1): 59-66. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SKXJ201201008.htm
[11]	张杰, 韩同春, 豆红强, 等. 基于分层假定入渗模型的边坡安全性分析[J]. 中南大学学报(自然科学版), 2014, 45(9): 3211-3218. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201409037.htm ZHANG Jie, HAN Tongchun, DOU Hongqiang, et al. Analysis slope safety based on infiltration model based on stratified assumption[J]. Journal of Central South University (Science and Technology), 2014, 45(9): 3211-3218. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201409037.htm
[12]	胡海军, 李博鹏, 田堪良, 等. 积水和降雨下非饱和重塑黄土水分入渗模拟[J]. 同济大学学报(自然科学版), 2019, 47(11): 1565-1573. doi: 10.11908/j.issn.0253-374x.2019.11.005 HU Haijun, LI Bopeng, TIAN Kanliang, et al. Simulation of water movement in unsaturated remolded loess under ponding infiltration and rainfall infiltration[J]. Journal of Tongji University (Natural Science), 2019, 47(11): 1565-1573. (in Chinese) doi: 10.11908/j.issn.0253-374x.2019.11.005
[13]	YAO W M, LI C D, ZHAN H B, et al. Time-dependent slope stability during intense rainfall with stratified soil water content[J]. Bulletin of Engineering Geology and the Environment, 2019, 78(7): 4805-4819. doi: 10.1007/s10064-018-01437-3
[14]	温馨, 胡志平, 张勋, 等. 基于Green-Ampt模型的饱和-非饱和黄土入渗改进模型及其参数研究[J]. 岩土力学, 2020, 41(6): 1991-2000. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202006023.htm WEN Xin, HU Zhiping, ZHANG Xun, et al. Modified infiltration model for saturated-unsaturated loess based on Green-Ampt model and its parametric study[J]. Rock and Soil Mechanics, 2020, 41(6): 1991-2000. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202006023.htm
[15]	CHO S E. Probabilistic stability analysis of rainfall-induced landslides considering spatial variability of permeability[J]. Engineering Geology, 2014, 171: 11-20. doi: 10.1016/j.enggeo.2013.12.015
[16]	JIANG S H, LI D Q, ZHANG L M, et al. Slope reliability analysis considering spatially variable shear strength parameters using a non-intrusive stochastic finite element method[J]. Engineering Geology, 2014, 168: 120-128. doi: 10.1016/j.enggeo.2013.11.006
[17]	GREEN W H, AMPT G A. Studies on soil physics: 1, flow of air and water through soils[J]. Journal of Agricultural Science, 1911, 4(1): 1-24. doi: 10.1017/S0021859600001441
[18]	MOORE I D, EIGEL J D. Infiltration into two-layered soil profiles[J]. Transactions of the ASAE, 1981, 24(6): 1496-1503. doi: 10.13031/2013.34480
[19]	王文焰, 王全九, 张建丰, 等. 甘肃秦王川地区土壤水分运动参数及相关性[J]. 水土保持学报, 2002, 16(3): 110-113. doi: 10.3321/j.issn:1009-2242.2002.03.029 WANG Wenyan, WANG Quanjiu, ZHANG Jianfeng, et al. Soil hydraulic properties and correlation in qingwangchuan area of Gansu Province[J]. Journal of Soil Water Conservation, 2002, 16(3): 110-113. (in Chinese) doi: 10.3321/j.issn:1009-2242.2002.03.029
[20]	MA Y, FENG S Y, SU D Y, et al. Modeling water infiltration in a large layered soil column with a modified Green-Ampt model and HYDRUS-1D[J]. Computers and Electronics in Agriculture, 2010, 71: 40-47. doi: 10.1016/j.compag.2009.07.006
[21]	DAMODHARA RAO M, RAGHUWANSHI N S, SINGH R. Development of a physically based 1D-infiltration model for irrigated soils[J]. Agricultural Water Management, 2006, 85(1/2): 165-174.
[22]	CAI J S, YEH T C J, YAN E C, et al. Uncertainty of rainfall-induced landslides considering spatial variability of parameters[J]. Computers and Geotechnics, 2017, 87: 149-162. doi: 10.1016/j.compgeo.2017.02.009
[23]	LALOY E, ROGIERS B, VRUGT J, et al. Efficient posterior exploration of a high-dimensional groundwater model from two-stage Markov chain Monte Carlo simulation and polynomial chaos expansion[J]. Water Resources Research, 2013, 49: 2664-2682. doi: 10.1002/wrcr.20226
[24]	豆红强, 韩同春, 龚晓南, 等. 降雨条件下考虑饱和渗透系数变异性的边坡可靠度分析[J]. 岩土力学, 2016, 37(4): 1144-1152. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201604030.htm DOU Hongqiang, HAN Tongchun, GONG Xiaonan, et al. Reliability analysis of slope stability considering variability of soil saturated hydraulic conductivity under rainfall infiltration[J]. Rock and Soil Mechanics, 2016, 37(4): 1144-1152. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201604030.htm
[25]	BROOKS R H, COREY A T. Hydraulic Properties of Porous Media[M]. Fort Collins: Colorado State University, 1964.
[26]	YUAN J, PAPAIOANNOU I, STRAUB D. Probabilistic failure analysis of infinite slopes under random rainfall processes and spatially variable soil[J]. Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 2019, 13(1): 20-33. doi: 10.1080/17499518.2018.1489059
[27]	SIMUNEK J, VAN GENUCHTEN M T, SEJNA M. The Hydrus-1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media, Version 4.16, HYDRUS Software Series 3[M]. Riverside: University of California Riverside, 2013.