基于有效应力原理的泡沫改良粗粒土不排水残余剪切强度计算模型

钟嘉政; 王树英; 冯志耀; 朱汉标

doi:10.11779/CJGE20230180

基于有效应力原理的泡沫改良粗粒土不排水残余剪切强度计算模型 English Version

钟嘉政^{1, 2,},
王树英^{1, 2, 3, ,},
冯志耀^{1, 2},
朱汉标^{1, 2}

1.
中南大学土木工程学院, 湖南长沙 410075
2.
中南大学隧地工程研究中心, 湖南长沙 410075
3.
中南大学轨道交通工程结构防灾减灾湖南省重点实验室, 湖南长沙 410075

基金项目:

国家自然科学基金项目 52022112

湖南省研究生科研创新项目 2020zzts152

详细信息

作者简介:
钟嘉政(1996—)，男，博士研究生，主要从事隧道及地下工程方面的研究工作。E-mail：jiazhengzhong@csu.edu.cn

通讯作者:
王树英, E-mail: sywang@csu.edu.cn

中图分类号: U455.43
计量
- 文章访问数: 391
- HTML全文浏览量: 49
- PDF下载量: 119
出版历程
- 收稿日期: 2023-02-28
- 网络出版日期: 2023-07-25
- 刊出日期: 2023-11-30

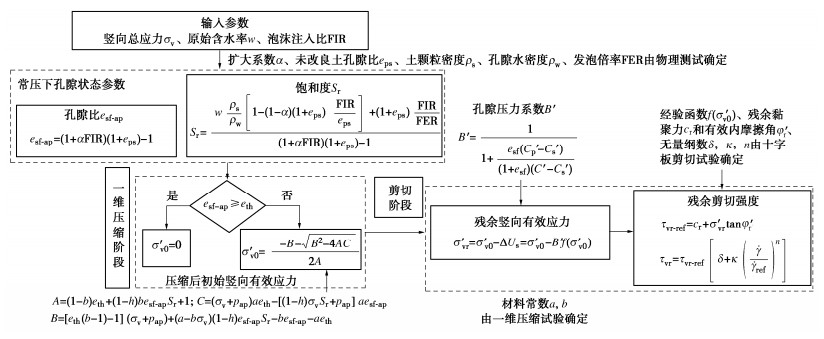
Analytical model for undrained residual shear strength of foam-conditioned coarse-grained soils in large deformation based on effective stress principle

ZHONG Jiazheng^{1, 2,},
WANG Shuying^{1, 2, 3, ,},
FENG Zhiyao^{1, 2},
ZHU Hanbiao^{1, 2}

1.
School of Civil Engineering, Central South University, Changsha 410075, China
2.
Tunnel and Underground Engineering Research Center of Central South University, Changsha 410075, China
3.
Hunan Provincial Key Laboratory for Disaster Prevention and Mitigation of Rail Transit Engineering Structures, Central South University, Changsha 410075, China

摘要

摘要: 泡沫常用于土压平衡盾构渣土改良，流动性良好的泡沫改良粗粒渣土有利于盾构进排土顺畅和土舱压力传递，进而避免地层过大变形和失稳。从泡沫改良粗粒土不排水压缩和剪切机理出发，推导了不排水条件下带压泡沫改良粗粒土流动大变形后的残余剪切强度统一理论模型。首先基于理想气体定律和土的有效应力-应变双曲线方程求解不排水一维压缩时的有效应力，然后推导不排水剪切引起的超孔隙压力和残余状态下剪切强度与有效应力的关系式，再构建剪切速率相关的残余剪切强度计算模型。采用不排水加压十字板剪切试验验证了计算模型的准确性，试验值与理论值的平均误差约10%，表明该计算模型可用于确定泡沫改良粗粒土连续流动时的残余剪切强度。最后开展了影响因素分析，竖向总应力增大能提高残余剪切强度，而泡沫注入比增加能降低残余剪切强度；残余状态下流动大变形泡沫改良粗粒土的屈服应力和塑性黏度均与竖向总应力呈正相关，而与泡沫注入比呈负相关。
- 泡沫改良粗粒土 /
- 剪切大变形连续流动 /
- 有效应力 /
- 率相关残余剪切强度 /
- 不排水加压十字板剪切试验
Abstract: Foam is usually used in soil conditioning of earth pressure balance shield tunnelling. The smooth muck discharge and chamber pressure transmission require foam-conditioned coarse-grained soils with suitable flowability to avoid face instability and excessive ground deformation. Inspired by undrained compression and shear mechanism, an analytical model is proposed for the undrained residual shear strength of foam-conditioned coarse-grained soils after large deformation under pressure. Firstly, the effective stress in one-dimensional undrained compression is obtained based on the ideal gas law and the hyperbolic equation for stress and strain. Then, the shear-induced excess pore pressure is calculated, and the relation between the residual shear strength and the vertical effective stress is derived. Furthermore, the analytical model for the residual shear strength dependent on shear rate is obtained. A series of undrained pressurized vane shear tests are performed to verify the analytical model. The average error between the analytical and experimental results is about 10%. It is proved that the analytical model is reliable in determining the residual shear strength under chamber pressure. Finally, the discussion of influencing factors manifests that the residual strength is raised by increasing the vertical total stress but reduced by increasing the foam injection ratio (FIR). It also revealed that the yield stress and plastic viscosity in the residual state are positively correlated with the vertical total stress but negatively correlated with FIR.
- foam-conditioned coarse-grained soil /
- continuous flow and large deformation /
- effective stress /
- rate-dependent residual shear strength /
- undrained pressurized vane shear test

HTML全文

0. 引言

非饱和土在世界各地的工程实践中均有涉及，土体的抗剪强度随含水率或吸力的变化对岩土结构的稳定性至关重要^[1-3]。基质吸力与含水率或者饱和度之间的关系被称之为土水特征曲线（soil-water characteristic curve, SWCC）或者土体持水曲线（soil-water retention curve, SWRC）。SWRC是体现非饱和土力学本构关系特征的重要响应曲线，其对土体的非饱和抗剪强度有显著影响^[4-7]。

不同非饱和土的微细观测试分析表明^[8]，SWRC受到孔径分布特征的影响，大致可区分为单峰SWRC和双峰SWRC。Cai等^[9]针对桂林红黏土联合轴平移技术、滤纸法和盐溶液蒸汽平衡法进行了宽广吸力范围内的持水特性试验，结果表明压实样呈现双孔隙结构，并具有双峰SWRC，而预固结试样呈现单一孔隙和单峰SWRC。Satyanaga等^[10]针对砂土和高岭土的混合物进行了一系列水力特性的测定试验，指出具有双孔隙结构的土体不一定呈现双峰SWRC，但双峰SWRC出现的必要条件是具备双孔隙结构。已有数据表明间断级配土体、粗砂-砾石混合物以及压实黏土等易呈现双峰SWRC。

过往的大量试验研究了抗剪强度随吸力的演化规律，其中土样普遍为具有单一孔径结构或单峰SWRC的土体。如张俊然等^[11]利用轴平移技术和盐溶液蒸汽平衡法对吸力范围在38 MPa内的南阳膨胀土进行了一系列常吸力三轴剪切试验，分析了峰值抗剪强度的演化规律并提出了预测模型；张季如等^[12]对不同应力路径下钙质砂抗剪强度进行了试验研究与机理分析；徐筱等^[13]对高吸力下黏性土的抗剪强度进行了三轴试验研究；Gao等^[14-15]研究了不同制样方法和不同初始干密度对非饱和土应力应变关系的影响。试验结果和理论分析表明吸力和强度之间往往呈现非线性关系^{[4, 16-17]}。对于粗粒土，利用SWRC将吸力乘以饱和度，孔隙应力扩为宏观应力时，强度包络线呈现直线特征，这是因为此时的宏观应力是有效应力的一部分。对于细粒土，毛细部分对剪切强度起主导作用^{[6-7, 16, 18-19]}，故而吸力乘以毛细饱和度才是骨架应力，或者有效应力的一部分。已有大量研究表明，结合上述有效应力，极限剪应力的临界状态线可以由唯一的强度包络线表征，即存在一组适用于饱和与非饱和状态的相同强度参数^{[5-7, 20]}。以上结论仅在具有单峰SWRC的土体中得到过验证。

近期对于具有双孔隙结构，特别是具有双峰SWRC土体力学特性的相关试验在陆续开展。Zhao等^[21]对间断级配粗粒土进行了低吸力段的三轴试验，并将其应力应变行为分为4个阶段；Ng等^[22]对具有双峰SWRC的压实黄土试样进行了一系列控制吸力的直剪试验。但上述土体的吸力-强度特性和具有单峰SWRC的土体能否统一还未有相关研究。

本文研究对象为同时具有双孔隙结构及双峰SWRC的土体（不仅限于压实膨胀土）。联合轴平移技术和盐溶液蒸汽平衡法在宽广吸力范围内对内乡膨胀土压实样进行了一系列的非饱和三轴剪切试验，探讨不同吸力对土体应力-应变行为及抗剪强度的影响特性。采用双峰SWRC模型区别毛细和吸附的影响效应，进而在毛细吸应力空间（毛细饱和度乘以吸力）分析土体的非饱和峰值抗剪强度，并利用双孔隙结构土体水力特性试验成果对峰值强度分析方法作评价与验证。

1. 试验概述

1.1 试验材料

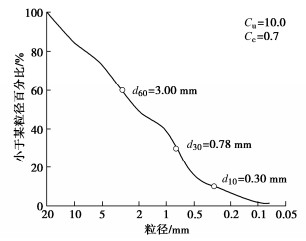
本试验选用膨胀土取自河南内乡县张岗村以西200 m处，是内乡220 KV变电站拟选站址，取土深度为地下5 m范围，天然干密度为1.69 g/cm³，天然含水率为22.74%。经过X射线衍射分析，内乡膨胀土的主要矿物成分为石英、黏土矿物，其次为斜长石和微斜长石。砂粒的含量为9.97%，粉粒含量为56.77%，黏粒含量为33.26%。粒径大于0.075 mm的颗粒质量为总质量的9.97%，小于50%，按照土的工程分类标准可判断该土样为细粒土，其它物理特性指标可见表 1。内乡膨胀土颗粒分布曲线如图 1所示，根据颗粒分布曲线及塑性指数，可知其为低液限黏土（CL）。

表 1 内乡膨胀土基本物理指标

Table 1. Index properties of Neixiang expansive soil

颗粒相对质量密度	液限/ %	塑限/ %	最大干密度/ (g·cm^-3)	最优含水率/%	自由膨胀率/%
2.74	45.1	25.3	1.70	21.2	59

下载: 导出CSV

| 显示表格

图 1 内乡膨胀土的颗粒分布曲线

Figure 1. Grain-size distribution curve of Neixiang expansive soil

下载: 全尺寸图片幻灯片

1.2 孔径分布与持水特性

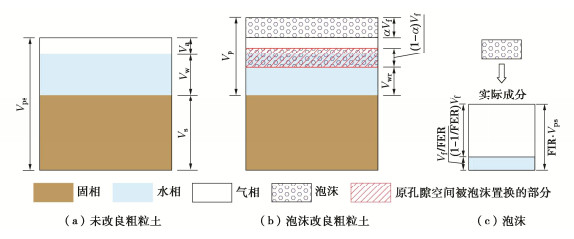
较早开展的压汞试验表明^[23]，内乡膨胀土的重塑预固结试样具有单峰孔径分布；与之不同的是，重塑压实样的微观结构为双孔隙结构，由集聚体间的大孔隙和集聚体内的小孔隙组成（如图 2（a））。联合轴平移技术（0~200 kPa）、滤纸法（200~8 MPa）和饱和盐溶液蒸汽平衡法（3.29~198.14 MPa）进行了宽广吸力范围的持水特性试验^[23]。结果显示，预固结样的持水曲线呈现单峰形态。压实样具有双峰持水曲线，即由两段斜率陡峭的曲线组成（双“S”分布），呈对数坐标下的两段半正态分布形式，中间有明显过渡区或者平台段。同时曲线上包括两个进气值AEV₁和AEV₂（分别对应空气进入到集聚体间和集聚体内孔隙时的孔隙气压力）以及两个残余饱和度R₁和R₂（如图 2（b））。本文进行三轴试验的试样为内乡膨胀土压实样，具有双孔隙结构和双峰持水曲线。

图 2 重塑压实样和重塑预固结样的孔径分布密度和持水曲线

Figure 2. PSDs and SWRCs of compacted and reconstituted specimens

下载: 全尺寸图片幻灯片

1.3 非饱和三轴试验方法

将自然风干土通过碎土机打碎，过2 mm筛，配制目标含水率为24%的湿土，放入密闭容器中静置两周待水分均匀后取用。试验采用击实法在三开模中制样，分为6层击实以保证均匀性，每一层通过175 g的落锤从300 mm的高度落下。试样直径38 mm，高76 mm，并控制其初始干密度为1.40 g/cm³。

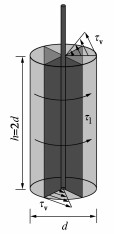
三轴试验采用HKUST双压力室的GDS UNSAT非饱和土三轴仪进行（如图 3），其压力室的底座嵌着进气值为500 kPa的陶土板。差压传感器（DPT）和HKUST双压力室（double-cell）系统量测非饱和土试样的体积变化。试验前进行标定，以消除非饱和土三轴试验系统中体变量测的系统误差。

图 3 GDS双压力室非饱和土三轴试验仪

Figure 3. GDS double-cell triaxial apparatus for testing unsaturated soils with HKUST

下载: 全尺寸图片幻灯片

为了实现全吸力范围抗剪强度的测定，联合采用轴平移技术法（0~500 kPa）和饱和盐溶液蒸汽平衡法（3.29~198.14 MPa）进行宽广范围吸力的控制。低吸力试验中，利用饱和陶土板的过水不过气的功能控制低吸力，同时轴平移技术避免孔隙水气化。应力路径如所示，从初始状态开始，首先施加 ${\sigma _{{\text{3n}}}}$ =20 kPa， $s$ =100，200 kPa进行吸力平衡（AB_i），吸力平衡之后施加 ${\sigma _{{\text{3n}}}}$ =200 kPa进行固结平衡（B_iC_i），变形稳定之后在恒定围压和吸力值下进行控制应变速率的三轴排水剪切（C_iD_i）。

图 4 宽广吸力范围内三轴试验应力路径示意图

Figure 4. Stress paths for triaxial tests over a wide suction range

下载: 全尺寸图片幻灯片

高吸力试验中，利用饱和盐溶液来控制密封干燥皿内空气的相对湿度^{[13, 24-26]}，从而控制土体的总吸力，不同的饱和盐溶液对应的吸力值见表 2^{[9, 25-26]}，在不考虑渗透吸力的情况下，总吸力近似等于基质吸力。依据每小时体积变化量小于0.01 cm³的平衡标准^{[11, 13-14]}，该过程耗时3~4个月。吸力平衡后把试样装在非饱和土三轴试验仪上，进行常含水率下的固结平衡和三轴剪切，此时可认为是等吸力试验^{[11, 13, 26]}。试样顶部通过孔隙气压控制管路和大气连通，试验中保证孔隙气压为0。采用不透水塑料薄膜将陶土板和试样隔开，保证含水率不变^{[11, 13]}。应力路径如图 4所示（仅展示控制吸力为3.29，21.82 MPa的路径），从初始状态开始，首先利用饱和盐溶液进行高吸力平衡（AX_i），吸力平衡之后施加围压 ${\sigma _{{\text{3n}}}}$ =200 kPa进行固结平衡（X_iY_i），变形稳定之后在恒定围压和常含水率下进行控制应变速率的不排水（排气）剪切（Y_i Z_i）。

表 2 饱和盐溶液及对应的吸力值

Table 2. Saturated salt solutions and corresponding suctions

饱和盐溶液	RH/%	总吸力/MPa
K₂SO₄	97.6	3.29
Na₂SO₃·7H₂O	90.8	13.10
KCl	85.1	21.82
NaCl	75.5	38.00
NaBr	59.1	71.20
K₂CO₃	43.2	113.50
CH₃COOK	23.1	198.14

下载: 导出CSV

| 显示表格

吸力平衡和固结平衡的标准根据进每2 h出水量小于0.01 cm³和每2 h体积变化量小于0.02 cm³确定。采取轴向应变控制三轴剪切加载模式。相关学者对宽广吸力范围内不同三轴剪切速率对峰值强度和体变的影响做了相关研究^{[11, 27-28]}，本试验选取轴向剪切速度约为0.00192 mm/min，保证剪切中孔隙水压完全消散。

2. 非饱和三轴试验结果

本文对重塑压实膨胀土样进行了不同吸力水平下的9组试验，显示不同常吸力下，三轴剪切过程中的应力应变关系和体变结果（压缩为正，剪胀为负）。结果表明，低吸力条件下（ $s$ =100 MPa， $s$ =200 kPa）以及中吸力条件下（ $s$ =3.29 MPa， $s$ =13.1 MPa），应力应变曲线呈现硬化现象，同时有明显的剪缩行为。随着吸力增加，剪缩体变逐渐减小。

图 5 三轴剪切过程中应力应变关系

Figure 5. Relationship between deviator stress, volumetric strain and axial strain from triaxial shear tests

下载: 全尺寸图片幻灯片

高吸力条件下（ $s$ 为21.82，38，71.2，113.5，198.14 MPa），应力应变曲线呈现峰值后软化现象，试样开始在经历了1%~3%的体积收缩变形之后开始出现明显剪胀。在高吸力状态下（ $s$ =113.5 MPa， $s$ =198.14 MPa），试样在较小应变的情况下很快达到峰值强度，随后软化至大应变时偏应力急剧降低。

随着吸力的增加，剪胀性逐渐增加（或剪缩性减弱）。应力应变曲线的峰后软化现象及体积剪胀现象可以归因于试样失水后孔隙比减小明显（特别是大孔隙收缩^[27]）或过度固结的应力历史^[11]。

中应力应变关系存在峰值，则峰值抗剪强度取偏应力最大值；若应力应变关系不存在峰值，则峰值抗剪强度取轴向应变为15%处的偏应力作为峰值抗剪强度（如）。在吸力 $s$ 小于21.82 MPa时，峰值和残余偏应力均增加，特别是在吸力 $s$ 介于200 kPa至21.82 MPa之间增幅较大。在吸力 $s$ 大于21.82 MPa时，峰值偏应力继续增加，残余偏应力开始下降。这是由于在恒定围压条件下，超过峰值剪应力的连续剪切形成的剪切带严重破坏了土体颗粒接触周围的空气-水弯液面系统，因此吸力对峰值强度的贡献往往大于残余状态。

图 6 不同吸力下内乡膨胀土峰值强度和残余强度

Figure 6. Peak and residual deviator stresses at different suctions of Neixiang expansive soil

下载: 全尺寸图片幻灯片

除了外部载荷外，吸力的增加往往会在土体颗粒的接触点上施加表面张力以及吸附作用，从而在土体颗粒之间产生额外的黏结，使土壤结构变得更加坚硬，在剪切过程中表现出脆性。以脆性指数评估土体脆性大小的方法如下^[29-30]：

${I_{\text{B}}} = \frac{{{q_{{\text{peak}}}} - {q_{\text{r}}}}}{{{q_{\text{r}}}}} 。$

(1)

式中： ${q_{{\text{peak}}}}$ 为峰值抗剪强度； ${q_{\text{r}}}$ 为残余抗剪强度。

从图 6，7可以清楚地看到试件的脆性随吸力的增加而增长，表明剪切破坏后破坏区域逐渐过渡，即在中低吸力下呈桶形或中心鼓形的延性破坏模式，在高吸力下发生应变局部化现象，并产生明显的剪切破坏面。此外，脆性增加了峰后软化的幅度，表现为图 6中峰值偏应力与残余破坏状态之间的差值增大。

图 7 不同吸力下试样剪切后状态

Figure 7. Typical failures of specimens at different suction states

下载: 全尺寸图片幻灯片

3. 峰值抗剪强度的分析与讨论

Bishop^[31]提出了经典的非饱和土有效应力公式：

${\mathit{\boldsymbol{\sigma}} '_{ij}} = {\mathit{\boldsymbol{\sigma}} _{ij}} - {u_{\rm{a}}}{\mathit{\boldsymbol{\delta}} _{ij}} + \chi s{\mathit{\boldsymbol{\delta}} _{ij}} \text{，}$

(2)

式中： ${\mathit{\boldsymbol{\sigma}} _{ij}}$ 为总应力张量； ${u_{\rm{a}}}$ 为孔隙气压力； $\chi$ 为有效应力参数， $s$ 为基质吸力； ${\mathit{\boldsymbol{\delta}} _{ij}}$ 为Kronecker符号。

式（2）的有效应力参数 $\chi$ 最初采用饱和度 $S_{\text{r}}^{}$ 加以量度，这种做法由于高估了吸力对骨架应力的作用，忽视了吸附吸力的存在^{[5-7, 16, 18-20]}，导致预测的峰值抗剪强度往往大于实际强度，特别是对于细粒土以及低饱和度的情况。为此，近来一些研究发现，可将总饱和度 $S_{\text{r}}^{}$ 的量度替换成毛细饱和度 $S_{\text{r}}^{{\text{cap}}}$ ^{[5-7, 20, 32-33]}以区分毛细和吸附不同作用的影响：

${\mathit{\boldsymbol{\sigma}} '_{ij}} = {\mathit{\boldsymbol{\sigma}} _{ij}} - {u_{\rm{a}}}{\mathit{\boldsymbol{\delta}} _{ij}} + S_{\text{r}}^{{\text{cap}}}s{\mathit{\boldsymbol{\delta}} _{ij}} 。$

(3)

研究表明，结合上述有效应力，极限剪应力的临界峰值强度状态线可以由唯一的强度包络线表征^{[5-7, 20]}（如图 8（a），即存在一组适用于饱和与非饱和状态的相同强度参数。唯一的强度包络线不仅在低吸力适用，也在高吸力范围内得到了验证，同时对于粗粒土和细粒土显示具有线性特征^[34]。

图 8 Madrid黏性砂土和内乡膨胀土峰值剪切强度特征

Figure 8. Peak shear strength behaviors for Madrid clayey sand and Neixiang expansive soil

下载: 全尺寸图片幻灯片

需要注意的是，以上研究仅针对大量具有单峰持水曲线的土体，而没有涉及具有双峰持水曲线的土体。这里利用笔者^{[5, 20, 23, 32]}提出的可以区分毛细和吸附饱和度的双峰持水曲线模型来计算毛细饱和度：

$S_{\text{r}}^{{\text{cap}}} = (1 - \alpha )A + (\alpha - \frac{{\alpha C(1 - B)}}{{1 - C(B - 1)}})B \text{，}$

(4)

$A = \frac{1}{2}{{\rm{erfc}}} \left( {\frac{{\ln (s/{s_{{\text{m1}}}})}}{{\sqrt 2 {\zeta _1}}}} \right) \text{，}$

(5)

$B = \frac{1}{2}{\text{erfc}}\left( {\frac{{\ln (s/{s_{{\text{m2}}}})}}{{\sqrt 2 {\zeta _2}}}} \right) \text{，}$

(6)

$C = \beta \left( {1 - \frac{{\ln s}}{{\ln {s_{\text{d}}}}}} \right) 。$

(7)

式中： ${s_{{\text{m1}}}}$ 为集聚体间中值孔径对应的基质吸力（kPa）， ${s_{{\text{m2}}}}$ 为集聚体内中值孔径对应的基质吸力（kPa）； ${\zeta _1}$ 为表征集聚体间孔径分布宽度的无量纲参数， ${\zeta _2}$ 为表征集聚体内孔径分布宽度的无量纲参数， ${\text{erf}}({\text{ }})$ 为误差函数； $\alpha = {\theta _{{\text{s2}}}}/{\theta _{{\text{s1}}}}$ ， ${\theta _{{\text{s1}}}}$ 为第一进气值对应的含水率，即土材料完全饱和时的体积含水率， ${\theta _{{\text{s2}}}}$ 为第二进气值对应的含水率，即集聚体内的饱和含水率； $\beta$ 为表征吸附作用大小的材料参数； ${s_{\text{d}}}$ 为干燥情况下的最大吸力，取 ${s_{\text{d}}} = {10^6}$ （kPa）。

参数 $\alpha$ 代表两种大小孔隙结构相对大小，技术上可以根据压汞试验进行标定。参数 $\beta$ 控制了吸附水在最大吸力处的变化速率，可以通过检测吸附水含量的变化确定，技术上可以通过核磁共振技术实现^[35]。参数 ${s_{\text{m}}}$ （ ${s_{{\text{m1}}}}$ ， ${s_{{\text{m2}}}}$ ）代表中等孔径对应的吸力值， $\zeta$ （ ${\zeta _1}$ ， ${\zeta _2}$ ）是对数坐标下孔径的标准差，这些参数可以通过微观试验，例如压汞试验进行测定^[36]。以上参数的标定方法都是基于相应的微观试验或者这些参数直接控制的测试结果来确定。然而，在未进行微观试验的状况下，模型参数可以通过对持水数据的拟合获得，即基于非线性拟合（详细的讨论见文献[37]）的方法进行，相同的参数标定流程见笔者对双峰持水曲线的建模过程^[23]。

表明，利用相同的表征方法利用毛细饱和度将吸力从孔隙应力扩为宏观应力时（参数见，其中 $\alpha$ ， $\beta$ ， ${\zeta _1}$ ， ${\zeta _2}$ 为无量纲参数），强度包络线由两条直线段组成，这一强度特征的微细观机理可解释为：由于具有双峰持水曲线的土体常存在集聚体结构，集聚体间大孔隙以毛细水占主导，集聚体内小孔隙赋存吸附水。对于毛细水，来源于空气-水弯液面提供的表面张力，能够在骨架间进行应力传递，完全贡献了第一段直线的强度；吸附作用主要源于3种不同的物理化学机制^[38-40]，即离子水化、内表面水化及颗粒表面水化，离子水化来源于原子尺度的电子力作用，内表面水化和颗粒表面水化受到范德华力影响。此种物理化学作用虽不能形成骨架应力，往往会产生额外的胶结作用，从而增加土体的第二段抗剪强度^[27]。

表 3 双峰持水曲线模型参数

Table 3. Parameters of bimodal water-retention curve

土体	s_m1/ kPa	s_m2/ kPa	${\zeta _1}$	${\zeta _2}$	$\beta$	$\alpha$
膨胀土	41.21	14500	1.05	0.74	0.95	0.70
黄土^{[17, 41]}	9.69	2097	1.00	1.24	0.20	0.59
M3^[10]	9.35	121.9	0.24	0.86	0.05	0.85
M5^[10]	14.22	135	0.19	0.77	0.05	0.87
M6^[10]	11.74	131.7	0.10	0.91	0.30	0.85
M8^[10]	0.53	28.12	0.23	1.34	0.38	0.84
红黏土^[42-43]	68.74	9430	1.22	0.74	0.48	0.79

下载: 导出CSV

| 显示表格

Ng等^{[22, 27]}对具有双峰SWRC的压实黄土试验进行了宽广范围的直剪试验；Satyanaga等^[10]对砂土和高岭土不同配比的混合物M3（70%砂土、30%高岭土）、M5（50%砂土、50%高岭土）、M6（40%砂土、60%高岭土）以及M8（20%砂土、80%高岭土）利用轴平移技术进行了三轴剪切试验；孙德安等^[42-43]对桂林红黏土进行了一系列土水特性试验和控制吸力的直剪试验，测试土体的基本物理指标见表 4，双峰SWRC的模型参数见表 3。基于土体持水特性和剪切试验的试验结果，在毛细吸应力空间重新整理峰值抗剪强度值（如图 9），结果显示强度随毛细吸应力的变化均由双段直线组成，第二段直线位于第一段直线的上方。这种现象的产生机理可同样归因于：对于具有双孔隙结构的土体，其持水曲线呈现双峰形态，高吸力下的峰值抗剪强度不仅由毛细作用形成的空气-水弯液面提供，还受到吸附作用引起的胶结作用增强。

表 4 具有双峰持水曲线土体的基本物理指标

Table 4. Physical properties of soils with bimodal SWRC

土体	液限/ %	塑限/ %	最大干密度/(g·cm^-3)	c/kPa	$\varphi$ /(°)
黄土^{[17, 41]}	36.0	19.0	1.30	0	27.7
M3^[10]	36.8	21.6	1.85	5.00	34.0
M5^[10]	46.7	27.4	1.75	9.00	26.0
M6^[10]	48.9	28.2	1.59	12.00	26.0
M8^[10]	57.8	33.6	1.45	16.00	25.0
红黏土^{[42, 43]}	77.8	42.1	1.52	1.57	32.1

下载: 导出CSV

| 显示表格

图 9 具有双孔隙结构和双峰SWRC土体的非饱和峰值强度特性（毛细吸应力-剪应力/偏应力空间）

Figure 9. Unsaturated shear strengths of soils with dual-porosity structure and bimodal SWRC

下载: 全尺寸图片幻灯片

试验数据和理论研究表明，对于具有双孔隙结构的土体，在集聚体间（低吸力范围），用毛细饱和度乘以吸力将吸力从孔隙应力扩为宏观应力时，能更为合理地量度吸力对有效应力的贡献；在集聚体内（高吸力范围），此时除毛细吸应力贡献峰值抗剪强度之后，还受到结构重组和胶结作用的影响（铁和锰氧化物的胶结^[27]）。后续研究需要考虑双孔隙结构以及胶结作用对抗剪强度的影响特性。

4. 结论

本文针对具有双孔隙结构及双峰SWRC的非饱和重塑膨胀土的抗剪强度开展了试验及理论研究。联合轴平移技术和盐溶液蒸汽平衡法对宽广吸力范围内膨胀土压实样进行了一系列的非饱和三轴剪切试验。同时对峰值抗剪强度在毛细吸应力空间（毛细饱和度乘以吸力与偏应力）进行了分析讨论。得到以下4点结论。

（1）中低吸力下的应力应变关系为应变硬化，伴随着剪缩行为，试样呈现中心鼓形的延性破坏模式；高吸力下为应变软化，伴随着剪胀现象，试样有明显的破坏剪切带。

（2）脆性随吸力的增加而增长，表现为峰后软化的幅度增大，即峰值抗剪强度与残余抗剪强度之间的差值增大。

（3）毛细吸应力能更为合理地揭示吸力对剪切强度的贡献，在毛细吸应力-强度空间，双孔隙结构非饱和土（不仅限于压实膨胀土）均呈现双段线性的强度特征。

（4）低吸力范围内，双孔隙结构非饱和土的抗剪强度由饱和强度与毛细吸应力贡献；高吸力范围内，抗剪强度应由饱和强度、毛细吸应力与胶结作用提供。

图 1 十字板剪切失效面示意

Figure 1. Failure interface of vane shear tests

下载: 全尺寸图片幻灯片

图 2 改良前后粗粒土多相示意图

Figure 2. Multiphase schematic diagram of coarse-grained soils with and without foam conditioning

下载: 全尺寸图片幻灯片

图 3 泡沫改良粗粒土残余剪切强度计算流程图

Figure 3. Calculation process of residual shear strength of foam-conditioned coarse-grained soils

下载: 全尺寸图片幻灯片

图 4 试验粗粒土级配曲线

Figure 4. Grain-size distribution curve of testing soils

下载: 全尺寸图片幻灯片

图 5 加压式十字板剪切仪

Figure 5. Pressurized vane shear apparatus

下载: 全尺寸图片幻灯片

图 6 一维压缩后初始孔隙比随竖向有效应力的变化

Figure 6. Variation of initial void ratio against vertical effective stress under compression

下载: 全尺寸图片幻灯片

图 7 剪切引起超孔隙压力随初始有效应力的变化

Figure 7. Variation of shear-induced excess pore pressure against initial effective stress

下载: 全尺寸图片幻灯片

图 8 残余状态十字板扭矩与竖向有效应力关系

Figure 8. Variation of vane torque against vertical effective stress

下载: 全尺寸图片幻灯片

图 9 无量纲十字板残余剪切强度随剪切速率的变化

Figure 9. Variation of residual strength against shear strain rate

下载: 全尺寸图片幻灯片

图 10 FIR=30%改良土残余剪切强度试验值与理论值对比

Figure 10. Comparison between analytical and experimental values of residual strength of conditioned soils with FIR=30%

下载: 全尺寸图片幻灯片

图 11 残余剪切强度随竖向总应力和有效应力的变化

Figure 11. Variation of analytical residual strength against vertical total stress and effective stress

下载: 全尺寸图片幻灯片

图 12 泡沫改良粗粒土残余状态下大变形屈服应力和塑性黏度随竖向总应力的变化

Figure 12. Variation of analytical yield stress and plastic viscosity of conditioned soils in large deformation against vertical total stress

下载: 全尺寸图片幻灯片

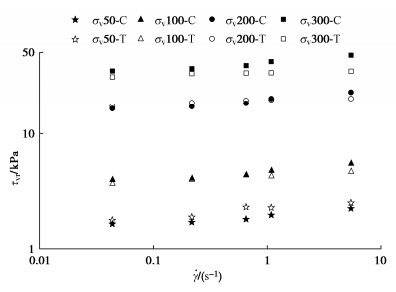
表 1 泡沫改良粗粒土初始状态参数和试验工况

Table 1 Initial parameters and test conditions of specimens

FIR/% α e_sf-ap S_r/% σ_v/kPa n/(r·min^-1)

20 0.186 0.827 35.7 50, 100, 200, 300 1/30, 1/5, 1, 3, 5, 25

30 0.366 0.955 32.4

40 0.523 1.130 28.7

下载: 导出CSV

参考文献(19)

[1]	张淑朝, 贺少辉, 朱自鹏, 等. 兰州富水砂卵石层土压平衡盾构渣土改良研究[J]. 岩土力学, 2017, 38(增刊2): 279-286. doi: 10.16285/j.rsm.2017.S2.039 ZHANG Shuchao, HE Shaohui, ZHU Zipeng, et al. Research on soil conditioning for earth pressure balance shield tunneling in Lanzhou sandy pebble strata with rich water[J]. Rock and Soil Mechanics, 2017, 38(S2): 279-286. (in Chinese) doi: 10.16285/j.rsm.2017.S2.039
[2]	王树英, 刘朋飞, 胡钦鑫, 等. 盾构隧道渣土改良理论与技术研究综述[J]. 中国公路学报, 2020, 33(5): 8-34. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202005002.htm WANG Shuying, LIU Pengfei, HU Qinxin, et al. State-of-the-art on theories and technologies of soil conditioning for shield tunneling[J]. China Journal of Highway and Transport, 2020, 33(5): 8-34. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202005002.htm
[3]	BEZUIJEN A. Foam used during EPB tunnelling in saturated sand, parameters determining foam consumption[C]//World Tunnel Congress 2012. Bangkok, 2012.
[4]	姜厚停, 龚秋明, 杜修力. 卵石地层土压平衡盾构施工土体改良试验研究[J]. 岩土工程学报, 2013, 35(2): 284-292. http://www.cgejournal.com/cn/article/id/14963 JIANG Houting, GONG Qiuming, DU Xiuli. Experimental study on soil conditioning in cobble layer by use of earth pressure balanced machine[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 284-292. (in Chinese) http://www.cgejournal.com/cn/article/id/14963
[5]	GALLI M, THEWES M. Rheological characterisation of foam-conditioned sands in EPB tunneling[J]. International Journal of Civil Engineering, 2019, 17(1): 145-160. doi: 10.1007/s40999-018-0316-x
[6]	钟嘉政, 王树英, 刘朋飞, 等. 泡沫改良砾砂渣土力学行为与流变模型研究[J]. 哈尔滨工业大学学报, 2021, 53(11): 84-92. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX202111011.htm ZHONG Jiazheng, WANG Shuying, LIU Pengfei, et al. Mechanical behavior and rheology model of foam- conditioned gravelly sand in EPB shield tunneling[J]. Journal of Harbin Institute of Technology, 2021, 53(11): 84-92. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX202111011.htm
[7]	孟庆琳, 屈福政, 李守巨. 土体旋转流变仪开发与土压平衡盾构改性土体塑性流动特性实验[J]. 岩土工程学报, 2011, 33(10): 1642-1648. http://www.cgejournal.com/cn/article/id/14215 MENG Qinglin, QU Fuzheng, LI Shouju. Development of soil rotational rheometer and experiment on plastic flow characteristics of conditioned soil in earth pressure balance shield[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(10): 1642-1648. (in Chinese) http://www.cgejournal.com/cn/article/id/14215
[8]	ZHONG J Z, WANG S Y, LIU P F, et al. Investigation of the dynamic characteristics of muck during EPB shield tunnelling in a full chamber model using a CFD method[J]. KSCE Journal of Civil Engineering, 2022, 26(9): 4103-4116. doi: 10.1007/s12205-022-1300-1
[9]	HU W, ROSTAMI J. Evaluating rheology of conditioned soil using commercially available surfactants (foam) for simulation of material flow through EPB machine[J]. Tunnelling and Underground Space Technology, 2021, 112: 103881. doi: 10.1016/j.tust.2021.103881
[10]	MORI L S, MOONEY M, CHA M S. Characterizing the influence of stress on foam conditioned sand for EPB tunneling[J]. Tunnelling and Underground Space Technology, 2018, 71: 454-465.
[11]	ZHONG J Z, WANG S Y, QU T M. Undrained vane shear strength of sand-foam mixtures subjected to different shear rates[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2023, 15(6): 1591-1602.
[12]	WANG Haibo, WANG Shuying, ZHONG Jiazheng, et al. Undrained compressibility characteristics and pore pressure calculation model of foam-conditioned sand[J]. Tunnelling and Underground Space Technology. 2021, 118: 104161.
[13]	WU Y L, NAZEM A, MENG F Y, et al. Experimental study on the stability of foam-conditioned sand under pressure in the EPBM chamber[J]. Tunnelling and Underground Space Technology, 2020, 106: 103590.
[14]	YANG Guangchang, BAI Bing, LIU Yang, et al. Constitutive modeling for undrained shear behavior of gassy sand considering energy dissipation at the mesoscopic level[J]. Ocean Engineering, 2021, 219: 108307.
[15]	LIU Kan, XUE Jianfeng, YANG Min. Deformation behaviour of geotechnical materials with gas bubbles and time dependent compressible organic matter[J]. Engineering Geology. 2016, 213: 98-106.
[16]	曹文贵, 李鹏, 张超, 等. 土的初始和再压缩曲线分析模型[J]. 岩石力学与工程学报, 2015, 34(1): 166-173. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201501018.htm CAO Wengui, LI Peng, ZHANG Chao, et al. Analysis models of initial compression and recompression curves of soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(1): 166-173. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201501018.htm
[17]	BISHOP A W. The influence of an undrained change in stress on the pore pressure in porous media of low compressibility[J]. Géotechnique, 1973, 23(3): 435-442.
[18]	杨益, 李兴高, 李兴春, 等. 基于Herschel-Bulkley流变模型的盾构螺旋输送机保压性能[J]. 湖南大学学报(自然科学版), 2021, 48(11): 195-204. https://www.cnki.com.cn/Article/CJFDTOTAL-HNDX202111021.htm YANG Yi, LI Xinggao, LI Xingchun, et al. Pressure maintaining performance of shield screw conveyor based on herschel-bulkley rheological model[J]. Journal of Hunan University (Natural Sciences), 2021, 48(11): 195-204. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HNDX202111021.htm
[19]	MESRI G, HAYAT T M. The coefficient of earth pressure at rest[J]. Canadian Geotechnical Journal, 1993, 30(4): 647-666.

施引文献(8)

期刊类型引用(2)

1.	张村，方尚鑫，贾胜，王永乐，王方田，白庆升. 基于CT扫描的三维重构煤体加载损伤演化特征及尺寸效应. 矿业科学学报. 2024(03): 413-425 . 百度学术
2.	李文新. 基于非饱和渗流特征的土体抗剪强度衰减预测研究. 矿产勘查. 2024(10): 1914-1920 . 百度学术