0.   引言

在经典的承载力理论中，条形基础的极限承载力q_u随基础宽度B的增大而线性增大，二者之间的关系可用通过原点的直线表示，如图 1中曲线C所示；承载力系数N_γ为极限承载力q_u与宽度的比例系数，其大小只与土体的内摩擦角有关，与B无关，在图 1的N_γ-B坐标中可用一条水平虚线H来表示。

图  1  基础尺寸效应示意图

Figure  1.  Sketch map of scale size effects in foundation

下载: 全尺寸图片 幻灯片

Golder等^[1]首次提出了尺寸效应问题，他通过试验研究发现：浅基础小比尺模型试验中得到的基础极限承载力q_u与B的关系如图 1中实线D所示，随着基础宽度的不断增大，曲线越来越靠近理论值线C；对于地基承载力系数，在基础宽度未达到一定值B₀时，随着基础尺寸的增大，承载力系数N_γ不断减小，在达到B₀之后，承载力系数不再随着基础尺寸的改变而改变，即地基承载力系数N_γ会随着基础宽度的增大而不断减小，并不是Terzaghi地基承载力公式中表现出来的一样，只与地基土体的内摩擦角有关，不随着基础宽度的改变而改变。这就是基础地基承载力尺寸效应问题。

很多学者从试验及数值模拟两个方面研究了基础尺寸效应问题^[1-7]。在试验方面，主要通过小比尺试验与离心机试验手段进行研究。Yamaguchi等^[2]通过对3，120 cm两种基础基底应变在形成滑动面时的差异进行观测，得出了基础尺寸效应产生的原因是地基的渐进性破坏，并得出可以忽略尺寸效应的基础极限宽度为B₀=90 cm；柳飞等^[3]分别在相对密实度为24%及78%的丰浦砂地基上进行了平板载荷离心机承载力试验，得到了考虑尺寸效应的修正后承载力公式, 并得到了B₀=110 cm；Kusakabe等^[4]对圆形和条形基础进行了研究，得出了基础形状对尺寸效应的影响；沈扬等^[5]对南海珊瑚砂进行室内承载力模型试验，在试验基础上提出了适用于珊瑚砂的地基承载力公式。在数值模拟方面，陈榕等^[6]利用有限元研究了密砂中圆形锚上拔的承载力尺寸效应；Fu等^[7]通过对干砂材料上平板载荷试验的离散元模拟，得出莫尔-库仑圆应力强度包线的非线性可能是尺寸效应产生的原因之一。

综上，已有的研究多集中对干砂地基中基础模型尺寸大于0.2 m的小比尺模型试验与模拟大比尺模型的离心机试验的尺寸效应研究，且针对海洋土力学中主要研究对象的饱和砂土地基研究较少，应用离散元研究尺寸效应的研究较少，对小比尺试验饱和砂土中条形基础的尺寸效应产生的机理尚不明确。

本文开展了不同密实度饱和砂土地基上条形基础宽度为0.01，0.02，0.05，0.1 m的小比尺模型试验，并利用离散元软件PFC对试验过程进行了模拟，利用尺寸效应评价指标，定量地讨论基础的尺寸效应问题，提出了考虑基础尺寸效应的承载力公式，为之后小比尺模型试验试验模型以及试验地基土的选取提供参考。

1.   试验设计

1.1   试验装置及模型地基制作方法

试验在2 m(长)×2 m(宽)×2 m(高)的混凝土浇筑的土槽中进行，槽内壁用防水涂层密封。试验使用的加载装置为天津大学自主研发的液压加载装置，如图 2所示。

图  2  试验装置示意图

Figure  2.  Test apparatus

下载: 全尺寸图片 幻灯片

地基材料使用饱和的福建标准砂。其饱和过程为：在模型槽底部及侧壁铺设一层土工布，防止槽内填土破坏防水层。模型槽底部填入0.3 m厚的碎石垫层，碎石粒径约10~20 mm。将一段PVC管(直径300 mm)插入碎石层作为排水井以控制水位。碎石层与试验土之间铺一层土工布，采用砂雨法向槽中均匀填砂，同时向槽中缓慢注水，控制水位和流速，使砂土缓慢饱和并防止管涌破坏，填土完成后，使水位略高于土面，保证试验过程中土体始终为饱和状态。标准砂物理性质颗粒级配曲线如图 3，表 1所示。

图  3  砂土级配曲线

Figure  3.  Grain-size distribution curve of sand

下载: 全尺寸图片 幻灯片

表  1  土体物理力学参数

Table  1.  Physical and mechanical parameters of soils

相对质量密度Gs	饱和重度γsat/(kN·m-3)	孔隙比e	相对密实度Dr/%	内摩擦角φ/(°)
2.65	19.7	0.85 0.73 0.71	0.32 0.65 0.75	28.0 33.4 38.2

下载: 导出CSV 

| 显示表格

1.2   试验方案及方法

在确定模型基础尺寸时，为避免边界效应确定了模型尺寸，如表 2所示，其中d为基础埋深，B为模型宽度。

表  2  试验方案

Table  2.  Test programs

组次	Dr	埋深比 d/B	基础形状	模型尺寸 (B×L)/m
1	0.32，0.65，0.75	0，0.5，1	条形	10×100
2	0.32，0.65，0.75	0，0.5，1	条形	20×200
3	0.32，0.65，0.75	0，0.5，1	条形	50×500
4	0.32，0.65，0.75	0，0.5，1	条形	100×1000

下载: 导出CSV 

| 显示表格

浅基础试验模型如图 4所示。

图  4  试验模型示意图

Figure  4.  Test model

下载: 全尺寸图片 幻灯片

试验步骤如下：

(1) 安装调试好设备后，将试验模型通过加载孔或加载螺栓与其上部压力传感器连接并测试正常。之后打开加载装置调整模型位置使基础底面贴合土表面。

(2) 启动加载装置对基础进行下压，此时测量系统开始监测基础沉降及压入阻力变化。对浅基础进行匀速下压，下压速度为0.1 mm/s，以该速度下压可以保证加载过程中地基土保持排水状态，进而更准确得到条形基础地基承载力。下压至各基础宽度0.5B时，停止下压。

(3) 记录收集数据，控制加载装置将浅基础上拔，整理试验器材，结束试验。

2.   试验结果及分析

2.1   荷载-位移曲线以及承载力确定方法

荷载-位移曲线中沉降使用s/B表示，即基础的实际沉降s与基础宽度B之比，条形基础承载力使用q表示，即使用传感器测得的力除以基础底面积得到。

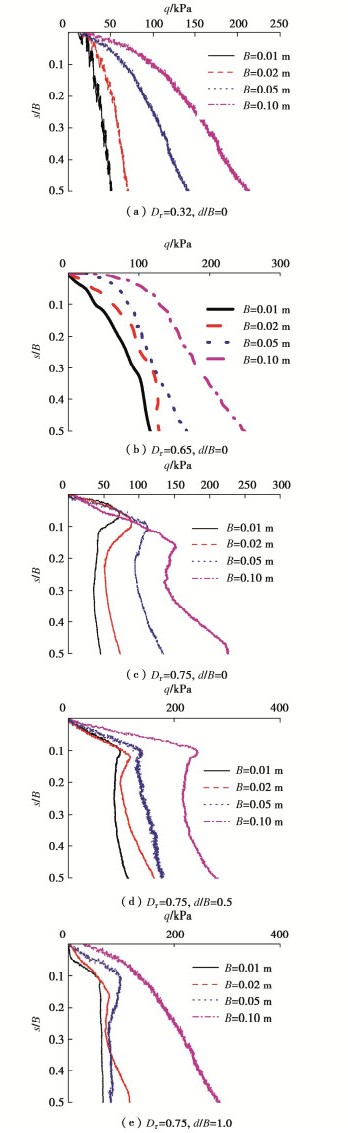
图 5为小比尺试验得到的条形基础荷载-沉降曲线。

图  5  条形基础荷载-沉降曲线

Figure  5.  Load-settlement curves of strip fonudations

下载: 全尺寸图片 幻灯片

由图 5荷载-位移曲线可知，对于条形基础，承载力随着基础宽度增大而增大。在地基砂土密实度较低时，即为松散或者中等密实时，荷载-沉降曲线均无峰值出现，此时地基破坏形式为局部剪切破坏或冲切剪切破坏；在密实程度为密实时，荷载-位移曲线均有较为明显的峰值出现，且峰值对应的沉降随着基础尺寸的增大而逐渐增大，地基破坏模式为典型的整体剪切破坏模式；地基为饱和密实砂土时，随着基础埋深的增加，地基承载力逐渐增大，地基破坏模式变化不大，基本上为整体剪切破坏，条形基础宽度为0.1 m且埋深为基础宽度时，荷载-位移曲线并未出现明显的拐点，破坏模式逐渐由整体剪切破坏向局部剪切破坏过渡。

根据荷载-沉降曲线确定地基极限承载力q_u的方法很多，如利用相对沉降法，以某一s/B值对应的荷载为极限承载力或者采用切线法确定等。本次试验，对于荷载-沉降曲线存在峰值的情况，将峰值荷载作为极限承载力；对于荷载-沉降曲线未出现峰值的情况，根据土工试验规范以及前人的研究成果，极限承载力取沉降量与基础宽度的比值即s/B=0.1~0.15时的承载力作为极限承载力，试验取s/B=0.1时承载力为基础的极限承载力，用q_u表示。试验结果如表 3所示。

表  3  不同地基密实度下条形基础的地基极限承载力

Table  3.  Bearing capacity of strip foundations with different D_r and d/B

相对密实度 Dr	基础宽度 B/m	相对埋深 d/B	极限承载力qu/kPa
0.32	0.01	0	24.88
	0.02	0	35.23
	0.05	0	65.08
	0.10	0	98.00
0.65	0.01	0	45.32
	0.02	0	65.28
	0.05	0	80.18
	0.10	0	125.32
0.75	0.01	0	69.89
		0.5	97.88
		1.0	149.32
	0.02	0	89.92
		0.5	117.90
		1.0	199.28
	0.05	0	109.88
		0.5	140.11
		1.0	250.18
	0.1	0	150.24
		0.5	230.05
		1.0	340.32

下载: 导出CSV 

| 显示表格

由表 3可以看出，在条形基础尺寸一定时，随着地基密实度的增大与基础埋深的增加，其地基极限承载力均随之增大；在地基密实度与基础埋深一定时，条形基础的地基极限承载力随着其尺寸的增大而不断地增大。

2.2   砂土密实度对尺寸效应的影响

Terzaghi极限承载力公式为

式中：c为黏聚力；N_c，N_q，N_γ为承载力系数；$\gamma '$为有效重度；d为基础埋深；B为基础宽度。对于饱和砂中的无埋深基础，极限承载力公式可简化为

由式(2)可得

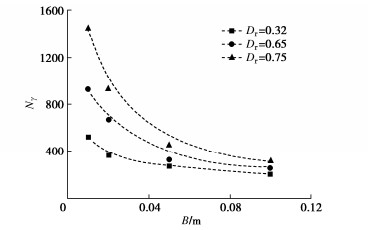
根据Terzaghi公式的基本假定，理想情况下${N_\gamma }$与土体内摩擦角相关，可根据承载力系数表确定，即默认一个内摩擦角对应一个承载力系数。而由以上小比尺试验不同密实度下条形基础极限承载力可得承载力系数${N_\gamma }$如图 6所示。

图  6  不同密实度下条形基础${N_\gamma }$变化图

Figure  6.  ${N_\gamma }$ trend of strip foundations with different D_r

下载: 全尺寸图片 幻灯片

由图 6可以看出，承载力系数${N_\gamma }$随着条形基础宽度的不断增大而逐渐减小，而这种减小的趋势是不断变缓的，并最终可能达到某一稳定值。密实度较高的饱和砂土地基，${N_\gamma }$的减小趋势明显，而松砂地基中${N_\gamma }$的减小趋势减弱。可以认为条形基础地基承载力的尺寸效应现象与地基密实度有较为明显的关系，即随着地基砂土密实度的增加，条形基础地基承载力尺寸效应越来越明显。

2.3   基础埋深对尺寸效应的影响

基础埋深对于地基承载力峰值与破坏模式均有较大影响。由图 5(c)~(e)可以看出，随着条形基础埋深的增加，地基的局部剪切破坏特性越来越显著。当基础相对埋深较小时，荷载-沉降曲线均有比较明显的峰值，破坏模式为整体剪切破坏，但在基础宽度为0.1 m时，基础相对埋深比为1时，表现出了较为明显的局部剪切破坏的特征。对于存在埋深的浅基础，式(1)可以写为

式(4)两边同时除以$\gamma 'B$/2可得

在理论上，对于相同的地基条件，在相同埋深情况下，式(5)右侧承载力系数之和应为定值，并不会随着基础宽度的变化而变化。为综合考虑有埋深情况下的尺寸效应问题，取一个新的承载力系数${N_{q\gamma }}$=2d/ B${N_q}$+${N_\gamma }$。然而根据小比尺试验结果，根据式(5)计算得到承载力系数${N_{q\gamma }}$变化如图 7所示。

图  7  不同相对埋深下浅基础${N_{q\gamma }}$变化图

Figure  7.  Trend of ${N_{q\gamma }}$ of strip foundations with different d/B

下载: 全尺寸图片 幻灯片

由图 7所示，在3种埋深试验条件下，不同尺寸条形基础的承载力系数${N_{q\gamma }}$均会随着基础宽度增大而减小；随着基础相对埋深的不断增大，基础尺寸效应随着基础宽度增加而不断减小的趋势越来越明显。

综上所述，小比尺试验中条形基础尺寸效应较为明显。随着地基砂土密实度的增大，尺寸效应越来越明显，在密实砂土中，尺寸效应表现得最为明显，而在松散与中等密实砂土中，尺寸效应相对不明显。基础相对埋深也会影响尺寸效应特性，随着基础相对埋深的增加，尺寸效应表现得越来越明显。

3.   考虑尺寸效应的承载力公式修正

以上研究表明，承载力系数${N_\gamma }$不仅与地基土的内摩擦角相关，而且与基础宽度和埋深相关，因此将基础的尺寸信息引入传统的地基承载力系数${N_\gamma }$，可有效考虑小比尺试验模型的尺寸效应。

综合前人部分研究成果^[1-7]，可以得到承载力系数${N_\gamma }$与进行归一化后的基础尺寸$\gamma B$/${p_{\text{a}}}$的关系式：

式中：A，β为试验结果的回归系数；${p_{\text{a}}}$为大气压值，${p_{\text{a}}}$=101.325 kPa。根据式(6)对不同密实度砂土试验结果与前人相关研究成果进行整理可得如表 4所示计算结果。

表  4  拟合公式

Table  4.  Fitting formula of ${N_\gamma }$

Dr	Nqγ拟合公式	R2
0.32	${N_\gamma } = 30{(\gamma B/{p_{\rm{a}}})^{ - 0.41}}$	0.997
0.51	${N_\gamma } = 32{(\gamma B/{p_{\rm{a}}})^{ - 0.44}}$ [2]	0.966
0.65	${N_\gamma } = 36{(\gamma B/{p_{\rm{a}}})^{ - 0.47}}$	0.975
0.75	${N_\gamma } = 40{(\gamma B/{p_{\rm{a}}})^{ - 0.5}}$	0.981
0.90	${N_\gamma } = 54{(\gamma B/{p_{\rm{a}}})^{ - 0.58}}$[4]	0.957

下载: 导出CSV 

| 显示表格

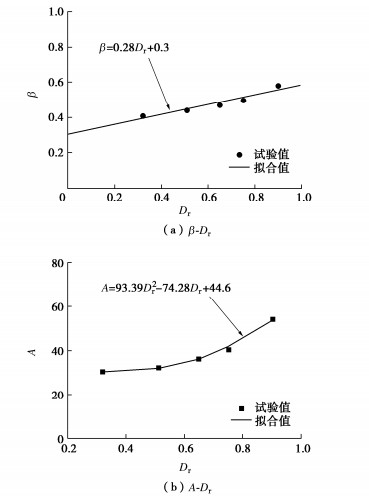
根据表 4绘制应力水平系数β与A和砂土密实度D_r关系图如图 8所示。

图  8  A，β，D_r的关系

Figure  8.  Relationship among A, β and D_r

下载: 全尺寸图片 幻灯片

由此可得小比尺试验中β与A和D_r关系如图 8中所示，可将图 8中计算得到的A，β代入式(6)得到${N_\gamma }$，最终确定考虑尺寸效应地基密实度影响的地基承载力。

对于基础存在埋深的情况，采用相同的拟合方法进行拟合，则综合承载力系数${N_{q\gamma }}$与进行归一化后的基础尺寸$\gamma B$/Pa的关系式：

式中：C，ζ为试验结果的回归系数，则对相对密实度为0.75不同埋深砂土试验结果进行整理可得如表 5所示计算结果。

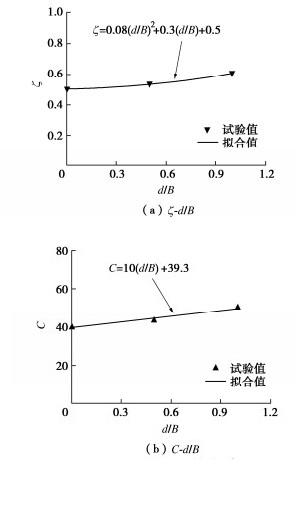
表  5  拟合公式

Table  5.  Fitting formula ${N_{q\gamma }}$

d/B	Nqγ拟合公式	R2
0	${N_{q\gamma }} = 40{(\gamma B/{p_a})^{ - 0.5}}$	0.981
0.5	${N_{q\gamma }} = 43{(\gamma B/{p_a})^{ - 0.53}}$	0.972
1.0	${N_{q\gamma }} = 50{(\gamma B/{p_a})^{ - 0.6}}$	0.965

下载: 导出CSV 

| 显示表格

根据表 5绘制C与ζ和基础埋深d/B关系图如图 9所示。

图  9  C，ζ，d/B的关系

Figure  9.  Relationship among C, ζ and d/B

下载: 全尺寸图片 幻灯片

由此可得小比尺试验中d/B，ζ和C关系如图 9所示，可将图 9中计算得到的C，ζ代入式(7)得到N_qγ，最终确定考虑尺寸效应埋深影响的地基承载力。

4.   尺寸效应的微观机理研究

离散单元法基于离散介质力学，立足于土颗粒的微观接触机制和运动规律，可以更加直观地反映地基破坏的机理。本文采用离散元软件PFC^2D，对试验中不同密实度砂土地基中，不同宽度条形基础的载荷试验进行数值模拟，通过分析地基破坏时的位移场、接触力链变化以及应力路径等进而研究小比尺试验中尺寸效应产生的机理。

4.1   室内试验细观参数标定

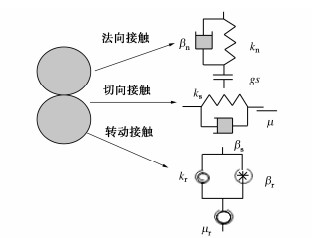
由于离散元软件考虑的是圆形颗粒之间的接触关系，其中不包括土的本构关系，因此选择适当的接触模型显得至关重要，根据试验所应用的密实砂土的性质，采用线性接触模型无法反映真实砂土颗粒较大的内摩擦角，因此本次模拟采用抗转动接触模型^[8]模拟，抗转动线性接触模型示意图如图 10所示。

图  10  抗转线性接触模型示意图

Figure  10.  Rolling resistance linear contact model

下载: 全尺寸图片 幻灯片

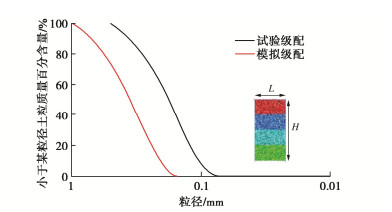
抗转线性接触模型最重要的参数有E^*，κ^*，μ_r，μ。其中，E^*为有效模量，κ^*为法向接触刚度和切向接触刚度的比值即刚度比，μ_r为颗粒间抗转动系数，μ为颗粒间摩擦系数。由于条形基础承载力问题可简化为平面应变问题，因此标定参数时采用双轴试验，剪切盒尺寸为80 mm×40 mm。颗粒形状为圆形，考虑到计算机计算效率问题并且为了更好地反映实际工况，此次模拟采用的平均粒径d₅₀为真实平均粒径的2倍，即0.34 mm。初始孔隙率为0.1，生成的颗粒数为26594个，模拟级配曲线与模拟前试样状态如图 11所示，其中，为方便区分，4种不同颜色代表分层成样中不同的层数，模拟颗粒均采用圆盘颗粒。

图  11  级配曲线与模拟模型

Figure  11.  Grain-size distribution curves of soils and DEM model

下载: 全尺寸图片 幻灯片

通过试错法，最终标定得到的细观参数如表 6所示。

表  6  细观参数设置

Table  6.  Microparameters of DEM

颗粒 总数	颗粒密度ρ/(kg·m-3)	有效模量E*/(N·m-3)	刚度比κ*	摩擦系数μ	抗转系数μr	目标孔隙比e	墙法向刚度kn/(N·m-1)	墙切向刚度ks/(N·m-1)	颗粒与墙摩擦系数μb-w	局部阻尼系数
158166(松) 146742(密)	970	2.0×108	1.5	1.0	0.35	0.1，0.2	1.5×109	1.0×109	0	0.7

下载: 导出CSV 

| 显示表格

通过双轴试验得到的离散元模拟结果与室内三轴试验得到的结果对比如图 12所示。

图  12  不同密实度下应力-应变曲线对比图

Figure  12.  Stress-strain curves with different D_r

下载: 全尺寸图片 幻灯片

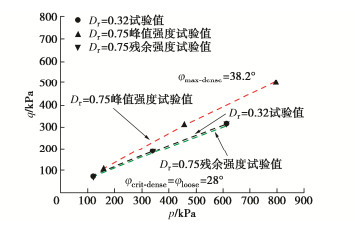
由图 12可以看出，双轴试验模拟得到的结果与真实三轴试验结果较为吻合，图 13给出了模拟地基土体的强度包线。

图  13  地基土强度包线

Figure  13.  Strength envelopes of soils

下载: 全尺寸图片 幻灯片

由图 13可以看出，土体强度的试验值与模拟值曲线误差很小，根据模拟得到的土体应力强度包线得到的峰值摩擦角与残余摩擦角与小比尺试验结果吻合良好，可见本次模拟使用的微观参数可以较为真实地反映试验用土的力学性质。

4.2   边界效应与粒径效应

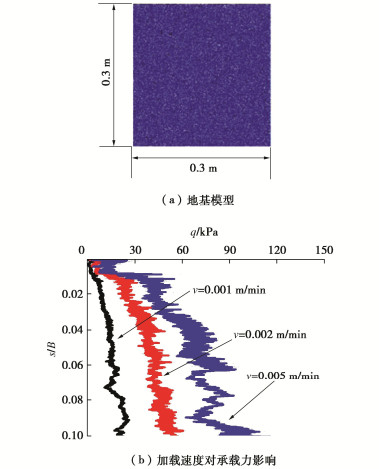
考虑地基对称性，取地基一半作为研究对象。为了保证试样的均匀性，采用分层压实法生成模型地基如图 14(a)所示。地基模型宽度为0.3 m，高度为0.3 m。地基模型宽度为最大尺寸条形基础宽度的6倍，可以忽略地基边界效应的影响^[9]，另外，模拟中最小基础宽度与平均粒径之比为B/d₅₀ =16，可以忽略粒径效应的影响^[10]。

图  14  地基模型与加载速度对承载力影响

Figure  14.  DEM model and influences of loading rate on bearing capacity

下载: 全尺寸图片 幻灯片

4.3   加载速度确定与结果验证

离散元数值模拟中，通过对墙体施加一定的速度进而实现加载，由于对土体加载存在率效应，因此需要对加载速度进行标定，以便于模拟结果可以更准确地模拟小比尺试验结果。以基础半宽为0.005 m的条形基础为模拟对象，分别采用3种不同速率(0.001，0.003，0.005 m/min)进行加载，最终得到的q-s/B曲线如图 14(b)所示。

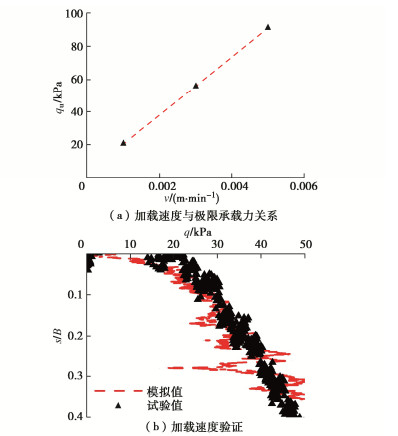
由图 14可以看出，随着加载速度的增加，q-s曲线不断向外扩张，地基极限承载力不断增大。根据小比尺试验中对极限承载力的取值方法，取s/B=0.1时对应的载荷为地基极限承载力，由此可得地基极限承载力与加载速度的关系式如图 15所示。

图  15  加载速度验证

Figure  15.  Verification of loading rate

下载: 全尺寸图片 幻灯片

由图 15(a)可以得出极限承载力与加载速度的关系式为q_u=1782.6v+2.2，将小比尺承载力试验得到的结果代入公式中，可得速度为0.0016 m/min。将离散元模拟中加载速度调整为0.0016 m/min之后重新进行加载计算，最终得到的荷载-沉降曲线与小比尺试验得到的结果如图 15(b)所示。可以看出，使用标定后的加载速度进行加载，得到的荷载-沉降曲线可以很好地模拟小比尺试验中的试验结果。因此，在其余的模拟中，将加载速度0.0016 m/min分别应用到不同基础宽度下的计算中，在加载速度相同，基础尺寸不同的情况下，土体的应变率是相同的，所不同的只是受影响的土体范围。此种情况下，土体参数是相同的，故在同一加载速度下研究地基承载力的尺寸效应是合理的。

4.4   离散元模拟结果

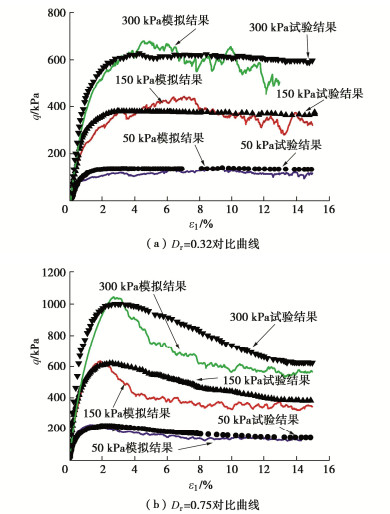
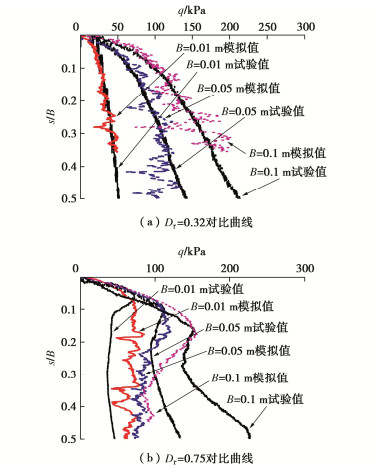
考虑到计算时长问题，为了更加明显反映承载力差异，离散元模拟计算了基础宽度为0.01，0.05，0.1 m情况下的基础承载力。经过模拟计算，得到的荷载-位移曲计算结果与小比尺试验结果对比如图 16所示。

图  16  模拟荷载-沉降曲线

Figure  16.  Load-settlement curves of simulation

下载: 全尺寸图片 幻灯片

由图 16可以看出，数值模拟得到的荷载-沉降曲线与小比尺试验得到的荷载-沉降曲线基本吻合。对于松砂地基，呈现出应变硬化的趋势并没有出现明显的拐点；对于密砂地基，基本都呈现出承载力先增大之后出现峰值荷载然后逐渐减小的趋势，不过离散元模拟得到的曲线与小比尺试验在峰后段出现一定的差距，这可能是由于离散元模型全部采用圆形颗粒来模拟土体颗粒以及二维离散元模拟与室内试验相比维度上存在不足，承载力数值变化上有一定的差异，但整体上可以反映出室内小比尺模型试验条形基础的承载特性。

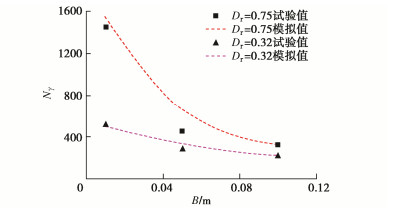
图 17为小比尺试验中基础尺寸效应与离散元模拟得到的结果的对比图。

图  17  尺寸效应对比图

Figure  17.  Comparsion of size effects

下载: 全尺寸图片 幻灯片

由上可知，数值模拟可以较好地反映真实小比尺试验得到的基础尺寸效应的结果，可作为下一步分析尺寸效应产生机理的基础。

4.5   尺寸效应产生微观机理分析

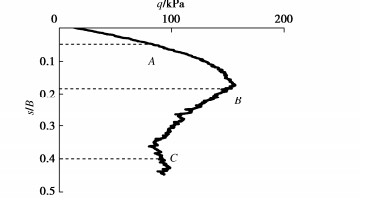
由4.4节离散元计算结果可以看出，对于密砂地基中的尺寸效应现象较为明显，以下针对密砂地基进行分析，通过比较不同尺寸浅基础在如图 18所示初始段A、峰值处B以及峰后稳定段C三个加载阶段位移场、力链场、应力路径的不同点进而探讨尺寸效应产生的原因。

图  18  尺寸效应对比图

Figure  18.  Comparsion of size effect

下载: 全尺寸图片 幻灯片

(1) 位移云图分析

地基土颗粒在受到上部荷载时，会通过移动和旋转的方式达到一个新的相对稳定状态来耗散能量以抵抗荷载。通过位移场的分析，可以得出地基土破坏时的整体破坏模式。

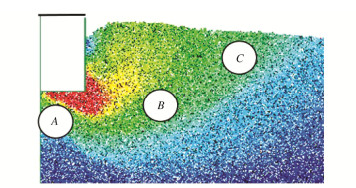
表 7为基础在3个阶段的位移场变化情况，越接近于红色代表地基土颗粒位移量越大，越接近于蓝色代表位移量越小。尺寸基础下土颗粒位移云图中最大位移为各基础的沉降，每个位移间间隔为0.001 m。

表  7  位移场分布变化

Table  7.  Variation of displacement contour

基础宽度/m	加载阶段
	A	B	C
0.01
0.05
0.10

下载: 导出CSV 

| 显示表格

由表 7可以看出，3个阶段下各个宽度的基础的破坏过程均为渐进性破坏，即塑性区并不是在一个瞬间产生和发展的，而是最先在基础正下方底部小范围形成三角压密区，随着沉降的增大，压密区逐渐挤向两侧，基础边缘首先产生塑性区，之后逐渐形成连续滑动面，之后不断向上延伸，最终延伸到地基土表面。由此可知，3个宽度下的基础的破坏模式符合整体剪切破坏模式。随着基础尺寸增大，破坏时深度与宽度影响范围随之增大，基础破坏时的模式符合太沙基地基破坏模式。在基础尺寸较小时，破坏时其最大位移可以由基础底部延伸到土体表面，并在宽度范围内扩展，随着基础尺寸的增大最大位移点逐渐由基础底部向各基础的角点移动，并且最大位移量都只是局限在基础角点位置，并没有延伸到地基表面，地基表面的位移量明显小于基础底部位移，并且3个尺寸下地基表面的最大隆起量与基础自身尺寸比值分别为50%，28%，26%，随着尺寸的增大，该比值逐渐减小。并且根据试验结果，基础宽度由0.01 m增大到0.05 m最后到0.1 m时，荷载-位移曲线的拐点变得越来越不明显，地基整体剪切破坏的特征越来越向局部剪切破坏的特征过渡。结合以上几点，说明地基的整体破坏模式越来越不明显，有逐渐向局部剪切破坏模式转化的趋势。由此可看出，基础尺寸效应的产生可能与地基破坏模式的变化有关。

(2) 力链分析

离散元的分析中，颗粒荷载的传递方式是通过颗粒之间的接触力链来表现的。接触力链根据数值大小可以分为强力链与弱力链，其中弱力链与强力链相连接，辅助维持强力链的剪切稳定性并参与强力链断裂之后的力链重分布。力链的粗细密集程度反映出力的大小，力链的走势反映出力的发展传递趋势。

表 8为基础在3个阶段的力链变化情况对比图，图中线条越粗，颜色越深表示力链强度越高。由表 8可以看出，3个尺寸的基础力链分布趋势大致相同，在最初加载阶段，基础墙体只与地基表层颗粒之间存在接触力链，随着荷载的增大，接触力链在基础底部逐渐增强、加密，形成较为明显的强力链并随着沉降继续增大，强力链逐渐向下方与侧方土体扩散，并逐步达到荷载峰值对应沉降，在应力-应变曲线的弱化与稳定阶段，可以看出，相比于峰值阶段，侧向强力链逐渐减少并逐渐集中与基础底部范围内，最终趋于稳定状态，这可能是由于土体在破坏的过程中产生了加载-卸载的过程，在地基承载力达到峰值强度之后，土体中开始形成连续的破坏面，此时破坏面周围的土体由于发生破坏，土颗粒之间的力链也随之断开。基础尺寸越大，下方力链强度越高，数目越多，强力链在水平与竖直方向的分布范围越广。

表  8  力链分布变化

Table  8.  Variation of force chain

基础宽度/m	加载阶段
	A	B	C
0.01
0.05
0.10

下载: 导出CSV 

| 显示表格

(3) 应力路径分析

根据位移云图在基底布置3个测量圆A，B，C如图 19所示。

图  19  测量圆布置

Figure  19.  Distribution of measuring circles

下载: 全尺寸图片 幻灯片

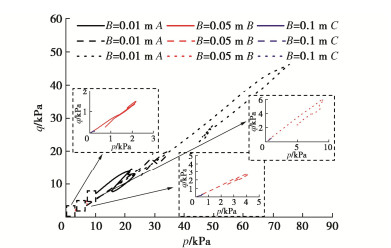
图 20为模拟过程中3种不同宽度基础基底下方测量圆应力路径。由图 20可以看出，在最初加载阶段，3种尺寸的条形基础均会出现加载效应，q-p曲线呈线性变化直到荷载达到极限承载力，在基底正下方的A点加载效应最为明显。根据应力路径图可以看出，3种尺寸的基础在峰值荷载后均出现了卸载效应，应力路径逐渐向左下方移动，说明此时已经发生了破坏现象。

图  20  应力路径

Figure  20.  Stress paths

下载: 全尺寸图片 幻灯片

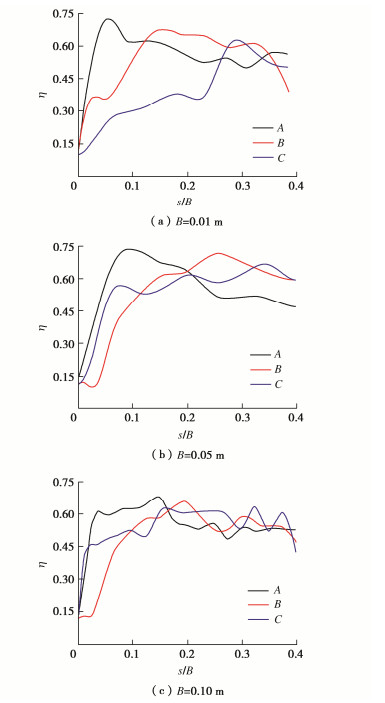
应力比定义为η=q/p，图 21为3种尺寸基础应力比随沉降比变化图。

图  21  不同宽度基础应力比变化

Figure  21.  Variation of stress ratio of foundation with different B

下载: 全尺寸图片 幻灯片

由于测量误差与理论假设，应力比最终变化峰值不一定都达到极大值，因此可以用峰值来判定各点破坏较为合理。由图 21可以看出，对于不同尺寸的基础，其应力比变化趋势较为相似，均是A点首先发生破坏，之后为B点，最后为靠近地基表面最接近的C点，其中A，B点破坏沉降较为接近，这是由于土体发生破坏时，其塑性区最先在基底的角点产生，之后分别向基底与地面延伸，A，B点与角点的距离较为接近因此会产生这种结果。由图 21可以看出，3种尺寸基础渐进破坏的速度是有区别的，基础宽度越大，同一点达到峰值时对应的沉降比越大，渐进破坏的速度越慢；另结合表 7中位移场变化可以看出，在基础宽度为0.01 m时，B点处塑性面已经延续到基础表面，位移最大点也有向基础表面延伸的趋势；而对于宽度为0.1 m基础。此时位移最大处出现在基础角点处，其塑性面虽然也达到了了基础表面，但不如基础宽度小时延伸的充分，结合以上两点，可知基础宽度大时其渐变速度较小这可能也是基础尺寸效应产生的原因之一。

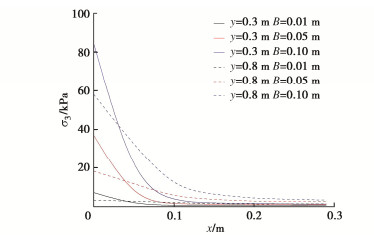
图 22为3种尺寸基础地基承载力达到峰值时一组不同深度处土体中球应力与距轴对称的水平向距离的关系曲线，球应力的大小反映了τ-σ坐标系中莫尔应力圆圆心距离坐标原点的距离。

图  22  不同深度土体中球应力分布

Figure  22.  Horizontal distribution of spherical stress at different depths

下载: 全尺寸图片 幻灯片

如图 22所示，不同深度土体中球应力变化趋势较为接近，均随着轴对称线距离的增大而减小，随着深度的增加，这种减小的趋势越来越不明显。条形基础宽度越大，浅层土体中球应力越大，莫尔应力圆圆心位置越远离原点，即莫尔-库仑强度包线上所对应的φ值越小，这与之前的研究结果一致，即可认为尺寸效应的产生与应力水平作用有关。

5.   结论

通过小比尺模型试验研究了条形基础的地基承载力尺寸效应问题，并得出了考虑基础尺寸效应的修正的地基承载力公式。利用离散元模拟讨论了尺寸效应产生的原因，主要得出3点结论。

(1) 小比尺砂土试验中承载力的尺寸效应较为明显，且随着地基砂土密实度的增大和基础埋深的增大，尺寸效应更加显著。

(2) 根据系列条形基础承载力试验结果，拟合得到了小比尺试验中与应力水平和砂土密实度与基础埋深相关的经验系数计算公式，从而基于太沙基条形基础承载力公式，建立了考虑小比尺试验尺寸效应的条形基础承载力计算方法。

(3) 利用离散元模拟了室内小比尺试验，并分析了破坏状态时的应力路径、应力比变化情况以及力链与位移云图，得出基础地基承载力尺寸效应的产生是应力水平变化、破坏模式改变以及渐进破坏程度综合作用的结果。