Prediction model for dilation behaviors of soft rock joints considering degradation of actual contact 3D roughness
-
摘要: 为预测岩石节理的剪胀变形行为,分析了恒法向荷载作用下实际接触微凸体三维粗糙度在剪切过程中的退化规律,提出了一个适用于软岩节理的剪胀曲线预测模型。在剪切荷载作用下节理法向位移的变化是节理在三角形微凸体侧面爬坡上升行为与爬越一些微凸体顶点后闭合行为的叠加,爬坡行为与闭合行为引起的位移都正比于节理最大可能剪胀角。最大可能剪胀角退化的实质是实际接触节理微凸体平均等效倾角的退化。通过分析初始剪切与残余应力阶段的节理形貌特征,提出了计算初始最大可能剪胀角与残余应力阶段剪胀角的模型。基于软岩节理不发生突然脆性破坏的假设,进一步通过研究剪切过程中节理微凸体退化规律,量化了最大可能剪胀角的变化规律。定量了节理爬坡行为、闭合行为与最大可能剪胀角之间的关系,进而提出了节理剪胀规律预测模型,通过试验验证了模型的有效性。模型可较准确预测软岩节理的剪胀规律,并可合理描述节理初始阶段剪切压密行为。Abstract: To predict the shear dilation characters of natural rock joints, a shear dilation prediction model suitable for soft rock joints is proposed to analyze the degradation laws of the actual three-dimensional contact roughness during the shear process under constant normal loads. The change of normal displacement of joints under shear loads is the superposition of joint climbing behaviors at the shear side of triangular asperities and joint closing behaviors after climbing some asperities. The displacement caused by the climbing and closing behaviors is proportional to the maximum possible dilation angle. The essence of the degradation of the maximum possible dilation angle is the degradation of the average equivalent dip angle of the actual contact joint asperities. By analyzing the joint morphology characteristics at the initial shear and residual stress stages, a model for calculating the initial maximum possible dilation angle and the dilation angle at the residual stress stage is proposed. Furthermore, based on the assumption that the soft rock joints do not experience sudden brittle failure, the variation of the maximum possible dilation angle is quantified by studying the degradation laws of the joint asperities during the shear process. The relationship among the joint climbing behaviors, the closing behaviors and the maximum possible dilation angle is quantified, and a joint shear dilation prediction model is proposed. The validity of the new model is verified by the test results. The new model can accurately describe the shear dilation behaviors and the initial shear compaction behaviors of joints.
-
Keywords:
- shear dilation of joint /
- surface degradation /
- asperity /
- 3D roughness /
- joint morphology
-
0. 引言
组成地壳的岩层和岩体在内、外动力地质作用下发生形变、变位,从而形成诸如褶皱、节理、断层、劈理以及其他各种面状构造,这些不连续构造在一定程度上对岩体强度和稳定性起控制作用[1]。Patton[2]对锯齿岩石节理进行了一系列直剪试验,并提出了一个双线性包络来预测岩石节理在法向应力下的抗剪能力。这项工作初步认识到,节理体积的增加,也称为膨胀,可以大大提高岩石节理的抗剪能力。此后,许多工作研究了节理剪切的形貌演化机制[3-7]。这些工作表明,岩石节理对剪切载荷的响应在很大程度上取决于节理所受的法向应力以及表面形貌。节理法向应力会使节理裂隙有闭合的趋势。同时由于节理表面不规则,剪切过程中会在节理壁之间产生膨胀,这使得节理张开度增大。两种相互作用共同影响着节理的剪胀行为。在剪切过程中,由于节理微凸体破坏,表面粗糙度也会降低,岩石节理的剪切行为随表面退化而变化很大[8]。
许多学者基于对与剪切行为相关的结构面形貌特征进行定量表征,从而对节理剪胀行为进行预测[9]。Barton等[10]提出了一种形态学参数,称为节理粗糙度系数(JRC),以对节理表面粗糙度的程度进行分类。由于它是实际中最常用的粗糙度参数,因此许多研究人员通过提出各种方法,例如统计分析[11-13]和分形分析[3, 14-15],继续改善了JRC的测定。然而上述提到的用于纯形貌量化的方法大多都倾向于低估节理的粗糙度,因为它们忽略了剪切过程中粗糙度改变的力学机理作用[16]。Li等[4]提出天然节理具有两个级别的粗糙度,即波纹度(第一阶)和不平整度(第二阶)。两种粗糙度都经历退化,导致岩石节理对剪切载荷的非线性响应。随着三维光学扫描技术的发展,一些学者提出了一系列的三维粗糙度指标来反映节理粗糙度。Belem等[17]定义了节理剪切倾角平均值θs、表面粗糙度系数Rs、各向异性度Ka、节理弯曲度Ts、平均正向坡度参数θp+与平均负向坡度参数θp-描述述节理三维粗糙度;Tang等[18]基于光照部分所占整个节理形貌面积的比值提出了三维粗糙度指标BAP。Grasselli[19]基于等效倾角的分布规律提出了三维粗糙度指标。研究结果表明节理在压剪作用下,仅仅是一小部分较陡微凸体发生接触而相互作用[1]。以往在描述粗糙度时是考虑整个形貌面微凸体的分布特点,这使得所得粗糙度指标弱化了较陡微凸体作用而强化了较平缓微凸体对剪切强度的作用(实际上大多平缓微凸体在剪切过程中未接触)。基于以上研究Ban等[1]提出了考虑实际接触节理分布特征的三维粗糙度指标,该指标可与剪切力学机理联系起来。
岩石节理对剪切作用反应还取决于法向应力[2, 20-22]。当法向应力较低时,由于粗糙面彼此相对滑动,导致岩石抗剪切作用节理失效。在这种情况下,剪胀是剪切破坏模式的主导。如果法向应力增长到足够高的水平,节理面上微凸体将发生严重破坏。岩石节理的剪切行为是由粗糙度的变化控制的,粗糙度的变化与剪切过程中的法向应力有关。对于在非极端法向应力条件下受到剪切作用的岩石节理来说,节理的剪胀和退化同时发生。已经提出了4种模型来量化节理粗糙的退化,其中大多数受到以下限制。①模型的适用性仅限于具有理想轮廓的二维形貌线[20, 23-24]。另外,Barton提出的通过视觉对比来判断二维粗糙度JRC的方法存在一定的主观性,且二维粗糙度JRC不能全面反映节理面的三维粗糙特征,这可能会导致微凸体对剪切行为的影响被低估。②现实情况是剪胀效应从节理峰前阶段开始就明显影响剪切强度与剪胀规律,并且初始阶段剪胀曲线会有闭合的趋势,然而大多数模型在出现峰值剪应力之前不考虑膨胀行为与初始阶段的闭合行为[25-27]。③这些模型是高度经验的,缺乏扎实的理论基础[4, 28-30]。这些已建立的公式通常包含一个或多个没有明确物理意义的系数,例如常用幂函数中的经验常数[6]。④很少有模型考虑实际接触节理三维粗糙度在剪切中的作用。实际接触节理三维粗糙度的退化决定着剪切应力随剪切过程的发展。
最近的一项研究[1]指出,节理的实际接触表面状况会极大地影响岩石节理的剪切行为,因此,应考虑实际接触节理三维粗糙度在剪切中的作用,以评估节理剪胀规律。提出了一种节理剪胀预测模型,该模型考虑了恒法向荷载作用下实际接触三维粗糙度在剪切过程中的退化规律,同时考虑了节理闭合与剪切爬坡行为对法向位移变化的影响。通过进行试验测试并与数值建模结果进行比较来评估所提议模型的性能。还将从文献中获得的一些试验数据与模型的仿真结果进行比较,以进行进一步的验证。
1. 节理法向位移-剪切位移模型
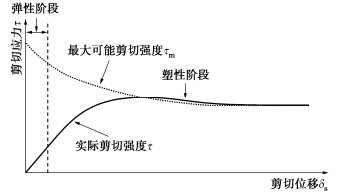
对于受剪切作用的岩石节理,存在一个最大可能的剪切强度τm,代表节理剪切时最大可达到的剪切应力。最大可能剪切强度对应最大可能剪胀角imob,随着节理形貌在剪切过程的变化而变化。最大可能剪切强度表示在某一剪切状态下节理有达到此剪切应力的能力,并不意味着实际剪切状态的剪切应力为最大剪切应力,类似于连续屈服模型[31],见图 1。在剪切位移达到峰值强度对应的位移之前,实际剪切强度小于最大可能剪切强度。此时,最大可能剪切强度仅与表面形态、材料性能和法向应力有关。尽管在这个阶段最大可能的剪切强度很大,但由于位移较小,实际强度尚未达到最大可能的抗剪强度。当节理剪切位移达到峰值强度对应的位移时,节理剪切强度等于最大可能剪切强度。
在剪切过程中只是一小部分节理微凸体接触,控制节理剪切行为的是实际接触节理微凸体之间的相互作用。在剪切过程中实际接触微凸体中的一部分发生剪断破坏。未发生剪断破坏的微凸体以最大可能剪胀角imob抵抗剪力,提供的剪切应力为σntan(φb+imob)。发生剪断破坏的微凸体以剪断形式抵抗剪力[25]。为计算节理剪断部分所提供的抵抗力,研究了实际接触微凸体剪断部分所提供的剪力。
实际接触微凸体的面积为[1]
Ac=Nσc=Aσnσc 。 (1) 式中:A为节理面名义面积;σn为法向应力;σc为单轴抗压强度。
根据剪切面积比as的定义[8],剪断微凸体面积为
Acs=asAσnσc。 (2) Xia等[32]观察剪切后的节理面证实,剪切过程中节理表面微凸体的磨损、剪断多是因拉裂引起。基于此现象这里假设节理微凸体的抗剪强度与材料抗拉强度相等。
则剪断部分所提供的剪切力为
Fcs=Acsσt=asAσnσcσt。 (3) 式中:σt为节理单轴抗拉强度。
则剪断面积所提供的剪应力为
τcs=asσnσcσt。 (4) as为塑性剪切位移δps的函数,τcs为塑性剪切位移从0进行到δps时剪断作用总提供的剪切应力。当剪切进行到某一塑性位移δps所对应的瞬时,剪断作用引起的剪应力为dasdδpsσ0σcσt(Δδs),剪断后的微凸体提供的剪切作用就消失。Δδs的大小取决于试验采集的频率与剪切速率,通常可认为是一个较小的数值,实际计算时发现dasdδpsσ0σcσt也是较小的数值,所以可以近似
假设某一剪切位移的瞬间,剪断作用提供的剪力为0。
因此仅考虑最大可能剪胀角的作用,剪切到某一剪切位移,最大可达到的剪应力为
τm=σntan(φb+imob)。 (5) 在弹性阶段,由于节理微凸体处于剪切弹性阶段,并没有损伤的发生。最大可能剪胀角imob保持数值为初始最大可能剪胀角im0(也就是剪切过程中实际接触节理平均倾角的最大值)不变。随着剪切位移的增大,节理剪切强度保持弹性状态继续增大。当剪切强度超过基本摩擦强度τ=σntanφb[5],实际接触节理发生磨损,粗糙度退化,节理进入塑性阶段,此时最大可能剪胀角imob开始减小。在剪切过程中imob的减小是因为实际接触节理微凸体平均倾角的减小,由初始剪切时的im0减小到残余剪胀角imr。
在弹性阶段,由于剪切强度未超过基本摩擦强度τ=σntanφb,节理的剪切强度全部由平直节理的基本摩擦角就可以抵抗,所以还未开始有微凸体爬坡效应的抵抗,此阶段爬坡效应引起的法向方向位移为0。弹性阶段的最大弹性位移为
δmaxe=σntanφbke 。 (6) 式中:ke为弹性阶段剪切刚度,可由剪切试验初始阶段刚度获取。
当剪切强度大于σntanφb时,节理的剪切强度除了由平直节理的基本摩擦角提供还需节理的爬坡效应提供,因此爬坡效应开始起作用。进入塑性阶段由爬坡效应引起的法向方向的位移Δδv1变化,
Δδv1=Δδpstanimob。 (7) 然而上部节理并不会随着倾角为imob的坡度一直抬高。随着剪切的进行,节理沿着倾角为imob的微凸体侧面爬越,当爬越超过一部分节理微元的顶峰时,由于法向应力的作用会使节理有闭合的趋势。最终节理法向位移的变化是节理在三角形微凸体侧面爬坡上升行为与爬越一些微凸体顶点后闭合行为的叠加。
节理粗糙面可等效为连续三角形微凸体,节理上所有实际接触微凸体的尺寸可认为是均匀连续变化,因此可以假设节理闭合位移也是随着剪切位移连续变化。对于爬越较小倾角的微凸体闭合位移较小,较大倾角的微凸体闭合位移较大。因此可假设闭合位移Δδv2与最大可能剪胀角imob成正比,
Δδv2=aΔδstanimob。 (8) 式中:a为节理剪切闭合系数。
则实际法向位移Δδv为
Δδv=Δδv1−Δδv2。 (9) 2. 最大可能剪胀角的退化规律
2.1 初始最大可能剪胀角
Barton等[10]提出了JRC-JCS模型,以建立起节理的粗糙度参数JRC与剪切强度之间的关系。但是JRC是二位粗糙度参数其无法充分的反映节理形貌的三维特征。
Grasselli[19]在岩石节理直剪试验中发现岩石三维形貌面参数“有效剪切角”可以与节理剪切强度很好的联系起来,同时提出了节理有效倾角分布函数。该分布函数表示了微元有效倾角大于θ*的微元面积总和与节理面面积比Aθ*与θ*的关系 [19],
Aθ∗=A0(θ∗max−θ∗θ∗max)C。 (10) 式中:A0为所有节理微元等效倾角大于0时的面积总和与节理表面面积总和之比;θmax*为沿剪切方向节理微元有效倾角最大值;C为公式拟合系数。
由式(10)可知,有效视倾角θ*的增大,使得有效视倾角大于θ*的所有微元面积比Aθ*不断减小,最终减小到0。Grasselli采用θmax*/C表征节理粗糙度,并建立起其与剪切强度之间的关系。
Ban等[1]发现节理在剪切过程中,仅有一部分微凸体发生相互作用来抵抗剪切荷载,未接触的部分不提供抵抗力。某一应力水平下接触时最小的视倾角[1]为
θ∗cr={1−10[lg(σn/σc)−lg(A0)]/C}θ∗max。 (11) 基于实际接触节理微凸体最小倾角与倾角的分布关系,实际接触部分节理微凸体倾角的平均值[1]为
¯θave =θ∗max{1−10[lg(σn/σc)−lg(A0)]/C}+θ∗max1+C{10[lg(σn/σc)−lg(A0)]/C}。 (12) Ban等[1]在验证上述角度时,文献中所选取的试验数据法向应力较小。忽略剪胀角的磨损作用,Ban等[1]提出上述平均角也为节理剪切过程中的峰值剪胀角ip。实际上¯θave为节理在刚施加剪切位移时的最大可能剪胀角im0。
2.2 残余剪胀角模型
随着剪切的进行,实际接触节理的微凸体中大于θcr*的部分发生塑性变形进而破坏。软岩节理脆性性质不明显,剪切时的损伤主要表现为节理微凸体的磨损。对于软岩节理实际接触节理的微凸体中大于θcr*的部分可假设其等效倾角是随着剪切位移的增大连续减小,并不发生脆性破坏突然降低到某一数值。基于此假设所得连续剪切模型仅适用于软岩节理连续破坏状态,通常为软岩节理在法向应力较低时的剪切过程。
将法向荷载的施加看作一个连续过程。实际接触等效倾角较大的节理微凸体由于在法向应力施加时最先达到屈服,微凸体受到剪切荷载作用后更加容易磨损,因此其等效倾角减小的速率较快。随着等效倾角因磨损而降低,这些微凸体所承受荷载状态会趋于稳定,等效倾角的减小速率也会逐渐减小,最终这些微凸体将减小到一个应力稳定状态,数值为θcr*。当节理经过剪切后达到残余强度时,实际接触节理的微凸体中大于θcr*的部分以不同的速率磨损为微凸体等效倾角为θcr*的微凸体。而未接触的部分未发生磨损。此时实际接触节理的平均等效倾角为θcr*,也即为残余剪切应力阶段的剪胀角。
上述假设正确的前提是岩石节理在剪切过程中发生连续塑性破坏,然而岩石在剪切过程中会表现出一定的弹脆性特征,例如在法向应力较大时,岩石的节理会在峰后发生突然的应力降,这会导致节理的残余强度小于以上分析结果。对于同一种岩石来说,岩石节理剪切强度与法向应力相关,法向应力越大,节理剪切强度越大,节理在峰后发生的破坏越大,相对于在低法向应力下来说,剪切脆性也更高。例如岩爆现象的产生,在高围压下比在低围压下的破坏程度要严重得多。由文献[33]可知,Grasselli在研究法向应力对摩擦角的影响试验中发现,当σn/σc大于0.3时,对于试验所用的几种岩石,摩擦角均不再随着σn/σc的增加而降低,这说明在法向应力为单轴抗压强度的0.3倍时,节理会发生磨平的现象。据文献[33]的研究,最大剪切强度发生时,法向应力为单轴抗压强度的0.3倍。本研究中,用节理抗剪强度与最大可能抗剪强度之比来表示剪切脆性系数,并用其来描述剪切脆性相对大小。
b=σntan(φb+¯θave)0.3σctanφb。 (13) 式中:b为剪切脆性系数;分子部分为实际抗剪强度[1];分母部分为最大抗剪强度[33]。
对于完全塑性的岩石节理,由以上分析可知,其残余剪胀角为θcr*。考虑脆性因素使岩石节理的残余剪胀角变小作用,残余剪胀角可假设为
imr=θ∗cr(1−b)。 (14) 2.3 最大可能剪胀角的退化函数
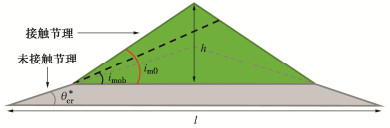
受剪切磨损作用的影响,最大可能剪胀角随着塑性位移的增大由im0减小到imr。将接触的节理面等效为连续的三角形网格,三角形网格的间距为实验室级别确定等效剪切倾角的网格间距(一般为0.2~0.5 mm[1])。三角形的倾角大小为实际接触节理的平均剪切倾角(图 2)。图 2中初始最大可能剪胀角为im0,经过剪切后,最大可能剪胀角为imob。
假设由塑性剪切位移增量引起的磨损面积增量dSr被认为与剩余粗糙度面积Sr成比例[25],即
dSrdδps=−cwSr。 (15) 式中:cw为磨损速率系数,磨损速率系数与节理材料性质和受力情况相关。假设:
cw=kσnσc。 (16) 式中:k为磨损速率常数。
那么磨损后剩余的面积为
Sr = S0e−kσnσcδps。 (17) 考虑到与微凸体长度l、高度h和初始粗糙度角im0的几何关系,见图 2。剩余节理粗糙度面积Sr为
Sr=l22(cotimob+cotim0)。 (18) 结合式(17),(18),最大可能剪胀角的变化规律为
tanimob =e−kσnσcδps2−e−kσnσcδpstanim0。 (19) 式中由边界条件确定系数k。塑性剪切位移为0时,imob=im0。当剪切位移取达到残余应力时位移δr时,imob=imr,进而可确定k。
k=σcσn[ln(tanimr+tanim0)−ln(2tanimr)]/(δr−δmaxe)。 (20) 通过总结试验结果,对于实验室尺度的剪切试验,残余强度位移可按10 mm确定。
3. 本文试验验证
由以上分析可知,节理法向位移可分为节理爬坡时张开位移与闭合位移的叠加,法向位移-剪切位移曲线为爬坡曲线减去闭合曲线。当剪切位移在(0,δmaxe)时,没有爬坡作用。当剪切位移大于δmaxe时,爬坡作用开始,爬坡作用引起的节理张开位移开始增加,需要注意的是节理的闭合位移Δδv2贯穿整个δmaxe时,闭合作用位移可由式(8)进行计算,这也对初始节理剪切压密行为做出了合理解释。
上述所提节理剪胀模型是以软岩节理微凸体连续破坏为基础进行理论推导所得。水泥砂浆人工节理一般材料抗压强度较低,接近于软岩节理的性质,因此为验证本文所提出节理剪胀模型的有效性,进行了水泥砂浆人工节理的制作与节理剪切试验来验证。
所研究岩石节理形貌面是由花岗岩经巴西劈裂试验得到。试验时,选取尺寸200 mm×100 mm×100 mm岩石试块,在100 mm的高度中间选择劈裂面。进行劈裂加载试验时竖向加载速率为0.5 mm/min,得到劈裂节理。按上述方法进行劈裂获取6组岩石试块,然后选取3组节理形貌特征较大的节理试样备用。
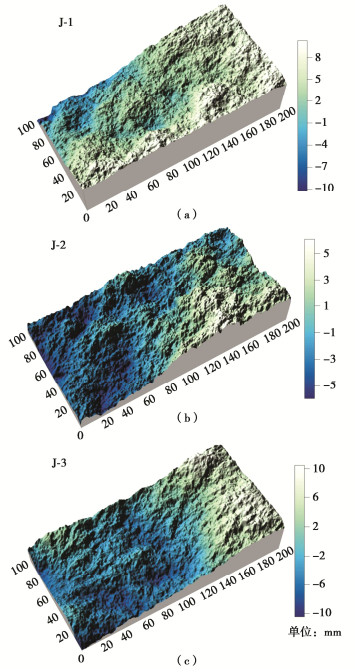
为定量表征岩石节理形貌面粗糙度,劈裂所得花岗岩节理扫描试验是在武汉大学自制的三维激光扫描仪上进行。最终获取节理形貌图见图 3。
3D打印技术具有精度高、成型快等特点,基于该技术制作了复制特定节理形貌面的模具。试验时,应用计算机三维软件设计出立体的节理样式,其节理形貌基于扫描获得的3组节理面数据,设置打印精度为0.2 mm,最终基于预设模型逐层打印出成型的3组模具。3D打印的优势在于试验的可重复性,可以精确复制模具来制作水泥砂浆节理。
为复制出节理微小的结构,材料选择42.5R基准水泥、标准砂和水,质量配合比为水︰水泥︰砂=1︰2.3︰4.5。试模采用铸铁试模,尺寸为200 mm×100 mm×100 mm。将搅拌均匀的水泥砂浆一层一层浇筑在打印模具表面并充分振捣。最后磨平铸铁模具顶面获得上盘节理。所得6组耦合节理面(每种形貌节理2组)。采用Grasselli形貌数据分析(式10),最终得到3组节理的三维形貌参数。其中,三组节理面J-1、J-2、J-3的形貌参数A0分别为0.46,0.54,0.55;θmax*分别为59.32°,72.03°,59.12°;C分别为7.81,10.92,6.80。
在节理试块制作过程中制备了6个标准圆柱砂浆试件。为保证材料性质一致,在制作过程中测试力学参数所用砂浆柱与剪切试验节理配合比相同、振捣过程一致,养护条件均一致。在岩石三轴伺服试验机上进行单轴压缩试验,测定其平均单轴抗压强度为29 MPa。由倾斜试验获得平均基本摩擦角为32°。
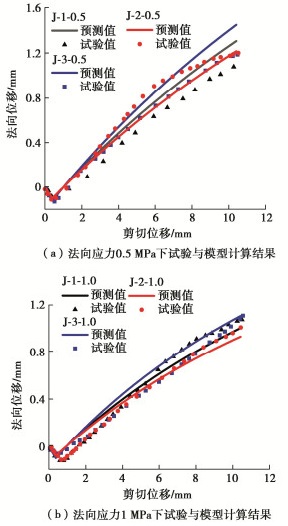
将6组试样按形貌面分为3组,每组进行法向应力分别为0.5,1 MPa的直剪试验。首先按照速率为0.10 kN/min在试块上施加法向荷载,达到预定值稳定后通过伺服调整荷载加载方式为位移加载,速率为0.5 mm/min施加切向荷载。试验过程中记录了剪切位移、法向位移、剪切荷载等试验数据。得到6组直剪试验剪胀曲线与模型所得剪胀曲线如图 4所示,其中初始剪切刚度由剪切应力-剪切位移曲线所得,分别为0.8,1.4,0.7,1.3,0.8,1.5 MPa/mm。
图 4中J-x-y为节理形貌x在法向应力为y MPa下的试验与预测结果,模型中a=0.6。由图 4可知,6组试验曲线与模型计算结果吻合度很好。水泥砂浆节理单轴抗压强度较低,在节理剪切试验中微凸体连续破坏表现为节理剪切后剪胀曲线较为光滑。本模型推导理论基础也是基于微凸体连续破坏,因此模型计算结果与试验结果吻合度较好。
4. 其他学者试验验证
上述试验对象为水泥砂浆复制节理,为进一步验证上述模型针对真实岩石节理的有效性,本文采用杨洁[34]进行的剪切试验所得结果进行验证。试验采用红砂岩节理进行定法向应力的剪切试验,节理在剪切方向上的尺寸为200 mm,红砂岩材料单轴抗压强度为65 MPa,节理基本摩擦角为28°,文献中报道了10组节理面在法向应力与单轴抗压强度为0.5%~5%下的剪切强度-剪切位移曲线。剪切强度-剪切位移曲线光滑变化,不存在突然大幅度的应力降,符合软岩节理特征。红砂岩节理是由200 mm×100 mm×100 mm红砂岩试块经巴西劈裂试验得到,10组节理形貌数据经激光扫描仪得到。采用Grasselli[19]形貌数据分析,最终得到10组节理形貌参数见表 1。
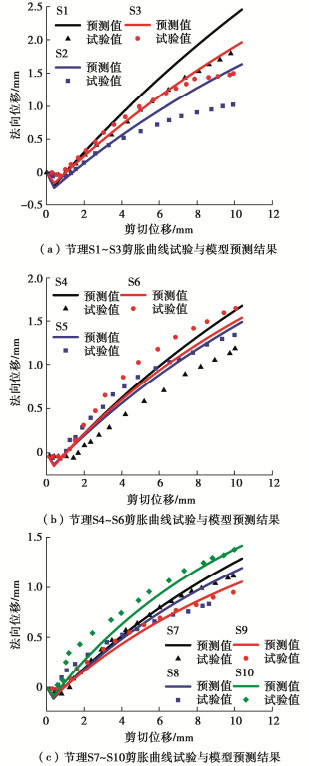
节理号 C θ∗max/(°) A0 σn/MPa S1 8.9 83.3 0.51 0.3 S2 7.6 82.3 0.61 0.7 S3 8.4 82.6 0.54 1.0 S4 8.9 83.9 0.49 1.3 S5 9.5 82.7 0.55 1.6 S6 7.9 81.6 0.58 2.0 S7 8.9 82.9 0.50 2.3 S8 8.8 83.5 0.47 2.6 S9 9.3 83.4 0.44 2.9 S10 8.3 84.2 0.51 3.3 采用本模型计算的法向位移-剪切位移曲线与试验结果对比见图 5。剪胀曲线试验值通过Getdata软件选取,模型所需的初始剪切刚度由试验所得剪切强度-剪切位移曲线获取,分别为0.8,1.6,1.9,2.2,2.5,3.3,3.3,3.7,3.8,4.7 MPa/mm。
图 5中预测结果为模型中a=0.6的计算结果,由图 5可知,S3,S5-10的预测精度很好,其中S7,S9计算曲线与试验曲线基本重合,这显示计算模型具有较好的合理性。然而试验结果与理论计算结果总有一定的误差。S1计算曲线与试验结果在剪切位移小于3 mm时重合度较高;当剪切位移大于3 mm时,计算曲线与试验结果有一定误差,计算结果较试验结果偏大,这可能的原因是由于岩石脆性性质,节理剪切过程中在剪切位移后期会出现一定的脆性破坏使得预测结果大于试验结果。S2计算曲线与试验结果在剪切位移小于4 mm时重合度较高;当剪切位移大于4 mm时,计算曲线与试验结果有一定误差,计算结果较试验结果偏大,这可能的原因是同节理S1。由S4图可知,计算曲线与试验结果有一定误差。试验剪胀曲线从剪切位移2 mm才开始剪胀,这显示试验结果的弹性位移高达2 mm,这显然不符合常规,可能出现的原因是节理初始不吻合导致。将试验曲线向左平移1 mm显示节理试验曲线与计算剪胀曲线吻合度较好,这说明本模型具有一定的合理性。
5. 讨论
5.1 创新点
通过理论与试验分析,探求了具有三维表面形貌的岩石节理的剪胀行为。新模型具有3个创新点:①该模型考虑了节理形貌三维粗糙度的影响,通过分析实际接触节理在剪切过程中的三维粗糙度变化,来反映最大可能剪胀角的变化。节理法向位移的变化是节理在三角形微凸体侧面爬坡上升行为与爬越一些微凸体顶点后闭合行为的叠加。爬坡行为与闭合行为引起的位移都正比于节理最大可能剪胀角。②提出了一种预测软岩节理残余剪胀角的方法。与Barton公式的比较表明了新方法的有效性。③确定初始最大可能剪胀角。对于中间过程,给出了最大可能剪胀角的变化规律。新模型能很好地反映软岩节理的剪胀特性。
此外,一些试验观察表明,在剪切荷载作用下,岩石节理在较小的剪切位移下表现出轻微的负膨胀[19, 31]。一些研究类似[4-5, 7, 22],忽略了负膨胀。由计算结果可知,该模型还可以对初始节理剪切压密行为进行描述,同时阐明了初始压密行为的原因。在剪切弹性阶段节理法向位移是节理张开位移与闭合位移构成,其中爬坡引起的张开位移为0,这是因为此阶段只依赖节理基本摩擦角就可以抵抗剪切力,不需要爬坡张开行为。此时节理闭合位移即为节理法向位移。
在新模型中,ke是从剪切试验中获得的参数,这是剪切试验中唯一需要获得的参数。在实际工程和实验室条件下,只需要获得节理在初始弹性阶段的剪切状态,然后就可以获得节理整个剪切阶段的剪胀规律。因此,新提出的模型具有预测能力。新模型表明,节理剪胀规律与实际接触节理粗糙度之间存在密切关系。
Li等[30]提出剪胀角是最大可能剪胀角的一定比例,在很大程度上依赖于法向应力的大小,进而提出一个正弦函数形式的剪胀角模型来预测节理剪切规律,
\left.\begin{array}{l} \frac{\tan d_{\mathrm{n}}^{\mathrm{w}}}{\tan i_{\mathrm{mob}}}=1-\sin \left(\frac{\sigma_{\mathrm{n}}}{\sigma_{\mathrm{T}}^{\mathrm{w}}} \cdot \frac{{\rm{ \mathsf{ π} }}}{2}\right), \\ \frac{\tan d_{\mathrm{n}}^{\mathrm{u}}}{\tan i_{\mathrm{mob}}}=1-\sin \left(\frac{\sigma_{\mathrm{n}}}{\sigma_{\mathrm{T}}^{\mathrm{u}}} \cdot \frac{{\rm{ \mathsf{ π} }}}{2}\right), \\ d_{\mathrm{n}}=d_{\mathrm{n}}^{\mathrm{w}}+d_{\mathrm{n}}^{\mathrm{u}}, \\ \Delta \delta_{\mathrm{v}}=\Delta \delta_{\mathrm{s}}^{\mathrm{p}} \tan d_{\mathrm{n}}。 \end{array}\right\} (21) 式中: d_{\mathrm{n}}^{\mathrm{w}} , d_{\mathrm{n}}^{\mathrm{u}} ,dn为临界波形度,临界不均匀度, \sigma_{\mathrm{T}}^{\mathrm{w}} , \sigma_{\mathrm{T}}^{\mathrm{u}} 为临界波形度和临界不均匀度的过渡应力。
式(21)给出了一个三角函数关系式来描述剪胀 \left( {\frac{{{\sigma _{\rm n}}}}{{\sigma _{\mathrm{T}}^{\mathrm{u}}}} \cdot \frac{{\rm{ \mathsf{ π} }} }{2}} \right) 的物理意义。
本文将节理法向位移由节理在三角形微凸体侧面爬坡上升位移减去爬越一些微凸体顶点后闭合位移所得。式(21)中的第一式减去一个三角函数的形式刚好佐证了法向位移可分解为两部分相减的假设。
对于红砂岩与水泥砂浆复制节理,其a的数值都是0.6。对于其他类型软岩节理,是否为0.6数值还需进一步去验证。确定a的数值后,a值不依赖于节理形貌与法向应力的变化,对于某种材料岩石节理,a的数值是稳定的,这显示该模型具有一定的预测能力。
5.2 不足之处
新模型虽然具有上述优点,但也存在局限性。这个模型是基于“实际接触节理平均倾角”连续变化理论推导出来的,主要适用于低法向应力下的软岩节理。然而,对于高法向应力下的软岩节理或脆性节理,剪切破坏主要转变为脆性破坏。在高法向应力下,脆性节理将发生剪切岩爆,像花岗岩等单轴抗压强度较大的岩石类型,其脆性性质较为明显。在剪切过程中,由于微凸体的脆性特点,节理表面上的大型微凸体突然破坏,导致剪切应力出现较大的应力降。对于这些情况,新模型的预测能力较差。
图 5中S1计算曲线与试验结果在剪切位移小于3 mm时重合度较高,但当剪切位移大于3 mm时,计算曲线与试验结果存在一定的误差,计算结果较试验结果偏大。这可能是由于节理剪切过程中在剪切位移后期会发生一定的脆性破坏,从而导致预测结果大于试验结果。
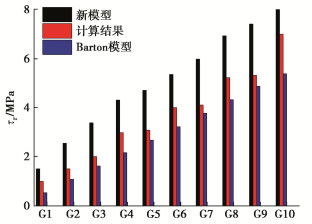
图 6为式(11)计算残余剪切强度与Barton公式和试验结果的对比。其中Barton提出残余摩擦角为φb,因此残余剪切强度为[21]
{\tau _{\text{r}}} = {\sigma _{\rm n}}\tan {\varphi _{\rm b}} 。 (22) 由图 6可知式(11)的计算结果大于试验结果,而Barton的计算结果小于试验结果。Barton公式的意义是节理经过剪切后其残余剪胀角为0,而本文的意义是经过剪切后其残余剪胀角为 \theta _{\rm{cr}}^* 。通过计算可知理论模型的平均误差为45%,Barton模型的平均误差为21%。这表明对于脆性岩石节理残余剪胀角更偏向于试验后节理磨损为平直节理。试验结果显示对于脆性岩石节理,其残余剪胀角介于0与 \theta _{\rm{cr}}^* 之间。可以认为脆性岩石节理残余剪胀角为Barton模型与式(11)关于脆性系数的加权平均,如下所示:
{\tau _{\rm r}} = {\sigma _{\rm n}}\tan ({\varphi _{\rm b}} + m\theta _{\rm{cr}}^*) 。 (23) 本文针对花岗岩节理,简单以Barton模型与式(11)的平均值作为其岩石节理的残余剪胀角计算残余剪切强度,结果见图 7。式(23)中m取为0.5,发现结果平均误差为13%,具有一定的准确度。但m的取值为0.5的物理意义需要进一步去探求。
6. 结论
为预测岩石节理的剪胀变形行为,分析了恒法向荷载作用下实际接触微凸体三维粗糙度在剪切过程中的退化规律,提出了一个适用于软岩节理的剪胀曲线预测模型,得到3点主要结论。
(1)在剪切过程中实际接触微凸体发生剪胀破坏和剪断破坏,剪胀破坏部分以最大可能剪胀角imob抵抗剪力,节理的剪胀行为是节理在三角形微凸体侧面爬坡上升行为与爬越一些微凸体顶点后闭合行为的叠加,爬坡行为与闭合行为引起的位移都正比于节理最大可能剪胀角。
(2)通过分析初始剪切与残余应力阶段的实际接触节理三维形貌特征,提出了计算初始最大可能剪胀角与残余应力阶段剪胀角的模型,最大可能剪胀角退化的实质是实际接触节理微凸体平均等效倾角的退化,通过研究节理微凸体在剪切过程中的退化规律,量化了最大可能剪胀角的变化规律。
(3)定量分析了节理爬坡上升行为和闭合行为与最大可能剪胀角之间的关联,进而基于最大可能剪胀角的退化规律提出了节理剪胀曲线模型,并且对初始节理剪切压密行为做出了合理解释,通过试验验证了新模型的有效性,且新模型可以较为精确地预测出节理剪胀规律。
该模型是基于剪切过程中节理不发生突然脆性破坏,假设实际接触节理平均等效倾角连续变化而推导获得,故该模型适用于法向应力较低时软岩节理的剪切行为分析。在预测脆性节理或高法向应力下软岩节理的剪切行为时,模型存在一定的局限性。关于脆性节理在高法向应力下的剪切变形规律还需进一步研究确定。
-
节理号 C /(°) /MPa S1 8.9 83.3 0.51 0.3 S2 7.6 82.3 0.61 0.7 S3 8.4 82.6 0.54 1.0 S4 8.9 83.9 0.49 1.3 S5 9.5 82.7 0.55 1.6 S6 7.9 81.6 0.58 2.0 S7 8.9 82.9 0.50 2.3 S8 8.8 83.5 0.47 2.6 S9 9.3 83.4 0.44 2.9 S10 8.3 84.2 0.51 3.3 -
[1] BAN L R, DU W S, QI C Z. A peak dilation angle model considering the real contact area for rock joints[J]. Rock Mechanics and Rock Engineering, 2020, 53: 4909-4923. doi: 10.1007/s00603-020-02193-1
[2] PATTON F D. Multiple modes of shear failure in rock[C]// Proceedings of the 1st ISRM Congress. Lisbon, 1966.
[3] KULATILAKE P H S W, BALASINGAM P, PARK J, et al. Natural rock joint roughness quantification through fractal techniques[J]. Geotechnical & Geological Engineering, 2006, 24(5): 1181-1202.
[4] LI Y, OH J, MITRA R, et al. A constitutive model for a laboratory rock joint with multi-scale asperity degradation[J]. Computers and Geotechnics, 2016, 72: 143-151. doi: 10.1016/j.compgeo.2015.10.008
[5] OH J, CORDING E J, MOON T. A joint shear model incorporating small-scale and large-scale irregularities[J]. International Journal of Rock Mechanics and Mining Sciences, 2015, 76: 78-87. doi: 10.1016/j.ijrmms.2015.02.011
[6] JING L, STEPHANSSON O, NORDLUND E. Study of rock joints under cyclic loading conditions[J]. Rock Mechanics and Rock Engineering, 1993, 26(3): 215-232. doi: 10.1007/BF01040116
[7] 肖维民, 余欢, 朱占元, 等. 薄层充填岩石节理剪胀特性试验研究[J]. 岩土工程学报, 2020, 42(8): 1499-1508. doi: 10.11779/CJGE202008015 XIAO Weimin, YU Huan, ZHU Zhanyuan, et al. Experimental study on shear dilatancy characteristics of thinly-infilled rock joints[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(8): 1499-1508. (in Chinese) doi: 10.11779/CJGE202008015
[8] LI Y C, TANG C A, LI D Q, et al. A new shear strength criterion of three-dimensional rock joints[J]. Rock Mechanics and Rock Engineering, 2020, 53(3): 1477-1483. doi: 10.1007/s00603-019-01976-5
[9] 尹宏, 王述红, 董卓然, 等. 引入因子分析的结构面粗糙度RBF复合参数模型[J]. 岩土工程学报, 2022, 44(4): 721-730. doi: 10.11779/CJGE202204015 YIN Hong, WANG Shuhong, DONG Zhuoran, et al. RBF composite parameter model for structural surface roughness with factor analysis[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(4): 721-730. (in Chinese) doi: 10.11779/CJGE202204015
[10] BARTON N, CHOUBEY V. The shear strength of rock joints in theory and practice[J]. Rock Mechanics, 1977, 10(1): 1-54.
[11] TSE R, CRUDEN D M. Estimating joint roughness coefficients[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1979, 16(5): 303-307.
[12] REEVES M J. Rock surface roughness and frictional strength[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1985, 22(6): 429-442.
[13] YANG Z Y, LO S C, DI C C. Reassessing the joint roughness coefficient (JRC) estimation using Z2[J]. Rock Mechanics and Rock Engineering, 2001, 34(3): 243-251. doi: 10.1007/s006030170012
[14] LEE Y H, CARR J R, BARR D J, et al. The fractal dimension as a measure of the roughness of rock discontinuity profiles[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1990, 27(6): 453-464.
[15] XIE H P, WANG J N, XIE W H. Fractal effects of surface roughness on the mechanical behavior of rock joints[J]. Chaos, Solitons & Fractals, 1997, 8(2): 221-252.
[16] HONG E S, LEE J S, LEE I M. Underestimation of roughness in rough rock joints[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32(11): 1385-1403. doi: 10.1002/nag.678
[17] BELEM T, HOMAND-ETIENNE F, SOULEY M. Quantitative parameters for rock joint surface roughness[J]. Rock Mechanics and Rock Engineering, 2000, 33(4): 217-242. doi: 10.1007/s006030070001
[18] TANG H M, GE Y F, WANG L Q, et al. Study on estimation method of rock mass discontinuity shear strength based on three-dimensional laser scanning and image technique[J]. Journal of Earth Science, 2012, 23(6): 908-913. doi: 10.1007/s12583-012-0301-2
[19] GRASSELLI G. Shear Strength of Rock Joints Based on Quantified Surface Description[D]. Zurich: Swiss Federal Institute of Technology, 2001.
[20] LADANYI B, ARCHAMBAULT G. Simulation of shear behavior of a jointed rock mass[C]//Proceedings of the 11th US Symposium on Rock Mechanics. Berkeley, 1970.
[21] BARTON N. Review of a new shear-strength criterion for rock joints[J]. Engineering Geology, 1973, 7(4): 287-332. doi: 10.1016/0013-7952(73)90013-6
[22] 刘丹, 张博文, 洪陈杰, 等. 岩石结构面两级形貌剪切特性研究[J]. 岩土工程学报, 2022, 44(8): 1434-1442. doi: 10.11779/CJGE202208008 LIU Dan, ZHANG Bowen, HONG Chenjie, et al. Shear properties of two-order morphology of rock joints[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(8): 1434-1442. (in Chinese) doi: 10.11779/CJGE202208008
[23] PLESHA M E. Constitutive models for rock discontinuities with dilatancy and surface degradation[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1987, 11(4): 345-362. doi: 10.1002/nag.1610110404
[24] SAEB S, AMADEI B. Modelling rock joints under shear and normal loading[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1992, 29(3): 267-278.
[25] LI Y C, SUN S Y, TANG C A. Analytical prediction of the shear behaviour of rock joints with quantified waviness and unevenness through wavelet analysis[J]. Rock Mechanics and Rock Engineering, 2019, 52(10): 3645-3657. doi: 10.1007/s00603-019-01817-5
[26] HABERFIELD C M, JOHNSTON I W. A mechanistically-based model for rough rock joints[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1994, 31(4): 279-292.
[27] PARK J W, LEE Y K, SONG J J, et al. A constitutive model for shear behavior of rock joints based on three-dimensional quantification of joint roughness[J]. Rock Mechanics and Rock Engineering, 2013, 46(6): 1513-1537. doi: 10.1007/s00603-012-0365-4
[28] SCHNEIDER H J. The friction and deformation behaviour of rock joints[J]. Rock Mechanics, 1976, 8(3): 169-184. doi: 10.1007/BF01239813
[29] ASADOLLAHI P, TONON F. Constitutive model for rock fractures: revisiting Barton's empirical model[J]. Engineering Geology, 2010, 113(1/2/3/4): 11-32.
[30] LI Y C, WU W, LI B. An analytical model for two-order asperity degradation of rock joints under constant normal stiffness conditions[J]. Rock Mechanics and Rock Engineering, 2018, 51(5): 1431-1445. doi: 10.1007/s00603-018-1405-5
[31] CUNDALL P, HART R. Analysis of block test No. 1 inelastic rock mass behavior: phase 2-A characterization of joint behavior (final report)[R]. Minneapolis: Itasca Consulting Group, 1984.
[32] XIA C C, TANG Z C, XIAO W M, et al. New peak shear strength criterion of rock joints based on quantified surface description[J]. Rock Mechanics and Rock Engineering, 2014, 47(2): 387-400. doi: 10.1007/s00603-013-0395-6
[33] GRASSELLI G, EGGER P. Constitutive law for the shear strength of rock joints based on three-dimensional surface parameters[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(1): 25-40. doi: 10.1016/S1365-1609(02)00101-6
[34] 杨洁. 结构面剪切渗流试验及其模型研究[D]. 武汉: 武汉大学, 2018. YANG Jie. Experimental and Modeling Study on Shear Flow Features of Structure Plane[D]. Wuhan: Wuhan University, 2018. (in Chinese)
-
期刊类型引用(0)
其他类型引用(1)
-
其他相关附件



 下载:
下载: