岩石结构面Grasselli二维粗糙度指标优化及其JRC估算

洪陈杰; 翁寒倩; 王凯; 黄曼; 陶志刚; 杜时贵

doi:10.11779/CJGE20230099

岩石结构面Grasselli二维粗糙度指标优化及其JRC估算 English Version

洪陈杰^1,,
翁寒倩¹,
王凯^{2, 3},
黄曼^{2, 3, ,},
陶志刚¹,
杜时贵⁴

1.
中国矿业大学(北京)隧道工程灾变防控与智能建养全国重点实验室, 北京 100083
2.
绍兴文理学院土木工程学院, 浙江绍兴 312000
3.
浙江省岩石力学与地质灾害重点实验室, 浙江绍兴 312000
4.
宁波大学土木与地理环境工程学院, 浙江宁波 315000

基金项目:

国家自然科学基金项目 42272333

国家自然科学基金项目 42277147

详细信息

作者简介:
洪陈杰(1994—)，男，博士研究生，主要从事岩体结构面粗糙度等方面的研究工作。E-mail: hongchenjie66@163.com

通讯作者:
黄曼，E-mail: hmcadx@126.com

中图分类号: TU45
计量
- 文章访问数: 415
- HTML全文浏览量: 62
- PDF下载量: 98
出版历程
- 收稿日期: 2023-02-07
- 网络出版日期: 2023-07-05
- 刊出日期: 2024-05-31

Updating Grasselli's 2D morphology parameter for estimating JRC of rock joints

HONG Chenjie^1,,
WENG Hanqian¹,
WANG Kai^{2, 3},
HUANG Man^{2, 3, ,},
TAO Zhigang¹,
DU Shigui⁴

1.
State Key Laboratory for Tunnel Engineering, China University of Mining and Technology, Beijing 100083, China
2.
School of Civil Engineering, Shaoxing University, Shaoxing 312000, China
3.
Key Laboratory of Rock Mechanics and Geohazards of Zhejiang Province, Shaoxing 312000, China
4.
School of Civil & Environmental Engineering and Geography Science, Ningbo University, Ningbo 315000, China

摘要

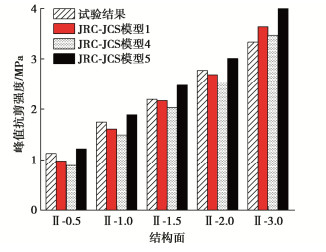
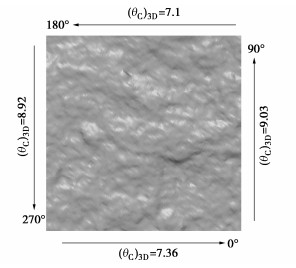
摘要: 采用只考虑迎剪侧表观倾角而忽略内部起伏角的Grasselli二维形貌参数 ${\theta _{\rm G}}$ 来估算结构面粗糙度系数JRC仍有待改进。从 ${\theta _{\rm G}}$ 的物理意义出发，发现爬坡区内部凸起高度对粗糙度的贡献可表示为其在总爬坡水平距离上的坡角，所有爬坡区提供的坡角之和定义为结构面内部起伏体粗糙贡献，将结构面迎剪侧表观平均倾角 ${\theta _{\rm G}}$ 和爬坡区内部平均坡角 ${\theta _{\rm H}}$ 叠加，提出岩石结构面粗糙度新指标 ${\theta _{\rm C}}$ 。通过获取十条标准JRC剖面线的 ${\theta _{\rm C}}$ ，分析其与JRC之间的关系，建立基于 ${\theta _{\rm C}}$ 的JRC估算式。计算不同采样间距和不同采样方向下的新指标 ${\theta _{\rm C}}$ ，结果显示 ${\theta _{\rm C}}$ 具有分形特征且能够反映结构面形貌各向异性。进一步将JRC估算式应用于JRC-JCS模型，通过对比已有研究得到的试验结果以及不同抗剪强度模型的预测效果，验证基于新指标 ${\theta _{\rm C}}$ 估算的JRC可以准确预测结构面峰值抗剪强度。最后，对二维指标 ${\theta _{\rm C}}$ 进行三维拓展，提出三维粗糙度新指标 ${({\theta _{\rm C}})_{\rm 3D}}$ ，并通过结构面形貌各向异性表征验证了其合理性。
- 岩石结构面 /
- 粗糙度 /
- 表观平均倾角 /
- 内部平均坡角 /
- 抗剪强度
Abstract: The Grasselli's 2D morphology parameter ${\theta _{\rm G}}$ used to estimate the joint roughness coefficient (JRC) is questionable, because it only considers the apparent inclination of the shear side and ignores the internal undulation angle. From the physical meaning of ${\theta _{\rm G}}$ , it is found that the contribution of internal bulge height in the climbing area to surface roughness can be expressed as the slope angle at the total climbing horizontal distance. The sum of the slope angles provided by all climbing areas is defined as the roughness of joint internal undulating. The apparent average inclination angle ${\theta _{\rm G}}$ and the internal average slope angle ${\theta _{\rm H}}$ are superimposed to propose a new roughness parameter ${\theta _{\rm C}}$ for rock joints. The ${\theta _{C}}$ of ten standard JRC profiles is obtained, and its relationship to JRC is then analyzed to establish an estimation formula for JRC based on ${\theta _{\rm C}}$ . The proposed parameter ${\theta _{\rm C}}$ under different sampling intervals and different sampling directions is calculated. The results show that ${\theta _{\rm C}}$ has fractal characteristics and can reflect the anisotropy of joint surface morphology. Further, the estimation formula for JRC is applied to the JRC-JCS model. By comparing the experimental results obtained from the existing researches and the predicted results under different shear strength models, it is verified that the estimated JRC based on ${\theta _{C}}$ can accurately predict the peak shear strength of joints. Finally, the new parameter ${\theta _{\rm C}}$ is extended to 3D form, and a 3D roughness parameter ${({\theta _{\rm C}})_{\rm 3D}}$ is proposed to capture the anisotropic characteristics of joint morphology.
- rock joint /
- joint roughness /
- apparent average inclination angle /
- internal average slope angle /
- shear strength

HTML全文

0. 引言

高温冻土是指由土颗粒基质、冰晶、未冻水和气体组成的温度介于-1.5℃~0℃的土体，通常表现出温度敏感性突出、力学性能低劣等特性，工程中极易引发建构筑物冻土地基产生非均匀沉降变形，甚至会导致上部结构开裂和破坏，严重威胁冻土工程安全设计与施工^[1]。因此，研究高温冻土本构模型具有重要工程意义，可为预测高温冻土地层变形特性从而避免工程灾害的发生提供重要手段。

朱元林等^[2]利用大量单轴压缩试验得出冻土应力-应变关系，结合曲线拟合与塑弹性理论建立了单轴压缩本构模型。苗天德等^[3]从微观视角出发，定义了压缩过程中的损伤因子，获得了冻土蠕变损伤本构关系。随后，诸多学者基于损伤力学理论，从细微观角度建立了冻土单轴唯像本构模型^[4]、细观损伤本构模型^[5]、宏细观本构模型^[6]、宏微观黏弹塑性本构模型^[7]。冻土体常在低围压条件下呈现出应变软化的变形特征，通过CT技术识别冻土内部变形过程中的损伤变量，可以描述冻土体蠕变过程中的损伤特征^[8-9]。对不同温度不同应变率下的冻土试件进行冲击压缩试验，可构建动荷载条件下的冻土本构关系^[10-11]。将加载-破坏屈服面及统一硬化参数整合，可建立冻土多相多面本构模型^[12]。空心圆柱仪试验可以科学量化不同应力水平条件下的冻土变形特征，为复杂应力条件下的本构关系构建提供了重要参考^[13]。

对于常规低温冻结，上述研究成果得到的本构模型基本能表征冻土不同应力状态下的力学状态^[14-15]。然而对于近相变区的高温冻土，冻结过程中冻结锋面、冰分凝锋面、冻结缘厚度随时间动态变化^[16-17]。当高温冻土未冻水含量相对较高时，内部的孔隙水压力增加较大使得作用在土骨架上的有效应力降低，表现出剪胀、应变软化特征；当高温冻土未冻水含量相对较低时，内部的孔隙水压力增加值小于总应力增加值，表现出剪缩、应变硬化特征，因此高温冻土同时存在剪缩、剪胀、硬化和软化特性^[18-19]。针对高温冻土，Liao等^[20]从强度随机分布出发，建立了可以反映冻土力学性质较强离散性的随机损伤本构模型，但将其作为弹性体的损伤本构模型研究存在一定的缺陷。Lai等^[21]从概率论与数理统计的视角出发，定义了材料截面内部的损失变量，提出了高温冻土损伤统计本构模型，但该模型难以对高低围压三轴应力路径下的高温冻土应力应变行为进行统一描述。

本文考虑黏聚力及内摩擦角的影响，以整体变形 $\varepsilon _{\text{v}}^{}$ -lnp曲线对冻土试样变形特征进行表征，建立了能够有效反映高温冻土剪缩、剪胀、硬化和软化特性的本构模型。该模型采用应力路径相关因子对等向固结路径条件下屈服面硬化参数进行修正，获得与应力路径无关的当前屈服面硬化参数，结合临界状态参数推导得到了能够体现高温冻土固有临界特性的参考屈服面硬化参数。自编程序计算了不同围压条件下高温冻土应力应变关系，利用试验数据对本文所构建的双屈服面统一本构模型进行了验证。

1. 本构模型建立

1.1 屈服函数

英国剑桥大学Roscoe等^[22]从能量方程推导出应力比与应变增量比的关系，结合正交法则、相关联流动法则及等向固结试验确定塑性应力应变关系，于1963年提出了原始剑桥模型。鉴于原始剑桥模型获得的屈服函数在 $p{\text{ - }}q$ 坐标系中与 $p$ 轴不正交，Roscoe等^[23]于1968年提出了塑性势函数(屈服函数)与 $p$ 轴正交的修正剑桥模型，定义了应力空间内 $g(p,q)$ 和 ${\text{(d}}\varepsilon _{\text{v}}^{\text{p}}{\text{,d}}\varepsilon _{\text{d}}^{\text{p}}{\text{)}}$ 的正交条件，表示为

。

${\text{d}}p{\text{d}}\varepsilon _{\text{v}}^{\text{p}} + {\text{d}}q{\text{d}}\varepsilon _{\text{d}}^{\text{p}} = 0 。$

(1)

荷载作用下塑性变形所消耗的功为

。

${\text{d}}{W^{\text{p}}} = p{\text{d}}\varepsilon _{\text{v}}^{\text{p}} + q{\text{d}}\varepsilon _{\text{d}}^{\text{p}} 。$

(2)

考虑到材料破坏时，也即临界状态下有

。

${q_{\text{f}}} = M(p + {p_r})\;\;\;({\text{d}}\varepsilon _{\text{v}}^{\text{p}} = 0) 。$

(3)

式中：M = $6\sin \varphi /(3 - \sin \varphi )$ ； ${p_{\text{r}}} = c\cot \varphi$ ，c， $\varphi$ 分别为土的黏聚力和内摩擦角。

将式（3）代入式（2）可得

$\begin{aligned} \mathrm{d} W^{\mathrm{p}} & =\left(p+p_{\mathrm{r}}\right) \mathrm{d} \varepsilon_{\mathrm{v}}^{\mathrm{p}}+q \mathrm{~d} \varepsilon_{\mathrm{d}}^{\mathrm{p}}=M\left(p+p_{\mathrm{r}}\right) \mathrm{d} \varepsilon_{\mathrm{d}}^{\mathrm{p}} \\ & =\left(p+p_{\mathrm{r}}\right) \sqrt{\left(\mathrm{d} \varepsilon_{\mathrm{v}}^{\mathrm{p}}\right)^2+\left(M \mathrm{~d} \varepsilon_{\mathrm{d}}^{\mathrm{p}}\right)^2} 。\end{aligned}$

(4)

整理式（4）可得

$\frac{{{\text{d}}\varepsilon _{\text{v}}^{\text{p}}}}{{{\text{d}}\varepsilon _{\text{d}}^{\text{p}}}} = \frac{{{M^2}{{(p + {p_{\text{r}}})}^2} - {q^2}}}{{2(p + {p_{\text{r}}})q}} 。$

(5)

求解方程（5）可得塑性势函数为

$g = {q^2} + {M^2}{(p + {p_{\text{r}}})^2} - C(p + {p_{\text{r}}}) = 0 。$

(6)

式中： $C$ 为积分常数， $C$ 取不同的值可得到不同的塑性势函数。

本文得到考虑高温冻土黏聚力及内摩擦角的修正剑桥模型塑性势面如图 1所示。

图 1 塑性势函数

Figure 1. Plastic potential function

下载: 全尺寸图片幻灯片

采用相关流动法则，当广义剪应力 $q = 0$ 时，令平均正应力 $p = {p_x}$ ，积分常数 $C = {M^2}({p_x} + {p_r})$ ，高温冻土屈服函数可进一步表示为

$f = {q^2} + {M^2}p(p + {p_r}) - {M^2}{p_x}(p + {p_r}) = 0 。$

(7)

变换式（7），并对两边取自然对数可得

$\ln \left[ {1 + \frac{{{q^2}}}{{{M^2}p(p + {p_r})}}} \right] = \ln {p_x} - \ln p 。$

(8)

1.2 屈服面参量及其修正

将高温冻土的等向固结试验（ ${\sigma _1} = {\sigma _2} = {\sigma _3}$ ）结果绘制在 ${\varepsilon _{\text{v}}}{\text{ - }}\ln p$ 坐标系中，如所示，回弹再加载曲线的斜率为 $\kappa$ ，记等向固结曲线NCL为

${\varepsilon _{\text{v}}} = \varphi \ln p 。$

(9)

图 2 ε_v-lnp平面中等向固结线NCL

Figure 2. Normal consolidation line in ε_v-lnp plane

下载: 全尺寸图片幻灯片

对式（9）进行微分可得

${\text{d}}{\varepsilon _{\text{v}}} = \varphi '(\ln p){\text{d}}\ln p 。$

(10)

弹性体积应变变化量为

${\text{d}}\varepsilon _{\text{v}}^{\text{e}} = \kappa d\ln p 。$

(11)

综合式（10），（11），得到塑性体积应变变化量为

${\text{d}}\varepsilon _{\text{v}}^{\text{p}} = {\text{d}}{\varepsilon _{\text{v}}} - {\text{d}}\varepsilon _{\text{v}}^{\text{e}} = (\varphi '\ln p - \kappa )d\ln p 。$

(12)

对式（12）进行变换并积分得到

$\int {\frac{{{\text{d}}\varepsilon _{\text{v}}^{\text{p}}}}{{\varphi '(\ln p) - \kappa }}} = \ln {p_x} - \ln {p_0} 。$

(13)

式中： ${p_0}$ 为与初始体积应变 ${\varepsilon _{{\text{v0}}}}$ 相对应的当前屈服面上的球应力，其决定了初始当前屈服面与 $p$ 轴的交点，其数值的确定在模型参数确定方法中详细介绍。

将式（13）代入式（8）得到屈服面函数为

$f = \ln \frac{p}{{{p_0}}} + \ln \left( {1 + \frac{{{q^2}}}{{{M^2}p(p + {p_r})}}} \right) - \int {\frac{{{\text{d}}\varepsilon _{\text{v}}^{\text{p}}}}{{\varphi '(\ln p) - \kappa }}} = 0 。$

(14)

根据式（14），高温冻土屈服面硬化参量可定义为

$H = \int {\frac{{{\text{d}}\varepsilon _{\text{v}}^{\text{p}}}}{{\varphi '(\ln p) - \kappa }}} 。$

(15)

为了使所要构建的高温冻土本构模型能够反映常压下的软化剪胀特性及塑性体积应变由剪缩阶段发展至剪胀阶段的特征状态分界线，模型中的硬化参量须包含能够有效反映特征状态的参数。根据姚仰平等^[24]提出的应力路径相关因子的方法，将应力路径相关因子设为

$R(\eta ) = \frac{{M_{\text{f}}^4}}{{{M^4}}}\frac{{{M^4} - {\eta ^4}}}{{M_{\text{f}}^4 - {\eta ^4}}} 。$

(16)

依据式（16）表征的应力路径相关因子，屈服面硬化参量修正为

$H = \int {\frac{1}{{R(\eta )}}\frac{{{\text{d}}\varepsilon _{\text{v}}^{\text{p}}}}{{\varphi '(\ln p) - \kappa }}} = \int {\frac{{{M^4}(M_{\text{f}}^4 - {\eta ^4})}}{{M_{\text{f}}^4({M^4} - {\eta ^4})}}\frac{{{\text{d}}\varepsilon _{\text{v}}^{\text{p}}}}{{\varphi '(\ln p) - \kappa }}} 。$

(17)

由此得到修正后的高温冻土当前屈服面函数：

$f=\mathrm{ln}\frac{p}{{p}_{0}}+\mathrm{ln}\left(1+\frac{{q}^{2}}{{M}^{2}p(p+{p}_{\text{r}})}\right)-{\displaystyle \int \frac{{M}^{4}({M}_{\text{f}}^{4}-{\eta }^{4})}{{M}_{\text{f}}^{4}({M}^{4}-{\eta }^{4})}\frac{\text{d}{\epsilon }_{\text{v}}^{\text{p}}}{{\phi }^{\prime }(\mathrm{ln}p)-\kappa }}。$

(18)

临界状态线在 $q{\text{ - }}p$ 空间中表示为一条不可逾越的应力比直线状态，在 ${\varepsilon _{\text{v}}}{\text{ - }}\ln p$ 空间中表示为一个稳定的非线性状态。通过三轴压缩试验可获得不同围压条件下由剪切开始至临界状态整个应力路径过程中冻土材料体积应变改变量与球应力p的关系，对达到临界状态时的球应力p取自然对数并统计与其相对应的体积应变可获得 ${\varepsilon _{\text{v}}}{\text{ - }}\ln p$ 空间中的CSL曲线，如图 3所示，记临界状态曲线CSL为

${\varepsilon _{\text{v}}} = \psi (\ln \bar p) 。$

(19)

图 3 ε_v-lnp平面中临界状态线CSL

Figure 3. Critical state line in ε_v-lnp plane

下载: 全尺寸图片幻灯片

可以看出，图 3中的高温冻土临界状态线与图 2中的等向压缩曲线形式相同，因此对其硬化参量的推导同式（13），可以得到

$\int {\frac{{{\text{d}}\varepsilon _{\text{v}}^{\text{p}}}}{{\psi '(\ln \bar p) - \kappa }}} = \ln {\bar p_x} - \ln {\bar p_0} 。$

(20)

式中： ${\bar p_0}$ 为与初始体积应变 ${\varepsilon _{{\text{v0}}}}$ 相对应的参考屈服面上的球应力，其决定了初始参考屈服面与 $p$ 轴的交点，其数值的确定在模型参数确定方法中详细介绍。

根据式（20）以及屈服函数式（8）便可推导得出参考屈服面函数为

$f = \ln \frac{{\bar p}}{{{{\bar p}_0}}} + \ln \left[ {1 + \frac{{{{\bar q}^2}}}{{{M^2}\bar p(\bar p + {p_{\text{r}}})}}} \right] - \int {\frac{{{\text{d}}\varepsilon _{\text{v}}^{\text{p}}}}{{\psi '(\ln \bar p) - \kappa }}} = 0 。$

(21)

参考屈服面硬化参量为

$\bar H = \int {\frac{{{\text{d}}\varepsilon _{\text{v}}^{\text{p}}}}{{\psi '\ln \bar p - \kappa }}} 。$

(22)

1.3 弹性应变增量

对于高温冻土本构模型的弹性部分，根据各向同性的假设，弹性应变增量可用张量表示为

${\text{d}}\varepsilon _{ij}^{\text{e}} = \frac{{1 + \nu }}{E}{\text{d}}{\sigma _{ij}} - \frac{\nu }{E}{\text{d}}{\sigma _{kk}}{\delta _{ij}} 。$

(23)

式中：E为弹性模量； $\nu$ 为泊松比。

根据标记法规则， ${\text{d}}{\sigma _{kk}} = {\text{d}}{\sigma _{11}} + {\text{d}}{\sigma _{22}} + {\text{d}}{\sigma _{33}}$ ，因此高温冻土体积应变与剪切应变增量形式为

${\text{d}}\varepsilon _{\text{v}}^{\text{e}} = \frac{{3(1 - 2\nu )}}{E}{\text{d}}p{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{d}}\varepsilon _{\text{d}}^{\text{e}} = \frac{{2(1 + \nu )}}{{3E}}{\text{d}}q 。$

(24)

将体积变形模型与剪切变形模量作为其计算参数，通过高温冻土等向固结试验（ ${\sigma _1} = {\sigma _2} = {\sigma _3}$ ），将结果绘制在 ${\varepsilon _{\text{v}}}{\text{ - }}\ln p$ 坐标系中，得到加载后回弹再加载曲线斜率 $\kappa$ ，则弹性体积应变增量公式为

${\text{d}}\varepsilon _v^e = \kappa d\ln p = \frac{\kappa }{p}{\text{d}}p 。$

(25)

对比式（24），（25）的数学表达计算式，模量K与模量G可进一步表示为

$K = \frac{{{\text{d}}p}}{{{\text{d}}\varepsilon _{\text{v}}^{\text{e}}}} = \frac{E}{{3(1 - 2\nu )}} = \frac{p}{\kappa } \text{，}$

(26)

$G = \frac{{{\text{d}}q}}{{3{\text{d}}\varepsilon _{\text{d}}^{\text{e}}}} = \frac{E}{{2(1 + \nu )}} = \frac{{3(1 - 2\nu )}}{{2(1 + \nu )}}K 。$

(27)

1.4 塑性应变增量

高温冻土在复杂应力状态下发生变形时，总应变可表示为

${\text{d}}{\varepsilon _{ij}} = {\text{d}}\varepsilon _{ij}^{\text{e}} + {\text{d}}\varepsilon _{ij}^{\text{p}} 。$

(28)

应力应变关系为

${\text{d}}{\sigma _{ij}} = C_{ijkl}^{\text{e}}{\text{d}}\varepsilon _{kl}^{\text{e}} = C_{ijkl}^{\text{e}}({\text{d}}{\varepsilon _{kl}} - {\text{d}}\varepsilon _{kl}^{\text{p}}) = C_{ijkl}^{{\text{ep}}}{\text{d}}{\varepsilon _{kl}} 。$

(29)

式中： $C_{ijkl}^{\text{e}}$ 为弹性张量； $C_{ijkl}^{{\text{ep}}}$ 为弹塑性张量。

由广义胡克定律可知弹性张量 $C_{ijkl}^{{\text{ep}}}$ 的具体表达式为

${C}_{ijkl}^{\text{e}}=\left(K-\frac{2}{3}G\right){\delta }_{ij}{\delta }_{kl}+G({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk})\text{ }。$

(30)

塑性应变增量由塑性位势理论确定, 因此存在如下数学关系：

${\text{d}}\varepsilon _{ij}^{\text{p}} = {\text{d}}\lambda \frac{{\partial g}}{{\partial {\sigma _{ij}}}} 。$

(31)

式中： ${\text{d}}\lambda$ 为塑性标量因子。

将屈服函数f简记为

$f({\sigma _{ij}},H(\varepsilon _{ij}^{\text{p}})) = 0 。$

(32)

对式（32）微分可得

${\text{d}}f = \frac{{\partial f}}{{\partial {\sigma _{ij}}}}{\text{d}}{\sigma _{ij}} + \frac{{\partial f}}{{\partial H}}\frac{{\partial H}}{{\partial \varepsilon _{ij}^{\text{p}}}}{\text{d}}\varepsilon _{ij}^{\text{p}} = 0 。$

(33)

将式（29），（31）代入式（33），并整理可得塑性标量因子 ${\text{d}}\lambda$ 的具体表达式为

${\text{d}}\lambda = \frac{{\frac{{\partial f}}{{\partial {\sigma _{ij}}}}C_{ijkl}^{\text{e}}{\text{d}}{\varepsilon _{kl}}}}{{ - \frac{{\partial f}}{{\partial H}}\frac{{\partial H}}{{\partial \varepsilon _{ij}^{\text{p}}}}\frac{{\partial g}}{{\partial {\sigma _{ij}}}} + \frac{{\partial f}}{{\partial {\sigma _{ij}}}}C_{ijkl}^{\text{e}}\frac{{\partial g}}{{\partial {\sigma _{kl}}}}}} 。$

(34)

将式（31），（34）代入式（29），并整理可得弹塑性张量 $C_{ijkl}^{{\text{ep}}}$ 的具体表达式为

$C_{ijkl}^{{\text{ep}}} = C_{ijkl}^{\text{e}} - \frac{{C_{ijmn}^{\text{e}}\frac{{\partial g}}{{\partial {\sigma _{mn}}}}\frac{{\partial f}}{{\partial {\sigma _{st}}}}C_{stkl}^{\text{e}}}}{{A + \frac{{\partial f}}{{\partial {\sigma _{ij}}}}C_{ijkl}^{\text{e}}\frac{{\partial g}}{{\partial {\sigma _{kl}}}}}} 。$

(35)

式中： $A = - \frac{{\partial f}}{{\partial H}}\frac{{\partial H}}{{\partial \varepsilon _{ij}^{\text{p}}}}\frac{{\partial g}}{{\partial {\sigma _{ij}}}}$ 。

1.5 应力应变关系

采用相关流动法则，只需对屈服函数f进行微分求导，根据复合函数求导法则有

$\frac{{\partial f}}{{\partial \sigma }} = \frac{{\partial f}}{{\partial {I_1}}}\frac{{\partial {I_1}}}{{\partial \sigma }} + \frac{{\partial f}}{{\partial \sqrt {{J_2}} }}\frac{{\partial \sqrt {{J_2}} }}{{\partial \sigma }} + \frac{{\partial f}}{{\partial \theta }}\frac{{\partial \theta }}{{\partial \sigma }} 。$

(36)

式中： ${I_1}$ 为第一主应力不变量； ${J_2}$ 为第二偏应力不变量； $\theta$ 为Lode角。

$\frac{{\partial \theta }}{{\partial \sigma }} = \frac{{\sqrt 3 }}{{2sin3\theta }}\left[ {\frac{1}{{{{({J_2})}^{{3 \mathord{\left/ {\vphantom {3 2}} \right. } 2}}}}}\frac{{\partial {J_3}}}{{\partial \sigma }} - \frac{{3{J_3}}}{{{{({J_2})}^2}}}\frac{{\partial \sqrt {{J_2}} }}{{\partial \sigma }}} \right] 。$

(37)

将式（37）代入式（36），整理可得

$\begin{gathered} \frac{\partial f}{\partial \sigma}=\frac{\partial f}{\partial I_1} \frac{\partial I_1}{\partial \sigma}+\left[\frac{\partial f}{\partial \sqrt{J_2}}+\frac{\partial f}{\partial \theta} \frac{\cot 3 \theta}{\sqrt{J_2}}\right] \frac{\partial \sqrt{J_2}}{\partial \sigma}+\frac{\partial f}{\partial \theta} \frac{\sqrt{3}}{2 \sin 3 \theta} . \\ \frac{1}{\left(J_2\right)^{3 / 2}} \frac{\partial J_3}{\partial \sigma} \end{gathered} 。$

(38)

考虑高温冻土当前屈服面函数形式的计算公式（14），（15），根据复合函数求导法则有

$\begin{gathered} \frac{\partial f}{\partial I_1}=\frac{\sqrt{3}}{2 \sin 3 \theta} \frac{1}{\left(J_2\right)^{3 / 2}} \frac{-2 q^2}{M(\theta)^3 p\left(p+p_r\right)+M(\theta) q^2}. \\ \frac{\partial M(\theta)}{\partial \theta} \end{gathered} 。$

(39)

由屈服函数中临界应力比 $M(\theta )$ 定义有

$\left.\begin{array}{l} M(\theta)=M\left(\theta=0^{\circ}\right)\left[\frac{2 \alpha^4}{1+\alpha^4-\left(1-\alpha^4\right) \cos 3 \theta}\right]^{\frac{1}{4}}, \\ \alpha=\frac{M\left(\theta=60^{\circ}\right)}{M\left(\theta=0^{\circ}\right)}=\frac{3-\sin \varphi}{3+\sin \varphi} 。 \end{array}\right\}$

(40)

对式（40）微分得

$\begin{aligned} \frac{\partial M(\theta)}{\partial \theta}= & {\left[\frac{2 \alpha^4}{1+\alpha^4-\left(1-\alpha^4\right) \cos 3 \theta}\right]^{\frac{5}{4}} } \\ & \frac{3\left(\alpha^4-1\right)}{8 \alpha^4} \sin 3 \theta \cdot M\left(\theta=0^{\circ}\right) 。\end{aligned}$

(41)

将式（40），（41）代入式（38）即可求得屈服函数f任一应力分量的一阶导数值。

根据式（16），（17）可得

$\begin{aligned} \frac{\partial f}{\partial H} \frac{\partial H}{\partial \varepsilon_{i j}^{\mathrm{p}}} \frac{\partial g}{\partial \sigma_{i j}} & =-\frac{M(\theta)^4\left(M(\theta)_{\mathrm{f}}^4-\eta^4\right)}{M(\theta)_{\mathrm{f}}^4\left(M(\theta)^4-\eta^4\right)} \frac{1}{\varphi^{\prime}(\ln p)-\kappa} .\\ & \frac{\partial \varepsilon_{\mathrm{v}}^{\mathrm{p}}}{\partial \varepsilon_{i j}^{\mathrm{p}}} \frac{\partial g}{\partial \sigma_{i j}} 。\end{aligned}$

(42)

因为 $\varepsilon _{\text{v}}^{\text{p}} = \varepsilon _{11}^{\text{p}} + \varepsilon _{22}^{\text{p}} + \varepsilon _{33}^{\text{p}}$ ，所以存在

$\left[ {\frac{{\partial \varepsilon _{\text{v}}^{\text{p}}}}{{\partial \varepsilon _{ij}^{p} }}} \right] = \left[ {1\;\;1\;\;1\;\;0\;\;0\;\;0} \right] 。$

(43)

将式（43）代入式（42），整理可得

$A=\frac{M{(\theta )}^{4}(M{(\theta )}_{\text{f}}^{4}-{\eta }^{4})}{M{(\theta )}_{\text{f}}^{4}(M{(\theta )}^{4}-{\eta }^{4})}\frac{1}{{\phi }^{\prime }(\mathrm{ln}p)-\kappa }\left(\frac{\partial g}{\partial {\sigma }_{11}}+\frac{\partial g}{\partial {\sigma }_{22}}+\frac{\partial g}{\partial {\sigma }_{33}}\right)。$

(44)

将式（30），（44）代入式（35）即可求得弹塑性张量 $C_{ijkl}^{{\text{ep}}}$ 的具体表达式。

1.6 模型参数及确定方法

根据高温冻土强度包线（直线）可确定内摩擦角 $\varphi$ 和黏聚力 $c$ ；泊松比 $\nu$ 可通过 $- \Delta {\varepsilon _r}/\Delta {\varepsilon _z}$ 获得；对于等向固结试验 ${\varepsilon _{\text{v}}}$ -lnp空间中回弹线斜率 $\kappa$ 可通过加载后回弹再加载试验确定； ${\varepsilon _{{\text{v0}}}}$ 为压缩固结完成开始剪切所对应的体积应变；伏斯列夫面(Hvorslev)斜率 ${M_{\text{h}}}$ 是 $q{\text{ - }}p$ 空间中不排水强度包线的斜率，通过冻土等向固结试验 $({\sigma _1} = {\sigma _2} = {\sigma _3})$ ，将结果绘制在 ${\varepsilon _{\text{v}}}{\text{ - }}p$ 坐标系中，便可获得等向固结曲线NCL，与初始体积应变 ${\varepsilon _{{\text{v0}}}}$ 对应的即为 ${p_0}$ 。通过多组不同压力等级下的三轴压缩试验，获得不同压力条件下的冻土临界体积应变与临界状态时球应力p的关系，将结果绘制于 ${\varepsilon _{\text{v}}}{\text{ - }}p$ 空间中，获得其临界状态曲线CSL，与初始体积应变 ${\varepsilon _{{\text{v0}}}}$ 对应的即为 ${\bar p_0}$ 。

2. 模型特性分析

2.1 固结参数与潜在强度

由式（21）推导可得参考应力点的球应力 $\bar p$ 为

$\bar p = {\bar p_0}\left( {\frac{{{M^2}}}{{{M^2} + \eta \eta '}}} \right)\exp \left( {\int {\frac{{{\text{d}}\varepsilon _{\text{v}}^{\text{p}}}}{{\psi '(\ln \bar p) - \kappa }}} } \right) 。$

(45)

式中： $\eta = q/(p + {p_r}) = \bar q/(\bar p + {p_r})$ ， $\eta ' = \bar q/\bar p$ 。

依据平面解析几何中直线与椭圆的基本关系，结合方程式（21）及 $\eta$ ，可求得 $\eta '$ 的具体表达式为

$\eta ' = \frac{{({M^2} + {\eta ^2})\eta {p_r}}}{{{M^2}{{\bar p}_0}\exp \left( {\int {\frac{{{\text{d}}\varepsilon _{\text{v}}^{\text{p}}}}{{\psi '(\ln \bar p) - \kappa }}} } \right) - {\eta ^2}{p_r}}} + \eta 。$

(46)

参照超固结土概念，定义高温冻土固结参数 $R$ 为参考应力点的球应力 $\bar p + {p_r}$ 与当前应力点的球应力 $p + {p_r}$ 的比值，即

$R = \frac{{\bar p + {p_r}}}{{p + {p_r}}} 。$

(47)

综合式（45），（46）可得高温冻土固结参数 $R$ 的具体表达式为

$R = \frac{1}{{p + {p_r}}}\left\{ {{{\bar p}_0}\left( {\frac{{{M^2}}}{{{M^2} + \eta \eta '}}} \right)\exp \left[ {\int {\frac{{{\text{d}}\varepsilon _{\text{v}}^{\text{p}}}}{{\psi '(\ln \bar p) - \kappa }}} } \right] + {p_r}} \right\} 。$

(48)

将高温冻土当前屈服面、参考屈服面、伏斯列夫面(Hvorslev)、临界状态线CSL绘制于同一坐标系（p-q）中，如所示。对于特定的应力状态点 $(p,q)$ ，潜在强度M_f与其相对应，并由参考应力点 $(\bar p,\bar q)$ 与冻土材料伏斯列夫面(Hvorslev)斜率共同决定，剪应力 ${q_{\text{f}}}$ 可表示为

${q_{\text{f}}} = M(\bar p + {p_r}) - {M_{\text{h}}}(\bar p - p) \text{，}$

(49)

${M_{\text{f}}} = \frac{{M(\bar p + {p_r}) - {M_{\text{h}}}(\bar p - p)}}{{p + {p_r}}} = M + (R - 1)(M - {M_{\text{h}}}) 。$

(50)

图 4 基于Hvorslev面的潜在强度M_f

Figure 4. Potential strength M_f based on Hvorslev surface

下载: 全尺寸图片幻灯片

图 5表明了高温冻土固结参数R、潜在强度M_f与硬化参数H之间的相互关系，由于不同的固结程度的高温冻土具有不同的潜在强度，所以固结参数R决定潜在强度M_f的大小；式（17）的硬化参数H中包含了潜在强度M_f，故M_f的变化直接影响硬化参数H；高温冻土在复杂应力作用下的硬化参数H决定着当前屈服面与参考屈服面状态及表达式，进而间接影响固结参数R。

图 5 高温冻土模型参数R，M_f，H相互关系

Figure 5. Relationship among model parameters R, M_f and H of warm frozen soil

下载: 全尺寸图片幻灯片

2.2 模型演化分析

微分当前屈服面硬化参量式（15）及参考屈服面硬化参量式（22）可得

${\text{d}}H = \frac{{{M^4}(M_{\text{f}}^4 - {\eta ^4})}}{{M_{\text{f}}^4({M^4} - {\eta ^4})}}\frac{{{\text{d}}\varepsilon _{\text{v}}^{\text{p}}}}{{\varphi '(\ln p) - \kappa }} \text{，}$

(51)

${\text{d}}\bar H = \frac{{{\text{d}}\varepsilon _{\text{v}}^{\text{p}}}}{{\psi '(\ln p) - \kappa }} 。$

(52)

对式（51），（52）进行整个应力路径中的分析，可得表 1所示的变化规律。

表 1 模型状态演化过程

Table 1. Evolution process of model states

状态阶段	应力比η、特征状态应力比M及潜在强度 ${M_{\text{f}}}$ 间关系	塑性体变增量 ${\text{d}}\varepsilon _{\text{v}}^{\text{p}}$ 、屈服面硬化参量增量增量 ${\text{d}}H$ 、 ${\text{d}}\overline H$
初始状态	$0 = \eta < M < {M_{\text{f}}}$	${\text{d}}\varepsilon _{\text{v}}^{\text{p}} > 0\;,\;{\text{d}}H > 0\;,\;{\text{d}}\bar H > 0$
剪缩、硬化阶段	$0 < \eta < M < {M_{\text{f}}}$	${\text{d}}\varepsilon _{\text{v}}^{\text{p}} > 0\;,\;{\text{d}}H > 0\;,\;{\text{d}}\bar H > 0$
特征状态	$0 < \eta = M < {M_{\text{f}}}$	${\text{d}}\varepsilon _{\text{v}}^{\text{p}} = 0\;,\;{\text{d}}H > 0\;,\;{\text{d}}\bar H = 0$
剪胀、硬化阶段	$0 < M < \eta < {M_{\text{f}}}$	${\text{d}}\varepsilon _{\text{v}}^{\text{p}} < 0\;,\;{\text{d}}H > 0\;,\;{\text{d}}\bar H < 0$
峰值应力状态	$0 < M < \eta = {M_{\text{f}}}$	${\text{d}}\varepsilon _{\text{v}}^{\text{p}} < 0\;,\;{\text{d}}H = 0\;,\;{\text{d}}\bar H < 0$
第一剪胀软化阶段	$0 < M < {M_{\text{f}}} < \eta$	${\text{d}}\varepsilon _{\text{v}}^{\text{p}} < 0\;,\;{\text{d}}H < 0\;,\;{\text{d}}\bar H < 0$
第二剪胀软化阶段	$0 < M = {M_{\text{f}}} < \eta$	${\text{d}}\varepsilon _{\text{v}}^{\text{p}} < 0\;,\;{\text{d}}H < 0\;,{\text{d}}\bar H < 0$
临界状态	$0 < M = {M_{\text{f}}} = \eta$	${\text{d}}\varepsilon _{\text{v}}^{\text{p}} = 0\;,\;{\text{d}}H = 0\;,\;{\text{d}}\bar H = 0$

下载: 导出CSV

| 显示表格

由此可见，建立在潜在强度M_f、特征状态应力比M和应力比η有关的硬化参数H的基础上，本文模型能够有效反映高温冻土的剪缩、剪胀、硬化和软化特性。

3. 模型试验验证

3.1 模型的试验验证Ⅰ

Ma等^[17]对兰州某地饱和冻结粉土进行了一系列三轴剪切室内试验，粉土干密度为1.75 g/cm³，三轴试验MTS810围压设定分别为1.0，2.0，6.0 MPa，高温冻结温度为-1.5℃；试验过程分为等向加载阶段和轴向应力加载阶段，围压约束的加载在5 min内完成，轴向应力以1.108 mm/min的速度加载，以试样轴向应变达到15%时作为试样破坏条件；本文所建模型需要6个参数和2条试验曲线，根据文献[，]及参数拟合： $c$ =112.3 kPa， $\varphi$ =25.8℃， $\nu$ =0.32， $\kappa$ =-8.8×10^-7， ${\varepsilon _{{\text{v0}}}}$ =1.72×10^-2， ${M_{\text{h}}}$ =1.17，等向固结曲线曲线 ${\varepsilon _{\text{v}}} =$ ${\text{2}}{\text{.18}} \times {\text{1}}{{\text{0}}^{ - {\text{6}}}} \cdot {\text{exp(0}}{\text{.726ln}}p{\text{)}}$ ，临界状态曲线曲线 ${\varepsilon _{\text{v}}} =$ ${\text{1}}{\text{.83}} \times {\text{1}}{{\text{0}}^{ - {\text{5}}}} \cdot {\text{exp(0}}{\text{.687ln}}p{\text{)}}$ ，

图 6（a）为-1.5℃条件下高温冻结粉土偏应力与轴向应变的模型预测结果与试验数据对比，可以看出，本文模型对1.0，2.0，6.0 MPa围压条件下剪切行为的预测结果与试验数据吻合度较高。在1.0 MPa围压条件下，高温冻结粉土偏应力一直增加（硬化），在6.0 MPa围压条件下，高温冻结粉土偏应力先增加后减小（软化）；在相同围压下，应力应变曲线主要呈三阶段变化，在初始阶段曲线呈线性变化，随着轴向应变的增加，曲线逐渐过渡到弹塑性阶段，此时试样内部以不可恢复的塑性变形为主。对于应变硬化的情况，应力逐渐到达最大值，曲线斜率近视趋近于零；对于应变软化的情况，当偏应力超过一定值时，曲线斜率由正转为负值，这是由于高温冻土特有的压融现象使得未冻水含量增加，试样内部超静孔隙水压力增加，颗粒之间的有效应力降低，剪切破坏极易发生。图 6（b）为-1.5℃条件下体积应变与轴向应变的模型预测结果与试验数据对比，可以看出，本文模型对1.0，2.0，6.0 MPa围压条件下体变行为的预测结果与试验数据吻合度较好。在围压较低时，试样因侧向变形受到的约束力较小而表现为稳定的剪缩特征；在围压较高时，试样因内部冰晶结构微裂隙及孔隙损伤开裂破坏而表现为特定的剪胀特征。综合图 6（a）和图 6（b）的试验数据和预测曲线，可以得出，-1.5℃条件下的高温冻结粉土在低围压条件下总体表现出剪缩硬化特性，在高围压条件下总体表现出剪胀软化特性，本文所建模型可以有效反映-1.5℃条件下的高温冻土剪缩、剪胀、硬化和软化特性。

图 6 模型预测结果与试验数据对比（-1.5℃）

Figure 6. Comparison between model results with experimental data (-1.5℃)

下载: 全尺寸图片幻灯片

3.2 模型的试验验证Ⅱ

宋丙堂等^[18]对兰州市安宁区某地冻结粉土进行了一系列三轴压缩加卸载试验，粉土干密度为1.70 g/cm³，液限和塑限分别为27.6%，19.4%，初始含水率为1.36%；饱和冻结处理后，试验含水率为22.28%，重度为0.017 kN/m³，孔隙比为0.73；MTS810三轴试验围压设定为0.3~6.0 MPa（共8组），高温冻结温度为-1.0℃；试验过程分为等向加载阶段和轴向应力加载阶段，围压约束的加载在5 min内完成，轴向应力以1.108 mm/min的速度加载，以试样轴向应变达到20%时作为试样破坏条件；当高温冻土轴向应变 ${\varepsilon _{\text{a}}}$ =3%时，卸载偏差应力到零，然后将轴向应变加载到5.75%，再进行第二次卸载，应变的加卸载增量步取2.75%，本文所建模型需要6个参数和2条试验曲线，根据文献[，]及参数拟合确定参数： $c$ =89.3 kPa， $\varphi$ =23.4℃， $\nu$ =0.35， $\kappa$ =-8.6×10^-7， ${\varepsilon _{{\text{v0}}}}$ = 2.14× 10^-2， ${M_{\text{h}}}$ =1.09，等向固结曲线 ${\varepsilon _{\text{v}}} = {\text{2}}{\text{.23}}$ × ${\text{1}}{{\text{0}}^{ - {\text{6}}}} \cdot$ ${\text{exp(0}}{\text{.689ln}}p{\text{)}}$ ，临界状态曲线 ${\varepsilon _{\text{v}}} = {\text{1}}{\text{.76}}$ × ${\text{1}}{{\text{0}}^{ - {\text{5}}}} \cdot$ ${\text{exp}}$ ${\text{(0}}{\text{.734ln}}p{\text{)}}$ ，

从图 7（a）可以看出，本文模型对1.4，2.0，4.0，6.0 MPa围压条件下剪切行为的预测结果与试验数据吻合度较好。在1.4，2.0 MPa围压条件下，高温冻结粉土偏应力一直增加（硬化），在4.0，6.0 MPa围压条件下，高温冻结粉土偏应力先增加后减小（软化）；在同一围压条件下，初始阶段曲线呈线性变化，试样内部以可恢复的弹性变形为主；随着轴向应变的增加，曲线逐渐过渡到弹塑性阶段，此时试样内部以不可恢复的塑性变形为主。对于应变硬化的情况，应力逐渐增加到最大值，曲线斜率近视趋近于零，可认为该强度即为-1.0℃的高温冻结粉土在该围压条件下的极限强度；对于应变软化的情况，当偏应力超过一定值时，曲线斜率由正转为负值，这是由于高温冻土中形成的不稳定冰晶在一定压力条件下发生破坏，试样内孔隙水压力增加，颗粒之间的有效应力降低，进而发生剪切破坏，强度降低。从图 7（b）可以看出，本文模型对体变行为的预测结果与试验数据吻合度较高。在1.4，2.0 MPa较低围压时，试样因侧向变形受到的约束力较小而表现为稳定的剪缩特征；在4.0，6.0 MPa较高围压时，试样在初始阶段因内部冰晶结构微裂隙及孔隙损伤开裂破坏而表现为特定的剪胀特征，随着轴向应变的增加，试样逐渐表现为稳定的剪缩特征。综合图 7（a），（b）可以得出，-1.0℃条件下的高温冻结粉土在低围压条件下总体表现出剪缩硬化特性，在高围压条件下总体表现出剪胀软化特性，本文所建模型可以有效反映-1.0℃条件下的高温冻土剪缩、剪胀、硬化和软化特性。

图 7 模型预测结果与试验数据对比（-1.0℃）

Figure 7. Comparison between model results with experimental data (-1.0℃)

下载: 全尺寸图片幻灯片

4. 结论

（1）与传统模型中使用的 $e{\text{ - }}\ln p$ 变形特征曲线相比，以 ${\varepsilon _{\text{v}}}{\text{ - }}\ln p$ 曲线对高温冻土试样变形进行描述后，NCL和CSL曲线表达简便，有利于双屈服面函数形式的简化表征及模型参数的方便获取。

（2）由当前屈服面与参考屈服面间的关系重新定义了能够反映高温冻土应力状态的固结参数及潜在强度，得到的双屈服面统一本构模型能够有效反映高温冻土的剪缩、剪胀、硬化和软化特性。

（3）本模型在经典修正剑桥模型基础上引入的新参数较少，可以通过常规三轴试验、等向固结试验、回弹再加载试验等基本土工试验获取，模型应用简便，试验结果验证了所建模型的合理性。

图 1 不同角度阈值的剖面线有效接触长度变化（改自文献[9]）

Figure 1. Change in potential contact length of profiles at different angle thresholds(modified from Reference [9])

下载: 全尺寸图片幻灯片

图 2 锯齿状结构面示意及其数值模拟结果

Figure 2. Schematic diagram of sawtooth-shaped joint and its numerical simulation results

下载: 全尺寸图片幻灯片

${\theta _{\rm G}}$ ， ${\theta _{\rm H}}$ 计算示意图

Calculation diagram of ${\theta _{\rm G}}$ and ${\theta _{\rm H}}$

下载: 全尺寸图片幻灯片

图 4 数字化标准剖面线

Figure 4. Digital standard profiles

下载: 全尺寸图片幻灯片

图 5 基于不同学者研究数据的计算结果对比

Figure 5. Comparison of calculated results based on different scholars' data

下载: 全尺寸图片幻灯片

${\theta _{\rm C}}$ 与JRC关系式

Relationship between ${\theta _{\rm C}}$ and JRC

下载: 全尺寸图片幻灯片

$\ln \Delta x$ 与 $\ln {\theta _{\rm G}}$ ， $\ln {\theta _{\rm H}}$ ， $\ln {\theta _{\rm C}}$ 线性关系

Relationship of $\ln \Delta x$ with $\ln {\theta _{\rm C}}$ , $\ln {\theta _{\rm G}}$ and $\ln {\theta _{\rm H}}$

下载: 全尺寸图片幻灯片

图 8 结构面剖面线提取位置

Figure 8. Location of 2D proﬁles extracted from joint surface

下载: 全尺寸图片幻灯片

图 9 结构面粗糙度各向异性

Figure 9. Anisotropy of joint roughness

下载: 全尺寸图片幻灯片

图 10 基于标准剖面线的不同JRC-JCS模型预测结果对比

Figure 10. Comparison between results predicted by different JRC-JCS models based on standard JRC profiles

下载: 全尺寸图片幻灯片

图 11 基于天然剖面线的不同JRC-JCS模型预测结果对比

Figure 11. Comparison between results predicted by different JRC-JCS models based on natural profiles

下载: 全尺寸图片幻灯片

基于 ${({\theta _{\rm C}})_{\rm 3D}}$ 计算的天然结构面粗糙度

Roughnesses of natural rock joint calculated by ${({\theta _{\rm C}})_{\rm 3D}}$

下载: 全尺寸图片幻灯片

表 1 模型细观力学参数^[16]

Table 1 Mesoscopic parameters of joint model^[16]

类别	参数	值
颗粒	颗粒直径/mm	0.14~0.21
	颗粒密度/(kg·m^-3)	2205
	有效模量/GPa	2.8
	摩擦系数	0.6
	刚度比	1.45
平行黏结模型	有效模量/GPa	2.8
	拉应力/MPa	20
	黏结应力/MPa	20
	刚度比	1.45
光滑节理模型	节理法向刚度/(MPa·mm^-1)	200
	节理切向刚度/(MPa·mm^-1)	50
	摩擦系数	0.78

下载: 导出CSV

不同JRC剖面线的 ${\theta _{\rm C}}$ ， ${\theta _{\rm G}}$ ， ${\theta _{\rm H}}$ 值

Values of ${\theta _{\rm C}}$ , ${\theta _{\rm G}}$ and ${\theta _{\rm H}}$ of different JRC profiles

JRC剖面线	标准JRC值	Δx=0.5 mm							Δx=1.0 mm
		正向分析			反向分析			平均值	正向分析			反向分析			平均值
		${\theta _{\rm G}}$	${\theta _{\rm H}}$	${\theta _{\text{C}}}$	${\theta _{\rm G}}$	${\theta _{\rm H}}$	${\theta _{\text{C}}}$	${\theta _{\text{C}}}$	${\theta _{\rm G}}$	${\theta _{\rm H}}$	${\theta _{\text{C}}}$	${\theta _{\rm G}}$	${\theta _{\rm H}}$	${\theta _{\text{C}}}$	${\theta _{\text{C}}}$
1	0.4	3.04	0.83	3.87	3.50	1.00	4.50	4.19	2.05	0.57	2.62	3.28	0.88	4.17	3.39
2	2.8	5.03	1.95	6.98	4.32	1.87	6.20	6.59	4.29	1.67	5.96	4.12	1.28	5.40	5.68
3	5.8	5.51	2.33	7.84	5.64	2.48	8.12	7.98	5.26	1.96	7.23	5.14	2.44	7.58	7.40
4	6.7	7.49	3.46	10.95	8.69	3.81	12.50	11.73	7.42	2.81	10.23	7.72	2.58	10.31	10.27
5	9.5	8.24	3.90	12.14	7.43	3.48	10.91	11.53	7.05	3.15	10.21	7.06	2.80	9.86	10.03
6	10.8	9.63	4.48	14.11	10.36	4.80	15.17	14.64	9.80	4.09	13.89	9.41	4.65	14.06	13.98
7	12.8	11.37	4.69	16.05	10.77	4.76	15.53	15.79	10.30	3.71	14.01	9.59	3.83	13.42	13.72
8	14.5	12.61	6.64	19.25	12.77	6.55	19.32	19.28	12.24	5.93	18.17	12.77	6.73	19.50	18.84
9	16.7	14.14	7.04	21.18	14.52	6.92	21.44	21.31	13.83	5.66	19.49	12.90	5.95	18.85	19.17
10	18.7	15.97	7.24	23.21	16.19	6.85	23.03	23.12	14.54	6.37	20.91	14.09	5.87	19.96	20.43

下载: 导出CSV

表 3 JRC=16~18剖面线在各采样间距下的粗糙度值

Table 3 Roughnesses of profiles with JRC of 16~18 at each.sampling interval

Δx/mm	0.5	1.0	1.5	2.0	2.5	3.0
${\theta _{\rm G}}$	14.33	13.36	12.13	11.49	10.86	9.99
${\theta _{\rm H}}$	6.98	5.81	4.13	4.11	3.82	3.88
${\theta _{\rm C}}$	21.31	19.17	16.26	15.60	14.68	13.87

下载: 导出CSV

基于 ${\theta _{\rm C}}$ 的10条标准JRC剖面线的分形维数

Table 4 Fractal dimensions of ten standard JRC profiles

JRC剖面线	标准JRC值	分形维数D
1	0.4	1.4427
2	2.8	1.3260
3	5.8	1.2729
4	6.7	1.3519
5	9.5	1.3384
6	10.8	1.1340
7	12.8	1.1546
8	14.5	1.1078
9	16.7	1.2449
10	18.7	1.2002

下载: 导出CSV

参考文献(26)

[1]	夏才初, 孙宗颀. 工程岩体节理力学[M]. 上海: 同济大学出版社, 2002. XIA Caichu, SUN Zongqi. Joint Mechanics of Engineering Rock Mass[M]. Shanghai: Tongji University Press, 2002. (in Chinese)
[2]	ZHANG G C, KARAKUS M, TANG H M, et al. A new method estimating the 2D Joint Roughness Coefficient for discontinuity surfaces in rock masses[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 72: 191-198. doi: 10.1016/j.ijrmms.2014.09.009
[3]	BARTON N. Review of a new shear-strength criterion for rock joints[J]. Engineering Geology, 1973, 7(4): 287-332. doi: 10.1016/0013-7952(73)90013-6
[4]	BARTON N, CHOUBEY V. The shear strength of rock joints in theory and practice[J]. Rock Mechanics, 1977, 10(1): 1-54.
[5]	ISRM. Suggested methods for the quantitative description of discontinuities in rock masses[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1978, 15(6): 319-368.
[6]	班力壬, 戚承志, 燕发源, 等. 岩石节理粗糙度新指标及新的JRC确定方法[J]. 煤炭学报, 2019, 44(4): 1059-1065. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201904010.htm BAN Liren, QI Chengzhi, YAN Fayuan, et al. A new method for determining the JRC with new roughness parameters[J]. Journal of China Coal Society, 2019, 44(4): 1059-1065. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201904010.htm
[7]	陈世江, 常建平, 姬长兴, 等. 两统计参数评估结构面粗糙度探讨及试验验证[J]. 岩石力学与工程学报, 2021, 40(3): 476-489. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202103003.htm CHEN Shijiang, CHANG Jianping, JI Changxing, et al. A two-parameter evaluation method of joint roughness and its experimental verification[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(3): 476-489. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202103003.htm
[8]	GRASSELLI G. Shear Strength of Rock Joints Based on Quantified Surface Description[D]. Lausanne: Ecole Polytechnique Federale De Lausanne, 2001.
[9]	TATONE B S A, GRASSELLI G. A new 2D discontinuity roughness parameter and its correlation with JRC[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(8): 1391-1400. doi: 10.1016/j.ijrmms.2010.06.006
[10]	唐志成, 刘泉声, 刘小燕. 节理的剪切力学性质与含三维形貌参数的剪切强度准则比较研究[J]. 岩土工程学报, 2014, 36(5): 873-879. doi: 10.11779/CJGE201405009 TANG Zhicheng, LIU Quansheng, LIU Xiaoyan. Shear behavior of rock joints and comparative study on shear strength criteria with three-dimensional morphology parameters[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(5): 873-879. (in Chinese) doi: 10.11779/CJGE201405009
[11]	YANG J, RONG G, HOU D, et al. Experimental study on peak shear strength criterion for rock joints[J]. Rock Mechanics and Rock Engineering, 2016, 49(3): 821-835. doi: 10.1007/s00603-015-0791-1
[12]	LIU Q S, TIAN Y C, LIU D F, et al. Updates to JRC-JCS model for estimating the peak shear strength of rock joints based on quantified surface description[J]. Engineering Geology, 2017, 228: 282-300. doi: 10.1016/j.enggeo.2017.08.020
[13]	BAN L R, DU W S, QI C Z, et al. Modified 2D roughness parameters for rock joints at two different scales and their correlation with JRC[J]. International Journal of Rock Mechanics and Mining Sciences, 2021, 137: 104549. doi: 10.1016/j.ijrmms.2020.104549
[14]	CHEN X, ZENG Y W, YE Y, et al. The physical meaning of Grasselli's morphology parameters and its correlations with several other 2D fracture roughness parameters[J]. International Journal of Rock Mechanics and Mining Sciences, 2021, 145: 104854. doi: 10.1016/j.ijrmms.2021.104854
[15]	GRASSELLI G, EGGER P. Constitutive law for the shear strength of rock joints based on three-dimensional surface parameters[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(1): 25-40. doi: 10.1016/S1365-1609(02)00101-6
[16]	BAHAADDINI M, SHARROCK G, HEBBLEWHITE B K. Numerical direct shear tests to model the shear behaviour of rock joints[J]. Computers and Geotechnics, 2013, 51: 101-115. doi: 10.1016/j.compgeo.2013.02.003
[17]	KWON T H, HONG E S, CHO G C. Shear behavior of rectangular-shaped asperities in rock joints[J]. KSCE Journal of Civil Engineering, 2010, 14(3): 323-332. doi: 10.1007/s12205-010-0323-1
[18]	TSE R, CRUDEN D M. Estimating joint roughness coefficients[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1979, 16(5): 303-307.
[19]	YANG Z Y, LO S C, DI C C. Reassessing the joint roughness coefficient (JRC) estimation using Z2[J]. Rock Mechanics and Rock Engineering, 2001, 34(3): 243-251. doi: 10.1007/s006030170012
[20]	YU X B, VAYSSADE B. Joint profiles and their roughness parameters[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1991, 28(4): 333-336.
[21]	孙辅庭, 佘成学, 万利台. Barton标准剖面JRC与独立于离散间距的统计参数关系研究[J]. 岩石力学与工程学报, 2014, 33(增刊2): 3539-3544. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2014S2019.htm SUN Futing, SHE Chengxue, WAN Litai. Research on relationship between JRC of barton's standard profiles and statistic parameters independent of sampling interval[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(S2): 3539-3544. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2014S2019.htm
[22]	张建明, 唐志成, 蒋景东, 等. 统计参数与JRC的定量关系研究[J]. 科学技术与工程, 2015, 15(14): 1-5. doi: 10.3969/j.issn.1671-1815.2015.14.001 (ZHANG Jianming, TANG Zhicheng, JIANG Jingdong, et al. A study of relationships between statistical parameters of typical rock-joint curves and JRC based on image analysis techniques[J]. Science Technology and Engineering, 2015, 15(14): 1-5. doi: 10.3969/j.issn.1671-1815.2015.14.001
[23]	葛云峰, 唐辉明, 王亮清, 等. 天然岩体结构面粗糙度各向异性、尺寸效应、间距效应研究[J]. 岩土工程学报, 2016, 38(1): 170-179. doi: 10.11779/CJGE201601019 GE Yunfeng, TANG Huiming, WANG Liangqing, et al. Anisotropy, scale and interval effects of natural rock discontinuity surface roughness[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(1): 170-179. (in Chinese) doi: 10.11779/CJGE201601019
[24]	王思敬. 论岩石的地质本质性及其岩石力学演绎[J]. 岩石力学与工程学报, 2009, 28(3): 433-450. doi: 10.3321/j.issn:1000-6915.2009.03.001 WANG Sijing. Geological nature of rock and its deduction for rock mechanics[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(3): 433-450. (in Chinese) doi: 10.3321/j.issn:1000-6915.2009.03.001
[25]	肖维民, 刘伟超, 朱占元. 基于正反向直剪试验的岩石节理JRC值计算研究[J]. 岩石力学与工程学报, 2021, 40(增刊2): 3098-3106. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2021S2010.htm XIAO Weimin, LIU Weichao, ZHU Zhanyuan. Study on calculation of rock joint JRC value based on forward and reverse direct shear tests[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(S2): 3098-3106. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2021S2010.htm
[26]	XIA C C, TANG Z C, XIAO W M, et al. New peak shear strength criterion of rock joints based on quantified surface description[J]. Rock Mechanics and Rock Engineering, 2014, 47(2): 387-400. doi: 10.1007/s00603-013-0395-6