A unified "p-y+M-θ " model for laterally loaded piles considering rigidities of various piles
-
摘要: 中国近海海上风电机组开发建设中，大直径单桩基础形式使用占比超70%。现行p-y曲线设计方法主要适用于小直径柔性桩，对大直径单桩侧向及桩底受荷描述能力不足，导致其严重低估刚柔性桩和刚性桩（分别常用于中国和欧洲的近海风电工程）的变形和承载能力，过于保守的设计给海上风电降本带来挑战。为此建立了能以统一的方式预测柔性、刚柔性和刚性单桩水平单调受荷响应的“p-y + M-θ”模型，并将该模型推广到循环荷载下单桩的响应分析。通过与相关试验结果比对发现，“p-y + M-θ”模型能较为准确地预测桩基水平加载响应。力图为水平受荷单桩工程设计提供简洁而可行的响应分析方法。
-
关键词:
- 软黏土 /
- "p-y + M-θ"模型 /
- 水平受荷桩循环加载 /
- 试验结果对比
Abstract: The large-diameter monopiles account for over 70% in construction of offshore wind turbines in China. The current p-y curve design method is primarily suitable for the small-diameter flexible piles. It has long been recognized that the method is inadequate to describe the lateral behavior of large-diameter monopiles, due to the ignorance of the soil resistances arising from base shear and base moment, which becomes more pronounced as the pile rigidity increases. Consequently, it will significantly underestimate the deformation and capacity of the semi-rigid and rigid piles (commonly used in offshore wind projects in China and Europe, respectively), bringing challenges for cost reduction. In light of these issues, the authors have proposed a "p-y+M-θ"model that aims to reasonably predict the lateral monotonic response of monopiles with a broad coverage of rigidities (or length-over-diameter ratios) in a unified way. An extension of the model is then made to enable the capability for predicting the cumulative lateral behavior under cyclic loadings. With the proposed "p-y+M-θ"model, the authors are invited by the Organizing Committee of 4th International Symposium on Offshore Geotechnical Engineering (ISFOG-2020) to participate in a blind Class-A prediction event, where the experimental data are generated from the centrifuge tests performed by University of Western Australia (UWA) on piles in soft clay under lateral monotonic and cyclic loadings. The results of some element tests for the same clay as used in the centrifuge tests are provided ahead of the Class-A prediction event, for calibrating the model parameters. All the measured responses of lateral piles under monotonic and cyclic loadings are found to be reasonably reproduced by the proposed "p-y+M-θ"model. Compared to the predictive capability of the other 28 models used by the parallel international teams participating in the prediction event, the "p-y+M-θ"model shows a leading performance in the context of monotonic and cyclic predictions. The proposed "p-y+M-θ"model constitutes an advantageous and simple alternative to the design of monopiles under lateral loads. -
0. 引言
大直径单桩是目前海上风电机组最为流行的基础形式，中国超70%、欧洲超80%的海上风电机组基础为大直径单桩基础。为了抵抗海上风、浪、流等产生的巨大荷载，单桩基础多采用5~10 m的桩径，由于欧洲海域大多为密实砂土和超固结黏土，单桩入土长径比的通常为4~8[1-2]，而中国海域一般为力学性质较差的软黏土和粉质黏土，因此单桩长径比一般为6~10。
黏土地基中水平受荷桩静力响应常用分析方法有极限状态法、弹性分析法、弹性地基反力法、p-y曲线法和有限元分析法等[3-4]。不同的方法各有其局限性：如极限状态法无法用于计算桩身变形，弹性分析法和弹性地基反力法仅适用于小变形状态下水平受荷桩响应分析，有限元分析法建模时间较长、本构模型依赖性大。p-y曲线法将弹性地基反力法中不同深度土弹簧力学特性用非线性的p-y曲线描述，考虑土体变形过程中的非线性，能便捷计算水平受荷桩响应。p-y曲线法已被美国石油协会的API规范以及挪威船级社的DNV规范所采用，广泛应用于实际工程设计中。然而，API规范推荐的黏土p-y曲线是基于Matlock[5]的小直径细长桩现场试验获得的，其低估了单桩水平初始刚度和极限承载力。为考虑“桩径效应”，在过去二十余年中，众多学者基于模型试验、数值模拟等[6-14]，通过在p-y曲线的刚度和极限抗力表达中考虑桩径修正，提出了改进的p-y曲线模型。笔者近期的研究发现，桩径的增大（改变刚度）不仅影响p-y曲线的刚度和抗力，还显著改变了桩周土体破坏模式；后者不能通过简单地在p-y曲线中引入桩径来描述。为了能以统一的方式描述黏土海床不同入土长径比单桩（涵盖柔性、半刚性和刚性桩）的水平单调受荷响应，笔者研究提出了双弹簧“p-y + M-θ”模型[15-17]。这一简单模型能非常容易嵌入到风电商业软件（如Bladed）和开源软件（如Open-FAST），形成叶片、主机传动系统、塔筒和桩体的一体化分析。而实现能准确描述桩土相互作用的海上风机整机一体化分析正是笔者提出“p-y + M-θ”模型的初衷。
在2020年第四届海洋岩土工程前沿国际研讨会期间，西澳大学（UWA）与澳大利亚国家岩土离心机机构（NGCF）联合举办了水平受荷桩离心机模型循环加载响应预测竞赛（cyclic loading prediction event）[18-19]，该竞赛旨在与全球相关学者共同交流对桩土作用模型的理解和应用经验，并力图通过离心机试验提升对海上风机单桩基础受荷响应的认识。竞赛组委会事先公布了试验所用土体的基本单元试验结果，并提供给参赛队伍，在未知离心机试验结果的情况下要求各参赛队伍对水平受荷桩离心机试验响应进行预测并提交预测结果，过程中不限定预测方法。最后，组委会公开试验实测结果，并将各队伍预测值与实测进行对比[19]。
本文首先介绍了“p-y + M-θ”分析模型，随后将该模型推广到循环响应分析，最后介绍应用所建立的分析模型参与国际预测竞赛的情况。通过与国际竞赛试验实测结果比对发现，本模型能准确高效地预测水平单调和循环受荷下单桩响应，且与其他各类分析模型相比，预测结果具有一定的先进性。本文所建立的模型为黏土海床水平受荷单桩工程设计提供了简洁可行的响应分析方法。
1. 桩周土体变形与破坏模式
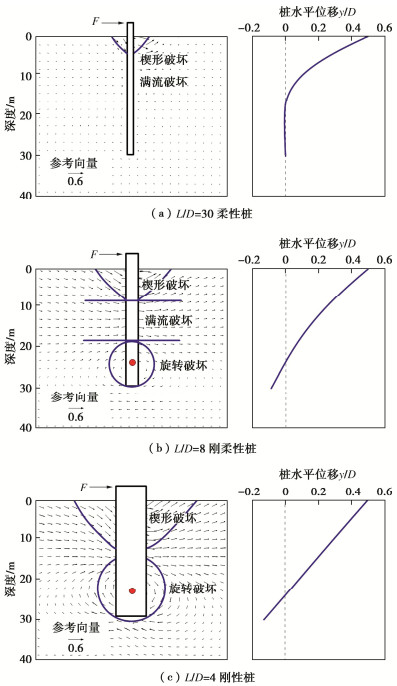
建立黏土海床单桩水平受荷静力分析模型的关键是准确揭示桩土真实的变形机制与破坏模式。各类研究分析表明，桩的长径比L/D是控制桩周土破坏模式最为重要的因素：在土质条件相同的情况下，L/D越小，桩表现得越刚，反之则越柔[15, 20]。图 1展示了黏土海床三维有限元分析所得的典型柔性桩（L/D=30）、刚柔性桩（L/D=8）和刚性桩（L/D=4）桩周土体破坏模式与对应桩身变形曲线[15]。
![]()
图 1 黏土海床桩-土破坏模式与桩身变形[15]Figure 1. Flow mechanism of soils and lateral displacement profile of piles in soft clay由图 1（a）可以看出，对于L/D=30的柔性桩，水平荷载作用桩周浅层土体表现楔形破坏模式，深层表现为绕桩流动的满流破坏[15, 20-22]，桩体变形主要为桩身材料变形为主的柔性变形。在深处，桩体基本无明显水平位移与转角，故土体抗力主要由上部楔形区和满流区的水平土阻力贡献。L/D减小时，桩从柔性桩向刚柔性桩过渡。图 1（b）展示了L/D=8的刚柔性桩典型响应。刚柔性桩-土破坏模式呈现“三区域”的分布，与柔性桩相比，除了上部的楔形、满流破坏区，在深处还存在竖向平面内的旋转破坏区[20]。
L/D进一步减小时，桩将完全呈刚性的响应，如图 1（c）所示。这时，桩周土体破坏模式为浅层楔形破坏，深层转动破坏，桩身变形完全表现为绕桩转动点的刚性转动，桩在转动点下方出现非常明显的反向踢脚。与刚柔性桩相比，刚性桩桩底处的水平位移和转角更大，这时桩底剪力、桩底反力弯矩对水平承载的贡献将进一步突显。由于忽略了这两项贡献，传统p-y曲线法在预测刚性桩时将更为显著地低估其承载性能。
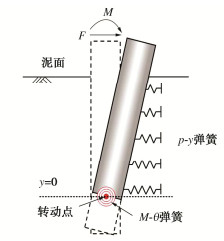
从桩-土实际变形和破坏模式出发[15-17]，提出了“p-y + M-θ”模型（图 2），该模型考虑了单桩抵抗水平载荷的3个最重要组成部分：全桩长水平土阻力、桩底剪力和桩底反力弯矩的额外抗力贡献。模型中，桩在转动点处截断，假设桩体在转动点仅发生转动。转动点以上的水平土阻力发挥用水平p-y弹簧来表征，转动点以下的土阻力发挥（包括桩底剪力和桩底反力弯矩）统一用一个集中旋转弹簧M-θ来表征。黏土海床中，刚柔性和刚性桩转动点通常比较固定（位于深度为（0.7~0.8）倍桩长处），这为“p-y + M-θ”模型的建立提供了便利。模型中，转动点上下不同破坏模式（从上到下分别为楔形区、满流区和转动区）的土体抗力采用了不同的弹簧表征。且若深层桩体不发生转动，M-θ弹簧不受力，模型将退化为传统p-y模型，因此“p-y + M-θ”模型能适用于不同入土深度与桩径比值的单桩。此外，模型基于土体强度发挥设计方法MSD（Mobilised Strength Design）思想[23-24]，可通过缩放地基土单元的应力-应变曲线，构建得到p-y曲线和M-θ曲线[17, 25-26]，模型输入简便。
![]()
图 2 单桩“p-y+M-θ”桩土分析模型Figure 2. Proposed"p-y + M-θ"pile-soil interaction model for analysis of monopile2. 基于分区破坏模式的极限阻力
2.1 满流区和楔形区极限土阻力pu
对于模型中的p-y曲线而言，构成p-y曲线的两个要素为极限土阻力pu（通常由无量纲水平承载力系数Np表达，Np= pu/suD）和归一化p-y曲线（即p/pu-y/D曲线）。本小节将阐述黏土地基中楔形区和满流区p-y曲线极限土阻力pu，并对楔形区和满流区的临界深度进行探讨。
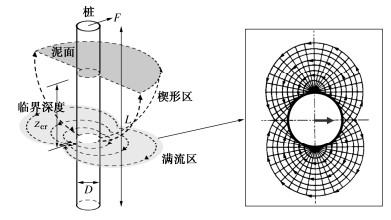
对于满流区（图 3），桩周土体表现为平面内的绕桩流动，桩后通常认为不产生空隙（流动土体填充）。基于塑性理论极限水平承载力系数Np的精确解[21]，近似可表达为
Np_f=pusuD = 9.14+2.8α。 (1) 式中：α为桩土界面粗糙度，位于0~1，0代表桩土界面完全光滑，1代表桩土界面完全粗糙。
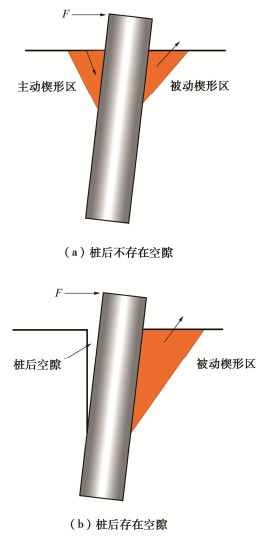
对于楔形区，其通常存在两种情况，如图 4所示。第一种情况：加载过程中桩后不存在空隙，多针对正常固结软黏土地基。此时，由于软黏土吸力作用，桩土界面不分离，因此表现为桩前一个被动楔形区和桩后的一个主动楔形区。考虑土体均质且各向同性，这两个楔形区大小形状一致。加载过程中，桩前桩后土体楔形区重力对桩水平承载的贡献相互抵消，此时，桩水平土阻力全部由桩前桩后楔形区土体强度决定。第二种情况：加载过程中桩后出现空隙，多针对超固结硬黏土地基情况。此时，由于桩后空隙的出现，只存在桩前的一个被动楔形区，此时，楔形区土体重力对桩的抵抗作用无法抵消。故此时，桩水平土阻力由桩前楔形区土体强度和土体重度共同决定。
基于三维上限法分析，可以得到上述两种情况下楔形区Np值的上限解，近似表达如下所示[22]：
Np\_w={2(11.94−8.72(1−(z/D14.5)0.6)1.35−(1−α))（桩后不存在空隙）(11.94−8.72(1−(z/D14.5)0.6)1.35−(1−α))+γ′zsu（桩后存在空隙）。 (2) 式中：γ′为土体有效重度；z为泥面下深度。
满流区桩土相互作用是一个平面应变问题，其能发挥的承载力最高，楔形区Np值须小于或等于满流区Np值（即Np_w≤Np_f，Np_f = 9.14+2.8α）。由此，可计算得到楔形区和满流区的无量纲临界深度zcr /D（图 3，Np_w=Np_f）。当深度小于zcr /D时，土体为楔形破坏；当深度大于zcr /D时，土体破坏模式转变为满流破坏。
对于刚柔性桩和刚性桩，其深层土体的破坏模式为竖向平面内的旋转剪切破坏（图 1（b），（c））。此时，桩转动点以下会出现反向的踢脚，该踢脚的存在会将桩后可能存在空隙闭合（图 4（b））。因此，对于桩后存在空隙的刚柔性桩和刚性桩，其楔形区最大深度应取桩转动点深度和式（2）判别所得临界深度这两者的较小值。
2.2 M-θ曲线极限承载弯矩Mult
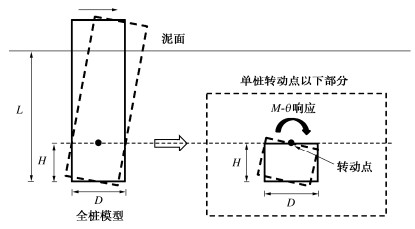
在本文模型中，M-θ弹簧代表的是桩转动点以下土体阻力对转动点的反力弯矩，其中土体阻力是转动点以下的水平土阻力、桩底剪力和桩底反力弯矩共同作用的结果。因此，分析M-θ曲线极限承载力距Mult时，可直接考虑单桩转动点以下部分，而忽略上覆桩土体，如图 5所示[17]。
对于刚柔性桩和刚性单桩，桩转动点以下土体破坏机制为绕转动点旋转流动的勺形破坏（Scoop-failure mechanism）[16]。此时，M-θ响应极限抗弯承载上限解Mult为底部勺形破坏面桩土剪切对转动点的力矩Mscoop和侧面桩土剪切对转动点的力矩Mside之和：
Mult=Mscoop+Mside 。 (3) 已解析获得M-θ曲线极限承载力Mult表达式，并通过有限元分析验证了其正确性[17]：
MR_ult=(16πD3su1+πsu1DH2)+k(12D2+2H2)2[38t+14sin(2t)+132sin(4t)]+0.73(2π3su1H3+kH4)。 (4) 式中：t=arcsin(D√D2+4H2)；su1为转动点处不排水强度；k为不排水强度随深度增长率。
3. “p-y + M-θ”分区抗力变形曲线
3.1 楔形区p-y曲线模型
2.1节确定了楔形区p-y极限土阻力pu，这节主要探究构成楔形区p-y曲线的另一个要素：归一化p-y曲线（即p/pu-y/D关系）。
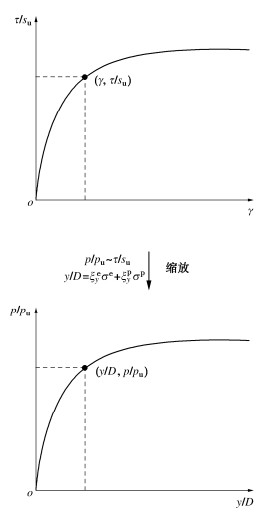
楔形区和满流区的p-y曲线可以通过缩放土单元应力-应变关系获得，如图 6所示。大量研究表明：土单元应力-应变曲线上的剪应力发挥度(τ/su)与p-y曲线土阻力发挥度(p/pu)相对应[16-17, 25-26]，
ppu∼τsu。 (5) ![]()
图 6 楔形区和满流区p-y曲线缩放模型[25]Figure 6. Scaling model for p-y curves in wedge and full-flow mechanism给定p/pu下，归一化水平位移y/D可通过缩放对应剪应变得到
yD=ξewγe+ξpwγp。 (6) 式中：ξew，ξpw分别为弹性剪切应变γe的和塑性剪应变γp的缩放系数。γe，γp按下式得到：
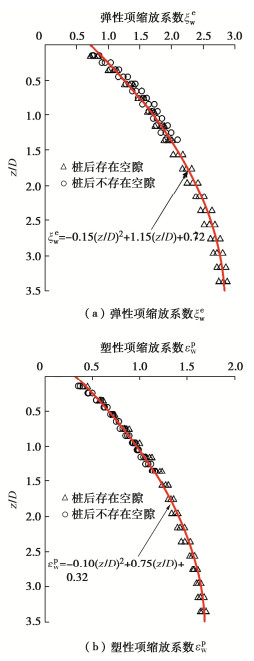
γe=τGmax=τ/suGmax/su， (7) γp=γ−γe。 (8) 采用上述方法，通过三维有限元分析[16]，算获得各个深度下楔形区归一化p-y曲线，并基于式（5）拟合p-y曲线和土体应力应变关系，拟合得到缩放系数ξew和ξpw，如图 7所示[16]。有限元分析中，考虑了桩后空隙存在与否的工况，以及不同的桩土粗糙度。由图 7可知，给定深度下，桩后空隙存在与否和桩土粗糙度对缩放系数ξew和ξpw的影响较小，可忽略。需指出的是，虽然桩后空隙对楔形区归一化p-y曲线影响可忽略，但其对p-y曲线极限土阻力有着显著的影响。
图 7仅适用于z/D≤3.5深度范围内楔形区p-y曲线，不宜外推。对于z/D > 3.5深度，基于缩放系数随深度趋于稳定的趋势，可近似采用z/D=3.5计算所得的缩放系数值。
3.2 满流区p-y曲线模型
针对满流区p-y曲线的缩放系数，Zhan等[25]已基于土体单元试验和有限元分析结果得
ξey=2.8， (9) ξpy=1.35+0.25α。 (10) 对比楔形区z/D < 3深度范围内的p-y曲线缩放系数（图 7），满流区p-y曲线缩放系数明显偏大，即楔形区p-y曲线要刚于满流区p-y曲线。这意味着，在传统p-y模型中，若沿桩身全长采用满流区p-y曲线，而不考虑楔形区p-y曲线，将低估桩水平承载的刚度。
3.3 M-θ曲线模型
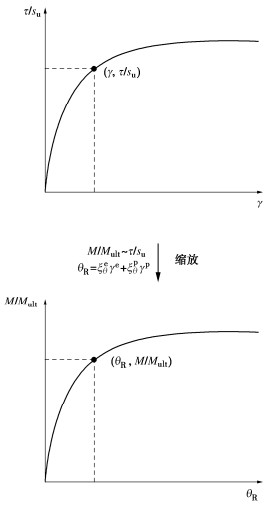
与p-y曲线类似，模型中的M-θ弹簧曲线也是基于土单元应力-应变曲线的缩放获得，如图 8所示。缩放模型中土单元应力-应变曲线上的剪应力发挥度（τ/su）与M-θ曲线弯矩发挥度（M/Mult）相对应，
MMult∼τsu。 (11) 类似3.1节中p-y曲线的做法，在给定的M/Mult下，桩体转角θ可通过缩放土单元应力-应变曲线上对应的剪应变得到
θ=ξeθγe+ξpθγp。 (12) 式中：ξeθ，ξpθ分别为弹性剪切应变γe和塑性剪应变γp的缩放系数，可根据式（7），（8）计算得到。
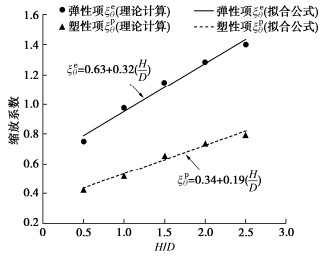
弹性项缩放系数ξeθ可通过解析得到，而塑性项缩放系数ξpθ则通过拟合有限元计算结果得到[16-17]。计算发现，这两个系数都和归一化的转动点下桩长（H/D）相关，如图 9所示。可以得到M-θ曲线的两个缩放系数ξeθ和ξpθ：
ξeθ=0.63+0.32(HD)， (13) ξpθ =0.34+0.19(HD)。 (14) ![]()
图 9 弹性缩放系数ξθe和塑性缩放系数ξθp与H/D关系Figure 9. Variation of elastic and plastic scaling factors with H/D ratio3.4 单桩转动点深度
3.2节、3.3节给出了“p-y+M-θ”模型中的p-y和M-θ曲线的表达式，完整“p-y+M-θ”模型的最后一个关键要素是确定单桩转动点深度。大量试验及数值研究表明，刚柔性单桩转动点深度在（0.7~0.8）L这一较窄的范围内，且与桩几何尺寸、地层条件和加载特性无明显关联[16-17]。这给“p-y+M-θ”模型的带来了极大的便利。在单桩初步设计阶段，本文推荐采用转动点深度z=0.8L作为模型构造条件[15]。
3.5 不排水强度各向异性问题讨论
本文提出的“p-y+M-θ”模型是在土体简化为各向同性材料的前提下建立的。然而，天然土体往往会表现出强度和应力-应变响应的各向异性，土体各向异性对模型预测结果的影响还有待进一步研究。此外，模型中p-y和M-θ曲线是基于土体应力-应变关系建立的，因此土体应力-应变曲线的选取较为重要。桩在承受水平荷载时桩周不同破坏模式的土体呈现不同的剪切模式，例如，被动楔形区土单元剪切模式主要为三轴伸长和单剪；主动楔形区主要为三轴压缩和单剪；满流破坏区主要为单剪；而旋转破坏区为单剪、三轴压缩和伸长的结合。从模型实用方便考虑，本文推荐采用土体单剪试验获得的应力-应变曲线作为模型输入，这主要因为单剪所得土单元应力-应变响应往往介于三轴伸长和三轴压缩之间，可看成是三者的平均值，具有很好的代表性[27-28]。这一做法已得到多个模型试验和现场试验验证[16]，具有良好的效果。还应当指出，所提出的基于土体力学特性的M-θ曲线是基于桩转动点以下的土层为单一土层且强度均匀或呈线性分布的假设。对于桩转动以下土体分层或强度分布不均的情况，需进行工程判断将其简化为单层均匀或线性分布。
4. 循环荷载分析模型
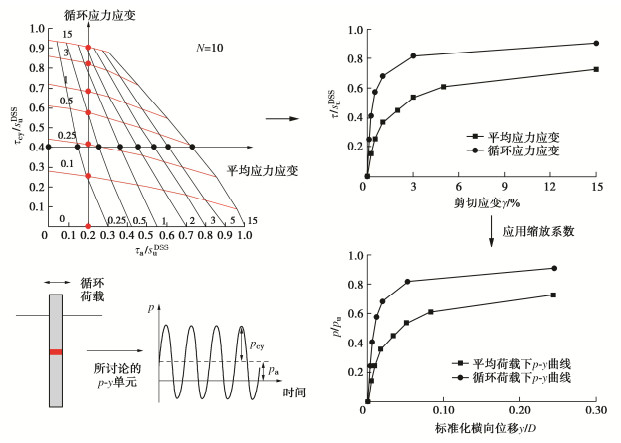
前面介绍的“p-y+M-θ”模型仅适用于分析单桩单调静力加载，为了使其具备循环荷载下单桩响应分析能力，需对模型进一步拓展。挪威土工所（NGI）结合近60 a的土体循环性状研究，系统建立了循环响应等值线理论框架[29]。结合应变等值图原理，可以将土体单剪状态下等效循环次数对应的应力-应变关系缩放为循环荷载下p-y曲线[30]。最近的进展是将其推广到包含平均水平荷载和循环荷载的等效p-y曲线，如图 10所示[26]。这里将循环应力幅值和平均应力分开，分别得到给定等效循坏次数下的应力应变曲线，通过第3节描述的相应缩放，用来分别计算桩基在平均荷载和循环荷载下的响应，最终叠加。对于本文模型，循环响应等值线理论框架也同样适用于构建循环M-θ曲线。基于等效循环次数下的循环p-y和M-θ曲线，也就可以用来分析循环荷载下的任意刚柔度桩基的响应。
![]()
图 10 基于循环响应等值线理论的循环p-y曲线确定[26]Figure 10. Deducing cyclic p-y curves from cyclic loading contours5. 离心机试验响应国际预测大赛
5.1 离心机试桩试验及土工试验
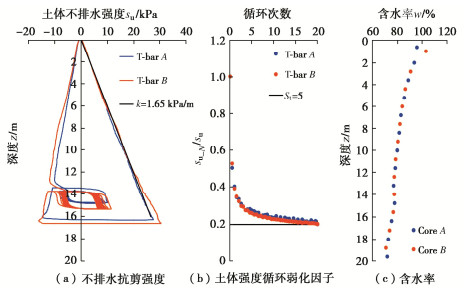
根据竞赛组委会提供的基本资料，离心机试验使用的是西澳大利亚西北大陆架的细粒土，塑性指数PI=22，相对质量密度Gs=2.76。将土体混合至140%含水率，以80g的加速度进行20 d的固结，形成正常固结黏土海床。图 11（a）显示了在80g离心模型试验下，用T-bar贯入试验测得的土体不排水抗剪强度，其强度梯度k为 1.65 kPa/m，其中T-bar系数取NT-bar=10.5。T-bar单调推进至原型尺寸为16~17 m深度，然后提升至14.5 m深度，共进行20个循环的T-bar试验。如图 11（b）所示，20次循环后，残余强度稳定在初始强度的0.2倍，可知土样灵敏度St为5[18-19]。完成循环T-bar试验后，即刻停机取样，测得的含水率沿深度变化结果如图 11（c）所示。
![]()
图 11 基于循环T-bar试验的不排水抗剪强度、土体强度循环弱化因子和土体含水率Figure 11. Undrained shear strength profile by cyclic T-bar tests (a), cyclic strength degradation factor (b) and water content profile (c)针对此次国际预测竞赛，西澳大学事先开展了大量土工试验，同时请独立第三方校核土体单剪试验结果。针对每个土工试验，制备含水率为140%的饱和土样，成浆后倒入土样桶中，在竖向压力30 kPa下完成固结。然后切样并装入单剪仪中，施加初始竖向固结应力30 kPa，待竖向变形稳定后，开展剪切试验。赛前，组委会将土工试验结果分发给各参赛团队，包括单调单剪试验、循环单剪试验、三轴压缩和伸长试验、共振柱试验。
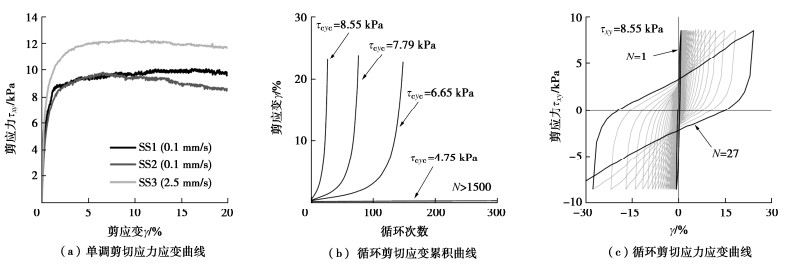
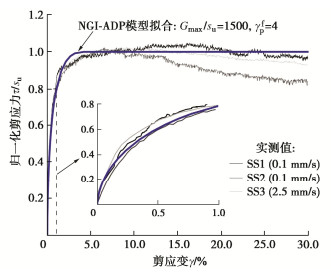
由于本次竞赛预测目标为单调和双向对称受荷试桩离心机试验，本文主要基于单调、循环单剪试验结果，标定获得p-y和M-θ模型参数。图 12（a）显示了不同单剪速率下试验土应力-应变试验结果。尽管土体应力-应变关系表现出一定的应变率效应，如将3条曲线中的剪应力用其不排水抗剪强度做归一化，3条曲线基本重合。图 12（b）, （c）分别显示了循环剪切试验中的应变累积和应力-应变关系。基于上述土单元试验结果，可以建立“p-y+M-θ”分析模型。
![]()
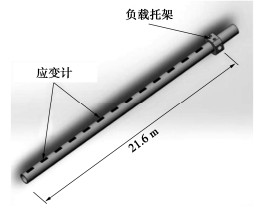
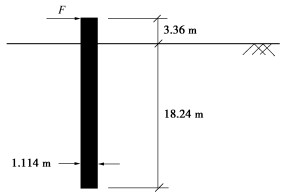
预测竞赛中，离心机试验模型桩由铝6061T6制成，弹性模量为68.9 GPa。图 13显示了模型桩尺寸，桩身安装有13组间距为20 mm的应变计，用于测量桩身弯矩响应。表 1总结了模型桩的相关参数。
表 1 模型桩尺寸Table 1. Dimensions of model pile尺寸 模型/mm 原型/m 长度 270.0 21.6 外径（铝桩） 12.00 0.96 壁厚（铝桩） 0.450 0.036 环氧树脂壁厚 0.960 0.0768 总外径 13.920 1.114 入土段长度 228.00 18.24 模型桩外周覆盖有环氧树脂用于防水。模型桩外径为13.92 mm（对应原型尺寸外径1.114 m）。西澳大学事先标定了未覆盖环氧树脂桩基的抗弯刚度EI，建议取770 MN·m2。组委会分析认为外层薄环氧涂层对桩基刚度影响不大[19]，故未告知参赛队伍。本文分析也不考虑这一变化，仍按原报告叙述。
图 14显示了离心机实验中，桩顶的加载位置以及桩基入土段的长度。桩顶水平荷载、位移分别通过加载臂上的轴力计、激光位移计测量获得。
5.2 试验内容及方法
试桩试验在西澳大学旋转半径为1.8 m的离心机中进行。试验使用的模型箱内部尺寸长650 mm、宽390 mm和高325 mm。模型箱底部铺有30 mm的砂层作为排水层，砂层上覆正常固结黏土层。该黏土层在80g下固结完成后，停机至1g，并将模型桩静力插入黏土层中，插入深度为228 mm（对应原型18.24 m）。为确保垂直插桩，并尽量减少插桩对周围土体的扰动，采用了如图 15所示的装备来垂直静压模型桩入土。当模型桩达到要求的嵌入深度时，移除桩的横向限制，取出钻头。桩身安装完毕后，水平加载装置安装于土床表面上方42 mm处（对应原型3.36 m），为叙述方便，在本文中水平加载的位置统称为桩顶。模型桩安装后，将离心机旋转至80g，待重固结完成后（约需1~2 h），在80g下开展静力或循环试桩试验。
表 2总结了所有离心机试验，包括了一个单调加载试验和3个双向循环加载试验。在模型尺度下，单调试验（MT）的桩头加载速率为1 mm/s。循环试桩包括两个位移循环试验（CT1和CT2）和一个力循环试验（CT3）。其中，CT1循环加载频率为1 Hz，CT2和CT3循环加载频率为0.5 Hz。每次循环试验持续时间为6.7~13.3 min，对应原尺模型29.6~59.3 d。组委会事先约定加载过程可视为不排水过程。
表 2 模型试验总结表Table 2. Test programs测试 测试类型 幅值 桩顶位移 模型尺度 原型尺度 静力加载（MT） 单调加载 1.07D 14.90 mm 1.19 m 循环测试1（CT1） 双向位移控制 0.02 D 0.22 mm 0.02 m 循环测试2（CT2） 双向位移控制 0.10 D 1.37 mm 0.11 m 循环测试3（CT3） 双向荷载控制 — 23.9 N 153 kN 5.3 模型参数标定
针对单桩静力加载预测，通过缩放土体静单剪归一化τ/su-γ曲线（图 16），获得p-y和M-θ模型参数。由图 16可得，不同剪切速率下的土单元归一化应力-应变曲线吻合良好。基于NGI-ADP模型[31]，采用参数Gmax/su=1500，γfp=0.04，可较好地描述该土体应力-应变曲线响应，故采用这些参数作为此次反分析中应力-应变曲线的输入。基于前述T-bar试验结果（图 11（a）），土体不排水抗剪强度沿深度变化速率取su=1.65z。
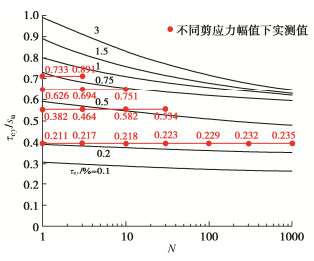
针对单桩双向循环加载的预测，“p-y+M-θ”模型的关键输入是土体循环响应等值线。基于本次竞赛组委会提供的4个不同剪应力幅值下的实测循环剪应变累积结果（图 12），通过数学插值，同时参考已有挪威Drammen clay（塑性指数PI=27）循环应力-应变包络面[29]，建立得到本次预测所用土单元循环响应等值线，如图 17所示。
在缺乏系统土单元循环实测数据情况下，上述这种基于有限实测数据点并结合现有应力-应变包络面构造得到对应所需土体应力-应变包络面的方法应用较为普遍，且精确度较好[26]。需指出，此处参考Drammen clay数据库的主要原因是，自20世纪80年代起，NGI对该种土体开展了系统且完善的土工试验，并实测建立得到了其循环应力-应变包络面，该数据库作为范本被广泛应用于其他不同土体循环响应等值线的建立。
基于图 17，结合第4节所述方法，便可建立得到“p-y+M-θ”模型中任意次循环荷载下的p-y和M-θ曲线，并用于预测该循环次数下单桩响应。
5.4 ISFOG—2020预测大赛结果分析
参赛队共提交了29组预测结果。其中20组预测基于p-y曲线法，8组预测基于有限元分析方法（FE），1组预测基于有限元和p-y曲线相结合的方法[19]。
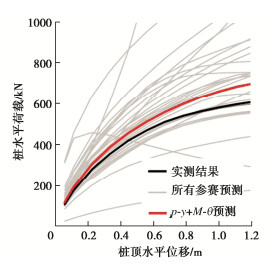
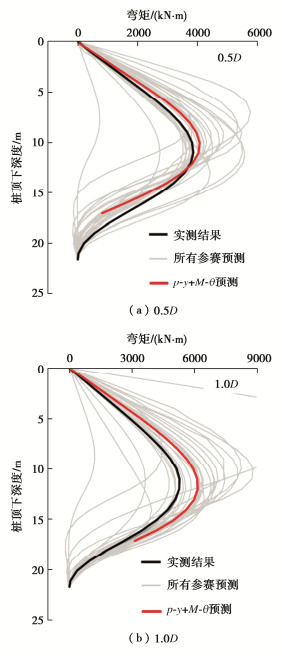
图 18展示了单调加载试验结果（黑线）和所有预测的荷载-位移曲线结果（灰线），其中本文“p-y + M-θ”模型预测结果用红线标出。由图 18可见，当桩顶位移加载至0.1D时，约70%的同行预测结果高估了桩顶荷载，所有预测的统计中值比实测值高22%，而本文“p-y + M-θ”模型预测结果比实测值仅高8%。当桩顶位移加载至1.0D时，约69%的同行预测结果高估了桩顶荷载，所有预测统计中值比实测值高26%，而本文“p-y + M-θ”模型预测结果比实测值仅高估13%。
图 19（a），（b）分别展示了桩顶水平位移加载至0.5D和1.0D时对应的桩身弯矩分布。当桩顶位移加载至0.5D时，约62%的同行预测结果高估了峰值弯矩，所有预测统计中值比实测值高6%，而本文“p-y + M-θ”模型预测的峰值弯矩仅比实测高4%，且预测的峰值弯矩所处深度更接近实测深度。当桩顶位移加载至1.0D时，72%的同行结果高估预测了峰值弯矩，所有预测统计中值比实测值高19%，而本文“p-y + M-θ”模型预测的峰值弯矩比实测仅高13 %，且预测的峰值弯矩所处深度与实测深度基本一致。
![]()
图 19 不同桩顶位移下单桩弯矩分布Figure 19. Profiles of monotonic bending moment in response to different pile head displacements: (a) 0.5D, (b) 1.0D综合上述单调加载分析结果可见，当桩顶加载位移较小时，“p-y + M-θ”模型更能准确预测桩顶荷载响应，且预测结果与实测荷载值基本一致。当桩顶发生较大位移时，“p-y + M-θ”模型则更能较为准确预测桩身峰值弯矩所处深度，但预测峰值弯矩会略大于实测值。总体看来，相比于其他同行预测结果，“p-y + M-θ”模型的预测效果处于最优行列。
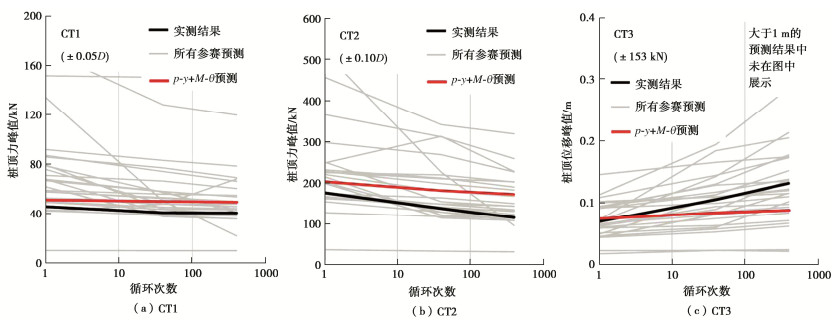
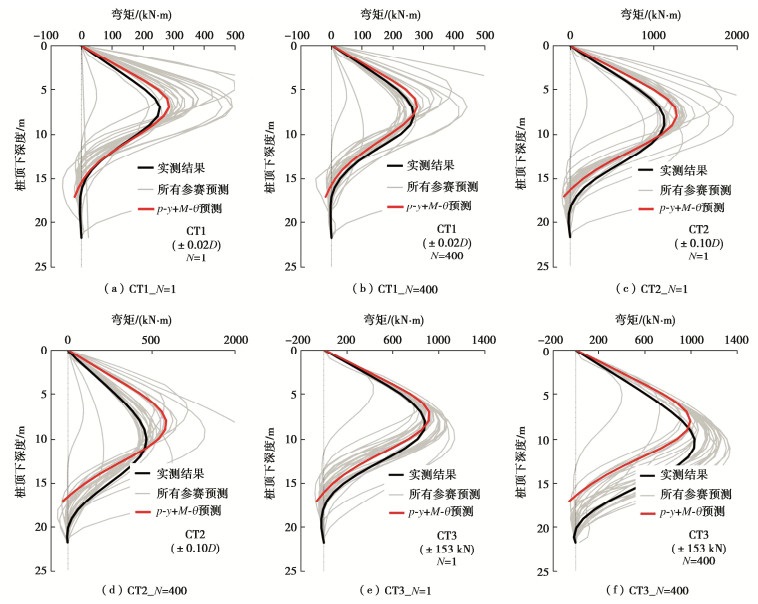
图 20，21分别对比了不同循环次数下预测和实测单桩的桩头响应和桩身弯矩分布。对于位移控制循环试验（CT1，CT2），预测结果表明：大多数同行高估了桩顶水平力和桩身峰值弯矩；相比而言，“p-y + M-θ”在预测循环加载的桩头响应和桩身弯矩时具有较好的预测效果，其精度在29个参赛模型中位居前5。对于力控制循环试验（CT3），“p-y + M-θ”模型预测也同样接近实测值，其精度在所有同行预测结果中位居前4。
![]()
图 20 不同循环次数下单桩桩头响应（循环次数N为1，40，400）Figure 20. Responses at pile head against number of cycles (N = 1, 40, 400)![]()
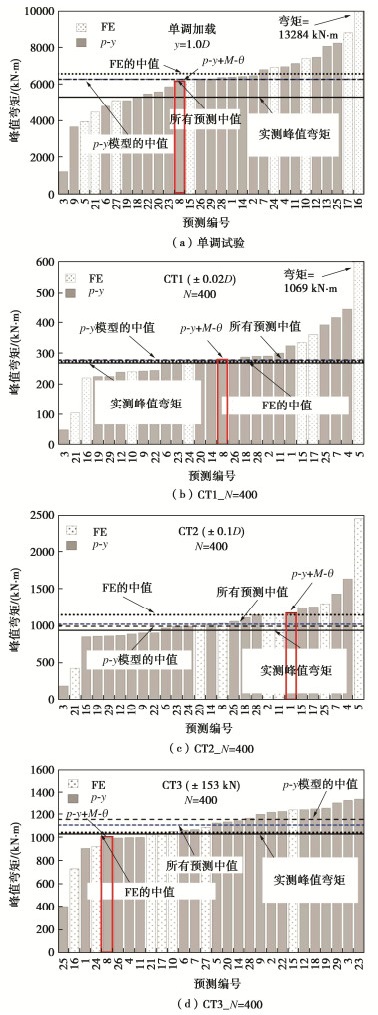
图 21 循环次数为N为1，400下桩身弯矩分布Figure 21. Profiles of bending moment for N = 1 and 400 for each cyclic test图 22以桩身峰值弯矩为指标，进一步对所有模型的预测效果进校了对比。图 22（a）展示了水平位移y=1.0D时单调试验的模型预测结果分布，图 22（b）~（d）呈现了循环加载N=400时CT1~CT3试验的预测结果分布。对比统计结果可以发现：过半数的预测模型均高估了单调试验和循环试验的峰值弯矩，并且p-y方法预测的效果略优于使用FE方法。而本文所建立的“p-y + M-θ”桩土作用分析模型具有良好的可靠性，能较为准确地描述单桩的单调和循环受荷响应，分析模型的预测准确度在所有参赛同行中位于前列。
![]()
图 22 桩身峰值弯矩预测值与测量值对比Figure 22. Comparison between observed and predicted peak bending moments综上，在单桩模型离心机加载国际预测竞赛中，“p-y+M-θ”模型在所有加载工况下均能根据所提供参数较好完成单桩响应计算。对于单调和循环加载下桩身弯矩分布、桩顶荷载和位移，“p-y + M-θ”模型均能取得较准确结果。特别在静力加载位移小于0.5D，循环加载位移小于0.1D时，模型预测效果较好。值得注意的是，本文分析模型目前仅考虑了特定的加载模式及较低荷载与较少循环次数的工况，下一步应进一步探索适于分析长期、复杂多变的多向荷载作用下桩基累积变形响应的模型。
6. 结论
介绍了一种考虑土体破坏模式的单桩水平响应统一预测分析方法，即p-y+M-θ法。区别于传统基于一种弹簧的桩土作用模型，本文模型耦合了两种弹簧作用：转动点以上的侧向土阻力由分布式p-y弹簧描述，转动点以下的综合土体阻力（包括桩底剪力和桩底反力弯矩）则整合到旋转点处的集中M-θ弹簧中。基于上述做法，实现了用统一的方式预测柔性、刚柔性和刚性单桩水平单调受荷响应。同时，p-y和M-θ曲线可以通过缩放土体单剪试验的应力-应变关系直接获得，便于工程设计。在此基础上，通过引入循环响应等值线理论框架，将该分析方法推广至循环荷载下单桩的响应分析。
通过与赛后公开发布的试验结果比对发现，p-y + M-θ模型能较为准确地预测桩基水平加载响应。在参赛国际团队所采用的29个模型中，本文模型对桩基的单调和循环响应预测效果位于最优之列。考虑到参与预测的部分方法如有限元等存在参数获取困难与运行耗时长等问题，p-y+M-θ模型因其理论简洁、使用便利、计算相对准确，而显示出较明显的优越性。
这一简单模型能非常容易嵌入到风电商业软件（如Bladed）和开源软件（如Open-FAST），形成叶片、主机传动系统、塔筒和桩体的一体化分析。而实现能准确描述桩土相互作用的海上风机整机一体化分析正是作者提出“p-y + M-θ”模型的初衷。
-
![]()
图 1 黏土海床桩-土破坏模式与桩身变形[15]
Figure 1. Flow mechanism of soils and lateral displacement profile of piles in soft clay
![]()
图 2 单桩“p-y+M-θ”桩土分析模型
Figure 2. Proposed"p-y + M-θ"pile-soil interaction model for analysis of monopile
![]()
图 6 楔形区和满流区p-y曲线缩放模型[25]
Figure 6. Scaling model for p-y curves in wedge and full-flow mechanism
![]()
图 9 弹性缩放系数ξθe和塑性缩放系数ξθp与H/D关系
Figure 9. Variation of elastic and plastic scaling factors with H/D ratio
![]()
图 10 基于循环响应等值线理论的循环p-y曲线确定[26]
Figure 10. Deducing cyclic p-y curves from cyclic loading contours
![]()
图 11 基于循环T-bar试验的不排水抗剪强度、土体强度循环弱化因子和土体含水率
Figure 11. Undrained shear strength profile by cyclic T-bar tests (a), cyclic strength degradation factor (b) and water content profile (c)
![]()
![]()
图 19 不同桩顶位移下单桩弯矩分布
Figure 19. Profiles of monotonic bending moment in response to different pile head displacements: (a) 0.5D, (b) 1.0D
![]()
图 20 不同循环次数下单桩桩头响应（循环次数N为1，40，400）
Figure 20. Responses at pile head against number of cycles (N = 1, 40, 400)
![]()
图 21 循环次数为N为1，400下桩身弯矩分布
Figure 21. Profiles of bending moment for N = 1 and 400 for each cyclic test
![]()
图 22 桩身峰值弯矩预测值与测量值对比
Figure 22. Comparison between observed and predicted peak bending moments
表 1 模型桩尺寸
Table 1 Dimensions of model pile
尺寸 模型/mm 原型/m 长度 270.0 21.6 外径（铝桩） 12.00 0.96 壁厚（铝桩） 0.450 0.036 环氧树脂壁厚 0.960 0.0768 总外径 13.920 1.114 入土段长度 228.00 18.24 
下载: 导出CSV
表 2 模型试验总结表
Table 2 Test programs
测试 测试类型 幅值 桩顶位移 模型尺度 原型尺度 静力加载（MT） 单调加载 1.07D 14.90 mm 1.19 m 循环测试1（CT1） 双向位移控制 0.02 D 0.22 mm 0.02 m 循环测试2（CT2） 双向位移控制 0.10 D 1.37 mm 0.11 m 循环测试3（CT3） 双向荷载控制 — 23.9 N 153 kN
下载: 导出CSV
-
[1] DOHERTY P, GAVIN K. Laterally loaded monopile design for offshore wind farms[J]. Proceedings of the Institution of Civil Engineers-Energy, 2012, 165(1): 7-17. doi: 10.1680/ener.11.00003
[2] MURPHY G, IGOE D, DOHERTY P, et al. 3D FEM approach for laterally loaded monopile design[J]. Computers and Geotechnics, 2018, 100: 76-83. doi: 10.1016/j.compgeo.2018.03.013
[3] 张磊, 龚晓南, 俞建霖. 水平荷载单桩计算的非线性地基反力法研究[J]. 岩土工程学报, 2011, 33(2): 309-314. http://cge.nhri.cn/cn/article/id/13920 ZHANG Lei, GONG Xiaonan, YU Jianlin. Solutions for laterally loaded single pile by nonlinear subgrade reaction method[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(2): 309-314. (in Chinese) http://cge.nhri.cn/cn/article/id/13920
[4] 苏静波, 邵国建, 刘宁. 基于P-Y曲线法的水平受荷桩非线性有限元分析[J]. 岩土力学, 2006, 27(10): 1781-1785. doi: 10.3969/j.issn.1000-7598.2006.10.028 SU Jingbo, SHAO Guojian, LIU Ning. Nonlinear finite element analysis of piles under lateral load based on P-Y curves[J]. Rock and Soil Mechanics, 2006, 27(10): 1781-1785. (in Chinese) doi: 10.3969/j.issn.1000-7598.2006.10.028
[5] MATLOCK H. Correlation for design of laterally loaded piles in soft clay[C]// Offshore Technology Conference, Houston, 1970.
[6] JEANJEAN P. Re-assessment of P-Y curves for soft clays from centrifuge testing and finite element modeling[C]// Offshore Technology Conference, Houston, 2009.
[7] TRUONG P, LEHANE B M. Effects of pile shape and pile end condition on the lateral response of displacement piles in soft clay[J]. Géotechnique, 2018, 68(9): 794-804. doi: 10.1680/jgeot.16.P.291
[8] 朱斌, 杨永垚, 余振刚, 等. 海洋高桩基础水平单调及循环加载现场试验[J]. 岩土工程学报, 2012, 34(6): 1028-1037. http://cge.nhri.cn/cn/article/id/14602 ZHU Bin, YANG Yongyao, YU Zhengang, et al. Field tests on lateral monotonic and cyclic loadings of offshore elevated piles[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(6): 1028-1037. (in Chinese) http://cge.nhri.cn/cn/article/id/14602
[9] 朱斌, 熊根, 刘晋超, 等. 砂土中大直径单桩水平受荷离心模型试验[J]. 岩土工程学报, 2013, 35(10): 1807-1815. http://cge.nhri.cn/cn/article/id/15299 ZHU Bin, XIONG Gen, LIU Jinchao, et al. Centrifuge modelling of a large-diameter single pile under lateral loads in sand[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1807-1815. (in Chinese) http://cge.nhri.cn/cn/article/id/15299
[10] 黄茂松, 马昊, 李森, 等. 软黏土中水平受荷桩的静力和循环p-y曲线[J]. 岩土工程学报, 2017, 39(增刊2): 9-12. doi: 10.11779/CJGE2017S2003 HUANG Maosong, MA Hao, LI Sen, et al. Static and cyclic p-y curves for laterally loaded piles in soft clay[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(S2): 9-12. (in Chinese) doi: 10.11779/CJGE2017S2003
[11] 黄茂松, 俞剑, 张陈蓉. 基于应变路径法的黏土中水平受荷桩p-y曲线[J]. 岩土工程学报, 2015, 37(3): 400-409. doi: 10.11779/CJGE201503002 HUANG Maosong, YU Jian, ZHANG Chenrong. p-y curves of laterally loaded piles in clay based on strain path approach[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(3): 400-409. (in Chinese) doi: 10.11779/CJGE201503002
[12] 张海洋, 刘润, 袁宇, 等. 海上大直径单桩基础p-y曲线修正[J]. 水利学报, 2020, 51(2): 201-211. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB202002008.htm ZHANG Haiyang, LIU Run, YUAN Yu, et al. A modified p-y curve method for offshore large-diameter monopile foundations[J]. Journal of Hydraulic Engineering, 2020, 51(2): 201-211. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB202002008.htm
[13] 王卫, 闫俊义, 刘建平. 基于海上风电试桩数据的大直径桩p-y模型研究[J]. 岩土工程学报, 2021, 43(6): 1131-1138. doi: 10.11779/CJGE202106017 WANG Wei, YAN Junyi, LIU Jianping. Study on p-y models for large-diameter pile foundation based on in situ tests of offshore wind power[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(6): 1131-1138. (in Chinese) doi: 10.11779/CJGE202106017
[14] 竺明星, 卢红前, 戴国亮, 等. 基于侧阻硬化与软化模型的大直径桩基水平承载力研究[J]. 岩土工程学报, 2018, 40(增刊2): 132-136. doi: 10.11779/CJGE2018S2027 ZHU Mingxing, LU Hongqian, DAI Guoliang, et al. Lateral bearing capacity of large-diameter pile foundation based on hardening and softening models of side resistance[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(S2): 132-136. (in Chinese) doi: 10.11779/CJGE2018S2027
[15] WANG L Z, LAI Y Q, HONG Y, et al. A unified lateral soil reaction model for monopiles in soft clay considering various length-to-diameter (L/D) ratios[J]. Ocean Engineering, 2020, 212: 107492. doi: 10.1016/j.oceaneng.2020.107492
[16] 赖踊卿. 软黏土地基海上风机大直径单桩水平受荷特性与分析模型[D]. 杭州: 浙江大学, 2021. LAI Yongqing. Modelling of Lateral Behaviour of Large-Diameter Monopiles Supporting Offshore Wind Turbines in Soft Clay[D]. Hangzhou: Zhejiang University, 2021. (in Chinese)
[17] LAI Y Q, WANG L Z, ZHANG Y H, et al. Site-specific soil reaction model for monopiles in soft clay based on laboratory element stress-strain curves[J]. Ocean Engineering, 2021, 220: 108437. doi: 10.1016/j.oceaneng.2020.108437
[18] ISFOG. Cyclic loading prediction event flyer[C]// International Symposium on Frontiers in Offshore Geotechnics, Austin, 2020.
[19] GUEVARA M, DOHERTY J P, GAUDIN C, et al. Evaluating uncertainty associated with engineering judgement in predicting the lateral response of conductors[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2022, 148(5): 05022001. doi: 10.1061/(ASCE)GT.1943-5606.0002759
[20] HONG Y, HE B, WANG L Z, et al. Cyclic lateral response and failure mechanisms of semi-rigid pile in soft clay: centrifuge tests and numerical modelling[J]. Canadian Geotechnical Journal, 2017, 54(6): 806-824. doi: 10.1139/cgj-2016-0356
[21] RANDOLPH M F, HOULSBY G T. The limiting pressure on a circular pile loaded laterally in cohesive soil[J]. Géotechnique, 1984, 34(4): 613-623. doi: 10.1680/geot.1984.34.4.613
[22] YU J A, HUANG M S, ZHANG C R. Three-dimensional upper-bound analysis for ultimate bearing capacity of laterally loaded rigid pile in undrained clay[J]. Canadian Geotechnical Journal, 2015, 52(11): 1775-1790. doi: 10.1139/cgj-2014-0390
[23] OSMAN A S, BOLTON M D. Simple plasticity-based prediction of the undrained settlement of shallow circular foundations on clay[J]. Géotechnique, 2005, 55(6): 435-447. doi: 10.1680/geot.2005.55.6.435
[24] 王立忠, 刘亚竞, 龙凡, 等. 软土地铁深基坑倒塌分析[J]. 岩土工程学报, 2020, 42(9): 1603-1611. doi: 10.11779/CJGE202009004 WANG Lizhong, LIU Yajing, LONG Fan, et al. Collapse of deep excavations for metro lines in soft clay[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(9): 1603-1611. (in Chinese) doi: 10.11779/CJGE202009004
[25] ZHANG Y H, ANDERSEN K H. Scaling of lateral pile p-y response in clay from laboratory stress-strain curves[J]. Marine Structures, 2017, 53: 124-135. doi: 10.1016/j.marstruc.2017.02.002
[26] ZHANG Y H, ANDERSEN K H, JEANJEAN P, et al. Validation of monotonic and cyclic p-y framework by lateral pile load tests in stiff, overconsolidated clay at the haga site[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(9): 04020080. doi: 10.1061/(ASCE)GT.1943-5606.0002318
[27] 王立忠, 叶盛华, 沈恺伦, 等. K0固结软土不排水抗剪强度[J]. 岩土工程学报, 2006, 28(8): 970-977. http://cge.nhri.cn/cn/article/id/12136 WANG Lizhong, YE Shenghua, SHEN Kailun, et al. Undrained shear strength of K0 consolidated soft clays[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(8): 970-977. (in Chinese) http://cge.nhri.cn/cn/article/id/12136
[28] 王立忠, 但汉波, 李玲玲. K0固结软土的循环剪切特性及其流变模拟[J]. 岩土工程学报, 2010, 32(12): 1946-1955. http://cge.nhri.cn/cn/article/id/9135 WANG Lizhong, DAN Hanbo, LI Lingling. Cyclic shearing behavior of K0-consolidated clay and its rheological simulation[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(12): 1946-1955. (in Chinese) http://cge.nhri.cn/cn/article/id/9135
[29] ANDERSEN K H. Cyclic soil parameters for offshore foundation design[C]//The 3rd McClelland Lecture, London, 2015.
[30] ZHANG Y, ANDERSEN K H, KLINKVORT R T, et al. Monotonic and cyclic p-y curves for clay based on soil performance observed in laboratory element tests[C]// Proc Offshore Technology Conf, Houston, 2016.
[31] GRIMSTAD G, ANDRESEN L, JOSTAD H P. NGI-ADP: Anisotropic shear strength model for clay[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2012, 36(4): 483-497.
-
期刊类型引用(1)
1. 章巍，储著宇，陈学奇，俞刚，张志帅，韩勃. 基于p-y曲线和实体有限元法的大直径单桩水平受荷性状研究. 水利水电技术(中英文). 2024(12): 193-202 . 
百度学术
其他类型引用(2)
计量
- 文章访问数: 519
- HTML全文浏览量: 78
- PDF下载量: 190
- 被引次数: 3
