Pressuremeter tests and parameter back analysis of deep silty clay
-
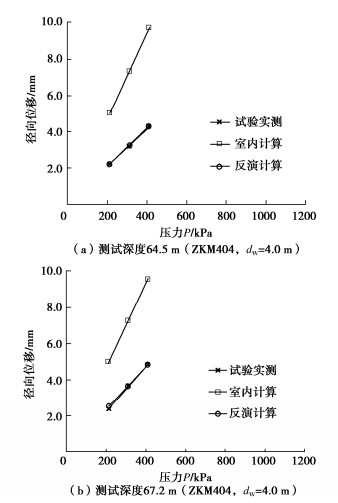
摘要: 深厚覆盖层土体具有显著的原位结构效应,如何考虑原位结构效应确定其本构模型参数,关系安全评价结果的可靠性。对覆盖层深部粉质黏土开展了原位旁压测试,测得了其荷载–位移曲线,确定了相应深度处初始压力、承载力特征值和旁压模量等力学指标特征值。联合原位旁压试验和室内三轴试验结果,采用基于和声算法的PBP3反分析程序,确定了覆盖层深部粉质黏土的本构模型参数。分别采用反分析参数和室内试验参数模拟了旁压试验过程,与实测荷载位移曲线进行了对比,论证了反分析参数的合理性。Abstract: The deep overburden layer has significant in-situ structural effects, and how to determine the constitutive model parameters by considering the in-situ structure effects is related to the reliability of safety assessment results. The in situ pressuremeter tests are carried out on the silty clay in deep overburden layer, and the load-displacement curves are measured, and the characteristic values of mechanical indexes such as bearing capacity characteristic value and pressuremeter modulus at corresponding depths are determined. Combined with the results of the in-situ pressuremeter tests and laboratory triaxial test, the constitutive model parameters of silty clay in deep overburden are determined by using the PBP3 back analysis program based on the harmony algorithm. The process of the pressuremeter tests is simulated by using the back analysis parameters and laboratory test parameters respectively, and the rationality of the back analysis parameters is demonstrated by comparing with the measured load-displacement curves.
-
0. 引言
土工离心模型试验技术是一项崭新的土工物理模型技术,通过施加在模型上的离心惯性力使模型的重度变大,从而使模型的应力与原型一致,这样就可以用模型反映、表示原型。离心模型是各类物理模型中相似性最好的模型,在国内外受到广泛重视,试验技术飞速发展与进步,研究内容涉及几乎所有的岩土工程研究领域,已成为岩土工程技术研究中的最主要、最有效、最广泛应用的研究手段[1]。
Biot动力固结方程是土力学的基本方程,包括动力平衡方程和连续方程。从连续方程出发,得到固结与孔隙水压力的扩散问题的时间比尺关系tp/tm=n2[2],这个关系的前提假设是,模型的渗透系数km是原型渗透系数kp的n倍,模型与原型的固结系数相等,这一假设存在争议,未得到试验完全证实。
Pokrovsky & Fyodorov认为离心模型的水力坡降im与原型的水力坡降ip相等,模型的渗透系数km是原型渗透系数kp的n倍,得到了tp/tm=n2的时间比尺关系;而Cargill等[3]则认为离心模型的水压力坡降im是原型的水压力坡降ip的n倍,模型的渗透系数km与原型渗透系数kp相等,令人奇怪的是,他们利用相互矛盾、相互对立的假定得到了相同的结论。
其实,Cargill等把达西定律中的“水力梯度(h/L)”用“水压力梯度(p/L)”来代替是错误的,因为水力梯度(无量纲)与水压力梯度(有量纲)并不相同。因而,模型渗透系数km与原型渗透系数kp的关系,成了问题的关键。即土的渗透系数(达西渗透系数)在高重力场下变不变?是否随加速度而增大?
从不同的研究目的出发,世界各国的离心模型试验专家进行了不懈的努力。Goodings[4]通过试验研究了灰坝的浸润线,Croce等[5]研究了土样的固结问题,Singh等[6]和Khalifa等[7]都研究过土的渗透系数随加速度的变化规律。令人不解的是,Singh等的结果表明,土的渗透系数随加速度而增大,而Khalifa等的结果却表明,在50g以下,土的渗透系数不随加速度变化。Singh等的试验装置不能防止水的蒸发,结果令人怀疑;Khalifa等的试验只进行到50g,也难以说明问题,不能令人信服。Sharma等[8]分析了离心机半径对变水头试验测得的渗透系数的影响。隋海宾等[9]总结了国外离心模型试验中土的渗透相似性研究成果,但没有自己的试验。Anderson等[10]研制了在离心机上进行土的渗透系数试验的装置,可以大大缩短试验时间。
国内外离心模型试验发展很快,离心模型试验中固结与孔隙水压力扩散问题的时间比尺问题一直未能得到有效的试验验证。固结与孔隙水压力扩散问题的时间比尺关系tp/tm=n2正确与否,归根结底就是高重力场条件下土的渗透特性与普通重力场条件下是否一致?如果不一致,土的渗透特性随离心加速度是怎样变化的?本文通过离心模型渗透试验,研究了土的渗透系数随离心加速度的变化规律,验证离心模型渗透相似理论,澄清固结与孔隙水压力扩散问题的时间比尺关系的一些模糊不清问题,对离心模型试验技术的发展具有十分重要的理论意义和应用价值。
1. 渗透相似理论
水在土体孔隙中的渗透采用达西定律描述,
v=kΔhL=ki, (1) 式中:v为渗透速度;k为渗透系数,其物理意义是当水力梯度等于1时的渗透速度;L为渗径长度;Δh为试样两端的水位差;i为水力梯度,它是沿渗透方向单位距离的水头损失,无量纲。
定义任一模型变量xm与原型变量xp的相似常数:
ηx=xp/xm。 (2) 将式(2)代入式(1),可以得到
ηvv=ηkηiki。 (3) 达西定律可以描述原型和模型,因此它对原型与模型来说都应当是正确的。只有当所有的η项系数都相等时,式(3)才与原方程式(1)相同,也就是,
ηv=ηkηi。 (4) 离心模型试验中,模型的渗透速度是原型的n倍,即ηv=1/n,而水力梯度无量纲,则ηi=1,得到
ηk=1/n。 (5) Muskat[11]、Lambe等[12]分别给出了渗透系数与流体重度的关系式:
k=Kγμ=Kρgμ。 (6) 式中:K为土体的内在渗透系数,是颗粒形状、直径和填料的函数;μ为流体的动力黏度;ρ为流体的密度;g为重力加速度。
由式(6)可以明显看出,渗透系数随土体的内在渗透系数、流体的动力黏度、流体的密度、重力加速度变化,模型和原型土体的内在渗透系数、流体的动力黏度、流体的密度相同,重力加速度为n倍,即,ηK=ημ=ηρ=1,ηg=1/n,因此,可得ηk=1/n。
2. 渗透离心模型试验
2.1 试验设备
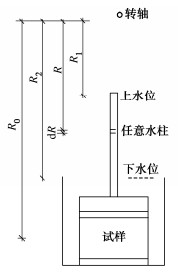
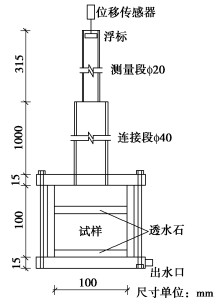
试验在南京水利科学研究院NHRI400 g·t土工离心机上进行。该机最大半径5.5 m,吊篮平台的尺寸为1100 mm×1100 mm,最大加速度200g,最大负荷2 t,容量400 g·t。为在离心机中进行渗透试验,研制出离心机渗透仪,渗透仪装置由渗透容器、变水头管、水头测量装置等组成(图 1)。渗透容器由金属圆筒(内径100 mm、高100 mm)、透水石、上盖和下盖组成,变水头管由连接段(内径40 mm)和测量段(内径20 mm)组成,水头测量装置由激光位移传感器和浮标组成。
2.2 试验方法
试验土样为低液限黏土(CL)、低液限粉土(ML)、粉土质砂(SM)3种,其物理性质指标见表 1。
表 1 土样的物理性质指标Table 1. Physical properties of soils土名 低液限黏土 低液限粉土 粉土质砂 含水率/% 29.0 26.2 20.5 密度/(g·m-3) 1.94 2.08 2.10 试样高度/mm 40 36 69 液限/% 42.2 24.8 塑性指数 20.7 6.6 颗粒组成
/%砂粒 12.8 39.0 55.3 粉粒 44.7 41.6 38.5 黏粒 42.5 19.4 6.2 将土样制备成饱和泥浆,放入试样筒内,采用预压方法进行固结成型,固结完成后土样的含水率、密度、试样高度见表 1。将安装好的渗透仪装置放置在模型箱内,以控制下水位,从而控制渗透水头。将渗透仪装置和模型箱放入离心机吊篮,接好激光位移传感器,启动离心机到设定加速度,通过位移传感器测试上水位下降过程。每种土样的试验加速度分别1g(常规)、10g、25g、50g、75g、100g、150g,每种工况进行2组平行试验。
2.3 渗透水头修正
离心惯性加速度场是通过离心机的旋转而产生的,离心机旋转产生的离心惯性加速场是沿旋转中轴形成的一个个圆形的柱面,在每个等半径的圆柱面上,其离心惯性加速场的惯性势是相等的,离心加速度也相同,离心加速度的大小与半径成正比。这样,在模型的不同高度上,所受到的离心惯性力是不同的。那么离心模型中,上、下水位差并不是真正的渗透水头,而必须进行修正。
如图 2所示,任意旋转半径R处的水柱dR,对试样中心产生的渗透压力增量dp可表示为,
dp=ρwa0R0RdR 。 (7) 式中dp为试样中心的渗透压力增量;ρw为水的密度;a0为试样中心的加速度;R0为试样中心的旋转半径;R为任意水柱的旋转半径;dR为任意水柱的高度。
对式(7)积分,可得土样中心产生的渗透压力为
p=∫R2R1ρwa0R0RdR=12ρwa0R0(R22−R21)。 (8) 式中,p为试样中心的渗透压力;R2为下水位的旋转半径;R1为上水位的旋转半径;其他符号意义同前。
因此,渗透水头为
Δh=pρwa0=R22−R212R0, (9) 式中,Δh为试样的渗透水头,其他符号意义同前。
变水头渗透系数按式(10)计算
kT=BLA(t2−t1)lnΔh1Δh2。 (10) 式中,kT为水温为T℃时试样的渗透系数;B为测量段变水头管的断面积;L为渗径,即试样高度;A为试样的断面积;t1,t2分别为测读水头的起始和终止时间;Δh1,Δh2分别为起始和终止渗透水头。
标准温度(20℃)下的渗透系数按式(11)计算
k20=kTηTη20。 (11) 式中,k20为标准温度时试样的渗透系数;ηT为T℃时水的动力黏滞系数;η20为20℃时水的动力黏滞系数。
3. 试验结果分析
3.1 渗透系数的变化规律
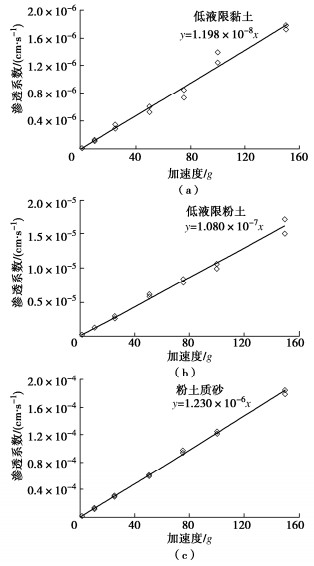
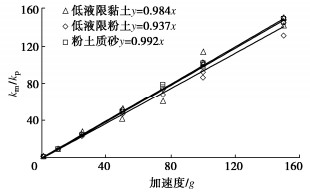
表 2列出了不同加速度下3种土样的渗透系数试验结果,图 3给出了3种土样的渗透系数随加速度的变化,从图中可以看出,3种土样的渗透系数随加速度的增加而线性增大,表明渗透系数与加速度呈正线性关系。把图 3的纵坐标改为ng时渗透系数与1g时渗透系数之比km/kp,如图 4所示,可以看出,km/kp与加速度具有良好的线性变化关系,可表示为
km/kp=χn, (12) 表 2 渗透系数试验结果Table 2. Test results of permeability coefficient (cm/s)土名 加速度/g 1 10 25 50 75 100 150 低液限黏土 1.21×10-8 1.24×10-8 1.28×10-7 3.58×10-7 6.16×10-7 8.50×10-7 1.40×10-6 1.79×10-6 1.29×10-8 1.25×10-8 1.14×10-7 2.97×10-7 5.26×10-7 7.57×10-7 1.26×10-6 1.73×10-6 低液限粉土 1.21×10-7 1.37×10-7 1.21×10-6 2.92×10-6 6.06×10-6 8.48×10-6 1.07×10-5 1.73×10-5 1.26×10-7 1.18×10-7 1.17×10-6 2.67×10-6 5.77×10-6 7.91×10-6 9.97×10-6 1.52×10-5 粉土质砂 1.32×10-6 1.18×10-6 1.29×10-5 2.99×10-5 5.99×10-5 9.44×10-5 1.22×10-4 1.85×10-4 1.50×10-6 1.09×10-6 1.13×10-5 3.10×10-5 6.16×10-5 9.81×10-5 1.26×10-4 1.79×10-4 式中,χ为比例系数。试验数据拟合得出,3种土样的χ分别0.984,0.937,0.992。除去试验仪器以及固结等因素的影响,比例系数χ≅1。因此,试验证明了离心模型试验渗透系数比尺为ηk=1/n。Singh等[6]利用小离心机变水头试验,也得出了类似的试验结果。
3.2 离心模型中达西定律的适用性
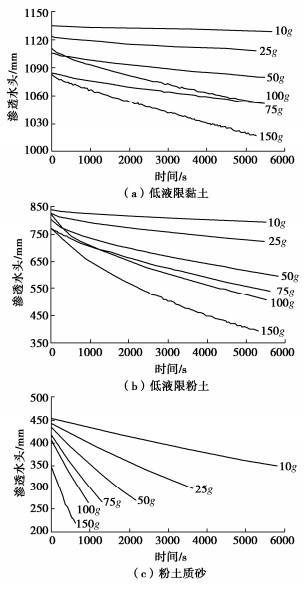
进行渗透试验时,渗透水头随时间的变化直接反映了试样的渗透稳定情况,图 5给出了不同加速度条件下3种土样的渗透水头过程线。试验结果表明,3种土样的渗透水头随时间的延长而逐渐下降,且下降速率基本一致,说明试样的渗透稳定。下降速率与离心机加速度和土性有关,加速度越大,下降速率越大,土样黏粒含量越大,下降速率越慢。
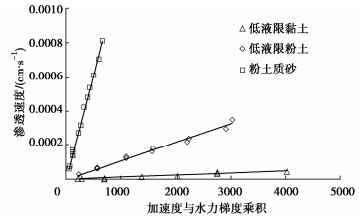
图 6给出了3种土样的渗透速度随加速度与水力梯度乘积的关系曲线,从图中可以看出,3种土样的渗透速度随加速度与水力梯度乘积的增加而线性增大,且线性关系相当好,增长速率与试样的黏粒含量有关,试样黏粒含量越大,增长速率越大,增长速率即为1g条件下试样的渗透系数。表 3列出了3种土样渗透试验最大加速度与水力梯度乘积,表明在这个范围内,离心模型试验渗透符合达西定律,试样黏粒含量越大,加速度与水力梯度乘积也越大。
表 3 3种土样渗透试验最大加速度与水力梯度乘积Table 3. Products of maximum acceleration and hydraulic gradients of three soil samples in permeability tests土名 d10/mm k/(cm⋅s-1) v/(cm⋅s-1) 试验最大加速度×水力梯度 低液限黏土 0.0014 1.22×10-8 4.81×10-5 4033 低液限粉土 0.0021 1.15×10-7 3.50×10-4 3037 粉土质砂 0.0112 1.24×10-6 8.14×10-4 661 4. 结语
离心模型渗透试验结果表明,渗透系数随加速度的增加而线性增大,离心模型试验渗透符合达西定律,模型的渗透系数与原型渗透系数之比km/kp随加速度成比例线性增大,比例系数≈1,从而验证了离心模型试验渗透系数比尺为ηk=1/n。虽然国外也得出了类似的试验结果,但我们试验的渗透水头比他们的大,土样类型也多。研究成果对离心模型试验具有重大理论和应用价值。
-
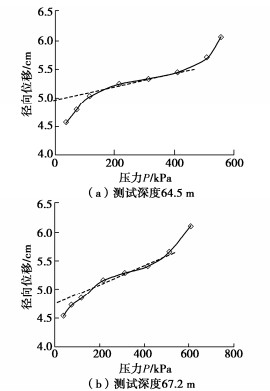
表 1 钻孔404旁压试验成果汇总表
Table 1 Summary of pressuremeter tests of borehole 404
编号 土层描述 试验深度H/m 上覆有效压力/kPa 临塑压力Pf/kPa 极限压力PL/kPa 承载力特征值Fak/kPa 旁压模量Em/MPa ③-2 粉质黏土 64.5 750 420 600 310 4.65 ③-2 粉质黏土 67.2 776 410 730 280 3.94 表 2 邓肯-张模型参数室内试验值
Table 2 Parameters of Duncan-Chang model obtained from laboratory tests
土样名称 土层类型 干密度/(g·cm-3) φd cd k n kb m Rf ③-2 粉质
黏土1.51 30.4 34.1 184 0.36 118 0.25 0.76 1.47 29.8 30.6 175 0.34 109 0.23 0.74 表 3 基于旁压试验的反分析邓肯-张模型参数值
Table 3 Parameter back analysis values of Duncan-Chang model based on pressuremeter tests
编号 土层
类型试验深度H/m 上覆压力/kPa k n kb m ③-2 粉质
黏土64.5 750 421 0.348 385 0.463 ③-2 粉质
黏土67.2 776 366 0.354 306 0.467 -
[1] 蒋彭年. 土的本构关系[M]. 北京: 科学出版社, 1982. JIANG Peng-nian. Constitutive Relation of Soil[M]. Beijing: Science Press, 1982. (in Chinese)
[2] 黄文熙. 土的工程性质[M]. 北京: 水利电力出版社, 1983. HUANG Wen-xi. Engineering Properties of Soil[M]. Beijing: Water Conservancy and Hydropower Press, 1983. (in Chinese)
[3] NAYLOR D J. Stress-Strain Laws for Soil, Development in Soil Mechanics[R]. Edited by Scott C R, 1975.
[4] 曾以宁, 屈智炯, 刘开明, 等. 土的非线性K-G模型的试验研究[J]. 成都科技大学学报, 1985, 17(4): 143–149. https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH198504019.htm ZENG Yi-ning, QU Zhi-jiong, LIU Kai-ming, et al. An experimental study of nonlinear K-G model for soils[J]. Journal of Chengdu University of Science and Technology, 1985, 17(4): 143–149. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH198504019.htm
[5] 谢定义. 土动力学[M]. 西安: 西安交通大学出版社, 1989. XIE Ding-yi. Soil Dynamics[M]. Xi'an: Xi'an Jiao Tong University Press, 1989. (in Chinese)
[6] 顾淦臣. 土石坝地震工程[M]. 南京: 河海大学出版社, 1989. GU Gan-chen. Earth Dam Earthquake Engineering[M]. Nanjing: Hohai University Press, 1989. (in Chinese)
[7] 刘小生, 汪闻韶, 赵冬. 饱和原状砂土的静、动力强度特性试验研究[J]. 水利学报, 1991, 22(11): 41–46. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB199111005.htm LIU Xiao-sheng, WANG Wen-shao, ZHAO Dong. Experimental study on static and dynamic strength characteristics of saturated sandy soil[J]. Journal of Hydraulic Engineering, 1991, 22(11): 41–46. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB199111005.htm
[8] 刘小生, 赵冬, 汪闻韶. 原状结构性对饱和砂土动力变形特性影响试验研究[J]. 水利学报, 1993, 24(2): 32–42. LIU Xiao-sheng, ZHAO Dong, WANG Wen-shao. Experimental study on dynamic deformation characteristics of saturated sand with shape structure[J]. Effects of in situ fabric on the dynamic deformation behavior of saturated sand[J]. Journal of Hydraulic Engineering, 1993, 24(2): 32–42. (in Chinese)
[9] 刘小生, 汪闻韶, 常亚屏. 饱和原状砂动力特性研究[R]. 国家自然科学基金重大项目"岩土与水工建筑物相互作用"研究成杲汇编, 1992. LIU Xiao-sheng, WANG Wen-shao, CHANG Ya-ping. Study on Dynamic Characteristics of Saturated Undisturbed Sand[R]. Compilation of the Research Achievements on the Interaction Between Rock and Soil and Hydraulic Structures in Major Projects of the National Natural Science Foundation of China, 1992. (in Chinese)
[10] 刘启旺, 杨玉生, 刘小生, 等. 考虑原位结构效应确定深厚覆盖层土体的动力变形特性参数[J]. 水利学报, 2015, 46(9): 1047–1054. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201509005.htm LIU Qi-wang, YANG Yu-sheng, LIU Xiao-sheng, et. al. Test of dynamic deformation parameters of deep alluvial soils considering in-situ structural effects[J]. Journal of Hydraulic Engineering, 2015, 46(9): 1047–1054. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201509005.htm
[11] 杨玉生, 刘小生, 赵剑明, 等. 考虑原位结构效应确定深厚覆盖层土体的动强度参数[J]. 水利学报, 2017, 48(4): 446–456. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201704008.htm YANG Yu-sheng, LIU Xiao-sheng, ZHAO Jian-ming, et al. Determination of liquefaction resistance of deep alluvial soils considering in-situ structure effects[J]. Journal of Hydraulic Engineering, 2017, 48(4): 446–456. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201704008.htm
[12] 杨玉生, 刘小生, 汪小刚, 等. 覆盖层地基和筑坝土石料本构模型参数反分析研究进展[C]// 第六届中国水利水电岩土力学与工程学术研讨会, 2016: 94–102. YANG Yu-sheng, LIU Xiao-sheng, WANG Xiao-gang, et al. Research progress on back analysis of constitutive model parameters of alluvial foundation and rockfill materials[C]// The 6th China Water Conservancy and Hydropower Geotechnical Mechanics and Engineering Symposium, 2016: 94–102. (in Chinese)
[13] 杨玉生, 刘小生, 赵剑明, 等. 基于计算结果和监测资料的坝基覆盖层沉降对比分析[C]// 土石坝工程—面板与沥青混凝土防渗技术交流会, 2015: 129–135. YANG Yu-sheng, LIU Xiao-sheng, ZHAO Jian-ming, et al. Comparative analysis of dam foundation settlement based on calculation results and monitoring data[C]// Proceeding for Earth Dam Engineering: Anti-seepage Technology in Face Slab and Asphalt Concrete, 2015: 129–135. (in Chinese)
[14] 刘小生, 汪小风, 马怀发, 等. 旁压试验反演邓肯-张模型参数方法研究[J]. 岩土工程学报, 2004, 26(5): 601–606. http://cge.nhri.cn/cn/article/id/11486 LIU Xiao-sheng, WANG Xiao-gang, MA Huai-fa, et al. Study on back-analysis method of constitutive parameters for Duncan-Chang model based on in -situ pressuremeter tests[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(5): 601–606. (in Chinese) http://cge.nhri.cn/cn/article/id/11486
[15] 马怀发, 孔俐丽, 侯淑媛, 等. 基于旁压试验反分析土体本构参数的有限元方法[J]. 水利水电技术, 2005, 36(6): 58–60, 64. https://www.cnki.com.cn/Article/CJFDTOTAL-SJWJ200506022.htm MA Huai-fa, KONG Li-li, HOU Shu-yuan, et al. FEM for inverse analysis on soil constitutive parameters based on pressuremeter test[J]. Water Resources and Hydropower Engineering, 2005, 36(6): 58–60, 64. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJWJ200506022.htm
[16] 杨志法, 王思敬, 冯紫良, 等. 岩土工程反分析原理及应用[M]. 北京: 地震出版社, 2002. YANG Zhi-fa, WANG Si-jing, FENG Zi-liang, et al. Principle and Application of Back Analysis in Geotechnical Engineering[M]. Beijing: Seismological Press, 2002. (in Chinese)
[17] 吕爱钟, 蒋斌松. 岩石力学反问题[M]. 北京: 煤炭工业出版社, 1998. LÜ Ai-zhong, JIANG Bin-song. Inverse Problem of Rock Mechanics[M]. Beijing: China Coal Industry Publishing House, 1998. (in Chinese)
[18] 杨玉生, 刘小生, 赵剑明, 等. 邓肯E-B模型参数敏感性分析[J]. 中国水利水电科学研究院学报, 2013, 11(2): 81–86. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGSX201302001.htm YANG Yu-sheng, LIU Xiao-sheng, ZHAO Jian-ming, et al. Parameter sensitivity analysis of Duncan E-B model[J]. Journal of China Institute of Water Resources and Hydropower Research, 2013, 11(2): 81–86. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGSX201302001.htm



 下载:
下载: