0.   引言

随着城市基础设施的不断发展和轨道交通的快速开发，已建运营隧道上方不可避免的会受到一些加、卸载工程扰动，地面应力状态的突然改变传递至下方隧道周围土体，会引起盾构隧道支护结构产生附加变形，严重时还会引发安全事故^[1]。目前很多学者针对地表堆载引起的下方既有运营隧道结构变形采用数值模拟，理论解析和室内试验等手段进行了研究，并取得了大量成果^[1-3]。然而这些分析大多采用均质材料进行研究，忽略了土体参数固有空间变异性对于地表堆载时下方隧道结构附加变形的影响。Vanmarcke^[4]通过引入相关距离和相关函数等概念，创造性地提出了随机场理论用以表征土体参数的空间变异性，并被诸多学者与其他数值方法结合使用。目前使用较多的方法主要有随机有限元法(Random Finite Element Method, RFEM)和随机有限差分法(Random Finite Difference Method, RFDM)，分析对象主要集中在边坡稳定性，隧道开挖和基坑开挖等领域^{[3, 5-6]}。Zhang等^[2]通过大量随机计算结果提出了3种针对盾构隧道收敛变形的简化计算方法；Cheng等^[7]分析了弹性模量的波动范围和变异系数对于隧道开挖后地表变形形态的影响；李建斌等^[8]以厦门地区典型风化花岗岩地层为例研究了双线盾构隧道开挖时地表以及隧道衬砌结构的变形。

然而这些研究大多局限于二维平面应变问题，对于三维空间中地表堆载时运营隧道轴向变形的影响规律尚不明确；此外，限于随机场的大规模计算，关于隧道可靠性方面的研究大多停留在定性、半定量的层面，很难与实际工程相结合。为此，本文建立了三维地表堆载—隧道模型，针对土体弹性模量的空间变异性进行随机场离散，采用随机有限元算法(RFEM)和蒙特卡洛(Monte-Carlo, MC)策略对各向同性相关结构下的隧道轴向变形的超标概率进行了概率分析，并提出了一种等效确定性计算方法，为类似工程考虑土体参数空间变异性提供了一种简化的计算思路。

1.   三维随机场模型生成

土体参数在沉积历史、应力条件、物理和化学风化等复杂地质作用下，即使在邻近的两点，土体参数也会存在差异，这种差异并非简单的纯随机性，而是表现为局部随机和整体相关两部分，称为空间变异性。实际工程中，限于场地条件和人力财力，往往无法获取工程范围内全部点的数据特征，为此，常采用随机场理论来模拟参数的这种空间变异特征。

常用的随机场建模方法有常用的随机场建模方法有局部平均法(Local Average Subdivision, LAS)，Karhunen-Loeve (K-L)级数展开法和协方差矩阵分解法等^[9]。鉴于矩阵分解法模拟过程简便，容易实现以及具有较高的模拟精度，本文利用矩阵分解法建立随机场，其基本步骤如下：

(1) 构建n阶自相关矩阵C，其中C中的任意元素$ {\rho _{{\tau _{ij}}}} $为空间中两点$ i $和$ j $的协方差，对于岩土参数，可以采用Markov相关函数计算，三维一阶Markov相关函数表达式为

其中：$ \tau $为两点在对应坐标系方向上的间距；$ \theta $为响应坐标系方向上的波动范围，可以通过对实测数据进行拟合得到。

(2) 对自相关矩阵进行Cholesky分解，得到上三角和下三角矩阵L和U：

式中，$ {\boldsymbol L^{\text{T}}} $为下三角矩阵L的转置矩阵。利用伪随机数生成器生成n阶正态分布随机数组成列向量R，则n阶标准正态分布随机场Y可以表示为

对式(3)进行等概率变换即可得到服从任意分布的随机场。

2.   地表堆载对运营隧道影响分析

2.1   数值计算模型

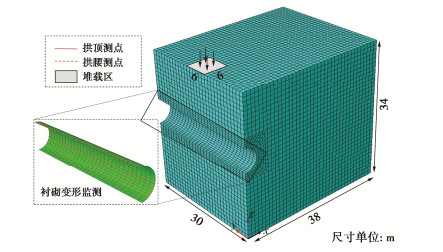
采用随机场模型与有限元软件ABAQUS相结合的方式对地表堆载时已有盾构隧道变形进行概率分析。在ABAQUS中建立三维堆载-隧道模型，如图 1所示，模型尺寸为38 m×34 m×30 m(长×高×宽)，盾构隧道直径D = 6 m，轴线埋深15 m。土体单元采用8节点立方体单元模拟，单元尺寸为1 m；衬砌采用shell单元模拟，厚度取0.3 m。在隧道顶部6 m×6 m范围内进行地表堆载，堆载压强为100 kPa，土体参数和衬砌材料参数见表 1所示。

图  1  地表堆载-隧道有限元模型

Figure  1.  FE model for ground surcharge and tunnel

下载: 全尺寸图片 幻灯片

表  1  土体和衬砌基本力学参数

Table  1.  Basic mechanical parameters of soils and linings

介质	重度/ (kN·m-3)	内摩擦角$ \varphi $/(°)	黏聚力c/kPa	弹性模量E/MPa	泊松比$ \nu $
土体	18.5	25	20	25(均值)	0.35
衬砌	24.5	—	—	20000	0.2

下载: 导出CSV 

| 显示表格

大量地质调查报告表明，土体弹性模量具有显著的空间变异性，对于隧道轴向沉降和横向收敛变形具有重要影响，因此本文将土体弹性模量离散为服从对数正态分布的一阶平稳随机场。根据Zhang等^[2]和Huang等^[9]的建议，取弹性模量E的均值$ {\mu _E} = 25{\text{ MPa}} $，变异系数(Coefficient of Variation) COV取0.3，此时弹性模量的对数lnE的均值$ {\mu _{\ln E}} $和标准差$ {\sigma _{\ln E}} $分别为

2.2   确定性分析

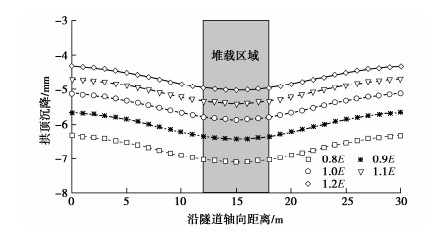
采用Mohr-Coulomb屈服准则对地表堆载时运营隧道衬砌结构的轴向变形进行研究，为验证弹性模量对于隧道变形的影响规律，采用不同的折减系数对弹性模量进行折减后计算。图 2分别给出了5个不同折减系数下地表堆载对于下方盾构隧道衬砌结构沿轴向方向的拱顶沉降。可见在地表堆载时，下部盾构隧道沿着轴向的拱顶沉降变形曲线关于地表堆载区域对称。随着弹性模量的增大，隧道轴向变形逐渐减小，结果研究可以为后续简化确定性计算方法的提出提供支撑。

图  2  确定性分析结果

Figure  2.  Deterministic analysis results

下载: 全尺寸图片 幻灯片

3.   隧道变形概率统计分析

实际工程中往往需要确定的变形控制指标作为衡量工程安全的关键，由以上随机分析结果可以发现对于任意一次随机分析，其得到的结果都是不同的，因此需要对盾构隧道变形的特征值展开可靠性分析，以确定合理安全的控制指标。采用随机解均值作为盾构隧道可靠度指标的方式会忽略那些与均值差异较大的数据，但这些偏离较大的数据往往并非异常值，而是有可能出现的，因此采用随机解均值表征盾构隧道变形特征值并不合理。统计学中认为，超过的5%的数据将被舍弃，取95%作为置信度的最高值，可以将瞬间的毛刺(尖峰)去掉，比使用均值更具真实意义^[7]。为此，取95%分位数(即超过该值的概率小于5%)作为盾构隧道轴向变形的特征值更为合理。参考边坡中的失效概率，以盾构隧道轴向拱顶沉降变形为例，定义不同计算工况下超出沉降特征值的超标概率${P_{\text{f}}}$为

式中，N为计算次数，在本文中取500，$I[ \cdot ]$为指示函数，当单次计算沉降最大值$\Delta s$超过沉降特征值${s_{\lim }}$时取1，否则取0。

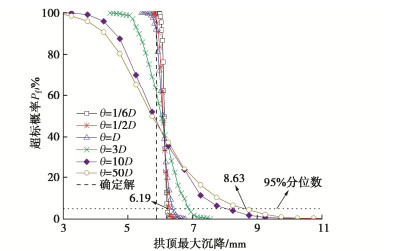
随机场中不同的波动范围对隧道拱顶沉降超标概率的影响如图 3所示，可以看出当波动范围$\theta \leqslant D$时，随机分析的结果波动性也很小，略大于确定性分析结果，当$\theta > D$时，随机分析的结果开始偏离确定解，而且偏离的程度随着波动范围的增大逐渐加剧。取95%分位数作为隧道受到地表堆载影响时沉降监测的控制值，θ = 1/6D时的控制值为6.19 mm，而θ = 50D的控制值为8.63 mm，两者相差28.27%，建议在波动范围大于隧道直径时考虑土体参数空间变异性。

图  3  各向异性系数对超标概率的影响(COV=0.3)

Figure  3.  Influences of anisotropy coefficient on probability of failure (COV=0.3)

下载: 全尺寸图片 幻灯片

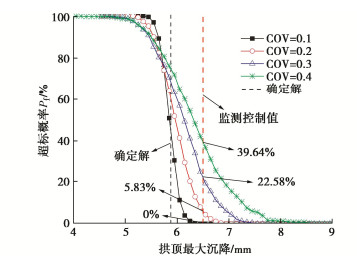
此外，土体由于受到的沉积历史和风化条件不同，其变异程度往往也是不同的，为了研究土体变异程度对于地表堆载时盾构隧道轴向变形的影响，分别取变异系数COV为0.1，0.2，0.3，0.4，研究不同变异系数对于隧道纵向变形特征值的影响。以${\theta _x} = {\theta _y} = $ ${\theta _z} = 3D$为例，图 4展示了4种不同的变异系数分别对应的隧道拱顶沉降超标概率分布图，可以看出当COV=0.1时，随机解的超标概率曲线几乎与确定解重合；而随着变异系数的增大，由于土体内部参数分布的离散程度增大，加剧了随机解的不确定性，进而导致隧道拱顶沉降的超标概率增大。若以6.5 mm作为监测控制值，变异系数为0.1和0.4分别对应的超标概率为0和39.64%，可见在高变异性土体中忽略土体参数的空间变异性会对严重低估隧道最大变形。

图  4  变异系数对于超标概率的影响

Figure  4.  Influences of COV on probability of failure

下载: 全尺寸图片 幻灯片

4.   隧道变形等效确定性分析法

采用有限元方法和蒙特卡洛策略相结合进行可靠度分析得到的结果虽然可信度高，然而庞大的计算成本使得随机场理论在实际工程中的应用极少。为了使随机场与实际工程的结合更为紧密，本文在对大量的随机分析结果进行概率统计的基础上，提出了一种计算在空间变异性土体中针对地表堆载引发的下方既有运营盾构隧道变形的等效确定性分析方法。

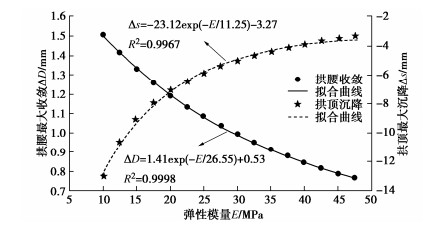
一般来说，受到土体参数低刚度占优效应^[6-7]的影响，随机分析得到的变形特征值往往会略大于确定解，根据图 3，4中的分析结果也可以看出确定性分析得到的结果普遍小于随机解。根据图 2中的确定性计算结果可以发现，这种差异可以将均质土层的弹性模量进行折损后消除，基于这种思想，将不同弹性模量均值计算得到的隧道拱顶沉降最大值$ \Delta s $和拱腰横向收敛最大值$ \Delta D $分别用散点图进行绘制，并且利用指数函数进行拟合，如图 5所示，可以发现，拱顶沉降最大值和拱腰收敛最大值的分布可以很好地用指数函数表征，拟合优度分别达到了0.9967和0.9998，拟合函数表达式分别为

图  5  变形最大值与弹性模量之间的关系

Figure  5.  Relationship between maximum deformation and elastic modulus

下载: 全尺寸图片 幻灯片

采用拟合方程，可以根据隧道轴向拱顶沉降和拱腰水平收敛快速求得单一土层中的等效均质弹性模量${E_{{\text{eq}}}}$。定义等效均质弹性模量${E_{{\text{eq}}}}$与确定性分析中使用的弹性模量${E_{\det }}$的比值为模量折损系数$\lambda $：

通过模量折损系数可以快速地对均质土体的弹性模量进行折减，从而使用一次确定性分析就能获得与随机解相近的计算结果。采用隧道轴向变形最大值的95%分位数作为变形特征值，代入拟合公式计算等效均质弹性模量与对应的模量折损系数，具体的结果如表 2所示。实际工程中，通过现场勘察与数据拟合得到相应的土体参数数字特征后，对表 2中的系数进行内插取值，可以为工程师在计算地表堆载引发运营隧道轴向变形时考虑土体参数空间变异性提供一种快速便捷的等效确定性分析方法。

表  2  随机解95%分位数对应的模量折损系数

Table  2.  Reduction coefficients corresponding to random solution

随机场变量		等效均质弹性模量${E_{{\text{eq}}}}$/MPa	模量折损系数$ \lambda $
\$$ \theta {\text{/}}D $ (COV=0.3)	1/6	24.2986	0.9719
	1/3	23.5905	0.9436
	1	22.2278	0.8891
	3	21.2447	0.8498
	10	18.0634	0.7225
	50	17.1241	0.6850
COV	0.1	24.7615	0.9905
	0.2	22.8765	0.9151
	0.3	22.2278	0.8891
	0.4	19.5565	0.7823

下载: 导出CSV 

| 显示表格

5.   结论

针对三维空间中地表堆载引起下方既有运营隧道轴向变形产生的影响，考虑土体弹性模量的空间变异性，利用随机有限元方法开展了隧道轴向变形概率分析，并提出了一种计算空间变异性土体中地表堆载引起下方隧道轴向变形的等效确定性分析方法。本文主要得到以下3点结论。

(1) 以随机分析中隧道轴向变形最大值的95%分位数作为变形特征值进行研究比均值更为合理，随着弹性模量波动范围增加，隧道轴向变形最大值的95%分位数也依次增大，隧道变形的超标概率也相应增加。

(2) 土体参数空间变异性对于隧道变形有着较大影响，在变异系数较高的土体中计算得到的隧道轴向变形与确定解差异较大，此时若忽略土体参数的空间变异性，会严重低估隧道变形的超标概率。

(3) 考虑到随机分析获得的结果往往大于确定性分析结果，以隧道轴向变形最大值的95%分位数表征随机分析结果，提出了一种等效确定性分析方法，并编制了对应计算工况的模量折损系数表，有效简化了复杂繁琐的随机分析，为工程师评估地表堆载对下方既有隧道产生的影响时考虑土体参数空间变异性提供了一种简便快捷的计算方法。