Temperature transfer characteristics of clearance space in hypergravity field of geotechnical model box
-
摘要: 寒区工程超重力试验设计与土工模型箱空气夹层空腔温度传递相关。通过建立夹层-土体的对流换热模型，基于Rayleigh-Benard对流模型和CFD数值仿真方法研究了超重力环境下，不同夹层厚度、不同超重力加速度对土体表面及夹层内部温度分布的影响，解释了超重力场对对流换热过程涡环成因及发展的现象。结果表明涡环的稳定分布与流场速度、压力及界面换热系数、温度等直接相关；不同间隙及过载下，努塞尔数均随时间降低；在传热初始阶段，夹层流场努塞尔数变化较大；在不同间隙状态下，随着超重力过载值变大，界面对流换热降低。研究获得了超重力对夹层热对流的影响，开展超重力场下试验设计时需综合考虑夹层尺度、超重力加速度等综合影响。
-
关键词:
- 夹层 /
- 超重力 /
- Rayleigh-Benard对流 /
- 涡环
Abstract: To study the temperature transfer laws of the air clearance space of the geotechnical model box in the hyper gravity field for design of the hyper gravity test platform tests in cold regions, the convection heat transfer model for clearance soil is established. Based on the Rayleigh-Benard convection model and the CFD numerical simulation, the effects of different clearance thicknesses and hypergravity acceleration on the temperature distribution on the soil surface and inside the clearance in the hypergravity environment are studied, and the phenomenon of the cause and development of the vortex ring in the convection heat transfer process is explained. The results show that the stable distribution of the vortex ring is directly related to the flow velocity, pressure, heat transfer coefficient of interface and temperature. The Nusselt number decreases with time under different clearances and overloads. In the start-up stage of the flow field, the Nusselt number changes greatly. In different gap states, the interfacial convective heat transfer decreases with the increase of the hypergravity acceleration. The influences of the hypergravity on the thermal convection in the slit are obtained, which can be used for the experimental design in the hypergravity field to consider the comprehensive influences of the slit scale and the hypergravity acceleration.-
Keywords:
- soil /
- hypergravity /
- Rayleigh-Benard convection /
- vortex ring
-
0. 引言
位于寒冷地区的水利工程，地基易受极端低温影响而发生冻胀现象，进而造成对水工建筑物结构的破坏。寒区工程超重力试验平台是利用离心力场模拟超重力场，具有克服小比尺模型的应力差异过大，避免了原位试验复杂耗时的优势，且具备热交换、干/湿环境模拟的功能，是开展寒区水利工程模型试验的重要设备。采用该设备进行寒区工程地基冻胀问题的模拟研究时，模型上方的热交换系统可在一定时间内持续为模型提供冷/热边界，利用热交换系统与模型表面间的之间的空气夹层上下表面温差进行热交换。
开展超重力场下寒区模型试验时，试验设计需了解土体与热交换系统间夹层空腔温度变化。而对空气夹层的换热过程可简化为不同尺寸的空腔及土体的耦合对流换热问题。对于空腔结构内部重力导致的对流问题，石峰等[1-2]研究了矩形腔体中Rayleigh-Benard对流结构，Ning等[3]研究了具有水平流的流体对流的周期行为问题，胡宇鹏等[4]研究了腔体内对流的稳定性问题，传统对此类的问题研究以常重力状态下为主[5-7]，对于超重力环境对低温边界下空气夹层-结构对流换热问题研究较少。由于土工模型箱内空气夹层换热过程较为复杂，易受到离心机工作状态的影响，获得超重力对低温对流换热的影响规律是设计试验面临的挑战问题。
本文基于数值模拟开展土体-夹层在超重力条件下对流换热仿真，通过分析土体界面的温度变化以及空腔内换热过程，获得模型表面温度随时间的变化规律，以及空腔内的温度场分布，获得了对换热过程对流、传导相关无量纲数变化的认识，可为开展寒区土体模拟试验提供参考。
1. 夹层传热计算模型
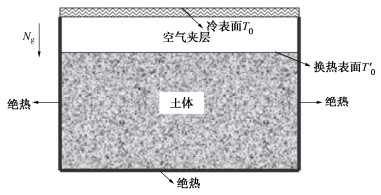
寒区工程超重力试验设备可简化描述为封闭空腔内自然对流传热的物理模型：模型箱内盛放一土体模型，此时模型加速度为Ng（常重力的倍数），方向由离心机主轴指向转臂。热交换板为冷表面，初始温度为T0；模型表面为光滑平面（热面），初始温度为T′0；模型表面与模型箱下表面的距离为L（夹层间隙厚度），该距离内形成一矩形密闭空腔。超重力场下的密闭空腔换热模型简化如图 1所示。
图 1中土体除上表面外均为绝热，空气夹层上表面为冷边界，土体与夹层界面通过对流及热传导进行热交换。可知空腔内流动包含两种运动：沿固壁的边界层运动以及围绕空腔中心的旋转运动，后者具有典型的Rayleigh-Benard（简称RB）对流的特征。RB对流是研究非平衡开放系统中对流运动的稳定性、时空结构、涡环（又称斑图）形成及非线性动力学特性的典型模型之一[1-4]，指在一个封闭的空腔内，其上表面温度恒定，下表面加热，由于底部流体被加热膨胀，相对于上部温度较低的流体其密度较小，下部流体上升，在上升中接触其他流体部分时消耗能量，温度变低密度变大。当底部温度继续升高，某些底部流体的温度足够大，密度足够小，能够上升到顶部而能量不至于全部耗散，从而形成温度差导致腔体内流体运动的流动现象[6]。需要指出的是，存在临界瑞利数（Ra），当空腔内局部Ra高于临界值时，才会出现RB对流[5-7]，如图 3所示，否则仅为热传导状态。
![]()
图 2 空腔界面温度在不同Ng、不同间隙时随时间变化Figure 2. Variation of temperature at interface with time under different Ng and clearances![]()
图 3 20 cm空腔50g状态换热末态时刻温度分布Figure 3. Temperature nephogram of 20 cm thick clearance at overload of 50g and last time step该物理问题与常重力场下的Rayleigh-Benard对流相似，仅重力加速度不同。在Boussinesq近似假设（认为浮力诱导的流体运动中，当温度足够小时，仅在浮力项中考虑密度变化）下，在Ng重力场下的流体力学基本控制方程如式（1）所示：
∇U=0 ，∂U/∂t+(U⋅∇)U=υ∇2U−∇P/ρ0+ρ/ρ0Ngg ，(U⋅∇)T+∂T/∂t=λ/ρ0CP∇2T 。} (1) 式中U为流体速度场；T为温度场；ρ为空气密度；g为重力加速度；υ为空气运动黏度；Cp为空气比热；t为时间；λ为导热系数。由于直接求解物理模型较为复杂，一般采用基于CFD（计算流体动力学）数值方法开展研究。
根据以上分析，模型箱的边界条件可以简化为：矩形方腔左右两侧绝热，上部为空气，下层为土体（密度为1.80 g/cm3，导热系数为2 W/m·℃，热容为4 MJ/m3·℃，热扩散系数为2.5×10-7 m2/s）。问题可简化为在Ng的超重力场下，研究矩形密闭空腔内的温度变化及温度场分布。考虑到空腔温度变化和从土体交换的热量直接相关，土体的热量与体积、质量等参数密切相关，因此建立考虑空气夹层与土体的温度分析模型，以模拟全场温度变化。同时，考虑到模型箱为长方体结构，取二维模型（侧向剖面）以表征真实三维结构，以降低计算量，提高仿真效率。计算模型的边界条件为：土体与夹层界面为换热边界，夹层上表面为-30℃，其它界面均为绝热边界，全场初始温度为10℃；即T0= -30℃；T′0=10℃，侧壁及底面均为绝热边界。根据试验状态取常重力及两种超重力状态，即Ng =1，10和50；根据土体情况取夹层厚度L =1，10和20 cm；针对两种参数组合共9种工况开展分析。
2. 夹层-土体对流换热分析
2.1 模型表面温度随时间变化
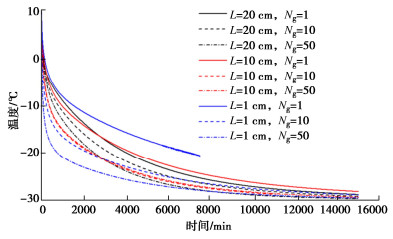
给出不同空气夹层厚度时界面温度在不同Ng值及间隙下随时间变化，如图 2所示。
图 2结果温度变化趋势与文献[8]一致。分析表明：随着Ng增大，界面降温加速，高Ng下降温速率大于低Ng工况，以20 cm为例，1g（常重力）、10g和50g状态下前2×105 s的平均降温速率分别为13.5，15，16.5℃/105 s；随着换热时间变长，降温速度随之降低，换热过程减速；降温速率与Ng并非线性关系：1，10，50g状态下200000~400000 s的平均降温速率分别为3.5，3，2℃/105 s；原因在于随着土体温度变低，土体界面与空气温差变小，导致温差驱动的对流换热的热量变小，导致降温过程随之减缓。
其次，在超重力状态下，随着夹层间隙减小，降温速率提升，小间隙下降温速率大于大间隙：以1 cm为例，1g，10g和50g状态下前2×105 s平均降温速率分别为12.5，15.5，17.5℃/105 s。空气与土体界面的换热热流率随间隙增大而减小，随Ng上升而上升：如10cm间隙时，初始阶段1g，10g和50g状态下，提取界面换热热流分别为78，165，325 W/m2；1 cm间隙时，10g和50g状态下界面热流率分别为520，630 W/m2，大于间隙较大时。界面对流换热系数变化趋势也一致。
需要指出的是，由于模型箱总容积一定，当夹层厚度较大时（20 cm），土体质量较小（总热容小），夹层厚度较小时，土体质量大（总热容大），导致通过对流及热传导将土体温度降低所需热量不同。
2.2 温度场分布特性
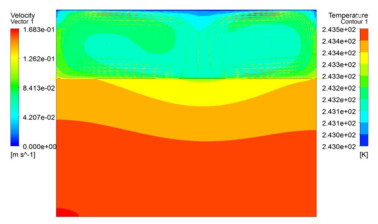
提取典型时刻全场温度分布及空腔流动速度，取具有代表性的20 cm空腔厚度和50g工况为例，如图 3所示，图 4给出了典型状态空腔内涡环的状态。
![]()
图 4 换热末态10 cm空腔50g状态涡环Figure 4. Vortex ring of 10 cm-clearance and overload 50g at last time step结合数值仿真结果及图 3，4可以看出：①20 cm间隙时，空腔内呈现典型的RB流动特征，形成两个对称的涡环，涡环外部流速较快，内部流速越来越小；出现涡环，超重力使得流动速度变快，1g，10g和50g下涡环中最大速度分别为0.028，0.65，1.02 m/s；在靠近壁面角落部位，会形成小的涡环，随着空腔流场的发展而变化。②10 cm间隙时，不同Ng下均会出现2对涡环；靠近侧边壁面处涡环较细长，中部涡环长宽比趋于1。③1 cm间隙时，1g状态有明显涡环成对出现；10g和50g状态下无明显的涡环发展过程，仅在靠近壁面交角附近出现较小涡环。④局部涡环会随着换热过程而发展。例如，在1 cm工况时，在初始阶段，先在靠近侧边壁面附近形成小的涡环，随之向空腔中部扩展；等到一定程度，涡环发展稳定；随着换热过程继续，涡环消失，仅在壁面附近形成较小的涡流，空腔气体温度随厚度方向变化明显，体现出传热为主的特征。涡环的稳定分布与流场速度、压力及界面换热系数、温度等直接相关。
2.3 空气夹层换热规律
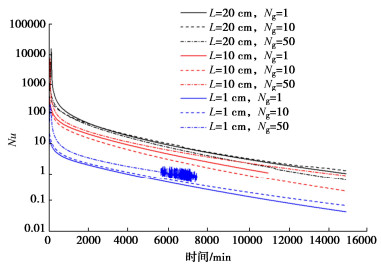
常用Nu数（努塞尔数）和Ra数（瑞利数）描述换热过程中的参数变化[8]，Nu数表征换热系统从流场中吸热的强弱，Ra数表征流场中自然对流的强弱。温度在空气和土体界面上并非完全均匀分布，因此界面上同一时刻对流换热系数、Nu数等并非均匀分布，计算时取界面中点数据。给出土体与空气界面上Nu数随时间的变化如图 5所示。
不同间隙及Ng下，Nu数均随时间降低，在夹层流场启动阶段，Nu数变化较大，表示初始状态流场对流换热较为显著，后续慢慢稳定降低；说明起始阶段（温差最大时刻）换热系统工作效率较高。
3. 结论
通过建立超重力下模型箱土体夹层换热模型，分析了不同厚度及Ng对换热过程的影响规律，研究获得以下结论：
（1）随着超重力Ng值增大，界面降温加速，高Ng值下降温速率大于低Ng值；随着夹层间隙厚度减小，降温速率提升，小间隙下降温速率大于大间隙。
（2）空气与土体界面的换热热量在一定时刻内随间隙增大而减小，随Ng上升而上升，与夹层空腔中涡环发展有关。
（3）超重力状态会使得传热规律发生变化。涡环的稳定分布与流场速度、压力及界面换热系数、温度等直接相关；20 cm间隙时，空腔内呈现典型的RB流动特征，形成两个对称的涡环，超重力使得流动速度变快；10 cm间隙时，不同Ng值下均会出现2对涡环；靠近侧边壁面处涡环较细长，中部涡环长细比小；1 cm间隙时，1g状态有明显涡环成对出现；高Ng值状态下无明显的涡环发展过程，热量传递主要以传热为主。
（4）不同间隙及Ng值下，Nu数均随时间降低，在流场启动阶段，Nu数变化较大；在不同间隙状态下，随着超重力Ng值变大，界面对流换热降低。
-
![]()
图 2 空腔界面温度在不同Ng、不同间隙时随时间变化
Figure 2. Variation of temperature at interface with time under different Ng and clearances
![]()
图 3 20 cm空腔50g状态换热末态时刻温度分布
Figure 3. Temperature nephogram of 20 cm thick clearance at overload of 50g and last time step
![]()
图 4 换热末态10 cm空腔50g状态涡环
Figure 4. Vortex ring of 10 cm-clearance and overload 50g at last time step
-
[1] 石峰, 宁利中, 王芳, 等. 矩形腔体中Rayleigh-Benard对流结构的分析[J]. 西安理工大学学报, 2008, 24(4): 484–489. https://www.cnki.com.cn/Article/CJFDTOTAL-XALD200804022.htm SHI Feng, NING Li-zhong, WANG Fang, et al. An analysis of the structure of Rayleigh-benard convection in a rectangular channel[J]. Journal of Xi'an University of Technology, 2008, 24(4): 484–489. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XALD200804022.htm
[2] 石峰, 宁利中, 王芳, 等. 具有不同来流形式的Rayleigh-Benard对流特性[J]. 水资源与水工程学报, 2008, 19(2): 56–59. https://www.cnki.com.cn/Article/CJFDTOTAL-XBSZ200802017.htm SHI Feng, NING Li-zhong, WANG Fang, et al. Research on the dynamic characteristics of Rayleigh-Benard Convection in a rectangular channel[J]. Journal of Water Resources and Water Engineering, 2008, 19(2): 56–59. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XBSZ200802017.htm
[3] NING Li-zhong, QI Xin, HARADA Yoshifumi, et al. A periodically localized traveling wave state of binary fluid convection with horizontal flows[J]. Journal of Hydrodynamics, 2006(2): 199–205.
[4] 胡宇鹏, 李友荣. 长方体腔内关于密度极值温度对称加热-冷却时冷水瑞利-贝纳德对流稳定性[J]. 力学学报, 2015, 47(5): 722–730. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201505002.htm HU Yu-peng, LI You-rong. Numerical investigation on flow stability of Rayleigh-bénard convection of cold water in a rectangular cavity cooled and heated symmetrically relative to the temperature of density maximum[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(5): 722–730. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201505002.htm
[5] 张淑芸, 宁利中, 周倩, 等. 重力变调作用对Rayleigh-Benard对流的影响[J]. 水资源与水工程学报, 2011, 22(2): 40–43. https://www.cnki.com.cn/Article/CJFDTOTAL-XBSZ201102010.htm ZHANG Shu-yun, NING Li-zhong, ZHOU Qian, et al. Influence of gravity modulation on Rayleigh-Benard convection[J]. Journal of Water Resources and Water Engineering, 2011, 22(2): 40–43. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XBSZ201102010.htm
[6] 余荔, 宁利中, 魏炳乾, 等. Rayleigh-Benard对流及其在工程中的应用[J]. 水资源与水工程学报, 2008, 19(3): 52–54. https://www.cnki.com.cn/Article/CJFDTOTAL-XBSZ200803014.htm YU Li, NING Li-zhong, WEI Bing-qian, et al. Rayleigh-Benard Convection and application in engineering[J]. Journal of Water Resources and Water Engineering, 2008, 19(3): 52–54. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XBSZ200803014.htm
[7] 孙亮, 孙一峰, 马东军, 等. 高瑞利数下水平自然热对流的幂律关系[J]. 物理学报, 2007, 56(11): 6503–6507. https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB200711059.htm SUN Liang, SUN Yi-feng, MA Dong-jun, et al. Power law of horizontal convection at high Rayleigh numbers[J]. Acta Physica Sinica, 2007, 56(11): 6503–6507. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB200711059.htm
[8] 张晨, 蔡正银, 黄英豪, 等. 输水渠道冻胀离心模拟试验[J]. 岩土工程学报, 2016, 38(1): 109–117. doi: 10.11779/CJGE201601011 ZHANG Chen, CAI Zheng-yin, HUANG Ying-hao, et al. Centrifuge modelling of frost-heave of canals[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(1): 109–117. (in Chinese) doi: 10.11779/CJGE201601011
下载:
计量
- 文章访问数: 72
- HTML全文浏览量: 28
- PDF下载量: 15
