基于离心机振动台试验的地震液化中砂土细观结构的演化机理分析

谢小丽; 王子凡; 叶斌

doi:10.11779/CJGE2022S2010

基于离心机振动台试验的地震液化中砂土细观结构的演化机理分析 English Version

同济大学地下建筑与工程系, 上海 200092

基金项目:

国家自然科学基金项目 41977225

详细信息

作者简介:
谢小丽(1994—)，女，博士研究生，主要从事岩土地震工程方面的科研工作。E-mail: xiexiaoli@tongji.edu.cn

通讯作者:
叶斌，E-mail: yebin@tongji.edu.cn

中图分类号: TU43
计量
- 文章访问数: 95
- HTML全文浏览量: 18
- PDF下载量: 22
出版历程
- 收稿日期: 2022-11-30
- 网络出版日期: 2023-03-26
- 刊出日期: 2022-11-30

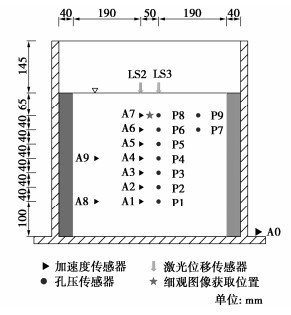
Centrifuge shaking table tests on evolution mechanism of sand mesostructure during earthquake liquefaction

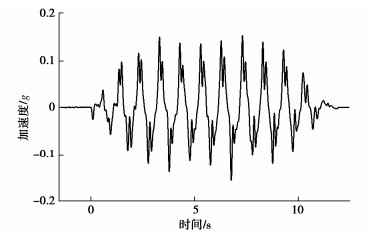
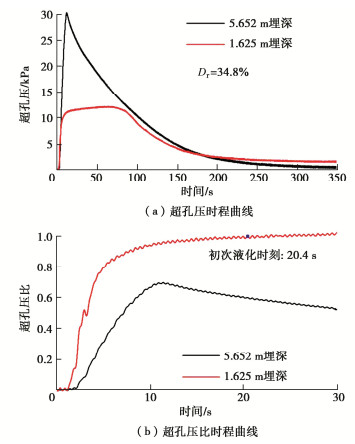
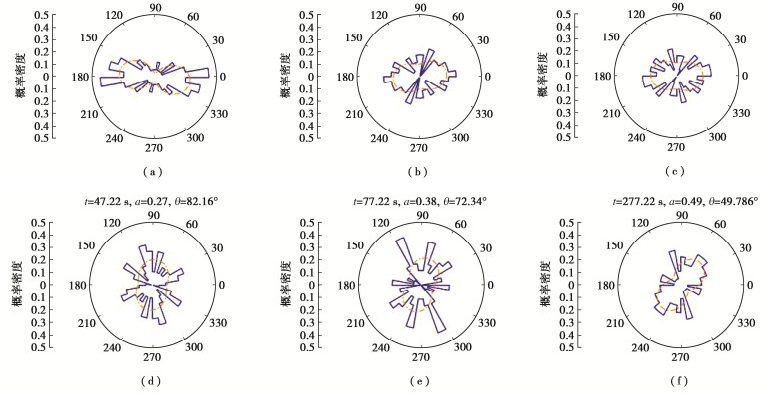
Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China

摘要

摘要: 已有研究表明地震液化历史是影响砂土抗液化能力的重要因素，相关研究学者认为这种影响的内在机理是砂土颗粒在前次地震液化后形成了稳定或者不稳定的细观结构，但是目前针对地震液化全过程中砂土细观结构演化行为的直接试验数据还很少。通过离心机振动台试验模拟了一个饱和砂土地基的地震液化现象，在试验过程中测试模型不同埋深处的加速度、孔压以及地表沉降，并基于细观图像获取设备记录了地震液化全过程中砂土细观数字图像。试验结果表明微振动会增加颗粒接触、减小颗粒间孔隙，随着振动强度增加，颗粒重新建立接触，颗粒间孔隙重新分布。受孔隙流体向上渗流作用，颗粒形成偏竖向和偏横向联通的大孔隙，偏竖向大孔隙周围的颗粒在渗流作用下长轴偏向竖直。
- 地震液化 /
- 离心机振动台试验 /
- 细观数字图像 /
- 砂土细观结构
Abstract: The existing studies demonstrate that the history of earthquake liquefaction is an important factor affecting the liquefaction resistance of sand. The researchers think the intrinsic mechanism of these effects is the generation of stable or unstable sand mesostructure after the previous liquefaction event. However, few studies have directly given the experimental results of the evolution behaviors of the sand mesostructure during the whole process of liquefaction. In this study, the centrifuge shaking table tests are conducted to model the earthquake liquefaction of a saturated sand deposit. The pore pressures and accelerations at different depths and the settlements of the sand deposit are measured. Besides, the mesoscopic digital images of the sand mesostructure are recorded simultaneously by a mesoscopic image acquisition system. The experimental results show that the small shaking increases the contacts and decreases the voids among sand particles. The particle contacts are reconstructed and the voids are redistributed with the larger shaking. Approximately vertically and horizontally linked large voids are caused by the upper seepage effects of the pore fluid. The sand particles nearby the approximately vertically large voids rotate vertically under the seepage effects.
- earthquake liquefaction /
- centrifuge shaking table tests /
- mesoscopic digital image /
- sand mesostructure

HTML全文

0. 引言

土的本构关系研究以及本构模型的合理建立是现代土力学的核心问题^[1]。本构关系的发展也先后历经了强度和变形分离考虑的传统土力学阶段和以剑桥模型^[2]、双屈服面模型^[3]、清华模型^[4]、统一硬化模型^[5]为代表的全面反映土的基本力学特性的现代土力学阶段,对土体复杂应力应变关系的描述效果有了明显的提高。但除了少数模型被普遍认可之外,大部分模型却都难以被广泛地应用。究其原因,主要有以下方面：①忽视了对土的基本力学特性共同变化规律的深入研究。土的基本力学特性是土区别于其他材料的标志,同时也是建立本构模型的重要基础和评价本构模型合理性的基本依据,而当前亟待解决的关键问题就在于基本力学特性的归一化处理。②传统本构理论中的基础假设与土的实际变形机制并不相符^[6]。比如认为塑性应变增量的方向与应力增量无关,仅取决于应力状态,但现在已通过试验证明了塑性应变增量方向的非唯一性。此外,在建立弹塑性模型过程中,对于屈服面的数目及如何选用、以及采取什么样的流动法则和硬化规律,均缺乏一个普遍认可的标准。③针对新的理论和方法,并未引起足够重视,而只是单纯地进行数学意义上的统计分析,缺乏理论背景的支撑。当前,大数据技术已广泛应用于各领域中,但在岩土工程领域尚处于发展初期,还需要一段时间的探索研究过程,但其特点和思想应受到业界的重视。

通过研究分析,未来土本构关系的发展可从以下方面考虑：①利用现代科学技术的发展成果,引入新的理论或技术,如神经网络、大数据技术等；②研究主应力轴旋转等复杂受力情况的力学特性及其本构模型；③考虑土体在受力过程中骨架相变和多场耦合问题^[7]。土的本构关系研究应尽可能的考虑它的实用性,但作为土力学中的基础性研究主要看它的创造性如何,看它是否能够促进该学科的发展^[8]。因此,为了更好地解决未来复杂岩土力学与工程问题,有必要开辟新的研究途径,为土的本构关系研究提供新的和更一般的理论。

近年来,大数据技术^[9]已经在诸多领域得到广泛应用,为我们提供了理解事物间关系的巨大可能性。特别是近几年大数据技术在岩土工程的特征挖掘与规律发现上^[10-12]表现了突出的能力,表明了大数据技术在土的本构关系研究上是可行的。笔者在研究剪缩型土本构模型的基础上,在本文中拟采用大数据技术,揭示剪胀型土应力应变关系试验结果的力学特性共同特征,并根据广义塑性力学建立一个更为科学合理的本构模型。

1. 基于Hadoop+Spark平台的分布式自适应自回归算法

在本文中,需要利用回归算法在剪胀型土的应力应变试验大数据基础上,建立关于塑性系数与其各影响因素之间的研究模型。但传统算法需要在已知函数结构的前提下才能回归处理,同时在进行大数据处理时,存在着效率低下等问题^[13]。因此,本文提出了一种基于Hadoop+Spark平台的Distributed Adaptive Auto Regression（DAAR）分布式自适应自回归算法。

1.1 基于Hadoop+Spark的大数据处理平台

Hadoop^[14]是一个基于分布式系统架构设计的数据管理平台,其核心组件为MapReduce并行计算框架和HDFS分布式文件系统。其中HDFS负责数据的存储功能,具有较高的容错性和可靠性。Spark^[15]则是一个专用于分布式计算的平台,相比于MapReduce,它可在内存中以接近“实时”的效率完成所有的数据分析。因此,结合研究实际,一方面利用HDFS作为分布式数据存储库,另一方面考虑到Spark的高效计算性能,选择其作为本研究中的大数据分布式计算工具。综上,本文搭建了一个Hadoop+Spark的处理平台,并采用Spark的YARN-Standalone集群模式开展剪胀型土试验大数据的处理,其工作流程步骤如图1所示。

图 1 Yarn-Standalone的工作流程图

Figure 1. Flow chart of work of Yarn-Standalone

下载: 全尺寸图片幻灯片

在传统回归算法中,每次迭代都必须要遍历所有数据,从而使得计算效率低下；而Hadoop+Spark的大数据处理平台一方面可利用Spark的全局共享内存来存储全计算过程中的所有数据,以解决数据重复遍历的问题；另一方面,可让集群中的各并行化支路以及工作节点共同参与到处理中,即原本需要花费5 h完成的任务,现在通过5条并行化支路花费1 h即可完成,从而大大提高了计算效率和稳定性。

1.2 基于大数据处理平台的DAAR算法

为了解决传统回归算法不能自适应回归处理的问题,首先利用泛函网络^[16],然后建立标准基函数池和泛函网络神经元调节机制^[17],最后引入可用于评判回归模型效果的AIC^[18]准则。

泛函网络是神经网络的一种拓展,但其神经元函数并不固定,之间也无联接权值。它可根据待求问题的数据特征建立一个标准基函数池。然后再通过调节机制,即隐层基函数的平均放电速率和隐层与输出层的互信息强度来对各神经元本身以及之间的连接结构进行优化,并通过AIC准则综合实现所求回归模型的最优化求解。

泛函网络的初始结构会对运算处理产生不同的影响。因此本文根据所处理试验大数据的不同特征,并结合剪胀型土的基本力学特性,建立了若干个泛函网络的初始结构。鉴于篇幅所限,下面主要介绍其中一种在给定泛函网络初始结构下的最优化处理过程。

首先设 $D = {(x_{r}, y_{r}) | r = 1, 2, \dots, k}$ 为待处理的数据样本集, $k$ 为样本数, $X = (x_{1}, x_{2}, \dots, x_{k})$ 为泛函网络的输入, $Y = (y_{1}, y_{2}, \dots, y_{k})$ 为输出,该泛函网络回归模型的初始结构为

$y_{r} = \sum_{i = 1}^{n} \sum_{j = 1}^{m} a_{i j} ϕ_{i j} (x_{r})$ ,

(1)

式中, $a_{i j}$ 为泛函网络回归模型的参数, $ϕ_{i j} (x_{r})$ 为从基函数池中选择的基函数。该回归模型与实际输出值之间总是存在误差 $ε_{r}$ ,再假设服从均值为0,方差为 $σ^{2}$ 的正态分布,即 $ε_{r}$ - $N (0, σ^{2})$ ,在此基础上则有

$y_{r}$ -

$N (\sum_{i = 1}^{n} \sum_{j = 1}^{m} a_{i j} ϕ_{i j} (x_{r}), σ^{2})$ ,

(2)

式（2）对应的极大似然函数可表示为

$L (Y, a_{i j}, σ^{2}) = \prod_{r = 1}^{k} \frac{1}{\sqrt{2 π} σ} \exp {- \frac{1}{2 σ^{2}} {(y_{r} - \sum_{i = 1}^{n} \sum_{j = 1}^{m} a_{i j} ϕ_{i j} (x_{r}))}^{2}},$

(3)

式中, $Y = {[y_{1}, y_{2}, \dots, y_{k}]}^{T}$ ,再对式（3）两边同时取对数可得

$\ln L = - \frac{k}{2} \ln 2 π - \frac{k}{2} \ln σ^{2} - \frac{1}{2 σ^{2}} \sum_{r = 1}^{k} {(y_{r} - \sum_{i = 1}^{n} \sum_{j = 1}^{m} a_{i j} ϕ_{i j} (x_{r}))}^{2} 。$

(4)

当式（4）最大时,可求得 $a_{i j}$ 和 $σ^{2}$ 的最优估计值,而与此同时,式（5）需要取得最小值,即

$S = \sum_{r = 1}^{k} {(y_{r} - \sum_{i = 1}^{n} \sum_{j = 1}^{m} a_{i j} ϕ_{i j} (x_{r}))}^{2} \to S_{\min}$ 。

(5)

因此,要使式（5）为最小值, $a_{i j}$ 就需要满足式（6）所示条件,即对 $a_{i j}$ 求偏导,并令其为0

$\frac{\partial S}{\partial a_{i j}} = - 2 \sum_{r = 1}^{k} (y_{r} - \sum_{i = 1}^{n} \sum_{j = 1}^{m} a_{i j} ϕ_{i j} (x_{r})) ϕ_{i j} (x_{r}) = 0$ 。

(6)

由式（6）等于0可求出 $a_{i j}$ ,而要使极大似然函数最大,还需要对 $σ^{2}$ 进行如下式所示的处理：

$\frac{\partial \ln L}{\partial σ^{2}} = - \frac{k}{2 σ^{2}} + \frac{1}{2 σ^{4}} {\sum_{r = 1}^{k} (y_{r} - \sum_{i = 1}^{n} \sum_{j = 1}^{m} a_{i j} ϕ_{i j} (x_{r}))}^{2}$ 。

(7)

然后,令式（6）,（7）分别等于0,可求得

$σ^{2} = \frac{1}{k} {\sum_{r = 1}^{k} (y_{r} - \sum_{i = 1}^{n} \sum_{j = 1}^{m} a_{i j} ϕ_{i j} (x_{r}))}^{2}$ ,

(8)

将式（8）代入式（3）,可得

$l (y | a_{i j}, σ^{2}) = - \frac{k}{2} \ln 2 π - \frac{k}{2} \ln σ^{2} - \frac{k}{2}$ 。

(9)

再根据式（10）,即可求得相应的AIC值。

$m_{AIC} = - 2 l (y | a_{i j}, σ^{2}) + 2 (n \times m)$ 。

(10)

式（1）～（10）表示了给定初始结构下参数 $a_{i j}$ 及对应AIC值的计算过程。但在本文中,为了得到最优化的回归模型,设计了多个初始结构,然后再在每一个初始结构下通过神经元调节机制对其结构进行不断优化,从而得到了若干个优化结构以及对应的AIC值,最后将所有优化结构对应的AIC值进行比较,综合分析后即可选出AIC值最小、结构最优化的回归模型。

综上可知,回归模型最优化选择的过程计算复杂度大、所占用计算资源多,因此可利用1.1节中建立的大数据平台以进行分布式的高效稳定处理。通过分析可知,整个运算过程有两个阶段可利用平台中的各并行化支路进行处理。第一个阶段是对若干初始结构进行并行化处理；第二个阶段是在给定的初始结构下,对若干个经过神经元调节机制后得到的优化结构进行并行化处理。

2. 基于试验大数据的土本构关系研究

根据广义塑性力学,不考虑洛德角和应力主轴旋转,可得到主空间上塑性应变增量与应力增量的关系。

$d ε_{v}^{p} = A d p + B d q$ ,

(11)

$d ε_{s}^{p} = C d p + D d q$ 。

(12)

式中, $A$ , $B$ , $C$ , $D$ 称为塑性系数。在传统塑性理论中,采用关联和非关联流动法则时,分别有

$A D - B C = 0, B = C$ ,

(13)

$A D - B C = 0, B \neq C$ 。

(14)

因此,业界认为土体材料的力学特性可用塑性系数来表达,如对剪缩型土有 $A > 0$ , $B > 0$ ,这都表明塑性系数与土本构关系的研究有着密切的联系。根据式（11）,（12）可知,只需确定4个塑性系数即可求得土体的塑性变形。通过对现有塑性系数计算模型的研究可知,其具有直观方便、理论明确等优势,但采用不合理的假设条件,在一定程度上虽然简化了本构模型的复杂性,但却限制了其在工程上的应用。特别地,当土的实际力学特性不能与其假设相符合时,基于这些假设建立的本构模型便不能有效地表达其本构关系,甚至还会产生较大的误差,从而影响实际应用中的安全性和经济性。因此,本文将基于剪胀型土试验大数据的特征关系,结合DAAR算法,对各塑性系数开展深度挖掘研究。首先可基于等压屈服的试验大数据,求得A的计算模型；然后利用式（11）,可求得B的计算值,再通过分析其影响因素,可建立起B的计算模型；通过简化假设和系数比较法,可求得D的计算模型；最后参考B的研究方法,再根据式（12）,即可建立起D的计算模型。

2.1 剪胀型土试验大数据的收集

剪胀型土试验大数据收集的代表性和可靠性是保证本文研究的重要条件。因此本文将分别从数据的来源、提取和检验3个过程进行严格控制。

数据来源的控制。考虑到噪声数据的不利影响,课题组综合了SJR和H-index指数,主要从表1所示的权威刊物发表的论文资料中进行筛选,相比于其他数据来源,可以说从源头上确保了数据的代表性和可靠性。

表 1 部分数据主要来源

Table 1. Main sources of data

序号	国家	期刊名称	SJR	H-index
1	英国	Geotechnique	2.571	114
2	中国	岩土工程学报	0.655	42
3	加拿大	Canadian Geotechnical Journal	1.753	100
4	英国	Computers and Geotechnics	1.946	79
5	日本	Soils and Foundations	1.246	64

下载: 导出CSV

| 显示表格

数据提取的控制。考虑到常规三轴压缩试验在实际应用中较为普遍,数据丰富并且较易获取。因此在本文研究中要求试验数据必须来源于常规三轴压缩试验的土样本。另一方面选择的土样本需要根据剪胀型土的基本力学特性,如体应变随轴向应变的增加呈先增大后减小的趋势等条件来去除不符合的试验数据。同时在提取试验数据点时,必须按照实际的试验点尽可能多地进行提取,因为如果数据点提取的过少,会影响到应力应变关系的真实表达。严格控制数据的提取过程进一步确保了数据的可靠性。

数据检验的控制。考虑到在第①和②过程中可能出现的人为因素影响,将课题组分为两个小组,严格按照上述过程再次进行交叉检验,最终得到了326个剪胀型土样本,并计算得到相应的试验数据。由于篇幅限制,部分剪胀型土样本试验数据如表2所示。

表 2 部分土样本的数据

Table 2. Data of some soil samples

编号	试验序列点	$d$	$p /kPa$	$q /kPa$	$d p /kPa$	$d q /kPa$	$ε_{v}^{p} /%$	$ε_{s}^{p} /%$	$\dots$
JZ-12	1	0.67	715.12	795.28	40.23	120.69	0.26	0.39	︙
	2	0.44	745.43	886.28	30.32	90.96	0.48	0.89	︙
	︙	︙	︙	︙	︙	︙	︙	︙	︙
	24	-0.02	820.84	1112.52	-2.51	-7.53	0.56	9.31	︙
	︙	︙	︙	︙	︙	︙	︙	︙	︙

下载: 导出CSV

| 显示表格

2.2 塑性系数 $A$ 的计算模型

根据杨光华^[1]关于剪缩型土中 $A$ 的研究可知,对于剪胀型土,在式（11）中,当位于 $p$ 轴上时 $d q = 0$ ,对应 $d ε_{v}^{p} = A d p$ ,再结合 $d ε_{v}^{p}$ 的变化规律,即此时 $d ε_{v}^{p}$ 为最大值,所以有

$A = A_{0} = \frac{d ε_{v}^{p}}{d p}$ 。

(15)

当土达到临界状态时,有 $d ε_{v}^{p} \to 0$ ,可知 $d ε_{v}^{p}$ 的变化是非线性的,因此可用一个变化系数 $a$ 来进行表征。综上分析,剪胀型土塑性系数 $A$ 可表示为

$A = A_{0} \cdot a$ 。

(16)

因为 $A_{0}$ 与剪胀型土的等压屈服特性有关,即可通过等压固结试验中的 $ε_{v}^{p}$ 和 $p$ 求得。首先进行归一化处理： ${\bar{p}}_{d} = p / p_{d- \max}$ , ${\bar{ε}}_{vd}^{p} = ε_{v}^{p} / ε_{v d-max}^{p}$ 。其中, ${\bar{p}}_{d}$ 和 ${\bar{ε}}_{v d}^{p}$ 表示归一化后的 $p$ 和 $ε_{v}^{p}$ 。 $p_{d- \max}$ 和 $ε_{v d-max}^{p}$ 分别表示在针对该类剪胀型土的一系列等压固结试验中,等向固结压力达到最大值时所对应的 $p$ 和 $ε_{v}^{p}$ 。

图2为 ${\bar{ε}}_{v d}^{p}$ - ${\bar{p}}_{d}$ 的大数据特征关系图,在其等压固结试验中, ${\bar{ε}}_{v d}^{p}$ 随 ${\bar{p}}_{d}$ 的增加逐渐增大,且 ${\bar{ε}}_{v d}^{p}$ 的变化速率逐渐减小,再根据DAAR算法,可得

${\bar{ε}}_{vd}^{p} = \frac{{\bar{p}}_{d}}{t_{1} + {\bar{p}}_{d}^{t_{2}}}$ ,

(17)

图 2

${\bar{ε}}_{v d}^{p}$ -

${\bar{p}}_{d}$ 的大数据关系

Figure 2. Big data relationship between

${\bar{ε}}_{v d}^{p}$ and

${\bar{p}}_{d}$

下载: 全尺寸图片幻灯片

式中, $t_{1}$ =-0.001, $t_{2}$ =0.628,拟合度为0.914。通过归一化处理的逆过程变换,便可得 $A_{0}$ ,即

$A_{0} = \frac{ε_{v d-max}^{p}}{p_{d- \max}} \cdot \frac{[t_{1} + {(\frac{p}{p_{d- \max}})}^{t_{2}}] - \frac{(t_{2} - 1) p^{2}}{{(p_{d- \max})}^{t_{2}}}}{{[t_{1} + {(\frac{p}{p_{d- \max}})}^{t_{2}}]}^{2}}$ 。

(18)

为了反映土的剪胀性,需要在模型中反映出 $d > 0$ 和 $d < 0$ 两种状态。因此在本研究中,将可反映剪胀特性的剪胀应力比 $M_{d}$ 引入到文献[6]的变化系数中：

$a = \frac{1 - {(η / M_{d})}^{2}}{1+ {(η / M_{d})}^{2}}$ ,

(19)

综上,可得到剪胀型土中 $A$ 的计算模型：

$A = \frac{ε_{v d-max}^{p}}{p_{d- \max}} \cdot \frac{[t_{1} + {(\frac{p}{p_{d- \max}})}^{t_{2}}] - \frac{(t_{2} - 1) p^{2}}{{(p_{d- \max})}^{t_{2}}}}{{[t_{1} + {(\frac{p}{p_{d- \max}})}^{t_{2}}]}^{2}} \cdot \frac{1 - {(\frac{η}{M_{d}})}^{2}}{1+ {(\frac{η}{M_{d}})}^{2}}$ 。

(20)

2.3 塑性系数 $B$ 的计算模型

在塑性系数的研究初期,学者普遍认为 $B$ 仅与 $q$ 有关。随着研究的深入,才发现 $p$ 和 $q$ 之间存在着耦合作用,因此又认为 $B$ 是关于 $p$ 和 $q$ 的函数。为了建立一个能更加准确反映土基本力学特性的计算模型,本文综合考虑了 $B$ 与各应力应变参数之间的关系。考虑到最大信息系数（MIC）^[19]。因此分别计算了它们之间的MIC值,并绘制了箱型图。

从图3可知, $B$ 与 $η$ 的MIC平均值明显高于其他因素,表明其相关性更高,因此将 $η$ 作为 $B$ 的显著性影响因素。又因为 $η$ 主要表现为剪应力的作用,为了避免重复影响,故在次要影响因素中不再考虑 $q$ 的作用,而将 $p$ , $d p$ , $d q$ , $ε_{v}^{p}$ , $ε_{s}^{p}$ 作为 $B$ 的次要影响因素研究。

图 3

$B$ 与应力应变参数之间的MIC值

Figure 3. Values of MIC between

$B$ and stress-strain parameters

下载: 全尺寸图片幻灯片

（1）塑性系数 $B$ 与显著性影响因素的相关性函数

在剪胀型土中, $B$ 随 $η$ 的变化过程如图4所示。

图 4

$B$ 随

$η$ 的变化过程

Figure 4. Change process of

$B$ with

$η$

下载: 全尺寸图片幻灯片

在剪胀型土中,峰值应力比 $M_{f}$ 记作 $M_{f- \max}$ 。由于 $η$ 差别较大,可以 $M_{f- \max}$ 作为归一化参数进行处理：

$\bar{η} = {η / M}_{f- \max}$ 。

(21)

由此可绘制出 $B$ 与 $\bar{η}$ 的大数据特征关系见图5。

图 5

$B$ 与

$\bar{η}$ 的大数据关系

Figure 5. Big data relationship between

$B$ and

$\bar{η}$

下载: 全尺寸图片幻灯片

从图5可知,在剪缩时, $B$ 随 $\bar{η}$ 的增大呈减小趋势,当 $\bar{η} \to {\bar{M}}_{d}$ （ ${\bar{M}}_{d}$ 为 $\bar{η}$ 所对应的剪胀应力比）, $B \to 0$ ；在剪胀时, $B$ 随 $\bar{η}$ 的增大继续减小,其减小速率更快,幅值更大。此时根据DAAR算法,可得

$B_{1} (η) = B_{η} = {(\frac{{\bar{M}}_{d}}{\bar{η}})}^{n_{1}} \cdot \frac{{\bar{M}}_{d}^{n_{2}} - {\bar{η}}^{n_{2}}}{{\bar{M}}_{d}^{n_{3}} + {\bar{η}}^{n_{3}}}$ ,

(22)

式中, $B_{η}$ 表示 $η$ 所对应的 $B$ 值, $B_{1} (η)$ 表示 $B_{η}$ 与 $η$ 的相关性函数, $n_{1}$ =41.066, $n_{2}$ =67.657, $n_{3}$ =-38.549,所得拟合曲线与试验值的拟合度为0.775。

（2）塑性系数 $B$ 与次要影响因素的相关性函数

在上节中,已研究了 $η$ 对 $B$ 的影响,并得到了 $B_{1} (η)$ 。本节中利用式（23）即可得到次要影响因素对 $B$ 的作用。

$B_{e} = B / B_{η} - 1$ ,

(23)

式中, $B_{e}$ 表示仅考虑 $η$ 时, $B$ 的残余误差,也是次要影响因素对 $B$ 影响的比例。本节主要利用相关性函数来研究 $B_{e}$ 与各次要影响因素之间的关系。

峰值状态时的 $p$ 可记作 $p_{p-max}$ 。由于样本中 $p$ 范围差别较大,因此可以 $p_{p-max}$ 为归一化参数。

$\bar{p} = p / p_{p-max}$ 。

(24)

由此可绘制 $B_{e}$ 与 $\bar{p}$ 之间大数据特征关系见图6。

图 6

$B_{e}$ 与

$\bar{p}$ 的大数据关系

Figure 6. Big data relationship between

$B_{e}$ and

$\bar{p}$

下载: 全尺寸图片幻灯片

在剪缩时, $B_{e}$ 随 $\bar{p}$ 的增加逐渐减小,且变化速率逐渐降低；在相变转换状态时, $B_{e} \to 0$ ；在剪胀时, $B_{e}$ 随 $\bar{p}$ 的增加快速减小,根据DAAR算法,可得

$B_{2} (p) = n_{4} \cdot \tan (n_{5} \cdot \bar{p} + n_{6})$ 。

(25)

式中, $B_{2} (p)$ 可表示 $B_{e}$ 与 $p$ 的相关性函数, $n_{4}$ =0.072, $n_{5}$ =-4.543, $n_{6}$ =3.105,拟合度为0.716。

剪胀型土中的 $ε_{v}^{p}$ 在临界状态和相变转换状态时可记作 $ε_{v}^{p}_{cs}$ 和 $ε_{v}^{p}_{pts}$ 。由于 $ε_{v}^{p}$ 的范围差别较大,因此可采用如式（26）所示的归一化方法进行处理。

${\bar{ε}}_{v}^{p} = \frac{ε_{v}^{p} - ε_{v}^{p}_{cs-min}}{ε_{v}^{p}_{pts-max} - ε_{v}^{p}_{cs-min}}$ 。

(26)

由此可绘制出 $B_{e}$ 与 ${\bar{ε}}_{v}^{p}$ 的大数据关系图（图7）。

图 7

$B_{e}$ 与

${\bar{ε}}_{v}^{p}$ 的大数据关系

Figure 7. Big data relationship between

$B_{e}$ and

${\bar{ε}}_{v}^{p}$

下载: 全尺寸图片幻灯片

在剪缩时, $B_{e}$ 随 ${\bar{ε}}_{v}^{p}$ 的增加逐渐减小,当达到相变转换状态时,有 ${\bar{ε}}_{v}^{p} = 1$ , $B_{e} \to 0$ ；在剪胀时, $B_{e}$ 随 ${\bar{ε}}_{v}^{p}$ 的减小呈先减小后增加的趋势,在临界状态,有 ${\bar{ε}}_{v}^{p} = 0$ , $B_{e} \to 0$ ,此时可根据DAAR算法分别对剪缩和剪胀阶段进行研究,然后可建立起全过程的 $B_{e}$ 与 ${\bar{ε}}_{v}^{p}$ 之间的相关性函数。

$\begin{matrix} B_{3} (ε_{v}^{p}) = H (M_{d} - η) \cdot (n_{7} + n_{8} \frac{\ln ({\bar{ε}}_{v}^{p})}{{\bar{ε}}_{v}^{p}}) + \\ H (η - M_{d}) \cdot (n_{9} {\bar{ε}}_{v}^{p}^{2} \ln ({\bar{ε}}_{v}^{p})) \end{matrix}$ ,

(27)

式中,

$\begin{array}{l} H (M_{d} - η) = \frac{1 + Sgn (M_{d} - η)}{2}, \\ Sgn (M_{d} - η) = {\begin{cases} 1 (M_{d} - η > 0) \\ - 1 (M_{d} - η < 0) \end{cases} 。 \end{array}}$

(28)

$B_{3} (ε_{v}^{p})$ 表示 $B_{e}$ 与 $ε_{v}^{p}$ 的相关性函数, $n_{7}$ =0.005, $n_{8}$ =-0.126, $n_{9}$ =2.170,拟合度为0.619。

由于 $ε_{s}^{p}$ 在临界状态时仍会继续增大,故将 $ε_{s}^{p}$ 的最大值记作 $ε_{s}^{p}_{max}$ 。然后以 $ε_{s}^{p}_{max}$ 作为归一化参数。

${\bar{ε}}_{s}^{p} = ε_{s}^{p} / ε_{smax}^{p}$ 。

(29)

由此可绘制出 $B_{e}$ 与 ${\bar{ε}}_{s}^{p}$ 的大数据特征关系见图8。

图 8

$B_{e}$ 与

${\bar{ε}}_{s}^{p}$ 的大数据关系

Figure 8. Big data relationship between

$B_{e}$ and

${\bar{ε}}_{s}^{p}$

下载: 全尺寸图片幻灯片

在剪缩时, $B_{e}$ 随 ${\bar{ε}}_{s}^{p}$ 的增加逐渐减小；在剪胀时, $B_{e}$ 随 ${\bar{ε}}_{s}^{p}$ 的增加先减小后增大,根据DAAR算法,有

$B_{4} (ε_{s}^{p}) = n_{10} \cdot cosh(n_{11} \cdot {\bar{ε}}_{s}^{p}) + n_{12} \cdot {\bar{ε}}_{s}^{p}$ 。

(30)

式中,cosh为双曲余弦函数, $n_{10}$ = 0.384, $n_{11}$ = 2.234, $n_{12}$ =-1.832,拟合度为0.710。

由于 $d p$ , $d q$ 范围差别较大,因此可选先期固结压力 $p_{c}$ 进行归一化处理,分别得到了 $\bar{d p}$ 和 $\bar{d q}$ 。

$\bar{d p} = \frac{d p}{p_{c}}, \bar{d q} = \frac{d q}{p_{c}}$ 。

(31)

由此可绘制出 $B_{e}$ 与 $\bar{d p}$ , $\bar{d q}$ 的大数据特征关系见图9。

图 9

$B_{e}$ 与

$\bar{d p}$ ,

$\bar{d q}$ 之间的大数据关系

Figure 9. Big data relationship between

$B_{e}$ ,

$\bar{d p}$ and

$\bar{d q}$

下载: 全尺寸图片幻灯片

$B_{e}$ 随 $\bar{d p}$ , $\bar{d q}$ 减小而逐渐减小,根据DAAR,有

$B_{5} (d p) = n_{13} \cdot \tan (n_{14} \cdot \bar{d p} + n_{15})$ ,

(32)

$B_{6} (d q) = n_{16} \cdot \tan (n_{17} \cdot \bar{d q} + n_{18})$ 。

(33)

式中, $B_{5} (d p)$ , $B_{6} (d q)$ 分别表示 $B_{e}$ 与 $d p$ , $d q$ 的相关性函数, $n_{13}$ =0.162, $n_{14}$ =4.191, $n_{15}$ =-0.671, $n_{16}$ =0.191, $n_{17}$ =1.316, $n_{18}$ =-0.653,拟合度分别为0.724和0.725。

（3）塑性系数 $B$ 计算模型的建立

从2.3节的研究可知,基于试验大数据建立的 $B$ 与各影响因素之间的相关性函数拟合度均较低,这表明不能只考虑单一因素的影响,而是需要考虑显著性因素和次要因素的综合影响作用。又因为 $B_{e}$ 与 $p$ , $ε_{v}^{p}$ , $ε_{s}^{p}$ , $d p$ , $d q$ 之间的相关性函数实际上包含了所有次要影响因素的作用,所以需要在 $B$ 的计算模型中根据它们的相关性差异进行加权处理。表3计算了 $B_{e}$ 与各次要影响因素之间的MIC值。

表 3

$B_{e}$ 与各次要影响因素之间的MIC值

Table 3. Values of MIC between

$B_{e}$ and secondary influencing factors

$m_{p - B_{e}}$	$m_{ε_{v}^{p} - B_{e}}$	$m_{ε_{s}^{p} - B_{e}}$	$m_{d p - B_{e}}$	$m_{d q - B_{e}}$
0.689	0.485	0.654	0.660	0.661

下载: 导出CSV

| 显示表格

由此可计算出各次要影响因素对 $B_{e}$ 的权重影响值,如下式所示：

$w_{p - B_{e}} = m_{p - B_{e}} / (m_{p - B_{e}} + m_{ε_{v}^{p} - B_{e}} + m_{ε_{s}^{p} - B_{e}} + m_{d p - B_{e}} + m_{d q - B_{e}})$ 。

(34)

式中, $w_{p - B_{e}} =0 .219$ ,表示 $p$ 对 $B_{e}$ 的影响权重值。同理可求得 $ε_{v}^{p}$ , $ε_{s}^{p}$ , $d p$ , $d q$ 对 $B_{e}$ 的影响权重值分别为0.154,0.207,0.210,0.210。

综上分析,根据剪胀型土的基本力学特性,结合 $B$ 的显著性影响因素和次要影响因素的相关性函数,加上各次要因素对 $B_{e}$ 的权重影响,综合建立了基于剪胀型土试验大数据的 $B$ 的计算模型。

$\begin{matrix} B = B_{1} (η) [1 + w_{p - B_{e}} B_{2} (p) + w_{ε_{v}^{p} - B_{e}} B_{3} (ε_{v}^{p}) + \\ w_{ε_{s}^{p} - B_{e}} B_{4} (ε_{s}^{p}) + w_{d p - B_{e}} B_{5} (d p) + w_{d q - B_{e}} B_{6} (d q)] \end{matrix}$ 。

(35)

2.4 塑性系数 $D$ 和 $C$ 的计算模型

要想求解A,B,C,D,只有式（11）,（12）两个有效方程是不够的,虽然可通过等压屈服试验求得A,进而求得B。但对于C,D仍然有无穷多解,此时可通过增加试验或是采用简化假设的方法来求解剩余的塑性系数。在本研究中,根据剪胀率的公式：

$d = \frac{d ε_{v}^{p}}{d ε_{s}^{p}}$ ,

(36)

可得

$\begin{matrix} d = \frac{d ε_{v}^{p}}{d ε_{s}^{p}} \Rightarrow d ε_{s}^{p} = \frac{d ε_{v}^{p}}{d} = \frac{A d p + B d q}{d} \\ = \frac{A}{d} d p + \frac{B}{d} d q = C d p + D d q \end{matrix}$ 。

(37)

式中,在理论上可通过系数比较法,求得C和D。但由于在B中含有dp和dq的影响,因此在实际处理时将存在较大的阻碍,而采用简化假设的方法,即假设dp和dq对B的影响很小,此时再用系数比较法,便可得

$D = B / d$ 。

(38)

这样不仅可减少计算的复杂度,也不用增加新的试验,同时还可以提高模型的适用性。但此处需要注意：不能直接令 $C = A / d$ ,因为这将直接等效为AD=BC,显然与土的实际变形机制不相符；此外,相比于A的计算模型精度,B是通过试验大数据的深度挖掘,考虑多因素综合影响建立的,所以认为B的精度更高,因此在本研究中认为首先利用简化假设和系数比较法求得 $D$ ,然后再根据式（12）求解 $C$ 更为合理。在得到 $C$ 的计算值之后,参考 $B$ 的计算模型研究方法,分别计算了 $C$ 与各应力应变参数之间的MIC值,并结合土的基本力学特性,将 $η$ 作为 $C$ 的显著性影响因素,而将 $p$ , $d p$ , $d q$ , $ε_{v}^{p}$ , $ε_{s}^{p}$ 作为 $C$ 的次要影响因素进行研究。

（1）塑性系数 $C$ 与显著性影响因素的相关性函数

根据前文计算出的 $\bar{η}$ ,可绘制 $C$ 与 $\bar{η}$ 的大数据关系见图10。

图 10

$C$ 与

$\bar{η}$ 的大数据关系

Figure 10. Big data relationship between

$C$ and

$\bar{η}$

下载: 全尺寸图片幻灯片

再根据DAAR算法,可得

$C_{1} (η) = C_{η} = \frac{{\bar{M_{d}}}^{l_{1}} - {\bar{η}}^{l_{1}}}{l_{2} {\bar{η}}^{l_{3}}} \cdot \sin (\frac{\bar{M_{d}}}{\bar{η}})$ ,

(39)

式中, $C_{η}$ 表示显著性影响因素 $η$ 所对应的 $C$ 值, $C_{1} (η)$ 表示 $C_{η}$ 与 $η$ 的相关性函数, $l_{1}$ =1.573×10^-8, $l_{2}$ =0.002, $l_{3}$ =-2.195,拟合度为0.736。

（2）塑性系数 $C$ 与次要影响因素的相关性函数

在上节中,已研究了 $η$ 对 $C$ 的影响,并得到了 $C_{1} (η)$ 。本节中利用式（40）即可得到次要影响因素对 $C$ 的影响。

$C_{e} = C / C_{η} - 1$ 。

(40)

$C_{e}$ 表示仅考虑 $η$ 的塑性系数 $C$ 的残余误差。根据前文得到 $\bar{p}$ ,可绘制 $C_{e}$ 与 $\bar{p}$ 之间大数据关系见图11。

图 11

$C_{e}$ 与

$\bar{p}$ 的大数据关系

Figure 11. Big data relationship between

$C_{e}$ and

$\bar{p}$

下载: 全尺寸图片幻灯片

再根据DAAR算法,可得

$C_{2} (p) = l_{4} \cdot \tan (l_{5} \cdot \bar{p} + l_{6})$ ,

(41)

式中, $C_{2} (p)$ 表示 $C_{e}$ 与 $p$ 的相关性函数, $l_{4}$ =-0.076, $l_{5}$ =4.408, $l_{6}$ =3.270,拟合度为0.712。根据前文计算的 $\bar{ε_{v}^{p}}$ ,可绘制出 $C_{e}$ 与 $\bar{ε_{v}^{p}}$ 的大数据关系见图12。

图 12

$C_{e}$ 与

$\bar{ε_{v}^{p}}$ 的大数据关系

Figure 12. Big data relationship between

$C_{e}$ and

$\bar{ε_{v}^{p}}$

下载: 全尺寸图片幻灯片

再根据DAAR算法,可得 $C_{e}$ 与 $\bar{ε_{v}^{p}}$ 的相关性函数：

$\begin{matrix} C_{3} (ε_{v}^{p}) = H (M_{d} - η) (l_{7} + l_{8} \frac{\ln (\bar{ε_{v}^{p}})}{\bar{ε_{v}^{p}}}) + H (η - M_{d}) \cdot \\ (l_{9} {\bar{ε_{v}^{p}}}^{2} \ln (\bar{ε_{v}^{p}})) \end{matrix}$ 。

(42)

$C_{3} (ε_{v}^{p})$ 表示 $C_{e}$ 与 $ε_{v}^{p}$ 的相关性函数, $l_{7}$ =-0.028, $l_{8}$ =-0.138, $l_{9}$ =2.146,拟合度为0.614。根据前文的 $\bar{ε_{s}^{p}}$ ,可绘制 $C_{e}$ 与 $\bar{ε_{s}^{p}}$ 的大数据关系图（图13）。

图 13

$C_{e}$ 与

$\bar{ε_{s}^{p}}$ 的大数据关系

Figure 13. Big data relationship between

$C_{e}$ and

$\bar{ε_{s}^{p}}$

下载: 全尺寸图片幻灯片

再根据DAAR算法,可得

$C_{4} (ε_{s}^{p}) = l_{10} \cdot \cosh (l_{11} \cdot \bar{ε_{s}^{p}}) + l_{12} \cdot \bar{ε_{s}^{p}}$ ,

(43)

式中, $C_{4} (ε_{s}^{p})$ 表示 $C_{e}$ 与 $ε_{s}^{p}$ 的相关性函数, $l_{10}$ =0.479, $l_{11}$ =2.181, $l_{12}$ =-2.161,拟合度0.705。根据前文的 $\bar{d p}$ 和 $\bar{d q}$ ,可绘制 $C_{e}$ 与 $\bar{d p}$ , $\bar{d q}$ 大数据关系见图14。

图 14

$C_{e}$ 与

$\bar{d p}$ ,

$\bar{d q}$ 之间的大数据关系

Figure 14. Big data relationship among

$C_{e}$ ,

$\bar{d p}$ and

$\bar{d q}$

下载: 全尺寸图片幻灯片

在图14所示的大数据特征关系基础上,根据DAAR算法,可得

$C_{5} (d p) = l_{13} \cdot \tan (l_{14} \cdot \bar{d p} + l_{15})$ ,

(44)

$C_{6} (d q) = l_{16} \cdot \tan (l_{17} \cdot \bar{d q} + l_{18})$ ,

(45)

式中, $C_{5} (d p)$ , $C_{6} (d q)$ 分别表示 $C_{e}$ 与 $d p$ , $d q$ 的相关性函数, $l_{13}$ =0.146, $l_{14}$ =4.385, $l_{15}$ =27.596, $l_{16}$ =0.137, $l_{17}$ =1.452, $l_{18}$ =21.317,拟合度分别为0.715和0.716。

（3）塑性系数 $C$ 计算模型的建立

根据2.4节的研究, $C$ 同样需要考虑显著性因素和次要因素的综合作用。因此参考 $B$ 的研究方法,即可分别得到次要因素对 $C_{e}$ 的权重影响值。然后可建立起剪胀型土中 $C$ 的计算模型。

$\begin{matrix} C = C_{1} (η) [1 + w_{p - C_{e}} C_{2} (p) + w_{ε_{v}^{p} - C_{e}} C_{3} (ε_{v}^{p}) + \\ w_{ε_{s}^{p} - C_{e}} C_{4} (ε_{s}^{p}) + w_{d p - C_{e}} C_{5} (d p) + w_{d q - C_{e}} C_{6} (d q)] \end{matrix}$ 。

(46)

3. 剪胀型土本构模型的建立与验证

3.1 模型的建立

总的应变增量可分解为弹性部分和塑性部分。

$d ε_{v} = d ε_{v}^{e} + d ε_{v}^{p}$ ,

(47)

$d ε_{s} = d ε_{s}^{e} + d ε_{s}^{p}$ 。

(48)

再根据广义胡克定律,有

$d ε_{v} = (A + 1/ K) d p + B d q$ ,

(49)

$d ε_{s} = C d p + (D + 1 / 3 G)d q$ ,

(50)

式中, $K$ 为弹性体积模量, $G$ 为弹性剪切模量,可分别通过式（51）和（52）求得

$K = E / 3 (1 - 2 ν)$ 。

(51)

$G = E / 2 (1+ ν)$ ,

(52)

式中, $E$ 和 $ν$ 分别为弹性模量和泊松比,在求得弹性变形的基础上,再结合第2节的研究内容,即可建立一个新的剪胀型土本构模型。

$\begin{array}{l} d ε_{v} = [A + 3 (1 - 2 ν) / E] d p + B d q, \\ d ε_{s} = C d p + [D + 2 (1 + ν) / 3 E] d q, \end{array}}$

(53)

式中,塑性系数 $A$ , $B$ , $C$ , $D$ 可分别通过式（20）,（35）,（46）,（38）求得。其中涉及到的模型参数可通过等压固结和常规三轴试验求得。各参数的具体求解方法已在2.2～2.4节中进行了研究,此处不再叙述。

3.2 模型的验证

为进一步检验本文模型的准确性和适用性,分别利用修正剑桥模型、考虑剪胀性的类剑桥模型^[20]以及本文模型对3组独立的未参与之前模型建立的剪胀型土试验数据^[21]进行预测研究。其中,修正剑桥模型和考虑剪胀性的类剑桥模型所需参数如表4所示。

表 4 验证试验的模型参数值

Table 4. Values of model parameters validation experiments

编号	$λ$	$κ$	$M$	$M_{d}$	$ν$
土1	0.0068	0.0042	1.66	0.95	0.31
土2	0.0161	0.0051	1.35	0.87	0.30
土3	0.0106	0.0049	1.58	0.89	0.32

下载: 导出CSV

| 显示表格

对于本文模型所需参数可通过2.2～2.4节中关于模型参数的确定方法求得；最后通过不同模型的验证试验,得到了如图15所示的试验结果。

图 15 预测曲线与试验值的比较

Figure 15. Comparison between predicted curves and experimental values

下载: 全尺寸图片幻灯片

从 $q$ - $ε_{1}$ 曲线可知,通过修正剑桥模型和考虑剪胀性的类剑桥模型得到的计算结果均比试验值偏大；由 $ε_{v}$ - $ε_{1}$ 曲线可知,修正剑桥模型得到的计算结果均为正值,即不能反映在剪胀阶段的力学特性,而考虑剪胀性的类剑桥模型虽然能够大致描绘剪胀型土的剪胀性及非线性,但与试验值仍然存在一定误差。相比之下,通过本文模型得到的计算结果与试验值均吻合较好。结果表明基于剪胀型土应力应变试验大数据建立的本构模型要优于修正剑桥模型和考虑剪胀性的类剑桥模型,并且对不同应力路径下剪胀型土的力学特性表达具有较强的适应性。

4. 讨论

在以往的研究中,鲜有从大数据技术的角度来研究本构关系。通过本文研究可知,新模型不仅能更好地反映剪胀型土的本构关系,还有效地突破了传统本构理论的束缚,具有更为广泛的理论意义。此外,从当前已完成工作来看,其有原理明晰、模型合理可靠等优点,不需考虑选用何种关联法则或屈服面,大大简化了建模的难度。本文研究虽然得到了模型参数一些定性的物理意义,但对于参数更为精确的物理意义,下一步还将重点进行研究探索。另外在本文中,研究的试验数据主要来源于常规三轴试验,应力加载范围多属于平均水平,也并未考虑应力主轴旋转等因素的影响。但笔者相信随着复杂应力路径下的综合试验数据库的建立和大数据技术在本构关系领域的进一步发展,本构模型的适用性问题势必会得到有效解决。

5. 结论

（1）建立了一个基于Hadoop+Spark的平台,然后在此基础上,提出了一种DAAR算法,有效解决了传统回归算法不能进行自适应回归,以及在处理大规模试验数据时的计算不稳定、效率低下等问题,为剪胀型土的本构关系研究提供了有力的技术支持。

（2）发现了塑性系数研究中存在的不足,在广义塑性力学的理论基础上,利用DAAR算法,考虑各塑性系数显著性影响因素和次要影响因素的综合作用,基于MIC权重计算,建立了一个新的剪胀型土本构模型。

（3）验证试验结果表明本文模型要优于修正剑桥模型和考虑剪胀性的类剑桥模型,并且可以较好地描述不同应力路径下剪胀型土的应力应变特性。本文模型的建立在大数据技术与土体本构关系的交叉研究领域、建模能力的增强与计算效率的提高等方面提供了新的思路。

图 1 饱和砂土模型的布局（模型尺寸）

Figure 1. Layout of model for saturated sand (in model size)

下载: 全尺寸图片幻灯片

图 2 输入地震波

Figure 2. Input seismic waves

下载: 全尺寸图片幻灯片

图 3 超孔压和超孔压比的时程曲线

Figure 3. Time histories of excess pore pressure and excess pore pressure ratio

下载: 全尺寸图片幻灯片

图 4 振动阶段砂土颗粒细观结构演化过程

Figure 4. Evolution of sand mesostructure during shaking

下载: 全尺寸图片幻灯片

图 5 砂土液化阶段颗粒细观结构演化过程

Figure 5. Evolution of sand mesostructure when r_u=1.0

下载: 全尺寸图片幻灯片

图 6 砂土不完全液化阶段颗粒细观结构演化过程

Figure 6. Evolution of sand mesostructure when r_u < 1.0

下载: 全尺寸图片幻灯片

图 7 颗粒长轴排列的各向异性与优势方向的演化过程

Figure 7. Evolution of fabric anisotropy and dominated direction of long axes of particles

下载: 全尺寸图片幻灯片

参考文献(8)

[1]	QUIGLEY M C, BASTIN S, BRADLEY B A. Recurrent liquefaction in Christchurch, New Zealand, during the Canterbury earthquake sequence[J]. Geology, 2013, 41(4): 419–422. doi: 10.1130/G33944.1
[2]	TOWHATA I, MARUYAMA S, KASUDA K I, et al. Liquefaction in the Kanto region during the 2011 off the Pacific coast of Tohoku earthquake[J]. Soils and Foundations, 2014, 54(4): 859–873. doi: 10.1016/j.sandf.2014.06.016
[3]	FINN W D L, BRANSBY P L, PICKERING D J. Effect of strain history on liquefaction of sand[J]. Journal of the Soil Mechanics and Foundations Division, 1970, 96(6): 1917–1934. doi: 10.1061/JSFEAQ.0001478
[4]	SUZUKI T. Effects of density and fabric change on reliquefaction resistance of saturated sand[J]. Soils and Foundations, 1988, 28(2): 187–195. doi: 10.3208/sandf1972.28.2_187
[5]	YE B, XIE X L, ZHAO T, et al. Centrifuge tests of macroscopic and mesoscopic investigation into effects of seismic histories on sand liquefaction resistance[J]. Journal of Earthquake Engineering, 2022, 26(8): 4302–4324. doi: 10.1080/13632469.2020.1826373
[6]	WANG R, FU P, ZHANG J-M, et al. Fabric characteristics and processes influencing the liquefaction and re-liquefaction of sand[J]. Soil Dynamics and Earthquake Engineering, 2019, 125: 105720. doi: 10.1016/j.soildyn.2019.105720
[7]	CHANEY R C, DEMARS K R, DEWOOLKAR M M, et al. A substitute pore fluid for seismic centrifuge modeling[J]. Geotechnical Testing Journal, 1999, 22(3): 196. doi: 10.1520/GTJ11111J
[8]	ROTHENBURG L, BATHURST R J. Analytical study of induced anisotropy in idealized granular materials[J]. Géotechnique, 1989, 39(4): 601–614. doi: 10.1680/geot.1989.39.4.601