震后地下结构在火灾下的力学性能初步分析

王国波; 刘强; 王鸿杰; 王建宁; 董正方

doi:10.11779/CJGE2022S2007

震后地下结构在火灾下的力学性能初步分析 English Version

1.
温州大学建筑工程学院, 浙江温州 325035
2.
中国机械工业集团有限公司, 北京 100080
3.
河南大学土木建筑学院, 河南开封 475004

基金项目:

国家自然科学基金项目 52078386

国家自然科学基金项目 51878529

详细信息

作者简介:
王国波(1979—)，男，湖北孝昌人，博士，教授，从事工程结构抗震研究。E-mail: wgb16790604@126.com

通讯作者:
董正方，E-mail: dzf@henu.edu.cn

中图分类号: TU435
计量
- 文章访问数: 124
- HTML全文浏览量: 21
- PDF下载量: 20
出版历程
- 收稿日期: 2022-11-30
- 网络出版日期: 2023-03-26
- 刊出日期: 2022-11-30

Preliminary analysis of mechanical properties of subway station under fire after earthquake

1.
College of Civil Engineering and Architecture, Wenzhou University, Wenzhou 325035, China
2.
China National Machinery Industry Co., Ltd., Beijing 100080, China
3.
School of Civil Engineering and Architecture, Henan University, Kaifeng, China

摘要

摘要: 地下结构等地下结构作为城市地下基础设施的重要组成部分，一旦遭受地震以及地震次生火灾会造成极大的经济损伤和人员伤亡，因此地下结构在地震以及地震火灾作用下的灾变行为亟待研究。基于某三跨两层车站建立其二维分析模型，首先对其进行了地震模拟，然后使用重启动分析，运用热-力耦合方法探讨了地下结构在地震次生火灾作用下响应。从地下结构中柱形变、层间位移等方面分析车站结构在地震及其次生火灾作用下灾变行为，讨论地震对地下结构抗火性能的影响，为地下结构受到地震以及次生火灾的性能评价提供参考。
- 地下结构 /
- 地震 /
- 地震次生火灾 /
- 性能评价
Abstract: As an important part of the urban underground infrastructure, the underground structures such as subway stations will cause great economic damage and casualties once they are subjected to earthquakes and earthquake-induced fires. Therefore, the catastrophic behaviors of the subway stations under the coupling of earthquakes and earthquake-induced fires needs to be studied. A two-dimensional analysis model is established based on a three-span two-story subway station. Firstly, the seismic simulation is carried out, and then the restart analysis is used to discuss the response of the subway station under the action of earthquake and the secondary fire by using the thermal-mechanical coupling method. The catastrophic behaviors of the subway station structure under earthquake and the secondary fire is analyzed from the aspects of column deformation and inter-layer displacement. The influences of earthquake on the fire resistance of the underground structures are discussed, which provides a reference for the performance evaluation of the underground structures under earthquakes and the secondary fire.
- subway station /
- earthquake /
- post-earthquake fire /
- performance evaluation

HTML全文

0. 引言

垃圾填埋场泄漏、化学品储罐事故、工厂排污以及采矿活动等造成的土壤和地下水污染会对人类的生存空间造成严重的威胁^[1]。目前污染土壤的修复工作具有难度大、周期长以及费用高等特点。对于已泄漏的或潜在的污染源,通常需要采取措施控制污染物通过地下水迁移,防止引发更大范围的污染。土工膜复合隔离墙是目前最为有效的污染场地管控技术之一,其工作原理是向开挖的沟槽中插入土工膜,并填入膨润土、土或水泥等混合料形成低渗透性垂直阻隔屏障,进而实现对污染水土的封装^[2]。由于土工膜渗透系数极低且耐化学性良好^[3-4],与传统的竖向隔离墙（如土-膨润土隔离墙、水泥-膨润土隔离墙等）相比,土工膜复合隔离墙具有更良好的防渗性能和耐久性^[5-8]。对于重点防渗区域,通常采用围护式复合隔离墙（图1）,同时需将墙体底部嵌入弱透水层,并采取良好的水头调控措施（如抽提墙内侧污水等）。基于此,穿过复合隔离墙的对流作用通常可以忽略不计,但是污染物依然会以分子扩散的方式击穿复合隔离墙,造成墙外水土污染^[5-6]。此外,由于土工膜对有机污染物的抗扩散性能显著弱于重金属离子^[9],因此对有机污染物在复合隔离墙中的迁移行为值得深入地研究。

图 1 概念模型图

Figure 1. Diagram of conceptual model

下载: 全尺寸图片幻灯片

一些学者对污染物在竖向隔离墙中的运移开展了研究。Neville等^[10]提出了污染物在竖向隔离墙中的稳态迁移模型,但该模型并不能反映污染物对周围环境的危害随时间变化的特征,因此采用瞬态模型更为合理。Acar等^[11]建立了污染物在竖向隔离墙中的瞬态迁移模型,但该模型假定隔离墙外侧界面通量为零,即污染物无法流出隔离墙,这与实际情况不符。Xie等^[12]、Chen等^[13]和Ding等^[14]构建了污染物在竖向隔离墙-含水层中的迁移模型,认为污染物迁移出隔离墙后,依然会在外侧的含水层中沿垂直于隔离墙的方向迁移。Peng等^[6]建立了有机污染物在复合隔离墙-含水层中扩散解析模型,该模型假定外侧含水层中地下水无渗流,即隔离墙外侧为无对流含水层边界条件。由于复合隔离墙的渗透系数远低于周围土体,外侧含水层中通常会形成沿隔离墙水平方向的地下水渗流通道^[15]（图1）,然而上述研究并未考虑地下水的影响。Zhan等^[5]分别建立了污染物在复合隔离墙中的一维扩散解析模型,该模型假定隔离墙外侧为零浓度边界条件,表明外侧含水层中地下水极其活跃,但未给出对应的地下水流速。由于含水层中地下水流速与地质条件及上下游水头差等因素密切相关,地下水并不一定处于流速为零或极其活跃的状态。因此,尽管Zhan等^[5]和Peng等^[6]均建立了复合隔离墙中污染物迁移模型,但他们关于隔离墙外侧含水层的假设导致其模型的应用存在一定的局限性,即不能解决任意地下水流速下污染物在复合隔离墙中的迁移问题。

本文考虑了复合隔离墙外侧含水层中地下水水平渗流（图1）,建立了有机污染物在复合隔离墙-含水层中的迁移数值模型,采用有限元软件COMSOL 5.3对该模型进行求解,并分析了含水层和复合隔离墙参数对污染物迁移的影响。

1. 计算模型

1.1 模型描述

复合隔离墙由垂直于地平面的3部分组成：内侧隔离墙、土工膜、外侧隔离墙,其厚度和长度分别为T_w,L,如图2所示。计算模型的主要假设：①隔离墙与含水层是均质、各向同性及饱和的多孔介质,且土工膜完整无孔；②由于复合隔离墙的渗透系数极低,当墙体底部嵌入弱透水层,且采用良好的水头调控措施,可以忽略穿过墙体的对流作用^[5-6]；③复合隔离墙外侧含水层中存在水平渗流的地下水,并服从达西定律；④本文所涉及的污染物浓度指的是溶解相浓度,且不存在相间传质；⑤假定内侧含水层污染物浓度在深度方向上一致,则污染物在复合隔离墙-含水层中的迁移方向是二维的（xy方向）。

图 2 数学模型图

Figure 2. Diagram of mathematical model

下载: 全尺寸图片幻灯片

基于上述假定,有机污染物的迁移路径描述如下：①以分子扩散的方式在内侧隔离墙中迁移；②在内侧隔离墙孔隙水与土工膜之间（y = L_g）进行分配；③以分子扩散的方式在土工膜内迁移；④在土工膜与外侧隔离墙孔隙水之间（y = L_g + T_g）再次进行分配；⑤以分子扩散的方式在外侧隔离墙中迁移；⑥以对流-弥散的方式在外侧含水层中迁移。

1.2 控制方程及边界条件

根据模型描述,建立有机污染物在各区域中的控制方程：

（1）在内侧隔离墙内（0≤ y ≤ L_g）

$\begin{matrix} R_{d,w} \frac{\partial C_{iw} (x, y, t)}{\partial t} = D_{w} (\frac{\partial^{2} C_{iw} (x, y, t)}{\partial x^{2}} + \frac{\partial^{2} C_{iw} (x, y, t)}{\partial y^{2}}) - \\ λ_{w} C_{iw} (x, y, t) \end{matrix}$ 。

(1)

（2）在土工膜内（L_g≤ y ≤L_g + T_g）

$\frac{\partial C_{g} (x, y, t)}{\partial t} = D_{g} (\frac{\partial^{2} C_{g} (x, y, t)}{\partial x^{2}} + \frac{\partial^{2} C_{g} (x, y, t)}{\partial y^{2}})$ 。

(2)

（3）在外侧隔离墙内（L_g + T_g ≤ y ≤ T_w）

$\begin{matrix} R_{d,w} \frac{\partial C_{ow} (x, y, t)}{\partial t} = D_{w} (\frac{\partial^{2} C_{ow} (x, y, t)}{\partial x^{2}} + \frac{\partial^{2} C_{ow} (x, y, t)}{\partial y^{2}}) - \\ λ_{w} C_{ow} (x, y, t) \end{matrix}$ 。

(3)

（4）在外侧含水层内（y > T_w）

$\begin{matrix} R_{d,a} \frac{\partial C_{a} (x, y, t)}{\partial t} = D_{ax} \frac{\partial^{2} C_{a} (x, y, t)}{\partial x^{2}} + D_{ay} \frac{\partial^{2} C_{a} (x, y, t)}{\partial y^{2}} - \\ v_{as} \frac{\partial C_{a} (x, y, t)}{\partial x} - λ_{a} C_{a} (x, y, t) \end{matrix}$ 。

(4)

式中C_i(x, y, t)（i = iw, g, ow, a）表示i区域中有机污染物溶解相瞬态浓度,其中iw,g,ow和a分别代表内侧隔离墙、土工膜、外侧隔离墙以及外侧含水层； $λ_{w}$ , $λ_{a}$ 为隔离墙和含水层中有机污染物的一阶降解常数；n_w,n_a为隔离墙和含水层的孔隙率；D_g为污染物在土工膜的扩散系数；v_as为外侧含水层地下水实际流速,v_as = v_a / n_a,其中v_a为地下水渗流速度；其他参数说明见下方。

D_w为隔离墙中的有效扩散系数,可表示为^[16]

$D_{w} = τ_{w} D_{0}$ ,

(5)

式中,τ_w为隔离墙的弯曲因子,D₀为污染物在水中的分子扩散系数。

D_ax,D_ay为污染物在外侧含水层中的水平和竖向水动力弥散系数^[17]

$D_{ax} = τ_{a} D_{0} + α v_{as}$ ,

(6a)

$D_{ay} = τ_{a} D_{0}$ 。

(6b)

式中τ_a为含水层的弯曲因子； $α$ 为纵向弥散度,Gelhar基于现场数据^[18],

$α {\begin{cases} \approx x_{α}^{2} / 100 (x_{α} < 100 m) \\ = 100 (x_{α} \geq 100 m) \end{cases}$ ,

(7)

其中,x_α为含水层长度。

R_d,w,R_d,a为污染物在隔离墙和含水层中的阻滞因子^[16]

$\begin{array}{l} R_{d,w} = 1 + \frac{ρ_{w} K_{d, w}}{n_{w}} ， \\ R_{d,a} = 1 + \frac{ρ_{a} K_{d, a}}{n_{a}} ， \end{array}}$

(8)

式中, $ρ_{w}$ , $ρ_{a}$ 为隔离墙和含水层的干密度,K_d,w,K_d,a为隔离墙和含水层对污染物的阻滞分配系数。

复合隔离墙和外侧含水层中污染物初始浓度为

${C_{i} (x, y, t) |}_{t = 0} = 0 (i = iw, g, ow, a)$ 。

(9)

模型入口边界条件为

$C_{iw} (x, y = 0, t) = C_{0}$ ,

(10)

式中,C₀为内侧含水层中污染物浓度。

模型左侧边界条件为

$\begin{array}{l} {\frac{\partial C_{i} (x, y, t)}{\partial x} |}_{x=0} = 0 & （ i =iw, g, ow), \\ {C_{a} (x, y, t) |}_{x=0} = 0 。 \end{array}}$

(11)

模型右侧边界条件为

${\frac{\partial C_{i} (x, y, t)}{\partial x} |}_{x \to + \infty} = 0 (i =iw, g, ow, a)$ 。

(12)

模型外侧边界条件为

${\frac{\partial C_{a} (x, y, t)}{\partial y} |}_{y = T_{w} + T_{a}} = 0$ 。

(13)

土工膜与邻近已污染介质之间的污染物分配可视为土工膜对污染物的吸附过程^[19]。当土工膜与内侧隔离墙孔隙水中污染物接触达到平衡,土工膜中污染物平衡浓度与内侧隔离墙孔隙水中的污染物平衡浓度之间关系符合Henry定律,

$K_{g} {C_{iw} (x, y, t) |}_{y = L_{g}} = {C_{g} (x, y, t) |}_{y = L_{g}}$ ,

(14)

式中,K_g为上游隔离墙与土工膜之间的分配系数。内侧隔离墙与土工膜之间污染物质量通量的关系为

${n_{w} D_{w} \frac{\partial C_{iw} (x, y, t)}{\partial y} |}_{y = L_{g}} = D_{g} {\frac{\partial C_{g} (x, y, t)}{\partial y} |}_{y = L_{g}}$ 。

(15)

污染物在土工膜与外侧隔离墙之间界面（y = L_g + T_g）的分配可视为污染物从土工膜上的解吸过程,同样也符合Henry定律,

${C_{g} (x, y, t) |}_{y = L_{g} + T_{g}} = {K^{'}}_{g} {C_{ow} (x, y, t) |}_{y = L_{g} + T_{g}}$ ,

(16)

式中, ${K^{'}}_{g}$ 为土工膜与下游隔离墙之间的分配系数,通常情况下,K_g = ${K^{'}}_{g}$ ^[20]。土工膜与外侧隔离墙之间污染物质量通量的关系为

${D_{g} \frac{\partial C_{g} (x, y, t)}{\partial y} |}_{y = L_{g} + T_{g}} = {n_{w} D_{w} \frac{\partial C_{ow} (x, y, t)}{\partial y} |}_{y = L_{g} + T_{g}}$ 。

(17)

外侧隔离墙与外侧含水层之间界面（y = T_w）的污染物浓度关系和质量通量关系为

${C_{ow} (x, y, t) |}_{y = T_{w}} = {C_{a} (x, y, t) |}_{y = T_{w}}$ ,

(18)

${n_{w} D_{w} \frac{\partial C_{ow} (x, y, t)}{\partial y} |}_{y = T_{w}} = {n_{a} D_{ay} \frac{\partial C_{a} (x, y, t)}{\partial y} |}_{y = T_{w}}$ 。

(19)

复合隔离墙外侧界面瞬态点通量可表示为

$F_{w} (x, t) = - {n_{w} D_{w} \frac{\partial C_{ow} (x, y, t)}{\partial y} |}_{y = T_{w}}$ 。

(20)

复合隔离墙外侧界面总通量可表示为

$M F_{w} (t) = - \int_{0}^{L} {n_{w} D_{w} \frac{\partial C_{w} (x, y, t)}{\partial y} |}_{y = T_{w}} d x$ 。

(21)

1.3 数值模拟方法及计算参数

笔者采用有限元计算软件COMSOL 5.3中多孔介质迁移分析模块（tds）对模型进行构建及计算。为了模拟半无穷右边界,假定模型长度为100 m。内侧含水层中污染物浓度（C₀）恒定为100 mg/L,并忽略污染物降解过程。选择垃圾填埋场和污染场地中常见的4种有机物作为目标污染物：甲基叔丁基醚（MTBE）、二氯甲烷（DCM）、三氯乙烯（TCE）以及氯苯（CB）,其中MTBE和DCM的亲水性显著强于TCE和CB。模型相关的几何参数^{[5, 21-22]}和污染物运移参数^{[4, 23-24]}参见表1,2。

表 1 模型几何参数^{[5, 21-22]}

Table 1. Geometrical parameters for model

几何参数		值
	复合隔离墙长度L/m	20
	土工膜厚度T_g/mm	1.5
	土工膜位置L_g/m	0.3
	隔离墙厚度T_w/m	0.6
	隔离墙孔隙率n_w	0.5
	隔离墙弯曲因子τ_w	0.4
	隔离墙密度ρ_w/(kg·m^-3)	1.34
	含水层厚度T_a/m	3
	含水层孔隙率n_a	0.55
	含水层弯曲因子τ_a	0.5
含水层隔离墙密度ρ_a/(kg·m^-3)		1.5

下载: 导出CSV

| 显示表格

表 2 有机污染物运移参数^{[4, 23-24]}

Table 2. Transport parameters for organic contaminant

污染物	分子扩散系数D₀/(10^-10 m²·s^-1)	HDPE土工膜中扩散系数D_g/(10^-13 m²·s^-1)	HDPE土工膜中分配系数K_g	隔离墙阻滞分配系数K_d,w/(mL·g^-1)	溶解度S/(mg·L^-1)
MTBE	7.92	7.74	0.57	0.20	48000
DCM	10.11	8.86	2.13	0.23	20000
TCE	9.40	5.45	63.24	0.52	1100
CB	10.40	3.96	108.94	0.20	500

下载: 导出CSV

| 显示表格

2. 含水层特性影响研究

本节以二氯甲烷（DCM）作为目标污染物。首先分析外侧含水层中地下水渗流速度对污染物在复合隔离墙中的迁移特征进行分析,并将本模型与基于零浓度边界条件的解析模型（Zhan的模型）及基于无对流含水层边界条件的解析模型（Peng的模型）进行对比；然后,分析纵向弥散度对污染物迁移的影响。

2.1 地下水渗流速度的影响

图3为50 a时复合隔离墙外侧界面（y = T_w）的相对浓度（C_w/C₀）随x变化图,考虑不同地下水渗流速度v_a（1×10^-9～1×10^-5 m/s）的影响。可以发现,渗流速度v_a增大会导致复合隔离墙外侧含水层中污染物浓度下降。这是由于地下水流会加速污染物在含水层中的迁移,减少污染物在含水层中的驻留。此外,由于受含水层左侧零浓度边界的影响,污染物浓度会沿着隔离墙长度方向（x方向）逐渐增大,并趋于稳定。当v_a=1×10^-9 m/s时,复合隔离墙外侧界面最大浓度为43.1 mg/L,且与Peng的模型计算结果吻合。当v_a=1×10^-5 m/s时,外侧界面浓度接近零,且与Zhan的模型计算结果十分吻合。

图 3 地下水渗流速度对墙外侧面浓度的影响

Figure 3. Effects of seepage velocity of groundwater on relative concentration at outside of CGCW

下载: 全尺寸图片幻灯片

图4为50 a时复合隔离墙最右侧剖面（x = L）相对浓度（C/C₀）。显然,v_a增大也会导致复合隔离墙内部浓度降低,说明活跃的地下水易导致污染物迁移出复合隔离墙。此外,当v_a为1×10^-9,1×10^-5 m/s时的复合隔离墙内部任意区域位置浓度分别与Peng的模型和Zhan的模型计算结果一致。另外还可以发现,土工膜两侧浓度存在显著的差异,这是由于土工膜对有机污染物的吸附和解吸导致的,说明土工膜能够对DCM的扩散具有一定的阻隔作用。

图 4 地下水渗流速度对墙最右侧剖面浓度的影响

Figure 4. Effects of seepage velocity of groundwater on concentration at right-most profile of CGCW

下载: 全尺寸图片幻灯片

图5表示复合隔离墙外侧界面末端（图2中点A）的瞬态相对浓度（C_wm/C₀）。可以发现,浓度C_wm随着时间的推移先增大后逐渐达到稳定；当v_a越大时,浓度越小且达到稳定的时间越短。此外,任意时刻v_a为1×10^-5,1×10^-9 m/s时的相对浓度（C_wm/C₀）分别与Zhan的模型和Peng的模型的计算结果一致。值得注意的是,当地下水流速较大时（v_a≥1×10^-5 m/s）,含水层中污染物浓度趋于零,此时无法采用浓度评价方法对复合隔离墙进行合理设计。基于此,有必要分析地下水渗流速度对复合隔离墙外侧界面末端的瞬态通量F_w的影响（图6）。可以发现,v_a增加会导致F_w增大,即加速污染物流出隔离墙进入含水层,不利于复合隔离墙阻隔污染物。当v_a≥1×10^-8 m/s,F_w随着时间推移先增大后趋于稳定。不同的是,当v_a≤1×10^-9 m/s时,F_w在27 a时达到最大值,随后不断降低,这是由于地下水流速较慢会导致污染物在含水层中驻留,造成隔离墙内浓度梯度减小,进而阻碍污染物迁移出复合隔离墙。此外,v_a为1×10^-5,1×10^-9 m/s时的通量分别与Zhan和Peng的模型的计算结果接近。

图 5 地下水渗流速度对墙外侧面末端瞬态相对浓度的影响

Figure 5. Effects of seepage velocity of groundwater on transient concentration at outside right-most point of CGCW

下载: 全尺寸图片幻灯片

图 6 地下水渗流速度对墙外侧面末端瞬态通量的影响

Figure 6. Effects of seepage velocity of groundwater on transient mass flux at outside right-most point of CGCW

下载: 全尺寸图片幻灯片

结合图3～6,可以认为：当外侧含水层地下水渗流速度v_a≥1×10^-5 m/s时,含水层可视为极其活跃,此时采用Zhan的模型进行复合隔离墙设计较为合理。当外侧含水层地下水渗流速度v_a≤1×10^-9 m/s时,复合隔离墙设计采用Peng的模型更合理。然而,当v_a在1×10^-9 m/s～1×10^-5 m/s时,若采用Zhan的模型进行设计将偏于保守,而采用Peng的模型进行设计将偏于危险。

2.2 含水层纵向弥散度的影响

污染物在含水层中的迁移机制包括对流作用和水动力弥散作用。本节基于纵向弥散度来研究水动力弥散系数的影响。根据Gelhar的研究,纵向弥散度 $α$ 与含水层长度x_α有关^[18]。本节假定含水层长度x_α分别为0,20,50,100 m,通过式（6）得到对应的纵向弥散度 $α$ 分别为0,4,25,100 m。图7为不同地下水渗流速度情况下,纵向弥散度对复合隔离墙外侧面末端（图2中点A）瞬态通量F_w的影响。可以发现当v_a为1×10^-7,1×10^-9 m/s时, $α$ 增加会导致F_w的增加,这是由于 $α$ 增加会导致污染物在含水层中水动力弥散系数增大,进而加速污染物的迁移；当v_a=1×10^-5 m/s时, $α$ 对F_w的影响较小,这是由于当流速较快时,对流作用主导污染物迁移,水动力弥散作用不明显；当v_a=1×10^-11 m/s时,由于含水层流速接近于零,水动力弥散系数近似等于有效扩散系数,导致 $α$ 对F_w的影响很小。

图 7 纵向弥散度对墙外侧面末端的瞬态通量的影响

Figure 7. Effects of longitudinal dispersion on transient mass flux at outside right-most point of CGCW

下载: 全尺寸图片幻灯片

3. 复合隔离墙特性影响研究

3.1 土工膜位置的影响

本节采用3个算例来研究HDPE土工膜位置的影响：①算例1,L_g = T_w/2,表示土工膜设置在复合隔离墙的中间位置（简称中置）；②算例2,L_g = T_w/6,表示土工膜设置在靠近复合隔离墙内侧界面（简称内置）；③算例3,L_g = 5T_w/6,表示土工膜设置在靠近复合隔离墙外侧界面（简称外置）。选择MTBE,DCM,TCE以及CB作为目标污染物。图8表示场地污染物为上述4种有机物时,不同土工膜位置情况下的复合隔离墙外侧界面瞬态总通量MF_w（式（21））,并考虑了外侧含水层地下水渗流速度的影响。从图中可以发现,改变土工膜位置会导致MF_w发生变化,并且在不同的污染物类别和含水层流速条件下,这种变化存在显著差异,为了便于对比,引入复合隔离墙外侧界面累积总通量CMF_w：

${CMF}_{w} = \int_{0}^{t_{d}} {MF}_{w} d t$ ,

(22)

图 8 土工膜位置对墙外侧面的瞬态总通量的影响

Figure 8. Effects of the geomembrane location on transient total mass flux at outside of CGCW

下载: 全尺寸图片幻灯片

式中,t_d为复合隔离墙的设计年限,本文假定为50 a,不同土工膜位置情况下的累积总通量CMF_w统计在表3中。

表 3 不同HDPE土工膜位置情况下的50 a内累积总通量及比较

Table 3. Comparison of cumulative mass fluxes at different locations of HDPE geomembrane during 50 years

L_g	MTBE(v_a/(m·s^-1))		DCM(v_a/(m·s^-1))		TCE(v_a/(m·s^-1))		CB(v_a/(m·s^-1))
L_g	1×10^-5	1×10^-9	1×10^-5	1×10^-9	1×10^-5	1×10^-9	1×10^-5	1×10^-9
T_w/2	343	211	702	396	704	357	854	442
T _w/6	318	192	684	391	720	391	887	488
T _w/6	-7.3% ↓	-8.9% ↓	-2.5% ↓	-1.1% ↓	2.3% ↑	9.6% ↑	3.9% ↑	10.5% ↑
5T_w/6	323	216	691	397	733	338	894	419
5T_w/6	-5.9% ↓	2.4% ↑	-1.5% ↓	0.3% ↑	4.1% ↑	-5.3% ↓	4.8% ↑	-5.3% ↓

下载: 导出CSV

| 显示表格

通过图8（a）和表3可以发现,对于MTBE,当v_a为1×10^-5 m/s时,将土工膜内置（L_g = T_w/6）和外置（L_g = 5T_w/6）时的瞬态通量MF_w比土工膜中置时（L_g = T_w/2）更低,且土工膜内置和外置时的累积总通量CMF_w比土工膜中置时分别低7.3%和5.9%,说明在这种情况下应当避免将土工膜中置,并建议将土工膜内置。当v_a=1×10^-9 m/s时,土工膜内置时的CMF_w比土工膜中置时低8.9%,但外置时却高了2.4%,说明将土工膜外置对复合隔离墙防污更为不利,建议将土工膜内置。对于DCM（图8（b））,尽管3种土工膜位置条件下的总通量MF_w十分接近,但通过累积总通量CMF_w发现土工膜的最佳和最不利位置与MTBE类似。对于TCE（图8（c））,不同地下水流速影响下的土工膜最不利位置和最佳位置各不相同：v_a为1×10^-5 m/s时,土工膜外置和中置分别为最不利位置和最佳位置；而v_a为1×10^-9 m/s时,土工膜内置和外置分别为最不利位置和最佳位置。对于CB（图8（d））,土工膜的最不利位置和最佳位置与TCE类似,并且不同位置之间的累积总通量CMF_w差异更为明显,特别是在地下水低流速条件下,土工膜内置和外置时的CMF_w比中置时分别高10.5%和低5.3%。通过上述分析,污染物类别及外侧含水层地下水流速均对土工膜的最佳位置和最不利位置有显著影响,不同土工膜位置条件下的累积总通量差异可达10%～20%。由于不同土工膜位置的设置不会对施工工程量和工程造价造成影响,因此基于掌握场地污染物类别及含水层地下水流速来确定最佳的土工膜位置,对于提升复合隔离墙的防污性能具有重要意义。

从图8和表3中还可以发现,复合隔离墙对亲水性有机物的阻隔效果较好,而对憎水性有机物阻隔效果较弱。例如,当HDPE土工膜中置且v_a=1×10^-5 m/s时,MTBE和CB的累积总通量CMF_w分别为343,854 mg/m。主要原因是HDPE土工膜中聚乙烯为非极分子,极性分子（亲水性有机物）较难穿透土工膜,而弱极性分子（憎水性有机物）则较容易通过^{[4, 19]}。

3.2 土工膜类别及厚度的影响

近年来,一些新型的土工膜正逐步应用于垃圾填埋场及污染场地的防污屏障中,如EVOH共聚土工膜^[25-26]。EVOH共聚土工膜是以乙烯-乙烯醇共聚物（Ethylene vinyl alcohol copolymer,简称EVOH）作为内核,以HDPE土工膜作为外层,合成了一种新型的土工膜。对于采用EVOH共聚土工膜的复合隔离墙和采用HDPE土工膜的复合隔离墙,分别简称为EVOH复合隔离墙和HDPE复合隔离墙。为了比较这两种复合隔离墙的优劣,本节给出了4种污染物（MTBE,DCM,TCE和CB）在这两种复合隔离墙中迁移的累积总通量CMF_w（图9）。其中MTBE、DCM、TCE和CB在EVOH共聚土工膜中的分配数分别为0.7,3.1,62.1,107.1,扩散系数分别为 5.5×10^-14,5.3×10^-14,1.7×10^-14,1.5×10^-14 m²/s^[25],土工膜厚度为1.5 mm。显然,当外侧含水层地下水流速增加,EVOH复合隔离墙外侧污染物累积总通量CMF_w也会相应上升。此外,EVOH复合隔离墙的防污性能显著强于HDPE复合隔离墙。例如v_a=1×10^-7 m/s时,采用HDPE和EVOH复合隔离墙时CB的CMF_w值分别为727,528 mg/m,表明采用EVOH土工膜复合隔离墙对CB的阻隔效率比采用HDPE土工膜高27%；而当污染物为MTBE时,EVOH复合隔离墙的阻隔效率比HDPE复合隔离墙高85%。

图 9 两种复合隔离墙外侧面累积总通量的比较

Figure 9. Comparison of cumulative mass fluxes at outside of two kinds of CGCW

下载: 全尺寸图片幻灯片

为了分析土工膜厚度的影响,引入增厚土工膜效率值R,

$R = \frac{| {{CMF}_{w} |}_{T_{g} = 3 mm} - {{CMF}_{w} |}_{T_{g} = 1.5 mm} |}{{{CMF}_{w} |}_{T_{g} = 1.5 mm}} \times 100 %$ ,

(23)

式中,CMF_w|_Tg=3mm和CMF_w|_Tg=1.5mm表示土工膜为3,1.5 mm时复合隔离墙50 a内的累积总通量。图10表示增厚土工膜对复合隔离墙性能的影响。可以发现外侧含水层流速对增厚土工膜效率值的影响很小。此外,对于不同的污染物,增厚HDPE土工膜对复合隔离墙性能的提升效果存在显著差异。例如当v_a=1×10^-7 m/s时,对于MTBE,DCM,TCE和CB这4种污染物,增厚土工膜效率值分别为33%,18%,9%,12%,说明对于憎水性有机物,增厚HDPE土工膜十分低效。当采用EVOH土工膜时,增厚土工膜效率值显著可以达到30%~50%。综上所述,在复合隔离墙中采用EVOH土工膜时的防污效果显著优于采用HDPE土工膜。

图 10 增厚土工膜对复合隔离墙性能的影响

Figure 10. Effects of thickening geomembrane on performance of CGCW

下载: 全尺寸图片幻灯片

3.3 隔离墙厚度及阻滞系数的影响

针对HDPE土工膜对憎水性有机物阻隔效果较差的特点,除了改变土工膜位置、厚度及类别,还可以通过改善隔离墙参数来提升复合隔离墙性能。本节选择TCE为目标污染物,外侧含水层地下水流速v_a为1×10^-7 m/s。假定隔离墙厚度T_w分别为0.6,0.9,1.2 m,阻滞分配系数K_d,w分别为0.52,1.56,4.68 mL/g,土工膜设置在隔离墙中间位置。图11表示隔离墙厚度与阻滞分配系数对隔离墙性能的影响。可以发现,随着墙厚T_w增大,复合隔离墙防污性能显著增强例如：K_d,w=0.52 mL/g时,T_w为0.9,1.2 m时的累积总通量CMF_w比T_w为0.6 m时低57.1%,82.2%。尽管增大墙厚可以有效提升复合隔离墙的防污性能,但是工程量和造价也会显著增加。

图 11 隔离墙厚度及阻滞系数的影响

Figure 11. Effects of distribution coefficient and thickness of wall

下载: 全尺寸图片幻灯片

同样地,增加阻滞分配系数K_d,w也会增强复合隔离墙防污性能。当T_w=0.6 m,K_d,w为1.56,4.68 mL/g时的累积总通量CMF_w比K_d,w为0.52 mL/g时低36.7%和83.2%。这是由于增大阻滞分配系数K_d,w将导致隔离墙的阻滞因子R_d增大,进而提升隔离墙对污染物的吸附性能。因此,隔离墙材料中添加改性材料可以有效降低复合隔离墙的设计厚度。

4. 讨论

由于土工膜复合隔离墙的渗透系数远低于周围土壤,隔离墙外侧含水层中通常会形成水平向地下水渗流通道,如图1所示。Zhan等^[5]和Peng等^[6]均建立了有机污染物在复合隔离墙中的迁移模型,他们分别假定外侧含水层中地下水极其活跃和不存在渗流。由于含水层中地下水流速与地质条件及上下游水头差等密切相关,上述假设均过于理想化,限制了他们方法在工程实际中的应用。针对这一问题,笔者建立了有机污染物在复合隔离墙-含水层中的迁移模型,考虑切下地下水渗流速度的影响。通过图3～11,可以发现地下水流速会显著影响污染物在复合隔离墙中的迁移,并且会影响土工膜在复合隔离墙中的最佳设置位置。因此在进行复合隔离墙设计前,应当掌握场地的土体类型、渗透系数及含水层长度等信息,估算复合隔离墙外侧含水层地下水流速。此外,本模型也存在一定的局限性：①本模型仅适用于穿越墙体的对流作用极其微弱的情况,对于墙内侧水头远高于外侧的情况,穿越墙体的对流作用无法忽略,本模型及本文结论暂不适用,今后需要对这一问题继续展开研究。②本模型只考虑了单一污染物的迁移,但很多污染场地存在多种污染物共存的复合污染情况（如垃圾填埋场）,污染物之间可能存在竞争性吸附及相互反应等情况,因此本文对于土工膜位置及厚度的设计建议仅适用于单一污染场地,对于复合污染场地需要根据实际情况进行分析。③本模型假定隔离墙材料和含水层均质且各向同性,但由于隔离墙的固结作用及含水层中存在不同类型的土层,隔离墙材料和含水层应当是非均质的,后续的研究中应当考虑这种情况。④含水层弥散度对计算结果有一定的影响,本文采用经验公式估算,弥散度取值除与尺度有关外,还受土的类型、地下水流速等影响,实际工程设计中应尽可能进行现场示踪试验确定弥散度取值。

5. 结论

本文建立了有机污染物在复合隔离墙-含水层中迁移数值模型,考虑污染物在复合隔离墙中的扩散作用及在含水层中的对流-弥散作用。该模型能够更准确地反映外侧含水层中地下水渗流对污染物在复合隔离墙中迁移的影响,对复合隔离墙设计和施工具有一定的指导意义。通过对含水层和复合隔离墙相关参数进行系统的分析,得到5点结论。

（1）外侧含水层中地下水流速增加会加速污染物迁移,进而导致复合隔离墙和含水层中污染物浓度降低以及复合隔离墙外侧界面污染物通量上升。当地下水渗流速度高于1×10^-5 m/s或低于1×10^-9 m/s时,可以分别采用基于零浓度边界条件的解析模型（Zhan的模型）和基于无对流含水层边界条件的解析模型（Peng的模型）进行初步设计；当流速处于1×10^-9～1×10^-5 m/s时,只能采用数值方法进行分析。

（2）复合隔离墙外侧界面污染通量随着含水层纵向弥散度增大而增加,但地下水流速高于1×10^-5 m/s时或低于1×10^-11 m/s时,纵向弥散度的影响可以忽略。

（3）不同HDPE土工膜位置情况下的复合隔离墙外侧界面累积总通量差异可达10%～20%,并且污染物类别和地下水流速均会影响土工膜的最佳位置和最不利位置。对于亲水性有机物MTBE和DCM,土工膜宜设置在靠近内侧。对于憎水性有机物TCE和CB,当地下水渗流速度较快时（v_a≥1×10^-5 m/s）,建议将土工膜设置在中间位置；当地下水渗流速度较慢时（v_a≤1×10^-9 m/s）,土工膜宜设置在靠近外侧。

（4）采用EVOH土工膜时的复合隔离墙防污性能显著优于采用HDPE土工膜,并且增厚EVOH土工膜对防污性能的提升效率也强于增厚HDPE土工膜。

（5）增加隔离墙厚度及在隔离墙中添加提升吸附性能材料均能提升复合隔离墙的防污性能。

图 1 地铁地下车站结构横截面主要尺寸和配筋图

Figure 1. Main dimensions and distributed steels of cross section

下载: 全尺寸图片幻灯片

图 2 C30混凝土本构曲线

Figure 2. Constitutive curves of concrete No. 30

下载: 全尺寸图片幻灯片

图 3 土−地铁车站相互作用体系有限单元划分

Figure 3. Finite elements of soil-underground structure

下载: 全尺寸图片幻灯片

图 4 输入荷载曲线

Figure 4. Curves of input loads

下载: 全尺寸图片幻灯片

图 5 地震作用下地下结构侧墙层间变形响应时程

Figure 5. Time histories of inter-story drift of station wall under earthquake

下载: 全尺寸图片幻灯片

图 6 火灾中地下结构变形情况及温度变化云图（15, 30, 60min）

Figure 6. Structural deformations and heat distribution of station in fire (15, 30, 60 min)

下载: 全尺寸图片幻灯片

图 7 火灾中地下结构温度变化各部位最高温度变化曲线

Figure 7. Temperature curves of components in fire

下载: 全尺寸图片幻灯片

图 8 火灾中结构层间位移时程

Figure 8. Time histories of structural inter-story drift in fire

下载: 全尺寸图片幻灯片

表 1 场地土层参数

Table 1 Site parameters

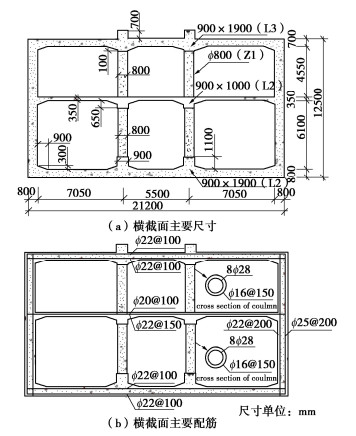
土层编号	土性	重度/(kN·cm^-3)	弹模/MPa	厚度/m	剪切波速/(m·s^-1)	动泊松比
1	素填土	19.4	15.3	3.0	200	0.49
2	黏土	19.4	15.3	4.0	200	0.49

下载: 导出CSV

表 2 C30混凝土材料参数

Table 2 Material parameters for concrete No. C30

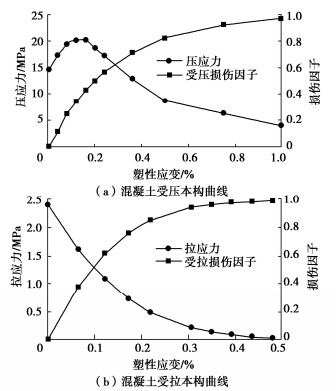
材料参数	参数值	材料参数	参数值
弹性模量	E₀ =3.0×10⁴ MPa	极限受压屈服应力	σ_cu =20.1 MPa
泊松比	ν = 0.2	初始受拉屈服应力	σ_t0 =2.4 MPa
密度	ρ =2450 kg/m³	受压刚度恢复系数	ω_c =1.0
膨胀角	Ψ=36.31°	受拉刚度恢复系数	ω_c =0.0
初始受压屈服应力	σ_c0 =13 MPa	损伤因子	d_c，d_t（图 2）

下载: 导出CSV

表 3 混凝土及钢筋的热工参数

Table 3 Thermal parameters of concrete and steel bars

温度/℃	混凝土热工参数			钢筋热工参数
温度/℃	导热系数	比热容	热膨胀系数	导热系数	比热容	热膨胀系数
20	1.96	913	6.16×10^-6	53.3	440	1.2×10^-5
100	1.81	964	6.8×10^-6	50.7	489	1.22×10^-5
200	1.63	1022	7.6×10^-6	47.3	530	1.25×10^-5
300	1.47	1075	8.4×10^-6	44.0	565	1.27×10^-5
400	1.33	1122	9.2×10^-6	40.6	606	1.30×10^-5
500	1.21	1164	1.0×10^-5	37.3	667	1.32×10^-5
600	1.10	1200	1.08×10^-5	34.0	760	1.35×10^-5
700	1.01	1231	1.16×10^-5	30.7	991	1.37×10^-5
800	0.93	1256	1.24×10^-5	27.4	795	1.40×10^-5
900	0.87	1275	1.32×10^-5	27.3	650	1.42×10^-5
1000	0.83	1289	1.40×10^-5	27.3	650	1.45×10^-5

下载: 导出CSV

表 4 构件变形

Table 4 Deformations of components

构件	峰值变形/mm	残余变形/mm
左侧墙	33.77	5.44
右侧墙	35.85	1.14
楼板	39.92	3.75
左柱	37.93	4.03
右柱	37.30	5.35

下载: 导出CSV

参考文献(18)

[1]	赵凯, 王秋哲, 王彦臻, 等. 可液化地基地下结构地震反应特征简化有效应力分析[J]. 振动与冲击, 2021, 40(21): 39–46. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202121006.htm ZHAO Kai, WANG Qiu-zhe, WANG Yan-zhen, et al. Effects of soil-underground structure interaction on seismic response of liquefiable sit around underground structure[J]. Journal of Vibration and Shock, 2021, 40(21): 39–46. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202121006.htm
[2]	唐柏赞, 李小军, 陈苏, 等. 可液化地基-非规则截面地下结构地震变形研究[J]. 振动与冲击, 2020, 39(11): 217–225. TANG Bai-zan, LI Xiao-jun, CHEN Su, et al. Seismic deformation characteristics of liquefaction soil-irregular section underground structure[J]. Journal of Vibration and Shock, 2020, 39(11): 217–225. (in Chinese)
[3]	李延涛, 田野, 宗金辉, 等. 受相邻上部结构影响的隧道-土体系振动台试验研究[J]. 振动与冲击, 2020, 39(3): 233–241, 259. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202003033.htm LI Yan-tao, TIAN Ye, ZONG Jin-hui, et al. Shaking-table tests for seismic response of tunnel-soil system affected by adjacent upper structure[J]. Journal of Vibration and Shock, 2020, 39(3): 233–241, 259. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202003033.htm
[4]	王建宁, 马国伟, 窦远明, 等. 异跨框架式地铁地下车站结构抗震性能水平与评价方法研究[J]. 振动与冲击, 2020, 39(10): 92–100. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202010013.htm WANG Jian-ning, MA Guo-wei, DOU Yuan-ming, et al. Performance levels and evaluation method for seismic behaviors of a large-scale underground subway station with unequal-span frame[J]. Journal of Vibration and Shock, 2020, 39(10): 92–100. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202010013.htm
[5]	陈素文, 李国强. 地震次生火灾的研究进展[J]. 自然灾害学报, 2008, 17(5): 120–126. https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH200805021.htm CHEN Su-wen, LI Guo-qiang. Advance in research on secondary fire of earthquake[J]. Journal of Natural Disasters, 2008, 17(5): 120–126. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZH200805021.htm
[6]	DANIELL J E, SCHAEFER A M, WENZEL F. Losses associated with secondary effects in earthquakes[J]. Frontiers in Built Environment, 2017, 3: 30.
[7]	陈适才, 田小明, 闫维明, 等. 建筑结构地震火灾效应分析方法[J]. 土木建筑与环境工程, 2011, 33(6): 90–95, 119. https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN201106016.htm CHEN Shi-cai, TIAN Xiao-ming, YAN Wei-ming, et al. A preliminary survey on analysis method of building structures under post-earthquake fire[J]. Journal of Civil, Architectural & Environmental Engineering, 2011, 33(6): 90–95, 119. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN201106016.htm
[8]	BURSI O S, FERRARIO F, PUCINOTTI R, et al. Seismic-induced fire analysis of steel-concrete composite beam-to-column joints: bolted solutions[C]// International Conference on Composite Construction in Steel and Concrete 2008. Reston, VA, 2008.
[9]	WEN B, WU B, NIU D T. Post-earthquake fire performance of reinforced concrete columns[J]. Structure and Infrastructure Engineering, 2016, 12(9): 1106–1126.
[10]	ARABLOUEI A, et al. Effect of fire insulation delamination on structural performance of steel structures during fire following an earthquake or an explosion[J]. Fire Safety Journal, 2016, 84: 40–49.
[11]	苗吉军, 王俊富, 刘才玮, 等. 损伤后混凝土框架结构火灾试验研究[J]. 建筑结构学报, 2012, 33(2): 1–9. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201202002.htm MIAO Ji-jun, WANG Jun-fu, LIU Cai-wei, et al. Experimental research on RC frame structure with damages due to elevated temperature[J]. Journal of Building Structures, 2012, 33(2): 1–9. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201202002.htm
[12]	李文婷, 陈清军. 地震次生火灾中城市地铁地下结构的灾变性能研究[J]. 振动与冲击, 2021, 40(14): 153–161, 179. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202114021.htm LI Wen-ting, CHEN Qing-jun. Damage performance of underground structures in earthquake-induced fire[J]. Journal of Vibration and Shock, 2021, 40(14): 153–161, 179. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202114021.htm
[13]	陈阳, 陈清军. 火灾后CFRP加固下地下结构结构的地震反应[C]//第28届全国结构工程学术会议论文集(第Ⅰ册). 南昌, 2019: 401–405. CHEN Yang, CHEN Qing-jun. Seismic response of subway station structures reinforced by CFRP after fire[C]//The 28th National Conference on Structural Engineering (VolumeⅠ). Nanchang, 2019: 401–405. (in Chinese)
[14]	赵丁凤, 阮滨, 陈国兴, 等. 基于Davidenkov骨架曲线模型的修正不规则加卸载准则与等效剪应变算法及其验证[J]. 岩土工程学报, 2017, 39(5): 888–895. doi: 10.11779/CJGE201705013 ZHAO Ding-feng, RUAN Bin, CHEN Guo-xing, et al. Validation of modified irregular loading-unloading rules based on Davidenkov skeleton curve and its equivalent shear strain algorithm implemented in ABAQUS[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(5): 888–895. (in Chinese) doi: 10.11779/CJGE201705013
[15]	LEE J, FENVES G L. Plastic-damage model for cyclic loading of concrete structures[J]. Journal of Engineering Mechanics, 1998, 124(8): 892–900.
[16]	WANG J N, et al. Influence of diaphragm wall on seismic responses of large unequal-span subway station in liquefiable soils[J]. Tunnelling and Underground Space Technology, 2019, 91: 102988.
[17]	李国强, 韩林海, 楼国彪. 钢结构及钢-混凝土组合结构抗火设计[M]. 北京: 中国建筑工业出版社, 2006. LI Guo-qiang, HAN Lin-hai, LOU Guo-biao. And Fire Resistance Design of Steel Structure and Steel-Concrete Composite Structure[M]. Beijing: China Architecture & Building Press, 2006. (in Chinese)
[18]	庄海洋, 任佳伟, 王瑞, 等. 两层三跨框架式地铁地下车站结构弹塑性工作状态与抗震性能水平研究[J]. 岩土工程学报, 2019, 41(1): 131–138. doi: 10.11779/CJGE201901014 ZHUANG Hai-yang, REN Jia-wei, WANG Rui, et al. Elasto-plastic working states and seismic performance levels of frame-type subway underground station having two layers and three spans[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(1): 131–138. (in Chinese) doi: 10.11779/CJGE201901014