Comparative analysis and parameter determination method of shear strength models for unsaturated clayey soils
-
摘要: 由于非饱和土强度随基质吸力变化剧烈、影响因素众多、机理复杂，学者们提出了多种不同的非饱和土强度表达模型，仍尚未形成共识。为了获得普适性较强、能够描述非饱和土强度在宽吸力范围内的非线性变化规律的模型，系统总结现有的非饱和土抗剪强度模型，并采用文献中的数据对其应用效果进行了比较，结果表明：①拟合模型的应用效果普遍高于预测模型；②在拟合模型中，双曲线模型在预测宽吸力范围内黏性土的抗剪强度中的实际应用效果最好。进一步，还对双曲线模型的参数确定方法进行了分析发现：①只需在3个饱和度水平下进行非饱和强度测量，就可以准确获得双曲线模型中的两个参数；②建议对饱和土样、饱和度0.7~0.4和饱和度0.1~0的3个土样进行非饱和强度测量。研究初步建立了一种较好的非饱和土强度模型参数确定方法，能够采用较少的试验数量在全吸力范围内获得比较准确的非饱和土强度演化规律，这对非饱和土力学行为的研究和工程应用都有着重要的意义。Abstract: Due to the great variation of strength of unsaturated soils with matric suction, the numerous influence factors and the complex mechanism, the worldwide scholars have proposed various unsaturated strength models, but no consensus has been reached. In order to obtain a universal model that can describe the nonlinear variation of strength of the unsaturated soils over a wide suction range, the existing unsaturated strength models are systematically summarized. Also, their application effects are compared with the data in the literature. The research results show that: (1) The fitting models are superior to the prediction ones; (2) Among the fitting models, the hyperbolic models are the best in predicting the shear strength of clayey soils. Furthermore, the parameter determination method for the hyperbolic model is analyzed. It is found that: (1) Two parameters of the hyperbolic model can be accurately obtained by measuring the unsaturated strength at three saturation levels. (2) It is recommended to measure the shear strength of soil samples within the saturation degrees of 1, 0.7 to 0.4 and 0.1 to 0. The determination method for the hyperbolic parameters is proposed. The parameters require a few of experimental data, which can obtain a relatively accurate evolution law of the strength in the full suction range. It is of great significance to the study on the mechanical behaviour and engineering application of unsaturated soils.
-
Keywords:
- unsaturated soil /
- shear strength /
- wide suction /
- nonlinear strength /
- hyperbolic model
-
0. 引言
自然界的大多数土体都处于非饱和状态，构筑或者承载着多种不同的土工建筑物。掌握非饱和土的强度特性，对评估这些土工建筑物的稳定性，优化其设计方案，提高其安全性和经济性至关重要。由于非饱和土性质复杂，通过试验的手段表征非饱和土的强度特性费时费力，同时需要精密的仪器和专业的知识，其强度理论至今尚不完善，难以直接应用于实际工程。为此，不少学者以理论知识或大量的试验数据为基础，建立了半经验或经验的非饱和土强度模型[1]，推动了非饱和土强度理论的发展。
目前，非饱和土抗剪强度模型表达形式众多，大体可分为预测模型和拟合模型两类[2]。其中，预测模型基于土体基本物理性质（例如土–水特征曲线等信息）对土体的强度进行预测, 通常与饱和度、有效饱和度或体积含水率有关。拟合模型给出了包含待定系数的非饱和强度表达，通过对实测强度数据拟合确定待定系数，从而得到确定的强度表达式，其中，沈珠江 [3]认为在预测宽吸力范围内非饱和土的抗剪强度时，采用拟合模型中的双曲线表达形式具有更好的应用效果，但模型中的参数难以确定，需要用到大量的试验数据拟合来得到。因此，如何基于有限的试验数据来确定模型的参数，进而建立预测宽吸力范围内非饱和土抗剪强度的简要模型，是拟合模型在简化问题上面需要重点考虑的。此外，对于现有的抗剪强度模型能否用于预测高吸力范围内非饱和抗剪强度的研究较少，有必要在宽吸力范围内讨论各种抗剪强度模型的优点和局限性。
本文首先基于脱湿过程中非饱和黏性土抗剪强度的非线性特征，对强度演化机理进行了分析。然后回顾了现有的非饱和土抗剪强度模型，并基于文献中的试验数据，对各种抗剪强度模型的优点和局限性进行了讨论。最后给出了一种双曲线模型参数的确定方法，该方法仅需使用饱和土强度参数和两组非饱和土强度的测量结果，即可实现在宽吸力范围内预测非饱和黏性土的抗剪强度。
1. 非饱和土强度模型对比分析
1.1 脱湿过程中黏性土抗剪强度的非线性特征及机理分析
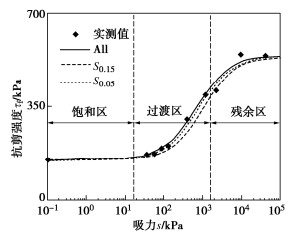
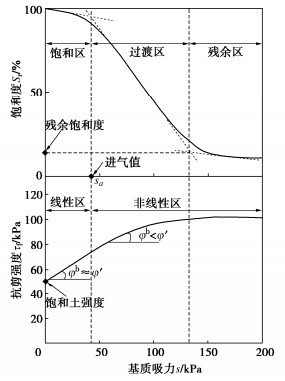
非饱和黏性土的抗剪强度主要由黏聚强度、颗粒间的摩擦强度及吸力强度构成，其中吸力强度的来源包括基质吸力、颗粒之间的胶结力等。如图 1所示，在脱湿过程中，黏性土的抗剪强度呈非线性增加，在SWCC残余区逐渐达到一个稳定值。
非饱和土孔隙水可分为毛细水和吸附水两大类。土体在脱湿过程中，在SWCC进气值之前，土体仍属于饱和状态，基质吸力对抗剪强度的作用可用饱和土的莫尔-库仑准则来进行分析；从过渡区开始到过渡区结束，气体开始进入土体，土体中开始出现水-气交界面，大孔隙中间的水逐渐被气体取代，随后小孔隙水开始逐渐被排出，相邻土颗粒之间形成液桥（毛细水），在该阶段，孔隙水的体积不断的减小，进而影响到基质吸力作用面积分数的降低，导致基质吸力有利增加抗剪强度的作用在不断降低，抗剪强度随基质吸力的增长率在减小，抗剪强度的包线呈现非线性的特性；SWCC从残余区开始到残余区结束，随着饱和度进一步的降低，颗粒间的液桥逐渐断开，毛细聚集作用逐渐消失，孔隙水紧密吸附在颗粒表面，此时土体孔隙水的主要形式为吸附水。由于吸附水包裹在土颗粒表面，吸附水压力几乎不影响土颗粒间的接触应力，吸附水对非饱和土抗剪强度的影响非常有限[4]。因此，在SWCC残余区，土体的抗剪强度处于一个相对稳定的状态。
1.2 现有非饱和土抗剪强度模型回顾
非饱和土抗剪强度模型主要分为预测模型和拟合模型两种。
（1）预测模型
代表性的预测模型为Bishop有效应力公式：
$$ {\tau }_{\text{f}}={\tau }_{\text{s}}+{\tau }_{\text{us}}={c}^{\prime }+\left[(\sigma -{u}_{\text{a}})+\chi s\right]\mathrm{tan}{\phi }^{\prime }\text{ }\text{，} $$ (1) 式中，c'为饱和土的黏聚力，$ \sigma $为法向总应力，φ'为饱和土的内摩擦角，s为基质吸力，ua为孔隙气压力，χ为有效应力系数，τs为饱和土强度，τus为与吸力直接相关的抗剪强度，可称为吸力强度。
式（1）最大的困难在于χ值难以确定。学者们通过统计回归给出了χ的经验表达，从而建立了相应的非饱和强度预测模型，如表 1所示。
表 1 非饱和土抗剪强度模型Table 1. Existing models for shear strength of unsaturated soils类型 模型名称 τus表达式 预测
模型Vanapalli预测模型(Eq.1)[5] $ s\tfrac{{{S_{\text{r}}} - {S_{{\text{re}}}}}}{{1 - {S_{{\text{re}}}}}}\tan \varphi ' $ Oberg预测模型[6] $ s{S_{\text{r}}}\tan \varphi ' $ Khalili预测模型[7] $ s{\left( {\tfrac{s}{{{s_{\text{a}}}}}} \right)^{ - 0.55}}\tan \varphi ' $ Tekinsoy预测模型[8] $ ({s_{\text{a}}} + {P_{{\text{at}}}})\ln \left[ {\tfrac{{s + {P_{{\text{at}}}}}}{{{P_{{\text{at}}}}}}} \right]\tan \varphi ' $ 拟合
模型Abramento拟合模型[9] $ \alpha {s^\beta } $ Vanapalli拟合模型(Eq.2)[5] $ sS_{\text{r}}^\kappa \tan \varphi ' $ Shen拟合模型[3] $ \tfrac{s}{{1 + ds}}\tan \varphi ' $ Miao拟合模型[10] $ \tfrac{{as}}{{1 + \tfrac{{1 - a}}{{{P_{{\text{at}}}}}}s}} $ Jiang拟合模型[11] $ \tfrac{s}{{a + ds}}\tan \varphi ' $ Alonso拟合模型[12] $ s\left\{ {\tfrac{{{S_{\text{r}}} - {S_{{\text{rm}}}}}}{{1 - {S_{{\text{rm}}}}}}} \right.\left. { + \tfrac{1}{\eta }\ln \left[ {1 + \exp \left( { - \eta \tfrac{{{S_{\text{r}}} - {S_{{\text{rm}}}}}}{{1 - {S_{{\text{rm}}}}}}} \right)} \right]} \right\}\tan \varphi ' $ 注：Sr为饱和度，Sre为残余饱和度，sa为进气值，Pat为大气压（101.3 kPa），α，β，κ，a，d，Srm，η为拟合参数。 （2）拟合模型
代表性的拟合模型是扩展莫尔-库仑准则：
$$ {\tau }_{\text{f}}={c}^{\prime }+(\sigma -{u}_{\text{a}})\mathrm{tan}{\phi }^{\prime }+s\mathrm{tan}{\phi }^{\text{b}}\text{，} $$ (2) 式中，φb为基质吸力引起的抗剪强度增量的摩擦角。
扩展莫尔-库仑准则使用简便，被证明在饱和度较高的情况下具有一定的适用性，但是存在两个缺陷：①无法退化为饱和土的有效应力原理；②在高吸力区间会严重高估土体的抗剪强度。因此，为了描述非饱和土强度的非线性特征，很多其它形式的拟合模型被很多学者提出，如表 1所示。
1.3 非饱和土抗剪强度模型的应用效果对比分析
（1）不同强度模型的应用效果
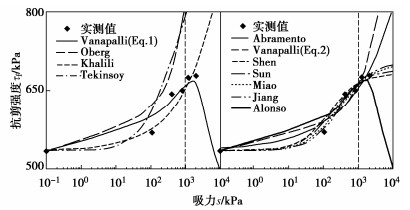
应用文献[13]马德里黏质砂土的试验数据对表 1中强度方程分别进行对比分析，如图 2所示。图 2中的黑色虚线表示为过渡区与残余区的分界线。
![]()
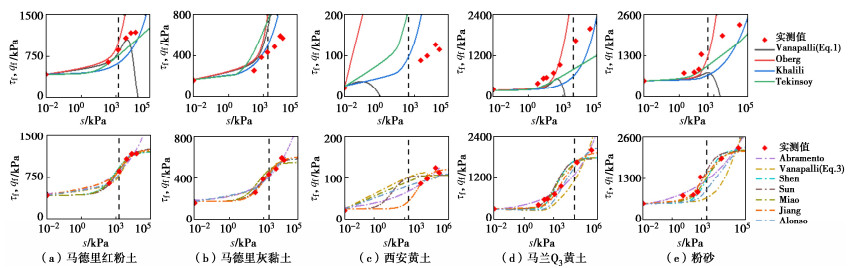
图 2 马德里黏质砂土的抗剪强度和模型预测Figure 2. Shear strengths of Madrid clayey sand and model predictions从图 2中可看出：①对于预测模型，其中Vanapalli预测模型能够合理预测在低吸力范围内的土体强度，但该方程并不适用于高吸力范围，这是因为采用有效饱和度计算χ时，χ值随着饱和度的减小而逐渐降低，而对于黏性土，在高吸力下土体的强度仍然保持着很高的水平。Oberg预测模型未考虑随着吸力增大饱和度减小的速率逐渐变慢的情况，预测强度明显高估实测强度。Khalili预测模型在高吸力区会出现高估实测值的现象。Tekinsoy预测模型整体高估了土体的强度。②对于拟合模型，只有Shen模型，Miao模型和Jiang模型等具有双曲线表达形式的模型，可很好地预测土体的强度。其他的一些方程，在宽吸力范围内的不同区段出现高估或低估实测值的现象。本文还用了Escario等[13]（马德里红粉土和灰黏土）、Ng等[14]（西安黄土）、孙德安等[15]（马兰Q3黄土）和Patil等[16]（粉砂）的试验数据，分别用预测型和拟合型强度模型进行应用效果对比，见图 3。从图 3中可看出，在实际应用过程中，预测模型在预估宽吸力范围内黏性土强度时会出现明显的高估或低估的现象，而拟合模型的应用效果整体要优于预测型，其中双曲线模型具有最优的拟合效果。
![]()
图 3 非饱和黏性土的抗剪强度模型应用效果对比Figure 3. Comparison of application effects of shear strength models for unsaturated clayey soils（2）不同强度模型的误差水平
本文使用平均相对误差ARE（The average relative error）来评价各强度模型的误差水平：
$$ \text{ARE}=\frac{1}{n}{\displaystyle \sum _{i=1}^{n}|\frac{{y}_{i}-{{y}^{\prime }}_{i}}{{y}_{i}}|}\times \text{100 }\text{，} $$ (3) 式中，yi为观察值，$ {y'_i} $为预测值。本文预测效果良好的定义为ARE≤20%。
基于图 2，3中的试验数据，采用式（3）对表 1中的强度模型进行评估。表 2总结了采用ARE准则对不同强度模型的评价结果。从表 2中可以看出：①拟合模型的平均误差要普遍小于预测模型。②预测模型中，效果最好的是Khalili预测模型。③拟合模型中，双曲线模型（包括Shen模型，Miao模型和Jiang模型等）的ARE值相对较小，其平均误差均小于10%，双曲线模型所能展现的曲线形状与土体强度的演化规律较为接近。其中，Jiang模型效果最佳，其平均误差为6.4%，最大误差为12.5%。
表 2 非饱和强度模型应用于6种黏性土强度数据后的平均相对误差ARE对比分析Table 2. Comparative analysis of ARE of unsaturated strength models (%)类型 学者 黏质砂土 灰黏土 红粉土 西安黄土 马兰Q3黄土 粉砂 平均误差 最大误差 预测
模型Vanapalli 1.9 56.5 17.8 7299.5 252.7 77.6 1284.3 7299.5 Oberg 17.7 126.1 41.5 1095.3 87.8 98.7 244.5 1095.3 Khalili 2.2 30.4 20.2 211.1 47.0 31.0 57.0 211.1 Tekinsoy 14.0 66.6 11.1 232.5 37.1 19.3 63.4 232.5 拟合
模型Abramento 2.2 8.9 6.5 14.4 10.4 16.9 9.9 16.9 Vanapalli 2.8 5.8 5.8 20.3 36.6 28.9 16.7 36.6 Shen 1.4 8.0 1.8 13.7 20.6 11.7 9.5 20.6 Miao 1.2 5.0 2.5 13.6 20.7 9.7 8.8 20.7 Jiang 1.2 5.6 1.7 7.6 12.5 9.8 6.4 12.5 Alonso 1.9 6.1 4.4 10.9 24.3 21.2 11.5 24.3 2. 双曲线模型的参数确定方法
第1.3节的分析表明：Jiang拟合模型的应用效果最佳。双曲线模型在推广和应用的过程中最大的瓶颈问题是模型的参数不明，需要通过大量的试验数据拟合得到，但是对于常规控制吸力的非饱和土强度试验，由于其吸力平衡时间过于漫长，使得通过试验的手段掌握宽吸力范围内非饱和土强度特性通常费时费力。因此，在保证强度模型预测精度的基础上，如果能采用有限的试验数据来确定双曲线模型的参数，这对于非饱和土强度模型的发展和应用具有重要的理论意义和实用价值。
Jiang双曲线拟合模型的原始表达式为
$$ {\tau }_{\text{f}}={c}^{\prime }+(\sigma -{u}_{\text{a}})\mathrm{tan}{\phi }^{\prime }+\left(\frac{s}{a+\text{d}s}\right)\mathrm{tan}{\phi }^{\prime }\text{，} $$ (4) 式中，a，d为拟合参数。
2.1 参数d的确定
本文采用3个试验数据点来确定参数。3个试验数据点的饱和度水平分别为位于饱和区、过渡区和残余区，代表着双曲线模型的首端（平缓段）、中部（上升段）和尾端（稳定段）。将不同区段的试验数据进行组合，对比不同拟合条件下ARE值，优选出不同区段的饱和度水平。
首先将式（4）中的c'与吸力强度τus合并：
$$ c={c}^{\prime }+\frac{s}{a+\text{d}s}\mathrm{tan}{\phi }^{\prime }\text{，} $$ (5) 式中，c为表观黏聚力。
当土体为干土时（Sr=0），假设吸力接近于∞，得到干土的表观黏聚力cult：
$$ \underset{s\to \infty }{\mathrm{lim}}c={c}_{\text{ult}}={c}^{\prime }+\frac{1}{d}\mathrm{tan}{\phi }^{\prime }\text{ }\text{，} $$ (6) $$ {c}_{\text{ult}}-{c}^{\prime }={\tau }_{\text{ult}}-{\tau }_{\text{s}}=\frac{1}{d}\mathrm{tan}{\phi }^{\prime }\text{ }\text{，} $$ (7) 式中，$ {\tau _{{\text{ult}}}} $为干土强度，选用标准为试验测量得到的最高吸力值对应的抗剪强度。
式（7）可表示为
$$ d=\frac{\mathrm{tan}{\phi }^{\prime }}{{\tau }_{\text{ult}}-{\tau }_{\text{s}}}\text{ }。 $$ (8) 从式（8）中可以看出，只需要饱和土的强度参数和一个位于残余区的土体强度，即可确定参数d。
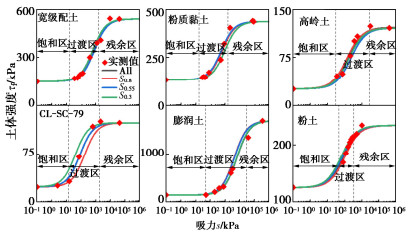
固定饱和区和过渡区的土体强度，研究在残余区内使得双曲线模型预测效果最佳的土体强度所对应饱和度水平的优选区间。以宽级配土的试验数据为例[17]，建立的试验数据组合及拟合效果如图 4和表 3所示。可以看出，在残余区内使得模型拟合效果最优的数据组合为S0.05，其平均相对误差为3.2%。
![]()
图 4 不同拟合条件下模型的预测效果对比图Figure 4. Comparison of model prediction effects under different fitting conditions表 3 残余区内不同试验数据组合的ARE值对比分析Table 3. Comparative analysis of ARE of different test data combinations in residual area (%)编号 组合 宽级配土 粉质黏土 高岭土 CL-SC-79 膨润土 粉土 平均误差 最大误差 All 所有数据点 3.0 3.6 5.5 5.6 5.8 5.4 4.8 5.8 S0.15 τs+τ0.7~0.4+τ0.2~0.1 5.3 7.2 6.5 6.1 14.3 5.8 7.5 14.3 S0.05 τs+τ0.7~0.4+τ0.1~0 3.2 3.8 7.5 5.7 9.8 5.5 5.9 9.8 注：S0.15代表在残余区选取的饱和度水平为0.2~0.1，S0.05为0.1~0。 基于以上思路，为了使得对比结果更具有普适性，本文又分别搜集了张禄乾[17]（粉质黏土）、王逍萌[18]（高岭土和CL-SC-79）、Zhang等[19]（膨润土）、Thu等[20]（粉土）的试验数据进行研究，通过对比各组合下ARE的平均值，明确在残余区内饱和度水平的优选区间。为了简单起见，本文将进气值对应的饱和度统一为0.9，残余饱和度统一为0.2。由于不同文献中测得抗剪强度对应的饱和度水平不同，本文定义τi~j代表着饱和度在i~j某一饱和度水平的土体强度。对比分析结果见表 3所示。从表 3中可以看出，S0.05组更接近All组的ARE值，其平均误差为5.9%，最大误差为9.8%。在残余区内，饱和度水平的优选范围为0.1~0。
2.2 参数a的确定
基于2.1节中对残余区内不同试验数据组合的对比分析结果。固定饱和区的土体强度τs和残余区的土体强度τ0.1~0，研究过渡区内使得双曲线模型应用效果最佳的饱和度水平区间，如图 5和表 4所示。从中可以看出，S0.55组的ARE平均值与All组最为接近，其平均误差为5.9%，最大误差为9.8%，具有最优的拟合效果，说明S0.55组的预测值与实测值最为接近。在过渡区建议选择饱和度水平在0.7~0.4的土体强度。
表 4 过渡区内不同试验数据组合的ARE值对比分析Table 4. Comparative analysis of ARE of different test data combinations in transition zone (%)编号 组合 宽级配土 粉质黏土 高岭土 CL-SC-79 膨润土 粉土 平均误差 最大误差 All 所有数据点 3.0 3.6 5.5 5.6 5.8 5.4 4.8 5.8 S0.8 τs+τ0.9~0.7+τ0.1~0 3.6 3.6 5.7 6.8 11.1 7.6 6.4 11.1 S0.55 τs+τ0.7~0.4+τ0.1~0 3.2 3.8 7.5 5.7 9.8 5.5 5.9 9.8 S0.3 τs+τ0.4~0.2+τ0.1~0 3.9 4.6 5.6 15.7 6.0 9.5 7.6 15.7 注：S0.8代表在过渡区选取的饱和度水平为0.9~0.7，S0.55为0.7~0.4，S0.3为0.4~0.2。 综合2.1节和2.2节的分析结果，在利用双曲线模型（4）预测非饱和土的抗剪强度时，仅需要知道饱和土的强度参数及饱和度在0.7~0.4和0.1~0内各一组土体的抗剪强度，即可以确定双曲线模型的参数a和d。该方法将极大地简化试验和节约测试时间。
3. 结论
（1）在宽吸力范围内，黏性土的抗剪强度包络线通常是非线性的，随着吸力的增大，抗剪强度的增长速率逐渐变缓，在SWCC残余阶段逐渐达到稳定，吸力对非饱和黏性土抗剪强度的贡献是有限的。
（2）现有的非饱和土抗剪强度模型可分为预测型和拟合型，在预估宽吸力范围内黏性土的强度时，拟合模型的应用效果整体优于预测模型，其中双曲线模型的平均相对误差最小，具有最优的拟合精度。
（3）本文提出了双曲线模型参数的确定方法，该方法使用来自饱和土的强度参数以及过渡区和残余区各一组的抗剪强度，具有一定的普适性。
-
![]()
图 2 马德里黏质砂土的抗剪强度和模型预测
Figure 2. Shear strengths of Madrid clayey sand and model predictions
![]()
图 3 非饱和黏性土的抗剪强度模型应用效果对比
Figure 3. Comparison of application effects of shear strength models for unsaturated clayey soils
![]()
图 4 不同拟合条件下模型的预测效果对比图
Figure 4. Comparison of model prediction effects under different fitting conditions
表 1 非饱和土抗剪强度模型
Table 1 Existing models for shear strength of unsaturated soils
类型 模型名称 τus表达式 预测
模型Vanapalli预测模型(Eq.1)[5] sSr−Sre1−Sretanφ′ Oberg预测模型[6] sSrtanφ′ Khalili预测模型[7] s(ssa)−0.55tanφ′ Tekinsoy预测模型[8] (sa+Pat)ln[s+PatPat]tanφ′ 拟合
模型Abramento拟合模型[9] αsβ Vanapalli拟合模型(Eq.2)[5] sSκrtanφ′ Shen拟合模型[3] s1+dstanφ′ Miao拟合模型[10] as1+1−aPats Jiang拟合模型[11] sa+dstanφ′ Alonso拟合模型[12] s{Sr−Srm1−Srm+1ηln[1+exp(−ηSr−Srm1−Srm)]}tanφ′ 注：Sr为饱和度，Sre为残余饱和度，sa为进气值，Pat为大气压（101.3 kPa），α，β，κ，a，d，Srm，η为拟合参数。 
下载: 导出CSV
表 2 非饱和强度模型应用于6种黏性土强度数据后的平均相对误差ARE对比分析
Table 2 Comparative analysis of ARE of unsaturated strength models (%)
类型 学者 黏质砂土 灰黏土 红粉土 西安黄土 马兰Q3黄土 粉砂 平均误差 最大误差 预测
模型Vanapalli 1.9 56.5 17.8 7299.5 252.7 77.6 1284.3 7299.5 Oberg 17.7 126.1 41.5 1095.3 87.8 98.7 244.5 1095.3 Khalili 2.2 30.4 20.2 211.1 47.0 31.0 57.0 211.1 Tekinsoy 14.0 66.6 11.1 232.5 37.1 19.3 63.4 232.5 拟合
模型Abramento 2.2 8.9 6.5 14.4 10.4 16.9 9.9 16.9 Vanapalli 2.8 5.8 5.8 20.3 36.6 28.9 16.7 36.6 Shen 1.4 8.0 1.8 13.7 20.6 11.7 9.5 20.6 Miao 1.2 5.0 2.5 13.6 20.7 9.7 8.8 20.7 Jiang 1.2 5.6 1.7 7.6 12.5 9.8 6.4 12.5 Alonso 1.9 6.1 4.4 10.9 24.3 21.2 11.5 24.3
下载: 导出CSV
表 3 残余区内不同试验数据组合的ARE值对比分析
Table 3 Comparative analysis of ARE of different test data combinations in residual area (%)
编号 组合 宽级配土 粉质黏土 高岭土 CL-SC-79 膨润土 粉土 平均误差 最大误差 All 所有数据点 3.0 3.6 5.5 5.6 5.8 5.4 4.8 5.8 S0.15 τs+τ0.7~0.4+τ0.2~0.1 5.3 7.2 6.5 6.1 14.3 5.8 7.5 14.3 S0.05 τs+τ0.7~0.4+τ0.1~0 3.2 3.8 7.5 5.7 9.8 5.5 5.9 9.8 注：S0.15代表在残余区选取的饱和度水平为0.2~0.1，S0.05为0.1~0。
下载: 导出CSV
表 4 过渡区内不同试验数据组合的ARE值对比分析
Table 4 Comparative analysis of ARE of different test data combinations in transition zone (%)
编号 组合 宽级配土 粉质黏土 高岭土 CL-SC-79 膨润土 粉土 平均误差 最大误差 All 所有数据点 3.0 3.6 5.5 5.6 5.8 5.4 4.8 5.8 S0.8 τs+τ0.9~0.7+τ0.1~0 3.6 3.6 5.7 6.8 11.1 7.6 6.4 11.1 S0.55 τs+τ0.7~0.4+τ0.1~0 3.2 3.8 7.5 5.7 9.8 5.5 5.9 9.8 S0.3 τs+τ0.4~0.2+τ0.1~0 3.9 4.6 5.6 15.7 6.0 9.5 7.6 15.7 注：S0.8代表在过渡区选取的饱和度水平为0.9~0.7，S0.55为0.7~0.4，S0.3为0.4~0.2。
下载: 导出CSV
-
[1] SHENG D C, ZHOU A N, FREDLUND D G. Shear strength criteria for unsaturated soils[J]. Geotechnical and Geological Engineering, 2011, 29(2): 145–159. doi: 10.1007/s10706-009-9276-x
[2] GAO Y, SUN D A, ZHOU A N, et al. Predicting shear strength of unsaturated soils over wide suction range[J]. International Journal of Geomechanics, 2020, 20(2): 04019175. doi: 10.1061/(ASCE)GM.1943-5622.0001555
[3] 沈珠江. 非饱和土力学的回顾与展望[J]. 水利水电科技进展, 1996, 16(1): 1–5, 20. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD199601000.htm SHEN Zhu-jiang. Review and prospect of unsaturated soil mechanics[J]. Advances in Science and Technology of Water Resources, 1996, 16(1): 1–5, 20. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD199601000.htm
[4] ZHOU A N, HUANG R Q, SHENG D C. Capillary water retention curve and shear strength of unsaturated soils[J]. Canadian Geotechnical Journal, 2016, 53(6): 974–987. doi: 10.1139/cgj-2015-0322
[5] VANAPALLI S K, FREDLUND D G, PUFAHL D E, et al. Model for the prediction of shear strength with respect to soil suction[J]. Canadian Geotechnical Journal, 1996, 33(3): 379–392. doi: 10.1139/t96-060
[6] OBERG A L, SALLFORS G. Determination of shear strength parameters of unsaturated silts and sands based on the water retention curve[J]. Geotechnical Testing Journal, 1997, 20(1): 40–48. doi: 10.1520/GTJ11419J
[7] KHALILI N, KHABBAZ M H. A unique relationship for χ for the determination of the shear strength of unsaturated soils[J]. Géotechnique, 1998, 48(5): 681–687. doi: 10.1680/geot.1998.48.5.681
[8] TEKINSOY M A, KAYADELEN C, KESKIN M S, et al. An equation for predicting shear strength envelope with respect to matric suction[J]. Computers and Geotechnics, 2004, 31(7): 589–593. doi: 10.1016/j.compgeo.2004.08.001
[9] ABRAMENTO M, CARVALHO C S. Geotechnical parameters for the study of natural slopes instabilization at Sierra do Mar-Brazilian Southeast[C]// Proceedings of the 12th International Conference on Soil Mechanics and Foundation Engineering, Rio de Janeiro, 1989: 1599–1602.
[10] MIAO L C, LIU S Y, LAI Y M. Research of soil–water characteristics and shear strength features of Nanyang expansive soil[J]. Engineering Geology, 2002, 65(4): 261–267. doi: 10.1016/S0013-7952(01)00136-3
[11] JIANG M J, LEROUEIL S, KONRAD J M. Insight into shear strength functions of unsaturated granulates by DEM analyses[J]. Computers and Geotechnics, 2004, 31(6): 473–489. doi: 10.1016/j.compgeo.2004.07.001
[12] ALONSO E E, PINYOL N M, GENS A. Compacted soil behaviour: initial state, structure and constitutive modelling[J]. Géotechnique, 2013, 63(6): 463–478. doi: 10.1680/geot.11.P.134
[13] ESCARIO V, SÁEZ J. The shear strength of partly saturated soils[J]. Géotechnique, 1986, 36(3): 453–456. doi: 10.1680/geot.1986.36.3.453
[14] NG C W W, SADEGHI H, JAFARZADEH F. Compression and shear strength characteristics of compacted loess at high suctions[J]. Canadian Geotechnical Journal, 2017, 54(5): 690–699. doi: 10.1139/cgj-2016-0347
[15] 孙德安, 徐钱垒, 陈波, 等. 广吸力范围内非饱和原状黄土的力学特性[J]. 岩土工程学报, 2020, 42(9): 1586–1592. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202009005.htm SUN De-an, XU Qian-lei, CHEN Bo, et al. Mechanical behavior of unsaturated intact loess over a wide suction range[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(9): 1586–1592. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202009005.htm
[16] PATIL U D, PUPPALA A J, HOYOS L R, et al. Modeling critical-state shear strength behavior of compacted silty sand via suction-controlled triaxial testing[J]. Engineering Geology, 2017, 231: 21–33. doi: 10.1016/j.enggeo.2017.10.011
[17] 张禄乾. 细粒含量和饱和度对非饱和土剪切特性影响的试验研究[D]. 北京: 北京交通大学, 2020. ZHANG Lu-qian. Experimental Study on the Influence of Fine Grain Content and Saturation on Shear Characteristics of Unsaturated Soils[D]. Beijing: Beijing Jiaotong University, 2020. (in Chinese)
[18] 王逍萌. 干燥过程中非饱和土强度变化特征试验研究[D]. 北京: 北京交通大学, 2018. WANG Xiao-meng. Experimental Study on Characteristics of Strength Changes of Unsaturated Soil During Drying[D]. Beijing: Beijing Jiaotong University, 2018. (in Chinese)
[19] ZHANG J R, NIU G, LI X C, et al. Hydro-mechanical behavior of expansive soils with different dry densities over a wide suction range[J]. Acta Geotechnica, 2020, 15(1): 265–278. doi: 10.1007/s11440-019-00874-y
[20] THU T M, RAHARDJO H, LEONG E C. Effects of hysteresis on shear strength envelopes from constant water content and consolidated drained triaxial tests[C]// Proceedings of the Fourth International Conference on Unsaturated Soils. Arizona, 2006: 1212–1222.
计量
- 文章访问数: 178
- HTML全文浏览量: 34
- PDF下载量: 35
