超前排气下杭州湾底水浅层气藏的气水界面运移特性

郭江涛; 王勇; 贾鹏飞; 来向华; 孔令伟

doi:10.11779/CJGE2022S1020

超前排气下杭州湾底水浅层气藏的气水界面运移特性 English Version

郭江涛^{1, 2,},
王勇^1, ,,
贾鹏飞³,
来向华⁴,
孔令伟¹

1.
中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室, 湖北武汉 430071
2.
陕西核工业工程勘察院有限公司, 陕西西安 710054
3.
西北大学地质学系大陆动力学国家重点实验室, 陕西西安 710069
4.
自然资源部第二海洋研究所, 浙江杭州 310012

基金项目:

国家自然科学基金项目 51979269

国家自然科学基金项目 52127815

详细信息

作者简介:
郭江涛(1996—)，男，硕士研究生，主要从事浅层气地质与工程危害防治方面的研究工作。E-mail：guo163jt@163.com

通讯作者:
王勇, E-mail: wang831yong@163.com

中图分类号: TU44
计量
- 文章访问数: 106
- HTML全文浏览量: 23
- PDF下载量: 14
出版历程
- 收稿日期: 2022-09-22
- 网络出版日期: 2023-02-06
- 刊出日期: 2022-11-30

Gas-water interface migration characteristics of shallow gas reservoirs in Hangzhou Bay during advanced exhaust

1.
State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics, Chinese Academy of Science, Wuhan 430071
2.
Shaanxi Nuclear Industry Engineering Survey Institute Co., Ltd., Xi'an, 710054
3.
State Key Laboratory of Continental Dynamics, Department of Geology, Northwestern University, Xi'an, 710069
4.
Second Institute of Oceanography, Ministry of Natural Resources, Hangzhou 310012

摘要

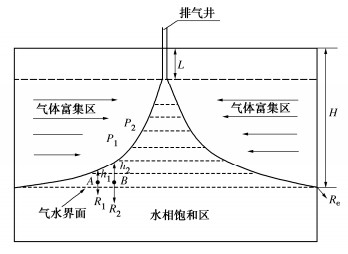
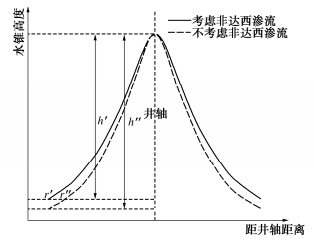
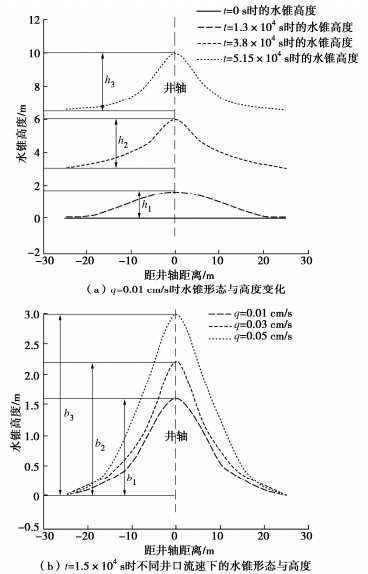
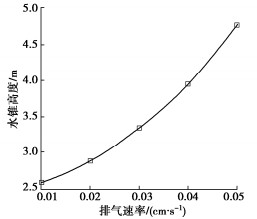
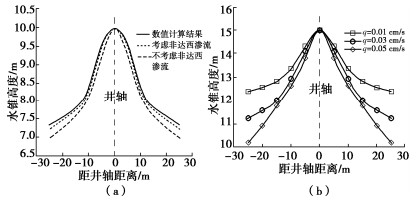
摘要: 探讨气体释放引起的气藏内部气水界面运移规律，对于工程超前排气井的布置和高效排气有重要意义。基于弹性水驱气藏渗流规律，结合两相流原理，对杭州湾底水浅层气藏的单井有控排气过程进行数值模拟分析，重点探讨排气过程中气藏内气水界面的“水锥”形成、形态和高度的演化规律。研究表明：有控排气过程中气藏内出现不同程度的水锥现象；井口流速是影响气水界面运移的最显著因素，与水锥波及面宽度呈负相关，与水锥高度呈正相关；井口流速越大，水锥形态越尖锐；反之，则越平缓；相同排气时间内，水锥波及面积越大，排气效果越好；水锥高度越高，越早发生“淹井”。实际工程中，工期允许条件下应控制较小的井口流速，避免过早淹井，达到高效排气目的。
- 浅层气 /
- 排气井 /
- 水气运移 /
- 水锥 /
- 两相流
Abstract: It is of great significance to study the water-gas interface migration in gas reservoirs caused by gas release for advanced exhaust wells. Based on the theory of elastic water drive gas reservoirs, a theoretical model describing the variation of gas-water interface in reservoirs is derived. The controlling gas exhaust of the reservoirs in Hangzhou Bay is simulated, and the evolution laws of water-coning formation, shape and height in the reservoirs under different wellhead velocities are emphatically discussed. The results show that different degrees of water coning occur in the process of the exhaust, and the water coning directly affects the efficiency of the exhaust wells. The wellhead velocity is the most significant factor affecting the shape and height of the water-coning, and it is negatively correlated with the water coning sweep area and positively correlated with the water-coning height. The larger the wellhead velocity, the sharper the shape of water coning. The smaller the wellhead velocity, the gentler the water coning shape. During the same exhaust time, the larger the water-coning sweep area, the better the exhaust effects. The higher the water-coning height, the faster the exhaust well flooded. In practice, a low wellhead flow-rate should be controlled to avoid premature well flooding so as to achieve the purpose of effective exhaust.
- shallow gas /
- gas well /
- water-gas migration /
- water coning /
- two-phase flow

HTML全文

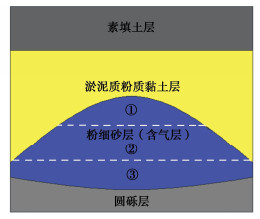
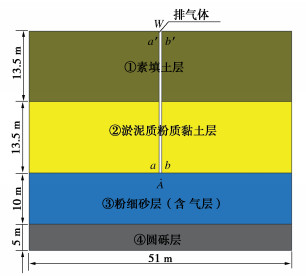
0. 引言

近年来，随着城市综合立体交通网的不断完善，地上地下多维联动的新格局逐步形成，地铁与市政桥桩的邻近建设工程变得愈发常见^[1]。新建桥桩跨越或紧邻地铁隧道施工，可能会对隧道的安全和稳定性带来不利影响。目前，全套管灌注桩具有无孔壁坍塌、断桩和缩径风险，施工扰动小等优点，已广泛应用于邻近地铁隧道的桩基工程中^[2-3]。然而，工程实践表明全套管灌注桩施工尤其是钢套管下放过程仍会引起地铁隧道变形^[4-5]，若变形过大，将引发管片裂损、渗漏水等问题，加剧地铁全寿命周期的工程风险，带来巨大的经济损失与社会影响。因此，桥桩施工对邻近既有地铁隧道的影响问题亟需引起高度重视。

国内外学者针对该问题开展了相关研究，如丁智等^[6]通过现场监测发现桥桩施工尤其工后沉降引起的隧道变形较大，且间距越近，造成的沉降漏斗半径越大。徐云福等^[7]基于实测数据，发现试桩施工引起隧道管片水平和竖向位增加，其中多数管片沉降，部分管片上浮。Yoo^[8]针对不同桥梁施工情况开展三维数值研究，提出桩–隧不同临界位置时隧道的变形与内力情况。路平等^[9]提出桥桩施工及运营荷载引起隧道整体性沉降，隧道截面发生逆时针扭曲变形和近桩侧拱腰方向被“压扁”而垂直方向被“拉长”的收敛变形。Lueprasert等^[10]根据不同地质条件和桩–隧位置下隧道水平和竖向变形的关系，初步提出新建桩基与既有隧道相邻的施工影响区。同时，引入一种隧道变形的评估方法，得到隧道断面椭圆化的规律^[11]。不难看出，现有研究大多以隧道水平或竖向变形作为评估施工影响的指标，而鲜少涉及隧道管片的内力、收敛变形等与隧道病害密切相关的横向性能。因此，为了合理评估隧道结构的健康状态和长期服役性能，有必要对隧道结构的横向受力与变形特征进行深入研究。

关于管片横向性能分析，主要有基于荷载–结构法提出的惯用法、修正惯用法、多铰环法、梁–弹簧模型法与梁–接头模型法等^[12-13]，并逐步发展为壳–弹簧模型、壳–接头模型等三维计算模型^[14-15]。此外，模型试验作为研究手段之一，可直观反映围压变化引起的隧道结构情况^[16]。值得一提的是，尽管隧道结构的横向性能特别是变形问题近些年已有研究^[17-18]，但涉及的工程多为运营荷载或近接堆卸载等工况，较少关注桥桩施工的动态过程影响，分析结果也不够全面。

基于此，本文以杭州软黏土地区某桥桩邻近地铁隧道建设工程为背景，根据桥桩施工附加应力的计算结果，提出考虑既有隧道刚度的附加围压计算公式。同时，建立管片三维有限元模型，从隧道附加围压的分布特征出发，探究桥桩钢套管施工动态过程中隧道管片横向变形与力学性能的变化规律，以期进一步明确隧道结构在桥桩施工影响下的安全状态。

1. 桥桩钢套管施工引起的地铁隧道附加围压计算

1.1 计算模型建立

根据丁智等^[19]的研究，采用全套管全回转工法的桥桩施工扰动主要来源于钢套管的施工过程。桥桩钢套管施工引起地铁隧道附加应力的因素主要包括桩端压力p、桩侧径向压力q和桩侧垂向摩阻力f。

本文以桥桩桩顶的圆周中心作为坐标原点建立坐标系，计算模型如图 1所示（考虑本文分析的重点为桥桩施工对既有地铁隧道的影响，因此绘制计算模型时适当放大了桥桩相对隧道的比例）。桥桩垂直于xoy平面，沿z轴正向施工，地铁隧道沿y轴纵向分布。桥桩的直径为d，钢套管的厚度为t，r_s=d/2+t，钢套管的长度为H；地铁隧道的半径为R，隧顶的埋深为H_t，轴线埋深为H_t0；桩—隧的相对净距为L，轴线净距为L₀。

图 1 计算模型示意图

Figure 1. Schematic diagram of computational model

下载: 全尺寸图片幻灯片

1.2 附加力计算

钢套管施工各附加力的简化计算参照丁智等^[19]的研究成果。

（1）根据黄大维等^[20]和张超等^[21]的研究，桩端压力计算依据施工工艺和土柱剪切破坏高度判断分为两种情况。

a）钢套管内土塞螺旋向上滑动

$p=\frac{K_1}{K_2}\left(\mathrm{e}^{\frac{K_2}{A} z_0}-1\right)+p_1 \mathrm{e}^{\frac{K_2}{A} z_0},$

(1)

$K_1=\frac{1}{\sqrt{n^2+1}} \frac{E t}{d_{\mathrm{s}}} \tan \varphi_{\mathrm{a}} U+\frac{1}{\sqrt{n^2+1}} c_{\mathrm{a}} U+\gamma A,$

(2)

$K_2=\frac{1}{\sqrt{n^2+1}} \frac{\mu}{1-\mu} \tan \varphi_{\mathrm{a}} U。$

(3)

b）钢套管内土塞竖直向上滑动

$p=\frac{K_1^{\prime}}{K_2^{\prime}}\left(\mathrm{e}^{\frac{K_2^{\prime}}{A} z_0}-1\right)+p_1 \mathrm{e}^{\frac{K_2^{\prime}}{A} z_0},$

(4)

$K_1^{\prime}=\frac{E t}{d_{\mathrm{s}}} \tan \varphi_{\mathrm{a}} U+c_{\mathrm{a}} U+\gamma A,$

(5)

$K_2^{\prime}=\frac{\mu}{1-\mu} \tan \varphi_{\mathrm{a}} U。$

(6)

式中， E为土体的弹性模量（MPa），d_s为桥桩直径与钢套管厚度之和（m），d_s=d+t，n为钢套管内壁与土塞的相对切向速度与竖向速度之比，一般取值为1，A为土塞的截面面积（m²），μ为土体的泊松比， ${c_{\text{a}}}$ 为土塞与钢套管内壁的黏聚力（kN/m²）， ${\varphi _{\text{a}}}$ 为土塞与钢套管内壁的摩擦角(°)，U为钢套管内壁的周长（m）， $\gamma$ 为土体的重度（kN/m³），z₀为土塞最底层土体的高度（m），p₁为土塞最底层土体的顶部应力（kN/m²）。

进一步，结合钢套管分节施工的特点，引入土塞高度折减系数 $\zeta$ ，建立土塞高度 ${z_{\text{s}}}$ 与钢套管分节施工高度 ${z_{\text{t}}}$ 之间的关系 ${z_{\text{s}}} = {z_{\text{t}}} \cdot \zeta$ ，并依据土塞单层或多层土体的分布特征，由土塞高度 ${z_{\text{s}}}$ 计算土塞最底层土体的高度 ${z_{\text{0}}}$ ，代入即得桩端压力的修正计算公式。

（2）考虑钢套管入土深度范围内挤土效应的强弱影响，分4区段（近空载段、软化段、稳定段和土塞段）对桩侧径向压力和桩侧垂向摩阻力进行修正，如图 2所示，修正计算公式为

图 2 钢套管施工附加力分布示意图

Figure 2. Distribution of additional force under construction of steel casing

下载: 全尺寸图片幻灯片

$q=\int_{H_1}^{H_2} \beta_i K_{0_i} \gamma_i \mathrm{~d} h+\int_{H_2}^{H_3} K_{0_i} \gamma_i \mathrm{~d} h+\int_{H_3}^{H_4} \eta_i K_{0_i} \gamma_i \mathrm{~d} h,$

(7)

$\begin{aligned} f= & \int_{H_1}^{H_2} \beta_i K_{0_i} \gamma_i \tan \delta_i \mathrm{~d} h+\int_{H_2}^{H_3} K_{0_i} \gamma_i \tan \delta_i \mathrm{~d} h+ \\ & \int_{H_3}^{H_4} \eta_i K_{0_i} \gamma_i \tan \delta_i \mathrm{~d} h, \end{aligned}$

(8)

式中，K₀为土体的静止侧压力系数， ${K_0} = \mu /(1 - \mu )$ ，h为土体的深度(m)， $\delta$ 为钢套管与土体的外摩擦角(°)， ${\beta _i}$ 为H₂段的软化系数， ${\eta _i}$ 为H₄段的强化系数，下标i为不同土体中各项参数不同取值的标识。

上述各参数取值及计算细节详见文献[19]，本文便不再赘述。

1.3 附加围压计算

（1）桥桩钢套管施工引起的附加应力计算

根据Mindlin解，一沿x，y或z轴正向的单位力作用于半无限空间体中(x₁, y₁, z₁)处，引起任一点(x, y, z)沿z轴方向和沿x轴方向的附加应力可由Mindlin应力解积分计算得到^[22]。

根据式（1）~（8）和Mindlin应力解，桩端压力p、桩侧径向压力q和桩侧垂向摩阻力f引起隧道某一点处的竖向附加应力计算公式分别为

$\sigma_{z-p}=\int_0^{r_{\mathrm{s}}} \int_0^{2 \pi} p r \cdot \sigma_{z z}(x, y, z, r \cos \theta, r \sin \theta, H) \mathrm{d} r \mathrm{d} \theta,$

(9)

$\sigma_{z-q_x}=\int_0^H \int_0^{2 \pi} q \cos \theta \cdot r_{\mathrm{s}} \cdot \sigma_{x z}\left(x, y, z, r_{\mathrm{s}} \cos \theta, r_{\mathrm{s}} \sin \theta, h\right) \mathrm{d} h \mathrm{d} \theta,$

(10)

$\sigma_{z-q_y}=\int_0^H \int_0^{2 \pi} q \sin \theta \cdot r_{\mathrm{s}} \cdot \sigma_{y z}\left(x, y, z, r_{\mathrm{s}} \cos \theta, r_{\mathrm{s}} \sin \theta, h\right) \mathrm{d} h \mathrm{d} \theta,$

(11)

$\sigma_{z-f}=\int_0^H \int_0^{2 \pi} f r_{\mathrm{s}} \cdot \sigma_{z z}\left(x, y, z, r_{\mathrm{s}} \cos \theta, r_{\mathrm{s}} \sin \theta, h\right) \mathrm{d} h \mathrm{d} \theta,$

(12)

式中， ${\sigma _{jk}}$ 为基于Mindlin应力解的附加应力表达式，其中下标j为单位力沿j轴正向的方向，k为单位力引起附加应力沿k轴正向的方向，r为桥桩圆周范围内任一微元体的半径，θ为桥桩圆周范围内任一微元体自x轴正向向y轴正向旋转的角度。

同理，水平向附加应力计算公式分别为

$\sigma_{x-p}=\int_0^{r_{\mathrm{s}}} \int_0^{2 \pi} p r \cdot \sigma_{z x}(x, y, z, r \cos \theta, r \sin \theta, H) \mathrm{d} r \mathrm{d} \theta,$

(13)

$\sigma_{x-q_x}=\int_0^H \int_0^{2 \pi} q \cos \theta \cdot r_{\mathrm{s}} \cdot \sigma_{x x}\left(x, y, z, r_{\mathrm{s}} \cos \theta, r_{\mathrm{s}} \sin \theta, h\right) \mathrm{d} h \mathrm{d} \theta,$

(14)

$\sigma_{x-q_y}=\int_0^H \int_0^{2 \pi} q \sin \theta \cdot r_{\mathrm{s}} \cdot \sigma_{y x}\left(x, y, z, r_{\mathrm{s}} \cos \theta, r_{\mathrm{s}} \sin \theta, h\right) \mathrm{d} h \mathrm{d} \theta,$

(15)

$\sigma_{x-f}=\int_0^H \int_0^{2 \pi} f r_{\mathrm{s}} \cdot \sigma_{z x}\left(x, y, z, r_{\mathrm{s}} \cos \theta, r_{\mathrm{s}} \sin \theta, h\right) \mathrm{d} h \mathrm{d} \theta 。$

(16)

综上，桥桩钢套管施工引起隧道某一点处的总竖向附加应力和总水平向附加应力计算公式分别为

${\sigma _z} = {\sigma _{z - p}} + {\sigma _{z - {q_x}}} + {\sigma _{z - {q_y}}} + {\sigma _{z - f}}\text{，}$

(17)

${\sigma _x} = {\sigma _{x - p}} + {\sigma _{x - {q_x}}} + {\sigma _{x - {q_y}}} + {\sigma _{x - f}}。$

(18)

（2）考虑隧道存在影响的附加围压计算

上述基于Mindlin解计算的附加应力是在不考虑既有隧道存在，假定土体为各向同性、均质连续的半无限空间弹性体基础上得到的结果。显然，这忽视了既有隧道刚度对附加应力场的影响。近年来，许多学者开始关注既有隧道存在引起的遮拦效应^[23]，发现其与桩基的遮拦效应有一定的相似性。廖少明等^[24]提出盾构穿越时由于既有隧道刚度远大于周围土体，将隧道视作弹性地基梁，可对下方土压力起到承担、分散的作用。通过假定隧道控制位移δ，可得到弹性地基梁作用下既有隧道底部附加应力的计算公式为

$\Delta \sigma_y=\frac{\delta B E}{2 \pi\left(1-\mu^2\right)}\left[\frac{1}{x^2-(B / 2)^2}\right],$

(19)

式中，B为隧道纵向影响区的长度，δ为假定的隧道控制位移。

同理，本文研究桥桩施工引起的隧道附加围压时，也要考虑侧方土体变形时既有隧道刚度的发挥作用，对围压进行修正。参照廖少明等^[24]的研究，假定桥桩施工引起的附加荷载分布于管片环向，其中远桩侧的水平向附加荷载予以折减，并基于弹性力学理论推导出隧道近桩侧承担的水平向附加应力，如图 3所示。

图 3 既有隧道承担水平向附加应力示意图

Figure 3. Horizontal additional stress borne by existing tunnel

下载: 全尺寸图片幻灯片

首先，将既有隧道的局部变形看作是刚体变形，则有边界条件：

$\left.\begin{array}{lll} x^{\prime}=0, & \left|y^{\prime}\right| \geqslant B / 2, & h=0, \\ x^{\prime}=0, & \left|y^{\prime}\right|<B / 2, & h=-\delta_{\circ} \end{array}\right\}$

(20)

其次，满足上述边界条件的傅里叶积分为

$x^{\prime}=0, \quad h\left(y^{\prime}\right)=\frac{2 \delta}{\pi} \int_0^{\infty} \frac{\sin \xi(B / 2)}{\xi} \cos \xi y^{\prime} \mathrm{d} \xi 。$

(21)

若假设应力函数为

$\mathit{\Phi}=\int_0^{\infty} \frac{1}{\xi^2}\left(C+D \xi x^{\prime}\right) \mathrm{e}^{-\xi x^{\prime}} \cos \xi y^{\prime} \mathrm{d} \xi 。$

(22)

则侧方土体变形引起的水平向附加应力为

$\begin{aligned} \sigma_{x^{\prime}}= & \frac{\delta E_{\mathrm{r}}}{2 \pi\left(1-\mu^2\right)}\left\{\frac{y^{\prime}+B / 2}{\left(y^{\prime}+B / 2\right)^2+x^{\prime 2}}-\frac{y^{\prime}-B / 2}{\left(y^{\prime}-B / 2\right)^2+x^{\prime 2}}+\right. \\ & \left.\frac{2\left(y^{\prime}+B / 2\right) x^{\prime 2}}{\left[\left(y^{\prime}+B / 2\right)^2+x^{\prime 2}\right]^2}-\frac{2\left(y^{\prime}-B / 2\right) x^{\prime 2}}{\left[\left(y^{\prime}-B / 2\right)^2+x^{\prime 2}\right]^2}\right\} 。 \end{aligned}$

(23)

进一步，取隧道近桩侧边缘点x=0，得到既有隧道近桩侧承担的水平向附加应力为

$\sigma_{x^{\prime}}=\frac{\delta B E_{\mathrm{r}}}{2 \pi\left(1-\mu^2\right)}\left[\frac{1}{y^{\prime 2}-(B / 2)^2}\right]。$

(24)

式（24）根据丁智等^[19]的研究，隧道变形的纵向区主要分布在±40 m左右，故B=80 m；E_r为隧道侧向土体的弹性模量，考虑注浆加固作用，E_r=20 MPa；μ为隧道侧向土体的泊松比；δ为假定的隧道控制位移，以水平位移1.0 mm为参考。

以隧道断面上近桩侧一点为例，定义荷载折减系数K为既有隧道近桩侧承担的水平向附加应力和所受的水平向附加应力之比与常数1的差值，那么远桩侧的水平向附加应力可通过荷载折减系数K予以折减。

$K=1-\left|\frac{\sigma_{x^{\prime}}}{\sigma_x}\right| 。$

(25)

因此，隧道管片各方向的附加荷载分布可由下式计算：

$\left.\begin{array}{l} P_z^{\prime}(\varpi)=\sigma_z^{\prime}(\varpi) & & \left(0 \leqslant \varpi<\frac{\pi}{2}, \frac{3 \pi}{2} \leqslant \varpi <2 \pi\right) \\ P_x^{\prime \prime}(\varpi)=K \cdot \sigma_x^{\prime \prime}(\varpi) & & (0 \leqslant \varpi<\pi) \\ P_x^{\prime}(\varpi)=\sigma_x^{\prime}(\varpi) & & (\pi \leqslant \varpi<2 \pi) \\ P_z^{\prime \prime}(\varpi)=\sigma_z^{\prime \prime}(\varpi) & & \left(\frac{\pi}{2} \leqslant \varpi<\frac{3 \pi}{2}\right) \end{array}\right\} \text ,$

(26)

式中， $\varpi$ 为隧道管片上任一点的角度(rad)，以拱顶为0，顺时针方向角度增大。

综上，根据隧道管片各方向的附加荷载分布，可得到隧道管片环向的附加围压计算公式为（以径向内围压为正）

$P_{\mathrm{r}}(\varpi)= \begin{cases}P_z^{\prime}(\varpi) \cos \varpi+P_x^{\prime \prime}(\varpi) \sin \varpi & \left(0 \leqslant \varpi<\frac{\pi}{2}\right) \\ -P_z^{\prime \prime}(\varpi) \cos \varpi+P_x^{\prime \prime}(\varpi) \sin \varpi & \left(\frac{\pi}{2} \leqslant \varpi<\pi\right) \\ -P_z^{\prime \prime}(\varpi) \cos \varpi-P_x^{\prime}(\varpi) \sin \varpi & \left(\pi \leqslant \varpi<\frac{3 \pi}{2}\right) \\ P_z^{\prime}(\varpi) \cos \varpi-P_x^{\prime}(\varpi) \sin \varpi & \left(\frac{3 \pi}{2} \leqslant \varpi<2 \pi\right)\end{cases}。$

(27)

2. 隧道管片有限元模型

2.1 模型概况

盾构隧道管片结构是由多环分片式管片和纵横向螺栓连接构成的预制装配式混凝土结构。以杭州地铁为例，整环管片结构采用3+2+1的分块方式错缝拼接，包括1块封顶块，圆心角为20°，2块邻接块，圆心角为68.75°，3块标准块，圆心角为67.5°。管片外直径6.2 m，内直径5.5 m，厚度0.35 m，幅宽1.2 m，典型结构如图 4（a）所示。管片混凝土等级C50，抗渗等级P10，钢筋等级HPB235、HRB335。环向管片间采用12个M30螺栓连接，纵向管片环间采用16个M30螺栓连接。

图 4 隧道管片结构

Figure 4. Structure of tunnel segment

下载: 全尺寸图片幻灯片

管片结构模型采用ANSYS有限元软件中的壳—弹簧模型，相比于传统的梁—弹簧模型更真实反映隧道管片及接头的空间力学性态，而且相比于三维实体模型建模更简单、计算量更小、通用性更好。管片采用三维壳单元（shell181壳单元）模拟，管片环向、纵向接头采用转动弹簧单元（combine39弹簧单元）模拟^[14]，示意如图 4（b）所示。环向、纵向接头弹簧单元分别沿管片的纵缝、环缝布置在对应节点对上，各组节点对之间允许有较小间隙。参考黄大维等^[25]和徐国文等^[26]的研究，考虑软土盾构隧道错缝拼装的特点，管片接头抗弯刚度取100 MN·m/rad。图 5为管片模型的网格划分图。

图 5 管片模型网格划分图

Figure 5. Meshing diagram of segment model

下载: 全尺寸图片幻灯片

2.2 材料参数

盾构隧道管片结构一般由钢筋混凝土材料制作，为了简化模型，本文仅考虑混凝土材料的特性。考虑材料的非线性特征，采用Hongnestad本构模型^[27]，上升段为二次曲线，下降段为斜直线。为了便于稳定计算，本文将下降段修正为平直段进行简化考虑。因此，混凝土材料的应力–应变关系为

$\sigma= \begin{cases}f_{\mathrm{c}}\left[2 \frac{\varepsilon}{\varepsilon_0}-\left(\frac{\varepsilon}{\varepsilon_0}\right)^2\right] & \left(\varepsilon \leqslant \varepsilon_0\right) \\ f_{\mathrm{c}} & \left(\varepsilon_0 \leqslant \varepsilon \leqslant \varepsilon_{\mathrm{u}}\right)\end{cases},$

(28)

式中， ${f_{\text{c}}}$ 为峰值压应力， ${\varepsilon _0}$ =0.002为峰值压应力对应的压应变， ${\varepsilon _{\text{u}}}$ =0.003为极限压应变。

混凝土材料的计算参数可根据混凝土结构设计规范等资料得到，C50混凝土主要物理力学参数：重度=25.0 kN/m³，泊松比=0.20，单轴抗压强度=23.10 MPa，单轴抗拉强度=1.89 MPa，初始切线模量=2.1945×10⁴ MPa。

2.3 接触边界

盾构隧道管片结构作为一种埋置于地层中的结构，其与周围土体之间的作用采用双向地层接触弹簧（combin39弹簧单元）模拟，并沿管片整环布置。土体抗力与地层位移之间呈线性变化关系，且该比例因子定义为土体抗力系数k，取值一般为0~10.0 MN/m³。结合本工程地质条件和取值建议^[28]，土体抗力系数k取5.0 MN/m³。此外，为了防止由于模型单元、施加荷载、边界条件等非完全对称而发生异常的刚体转动，隧道管片模型的纵向方向（z方向）施加了约束。

3. 工程案例分析

3.1 工程概况

风情大道改建工程作为杭州南北向主通道之一，是杭州“四纵五横”快速路网的重要组成部分。由于部分高架桥桩距离地铁区间隧道较近，项目在正式施工前进行了试成桩，选取对应地铁隧道左线（下行线）里程桩号K1+343.7—K1+373.7作为试桩位置。试桩与隧道的平面和剖面位置关系如图 6，7所示，工程地质参数如表 1所示。

表 1 地层参数表

Table 1. Parameters of rock and soil layers

编号	地层名称	层厚/m	重度γ/(kN·m^-3)	压缩模量E_s/MPa	黏聚力c/kPa	内摩擦角φ/(°)	泊松比μ	地基承载力/kPa
①	杂填土	2.8	(18.0)	(3.00)	(5.0)	(8.0)	0.23	—
①₁	粉质黏土	4.7	19.2	5.10	22.0	15.2	0.26	90~100
②	淤泥质黏土	9.8	17.4	2.27	13.1	8.7	0.38	60
③₁	淤泥质粉质黏土	9.4	17.6	2.80	15.8	10.2	0.33	70
⑤₂	粉质黏土	9.8	18.5	3.88	25.1	14.2	0.26	90
⑥₁	粉砂	4.8	19.7	11.18	4.6	27.7	0.20	180
⑨₁	圆砾	15.0	(20.0)	(10.00)	(5.0)	(30.0)	0.18	400
⑤₃	含砂粉质黏土	4.2	20.0	5.98	29.4	20.7	0.21	190
⑨₁	圆砾	1.9	(20.0)	(10.00)	(5.0)	(30.0)	0.18	400
⑩_2b	强风化砂岩	1.6	20.1	4.96	(25.0)	(15.0)	0.29	400
⑩_3b	中等风化砂岩	10.0	(22.0)	(40.00)	(5.0)	(35.0)	0.15	1000~1200
注：（）内为经验值。

下载: 导出CSV

| 显示表格

图 6 试桩与隧道平面位置关系

Figure 6. Plane position relationship between test pile and tunnel

下载: 全尺寸图片幻灯片

图 7 试桩与隧道剖面位置关系

Figure 7. Profile position relationship between test pile and tunnel

下载: 全尺寸图片幻灯片

本工程既有隧道轴线埋深为19.37 m，半径为3.1 m。以试桩-1为例，其桩基直径为1.5 m，桩长约70.0 m，套管厚度30.0 mm，采用全长套管全回转钻机旋挖成孔工艺（套管不拔除），里程号为K1+371，与地铁隧道水平净距最近为5.0 m，桩—隧轴线净距为8.88 m。主要计算参数取值：钢套管分节高度=8.0 m，土塞高度折减系数 $\zeta$ =0.6，软化系数 ${\beta _i}$ =0.66，强化系数 ${\eta _i}$ =1.02，四区段取值H₁=0.10H，H₂=0.30H，H₃=0.50H，H₄=0.10H。

3.2 模型验证

为了验证本文方法的可靠性，基于上述工程案例和附加围压公式，计算隧道纵向y=0处的管片环向附加围压，并将附加围压施加到隧道管片三维数值模型上，开展桥桩施工过程中隧道管片的横向性能分析。

图 8为桥桩钢套管施工至70.0 m时隧道管片的水平与竖向变形云图（放大系数2000）。此时，管片产生了较大的远离桥桩方向的偏移与沉降，隧道拱顶和拱底分别达到最小绝对水平位移0.041 mm和最大绝对水平位移0.464 mm，左拱腰下侧达到最大竖向位移1.612 mm，右拱腰达到最小竖向位移0.922 mm，断面出现“竖鸭蛋”式变形。从数值上看，计算得到的隧道水平和竖向位移最大值与实测的最大水平位移0.5 mm和最大竖向位移1.6 mm相近。

图 8 施工深度70 m时隧道变形云图

Figure 8. Deformation cloud map of tunnel at construction depth of 70 m

下载: 全尺寸图片幻灯片

图 9为桥桩钢套管施工至70.0 m时隧道断面相对变形的结果对比曲线（放大系数10³）。对比发现，本文计算得到的隧道断面变形规律与实测基本吻合，而且从实测值4个点可以看出两者数值也相差无几。此外，从图 10桥桩钢套管施工过程中隧道管片水平收敛对比曲线（收敛值以伸长为正，缩短为负，下同）可以看出，管片收敛的数值与实测变化趋势基本一致，都是先水平伸长而后缩短，数值也较为接近，仅在隧道底部附近出现波动差异。可能原因在于该阶段实测数据的统计节点间隔较大，收集数据无法及时反映阶段性的施工影响，造成了变化的差异性。

图 9 施工深度70 m时隧道断面相对变形图

Figure 9. Relative deformations of tunnel section at construction depth of 70 m

下载: 全尺寸图片幻灯片

图 10 套管施工过程中隧道管片水平收敛的实测对比曲线

Figure 10. Comparison between measured and calculated curves of horizontal convergence of tunnel segments during casing construction

下载: 全尺寸图片幻灯片

总体而言，通过上述各方面比较，本文方法得到的计算结果与实测中隧道管片的横向变形特征相近，可有效为施工风险评价和安全防控提供理论支持。

4. 桥桩钢套管施工全过程下隧道管片的横向性能分析

4.1 横向变形

为了厘清桥桩钢套管施工过程中管片横向变形的动态趋势，笔者统计了施工不同深度下隧道管片的整体变形情况，绘制曲线如图 11所示（放大系数10³）。

图 11 隧道管片整体变形曲线

Figure 11. Curves of overall deformation of tunnel segment

下载: 全尺寸图片幻灯片

由图 11可知，随着施工深度的增加，管片先发生小幅度左移后发生倾斜右移，管片整体沉降且表现为竖椭圆变形，这与翁效林等^[29]的离心机模型试验结果类似。当施工深度高于隧道顶部，端部压力和桩侧摩阻力主要引起隧道沉降，而桩侧压力引起隧道上方土体侧移继而影响隧道左移。当套管施工至隧道正侧面深度时，桩侧压力主要引起隧道右移。随着施工深度继续增加，桩身底部范围的桩侧压力影响甚微，管片发生不均匀侧移，加之桩侧摩阻力引起的管片沉降，管片整体最终表现为竖椭圆变形。

图 12为桥桩钢套管施工过程中隧道管片收敛位移曲线。可知，隧道水平与竖向收敛变化规律相似，数值相反，表明隧道椭圆化变形步调一致。当套管施工至距隧道轴线埋深上方0.5D范围时，管片水平和竖向收敛达到极值，此时隧道横椭圆变形明显。而随着施工深度继续增加，收敛值逐渐趋近于0，椭圆化变形有所缓解。水平与竖向收敛均在套管施工至隧道轴线埋深附近时达到零点，笔者认为该节点是隧道由横椭圆向竖椭圆转变的临界点。至此以后，隧道水平收敛急剧减小，竖向收敛急剧增大，并于隧道轴线埋深下方0.75D范围达到极值，隧道竖椭圆变形显现，又于隧道轴线埋深下方1.25D附近稍有回落，随后趋于平缓。可见，桥桩钢套管施工至隧道埋深附近时，扰动影响最为剧烈，结构变形速率也较快，是隧道横向变形发展的不易控制阶段，现场施工尤要引起重视。

图 12 套管施工过程中隧道管片收敛位移曲线

Figure 12. Curves of convergence of tunnel segment during casing construction

下载: 全尺寸图片幻灯片

4.2 横向内力

图 13分别显示了桥桩钢套管施工过程中隧道管片横断面的轴力、弯矩和剪力。内力的方向规定如下：①轴力的正值和负值分别表示拉伸和压缩；②若弯矩引起管片的外边缘受拉，内边缘受压，则视为正，否则视为负；③若剪力引起管片顺时针旋转则视为正，否则视为负。

图 13 套管施工过程中隧道管片横断面内力图

Figure 13. Internal forces of tunnel segment section during casing construction

下载: 全尺寸图片幻灯片

由图 13（a）可知，轴力曲线环向多为负值，表明管片长期受压，且随着施工深度增加，轴力出现了绝对值先增大后减小的趋势。笔者推断，管片轴力的非对称性变化与隧道的椭圆化变形程有关，隧道断面接近圆形时环向轴力受压，而发生斜椭圆变形时各分块管片间产生了环间张开，轴力由压向拉转变。另外，管片左拱腰处轴力变化较敏感，结合图 8变形可知，管片左拱腰下侧作为变形的最大值点，轴力也最大。

比较图 13（b），图 13（c）可以发现，弯矩与剪力的曲线类似，表现出一致的规律性和非对称性变化特征。桥桩钢套管施工过程中，隧道拱腰由外侧受拉、内侧受压的正弯矩向内侧受拉、外侧受压的负弯矩变化，拱顶拱底由内侧受拉、外侧受压的负弯矩向由外侧受拉、内侧受压的正弯矩变化。因此，弯矩曲线表现为拱腰两侧逐渐缩进，拱顶拱底逐渐外扩的特征。最终，隧道拱顶最大正弯矩为+3.896 kN·m/m，拱底最大正弯矩为+3.947 kN·m/m，左拱腰最大负弯矩为-5.477 kN·m/m，右拱腰最大负弯矩为-3.165 kN·m/m。

此外，弯矩零点出现在环向55°，155°，238°，325°处，对应于剪力的最值位置。这些位置大多位于隧道管片相邻块的拼接处附近，因此接缝处受剪力较大，更易发生张开错台、渗漏水等病害^[30]。最终，管片最大正剪力分别为+1.573，+3.813 kN/m，最大负剪力分别为-3.021，-2.788 kN/m。

4.3 旋转变形

图 8变形云图显示了桥桩施工至70.0 m时隧道整体的偏转情况。可见，桥桩邻近地铁隧道施工不仅会引起隧道横向变形，还会引起隧道发生偏转变形。

为了识别隧道的旋转行为，笔者参考文献[31]，提出了一种定性的评估方法（图 14）：

图 14 定义既有隧道的旋转指数^[31]

Figure 14. Rotation index of existing tunnel

下载: 全尺寸图片幻灯片

$w=\tan \alpha=\frac{u_{x 1}+u_{x 2}}{D},$

(29)

$w^{\prime}=\tan \alpha^{\prime}=\frac{u_{y 1}+u_{y 2}}{D},$

(30)

式中，w， $w'$ 分别为横向与竖向旋转指数， $\alpha$ ， $\alpha '$ 分别为隧道横向与竖向旋转角度，u_x1，u_x2分别为隧道拱顶和拱底的水平位移（m），u_y1，u_y2分别为隧道右侧拱腰和左侧拱腰的竖向位移（m），D为隧道的直径（m）。

根据式（29），（30）计算，图 15显示了桥桩钢套管施工过程中隧道管片的横向与竖向旋转指数分布情况（其中，以隧道顺时针旋转时旋转指数为正，逆时针旋转时旋转指数为负）。

图 15 桥桩钢套管施工过程中隧道管片旋转指数分布

Figure 15. Distribution of rotation index of tunnel segment during casing construction

下载: 全尺寸图片幻灯片

由图 15可知，隧道管片整体经历了从顺时针旋转到逆时针旋转的转变，其临界点位于隧道轴线埋深下方0.85D范围。施工高于临界点时，随着深度的增加，管片旋转指数先增大后减小，最大值位于隧道轴线埋深附近。这是因为本文评估方法是以隧道轴线为界划分的，一旦施工深度超过隧道轴线埋深，管片力学状态重新调整，轴线以下部分受侧向力作用产生了抵抗顺时针旋转的力矩。当施工深度继续增加至超过临界点时，轴线以下部分的力矩进一步增大使得管片发生逆向旋转，且旋转指数逐渐变大。显然，对于桥桩邻近既有地铁隧道施工的工况，隧道管片不仅发生弯矩和剪切的横向变形，而且发生整体移动和旋转变形，这与路平等^[9]的研究结论较为一致。

值得注意的是，较大的偏转行为极易引起管片接缝的张开错位，甚至造成纵向不均匀偏转及局部扭转变形，严重威胁地铁的行车与运营安全。当前研究者在隧道的横向变形与受力方面做了较多有意义的工作，却极少关注侧向桥桩施工引起的管片偏转行为。因此，笔者希望借由本文对隧道管片旋转变形行为的讨论，提醒工程和研究人员不仅要注意隧道的横向性能，还要注意隧道局部的偏转与扭转变形。

5. 结论

本文基于壳—弹簧模型建立管片三维数值模型，针对桥桩钢套管施工过程引起的隧道附加围压分布，探究管片结构整体与收敛变形、内力以及旋转变形等横向性能的变化规律，得到3点结论。

（1）随着桥桩钢套管施工深度的增加，隧道先发生小幅度左移后发生倾斜右移，隧道整体产生沉降及“竖椭圆”变形。隧道水平与竖向收敛变化规律相似，数值相反，均在套管施工至隧道轴线埋深附近时达到零点。该节点认为是隧道由“横椭圆”向“竖椭圆”转变的临界点，随后进入隧道横向变形急剧发展的不易控制阶段，现场施工尤要引起重视。

（2）隧道管片弯矩曲线表现为拱腰两侧逐渐缩进，拱顶拱底逐渐外扩的非对称性变化特征，剪力图类似。弯矩零点对应剪力的最值位置，大多位于管片相邻块的拼接处附近，故接缝处受剪力较大更易发生张开错台、渗漏水等病害。

（3）根据一种识别隧道旋转行为的评估方法，发现桥桩钢套管施工过程中隧道管片经历了从顺时针旋转到逆时针旋转的转变，其临界点位于隧道轴线埋深下方0.85D范围。隧道管片局部较大的偏转与扭转变形应予以关注。

图 1 杭州湾底水浅层气藏的赋存示意图

Figure 1. Schematic of shallow gas reservoirs in bottom water of Hangzhou Bay

下载: 全尺寸图片幻灯片

图 2 气井打开理论模型(改自谢林峰等^[9])

Figure 2. Theoretical model for gas well opening (Adapted from Xie et al^[9])

下载: 全尺寸图片幻灯片

图 3 气水界面理论形态

Figure 3. Theoretical form of gas-water interface

下载: 全尺寸图片幻灯片

图 4 排气井数值模型

Figure 4. Model of an exhaust shaft for numerical analysis

下载: 全尺寸图片幻灯片

图 5 气体排放过程中水锥形态及高度的变化曲线

Figure 5. Distribution of water-coning shape and height during gas emission

下载: 全尺寸图片幻灯片

图 6 井口流速与水锥高度关系

Figure 6. Relationship between wellhead velocity and water-coning height

下载: 全尺寸图片幻灯片

图 7 淹井时的水锥形态曲线

Figure 7. Distribution of water-coning curve at flooding time

下载: 全尺寸图片幻灯片

参考文献(16)

[1]	丁国生, 田信义. 中国浅层天然气资源及开发前景[J]. 石油与天然气地质, 1996, 17(3): 226–231. doi: 10.3321/j.issn:0253-9985.1996.03.011 DING Guo-sheng, TIAN Xin-yi. China's shallow gas resources and exploration prospects[J]. Oil & Gas Geology, 1996, 17(3): 226–231. (in Chinese) doi: 10.3321/j.issn:0253-9985.1996.03.011
[2]	郭爱国, 孔令伟, 沈林冲, 等. 地铁建设中浅层气危害防治对策研究[J]. 岩土力学, 2013, 34(3): 769–775. doi: 10.16285/j.rsm.2013.03.022 GUO Ai-guo, KONG Ling-wei, SHEN Lin-chong, et al. Study of disaster countermeasures of shallow gas in metro construction[J]. Rock and Soil Mechanics, 2013, 34(3): 769–775. (in Chinese) doi: 10.16285/j.rsm.2013.03.022
[3]	王晓冬. 渗流力学基础[M]. 北京: 石油工业出版社, 2006. WANG Xiao-dong. Foundation of Seepage Mechanics[M]. Beijing: Petroleum Industry Press, 2006. (in Chinese)
[4]	葛家理. 现代油藏渗流力学原理[M]. 北京: 石油工业出版社, 2003. GE Jia-li. The Modern Mechanics of Fluids Flow in Oil Reservoir[M]. Beijing: Petroleum Industry Press, 2003. (in Chinese)
[5]	王勇, 孔令伟, 郭爱国, 等. 气体释放速率对浅层气藏中气水运移的影响[J]. 浙江大学学报(工学版), 2010, 44(10): 1883–1889. doi: 10.3785/j.issn.1008-973X.2010.10.007 WANG Yong, KONG Ling-wei, GUO Ai-guo et al. Effects of gas release rate on gas-water migration in shallow gas reservoir[J]. Journal of Zhejiang University (Engineering Science), 2010, 44(10): 1883–1889. (in Chinese) doi: 10.3785/j.issn.1008-973X.2010.10.007
[6]	王会强, 李晓平, 杨琪, 等. 底水气藏见水时间预测方法[J]. 新疆石油地质, 2007, 28(1): 92–93. https://www.cnki.com.cn/Article/CJFDTOTAL-XJSD200701025.htm WANG Hui-qiang, LI Xiao-ping, YANG Qi et al. A prediction of water breakthrough time in gas reservoirs with bottom water[J]. Xinjiang Petroleum Geology, 2007, 28(1): 92–93. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XJSD200701025.htm
[7]	SOBOCINSKI D P, CORNELIUS A J. A correlation for predicting water coning time[J]. Journal of Petroleum Technology, 1965, 17(5): 594–600. doi: 10.2118/894-PA
[8]	徐耀东. 底水气藏气井见水时间预测方法[J]. 内蒙古石油化工, 2012, 38(2): 149–151. https://www.cnki.com.cn/Article/CJFDTOTAL-NMSH201202065.htm XU Yao-dong. Prediction of water coning time for gas well in bottom-water gas reservoir[J]. Inner Mongolia Petrochemical Industry, 2012, 38(2): 149–151. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-NMSH201202065.htm
[9]	谢林峰, 李相方. 底水气藏水锥高度与形状计算新方法[J]. 天然气工业, 2004, 24(4): 54–56, 8. doi: 10.3321/j.issn:1000-0976.2004.04.019 XIE Lin-feng, LI Xiang-fang. New calculating method of highness and shape of water cone for gas pool driven by bottom water[J]. Natural Gas Industry, 2004, 24(4): 54–56, 8. (in Chinese) doi: 10.3321/j.issn:1000-0976.2004.04.019
[10]	陈军, 刘太雷. 底水气藏气井水锥动态模拟及见水时间预测[J]. 大庆石油地质与开发, 2019, 38(1): 84–88. https://www.cnki.com.cn/Article/CJFDTOTAL-DQSK201901012.htm CHEN Jun, LIU Tai-lei. Modeling of the water coning dynamics and the prediction of the water breakthrough time for the gas well in bottom-water gas reservoirs[J]. Petroleum Geology & Oilfield Development in Daqing, 2019, 38(1): 84–88. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DQSK201901012.htm
[11]	朱瑶宏, 黄燕庆, 曾洪贤, 等. 杭州湾大桥南岸工程地质特征与浅层气分布[J]. 岩土力学, 2002, 23(增刊1): 215–219. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2002S1062.htm ZHU Yao-hong, HUANG Yan-qing, ZENG Hong-xian et al. Engineering geological features and shallow gas distribution in south bank of Hangzhou bay bridge[J]. Rock and Soil Mechanics, 2002, 23(S1): 215–219. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2002S1062.htm
[12]	勇振明, 金柏范, 王旭东, 等. 杭州湾地区第四系超浅层气的开发及营销[J]. 天然气工业, 1997, 17(3): 36–38. https://www.cnki.com.cn/Article/CJFDTOTAL-TRQG703.008.htm YONG Zhen-ming, JIN Bai-fan, WANG Xu-dong et al. The development and management of quaternary extrashallow gas reservoirs in Hangzhou bay[J]. Natural Gas Industry, 1997, 17(3): 36–38. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TRQG703.008.htm
[13]	WANG Y, KONG L W, WANG Y L, et al. Deformation analysis of shallow gas-bearing ground from controlled gas release in Hangzhou Bay of China[J]. International Journal of Geomechanics, 2018, 18(1): 04017122-1-13.
[14]	孔令伟, 郭爱国, 陈守义, 等. 浅层天然气井喷对地层的损伤影响与桩基工程危害分析[J]. 防灾减灾工程学报, 2004, 24(4): 375–381. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK200404004.htm KONG Ling-wei, GUO Ai-guo, CHEN Shou-yi et al. Influence of shallow natural gas blowout on stratum damage and hazard analysis of pile foundation[J]. Journal of Disaster Prevention and Mitigation Engineering, 2004, 24(4): 375–381. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK200404004.htm
[15]	杨筱璧, 李祖友, 鲁敏蘅, 等. 高速非达西流气井产能方程的新形式[J]. 特种油气藏, 2008, 15(5): 74–75, 83, 109. https://www.cnki.com.cn/Article/CJFDTOTAL-TZCZ200805021.htm YANG Xiao-bi, LI Zu-you, LU Min-heng et al. New deliver ability equation for gas wells with high velocity Non-Darcy flow[J]. Special Oil & Gas Reservoirs, 2008, 15(5): 74–75, 83, 109. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TZCZ200805021.htm
[16]	郭爱国, 沈林冲, 张金荣, 等. 浅层气对杭州地铁施工的影响模式分析[J]. 铁道工程学报, 2010, 27(9): 78–81. https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201009017.htm GUO Ai-guo, SHEN Lin-chong, ZHANG Jin-rong, et al. Analysis of influence mode of shallow gas on construction of Hangzhou metro[J]. Journal of Railway Engineering Society, 2010, 27(9): 78–81. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201009017.htm