0.   引言

一维固结试验中测试试样底部超静孔隙水压力（本文简称孔压）可用于判断主固结完成和分析固结性状等^[1-2]。已有研究发现，荷载施加于试样顶部后，底部孔压随固结时间先增长至峰值，然后才开始消散，称为“时间滞后”现象^[3-5]。

早在20世纪五六十年代，一些研究者探讨了测压管式孔压计的测量系统刚度对孔压时间滞后的影响，发现测量系统刚度不足是引起孔压滞后的一个不可或缺的原因^{[4, 6]}。之后，Robinson^[1]通过系列测试试样底部孔压的一维固结试验发现，相同孔压传感器的条件下，孔压滞后时间随试样渗透系数增加而减小。Simoeni^[7]通过隔膜式孔压计进行的三轴不固结不排水系列试验发现，孔压在约6 min的短暂响应时间内便增长至荷载增量水平。因此，孔压滞后不能完全归结于孔压测量系统刚度，孔压时间滞后机理与主要影响因素尚不明确。

为探讨一维固结试验中饱和黏性土试样底部孔压性状与时间滞后主要影响因素，本文基于已有的理论分析方法，对比了不同测试系统刚度对孔压测量的影响，发现一维固结试验孔压滞后主要归结于施加荷载时试样顶部的排水固结，进而探讨了固结过程中试样渗透性、压缩性对孔压滞后的影响规律。

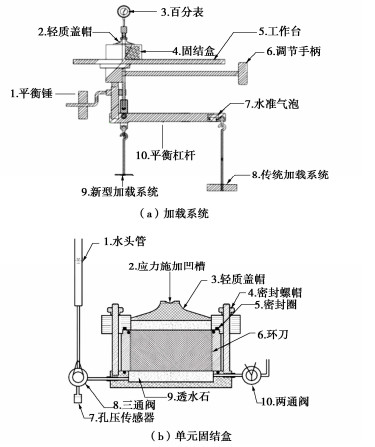
1.   孔压滞后性状

本研究开展了17组重塑土固结试验，连同Zeng等^[8]用于探讨固结过程体积应变随固结时间的变化规律的13组数据，分析孔压滞后性状，如表 1所示。重塑土的液限（w_L）分布范围为37%~100%，初始含水率（w₀）为0.8 w_L~1.8 w_L。表 1的一维固结试验数据均采用低应力起始固结仪获得，固结过程测量试样底部孔压。该固结仪含有两个加载系统，通过位于试样中心点的加载系统施加0.5~12.5 kPa的固结压力，应力水平达到12.5 kPa之后，利用传统的杠杆加载系统，施加25~1600 kPa的固结压力。试样高度4 cm，直径6.18 cm，底部两端分别连接三通阀和两通阀，其中两通阀控制排水，三通阀连接试样底部、孔压传感器和水头管，通过控制三通阀开关，实现对孔压传感器和透水石中的气泡排除以及对试样底部孔压的测量。仪器示意图见图 1所示。更多仪器细节和试验方法参考Hong等^[9]和Zeng等^[10]。

表  1  重塑土试样的基本物理指标

Table  1.  Basic physical properties of reconstituted clays

土样	相对质量密度 Gs	液限 wL/%	塑限 wP/%	初始含水率 w0/%	试验 组数	数据来源
南京土	2.71	37.0	21.0	38.3~68.6	3	本研究
蚌埠土A	2.71	42.0	22.0	43.4~75.3	3
蚌埠土B	2.69	48.0	24.0	50.8~71.7	2
蚌埠土C	2.71	57.0	30.0	54.6~103.3	3
连云港土	2.72	63.0	31.0	65.4~114.3	3
五河土	2.75	56.3	28.0	45.3~93.3	3
Huaian clay A	2.70	100.1	38.8	80.6~179.6	6	Zeng等[8]
Huaian clay B	2.70	70.8	33.5	85.0~114.2	3
Lianyungang clay	2.70	55.6	28.8	44.5~88.8	4

下载: 导出CSV 

| 显示表格

图  1  低应力起始固结仪示意图^[9]

Figure  1.  Schematic diagram of modified oedometer^[9]

下载: 全尺寸图片 幻灯片

为了清晰探讨孔压性状，本文仅采用有效应力水平（${\sigma '_{\text{v}}}$）大于重塑屈服压力（${\sigma '_{{\text{yr}}}}$）的底部超静孔压（${u_{\text{b}}}$）随固结时间（t）变化的测试数据。根据Hong等^[9]所建议的重塑屈服压力经验关系式：${\sigma '_{{\text{yr}}}} =$$5.66/$ ${({e_0}/{e_{\text{L}}})^2}$，采用初始孔隙比（e₀）和液限孔隙比（e_L）进行计算。本文分析所使用的数据均为正常固结状态下饱和黏性土的一维固结试验数据。

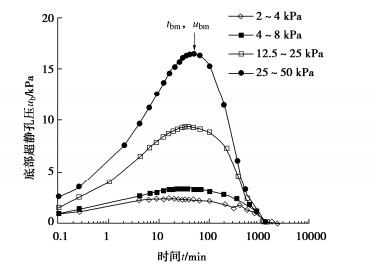
孔压的“时间滞后”现象在饱和黏性土的一维固结试验中十分常见。图 2显示了给定液限和初始状态下（w_L=57%，w₀=103.3%）的典型底部超静孔压随固结时间变化曲线（${u_{\text{b}}}$-t）随荷载的变化，瞬时加载后孔压随固结时间先增长至峰值（${u_{{\text{bm}}}}$），然后才开始消散。孔压“时间滞后”性状通常以孔压测量值出现峰值的时间（${t_{{\text{bm}}}}$），作为评价孔压时滞性状的参数^{[1, 7]}。从图 2可见，随荷载水平增加，${t_{{\text{bm}}}}$增长。

图  2  不同荷载等级下底部超静孔压随固结时间的变化曲线

Figure  2.  Variation of excess pore water pressure with time under different loading increments

下载: 全尺寸图片 幻灯片

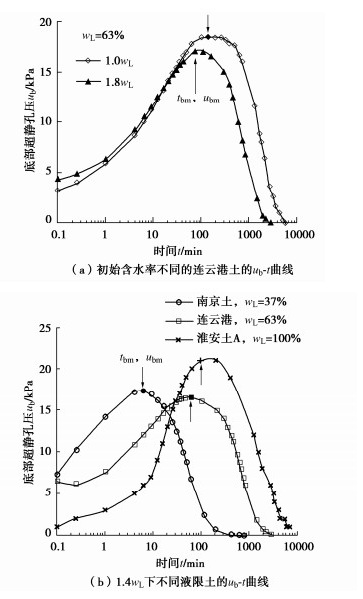
图 3显示相同荷载等级（25~50 kPa）下典型土的u_b-t变化曲线。对于液限w_L相同的土，试样的初始含水率越高，孔压滞后时间t_bm越短；对于相同初始含水率的试样，液限w_L越低，孔压滞后时间t_bm越短。

图  3  相同荷载等级下典型底部超静孔压与时间的变化关系

Figure  3.  Typical variation of excess pore water pressure with time under same loading level

下载: 全尺寸图片 幻灯片

上述试验结果说明具有不同液限的不同种类土、不同初始含水率与应力水平均对孔压滞后性状有显著影响。

2.   孔压测量系统刚度影响分析

目前常用的孔压计有测压管式和隔膜式两大类^[11]。测压管式孔压计通过水头的高低来反映孔压的大小，由于水体在压力作用下需要一定的时间在土体和测压管间完成补偿过程，在实际应用中表现出明显的时间滞后现象^[6]。隔膜式孔压计通过作用在承压膜上的水压直接进行测量，只需要很少的水便可以将孔压传递到感应膜片上^[12]，若膜片刚度不足，在压力下产生变形，使得孔压计腔体体积改变，则需要土体中的水进行补偿，也会引起测量孔压时间滞后的现象^[3-5]。上述解释将孔压滞后归因于孔压计存在平衡时间，平衡时间取决于孔压测量系统在压力作用下发生体积变化的灵敏程度，即孔压测量系统刚度。

Gibson^[4]针对三轴不排水固结的情况，提出了考虑测量系统刚度影响的孔压滞后时间理论解。实际上，试样在不排水条件下受压时，若孔压测量系统刚度不足导致测量系统腔体（液体压力传递空间）发生体积变化，则试样底部（与孔压计相连）将允许土中水排出，此时边界条件改变。根据水流连续性原理，单位时间内的腔体体积改变量与试样底部排水边界排出的流量相同，即$\lambda \frac{{{\text{d}}\sigma }}{{{\text{d}}t}} = A\frac{{{k_{\text{v}}}}}{{{\gamma _{\text{w}}}}}{\left( {\frac{{\partial u}}{{\partial x}}} \right)_{x = 0}}$，可以得到试样底部边界条件，${k_{\text{v}}}\frac{{\partial u}}{{\partial x}} - \frac{{\lambda {\gamma _{\text{w}}}}}{A}\frac{{{\text{d}}\sigma }}{{{\text{d}}t}} = 0;x = 0, t > 0$，其中，$\sigma$为孔压计测得压力，u为试样中孔压，$\lambda$为单位压力下测量系统腔体的体积改变量，A为试样的横截面积，k_v为试样的渗透系数，${\gamma _{\text{w}}}$为水的重度。

基于太沙基一维固结理论解析解，Gibson^[4]考虑由测量系统刚度不足所导致的体积改变对边界条件的影响，提出了分析试样在三轴不固结不排水情况下底部孔压增长的滞后时间的理论解答：

式中：E为t时刻测得的滞后孔压与荷载增量的比值，代表孔压测量系统腔体达到平衡所需要补偿的比值，下文简称孔压平衡比；$\sigma (0)$为加载前测试系统的初始孔压；$\sigma (\infty )$为加载后测量系统腔体达到平衡后的最终孔压；$\sigma (t)$为腔体平衡过程中测试系统在t时刻的孔压；$T = \frac{{{C_{\text{v}}}t}}{{{H^2}}}$，为时间因数，C_v为试样的固结系数，H为试样高度；${\alpha _n}\cot {\alpha _n} = - \eta$，当传感器刚度为无穷大时，${\alpha _n} = n{ {\rm{ \mathsf{ π} }}}$；$\eta = \frac{{{m_{\text{v}}}AH}}{\lambda }$，称为刚度比，物理意义是单位压力下试样的体积变形量与测试系统的体积变形量之比^[4]，m_v为土骨架的体积压缩系数。本研究采用该理论解对考虑“时间滞后”影响的孔压变化规律进行计算分析。

对于不同类型孔压计，单位压力下体积改变量λ的计算方法如下：对于测压管式孔压计，在已知测压管截面积A_e的条件下，$\lambda = {A_{\text{e}}}/{\gamma _{\text{w}}}$；对于隔膜式孔压计，赵慈义等^[13]基于弹性理论，考虑系统刚度不足时弹性膜片在流体压力作用下产生挠曲变形，腔体体积相应增加，给出膜片刚度因数α的计算方法，其物理意义与$\lambda$一致：

式中：a为膜片的半径；$D = \frac{{E{\delta ^3}}}{{12(1 - {\mu ^2})}}$，为膜片的弯曲刚度；δ，E，μ分别为膜片的厚度、杨氏模量、泊松比。

根据定义分别计算测压管式和隔膜式孔压计的刚度比η。测压管的内径一般大于2 mm，此处取2 mm计算测压管截面积A_e，λ为3.14 cm³/MPa；本文试验所使用的隔膜式孔压计的感应膜片材料为316 L不锈钢，相关参数取值为a=0.25 cm，δ=0.5 mm，μ=0.3，E=200 GPa，故刚度因数α约为1.746×10^-6 cm³/MPa。根据《工程地质手册》^[14]，黏性土的体积压缩系数m_v范围大致在1/16~1 MPa^-1。假定试样高度为4 cm，直径6.18 cm，计算可得测压管式孔压计的η大致范围为2~40；隔膜式孔压计的η大致范围为4.30×10⁶~6.87×10⁷。

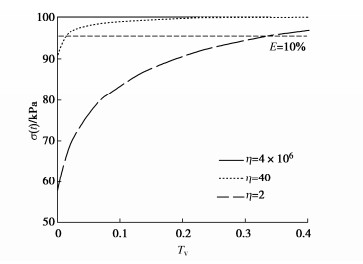
分别取η=2，40，4×10⁶，代入式（1）计算分析三轴不固结不排水情况下测试系统刚度对孔压滞后时间的影响。α_n采用逐次逼近法获得，由于级数收敛较快，求和时令n=4已足够精确，所得数组的值见表 2。

表  2  不同η值对应的α_n值

Table  2.  Corresponding values of α_n at different values of η

η	2	40	4×106
α1	2.2889	3.0651	3.1416
α2	5.0870	6.1311	6.2823
α3	8.0962	9.1987	9.4248
α4	11.1727	12.2688	12.5664

下载: 导出CSV 

| 显示表格

采用表 2中数据计算荷载等级50~100 kPa时测量系统中孔压$\sigma (t)$随时间因数T_v的变化，结果绘制于图 4。实线对应隔膜式孔压的最小刚度比，点线、虚线分别为测压管式孔压计对应刚度比的最大值和最小值。可以看到，不同刚度比对孔压滞后时间的影响显著：在测压管式孔压计的刚度比范围内，孔压平衡比E达到10%时时间因数的差异高至3倍以上；随刚度比增加，孔压滞后越来越短，隔膜式孔压计对应刚度比的孔压几乎在加载瞬间增长至上覆荷载水平。

图  4  不同刚度比下三轴不固结不排水试验的孔压计算结果

Figure  4.  Results of calculated pore pressure in triaxial unconsolidated and undrained tests with different stiffness ratios

下载: 全尺寸图片 幻灯片

上述计算结果说明，隔膜式孔压计刚度足够大，不排水条件下孔压测量值在加压瞬间完成增长；测压管式孔压计刚度不足，孔压测量值需要一定响应时间增长至最大值。由于Gibson理论解是不排水条件下考虑边界条件受测试系统刚度影响时的孔压增长滞后时间，即孔压计腔体体积达到平衡、孔压数值上升到稳定值所需要的响应时间，故认为由孔压计系统刚度不足引起的孔压时间滞后是仪器带来的系统误差。基于上述分析可知，相较测压管式孔压计，隔膜式孔压计受测试系统刚度的影响可以忽略不计。

3.   一维固结底部孔压时间滞后机理分析

以上理论分析结果表明，采用三轴仪进行固结试验时，施加荷载前可以通过关闭上下排水阀实现试样不排水，隔膜式孔压计测试系统刚度足够大，孔压测试值出现“时间滞后”的现象不明显。Simeoni^[7]通过三轴固结试验验证了这一结论，试验结果显示不排水条件下，远离加载端的孔压响应时间很短，一般在几分钟内，稍稍滞后的原因可以归结于孔压在试样内部传递需要时间。已有结果表明处于封闭状态的饱和土体，孔压在短暂响应时间内便能增长至上覆荷载水平^[15-16]。也就是采用三轴仪进行固结试验，测量的孔压随时间的变化能够反映真实的孔压性状。

一维固结试验目前还是土体固结试验的主要手段之一。采用一维固结仪进行固结试验，无法实现施加荷载前试样上下边界均处于不排水状态。试验底部可以关闭排水阀，连通隔膜式孔压传感器，测量试样底部孔压，实现底部不排水条件。但是，试样顶部一直处于自由排水边界面状态，施加荷载的同时，试样顶部就开始固结。也就是在试样顶部施加荷载后，产生的孔压在向试样底部传递的过程中，部分孔压通过试样顶部边界消散，越靠近试样顶部，孔压消散的时间越短。

施加荷载时一维固结试验、三轴固结试验边界条件的不同，和已有的一维固结、三轴固结孔压时间滞后性状不同的试验结果，说明施加荷载时试样顶部边界的不同是导致一维固结和三轴固结孔压时间滞后性状不同的不可或缺的原因。采用一维固结仪开展固结试验时，顶部施加荷载后，部分孔压从顶部边界消散，改变了试样内部传递孔压的水力梯度，影响孔压传递的时间，诱发试样内部超静孔压分布不均匀。采用三轴固结仪开展固结试验时，顶部施加荷载后，孔压不会从顶部边界消散，施加荷载引起的水力梯度向下传递，在很短的时间内均匀地分布于试样，孔压达到施加荷载水平后，打开顶部排水阀门，孔压开始消散。

根据太沙基一维固结理论，施加荷载的同时，试样的孔压达到荷载水平的峰值，然后随着固结时间而逐渐消散减小，也就是孔压随固结时间单调降低，固结过程试样的孔压呈现从排水面到不排水面逐渐增大的分布性状，直至孔压消散完成。因此，一维固结过程中，试样底部的孔压在理论上应该随固结时间单调减小，与试验实测的试样底部的孔压时间滞后性状相悖。

一维固结试验中发现的试样底部孔压时间滞后性状是由固结试验设备的条件制约导致的，时间滞后过程的试样底部测点的孔压性状不能用于整个试样的固结性状分析。试样底部测点的孔压达到峰值后，孔压随固结时间单调减小，变化规律符合太沙基固结理论，理论与试验的对比分析有待于今后进一步开展。

另外应该指出，三轴固结试验与一维固结试验的另外一点不同，一维固结试验中，尽管采用硅脂/凡士林润滑以减少试样与固结环刀之间的摩擦，测试的固结性状仍或多或少受到侧面边界摩擦的影响。问延煦等^[15]通过对比不同侧壁摩阻力下一维固结试验的结果，发现侧壁摩阻力更小时，孔压峰值更高，但滞后时间没有太大变化，也就是侧壁摩阻或多或少导致部分外加荷载没有施加在试样上，但不是试样底部孔压时间滞后的主要影响因素。

4.   孔压时间滞后主要影响因素分析

根据经典太沙基固结理论，饱和黏性土的排水固结过程主要受试样的渗透性和压缩性影响^{[9-10, 17-19]}。为探讨表 1中不同试样在各级荷载下孔压滞后性状的主要影响因素，分别考虑渗透系数（k_v）、压缩指数（C_c）对孔压滞后时间（t_bm）的影响。

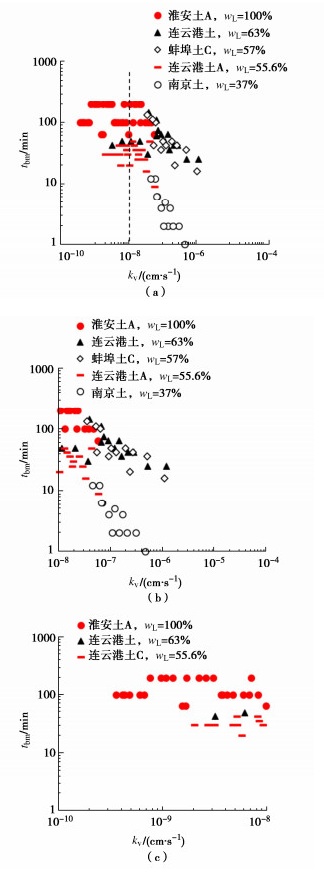
图 5显示典型孔压测量值到达峰值的时间随渗透系数的变化规律（lg t_bm-lg k_v）。由于表 1中试样未进行渗透试验，采用Zeng等^[19]提出的经验关系式（3）计算渗透系数（k_v），

图  5  典型孔压测量值到达峰值时间随渗透系数的变化规律

Figure  5.  Typical relationship between time reaching maximum pore water pressure and hydraulic coefficient

下载: 全尺寸图片 幻灯片

式中：e为施加当级荷载前的孔隙比；e_L为液限孔隙比。

整体而言，t_bm随k_v减小而增大，与Robinson^[1]所得结果一致。不同数值范围的k_v对t_bm的影响程度不同：当k_v较大时，lg t_bm-lg k_v近似线性，为近似幂函数关系，如图 5（b）所示；当k_v大致小于1×10^-8 cm/s后，虽然整体上仍表现为t_bm随k_v减小而增大，但lgt_bm- lgk_v斜率减缓，k_v对t_bm的影响程度明显变小，且数据具有一定程度的离散，如图 5（c）所示。容易发现，大部分数据的孔压滞后时间t_bm变化范围为20~200 min，但南京土（w_L=37%）的孔压滞后时间t_bm明显小于20 min，这一情况将在后文中分析说明。

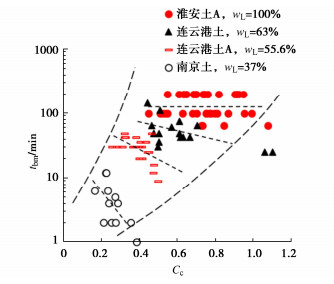
图 6显示典型孔压测量值到达峰值的时间t_bm随压缩指数C_c的变化规律。可以看到，t_bm随C_c的变化规律整体呈正相关趋势。但对于液限w_L相同的土，t_bm随C_c的减小而增大，与整体变化趋势相反，与此同时，随w_L增加，lg t_bm-C_c斜率由陡变缓。此外，C_c相近时，w_L越大，t_bm越大。这是因为w_L越大的试样渗透系数k_v越小，t_bm随C_c的变化规律受到k_v影响，说明t_bm是受到k_v和C_c共同影响。

图  6  典型孔压测量值到达峰值时间随压缩指数的变化规律

Figure  6.  Typical relationship between time reaching maximum pore water pressure and compression index

下载: 全尺寸图片 幻灯片

结合t_bm关于k_v，C_c的变化规律进行分析。对于给定液限w_L土样，t_bm随k_v，C_c减小而增大，这与t_bm关于k_v的整体规律一致，与t_bm关于C_c的整体规律相反。说明k_v对t_bm的影响程度更大，并且对t_bm关于C_c变化规律的影响不可忽视。但当k_v大致小于1×10^-8 cm/s时，lg t_bm-lg k_v斜率减缓，k_v的影响程度变小，C_c的影响程度变大。另一方面，随试样液限w_L增加，lg t_bm-C_c的斜率逐渐减缓，根据式（3），此时k_v减小，同样表明k_v对lg t_bm-C_c的影响减弱。

结合上述分析，对南京土（w_L=37%）的孔压滞后时间t_bm不超过20 min的情况进行分析说明。通过图 5，6发现，南京土不仅渗透系数k_v较大而且压缩指数C_c较小，因此施加荷载后产生的孔压能够较快传递到试样底部，且试样压缩性小、受压产生的变形小，即顶部排出的水量较小，故受试样顶部排水固结的影响较小。

需要注意的是，淮安土A的滞后时间t_bm较为离散，趋势线接近水平，可能是因为土样液限高，黏粒含量高，压缩性高、渗透性差，滞后时间长，固结压力大于50 kPa后测得的t_bm均大于100 min，但由于固结试验过程中100 min附近的记录点少、时间间隔长，导致t_bm均为100 min或200 min的固定值。

综上分析，孔压滞后时间t_bm受试样渗透性、压缩性综合影响。整体而言，t_bm受k_v的影响更显著。C_c的影响不可忽视，会影响k_v对t_bm的影响程度。关于渗透系数、压缩指数对孔压时间滞后影响的定量分析有待进一步探索。

5.   结论

（1）基于Gibson所给出的理论解答，分析了不同孔压测试系统刚度对孔压滞后时间的影响，结果表明隔膜式孔压计刚度足够大，所引起的孔压时间滞后可忽略不计。

（2）三轴固结试验在不排水条件下孔压响应时间很短，而一维固结试验在试样顶部处于排水条件下，试样底部孔压达到峰值的时间比三轴固结试验在不排水条件下的时间大得多，大多数情况下，对应于孔压峰值的固结时间为数十至数百分钟，两者的差异主要由试样顶部排水条件的不同引起。因此，一维固结试验中的试样底部孔压时间滞后主要归结于试样顶部的自由排水边界条件。

（3）底部孔压峰值滞后时间受试样渗透性、压缩性影响。滞后时间随渗透系数减小和压缩指数增大而增大。基于已有的试验数据分析发现，渗透系数的影响比压缩指数的影响更为显著。