Seismic response of subway station structures under straight-down near-fault
-
摘要: 目前在近断层场地中地下地铁车站抗震性能水平认识方面相对匮乏,鉴于此,提出了一种考虑发震断层-地下结构全过程地震响应的IBE-FEM联合求解分析方法。首先,基于运动学有限断层模型,采用间接边界元方法(IBE)求解直下型走滑断层错动作用下上覆软土沉积层场地内的地震波场,并验证了有限元法(FEM)间接求解地震波场的可行性;在此基础上,通过建立土-地下连续墙-主体结构非线性静-动力耦合的二维整体时域有限元模型,初步探究了断层-软土场地耦合效应对地铁车站抗震性能的影响规律。结果表明:在近断层区域,地铁车站结构震害具有典型的断层上盘效应和震害集中效应,更容易进入塑性变形发展阶段;在远断层区域,由于断层-场地效应耦合作用,断层下盘场地内地震波场衰减较缓,其内车站结构整体震害略大于断层上盘。本文研究方法为近断层场地条件下地下结构地震响应分析开辟新思路,也可为相关场地区域内的地下结构抗震设计提供技术参考。
-
关键词:
- 间接边界元-有限元法 /
- 全过程地震反应分析 /
- 土-地下结构动力相互作用 /
- 走滑断层 /
- 场地效应
Abstract: Given the deficiencies of knowledge on the seismic performance level of shallow-buried subway station structures in the near-fault site, the indirect boundary element method and the finite element method (IBE-FEM) integrated solution approach that considers the seismic response of the whole process of seismogenic fault-underground structures is proposed. First, based on the kinematic finite fault model, the IBE is used to solve the seismic wave field in the overlying soft soil site under the dislocation of straight-down strike-slip fault, and the feasibility of indirectly solving the seismic wave field by using the FEM is verified. On this basis, the influence laws of the fault-soft soil site coupling effects on the seismic performance of the subway station are preliminarily investigated by establishing a two-dimensional finite element model for the soil-diaphragm wall-underground structure nonlinear static dynamic coupling interaction system. The results show that in the near-fault region, the seismic damage of the subway station structures has typical hanging wall effects and concentration effects, and it's more likely to enter the stage of plastic deformation development. In the far-fault region, due to the fault-site coupling effects, the seismic wave field attenuation is slower in the footwall site, and the overall seismic damage of the station structures in the footwall is slightly larger than that in the hanging wall. This study may provide a new idea for the seismic response analysis of underground structures under near-fault site conditions, and it is of great significance for the seismic design of underground structures in the related site. -
0. 引言
当前,全球正处于地震多发期,大量震害资料表明,近断层地震是发生概率最高的一种地震类型;在中国众多重要城市区域内分布着许多大型活动断层,总长约为4915 km,时刻面临地震灾害的威胁。当近断层地震发生时,由于局部场地震源距大幅减小,大量断层破裂能量在短时间内传入其中,从而导致场地效应与断层效应耦合作用显著增强,场地内部地震波场时空分布更为复杂,造成远超震级的震害,出现典型的震害集中以及长周期速度大脉冲现象;以往关于远场地震研究所得到的规律以及相关规范可能不再适用。近年来,地震灾害情景构建已然成为地震学和地震工程领域的热门研究课题,中国发布的“十四五”国家防震减灾规划将“增强城市韧性,推进地震灾害风险情景构建技术”作为重点工作之一;因此,建立“震源破裂-地壳层传播-场地条件-地下结构”这一全过程地震响应分析方法,可进一步完善地铁地下车站结构抗震性能水平和破坏机理的相关研究,为城市规划、结构抗震以及震害预防提供技术参考,对于推进韧性城乡建设工作具有重要意义。
针对近断层地震作用下地下结构抗震响应分析这一研究课题,目前已取得大量的研究成果。Qiu等[1]采用实测近场地震动记录来研究近断层场地效应对土-车站结构相互作用系统非线性变形的影响机制;崔臻等[2]提出一种人工合成近断层场地地震波场的可行性方法,并将其作为地下洞室结构数值模型的动力输入,针对近场场地中地下洞室群的失稳破坏危险性进行深入研究;Zhao等[3]和Mei等[4]提出简化脉冲模型和速度脉冲等效模型,以揭示近断层脉冲地面运动作用下地下结构的地震响应;梁建文等[5]将断层错动量施加到隧道模型中,采用静力弹塑性分析方法研究了断层错动下盾构隧道的抗震措施。
值得注意的是,上述对于近场地下结构抗震性能的研究所采用的动力输入多为其他地区记录的地震波或者依据规范要求的反应谱人工合成地震波,又或者直接将断层上、下盘的相对错动作为数值求解的边界条件进行拟静力分析。然而在实际地震中,不同地域地震波场因其震源破裂机理、传播介质以及场地条件的不同而存在一定的差别;对于缺乏地震动记录区域内相关地下结构近场地震响应的研究,采用现有研究方法是不确切的。此外,直接将断层上、下盘相对错动作为数值模型边界条件的拟静力分析方法仅可宏观上反映出地下结构可能存在的震害,无法准确描述断层不均匀破裂的具体过程以及充分考虑断层效应与场地效应耦合作用机制。在近断层场地中,地铁车站结构周围土体变形与破坏以及土-结构动力相互作用机理更为复杂,这将决定地铁车站等地下结构的震害程度;因此,亟需建立考虑发震断层-地下结构全过程地震响应的可行性分析方法,为地下结构近场地震反应分析提供一种新思路。
鉴于此,本文基于运动学有限断层理论和土-结构非线性动力相互作用理论,提出了一种考虑震源-地下结构全过程地震响应分析的IBE-FEM联合求解分析方案,研究了断层-场地-地下结构相互作用系统耦合机制。该方案首先基于运动学有限断层模型,采用IBE方法求解直下型走滑断层错动作用下上覆软土沉积层场地内的地震波场[6];在此基础上,采用静-动力耦合分析的FEM方法间接求解断层作用下地表地震响应,并与IBE结果进行对比,验证本文所述的IBE-FEM联合求解方法的合理性;最后,采用有限元软件ABAQUS建立土-两层三跨地铁车站结构动力相互作用系统的整体分析模型,系统研究了近断层上覆软土沉积层场地中地铁车站结构的侧墙相对位移、结构加速度响应以及关键截面应力等地震反应特性,初步探究了断层-软土场地耦合效应对地铁车站抗震性能的影响机制,相关研究成果可为近场场地条件下地下车站结构抗震性能以及地震安全评估提供指导与参考,为城市生命线工程安全运营与可持续发展提供有力保障。
1. 断层-软土场地地震动求解
目前,近断层大型场地宽频地震动模拟的可靠性主要取决于断层震源模型以及所采用的计算技术,要求震源模型具备激发宽频地震波场的能力,所选用的计算技术可同时兼顾计算效率及其计算精度。综合考虑,本文基于GP14.3的混合震源[7-8]运动学有限断层模型,采用具有降维、节省计算内存、自动满无限远辐射条件、无高频数值频散等优势的IBE方法进行直下型走滑断层-上覆软土沉积层场地地震波场的模拟。下文将详细介绍混合震源运动学有限断层模型以及断层-上覆软土沉积层场地计算模型的具体参数。
1.1 震源模型
本文所采用的运动学有限断层震源模型是由Haskell在1964年首次提出[9],其表达式如下:
D(t)=D∞G(t−xl/vr)。 (1) 式中:D(t)为在t时刻、距震源点xl处断层单元的错动值;G(t−xl/vr)为震源时间函数[6],上升时间取值为1.3 s;vr为破裂速度,取值为1800 m/s。
需要注意的是,常规震源模型在反映场地地震波场高频特性方面存在一定的缺陷。因而本研究在上述震源模型的基础上,通过在空间域内引入确定性单凹凸体震源位错以及含有高频随机成分的GP14.3混合震源模型,并在时间域内引入均值为0、方差为1的高斯白噪声,记作G1(t),来近似模拟由断层成核区(震源)初始位移引起的各子断层单元的自由振动(阻尼衰减)。基于上述断层错动时空高频成分的引入,得以确保所合成宽频地震激励带宽的有效性。下文将详细介绍有限断层混合震源模型中断层错动空间不均匀分布模式。
基于姜伟等[10]关于震源参数的研究,本文假设断层两盘的平均永久相对位错Dav∞为1 m,局部震源参数及其定标律见表 1。
在确定性单凹凸体断层错动空间分布基础上,引入由Graves等[7]提出的GP14.3混合震源模型,该模型对近断层地震动宽频模拟的有效性已由巴振宁等[8]验证,本文对其进行适当简化,具体实现步骤如下:
首先,基于表 1得到的确定性凹凸体震源空间分布D(x),对其采用快速傅里叶变换来实现空间-波数域转换,得到确定性震源滑动波数谱D(k):
D(k)=∫D(x)e−ikxdx。 (2) 式中:k为沿断层倾向的波数;x为以断层面为坐标轴的局部坐标。
同时引入波数衰减满足von Karman自相关函数的A(k)和波数结合函数W(k),其中A(k)用于确定震源滑动波数谱的高波数随机成分,W(k)用于选择震源滑动波数谱中确定成分与随机成分占比:
A(k)=(1+ak2)−0.5(H+1)eiθ, (3) W(k)=[1+(k2/k2d)N]−1。 (4) 式中:H为Hust指数,取值为0.75;θ为均匀分布在[−π,π]之间的随机因子;a为与震级Mw相关的经验系数,即lg10 a=0.333Mw−0.7,其中Mw可由Dav∞推导得出[11];N为控制结合锐度,取值为1;kd为拐角波数,在波数谱中代表高、低波数的分界点,取值为kd=2/as,其中as为断层倾向长度。
在此基础上,整合整个波数域内确定性低波数谱和随机性高波数谱,利用傅里叶逆变换进行波数-空间域转换:
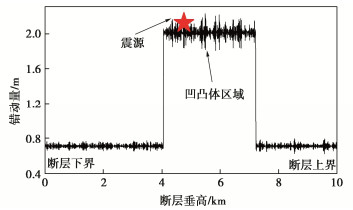
DF∞=1/((2π ))2∫[D(k)W(k)+A(k)−A(k)W(k)]e−ikxdk, (5) 由此所得到的断层错动空间分布如图 1所示。
综上所述,基于确定性凹凸体震源以及随机性GP14.3混合震源模型建模方法,本文所采用的运动学有限断层震源模型可描述为
d(t)=DF∞[G(t−xl/vr)+G1(t)]。 (6) 1.2 断层-软土场地计算模型
为缩短大型场地模型计算周期,在此假设基岩以及上覆软土沉积介质由均匀、各向同性和线弹性材料构成,且材料特性和几何结构在出平面方向上不发生变化,因而可进一步简化为二维平面计算模型;同时假设层状沉积场地、基岩、断层上盘、下盘之间的界面均能紧密结合。本文所研究的直下型断层-软土沉积层场地模型图如图 2所示。在基岩上方存在厚度为800 m的软土沉积层,其地表长度为100 km;同时,在基岩内存在垂直高度H1为10 km,断层倾角α为80°的直下型走滑断层;断层上界埋深H2为5 km,其坐标点为(0,5000)。基岩介质的密度、剪切波速、阻尼系数分别为3000 kg/m3,2400 m/s,2%,与上覆软土沉积层介质密度比、波速比、阻尼系数比分别为1.5,4,0.67。
采用IBE方法求解时,首先需要离散各接触面边界以及地表界面,基于单层位势理论,给每个离散单元施加虚拟均布荷载,并利用傅里叶变换原理将震源错动空间函数转换到波数域内,构造各边界单元虚拟均布荷载在震源错动稳定状态下的频域边界条件,求解断层-上覆软土沉积层场地边界单元的频域波源密度,进而得到在断层左旋走滑动态错动作用下的场地地震波场的频域分布;在频域求解的基础上,结合震源错动时间函数,利用傅里叶逆变换进行频-时转换,即可得到近断层区域内上覆软土沉积层场地以及基岩场地内的时域地震响应,相关计算原理参见文献[6]。
2. 断层-地铁车站结构数值分析方法
2.1 数值计算模型
本文研究的南京地区两层三跨地铁车站结构埋深为3 m,结构两侧由高30 m、厚0.8 m的地下连续墙支撑;原型车站结构的中柱沿结构纵向间隔9.12 m均匀布置,在进行二维横断面分析时,中柱刚度等效折减为0.8 m厚的墙体;土层物理力学参数、车站横断面结构特征及配筋情况等相关参数参见文献[12]。此外,为尽可能地减小侧向边界对地下结构动力反应的不利影响,综合考虑地下结构模型尺寸和计算精度,本研究中模型场地尺寸取值为200 m(宽)×80 m(埋深)[12]。
为提高整体模型计算效率,本文采用平面应变减缩积分单元(CPE4R)模拟土体和车站结构;采用梁单元(B21)模拟钢筋,其嵌入车站结构中,忽略两者间的相对滑移与分离;采用瑞雷阻尼来考虑材料的阻尼特性,其中,土体的阻尼系数取为3%,混凝土的初始阻尼系数取为2%。此外,为保障计算结果的准确性,综合考虑地震波场频谱特性以及车站结构的地基场地条件,基于Kuhlemeyer关于单元网格尺寸与剪切波长关系的研究[13],本文模型的土体单元尺寸介于1~2 m,车站结构单元尺寸为0.2 m,地连墙单元尺寸和钢筋网格尺寸均为0.3 m,网格划分详图如图 3所示。土体与车站结构、车站结构与地连墙之间的接触特性以及土-地下结构动力相互作用系统的边界转换条件见文献[12]。
2.2 材料动力本构模型
土体动力本构模型采用由庄海洋等[14]建立的软土记忆性黏塑性嵌套面动本构模型,该模型基于土体广义塑性理论,采用等向硬化-随动硬化的耦合硬化准则,建立总应力增量形式的土体黏塑性动本构模型。目前,该模型已采用Fortran语言进行二次开发,实现与ABAQUS有效对接;本构模型有效性和优越性已通过动三轴试验和自由场地数值模型等效线性分析进行对比验证。混凝土材料本构模型采用由Lee等[15]所建立的混凝土塑性动力损伤模型,该模型通过定义受拉、受压两种损伤变量和损伤因子来描述混凝土实际受力状态中的刚度退化规律,即在压缩状态下拉伸损伤可完全恢复,拉伸状态下压缩损伤不可恢复;同时使用多个强化变量来修正本构模型中的屈服函数方程,可更好的反映出混凝土结构强震动力作用中的损伤演化过程。本文地铁车站结构中除圆形中柱采用C40混凝土浇筑外,其余混凝土构件均采用C30混凝土浇筑。上述土体非线性动力本构模型和混凝土动力损伤模型详细参数见文献[12]。
2.3 IBE-FEM动力求解
基于上述大型断层-上覆软土沉积层场地边界元模型和土-地下结构动力相互作用有限元模型,本节将详细介绍考虑发震断层-地下结构全过程地震响应的IBE-FEM联合求解方法具体步骤。首先,采用IBE方法求解上覆软土沉积层场地在直下型左旋走滑断层错动作用下的地震波场。然后,提取软土沉积层埋深80 m处的土体地震反应作为土-地下车站结构相互作用系统的动力输入,本研究在断层距45 km范围内间隔1 km提取(为方便观测点断层距的数据统计,本文将观测点断层距定义为观测点与断层上界之间的地表投影距离),断层上盘、下盘共提取91组数据,示意图如图 4所示。本文所研究的地铁车站横断面与断层走向平行,动力输入方向为基底水平方向,示意图见图 5;不同断层距观测点处的动力输入即代表地下车站结构的不同断层距工况。最后采用静-动力耦合时程分析法研究断层-软土沉积层场地中地下车站结构地震反应特性。
2.4 精度验证
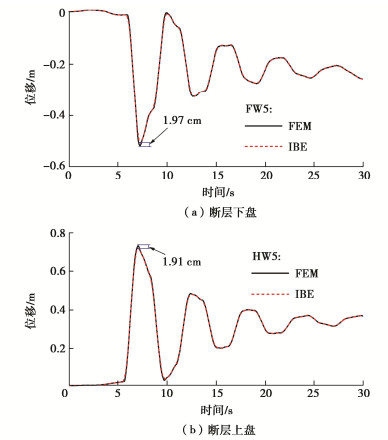
为验证采用FEM间接求解地表地震反应的可行性,首先建立200 m(宽)×80 m(埋深)的自由场场地模型,土体参数与断层-软土场地计算模型中沉积层介质保持一致;然后间隔5 km提取观测点地震波场(共19组数据)作为自由场地模型时程分析的动力输入(如提取断层上盘断层距10 km处的观测点,简称“HW10”;同理,断层下盘同一断层距的观测点简称“FW10”),并采用FEM间接求解地表位移反应。
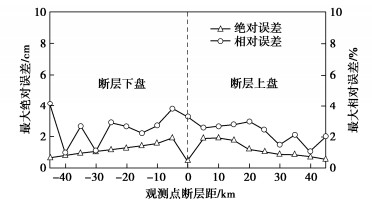
图 6给出了采用IBE直接求解和FEM间接求解的HW5、FW5场地地表位移时程对比,图 7给出了不同断层距工况下两种方法求解的地表位移最大绝对误差及其最大相对误差。从对比结果可以看出,采用本文所述的静-动力耦合方法及边界处理方式间接求解近断层场地地震响应与IBE直接求解相差不大,最大相对误差保持在4.5%以内,故本文所述考虑震源的地下结构全过程地震反应分析方法可信度高、实际操作性强、且易于普及使用,可为地下结构全过程地震响应分析提供新思路。
3. 计算结果分析
3.1 主体结构侧向变形反应
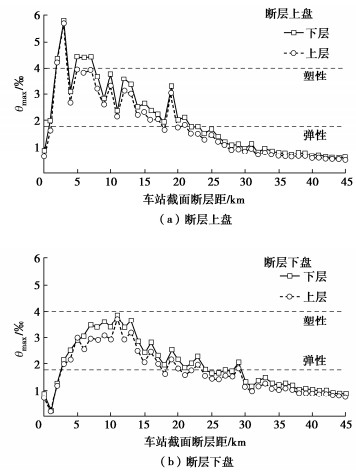
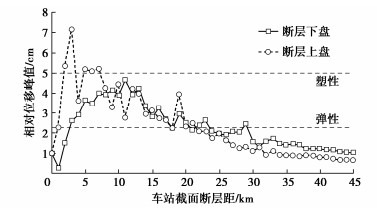
图 8,9给出了不同断层距工况下车站结构的层间位移角峰值和侧墙顶底相对位移峰值。根据《地下结构抗震设计标准:GB/T51336—2018》中表 6.9.1关于地下结构弹塑性变形发展阶段层间位移角限值的规定,位于断层上盘、断层距介于2~7 km的地铁车站结构侧墙顶底相对位移最大值为7.14 cm,其层间位移角大于结构塑性破坏限值,车站结构可能发生较为严重的塑性变形;而位于断层下盘相同断层距区域范围内的车站结构在地震过程中产生的侧向变形介于弹性破坏与塑性破坏限值之间,且其层间位移角均小于断层上盘工况。
产生上述震害的主要原因是:在断层上盘、下盘断层距相等的观测点处,断层上盘观测点的震源距略小于断层下盘观测点;此外,在近断层区域内,断层破裂能量在断层面-地表间产生的多次反射叠加可进一步放大断层上盘地震波场,因而位于断层上盘近断层区域内的地下地铁车站结构在地震过程中产生的侧向变形明显大于断层下盘,其震害具有典型的断层上盘效应。
整体上看,车站结构侧向极限相对变形随其断层距的增加呈先快速减小随后维持稳定的趋势;断层上盘、下盘远断层区域(HW44~45、FW44~45)侧墙顶底相对位移峰值较近断层区域分别减小91%,78%;值得注意的是,由于断层效应-场地效应的耦合作用,上覆软土沉积层场地的地震动放大效应存在明显的不均匀性,从而导致车站结构侧向极限相对变形随着断层距的增加存在一定的波动现象。
此外,根据Xie等[16]关于断层破裂方向性效应的研究,观测场点所在方向与断层破裂传播方向夹角θ小于90°时属于断层破裂前方,反之则属于断层破裂后方。本文断层倾角为80°,属于高倾角直下型断层,在断层上盘近断层区域内属于断层破裂前方;随着观测场点断层距的增大,其所在方向与断层破裂传播方向夹角θ逐渐增大,所在区域也由断层破裂前方逐渐转变为破裂后方;而断层下盘区域相应观测场点处的θ值与之始终相差10°,所有观测场点均处于断层破裂前方。在远断层区域内,由于破裂方向性效应的影响,加之断层上盘效应的逐渐弱化,导致断层下盘地震波场能量衰减速度略低于断层上盘,其内波场长周期成分更为丰富,场地内的速度脉冲幅值以及加速度峰值(PGA)均略高于断层上盘,因而位于断层下盘远断层区域内的车站结构侧墙极限相对变形略大于断层上盘工况。
3.2 主体结构加速度反应
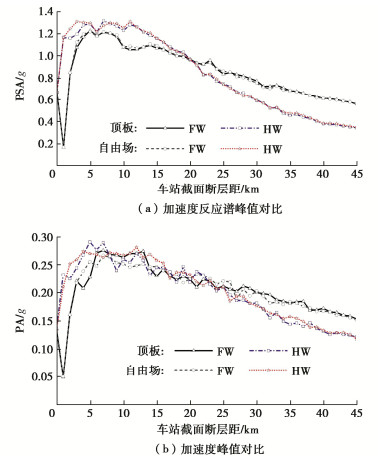
结构加速度响应在一定程度上可真实反映其在地震过程中所承受的动力作用大小,鉴于此,图 10给出了不同断层距工况下结构顶板加速度反应谱幅值(PSA)、加速度幅值(PA)与自由场对应位置处幅值对比;图 11给出了近、远断层区域车站结构顶板加速度时程及其加速度反应谱(SA)。
由图 10可知,在FW1附近区域内,车站结构顶板的PA、PSA值普遍偏小。这主要是因为该区域位于断层上界地表投影点附近,属于断层上、下盘分界区域;分界区域处的震源运动学表现为断层上、下盘震动方向相反,本文断层上界埋深5 km,地震波场在断层分界区域的上覆软土场地传播中因波的相干效应而异向相消,地震波动能量在该区域的衰减速率远大于非分界区域,从而导致断层分界区域上覆软土场地的地震动强度普遍降低,并在地表近断层区域形成一定范围的弱震区。
随着车站结构断层距的增加,顶板加速度响应先快速增长、随后缓慢下降、最终维持稳定。在断层上盘效应-破裂方向性效应耦合作用下,结构顶板加速度响应变化规律与其侧向变形反应近似相同;即在近断层区域,位于断层上盘的车站结构顶板加速度反应较强,位于下盘的车站结构顶板加速度反应次之,断层上盘车站结构顶板PA、PSA值较断层下盘增加高达28%,22%;远断层区域(断层距大于25 km)的车站结构顶板加速度反应强弱变化规律与近断层区域正好相反。此外,近断层区域的车站结构顶板PA值略大于自由场对应位置处的加速度反应,断层上盘、下盘车站结构顶板PA值较自由场地增幅高达10%;表明在强震作用下,土体可能发生较大的非线性变形,地下结构在土-结构动力相互作用的影响下,将进一步放大来自周围土体的动力作用,从而产生震动幅值更大的地震反应。整体上看,车站结构顶板PSA值与自由场地相差不大。
由图 11可知,在近断层区域,场地地震波场能量受断层上盘效应影响较大,从而导致位于断层上盘的车站结构顶板加速度反应大于断层下盘;在远断层区域内,断层上盘效应逐渐弱化,由破裂方向性效应引起的断层下盘场地内部地震波场的持续叠加效应逐渐显现,致使位于断层下盘的车站结构顶板加速度反应明显大于断层上盘,就断层距39 km处的车站结构而言,位于断层下盘的车站结构顶板PSA值较断层上盘增加58%。结构顶板加速度反应的整体变化规律表明:在近断层场地中,断层上盘效应与破裂方向性效应耦合作用呈现一定的空间互补性,从而进一步增加场地内部地震动的空间复杂性及其相关地下结构的震害多变性。此外,软土场地对地震波场具有强烈的滤波效应,从而导致车站结构顶板加速度反应谱在短周期范围内(T < 1 s)的幅值大幅缩减,长周期范围内幅值明显放大,加速度的高频震动衰减显著。
综上所述,在断层-软土场地耦合效应作用下,高倾角走滑断层近场区域内,位于断层上盘的地下结构产生的震害更强;远场区域内,位于断层下盘的地下结构震害略大于断层上盘。
3.3 主体结构内力反应
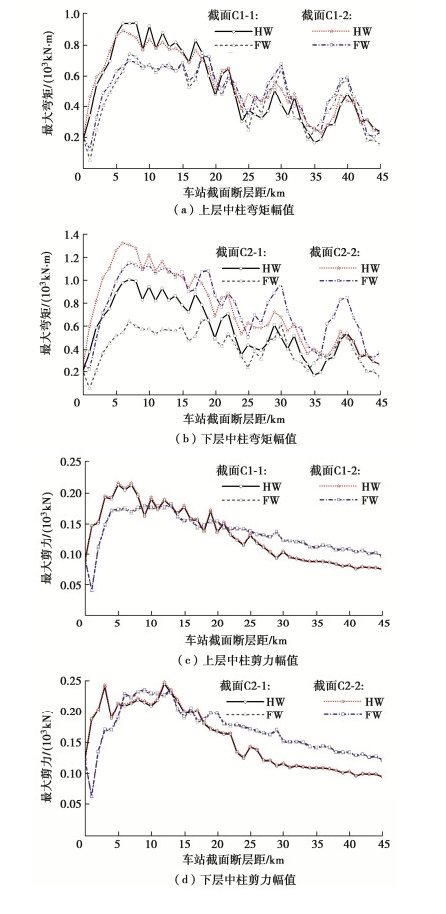
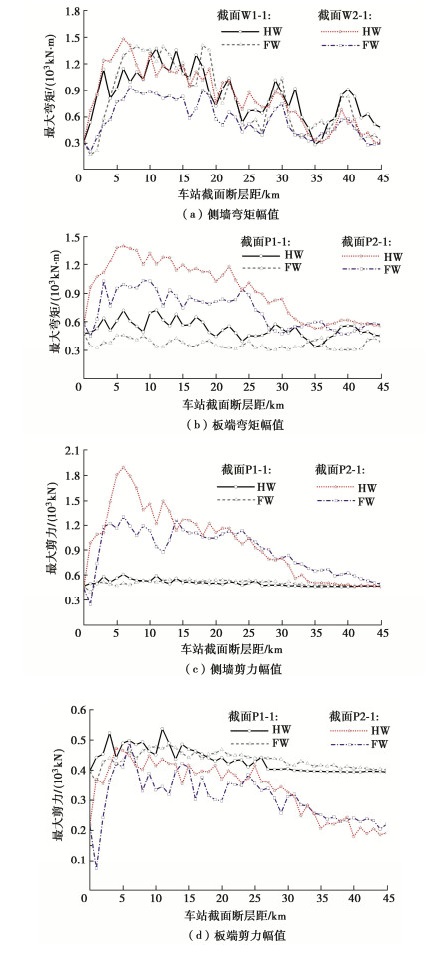
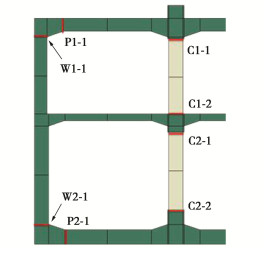
为进一步分析断层-软土场地耦合效应作用下地下结构地震内力变化特性,图 12,13依次给出了不同断层距工况下车站结构中柱端部、侧墙端部以及顶、底板端部的弯矩、剪力幅值,其中所涉及到的观测截面详图见图 14。
由图 12可知,在近断层区域内,中柱顶、底端截面C1-1、C2-2在地震过程中产生的弯矩幅值略大于与纵梁连接处的中柱端部截面C1-2、C2-1。由于断层上盘效应的影响,位于断层上盘车站结构中柱截面C1-1、C2-2处弯矩幅值较下盘最少提升25%,13%。在远断层区域内,软土场地对地震波能量的放大效应存在明显的不均匀性,从而导致车站结构中柱弯矩幅值随其断层距的增加呈非线性衰减趋势。断层上盘效应在远断层区域弱化现象以及断层破裂方向性效应对于中柱顶、底端截面弯矩幅值影响较大,对纵梁连接处的中柱端部截面弯矩幅值影响次之;在远断层区域内具体表现为,断层距相等的车站结构中柱截面C1-1、C2-2弯矩幅值断层上盘、下盘之间的差值明显大于截面C1-2、C2-1。
整体上来看,由于近断层场地内的震害集中效应,位于断层上盘的车站结构中柱弯矩幅值随着其断层距的增加存在明显的衰减阶段(HW20~HW30);在断层破裂方向性效应的影响下,断层下盘的中柱弯矩幅值随断层距的增加而衰减的速度略缓于断层上盘。
中柱剪力幅值变化规律与其弯矩幅值基本相同,值得注意的是,断层上盘效应对于上层中柱剪力幅值影响更为明显,断层距在10 km以内,位于断层上盘的车站结构上层中柱剪力幅值均明显大于断层下盘,其幅值较断层下盘增幅达38%;断层上盘效应对于下层中柱剪力幅值的作用范围将缩减至5 km以内。下层中柱内力反应大于上层,这表明在地震过程中,下层车站结构将更易产生较为严重的震害,这与不考虑断层效应的地铁地下车站结构中柱地震反应规律相一致[12]。
由图 13可知,在近断层区域内,位于断层上盘的车站结构侧墙底部截面W2-1的弯矩、剪力幅值较断层下盘最少提升20%,17%,底板截面P2-1的弯矩、剪力幅值较断层下盘最少提升16%,14%;而结构侧墙-顶板连接处的内力反应受震害集中效应以及断层上盘效应的影响较小,具体表现为该连接处观测截面P1-1、W1-1断层上、下盘间的内力幅值相差不大,且随着断层距的增加,内力幅值衰减趋势不明显。上述现象表明,侧墙-底板连接处对于输入地震动频谱幅值特性变化更为敏感,在近断层区域内的内力反应明显大于远断层区域,具有明显的震害集中效应,在强震过程中消耗主要的地震动能量,因而极易发生弹塑性变形,产生较为严重的震害。
4. 结论
本文基于运动学有限断层理论,采用IBE方法求解含有高频随机震动成分的单凹凸体直下型走滑断层-上覆软土场地内的地震波场;其次,基于土-结构动力相互作用理论,通过建立土-两层三跨地铁车站结构动力相互作用有限元模型,采用静-动力耦合时程分析的FEM方法,初步探究了断层-软土场地耦合效应对地铁地下车站抗震性能的影响规律,主要得到以下4点结论。
(1)通过对比分析,验证本文提出的一种考虑发震断层-地下结构全过程地震响应的IBE-FEM联合求解分析方法能够实现考虑震源的地下结构全过程地震反应分析,可信度高、实际操作性强、且易于普及使用,可为地下结构全过程地震响应分析提供新思路。
(2)对于破裂未出露地表的直下型走滑断层,断层上、下盘分界区域地震波传播过程中因波的相干效应异向相消,以致近断层地表存在一定范围的弱震区,本文计算模型弱震区主要分布在FW1附近,这一区域的地下结构层间位移角显著降低,结构整体震害较轻。
(3)在直下型走滑断层场地近断层区域内,由于断层上盘效应和震害集中效应,使得位于断层上盘的车站结构侧向变形进入塑性发展阶段;结构顶板加速度反应更为强烈,其PA、PSA值较下盘增加高达28%,22%;结构中柱内力幅值较断层下盘大幅提升。
(4)在高倾角走滑断层作用下的远断层区域内,由破裂方向性效应引起的地震波场的持续叠加效应显著增强,断层下盘场地内地震波场能量衰减相对较缓、长周期成分更为丰富,该区域内观测场点PGA、结构顶板PA、PSA均大于断层上盘。
-
-
[1] QIU D, CHEN J, XU Q. 3-D numerical analysis on seismic responses of the underground large scale frame structure under near-fault ground motions[J]. Tunnelling and Underground Space Technology, 2019, 91: 103020. doi: 10.1016/j.tust.2019.103020
[2] 崔臻, 盛谦, 冷先伦, 等. 近断层地震动对大型地下洞室群地震响应的影响研究[J]. 岩土力学, 2013, 34(11): 3213-3220, 3228. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201311029.htm CUI Zhen, SHENG Qian, LENG Xianlun, et al. Effects of near-fault ground motion on seismic response of underground cacerns[J]. Rock and Soil Mechanics, 2013, 34(11): 3213-3220, 3228. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201311029.htm
[3] ZHAO W S, CHEN W Z. Effect of near-fault ground motions with long-period pulses on the tunnel[J]. Journal of Vibro-engineering, 2015, 17(2): 841-858.
[4] MEI X, SHENG Q, CUI Z. Effect of near-fault pulsed ground motions on seismic response and seismic performance to tunnel structures[J]. Shock and Vibration, 2021: 1-18.
[5] 梁建文, 吴泽群, 辛钰, 等. 断层错动下盾构隧道抗震措施研究[J]. 地震工程与工程振动, 2020, 40(1): 1-11. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC202001001.htm LIANG Jianwen, WU Zequn, XIN Yu, et al. Seismic countermeasures of shield tunnel under fault movement[J]. Earthquake Engineering and Engineering Vibration, 2020, 40(1): 1-11. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC202001001.htm
[6] 刘中宪, 刘英, 孟思博, 等. 基于间接边界元法的近断层沉积谷地地震动模拟[J]. 岩土力学, 2021, 42(4): 1141-1155, 1169. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202104028.htm LIU Zhongxian, LIU Ying, MENG Sibo, et al. Near-fault ground motion simulation of alluvial valley based on indirect boundary element method[J]. Rock and Soil Mechanics, 2021, 42(4): 1141-1155, 1169. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202104028.htm
[7] GRAVES R, PITARKA A. Refinements to the Graves and Pitarka (2010) broadband ground-motion simulation method[J]. Seismological Research Letters, 2014, 86(1): 75-80.
[8] 巴振宁, 刘悦, 赵靖轩, 等. 2021年漾濞6.4级近断层宽频地震动模拟: 一种改进的FK方法[J]. 岩土工程学报, 2023, 45(4): 709-719. doi: 10.11779/CJGE20211574 BA Zhenning, LIU Yue, ZHAO Jingxuan, et al. Near-fault broadband ground-motion simulation of 2021 Yangbi M6.4 earthquake: an improved FK method[J]. Chinese Journal of Geotechnical Engineering, 2023, 45(4): 709-719. (in Chinese) doi: 10.11779/CJGE20211574
[9] HASKELL N A. Total energy and energy spectral density of elastic wave radiation from propagating faults[J]. Bulletin of the Seismological Society of America, 1964, 54(6A): 1811-1841. doi: 10.1785/BSSA05406A1811
[10] 姜伟, 陶夏新, 陶正如, 等. 有限断层震源模型局部参数定标律[J]. 地震工程与工程振动, 2017, 37(6): 23-30. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201706003.htm JIANG Wei, TAO Xiaxin, TAO Zhengru, et al. Scaling laws of local parameters of finite fault source model[J]. Earthquake Engineering and Engineering Dynamics, 2017, 37(6): 23-30. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201706003.htm
[11] 刘启方. 基于运动学和动力学震源模型的近断层地震动研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2005. LIU Qifang. Studies on Near-Fault Ground Motions Based on Kinematic and Dynamic Source Models[D]. Harbin: Institute of Engineering Mechanics China Earthquake Administration, 2005. (in Chinese)
[12] ZHUANG H Y, WANG R, SHI P X, et al. Seismic response and damage analysis of underground structures considering the effect of concrete diaphragm wall[J]. Soil Dynamics and Earthquake Engineering, 2019, 116: 278-288. doi: 10.1016/j.soildyn.2018.09.052
[13] KUHLEMEYER R L, LYSMER J. Finite element method accuracy for wave propagation problems[J]. Journal of the Soil Mechanics and Foundations Division, 1973, 99(5): 421-427. doi: 10.1061/JSFEAQ.0001885
[14] ZHUANG H Y, CHEN G X. A viscous-plastic model for soft soil under cyclic loadings[C]//Geotechnical Special Publication of ASCE, Soil and Rock Behavior and Modeling Proceedings of the Geo-Shanghai Conference. Shanghai, 2006: 343-350.
[15] LEE J, FENVES G L. Plastic-damage model for cyclic loading of concrete structures[J]. Journal of Engineering Mechanics, 1998, 124(8): 892-900. doi: 10.1061/(ASCE)0733-9399(1998)124:8(892)
[16] XIE J J. Strong‐motion directionality and evidence of rupture directivity effects during the Chi‐Chi Mw 7.6 earthquake directionality and rupture directivity effects during the Chi‐Chi Mw 7.6 earthquake[J]. Bulletin of the Seismological Society of America, 2019, 109(6): 2367-2383. doi: 10.1785/0120190087
-
期刊类型引用(0)
其他类型引用(2)
-
其他相关附件



 下载:
下载: