考虑岩土参数随机性的三维沉积盆地地震动高效模拟方法

刘中宪; 孟思博; 李文轩; 赵嘉玮; 黄振恩

doi:10.11779/CJGE20221399

考虑岩土参数随机性的三维沉积盆地地震动高效模拟方法 English Version

1.
天津城建大学天津市软土特性与工程环境重点实验室, 天津 300384
2.
天津城建大学天津市土木建筑结构防护与加固重点实验室, 天津 300384
3.
天津城建大学土木工程学院, 天津 300384
4.
天津大学建筑工程学院, 天津 300072

基金项目:

国家自然科学基金项目 U2139208

国家自然科学基金项目 52208497

天津市科技计划项目 19YFZCSN01180

天津市项目加团队 2020

详细信息

作者简介:
刘中宪(1982—)，男，博士，博士后，教授，主要从事地震工程、工程防护等方面的研究。E-mail: zhongxian1212@163.com

通讯作者:
孟思博, E-mail: sibomeng@yeah.net

中图分类号: TU43
计量
- 文章访问数: 323
- HTML全文浏览量: 55
- PDF下载量: 97
出版历程
- 收稿日期: 2022-11-10
- 网络出版日期: 2023-04-23
- 刊出日期: 2024-02-29

Evaluation method for stochasticity in seismic response of 3D sedimentary basins based on artificial neural network

1.
Tianjin Key Laboratory of Soft Soil Characteristics and Engineering Environment, Tianjin Chengjian University, Tianjin 300384, China
2.
Tianjin Key Laboratory of Structural Protection and Reinforcement, Tianjin Chengjian University, Tianjin 300384, China
3.
School of Civil Engineering, Tianjin Chengjian University, Tianjin 300384, China
4.
School of Architectural Engineering, Tianjin University, Tianjin 300072, China

摘要

摘要: 沉积盆地对地震波的散射导致盆地放大效应，增大结构震害。盆地的岩土参数通常具有显著的随机特征，导致盆地响应的可变性。旨在基于快速多极边界元法（FM-IBEM）和人工神经网络（ANN），提出一种考虑岩土参数不确定性的三维沉积盆地地震动有效模拟方法。首先，以岩土参数、入射波频率和地表位置为输入参数，以三维沉积盆地响应为输出参数，建立了人工神经网络模型。其次，利用蒙特卡罗模拟（MCS）来评估沉积盆地地面运动的随机性，并使用ANN模型和数据集中现有的结果来代替数值模拟来求解样本，通过减少计算时间来提高随机问题的计算效率。结果表明，该方法可用于求解和评估考虑岩土参数随机性的三维沉积盆地地震响应，计算效率高。岩土参数的随机性对沉积盆地地震响应的影响不容忽视，沉积盆地地表响应的可变性与地表点的位置、入射频率和分布有关，表现出与均值分布非线性相关的特征。岩土参数的随机性对高频入射波作用下盆地地震动有显著影响，放大效应变异系数可达0.3，是岩土参数变异系数的3倍；与平均值相比，对应于95%置信水平的盆地峰值加速度增加了56%。
- 盆地效应 /
- 人工神经网络 /
- 岩土参数随机性 /
- 快速多极边界元法
Abstract: The scattering of seismic waves by sedimentary basins leads to basin amplification effects and increases earthquake damage of structures. The geotechnical parameters of the basins generally have significantly stochastic characteristics, resulting in the variability of the basin response. This study aims to propose an efficient simulation method for ground motions of 3D sedimentary basins considering geotechnical uncertainty based on the fast multipole boundary element method (FM-IBEM) and artificial neural network (ANN). Firstly, an ANN model is constructed with geotechnical parameters, incident wave frequency and surface location as the input parameters and 3D sedimentary basin response as the output parameter. Secondly, a Monte Carlo simulation is utilized to evaluate the randomness of ground motions in sedimentary basins, and the ANN model and the existing results in the dataset are used instead of numerical simulations for sample solutions, which improves the computational efficiency of stochastic problems by reducing the computational time. The results indicate that the proposed method can be used to solve and evaluate the seismic response of 3D sedimentary basins considering the randomness of geotechnical parameters with high computational efficiency. The influences of randomness of geotechnical parameters on the seismic response of sedimentary basins are not negligible, and the variability of surface response of sedimentary basins is related to the location of surface points, incident frequency and distribution. It shows non-linear correlation characteristics with mean value distribution. The randomness of geotechnical parameters has a significant effect on ground motions of the basin under high-frequency incident waves. The coefficient of variation of the amplification effects can reach 0.3, which is three times the coefficient of variation of geotechnical parameters. The peak acceleration of the basin corresponding to 95% of confidence level increases by 56% compared to the mean value.
- basin effect /
- artificial neural network /
- geotechnical parameter stochasticity /
- FM-IBEM

HTML全文

0. 引言

沉积盆地是一种典型的局部复杂场地，已有理论分析和实际震害表明，沉积盆地对地震波的散射将引起盆地中心聚焦效应和边缘放大效应，并导致沉积盆地地震动表现出长周期、长持时特性^[1-3]。同时，受限于钻孔数量、土波速试验条件，岩土参数确定通常存在很大的随机性，并在地震波传播过程中发生随机性传递，增大了盆地效应定量分析的难度。因此，开展沉积盆地地震动随机模拟与评估具有重要意义。

国内外学者基于解析法和数值法对确定性参数下沉积盆地放大效应开展了大量研究。一维波动理论或二维模型求解盆地地震响应无法充分考虑介质横向不均匀性引起的盆地内地震波反射、折射和三维聚焦现象，可导致地表位移幅值相差3.5~4.2倍^[4]，因此多基于三维模型求解沉积盆地地震响应。针对三维沉积盆地，赵成刚等^[5]基于波函数展开法获得了层状饱和沉积场地对Rayleigh波散射的解析解，分析了入射波频率、层状沉积层排列顺序、相对刚度和厚度等因素对散射效应的影响；Mossessian等^[6]采用间接边界积分法研究了三维沉积盆地对P、SV和SH波的散射，分析了入射频率、入射角对沉积盆地地表位移幅值的影响规律；Liang等^[7]采用间接边界元法求解了层状横向各向同性半空间中任意形状沉积河谷对地震波的散射。此外，刘启方^[8]、韩天成等^[9]采用有限元法、谱元法等域离散法分别研究了远场、近场地震作用下三维沉积盆地地震响应。

值得指出的是，岩土参数随机性将引起沉积盆地地震动随机性。已有研究基于MCS分析了剪切波速、剪切模量和阻尼比随机性对三维沉积盆地地震响应的影响，考察指标包括地震动峰值加速度（PGA）和谱加速度^[10]。理论上，MCS适用于任意随机性问题，其缺点是计算量较大，尤其是基于三维盆地模型求解场地地震反应时，由于单个样本计算时间较长，MCS计算效率低下。因此，一些学者采用响应面法、乘子降维法开展场地岩土参数随机性评估^[11-12]，通过降低所需样本数量提高计算效率，研究对象包括三维水平成层场地和二维沉积河谷，结果表明岩土参数随机性可导致层长场地PGA变异系数达到25%^[11]、高频波作用下二维沉积河谷地表位移幅值变异系数超过20%^[12]。但此类方法处理强变异性问题的适用性、求解三维沉积盆地地震动的有效性有待进一步验证。综上所述，有必要建立考虑岩土参数随机性的三维沉积盆地地震动高效模拟方法。

近年来，ANN被应用于局部场地效应预测模型构建，大多基于二维场地模型^[13-14]；三维模型方面，Zhou等^[15]研究了ANN模型预测含随机起伏地形几何参数的三维高山峡谷场地地震动的适用性，Hamidreza等^[16]结合有限元法和ANN，分析了不同岩土参数对伊朗克尔曼地区PGA的影响。以上研究均显示ANN可实现局部复杂场地地震动响应有效评估。

鉴于此，本文基于ANN建立一种可考虑岩土参数随机性的三维沉积盆地地震动模拟方法。首先，确定随机岩土参数，采用FM-IBEM求解三维沉积盆地地震响应以构建数据集；然后，基于ANN建立沉积盆地地震响应代理模型；最后，采用MCS求解考虑岩土参数随机性的三维沉积盆地地震响应，其中单次样本基于代理模型求解或直接提取所建数据集已有结果，通过提高单次样本计算效率大幅降低MCS计算成本。在验证方法有效性基础上，以半椭球形沉积盆地为例，从频域和时域两个方面，研究了SV波垂直入射下三维沉积盆地随机地震动变异性分布特征。

1. 随机岩土参数下三维沉积盆地地震动模拟方法

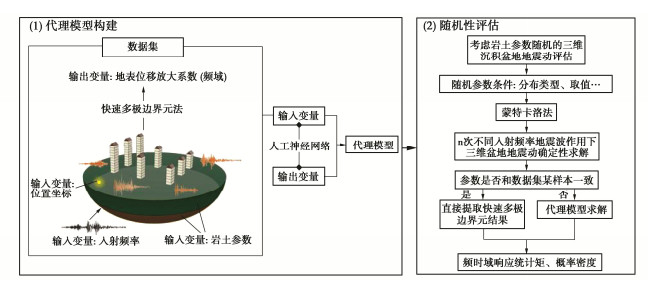
考虑岩土参数随机性的三维沉积盆地地震动模拟方法框架如图 1所示。首先，确定随机岩土参数，将其和入射频率、地表点位置坐标设置为ANN的输入参数，并通过FM-IBEM求解每组随机输入参数下三维沉积盆地地震响应，将某地表点位移放大系数（DAF）设置为输出参数，其定义为盆地某地表点位移幅值绝对值与入射波振幅的比值；建立数据集后，基于ANN构建求解沉积盆地地表DAF的代理模型；然后，假定随机岩土参数概率分布、统计矩，采用MCS开展沉积盆地随机地震动模拟，确定性参数下单次样本计算基于代理模型实现或直接提取所建数据集已有结果，以代替常规的数值模拟，通过提高单次样本计算效率降低MCS计算时间。沉积盆地PGA可由傅里叶逆变换求得。

图 1 本文所建方法流程图

Figure 1. Flow chart of proposed method

下载: 全尺寸图片幻灯片

1.1 确定性参数下三维沉积盆地地震动模拟方法

（1）计算模型

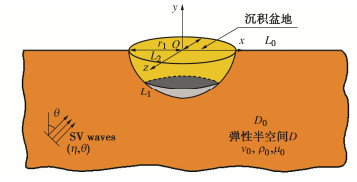
如图 2所示，三维沉积盆地位于基岩半空间，假设半空间为各向同性均匀弹性介质，坐标系原点位于沉积盆地地表中心点。盆地地表半径为r₁，L₀为弹性半空间地表，L₁表示沉积域与弹性半空间交界面，L₂表示沉积盆地地表。

图 2 三维沉积盆地计算模型

Figure 2. Computational model for 3D sedimentary basin

下载: 全尺寸图片幻灯片

（2）快速多极间接边界元法

在求解沉积盆地地震动问题时，首先对L₁，L₂交界面进行单元划分；然后假设不存在沉积盆地，求解自由波场；进而将虚拟荷载施加在离散单元表面上，利用边界条件和格林函数求解散射波场；最后叠加自由波场和散射波场获得总波场。自由波场求解参考文献[17]，重点阐述散射波场求解过程。地震波入射下沉积盆地中任意点位移和应力均可表示为

，

$u_i^{(s)}(x) = \int\limits_S {{\phi _j}(y){G_{ij}}(x,y){\text{d}}{S_A}} \text{，}$

(1)

。

$t_i^{(s)}(x) = \int\limits_S {{\phi _j}(y){T_{ij}}(x,y){\text{d}}{S_A}} 。$

(2)

式中：上标s为散射场； ${\phi _j}$ 为边界表面上的虚拟荷载密度；S_A为每个离散单元的面积；G_ij和T_ij分别为位移和应力格林函数；x和y分别为场点和源点。

地震波入射下三维沉积盆地散射波场满足边界条件：自由地表面牵引力为零，半空间域和沉积域的交界面应力和位移连续，盆地内表面牵引力为零，可表示为

$\left[\begin{array}{cc}{T}_{\text{s}}{}^{\text{D}}(3{L}_{0},3M)& 0\\ \begin{array}{c}{F}_{\text{s}}{}^{\text{D}}(6{L}_{1},3M)\\ 0\end{array}& \begin{array}{l}{F}_{\text{s}}{}^{\Omega }(6{L}_{1},3N)\\ {T}_{\text{s}}{}^{\Omega }(3{L}_{2},3N)\end{array}\end{array}\right]\left[\begin{array}{c}{\varphi }^{\text{D}}(3M)\\ {\varphi }^{\Omega }(3N)\end{array}\right]=\left[\begin{array}{c}0\\ -{F}_{\text{f}}^{\text{D}}(6{L}_{1})\\ 0\end{array}\right]。$

(3)

式中：T为半空间地表牵引力矢量；F；交界面上牵引力和位移作用； $\phi$ 为虚拟荷载密度，上角标D代表半空间域对边界面的作用； $\varOmega$ 为沉积域对边界面的作用；下角标f表示自由场。 $M = {L_0} + {L_1},N = {L_1} + {L_2}$ 。通过求解式（3）即可得到虚拟荷载密度，从而求得散射场应力和位移。

然而，此方法求解计算量和存储量需求较高，当模型自由度较多时计算效率较低，因此引入FM算法以降低计算量和存储量，实现三维沉积盆地地震动高效求解。

FM引入分层树结构中的细胞节点将单元之间的直接作用转换为以细胞节点为中间点的间接作用，需对应力和位移格林函数进行快速多极展开，球面波势函数展开后可表示为

$f(q,r) = \frac{{{{\text{e}}^{ - iqr}}}}{r} 。$

(4)

式中：q为纵波或横波的波数；r为场点和源点间距离。针对三维高频弹性波散射问题，基于平面波展开理论^[18]，对势函数进行平面波展开，可得

$f(q,x,y) = \frac{{iq}}{{2(2p + 1)}}\sum\limits_{n = 0}^p {\sum\limits_{m = 0}^{2p} {{\omega _n}R_n^m(q,\overrightarrow {y{y_0}} )} } \times$

$T_n^m(q,\overrightarrow {{y_0}{x_0}} )S_n^m(q,\overrightarrow {{x_0}x} ) \text{，}$

(5)

$R_n^m(q,\overrightarrow {y{y_0}} ) = {{\text{e}}^{iq({y_0} - y) \cdot \hat k_n^m}} \text{，}$

(6)

$S_n^m(q,\overrightarrow {{x_0}x} ) = {{\text{e}}^{iq({x_0} - x) \cdot \hat k_n^m}} \text{，}$

(7)

$T_n^m(q,\overrightarrow {{y_0}{x_0}} ) = \sum\limits_{l = 0}^p {{i^l}(2l + 1)h_l^{(2)}(qr){p_l}(\hat r \cdot \hat k_n^m)} 。$

(8)

式中： $\hat k_n^m = (\sin {\theta _n}\cos {\phi _m},\sin {\theta _n}\sin {\phi _m},\cos {\phi _m})$ ； ${\theta _n} =$ $a\cos {x_n}$ ； ${\phi _m} = 2{\rm{\mathsf{π}}}m/(2p + 1)$ ； ${x_n}$ 为[-1，1]范围内高斯积分水平坐标， ${w_n}$ 为[-1-1]范围内高斯积分权重系数， $\hat r = \overrightarrow {{y_0}{x_0}} /\left| {\hat r} \right|$ ， $r = \left| {\hat r} \right|$ ，同时满足 $\left| {\overrightarrow {y{y_0}} } \right| \lt \left| {\overrightarrow {{y_0}{x_0}} } \right|$ 和 $\left| {\overrightarrow {x{x_0}} } \right| <$ $\left| {\overrightarrow {{y_0}{x_0}} } \right|$ 。 $h_l^{(2)}$ 为二阶Hankel函数， ${p_l}$ 为l阶Legendre函数。

FM-IBEM具体步骤可参考文献[19]，在此不再赘述。

1.2 基于ANN代理模型的三维沉积盆地地震动模拟

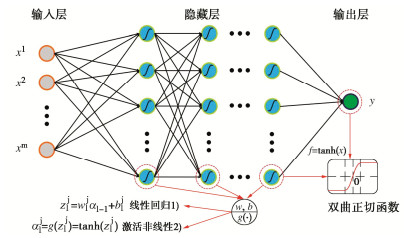
MCS需求解大量确定性样本，进行统计分析获取响应矩和概率信息。为提高单次样本求解速度，采用ANN代理模型或构建ANN模型时数据集中已有结果代替数值模拟，建立基于ANN代理模型的三维沉积盆地地震动高效模拟方法。本文所用ANN类型为前馈神经网络，由输入层、隐藏层和输出层中相互连接的神经元组成^[15]（图 3）。对于三维沉积盆地，具有随机性的场地介质参数、入射波相关参数均可作为输入层元素，输出层元素为沉积盆地地震响应量。

图 3 ANN结构示意图

Figure 3. Diagram of ANN structure

下载: 全尺寸图片幻灯片

第L个隐藏层中神经元的输出为

${\theta ^L} = {\left[ {\begin{array}{*{20}{c}} {{\theta _1}}&{{\theta _2}}& \cdots &{{\theta _n}} \end{array}} \right]^{\text{T}}} 。$

(9)

式中：n代表第L个隐藏层中神经元的数量，初始权重可写为^[15]

${\omega ^L} = \left[ {\begin{array}{*{20}{c}} {\omega _{11}^{(L)}}&{\omega _{12}^{(L)}}&{\begin{array}{*{20}{c}} \ldots &{\omega _{\ln }^{(L)}} \end{array}} \\ \begin{gathered} \omega _{21}^{(L)} \hfill \\ \vdots \hfill \\ \end{gathered} &\begin{gathered} \omega _{22}^{(L)} \hfill \\ \vdots \hfill \\ \end{gathered} &\begin{gathered} \begin{array}{*{20}{c}} \ldots &{\omega _{2n}^{(L)}} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} \hfill \\ \end{gathered} \\ {\omega _{r1}^{(L)}}&{\omega _{r2}^{(L)}}&{\begin{array}{*{20}{c}} \ldots &{\omega _{rn}^{(L)}} \end{array}} \end{array}} \right] 。$

(10)

式中： ${\omega _{ij}}{\text{(}}i = 1,{\text{ }}2, \cdots ,r;j = 1,{\text{ }}2, \cdots ,n{\text{)}}$ 为第L个隐藏层、第i个神经元到第（L+1）层、第j个神经元的权重，权重累计值可写为^[15]

${\lambda }_{i}^{（L+1)}={\displaystyle \sum _{j=1}^{n}{\omega }_{ij}^{(L)}{\theta }_{j}^{(L)}+{b}_{i}^{(L)}} 。$

(11)

式中： $\lambda _i^{(L + 1)}$ 为第（L+1）层第i个神经元的权重之和， $b_i^{(L)}$ 为第（L+1）层第i个神经元的偏差。

2. 方法验证

本节开展两方面验证：①验证求解确定性岩土参数下三维沉积盆地地震响应FM-IBEM方法的正确性；②验证ANN代理模型对沉积盆地任意地表点地震响应的预测性能和泛化能力。

2.1 FM-IBEM方法验证

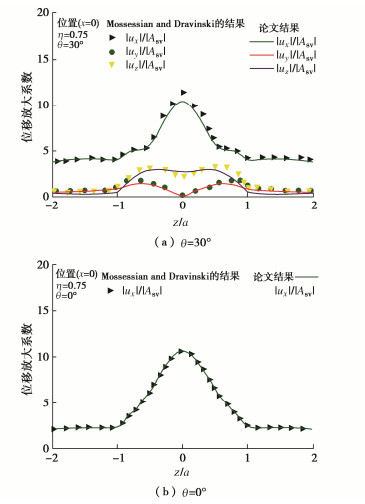
采用FM-IBEM求解SV波入射下半球形三维沉积盆地地表位移幅值（确定性分析）。无量纲频率η定义为η=ωr₁/πc₁，其中ω是圆频率，r₁是盆地半径，c₁是半空间中的剪切波速。参数设置与文献[6]相同：r₁=1，沉积盆地内外泊松比为1/3，密度比为2/3，横波速度比为1/2，黏滞阻尼取为0.005，入射角分别为 $\theta$ =60°和90°，入射波在xy平面内。

图 4给出了沿盆地中心线z向（图 2）地表DAF。由图 4可知，FM-IBEM求解结果与文献结果[6]具有良好的一致性，验证了本文FM-IBEM方法的准确性。

图 4 本文结果与文献[6]结果对比

Figure 4. Comparison between results in this study and those in literature ^[6]

下载: 全尺寸图片幻灯片

2.2 ANN代理模型精度验证

计算模型为一半椭球形沉积盆地，盆地地表为圆形，无量纲盆地半径为1、无量纲盆地深度为0.6。弹性半空间介质泊松比为1/3，沉积内外密度比为2/3，考虑SV波垂直入射。将入射频率、盆地内泊松比和阻尼比、沉积盆地与半空间之间的剪切波速度比、盆地地表位置坐标设置为输入参数，取值范围见表 1。选取沉积盆地任意地表点DAF作为输出参数。

表 1 验证模型输入参数

Table 1. Input parameters for validation model

参数	符号	名称	分布类型	均值	均方差	范围
参数	符号	名称	分布类型	均值	均方差	下限	上限
入射频率	η	入射频率	均匀分布	1.560	0.844	0.10	3
场地介质	μ	沉积盆地内泊松比	均匀分布	0.340	0.066	0.30	0.38
	β	沉积盆地内外剪切波速比	均匀分布	0.493	0.096	0.33	0.67
	ξ	沉积盆地内阻尼比	均匀分布	0.021	0.003	0.015	0.025
位置相关参数	x	x轴方向笛卡尔坐标	—	—	—	—	—
位置相关参数	z	z轴方向笛卡尔坐标	—	—	—	—	—

下载: 导出CSV

| 显示表格

采用FM-IBEM进行500次三维沉积盆地地震响应的确定性求解，每次求解岩土参数、入射频率均随机确定，且取值在表 1所示范围内。训练集、测试集比例为90%，10%。综合考虑模型的复杂性、训练精度和成本，隐藏层取为三层，经试算后，将ANN结构设置为6×38×32×20×1。采用均方根误差（RMSE）评估单个样本和测试集的预测值和实际值，表达式为

${\text{RMSE}}(\psi ',\psi ) = \sqrt {\frac{1}{m}\sum\limits_{i = 1}^m {{{({\psi ^{(i)}} - {{\psi '}^{(i)}})}^2}} } 。$

(12)

式中：ψ⁽ⁱ⁾为第i个采样点的实际值；ψ'⁽ⁱ⁾为相应的预测值；m为测试集样本个数。

采用决定系数R²衡量自变量对因变量的变化程度，表达式为

${R^2}(\psi ',\psi ) = 1 - \frac{{\sum\limits_{i = 1}^m {{{({\psi ^{(i)}} - {{\psi '}^{(i)}})}^2}} }}{{\sum\limits_{i = 1}^m {{{({\psi ^{(i)}} - \overline \psi )}^2}} }} 。$

(13)

式中： $\overline \psi$ 为基线模型。

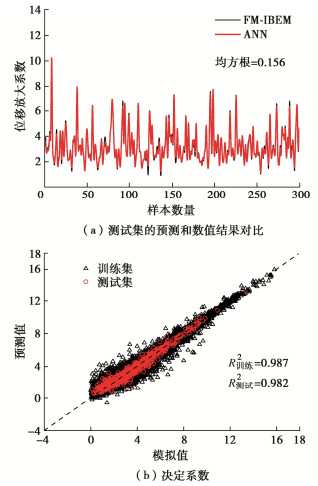
图 5（a）给出了测试集中随机选取300组输入参数对应的地表DAF，图 5（b）给出了ANN训练集、测试集决定系数R²。由图 5可知，ANN代理模型与FM-IBEM结果均方根误差为0.156，训练集和测试集决定系数R²分别为0.987和0.982，表明所建ANN模型具有很好的预测能力和泛化性能，可作为求解三维沉积盆地随机地震响应的代理模型。

图 5 ANN代理模型性能验证

Figure 5. Performance verification of ANN model

下载: 全尺寸图片幻灯片

3. 算例

本节以2.3节所述模型为例，采用所建方法开展沉积盆地随机地震动模拟及关键参数影响分析。随机岩土参数包括沉积盆地内泊松比和阻尼比、沉积盆地内外剪切波速比，假设均服从截断正态分布^[20]，变异系数为0.1，均值、变异系数见表 2。

表 2 随机岩土参数信息

Table 2. Information of random geotechnical parameters

符号	名称	分布类型	均值	均方差变异系数	范围
符号	名称	分布类型	均值	均方差变异系数	下限	上限
μ	沉积盆地内泊松比	正态分布	0.339	0.034 0.100	0.300	0.380
β	沉积盆地内外剪切波速比	正态分布	0.493	0.049 0.100	0.330	0.670
ξ	沉积盆地内阻尼比	正态分布	0.020	0.002 0.100	0.015	0.025

下载: 导出CSV

| 显示表格

3.1 计算效率对比

根据沉积盆地地震响应均值、均方差收敛性分析，针对本算例，采用MCS进行单一频率入射波作用下盆地随机地震响应求解平均需500个样本（与入射频率有关）；时域分析时，入射波无量纲频带取为0.1~3.0，频率间隔为0.1，故共需完成30⊆500个样本求解。采用常规MCS需进行15000次三维沉积盆地地震响应数值模拟，FM-IBEM求解单个样本平均时间约为15 min（8 GB内存、2.0 GHz主频），总时间约为225000 min。本文所建方法将此问题转化为500次三维沉积盆地地震响应的数值模拟（建立数据集）、14998次ANN代理模型求解和2次直接提取建立数据集时模拟结果，ANN代理模型求解单个样本时间仅1秒，总时间约为7750 min，仅为常规方法的3.4%。

3.2 频域结果与分析

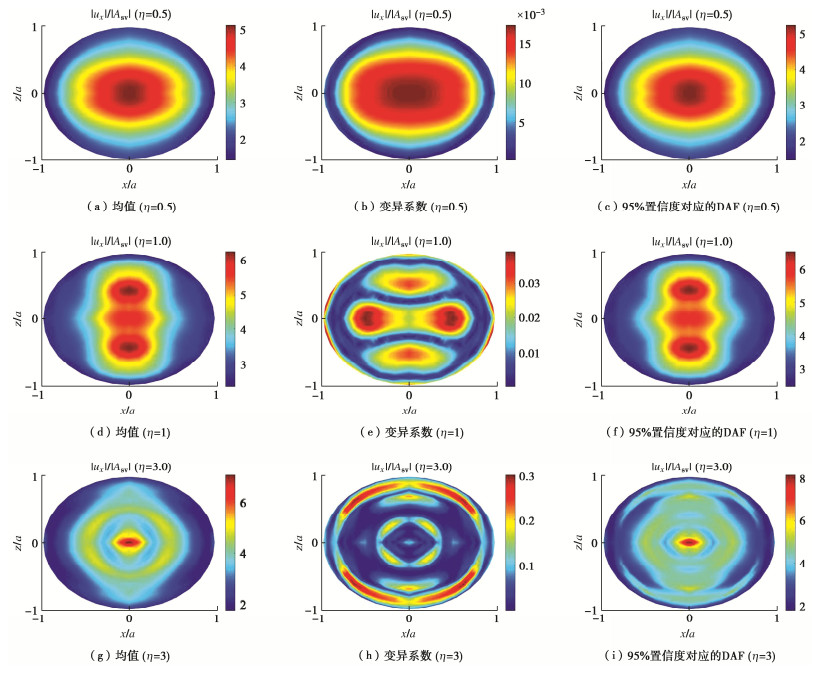
图 6给出了不同频率SV波入射下三维沉积盆地水平x向DAF均值、变异系数。根据概率分布函数可求得任意置信度对应的响应值，本算例以95%置信度为例进行结果分析，因此图 6同时给出了95%置信度对应的水平x向地表DAF。

图 6 低、中、高频SV波入射下沉积盆地水平x向DAF均值、变异系数和95%置信度对应的DAF

Figure 6. Mean values and COVs of DAFs, and DAFs corresponding to confidence of 95% of sedimentary basins at horizontal x-direction under low-, medium-, and high-frequency SV waves

下载: 全尺寸图片幻灯片

由图 6可知，当η=0.5和3.0时，沉积盆地地震动水平x向DAF均值表现出中心聚焦现象，与确定性参数下DAF分布类似。原因在于地震波反复折射导致其在盆地中心产生聚集，而由于地震波向外传播的过程中的能量耗散，盆地边缘DAF均值与自由场结果近似。盆地DAF变异性与位置、入射频率有关。当η=0.5时，变异系数峰值出现在盆地地表中心点，与均值结果一致；当η=1.0和3.0时，地表DAF变异系数分布与均值分布存在显著差异，例如，当η=3.0时，盆地边缘地震动表现出更强的变异性。数值上看，当η=0.5时，盆地水平x向DAF基本不受岩土参数随机性影响，变异系数在10^-3数量级，因此95%置信度对应的DAF与均值基本一致；当η=1.0时，盆地水平x向DAF变异系数最大值为0.04，变异性较入射波频率为0.5对应结果有所增大，但仍小于设定的岩土参数变异性（0.1）；当η=3.0时，盆地水平x向DAF变异系数最大值约为0.3，导致95%置信度对应的DAF约为4.0，相比均值增大了约60%，盆地中心点DAF变异系数约为0.1，导致95%置信度对应的DAF达到8.18，大于此位置的DAF均值（7.09）。

图 7 典型沉积盆地地表观测点DAF频谱

Figure 7. Frequency spectra of DAF of surface observation points in typical sedimentary basins

下载: 全尺寸图片幻灯片

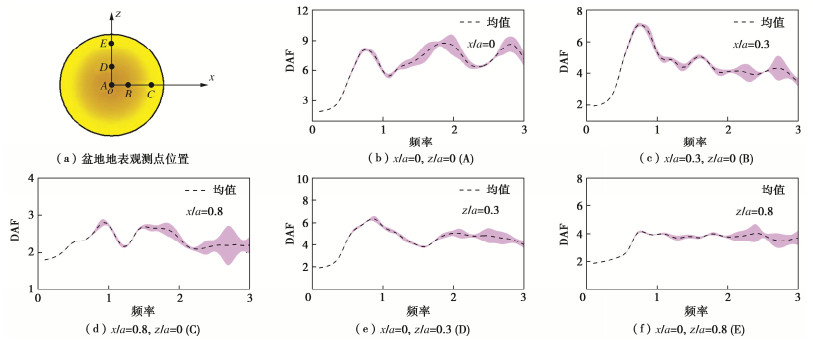
图 7给出了沉积盆地地表观测点水平x向DAF频谱，紫色区域为均值±均方差。由图 7可知，当入射波频率η < 1.0时，DAF受岩土参数随机性影响非常有限；当入射波频率η在1.0~2.0时，观测点A和B处DAF变异性有所增大；当入射波频率η > 2.0时，5个观测点DAF变异性均增幅明显，如当η=2.7时，观测点A，C处DAF均值±均方差范围分别可达1.6，2.1，而在相同频率下，观测点D，E处DAF均值±均方差范围则为1.3，1.2。结果表明，中高频入射波作用下，岩土参数随机性在地震波传播和散射过程中进行了传递，且表现出显著放大现象，但在低频地震波入射时，随机性基本未引起盆地地震响应较大离散，此特征与文献[12]中对于含随机岩土参数的二维沉积河谷地震动模拟所得结论类似。

3.3 时域结果与分析

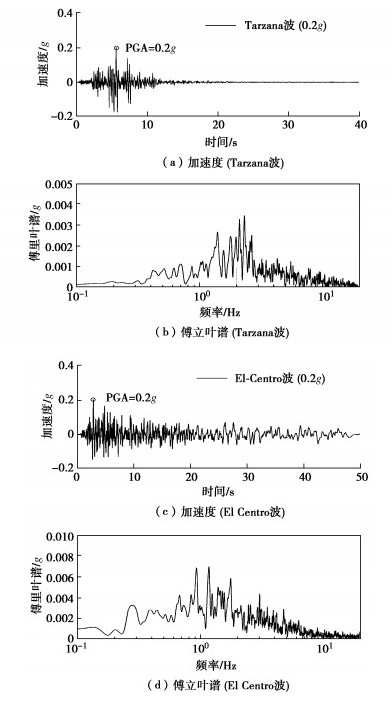
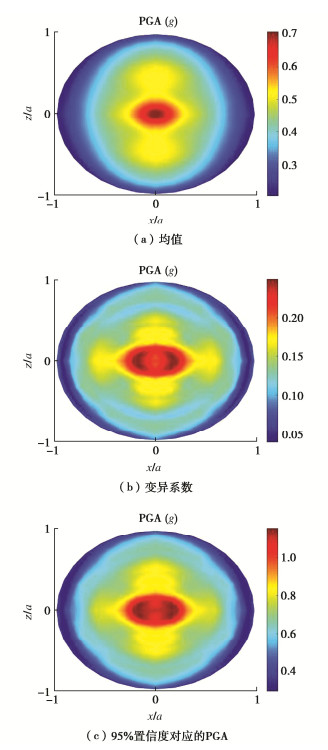
本节以PGA为考察指标，在时域内利用随机岩土参数对三维沉积盆地地震动的影响进行评估，需要指出的是，此处主要分析静力一致条件的参数尺度关系，对于动力一致条件的参数尺度关系还有待进一步研究。分别选择Tarzana波和El Centro波作为输入，PGA均调幅至0.2g，加速度时程和傅里叶幅值谱见图 8。由图 8可知，El Centro波携带的能量高于Tarzana波，Tarzana波能量集中于1~3 Hz，而El Centro波中高频能量更显著。图 9，10分别给出了Tarzana和El Centro地震波作用下三维沉积盆地PGA均值、变异系数和95%置信度对应的PGA。

图 8 Tarzana和El Centro地震波加速度时程和傅里叶幅值谱

Figure 8. Time histories of acceleration and spectra of Fourier amplitude of Tarzana and El Centro waves

下载: 全尺寸图片幻灯片

图 9 Tarzana波作用下沉积盆地PGA均值、变异系数和95%置信度对应的PGA

Figure 9. Mean values and COVs, and PGAs corresponding to confidence of 95% of sedimentary basins under Tarzana waves

下载: 全尺寸图片幻灯片

图 10 El Centro波作用下沉积盆地PGA均值、变异系数和95%置信度对应的PGA

Figure 10. Mean values and COVs, and PGAs corresponding to confidence of 95% of sedimentary basins under El Centro waves

下载: 全尺寸图片幻灯片

由图 9，10可知，沉积盆地PGA均值峰值出现在盆地地表中心点，表现出中心聚焦现象，地表中心点及其附近位置点PGA变异性较大，变异系数峰值出现在x/a=0.2，z/a=0处，约为0.24。由于Tarzana波和El Centro波在频域能量分布不同，沉积盆地PGA均值、变异系数空间分布均存在差异：Tarzana波作用下，盆地地表中心点PGA均值和95%置信度对应的PGA分别为0.71g和1.11g，而在El Centro波作用下同样的响应则是0.98g和1.31g，95%置信度对应的PGA较均值分别增大了56%和34%，El Centro波更高的能量引起了更大的盆地PGA均值。

随机性在地震波传播过程中可能产生放大或减弱，变化情况与盆地地表位置、基岩入射波能量分布均有关，虽然两种入射波作用下盆地地表PGA变异系数峰值近似，但其空间分布差异显著。本算例中，盆地边缘受岩土参数随机性影响有限，而盆地地表中心区域PGA变异性较强，且变异性和均值呈现非线性相关，尤其是El Centro波作用下，盆地z轴附近地表点均表现出强变异性，与均值分布差别较大。总体上，95%置信度对应的盆地PGA在数值以及空间分布上均和PGA均值差异显著。结果表明，岩土参数随机性对盆地PGA影响不可忽略，有必要在沉积盆地地震动参数确定时对其进行科学量化。

4. 结论

本文基于快速多极边界元法和人工神经网络，建立了一种考虑岩土参数随机性的三维沉积盆地地震动高效模拟方法，此方法可进一步拓展到其他复杂场地随机地震动模拟。结果表明：

（1）ANN可作为求解三维沉积盆地地震响应的代理模型，测试集决定系数可达0.982；本文所建方法适合处理含随机参数的沉积盆地地震动参数确定问题，具有良好的精度和稳定性，所分析算例的计算时间仅为常规蒙特卡洛模拟的3.4%。

（2）沉积盆地地表位移放大系数变异性与位置、入射频率有关：地表位移放大系数均值空间分布呈现中心聚焦现象，但变异性分布与均值存在显著差异；整体上看，地表位移放大系数变异性随入射频率增大而增大，低频波入射下，其受岩土参数随机性影响非常有限；当入射波无量纲频率η > 2.0时，盆地中心位移放大系数为6.5，远大于盆地边缘，但盆地边缘附近变异系数可达0.3，为岩土参数变异系数的3倍。

（3）沉积盆地PGA变异性与地表点位置、入射波能量分布有关。盆地PGA变异系数和均值分布呈现非线性相关特征，盆地边缘PGA受岩土参数随机性影响较小，而盆地地表中心区域PGA变异性显著，导致95%置信度对应的PGA可较均值增大56%，量化岩土参数随机性对沉积盆地地震动的影响具有重要意义。

图 1 本文所建方法流程图

Figure 1. Flow chart of proposed method

下载: 全尺寸图片幻灯片

图 2 三维沉积盆地计算模型

Figure 2. Computational model for 3D sedimentary basin

下载: 全尺寸图片幻灯片

图 3 ANN结构示意图

Figure 3. Diagram of ANN structure

下载: 全尺寸图片幻灯片

图 4 本文结果与文献[6]结果对比

Figure 4. Comparison between results in this study and those in literature ^[6]

下载: 全尺寸图片幻灯片

图 5 ANN代理模型性能验证

Figure 5. Performance verification of ANN model

下载: 全尺寸图片幻灯片

图 6 低、中、高频SV波入射下沉积盆地水平x向DAF均值、变异系数和95%置信度对应的DAF

Figure 6. Mean values and COVs of DAFs, and DAFs corresponding to confidence of 95% of sedimentary basins at horizontal x-direction under low-, medium-, and high-frequency SV waves

下载: 全尺寸图片幻灯片

图 7 典型沉积盆地地表观测点DAF频谱

Figure 7. Frequency spectra of DAF of surface observation points in typical sedimentary basins

下载: 全尺寸图片幻灯片

图 8 Tarzana和El Centro地震波加速度时程和傅里叶幅值谱

Figure 8. Time histories of acceleration and spectra of Fourier amplitude of Tarzana and El Centro waves

下载: 全尺寸图片幻灯片

图 9 Tarzana波作用下沉积盆地PGA均值、变异系数和95%置信度对应的PGA

Figure 9. Mean values and COVs, and PGAs corresponding to confidence of 95% of sedimentary basins under Tarzana waves

下载: 全尺寸图片幻灯片

图 10 El Centro波作用下沉积盆地PGA均值、变异系数和95%置信度对应的PGA

Figure 10. Mean values and COVs, and PGAs corresponding to confidence of 95% of sedimentary basins under El Centro waves

下载: 全尺寸图片幻灯片

表 1 验证模型输入参数

Table 1 Input parameters for validation model

参数	符号	名称	分布类型	均值	均方差	范围
参数	符号	名称	分布类型	均值	均方差	下限	上限
入射频率	η	入射频率	均匀分布	1.560	0.844	0.10	3
场地介质	μ	沉积盆地内泊松比	均匀分布	0.340	0.066	0.30	0.38
	β	沉积盆地内外剪切波速比	均匀分布	0.493	0.096	0.33	0.67
	ξ	沉积盆地内阻尼比	均匀分布	0.021	0.003	0.015	0.025
位置相关参数	x	x轴方向笛卡尔坐标	—	—	—	—	—
位置相关参数	z	z轴方向笛卡尔坐标	—	—	—	—	—

下载: 导出CSV

表 2 随机岩土参数信息

Table 2 Information of random geotechnical parameters

符号	名称	分布类型	均值	均方差变异系数	范围
符号	名称	分布类型	均值	均方差变异系数	下限	上限
μ	沉积盆地内泊松比	正态分布	0.339	0.034 0.100	0.300	0.380
β	沉积盆地内外剪切波速比	正态分布	0.493	0.049 0.100	0.330	0.670
ξ	沉积盆地内阻尼比	正态分布	0.020	0.002 0.100	0.015	0.025

下载: 导出CSV

参考文献(20)

[1]	李平, 薄景山, 李孝波, 等. 安宁河河谷及邛海地区土层场地对地震动的放大作用[J]. 岩土工程学报, 2016, 38(2): 362-369. doi: 10.11779/CJGE201602022 LI Ping, BO Jingshan, LI Xiaobo, et al. Amplification effect of soil sites on ground motion in Anning River valley and Qionghai Lake area[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(2): 362-369. (in Chinese) doi: 10.11779/CJGE201602022
[2]	高玉峰, 代登辉, 张宁. 河谷地形地震放大效应研究进展与展望[J]. 防灾减灾工程学报, 2021, 41(4): 734-752. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK202104007.htm GAO Yufeng, DAI Denghui, ZHANG Ning. Progress and prospect of topographic amplification effects of seismic wave in canyon sites[J]. Journal of Disaster Prevention and Mitigation Engineering, 2021, 41(4): 734-752. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK202104007.htm
[3]	赵登科, 王自法, 刘渊, 等. 基于新西兰实际震害资料的地震损失不确定性分析[J]. 地震工程与工程振动, 2021, 41(2): 84-95. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC202102009.htm ZHAO Dengke, WANG Zifa, LIU Yuan, et al. Earthquake loss uncertainty based on detailed loss data in New Zealand[J]. Earthquake Engineering and Engineering Vibration, 2021, 41(2): 84-95. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC202102009.htm
[4]	SMERZINI C, PAOLUCCI R, STUPAZZINI M. Comparison of 3D, 2D and 1D numerical approaches to predict long period earthquake ground motion in the Gubbio plain, Central Italy[J]. Bulletin of Earthquake Engineering, 2011, 9(6): 2007-2029. doi: 10.1007/s10518-011-9289-8
[5]	赵成刚, 韩铮. 半球形饱和土沉积谷场地对入射平面Rayleigh波的三维散射问题的解析解[J]. 地球物理学报, 2007, 50(3): 905-914. doi: 10.3321/j.issn:0001-5733.2007.03.032 ZHAO Chenggang, HAN Zheng. Three-dimensional scattering and diffraction of plane Rayleigh-waves by a hemispherical alluvial valley with saturated soil deposit[J]. Chinese Journal of Geophysics, 2007, 50(3): 905-914. (in Chinese) doi: 10.3321/j.issn:0001-5733.2007.03.032
[6]	MOSSESSIAN T K, DRAVINSKI M. Amplification of elastic waves by a three-dimensional valley: Part 1: Steady state response[J]. Earthquake Engineering Structural Dynamics, 1990, 19(5): 667-680. doi: 10.1002/eqe.4290190504
[7]	LIANG J W, WU M T, BA Z N, et al. Surface motion of a layered transversely isotropic half-space with a 3D arbitrary-shaped alluvial valley under qP-, qSV-and SH-waves[J]. Soil Dynamics and Earthquake Engineering, 2021, 140: 106388. doi: 10.1016/j.soildyn.2020.106388
[8]	刘启方. 2014年鲁甸地震龙头山镇盆地共振效应研究[J]. 地震工程与工程振动, 2021, 41(2): 43-52. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC202102005.htm LIU Qifang. Study on the basin resonance effect in Longtoushan Town during the 2014 Ludian earthquake[J]. Earthquake Engineering and Engineering Vibration, 2021, 41(2): 43-52. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC202102005.htm
[9]	韩天成, 于彦彦, 丁海平. 直下型断层的破裂速度对盆地地震效应的影响[J]. 地震学报, 2020, 42(4): 457-470, I0002. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXB202004007.htm HAN Tiancheng, YU Yanyan, DING Haiping. Influence of rupture velocity of the directly-beneath fault on the basin seismic effect[J]. Acta Seismologica Sinica, 2020, 42(4): 457-470, I0002. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXB202004007.htm
[10]	BARANI S, DE FERRARI R, FERRETTI G, et al. Assessing the effectiveness of soil parameters for ground response characterization and soil classification[J]. Earthquake Spectra, 2008, 24: 565-597. doi: 10.1193/1.2946440
[11]	LIU W X, HSEIN JUANG C, CHEN Q S, et al. Dynamic site response analysis in the face of uncertainty: an approach based on response surface method[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2021, 45(12): 1854-1867. doi: 10.1002/nag.3245
[12]	MENG S B, LI W X, LIU Z X. A probability-based efficient assessment of seismic wave scattering in complex topography with geo-property uncertainty[J]. Waves in Random and Complex Media, 2022. DOI: 10.1080/17455030.2022.2086321.
[13]	罗仁昱, 陈继锋, 尹欣欣. 机器学习在地震事件自动检测中的应用综述[J]. 地球物理学进展, 2021, 36(3): 923-932. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ202103008.htm LUO Renyu, CHEN Jifeng, YIN Xinxin. Review of the applications of machine learning in automatic detection of seismic events[J]. Progress in Geophysics, 2021, 36(3): 923-932. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DQWJ202103008.htm
[14]	孟思博, 赵嘉玮, 刘中宪. 基于差分进化-人工神经网络的沉积河谷地震动放大效应预测模型[J]. 地震学报, 2022, 44(1): 170-181. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXB202201016.htm MENG Sibo, ZHAO Jiawei, LIU Zhongxian. Prediction model of seismic amplification effect in sedimentary valley based on differential evolution-artificial neural network[J]. Acta Seismologica Sinica, 2022, 44(1): 170-181. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXB202201016.htm
[15]	ZHOU H, LI J, CHEN X. Establishment of a seismic topographic effect prediction model in the Lushan Ms 7.0 earthquake area[J]. Geophysical Journal International, 2020, 221(1): 273-288. doi: 10.1093/gji/ggaa003
[16]	HAMIDREZA T, SAMAN S K. Evaluation of effect of soil characteristics on the seismic amplification factor using the neural network and reliability concept[J]. Arabian Journal of Geosciences, 2015, 8(6): 3881-3891. doi: 10.1007/s12517-014-1458-z
[17]	WOLF J P. Dynamic Soil-Structure Interaction[M]. Englewood Cliffs, NJ: Prentice-Hall, 1985.
[18]	ROKHLIN V. Diagonal forms of translation operators for the Helmholtz equation in three dimensions[J]. Applied and Computational Harmonic Analysis, 1993, 1(1): 82-93. doi: 10.1006/acha.1993.1006
[19]	LIU Z X, HUANG Z E, ZHANG Z, et al. Three-dimensional preconditioned FM-IBEM solution to broadband-frequency seismic wave scattering in a layered sedimentary basin[J]. Engineering Analysis with Boundary Elements, 2021, 133: 1-18.
[20]	BAZZURRO P, CORNELL C A. Ground-motion amplification in nonlinear soil sites with uncertain properties[J]. Bulletin of the Seismological Society of America, 2004, 94: 2090-2109.