0.   引言

由于复杂的地质和水文条件，在隧洞施工中经常会因遇到岩溶、破碎带、暗河等异常地质体而造成的塌方、突水突泥等各种地质灾害，造成严重的人员伤亡和财产损失。因此，在隧洞掘进过程中，准确获取掌子面前方岩体的物性参数，推断地质构造形态和潜在的地质风险，是目前隧洞工程研究的重点和难点^[1]。基于地震波法的超前地质预报方法具有探测距离长、预报精度高等优点，是目前应用最广泛的方法。其中，纵波速度是岩体物性参数中最基础、最重要的参数。但是由于数据处理方法的限制，目前主流技术主要采用速度分析、层析成像等只利用地震数据走时信息的方法对岩体速度信息进行提取，其精度有限；对于异常地质体界面的成像方法主要采用基于单程波的Kirchhoff积分法偏移，该方法对于远距离构造成像精度不高且依赖于精确的走时信息，而精确的走时信息同样依赖于精确的速度模型。因此，对于隧洞掌子面前方岩体的高精度速度建模和成像是亟待解决的问题。

油气地震勘探领域的全波形反演（FWI）技术利用叠前地震数据的全部运动学和动力学信息（振幅、相位、走时等），将强非线性反演问题近似线性化求解，通过构建目标函数对初始模型进行基于梯度下降的迭代更新，实现对被探测区域内介质物性参数的高精度建模^[2-3]。FWI是一个基于Born近似下的针对弱散射介质的局部优化问题，这使得FWI对于初始模型的精度依赖性很高。当初始模型与真实岩体速度分布相差较大或地震数据中缺少足够的低频分量时，FWI会产生周期跳跃现象，导致基于局部优化算法的FWI收敛到局部极值而无法跳出^[4]。基于频率尺度分解的多尺度反演策略是提升FWI收敛性、减弱FWI对初始模型和低频信息依赖性的重要手段。Bunks提出用低通滤波器分频段将地震数据分解为不同频率尺度，采用在时间域从低频段到高频段的反演策略可以使FWI目标函数更好的收敛，减少了局部极值的出现，缓解了周期跳跃问题^[5]。Boonyasiriwat等^[6]提出利用维纳滤波对地震数据进行频带分解，研究并给出了最佳频带选择策略来进行多尺度FWI。郭雪豹等^[7]提出在将地震数据变换到频率域并进行指数衰减以实现不同频段数据在时间域的FWI。

相比于单程波偏移成像，基于双程波动方程矢量波动理论的逆时偏移（RTM）技术可以模拟更加复杂介质的情况，能够对多次波、回转波等进行成像，可以更好地恢复地质构造形态，且不受倾角限制，对陡倾角和强横向变速体都有很好的成像效果，同时具有保幅优势，可以对精微构造和复杂构造进行高精度成像。逆时偏移在20世纪80年代由Whitmore^[8]首先提出，McMechan等^[9]利用二维声波方程在连续和变速介质中实现了逆时偏移。刘红伟等^[10]提出利用拉普拉斯算子进行滤波消除成像过程中产生的低频噪声，提高成像的分辨率。Chen等^[11]利用坡印廷矢量将波场上下行波和左右行波进行分离，并结合互相关成像成像条件，压制成像结果中的低频噪声。

为提高隧洞地震波法超前地质预报的精度和距离，需要在隧洞施工现场采集多炮地震数据提高覆盖次数和照明强度。由于炮孔质量不同、炸药剂量差异、以及炸药与围岩耦合情况不同等因素，检波器接收到的来自不同炮孔的数据存在能量差异；另外，震源激发时产生的高频声波干扰通过隧洞空间内的空气传播至检波器，造成接收数据中有效反射信号被高频噪声干扰。因此，本文提出将互相关目标函数取代常规最小二乘目标函数进行FWI，该目标函数可以减弱振幅信息准确性对反演结果的影响，并具有很强的抗噪性。FWI的计算耗时主要集中在正演模拟部分，炮数越多则计算耗时越长。①一方面，隧洞超前地质预报对时效性要求很高；②另一方面，隧洞现场的计算硬件条件有限，难以满足大规模并行计算的要求。因此，提出隧洞地震数据混合震源编码策略，将所有单炮记录按照一定编码规则组合成一个混合地震记录，从而将一次迭代过程中的多次单炮正演缩短为一次混合震源正演，在保证反演结果精度的前提下极大地提高了FWI的计算效率。为提高异常地质体的成像精度，本文提出利用FWI提供的高精度隧洞岩体超前速度模型进行基于震源-检波器双向照明补偿互相关成像条件的RTM对隧洞掌子面前方异常地质体构造界面进行精准成像。本文设计了4种隧洞常见地质体模型，并通过多组数值试验验证了本文提出方法的有效性和先进性，并为实际隧洞工程应用提供了理论支撑。

1.   时间域FWI方法

1.1   常规时间域FWI

常规FWI的最小二乘目标函数可表示为

式中：J为目标函数；v为岩体纵波速度；t为时间变量，N_r和N_s分别为总检波器数和总炮数；${d_{{\text{syn}}}}$和${d_{{\text{obs}}}}$分别为初始模型上正演得到的模拟数据和隧洞中实际采集到的观测数据。FWI中梯度是决定模型参数更新方向的核心。为了得到目标函数的收敛方向即梯度，需要计算其对反演所需要的地下介质物性参数的导数，可以表示为

式中，$\left\langle \cdot \right\rangle$表示内积。为减少计算耗时采用伴随状态法计算梯度，其中常规FWI的伴随源可以表示为

式中，$\lambda$为伴随源。则常规FWI的迭代过程可以表示为

式中：k为迭代次数；$\alpha$和g分别为步长和梯度。

1.2   互相关目标函数及梯度

为减弱不同单炮记录之间能量差异的影响并提高反演过程的抗噪性，采用互相关目标函数（Choi等^[12]）代替常规最小二乘目标函数来进行隧洞地震数据的FWI。互相关目标函数可表示为

根据伴随状态法求取梯度，目标函数对速度参数的导数可以表示为

式中，χ为伴随源

则时间域FWI梯度公式可以被简化为

式中：${u_{\text{f}}}$为震源正传播场；$u_{\text{b}}^\chi$为以χ为伴随源的逆时反传波场。

1.3   混合震源编码策略

为满足隧洞超前地质预报的时效性，缩短时间域FWI的计算时间，借鉴地震勘探领域的“超级炮”概念（张盼等^[13]），提出隧洞地震数据混合震源编码策略。一次地震波法超前地质预报所使用震源数量为s，则组合为一个混合震源后计算时间缩短至原来的1/s，将极大地提升全波形反演的计算效率。如果将多个单炮记录简单地线性叠加则会产生较强的串扰噪声，影响反演结果精度。因此，采用动态混合震源编码策略方法压制串扰噪声，则一个混合震源数据可以表示为

式中：S为一个混合震源数据；s_i为第i个震源的单炮记录；A_rand为随机振幅极性编码；s_i(x, z, t)为在震源位置(x, z)处的函数；δ(t-Δt_rand)为随机延迟时间为Δt_rand的δ函数；$\cdot$表示乘积；*表示褶积；PH_rand(·)为随机相位编码算子，可以表示为

式中：${\theta _{{\text{rand}}}}$为随机相位旋转角；H(α)为信号α的希尔伯特变换。在反演迭代时，设置迭代次数k为10的整数倍时对观测数据重新进行一次编码，以保证地震照明的均匀性。

2.   RTM成像方法

RTM技术是通过双程波波动方程在时间上对信接收号进行反向外推来实现偏移过程，其波场模拟更加符合复杂隧洞岩体构造的情况，可以更好地对多种异常地质体结构面进行精细刻画。采用炮点和检波点双向照明补偿的互相关成像条件提高远距离预报时地质体的成像精度：

式中：Image表示成像条件；${u_{\text{s}}}$和${u_{\text{r}}}$分别为震源波场和检波点波场。为消除成像结果中由震源波场和检波点波场同方向行波相关产生的低频噪声，对成像结果进行四阶Laplace滤波以消除噪声干扰，提高成像精度：

式中：I和I_L分别为Laplace滤波前后的成像结果；ω为角频率；θ为入射角。对I_L乘以v⁴进行速度补偿，进一步提高成像结果中的高波数成分。

3.   数值试验

3.1   隧洞观测系统及多种地质模型FWI试验

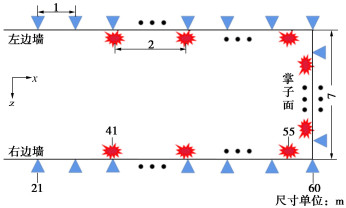
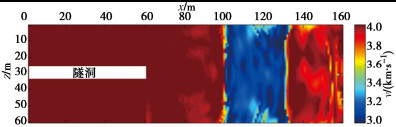
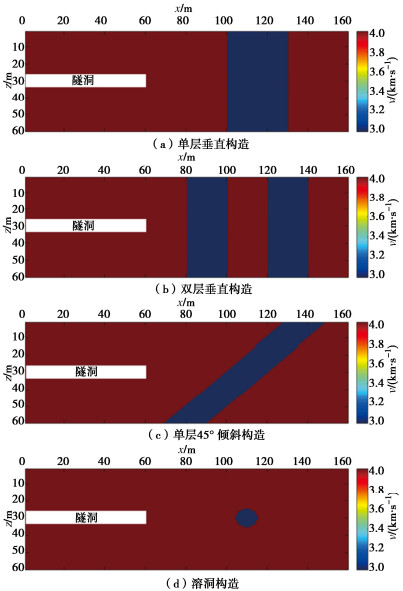
为测试本文所提出方法的有效性，设计了4种隧洞常见地质体模型（图 1）进行隧洞岩体纵波速度FWI和RTM的数值试验。图 1（a）~（d）分别是常见的隧洞单层垂直构造、双层垂直构造、单层倾斜构造和溶洞地质体模型，模型网格大小为60×160，网格间距为1 m，其中隧洞洞身长60 m，宽7 m，隧洞掘进方向为x轴正方向。初始模型采用速度为4 km/s的均匀速度模型。观测系统如图 2所示，在左右边墙21~60 m处以及掌子面上布设检波器，检波器间距为1 m，共布设87个检波器；在左右边墙41~55 m处及掌子面上布设震源，震源间距为2 m，共布设20个震源。震源子波使用主频为200 Hz的雷克子波，正演计算采用10阶精度交错网格有限差分算法结合20层PML边界条件。总采样时间为1 s，采样间隔为0.0001 s。反演方法采用本文提出的结合了混合震源编码策略和互相关目标函数的FWI对速度模型进行迭代更新，并使用从低频段到高频段的多尺度反演步骤。在更新速度模型时，只对掌子面前方岩体的纵波速度参数进行更新，洞身所对应的岩体速度保持固定。

图  1  4种隧洞常见地质体构造模型

Figure  1.  Four kinds of frequent geological models in tunnel engineering

下载: 全尺寸图片 幻灯片

图  2  隧洞地震观测系统

Figure  2.  Geometry of tunnel seismic detection

下载: 全尺寸图片 幻灯片

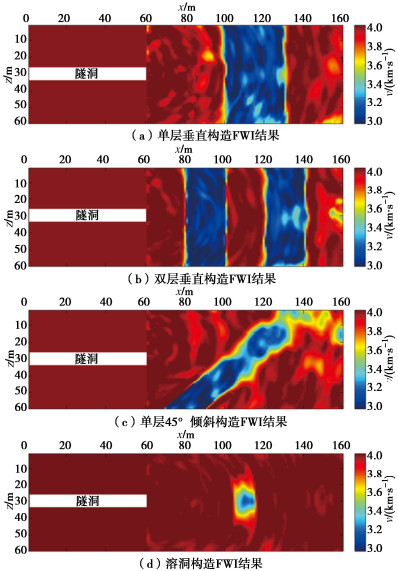
图 3（a）为单层垂直构造模型的FWI结果，其中垂直构造与均匀围岩的交界面清晰，垂直构造内部的低速异常被准确地反演出来，且没有出现由周期跳跃现象产生的假异常；图 3（b）为双层垂直构造模型的FWI结果，其中两个垂直构造与围岩的交界面均被清晰地刻画出来，两个垂直构造内部的低速异常均被准确地反演出来，两个异常体之间的均匀围岩速度没有产生错误的扰动；图 3（c）为单层45°倾斜构造模型的FWI结果，其中低速异常体的速度值和构造倾角均被准确反演出来，且异常体靠近掌子面一端的反演精度高于其远离掌子面一端的反演精度；图 3（d）为隧洞轴线方向溶洞模型的FWI结果，其中溶洞构造的球状低速异常被准确地反演出来，且未在其它位置产生假异常。由于隧洞狭窄观测孔径的限制，垂直于隧洞轴线方向的异常体边界反射波信号可以被布置在隧洞内及掌子面的检波器有效地接收到，随着异常体边界倾角与隧洞轴线方向逐渐减小，有效反射信号越来越难以被检波器接收到。因此，当观测系统全部布置在隧洞内时，FWI对于异常体垂直于隧洞轴线方向的边界反演精度高，而对平行与隧洞轴线方向的边界反演精度较低。从而对于垂直构造FWI结果更为精确；对于溶洞模型在x方向边界位置及形态反演较为准确，而在z方向边界位置及形态反演结果欠佳；对于倾斜构造模型，其边界反射波方向与倾斜面垂直，因此靠近掌子面一侧的异常体边界的反射信号可以被隧洞内检波器有效地接收到，而越远离掌子面一侧的异常体边界其反射波通过的隧洞内检波器少，从而导致倾斜构造在靠近掌子面一侧反演精度高，而在远离掌子面一侧反演精度较低。

图  3  图 1所示4种隧洞常见地质体构造模型的FWI结果

Figure  3.  FWI results of 4 kinds of frequent geological models in tunnel engineering shown in Fig. 1

下载: 全尺寸图片 幻灯片

3.2   观测数据能量不均及含噪情况的FWI试验

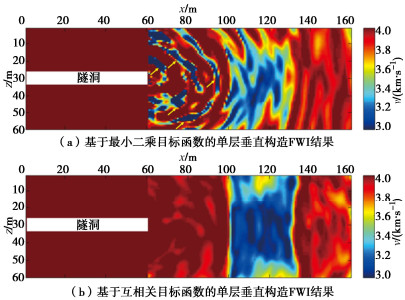
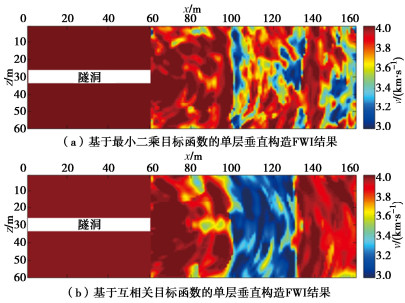
为模拟实际隧洞地震波法超前地质预报工作中震源能量不均的情况，对基于式（9）进行混合震源编码后的观测数据再进行一次随机振幅能量编码，使之与模拟数据对应单炮记录的能量存在差异。以图 1（a）所示单层垂直构造模型为真实速度模型测试观测数据能量不均情况下不同目标函数FWI结果。图 4（a）为基于最小二乘目标函数的单层垂直构造模型反演结果，其中存在明显的假异常（图中黄色箭头标识处），这些位置出现了与真实速度模型（4 km/s）明显偏离的多个弧状低速体，且低速层状异常体的构造形态并未准确的反演出来。由于最小二乘目标函数是观测数据和模拟数据在对应时间轴上点对点相减计算的，其对模拟数据振幅信息的准确度依赖性强。因此，观测数据震源能量不均影响FWI的收敛，得到不准确的速度模型。基于互相关目标函数的FWI通过归一化过程减弱振幅信息对反演的影响，突出线性程度更高的相位信息对梯度计算的权重，可以避免错误振幅信息对FWI收敛性的影响，在观测数据震源能量不均时依然能得到准确的反演结果（图 4（b）。

图  4  震源能量不均时两种目标函数FWI结果对比

Figure  4.  FWI results of global-correlation misfit function and least squares misfit function under different energies of seismic source

下载: 全尺寸图片 幻灯片

对纯净的地震记录加入强噪声以测试基于互相关目标函数FWI的抗噪性。以图 1（a）所示单层垂直构造模型为真实速度模型测试观测数据含强噪声（加噪后的观测数据信噪比为-1.2）情况下不同目标函数FWI结果。图 5（a）显示了基于最小二乘目标函数的单层垂直构造模型反演结果。由于最小二乘目标函数对噪声敏感，强噪声严重影响反演结果的精度，模型中的低速层状结构未能被准确建模，且在隧洞里程140~160 m内出现了假低速异常体。图 5（b）中所示FWI结果与真实模型相近，但相较于纯净数据FWI结果（图 3（a））精度有所降低。强噪声掩盖并破坏了纯净数据中的来自于异常地质体的有效反射信号，虽然基于互相关目标函数的FWI可以在一定程度上突出有效信号、减弱噪声的影响，但并不能将噪声的干扰完全消除，因此图 5（b）所示FWI结果中局部出现了因噪声干扰产生的小尺度假异常，但主要异常体低速层状构造被准确地还原出来。

图  5  观测数据含噪时两种目标函数FWI结果对比

Figure  5.  FWI results of global-correlation misfit function and least squares misfit function under observed data contaminated by strong random noise

下载: 全尺寸图片 幻灯片

3.3   混合震源编码与单炮FWI对比

以图 1（a）所示单层垂直构造模型为真实速度模型测试了基于单炮隧洞地震数据和基于混合震源隧洞地震数据的FWI计算效率及反演精度。图 6为基于单炮隧洞地震数据的FWI结果。为了衡量反演结果与真实模型之间的差距，定义一个误差系数：

图  6  单炮隧洞数据FWI结果

Figure  6.  FWI results of seismic data of tunnel with a single source

下载: 全尺寸图片 幻灯片

式中：p为误差系数；${v_{{\text{inv}}}}$和${v_{\text{t}}}$分别为反演结果和真实模型；X和Z分别为模型x和z方向的网格点总数。分别将图 1（a）所示真实模型和图 3（a），6所示FWI结果代入式（13）中，可分别得到基于单炮隧洞地震数据和混合震源隧洞地震数据FWI结果的误差系数。表 1为单炮数据与混合震源数据FWI对比，可见单炮数据反演耗时远高于混合震源数据，其耗时为混合震源的20倍即单炮数据的震源总数。虽然单炮数据反演精度略高于混合震源数据，但两者误差系数相差小于0.1%，相比于混合震源编码提升计算效率的程度，反演精度的降低在可接受范围内，并不影响后续的地质解译和潜在地质灾害预警。本节试验验证了本文所提出的隧洞地震数据混合震源编码策略可以实现在保证反演精度的前提下显著提升计算效率。

表  1  单炮数据与混合震源数据FWI对比

Table  1.  Comparison of FWI between single-source and multi- source data

类型	震源/ 个	单次正演耗时/s	迭代次数/次	反演 总耗时/s	误差系数/%
单炮 数据	20	5.6	160	36800	1.38
混合震源数据	1	5.6	160	1840	1.46

下载: 导出CSV 

| 显示表格

3.4   常见隧洞地质体模型RTM成像试验

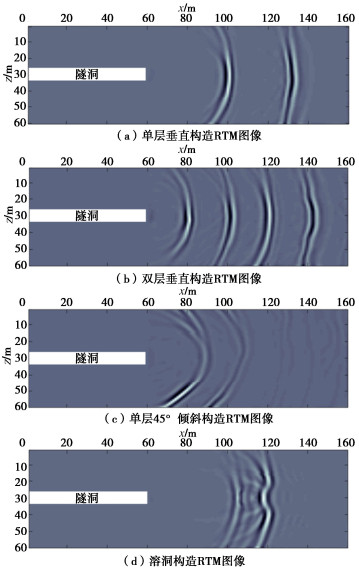
本节利用基于本文提出的FWI方法（图 3）获得的4种常见隧洞地质体速度模型进行RTM成像，成像条件为第3节中所述双向照明补偿的互相关成像条件，并采用4阶Laplace滤波对偏移图像进行低频噪声压制。图 7（a）为单层垂直构造模型RTM图像，其中成像点准确收敛于围岩速度变化的交界面（隧洞里程100，130 m处），且没有低频噪声干扰；图 7（b）为双层垂直构造模型RTM图像，其中成像点准确收敛于两个低速异常体与围岩交界面（隧洞里程80，100，120，140 m处），且没有低频噪声干扰；图 7（c）为单层45°倾斜构造模型RTM图像，在低速异常体靠近掌子面一侧的成像位置较准确，而由于隧洞狭小的观测孔径以及异常体倾斜角度较大，检波器难以接收来自异常体远离掌子面一侧的有效反射信号，因此在RTM图像中远离掌子面一侧的成像效果欠佳；图 7（d）为溶洞构造模型RTM图像，其中掌子面前方存在明显的球状同相轴，溶洞的形态和位置被准确成像出来，且没有低频噪声干扰。

图  7  以图 3所示FWI结果为速度模型的图 1所示4种隧洞常

Figure  7.  RTM images of 4 kinds of frequent geological models in tunnel engineering shown in Fig. 1 based on velocity models shown in Fig. 3

下载: 全尺寸图片 幻灯片

作为对比，图 8给出了直接利用常速度（4 km/s）为速度模型的4种隧洞常见地质体构造模型的RTM图像。图 8（a），（b）中可以看到由于速度模型中不存在低速异常体，无论是单层垂直构造还是双层垂直构造，除了离掌子面最近的边界位置正确以外，其它边界位置都因为速度值过高而产生了不同程度的后移，造成了异常体边界位置的错误成像；图 8为单层45°倾斜构造RTM结果，相比于图 7（c）所示RTM结果，单层45°倾斜构造在远离掌子面一侧的边界位置出现了后移，且边界倾角有所增大；图 8（d）所示溶洞构造RTM结果完全没有将溶洞的弧形边界刻画出来，其成像结果易被误判为层状构造。

图  8  以常速度（4 km/s）为速度模型的图 1所示4种隧洞常见

Figure  8.  RTM images of 4 kinds of frequent geological models in tunnel engineering shown in Fig. 1 based on initial velocity model (4km/s)

下载: 全尺寸图片 幻灯片

本节试验一方面验证了基于本文提出的FWI方法所获得的的速度模型是准确可靠的，另一方面验证了基于双程波的RTM技术应用于隧洞中可以实现岩体构造分界面的准确成像。

4.   结论

本文将油气勘探领域前沿的全波形反演技术和逆时偏移技术应用于隧洞超前地质预报中，解决了隧洞地震波法超前地质预报工程实践中遇到的关键问题和特有问题，得到以下3点结论。

（1）基于互相关目标函数的隧洞地震数据FWI方法有效减弱了反演对于子波振幅准确性的依赖并提高了反演过程的抗噪性，提升了反演结果的精度。

（2）基于混合震源编码的隧洞地震数据FWI方法在保证反演结果精度的同时极大地提升了计算效率，满足隧洞超前地质预报对于时效性要求。

（3）在FWI提供的精准速度模型的基础上，采用RTM技术对异常地质体边界进行精准刻画，并结合双向照明补偿和四阶Laplace滤波进一步提升成像精度。