Flexural tests and numerical simulations of prestressed concrete pipe piles with partial hybrid reinforcement based on support of foundation pits
-
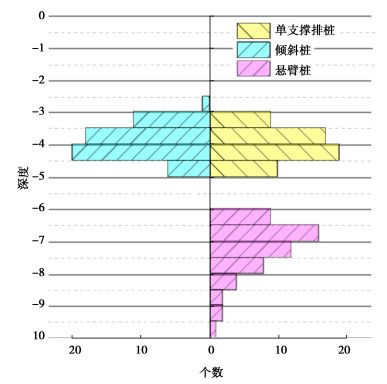
摘要: 复式配筋预应力混凝土管桩（PRC管桩）作为基坑支护桩使用时，为提高非预应力钢筋的利用效率，提出将区段配置非预应力钢筋的管桩作为基坑支护桩。通过对天津地区80个基坑工程中的支护桩弯矩分布情况统计分析，并对区段复式配筋预应力混凝土管桩（PR-PHC管桩）进行足尺抗弯试验及有限元分析，研究区段配筋的可行性和PR-PHC管桩的抗弯性能。研究表明，单支撑排桩、倾斜桩及悬臂桩的桩身弯矩区间分布具有规律性。PR-PHC管桩区段配置的非预应力筋，可以提高其抗弯极限承载力及其抗弯刚度，并有效改善桩身裂缝的展开情况，构建的数值模型可以较好地反映试验的实际情况。并对PR-PHC管桩在实际应用中可能遇到的不利工况做了影响分析。研究结果表明可以在基坑工程中使用PR-PHC管桩替代PRC管桩，减少钢筋使用量，促进碳减排。Abstract: When the prestressed concrete pipe piles with hybrid reinforcement (PRC pipe pile) are used as the supporting piles of foundation pits, in order to improve the utilization efficiency of non-prestressed reinforcement, it is proposed to use the pipe pile with non-prestressed reinforcement in the section as the supporting piles. Through the statistical analysis of the moment distribution of the supporting piles in 80 foundation pit projects in Tianjin, the full-scale bending tests and finite element analyses of the prestressed high-strength concrete pipe piles with partial hybrid reinforcement (PR-PHC pipe piles), the feasibility of the sectional reinforcement and the bending resistance of the PR-PHC pipe piles are studied. The research results show that the interval distribution of the bending moment of the pile shaft of single support row piles, inclined piles and cantilever piles has regularity. The non-prestressed reinforcement configured in the section of PR-PHC pipe piles can improve its ultimate bending bearing capacity and bending stiffness, and effectively improve the spread of pile cracks. The proposed numerical model can better reflect the actual situation of the tests. In addition, the adverse working conditions that may be encountered in the practical application of PR-PHC pipe piles are analyzed. It is proved that the PR-PHC pipe piles can be used to replace the PRC ones in foundation pit engineering, which reduces the use of reinforcement and promotes the carbon emission reduction.
-
0. 引言
由于岩土体形成过程涉及多形式且复杂的物化作用，导致岩土体参数存在空间变异性，该变异性对岩土结构物（如：边坡、桩基础、隧道等）具有较大影响，这一事实已逐渐被人们所认识[1-6]。如何准确地表征岩土体参数空间变异性，并进行高效边坡可靠度分析已成为岩土工程领域目前研究热点之一。
岩土体的空间变异性可在随机场理论体系中进行模拟，其中Karhunen-Loève（K-L）级数展开法具有较好的多参数适应性，可以在考虑波动范围的情况下对随机场进行较好的离散[7]。另一方面，为有效地进行边坡可靠度分析，采用代理模型可减少边坡确定性分析模型的调用次数达到降低计算量的目的。代理模型以少量样本点构建近似边坡极限状态函数，进而以代理模型响应值评估边坡失效概率Pf[8]。常用代理模型中的多元自适应回归样条（简称MARS）可以根据输入输出变量之间的关系构建精度较高的模型，无需进行函数形式预设[9-10]。代理模型针对整个样本空间进行选点建模，在不同子空间中精度不同，尤其是在失效域附近样本点较少。为此，部分学者提出在失效域附近进行代理模型的优化，如：苏永华等[11]提出基于Kriging的边坡稳定可靠度主动搜索法；张天龙等[12]提出引入径向基插值函数，结合主动学习的策略，建立数值分析模型的显式代理模型。然而，上述方法均忽略了土体参数的空间变异性，这必将导致评估结果不准确。在考虑边坡土体参数空间变异时，随机场离散的随机变量矩阵往往具有较高的维度，这将导致模型陷入高维诅咒[13]。为解决该问题，部分学者提出对输入的随机变量矩阵进行降维处理。Li[14]提出的充足降维法中的分段逆回归具有较高的可靠性并易于实现而得到广泛的应用。此外，在实际岩土工程中，常会遇见边坡Pf较小的情况，使用传统蒙特卡洛模拟（简称MCS）方法选取计算样本，会出现计算机内存溢出情况，限制了代理模型的应用。
为在考虑参数空间变异性情况下准确高效地开展小失效概率的边坡可靠度分析，本文提出了一种基于分段逆回归的主动学习多元自适应回归样条法与子集模拟结合的边坡可靠度分析方法。首先，介绍了采用K-L展开法模拟土体参数空间变异性的理论。接着，通过分段逆回归方法（简称SIR）降维，将降维后的随机变量矩阵与安全系数（FS）矩阵相结合构建初始MARS模型。其次，利用主动学习函数反复选取最优样本点更新MARS模型，当模型达到阈值要求时，采用子集模拟方法（简称SS）对边坡进行可靠度分析。最后，采用两个典型边坡算例，验证本文所提方法的准确性与稳健性。
1. 岩土体参数空间变异性表征
1.1 岩土体参数的空间变异性
岩土体内各点之间存在一定的相关性，土体内任意两点之间的关系通常采用自相关函数表示。高斯型自相关函数具有连续可导的优点[14]，本文选取该自相关函数，具体的表达式为
$$ \rho ({\psi _{\boldsymbol{x}}},{\psi _y}) = 1/\exp \left[ {\frac{{\nu _x^2}}{{\lambda _h^2}} + \frac{{\nu _y^2}}{{\lambda _v^2}}} \right] 。 $$ (1) 式中：ρ(ψx, ψy)为自相关函数；$ \lambda _h^{} $和$ \lambda _v^{} $分别为水平与垂直相关距离；νx和νy分别为岩土体内两点对应坐标的差值。
1.2 基于Karhunen-Loève展开法的空间变异岩土体特征参数模拟
在保证精度的前提下，通常截取前r个较大的特征值和相对应的特征向量，以提高计算效率。将对数随机场H离散为一组独立标准随机变量，对于第i（i=1, 2, 3, …, N）个随机场K-L离散结果可表示为[7]
$$ {\boldsymbol{\tilde H}}_i^{}(x,y) = \exp ({\mu _{\ln i}} + \sum\limits_{j = 1}^r {{\sigma _{\ln i}}\sqrt {{\lambda _i}} {f_j}(x,y){\chi _{i,j}}} )\;\;\;({\text{ }}i = c,\varphi ) 。 $$ (2) 式中：i为需要离散的参数；${\lambda _j}$和${f_j}(x,y)$分别是自相关函数中第j个特征值和特征函数；c和φ分别为土体的黏聚力与内摩擦角；${\chi _{i,j}}$为相关标准正态随机变量，由独立标准正态随机样本矩阵转化得到；${\mu _{\ln i}}$和${\sigma _{\ln i}}$分别为对应标准正态分布参数lni的均值与标准差，${\mu _{\ln i}} = \ln {\mu _i} - 0.5\sigma _{\ln i}^2$，${\sigma _{\ln i}} = \sqrt {\ln (1 + {{({\sigma _i}/{\mu _i})}^2})} $。${\mu _i}$和${\sigma _i}$分别为土体参数的平均值和标准差。
2. 基于分段逆回归的主动学习多元自适应回归样条法介绍
本节选择SIR法用于降维，再结合代理模型，构建能解决高维问题且计算效率高的代理模型。
2.1 分段逆回归降维方法
SIR方法的降维思想是以输入变量及因变量的相关关系，将原始空间划为整合，在高维变量中构造少量的线性组合，基于这些线性组合得到新的变量表示原高维空间信息[14]。
首先计算训练样本均值${{\boldsymbol{\bar {\xi} }}_l}$的协方差矩阵$ {\boldsymbol{\hat C}} $。求解矩阵${\boldsymbol{\hat C}}$的特征值及对应的特征向量，据此找到主方向。根据SIR主方向，将输入变量x线性组合得到新变量。每一个方向向量对应一个变量。前k个方向向量为$[{\boldsymbol{\hat \beta} _1},{\boldsymbol{\hat \beta} _{\mathit{\pmb{2}}}}, \cdots ,{\boldsymbol{\hat \beta} _k}]$，可得
$$ {\omega _Q} = \boldsymbol{\hat \beta} _1^{'}x = {\hat \beta} _{11}^{'}{x_1} + {\hat \beta} _{12}^{'}{x_2} + , \cdots , + {\hat \beta} _{1r}^{'}{x_r}{\text{ }}(Q = 1,2, \cdots ,k) \text{，} $$ (3) 式中，$ {\omega _Q} = \boldsymbol{\hat \beta} _1^{'}x $为第Q个SIR变量。求解并且找到最大的特征值是SIR降维是否有效的关键所在[15]。
2.2 多元自适应回归样条法
多元自适应回归样条法是一种基于分段策略的非线性、非参数回归方法[13]。在系统中，实函数$f\left( \xi \right)$可以表示为
$$ f(\xi ) \approx \hat f(\xi ) = {a_0} + \sum\limits_{m = 1}^M {{a_m}{B_m}(\xi )} 。 $$ (4) 式中：$ \hat f(\xi ) $为MARS模型输出的预测值；$\xi = $ $({\xi _1},{\xi _2}, \cdots ,{\xi _t})$为一组输入变量；${a_m}$为第m个基函数的系数，系数${a_m}$通过训练样本的最小二乘拟合获得。
MARS算法分为前向选择和后向剪枝两个过程。前向过程算法只从一个常数项基${B_0}(x) = 1$开始，每次迭代产生两个新的基函数，然后对新的基函数进行标识，最后得到近似模型。每次迭代更新的模型如下：
$$ \begin{aligned} \hat{f}(\xi)=a_0+ & \sum\limits_{m=1}^M a_m B_m(\xi)+\hat{a}_{m+1} B_i(\xi) . \\ & \max \left(0, x_j-t\right)+\hat{a}_{m+2} B_i(\xi) \max \left(0, t-x_j\right) 。 \end{aligned} $$ (5) 式中：${\hat a_{m + 1}}$与${\hat a_{m + 2}}$可以对输入样本进行最小二乘拟合计算；${B_i}(\xi )$为先前确定的基函数，$0 \leqslant l \leqslant M$。
一般来说，前向过程算法会产生过拟合模型，因为MARS算法允许使用前一个基函数构造新的基函数，导致初始基函数的贡献减小。因此，应采用后向过程算法来提高模型的预测能力。后向过程算法采取的是每次循环，将原有的基函数删除，得到子模型，使用的是泛化交叉实验准则（GCV），GCV最小时模型最优[17]，具体形式表示如下：
$$ {\rm GCV} = {{\frac{1}{N}\sum\limits_{i = 1}^N {{{\left[ {{y_i} - {{\hat f}_M}({x_i})} \right]}^2}} } \mathord{\left/ {\vphantom {{\frac{1}{N}\sum\limits_{i = 1}^N {{{\left[ {{y_i} - {{\hat f}_M}({x_i})} \right]}^2}} } {{{\left[ {1 - \frac{{C(M)}}{N}} \right]}^2}}}} \right. } {{{\left[ {1 - \frac{{C(M)}}{N}} \right]}^2}}} 。 $$ (6) 式中：d为惩罚因子，一般取3；C(M)为该模型有效系数的个数；${\hat f_M}({x_i})$为在样本点${x_i}$对应的预测值。
2.3 主动学习函数
主动学习函数选取的样本点是模型收敛快慢的影响因素之一。当样本点选取在失效临界面附近，可以获得需要的有效信息加快模型收敛，并且每次选取的最优样本点之间有一定的距离防止重复取点。Li等[16]提出了一种考虑样本点相关距离主动学习函数：
$$ {\boldsymbol{u}}_{\rm{a}} = \underset{\boldsymbol u}{\arg \min } \frac{{(1 + \left\| {\boldsymbol{u}} \right\|)|\hat G({\boldsymbol{u}};{T_{N - 1}})|}}{{\frac{{d({\boldsymbol{u}},{T_{N - 1}})}}{{1 + \exp \{ - 20[d({\boldsymbol{u}},{T_{N - 1}}) - {d_{\min }}({T_{N - 1}})]\} }}}} 。 $$ (7) 式中：$ d({\boldsymbol{u}},{T_{N - 1}}) $为样本池集中点与独立标准正态空间中样本点之间的最小距离；$ \hat G({\boldsymbol{u}};{T_{N - 1}}) $为代理模型的预测值；$ {d_{\min }}({T_{N - 1}}) $为最优样本点间最小距离[17]。
2.4 模型终止条件
收敛条件对于构造代理模型尤为重要，因为及时停止最优样本点的增加可以减少计算迭代次数，提高模型构建的效率。通常在失效域与安全域的交界处取得足够的采样点，并且要保证迭代次数与得到的模型精度达到最优。而且计算迭代终止后，模型的参数指标波动范围较小。本文截取计算迭代过程最后5次计算的失效概率$P_{\rm{f}}^{{\rm{LAT}}(5)}$。当$P_{\rm{f}}^{{\rm{LAT}}(5)}$的变异系数小于或等于某个阈值${\varepsilon _{\rm{end}}}$，本次设计阈值选取${\varepsilon _{\rm{end}}} = 0.0001$作为迭代终止条件，最后5次计算值的变异系数${{\rm{COV}}_{P_{\rm{f}}^{{\rm{LAT}}(5)}}}$可表示为
$$ {{\rm{COV}}_{P_{\rm{f}}^{{\rm{LAT}}(5)}}} = \frac{{{\sigma _{P_{\rm{f}}^{{\rm{LAT}}(5)}}}}}{{\mu {}_{P_{\rm{f}}^{{\rm{LAT}}(5)}}}} \leqslant {\varepsilon _{\rm{end}}}。 $$ (8) 式中：${\sigma _{P_{\rm{f}}^{{\rm{LAT}}(5)}}}$为最后5次计算值的方差；$\mu {}_{P_{\rm{f}}^{{\rm{LAT}}(5)}}$为最后5次计算值的均值。
2.5 子集模拟
当最优样本点选取程序终止，SIR-AMARS模型可直接根据样本点集合预测FS。SS方法是将概率空间划分成一系列子集，子集的生成是通过中间失效事件，将小失效概率分解为若干个较大条件概率的乘积，且这些较大的条件概率较易获得。具体形式如下：
$$ {P_{\rm{f}}} = P({F_{\rm{S}}}(x) - 1 < 0) = P({F_1})\prod\limits_{l = 2}^s {P({F_l}|{F_{l - 1}})} 。 $$ (9) 式中：s为子集模拟层数；$P( \cdot )$为某事件的概率；${F_l} = \{ {F_{\rm{S}}}({\boldsymbol{x}}) - 1 < {g_l}(x),l = 1,2,3, \cdots ,s\} $；$P({F_1})$可使用MCS直接进行计算，可表示为
$$ P({F_1}) = \frac{1}{{{N_{\rm{all}}}}}\sum\limits_{t = 1}^{{N_1}} {{I_{{F_1}}}} (x_t^{(1)}){\text{ }}(k = 1,2,3, \cdots ,{N_{\rm{all}}}) 。 $$ (10) 式中：$ x_t^{(1)} $为独立同分布样本点，由概率密度分布函数计算得到；$ {I_{{F_1}}}( \cdot ) $为指示函数。
3. SIR-AMARS-SS方法执行步骤
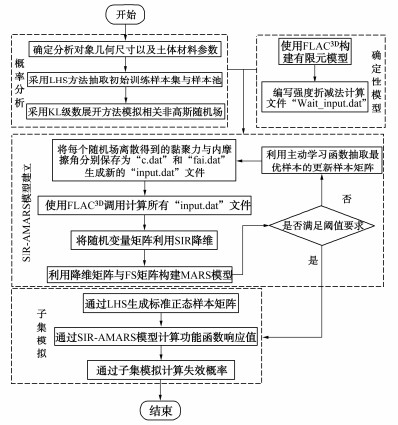
本节给出了基于SIR-AMARS-SS的边坡可靠度分析方法的具体过程，图 1为相应的计算流程图，具体步骤如下：
![]()
图 1 SIR-AMARS-SS边坡可靠度计算流程图Figure 1. Flow chart for calculation of slope reliability by SIR-AMARS-SS（1）确定分析对象的几何尺寸，以及土体材料特征参数及其统计特征（如黏聚力c、内摩擦角φ、密度，以及其均值、方差、波动范围等）
（2）借助FLAC3D软件，根据几何参数构建边坡模型，并且编写MATLAB程序提取各个单元形心点坐标$({x_{\boldsymbol{t}}},{y_{\boldsymbol{t}}})$，其中t=1，2，3, …，m, m为单元数。使用Fish语言编写待输入各个单元参数值的强度折减法（SRM）程序，保存程序文件名为“input.dat”。
（3）使用拉丁超立方抽样（LHS）抽取大小为$(M \times {N_{\rm m}}) \times {N_{\rm S}}$的初始样本矩阵$ \xi $与大小为$(M \times {N_{\rm F}}) \times $ ${N_{\rm T}}$初始样本池矩阵T。M为K-L展开法截断后留下的项数，${N_{\rm m}}$为边坡有限元模型单元个数，${N_{\rm S}}$为建立初始代理模型需要的样本点个数，${N_{\rm T}}$为样本池中样本点个数。随后将矩阵$ \xi $标准化，得到矩阵Γ。
（4）根据已知信息，使用K-L展开法生成随机场，并保证离散后的随机场大小与有限元模型单元数${N_{\rm m}}$一致。将每一个随机场模型的单元c、φ值保存为文件“c.dat”和“f.dat”，并生成${N_{\rm S}}$个新的“input.dat”文件。
（5）使用FLAC3D软件调用“input.dat”文件，将文件“c.dat”和“f.dat”中的参数赋值于各个单元。随后进行SRM计算，得到${N_{\rm S}}$个FS。
（6）利用SIR对独立标准正态的随机样本矩阵$ \xi $进行降维操作，采用2.1节所给出的步骤得到k维的随机样本矩阵η。
（7）根据随机样本矩阵η和矩阵FS，采用2.2节所介绍的方法构建最初的MARS模型，并根据2.4节所给出的阈值验证模型的精确性。
（8）如果模型不满足阈值所需要的精确度要求，则采用2.3节介绍的方法调用主动学习函数，选取样本池中最优点xt，加入到初始训练样本集内，再次更新MARS模型。
（9）当模型达到迭代停止的阈值要求，将最终得到的SIR-AMARS模型与SS结合，计算Pf。
4. 算例一：单层c-φ边坡
本节的研究对象为单层c-φ边坡，考虑岩土体抗剪强度参数空间变异性进行边坡可靠度分析。此外，验证不同互相关系数情况下模型的鲁棒性。
4.1 算例一边坡的描述与确定性分析
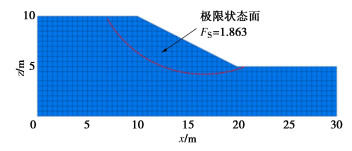
图 2给出了所研究的边坡几何形状，坡高5 m，边坡水平长度为10 m。土体弹性模量E=100 MPa，土体重度$ \gamma $=20 kN/m3，泊松比$ \nu $=0.3。假定c与φ均服从对数正态分布。稳定性分析所需的土体参数统计特征见表 1。本次边坡可靠度分析仅考虑土体c和φ参数的空间变异性，边坡FS计算基于弹塑性模型以及莫尔库仑破坏准则，其余土体参数均以常数赋值。根据表 1土体参数均值建立初步模型，借助FLAC3D建模，并利用SRM计算得到FS为1.863，图 2给出了破坏时的滑动面位置以及形状。与Jiang等[18]得到的1.78相近，安全系数相对误差为4.66%，表明所建立的边坡确定性模型的正确性。
表 1 算例一岩土体参数统计特征Table 1. Statistical characteristics of geotechnical parameters for Example Ⅰ土体参数 均值 变异系数 分布情况 互相关系数 c 10 kPa 0.3 对数分布 0 φ 20° 0.2 对数分布 图 2给出了建立模型时网格划分情况，本次建模包含910个单元。为与先前学者研究结果对比，网格划分情况与Jiang等[19]模型划分情况保持一致。并且假设波动范围分别为δh=25 m，δv=2.5 m，采用K-L展开方法对边坡c-φ随机场进行离散，此过程将参数赋予每个单元质心，以质心参数代表整个单元的土体参数值。基于以上所述条件进行边坡可靠度分析。
4.2 算例一边坡可靠度结果分析
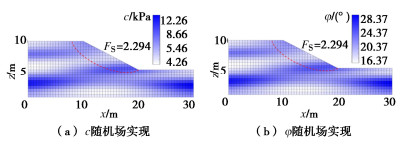
根据表 1中土体参数，采用K-L展开法进行随机场的实现，为保证随机场离散化精度，随机场中土体参数c与φ的截断展开项数均为21，从而得到42个随机变量。图 3给出了所研究的边坡抗剪强度参数随机场一次典型实现及稳定性分析结果。
一般情况下，面对维度较高的问题，代理模型会陷入高维诅咒。因此，在构建代理模型之前，将随机变量矩阵进行降维处理。而降维会舍去一部分信息量，模型精度可能会受到一定量的损伤。为找到降维效果最为显著（即降维数最小，且不会对可靠度分析结果几乎不会造成影响）的维数k，并得到初始样本数最少且精度较高的平衡点，需要有一个指标评价模型在不同情况下的准确性。本文中采用均方根误差RMSE评估SIR-AMARS代理模型的精确度，计算公式如下：
$$ {\rm {RMSE}} = \sqrt {\frac{{\sum\limits_{s = 1}^{{N_s}} {{{({{\rm FSS}_s} - {{\rm FSP}_s})}^2}} }}{{{N_s}}}} 。 $$ (11) 式中：${{\rm FSS}_s}$为利用SIR-AMARS代理模型预测得到的安全系数；${{\rm FSP}_s}$为通过SRM计算得到的安全系数；Ns为用于计算均方根误差的样本数目。
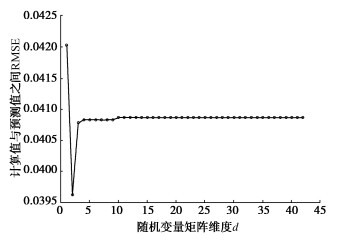
为确定模型降维效果最为显著的维数，设置初始训练样本数1000个，使用SIR将随机变量矩阵降维后，与使用SRM计算所的FS构建MARS模型。另取1000个样本，改变模型设置中降维后的维数k，计算预测值与无偏估计值之间在不同维度下的RMSE，结果如图 4所示。由于当k=4时，RMSE的值为0.0408，此时的代理模型已经非常准确，因此本次研究将维度降为4。
![]()
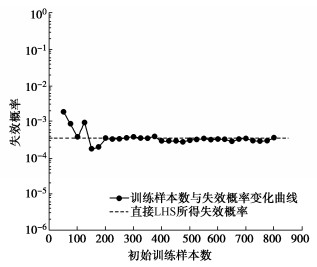
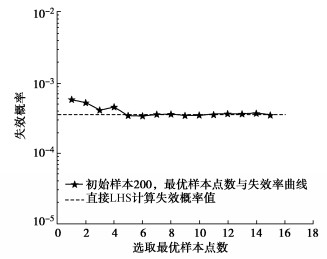
图 4 均方根误差与降维变化对比图Figure 4. Comparison diagram of root mean square error and dimensionality reduction模型预测能力的优劣，关键因素之一是用于构建代理模型的训练样本点数，用于构建代理模型的初始样本点数量与模型预测结果精度呈正比。但是用于构建模型的训练样本需要经过SRM进行计算，而训练模型的初始样本点数与构建模型所需要的时间呈正比，所以需要找到在不影响模型精度的前提下初始训练样本最少的数量。为寻求构建模型样本数的最优值，采用LHS抽取生成1000个独立标准正态分布样本矩阵$ \xi $，通过随机场离散获得对应边坡随机场实现，进而利用SRM计算FS。设置初始训练样本数从50开始，随着训练样本的增加边坡Pf的变化如图 5所示。从图 5中可以看出，当初始训练样本达到200时，Pf值基本稳定。所以，在本节中，选取200个初始训练样本用于构建代理模型。
![]()
图 5 初始训练样本数与失效概率变化对比图Figure 5. Comparison diagram of number of initial training samples and change of failure probability当初始训练样本确定为200个，最优样本点的选取个数为9时模型构建已完成，为证明此时的模型已经达到收敛状态，继续抽取6个最优样本点。图 6给出了随着最优样本点个数增加，Pf的变化情况。由图 6可知，当抽取最优样本点数为9时，所得到的结果已经满足主动学习函数的阈值，停止选取样本点，并且计算结果已经趋于稳定。
![]()
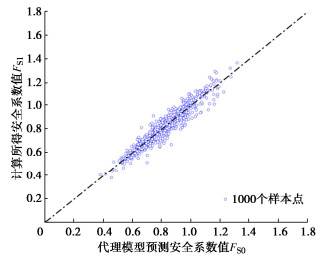
图 6 最优样本点增加与失效概率变化对比图Figure 6. Comparison diagram of increase of optimal sample points and change of failure probability使用LHS任意抽取1000组样本，并得到其对应的边坡随机场实现，利用FLAC3D软件计算得到安全系数的无偏估计值矩阵FS0，再将训练样本使用上述得到的SIR-AMARS模型进行预测，得到预测安全系数矩阵FS1，将无偏估计值矩阵FS0与预测安全系数矩阵FS1进行对比，结果可见图 7。不难发现，当维度最终降为4，且初始训练样本数为200，利用主动学习函数抽取最优样本点9个时（即最终使用209个训练样本构建SIR-AMARS模型），已经能得到精准度较高的SIR-AMARS模型。随后，将最终得到的SIR-AMARS模型与SS结合，设置计算样本数为3000，最终得到此边坡Pf为3.556×10-4。
![]()
图 7 计算所得安全系数与代理模型预测安全系数值对比图Figure 7. Comparison between calculated safety factor and predicted safety factor by surrogate model为证明本文所提方法的准确性以及计算的高效性，将本文所述方法与二阶Hermite混沌展开多项式（二阶PCE）（训练样本数462个和2500个，两种情况）、三阶Hermite混沌展开多项式（三阶PCE）、直接拉丁超立方模拟对此边坡计算Pf结果进行对比。为比较不同分析方法之间的差异，本文使用直接LHS抽取1×105个样本，使用FLAC3D直接计算得到了Pf无偏估计值，再将各种分析方法算得的Pf与其对比，采用了相对误差∆用于比较各种方法的准确度。相对误差的计算公式如下：
$$ \varDelta=\left|\frac{\mathrm{PF}_{\mathrm{c}}-\mathrm{PF}_{\mathrm{p}}}{\mathrm{PF}_{\mathrm{p}}}\right| \times 100 \% 。 $$ (12) 式中：$\varDelta $为相对误差值；$\mathrm{PF}_{\mathrm{c}}$为代理模型计算得到的失效概率；$\mathrm{PF}_{\mathrm{p}}$为直接LHS方法算得的失效概率。计算结果见表 2。
表 2 不同分析方法对算例一计算失效概率结果Table 2. Failure probability results calculated by different analysis methods for Example Ⅰ由表 2可知，本文所提方法在训练代理模型时，所需要的训练样本数最少，仅需要209个。并且，本文所提方法与使用直接LHS计算得到的Pf之间的相对误差仅为1.22%，优于其他方法。并且所使用的训练样本数及计算样本数最少，说明了本文所提方法具有高效计算能力以及精准度。需要特别说明的是，如果需要更高的计算精度，例如计算样本数大于108时，计算样本的模拟内存将超过设备物理内存（计算机内存条16 GB），导致内存溢出情况，因此在概率更小的问题时，使用MCS模拟法存在局限性[18]。但基于SIR-AMARS模型的SS方法，在与MCS法计算结果相近的情况下，仅需要3×103个计算样本，很好地解决了其他代理模型计算小失效概率事件导致内存溢出无法计算的问题。为增加处理问题高效性，以下研究均基于SIR-AMARS-SS模型。
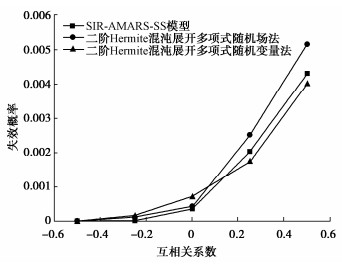
为研究抗剪强度参数之间的相关程度对边坡可靠度分析的影响，本文选取-0.5 ≤ρcφ ≤ 0.5，假定$ {\lambda _{\rm{h}}} $=25 m，$ {\lambda _{\rm{v}}} $=2.5 m，对比了二阶Hermite混沌展开多项式随机变量法、二阶Hermite混沌展开多项式随机场法与基于SIR-AMARS-SS模型随机场法计算结果。图 8比较了3种方法随着的ρcφ变化Pf的结果，由图 8可知，在互相关系数ρcφ从-0.5逐渐变为0.5，Pf变化几个数量级（Pf从3.9×10-6变至4.32×10-3），说明抗剪强度参数之间的互相关系数对边坡失效概率影响较大。并且二阶Hermite混沌展开多项式随机变量法在c与φ处于较大正相关系数时，低估了边坡的Pf，所得结果与Jiang等[18]得到的结论一致，同时也证明本文所提方法在面对土体强度参数相关性不同的情况下，依然有较好的预测能力。由此表明，本文所提方法，训练样本数以及计算样本数需求量最低，节省计算量明显，并且能适用于土体抗剪强度不同的相关性情况。
![]()
图 8 不同分析方法随ρcφ变化失效概率对比图Figure 8. Comparison diagram of failure probability by different analysis methods with change of ρcφ4.3 降维对安全系数的影响分析
在本节算例中，采用了SIR降维，随机变量矩阵维度从42降至4，在此过程中，必然会有一部分信息丢失，为确定降维是否会对边坡可靠度分析造成较大的影响，必须讨论降维前后FS变化情况。
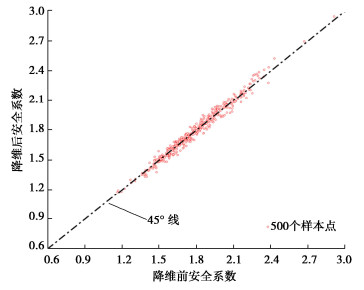
基于上述模型，使用拉丁超立方随机抽取500个初始样本生成随机场，首先使用SRM直接计算得到安全系数FSN，使用已经构建的SIR-AMARS模型进行预测，得到预测安全系数FSS。在本节中，采用决定系数R2表示降维对FS的影响，其中R2∈(0, 1)。R2越接近1，表示SIR降维对失效概率影响越低。其中R2的计算公式为
$$ R^2=1-\frac{\sum\limits_{i=1}^N\left(\mathrm{FS}_S-\mathrm{FS}_N\right)^2}{\sum\limits_{i=1}^N\left(\mathrm{FS}_N-\overline{\mathrm{FS}}\right)^2} $$ (13) 式中，N是样本数目；FSS是使用SIR-AMARS模型预测得到的安全系数；FSN使用SRM直接计算得到安全系数；FS是FSN的均值。最终算得的决定系数R2=0.9773，并且将安全系数矩阵FSN与预测安全系数矩阵FSS依次对应画图，最终结果可见图 9，由决定系数值及图 9可知，降维对FS的计算结果没有造成大的影响。
![]()
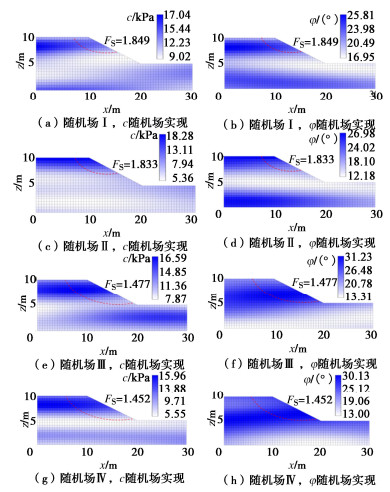
图 9 降维前后安全系数对比图Figure 9. Comparison diagram of safety factor before and after dimension reduction为进一步讨论降维对边坡可靠度分析的影响，随机选择两组随机变量矩阵，模拟降维前后c与φ的随机场。具体的模拟情况可见图 10，随机场Ⅱ与Ⅳ分别是随机场Ⅰ与Ⅲ降维后的情况，随机场内的空间变异性程度有所降低，但降维并没有导致FS有较大的变化。造成空间变异性程度降低主要是因为在降维时，SIR会丢弃一部分不重要的信息。在边坡安全系数的计算中，影响其数值大小最关键的一部分就是滑动面底部的参数情况[19]。
![]()
图 10 降维前后随机场对比图Figure 10. Comparison of random field before and after dimension reduction5. 算例二：双层非均质边坡
本节的研究对象为双层边坡，仅考虑c的空间变异性，进行边坡可靠度分析。
5.1 算例二边坡的描述于确定性分析
本节研究对象为双层非均质边坡，边坡高度为24 m，坡角为36.87°(3h∶4v)。c的变异系数均为0.4，上下层c的分布类型均为高斯型，土体重度为19 kN/m3。建模所需要的土体抗剪强度参数见表 3，将边坡划分为1296个单元。
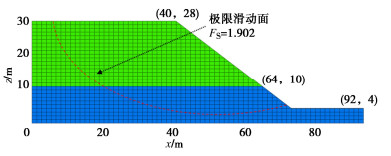
表 3 算例二岩土体抗剪强度参数统计表Table 3. Statistical table of shear strength parameters of slope soil for Example Ⅱ参数 均值 自相关距离 分布类型 黏聚力c 上层，120 kPa λh = 20 m 对数正态分布 下层，160 kPa λv = 2 m 本文采用FLAC3D计算FS，得到边坡安全系数为1.902。具体的破坏滑面可见图 11所示，滑动面穿过两层土体，并且滑动面沿着底部边界，破坏形式和FS与文献[20，21]的滑动面形状与FS值2.02和1.993基本保持一致，验证了本节建模的准确性。
5.2 算例二边坡可靠度结果分析
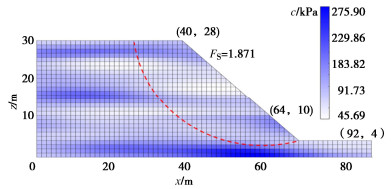
为将参数空间变异性考虑进边坡可靠度分析，本节依旧使用K-L展开法进行随机场模拟，本节算例仅考虑了c的空间变异性，为满足离散化精度，需要产生65个随机变量，其中上层随机变量为36个，下层随机变量为29个。图 12展现了一次典型随机场实现形式。
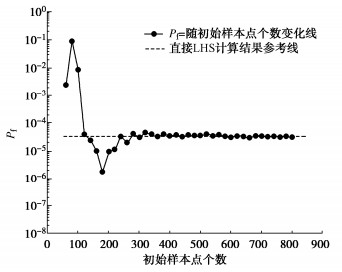
为确定本文所提方法针对本节算例所需要的最少样本数，首先利用LHS抽取生成3×104个独立的标准正态分布样本矩阵$ \zeta $。进而获得边坡随机场实现，通过SRM计算FS，直接计算得到失效概率。将样本矩阵从前往后，从60个初始训练样本开始，依次增加训练样本数，直至训练样本数到800个结束，每次都使用训练样本构建新的SIR-AMARS模型。构建模型时，SIR降维后随机变量矩阵的维数k=10，将每次得到的模型与SS结合计算失效概率（其中SS的计算样本数定为3000），构建训练样本数与Pf相关关系如图 13所示。从图 13中可以看出，当初始训练样本为300时，模型已经趋于稳定，可以应用于本节双层边坡可靠度分析之中。当初始训练样本确定为300个时，最优样本点的选取个数为13时（即用于构建代理模型的训练样本数为313个），模型已经完成构建，此时随机场的随机变量矩阵维数k=10。将样本矩阵$ \zeta $的前300个样本作为训练样本，构建SIR-AMARS模型，最后将此模型结合SS，抽取的样本数为3000，计算失效概率。
为进行对比，选取二阶Hermite响应面方法，人工神经网络对本节算例进行可靠度分析，由于本节算例将土体参数离散有65个随机变量，二阶Hermite的待定系数为67!/2!65! = 2211项。二阶Hermite随机多项式4500个样本，神经网络选取500个样本作为对比。最终的计算结果见表 4。从表 4可知，本文所提方法计算得到的Pf与直接LHS计算所得的Pf相最为接近，在保证精度的情况下，使用的训练样本数最少，计算耗时最短（基于电脑配置为I7-10700，16 G运行内存情况）。这进一步验证了所提方法的高效性。
表 4 不同分析方法对算例二计算失效概率结果Table 4. Failure probability results of Example Ⅱ calculated by different analysis methods分析方法 训练样本 失效概率 计算耗时/h 二阶Hermite 4500 4.10×10-5 225 人工神经网络 500 4.91×10-5 25 SIR-AMARS-MCS 313 3.56×10-5 15.65 LHS 3×104 3.33×10-5 1500 6. 结论
为在考虑参数空间变异性情况下准确高效地开展小失效概率的边坡可靠度分析，本文提出了一种基于SIR-AMARS-SS代理模型的分析方法，并验证了所提方法的有效性，得到以下3点结论。
（1）在考虑参数空间变异性情况下进行小失效概率边坡可靠度分析时，所提方法可以较少的训练样本以及计算样本得到较为精准的结果，极大地降低了调用原边坡有限元模型计算次数，并且避免由于抽样个数过多而导致的物理内存溢出情况。
（2）本文所提方法在面对高维度问题，不会陷入高维灾难，且在高维情况下得到快速收敛的结果，所得结果具有较高的计算精度。
（3）在使用SIR降维时，会导致随机变量矩阵丢失一部分信息，造成随机场的空间变异性变低，但是对模型预测FS影响较小。
-
![]()
图 1 3种支护桩型最大弯矩点分布图
Figure 1. Distribution of maximum bending moment of three types of retaining piles
![]()
图 3 单支撑排桩弯矩区间分布图
Figure 3. Interval distribution of bending moment of single support.row pile
![]()
图 4 悬臂桩和倾斜桩弯矩区间分布图
Figure 4. Interval distribution of bending moment of cantilever pile and inclined pile
![]()
图 5 单支撑排桩各弯矩区域占桩身范围随坑深的变化情况
Figure 5. Variation of proportion of each bending moment area of single support row pile to pit depth
![]()
图 8 PHC和PRC管桩模拟及实测荷载-位移图
Figure 8. Simulated and measured load-displacement of PHC and PRC pipe piles diagrams
![]()
图 9 各试验管桩荷载-位移曲线模拟值对比
Figure 9. Comparison of simulated values of load-displacement curves of pipe piles
![]()
图 10 直、斜桩70%最大弯矩区间随堆载值变化图
Figure 10. Variation of maximum bending moment interval of 0.7 times with load value of straight and inclined piles
![]()
图 11 直、斜桩70%最大弯矩区间随超挖深度变化图
Figure 11. Variation of maximum bending moment interval of 0.7 times with over excavation depth of straight and inclined piles
![]()
图 12 直、斜桩70%最大弯矩区间降雨前后变化图
Figure 12. Variation of straight and inclined piles before and after rainfall at interval of 0.7 times maximum bending moment
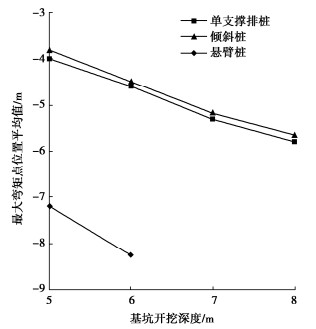
表 1 最大弯矩点位置与地表至桩底深度比值表
Table 1 Ratios between position of maximum bending moment and depth from surface to pile bottom
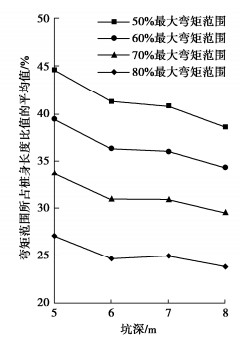
基坑深度/m 单支撑排桩/% 倾斜桩/% 悬臂桩/% 5 38.53 36.73 43.40 6 36.16 35.34 40.91 7 35.84 34.85 8 34.41 33.56 
下载: 导出CSV
表 2 3种支护桩型不同弯矩区域所占桩身比值的平均数
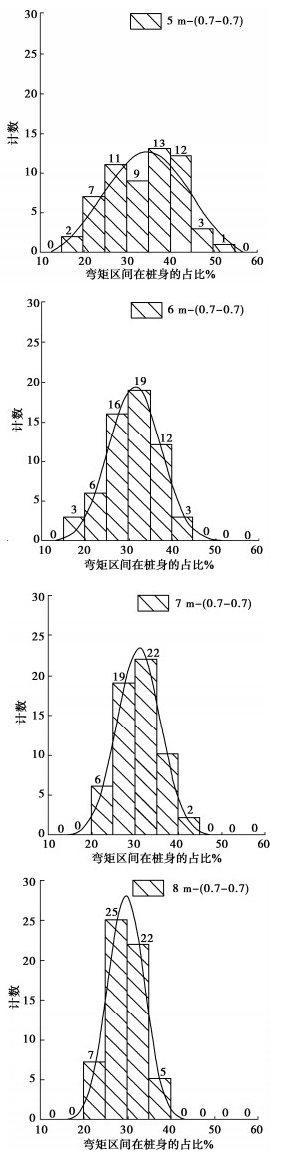
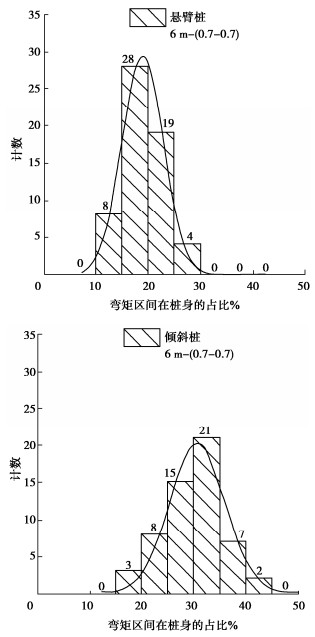
Table 2 Average values of ratio of three types of retaining pile to different bending moment areas
支护类型 坑深/m 0.5Mmax区域/% 0.6Mmax区域/% 0.7Mmax区域/% 0.8Mmax区域/% 单支撑排桩 5 44.58 39.41 33.60 27.07 6 41.34 36.33 30.95 24.69 7 40.77 36.03 30.87 25.05 8 38.63 34.28 29.50 23.84 倾斜桩 5 42.53 37.58 32.13 26.19 6 39.46 35.13 29.68 24.32 7 38.82 34.23 29.44 23.81 8 37.00 32.88 28.18 22.89 悬臂桩 5 30.17 25.61 21.28 16.74 6 26.76 22.65 18.97 15.00
下载: 导出CSV
表 3 试验桩纵筋钢筋配置表
Table 3 Longitudinal reinforcement of test piles
试验桩型 预应力筋配置 HRB400非预应力筋配置 备注 配置数量 配置位置/m 对照组 PHC AB 400 7ΦD10.7 — — 全长配非预应力筋 PRC AB 400 7ΦD10.7 
0~8 试验组一 PR-PHC AB 400(0.6~0.6) 7ΦD10.7 2.74~5.26 60%最大弯矩区域配非预应力筋 PR-PHC AB 400(0.7~0.7) 7ΦD10.7 2.93~5.07 70%最大弯矩区域配非预应力筋 PR-PHC AB 400(0.8~0.8) 7ΦD10.7 3.12~4.88 80%最大弯矩区域配非预应力筋 试验组二 PR-PHC AB 400(0~0.6) 7ΦD10.7 0~5.26 桩端至60%弯矩配非预应力筋 PR-PHC AB 400(0~0.7) 7ΦD10.7 0~5.07 桩端至70%弯矩配非预应力筋 PR-PHC AB 400(0~0.8) 7ΦD10.7 0~4.88 桩端至80%弯矩配非预应力筋 验证组 PR-PHC AB 400(0.5~0.5) 7ΦD10.7 2.55~5.45 50%最大弯矩区域配非预应力筋 PR-PHC AB 400(0~0.5) 7ΦD10.7 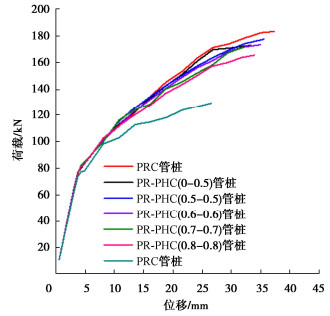0~5.45 桩端至50%弯矩配非预应力筋
下载: 导出CSV
表 4 各试件受弯试验结果
Table 4 Flexural test results of specimens
桩型 抗裂弯矩 极限弯矩 弯矩值/(kN·m) 弯矩值/(kN·m) 裂缝数量 裂缝平均间距/mm 对照组 PHC AB 400 63.66 115.34 6 354 PRC AB 400 83.15 188.68 20 144 试验组一 PR-PHC AB 400 (0.8~0.8) 65.37 150.96 13 183 PR-PHC AB 400(0.7~0.7) 72.59 158.47 15 183 PR-PHC AB 400(0.6~0.6) 72.59 173.57 14 196 试验组二 PR-PHC AB 400(0~0.8) 72.59 158.47 14 196 PR-PHC AB 400(0~0.7) 65.37 188.68 18 146 PR-PHC AB 400(0~0.6) 76.29 196.28 18 160 验证组 PR-PHC AB 400(0.5~0.5) 76.29 188.68 19 151 PR-PHC AB 400(0~0.5) 76.29 188.68 19 164
下载: 导出CSV
表 5 混凝土本构参数表
Table 5 Constitutive parameters of concrete
弹性模量/MPa 泊松比 膨胀角/(°) 偏心率 fb0fc0 屈服常数 黏性系数 38000 0.2 30 0.1 1.16 0.6667 0.001
下载: 导出CSV
表 6 钢筋材料参数表
Table 6 Parameters of rebar materials
钢筋种类 Es/MPa fy/MPa εy k1 k2 k3 k4 预应力钢棒 200000 1342 0.0069 1 4.9 5.1 1.09 非预应力筋 195000 484 0.0024 10.2 48.3 56.8 1.21
下载: 导出CSV
表 7 管桩极限弯矩模拟值与实测值对比
Table 7 Comparison between simulated and measured ultimate bending moments of pipe piles
管桩型号 极限弯矩实测值/(kN·m) 极限弯矩模拟值/(kN·m) 实测值/模拟值 PRC-400-AB 188.68 174.39 1.08 PR-PHC-400-AB（0-0.5） 188.68 164.50 1.15 PR-PHC-400-AB（0.5-0.5） 188.68 168.82 1.12 PR-PHC-400-AB（0.6-0.6） 173.60 164.88 1.05 PR-PHC-400-AB（0.7-0.7） 158.47 163.03 0.97 PR-PHC-400-AB（0.8-0.8） 150.96 157.34 0.96 PHC-400-AB 126.59 123.00 1.03
下载: 导出CSV
-
[1] 何永福, 朱进军. 管桩在连云港地区基坑支护中的应用及实测分析[J]. 建筑结构, 2009, 39(7): 57-59. HE Yongfu, ZHU Jinjun. Application and observational analysis of pipe-pile for excavation support system in Lianyungang district[J]. Building Structure, 2009, 39(7): 57-59. (in Chinese)
[2] 李绥林, 刘合伍, 陈昌文. PHC管桩在某基坑支护工程中的设计与施工[J]. 施工技术, 2010, 39(增刊1): 13-16. LI Suilin, LIU Hewu, CHEN Changwen. The design and construction of PHC pipe pile technique in one deep foundation pit supporting engineering[J]. Construction Technology, 2010, 39(S1): 13-16. (in Chinese)
[3] 沈晞, 周建凡, 夏亮. PHC管桩在基坑支护工程中的应用研究[J]. 国外建材科技, 2007, 28(1): 70-73. SHEN Xi, ZHOU Jianfan, XIA Liang. Research on application of PHC piles in foundation pit supporting[J]. Science and Technology of Overseas Building Materials, 2007, 28(1): 70-73. (in Chinese)
[4] 张忠苗, 刘俊伟, 邹健, 等. 加强型预应力混凝土管桩抗弯剪性能试验研究[J]. 浙江大学学报(工学版), 2011, 45(6): 1074-1080. ZHANG Zhongmiao, LIU Junwei, ZOU Jian, et al. Experimental study on flexural and shearing property of reinforced prestressed concrete pipe pile[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(6): 1074-1080. (in Chinese)
[5] 王新玲, 高会宗, 周同和, 等. 新型混合配筋预应力混凝土管桩抗弯性能试验研究[J]. 工业建筑, 2012, 42(8): 64-68. WANG Xinling, GAO Huizong, ZHOU Tonghe, et al. Experimental studies of flexural behavior of new type prestressed concrete pipe pile with compound unprestressed reinforcement[J]. Industrial Construction, 2012, 42(8): 64-68. (in Chinese)
[6] 杜新喜, 胡锐, 袁焕鑫, 等. 混合配筋预应力混凝土管桩抗弯承载性能研究[J]. 土木工程学报, 2019, 52(1): 44-52. DU Xinxi, HU Rui, YUAN Huanxin, et al. Study on flexural behavior of prestressed concrete pipe pile with hybrid reinforcement[J]. China Civil Engineering Journal, 2019, 52(1): 44-52. (in Chinese)
[7] 徐金, 何晶. 增加非预应力筋的混凝土管桩抗弯抗剪性能研究[J]. 工业建筑, 2016, 46(10): 109-112, 130. XU Jin, HE Jing. Research on flexural and shear behavior of prestressed concrete pipe pile with non prestressed reinforcement[J]. Industrial Construction, 2016, 46(10): 109-112, 130. (in Chinese)
[8] 张忠苗, 刘俊伟, 谢志专, 等. 新型混凝土管桩抗弯剪性能试验研究[J]. 岩土工程学报, 2011, 33(增刊2): 271-277. http://cge.nhri.cn/cn/article/id/14363 ZHANG Zhongmiao, LIU Junwei, XIE Zhizhuan, et al. Experimental study on flexural and shearing properties of modified concrete pipe piles[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(S2): 271-277. (in Chinese) http://cge.nhri.cn/cn/article/id/14363
[9] 黄汉林, 卢玉南. 混合配筋预应力混凝土管桩在深基坑支护工程中的应用[J]. 工程勘察, 2022, 50(8): 13-16, 27. HUANG Hanlin, LU Yunan. Application of prestressed reinforced concrete pipe piles in retaining of deep foundation pit[J]. Geotechnical Investigation & Surveying, 2022, 50(8): 13-16, 27. (in Chinese)
[10] 蔡磊, 梁世德, 顾明, 等. 预制高性能混合配筋预应力混凝土管桩在某深基坑支护中的应用[J]. 工程勘察, 2018, 46(12): 25-29. CAI Lei, LIANG Shide, GU Ming, et al. Application of high reinforced prestressed concrete compounded pipe piles in deep foundation pit[J]. Geotechnical Investigation & Surveying, 2018, 46(12): 25-29. (in Chinese)
[11] 常玉军, 刘毅, 张吉庆, 等. PRC管桩在基坑支护工程中的应用[J]. 探矿工程(岩土钻掘工程), 2017, 44(6): 78-83. CHANG Yujun, LIU Yi, ZHANG Jiqing, et al. Application of PRC pipe pile in foundation pit support engineering[J]. Exploration Engineering (Rock & Soil Drilling and Tunneling), 2017, 44(6): 78-83. (in Chinese)
-
期刊类型引用(3)
1. 陈敏. 基于BP神经网络的边坡可靠度分析. 黑龙江交通科技. 2024(07): 31-34 . 
百度学术
2. 汪卫，廖志浩，廖杰林. 基于随机场模型的土石坝失效概率分析研究进展. 人民珠江. 2024(10): 114-123 . 百度学术
3. 彭宗桓 ，盛建龙 ，叶祖洋 ，李硕 . 基于t-SNE-AMARS-MPM的空间变异性边坡可靠度分析及大变形破坏模式研究. 力学学报. 2024(11): 3274-3289 . 百度学术
其他类型引用(4)
-
其他相关附件
-
本文英文pdf
20240220-G22-1359英文发布稿 点击下载(561KB)
-
计量
- 文章访问数: 413
- HTML全文浏览量: 48
- PDF下载量: 119
- 被引次数: 7
