Variation characteristics of deformation and water content of remolded unsaturated expansive soils in Nanyang
-
摘要: 为研究水-力作用下非饱和土变形和含水率变化特性，采用非饱和土三轴仪，对非饱和膨胀土开展了吸力平衡、等向固结和三轴剪切试验，实时监测土的变形和含水率变化，综合分析了水-力作用下土的变形和含水率随时间的变化规律，并以“双孔”模型为基础框架，揭示了水-力作用下土的变形和含水率变化机制。研究表明：在吸力平衡和等向固结过程，非饱和土的变形和含水率随时间变化规律不同，变形在相对较短时间内达到平衡，而含水率达到平衡耗时更长；在三轴剪切过程，剪缩变形量与孔隙水排出量随时间基本上呈线性变化。随着吸力增大，含水率达到平衡所需时间增长，但对变形达到稳定耗时影响不大。净围压增大会增长含水率达到平衡的时间，然而对变形达到稳定的耗时影响不大。改进“双孔”模型，外力基本上只影响集聚体间孔隙；含水率变化会引起土颗粒重新排列，进而影响集聚体间孔隙；集聚体间孔隙水迁移速率相对较大，颗粒间孔隙水迁移速率相对较小。Abstract: In order to study the variation characteristics of the deformation and water content of unsaturated soils under hydro-mechanical effects, the unsaturated soil triaxial apparatus is used to carry out suction equilibrium, isotropic consolidation and triaxial shear tests on unsaturated clay. The variation of deformation and water content of expansive soils is real-time monitored, and that with time under hydro-mechanical action is comprehensive analyzed. Based on the "double-pore structure" model, the mechanisms of soil deformation and water content variation under hydro-mechanical action are revealed. The results show that in the process of suction equilibrium and isotropic consolidation, the deformation and water content of unsaturated soils vary with time. The deformation reaches the equilibrium in a relatively short time, but the water content reaches the equilibrium in a longer time. In the triaxial shear process, the amount of shear deformation and the discharge of pore water are basically linear with time. With the increase of suction, the time for the moisture content to reach the equilibrium increases, which has few effects on the time for the deformation to reach stability. The increase of the net confining pressure increases the time for water content to reach the equilibrium, but it has few effects on the time for deformation to reach stability. The "double-pore structure" model is modified, and the external force basically only affects the inter-aggregate pores. The variation of water content causes the rearrangement of soil particles, and then affect the macropores in the soil. The migration rate of pore water between aggregates is relatively large, and the migration rate of pore water between particles is relatively small.
-
Keywords:
- unsaturated soils /
- deformation /
- water content /
- triaxial test /
- double-pore structure model
-
0. 引言
非饱和土不单是固-液两相，还增加了气相，使非饱和土的水-力性质变得十分复杂，饱和土的本构模型也就不能适应非饱和土的复杂情况。非饱和土的水-力作用会引起土中孔隙结构的变化，反之，土中孔隙结构的变化也会改变非饱和土的水-力特性[1]。非饱和土水-力特性和孔隙结构之间的耦合作用是建立非饱和土宏微观力学之间联系的基础[2]，因此近几十年受到广泛关注。但是，目前关于水-力作用与孔隙结构之间的耦合作用还存在很多争议，仍然有很多地方需要新的试验数据证明和更先进的理论解释。
现阶段，水-力作用下非饱和土的水分迁移和变形问题已有大量研究。变形方面，陈正汉等[3]通过三轴试验和侧限压缩试验研究了原状Q3黄土湿陷特性（增湿到饱和）和增湿变形特性（增湿到不同含水率），除此之外，也有一些学者进行了相关增湿试验变形研究[4-6]；谈云志等[6]开展了干湿循环与上覆荷载共同作用下的压缩特性试验，揭示了泥岩孔隙-水分-荷载的相互作用机制；陈康等[7]开展了不同围压及动应力下饱和红层泥岩填料的动三轴试验，并讨论了围压和动应力对填料累积变形特性的影响；宋朝阳等[8]基于考虑土颗粒间物理化学作用的粒间应力方程，建立考虑孔隙盐溶液浓度影响的饱和黏土统一压缩模型。同时，也有大量试验从微细观角度分析水-力作用下孔隙结构演化并基于演化模型建立宏观变形模型[9]。
土孔隙中水受到力-温度-化学等因素会发生流动。从能量角度，土中孔隙水由于不同孔隙的能量存在差异会发生迁移[10]；水-力学特性上，土中孔隙水主要受吸力和变形控制（忽略热和化学势能等影响）[11]。郭剑峰等[12]以非饱和土增量非线性固结理论为基础，考虑干密度在固结过程中的变化，对高填方土体进行变形和水分迁移的耦合分析；高游等[13]研究了不同初始孔隙比和水力路径对非膨胀性黏土水分迁移规律的影响，提出了考虑初始孔隙比影响的非饱和土滞回特性的模拟方法；Zhou等[14]从理化角度出发研究了化学势能对水分迁移的影响；吸力作用下土中水分迁移主要表现在土的持水曲线[15]和非饱和土渗透特性[16]，该方面研究取得了很大进展；外力对土种孔隙水的影响主要表现在土的固结特性[17]，由于非饱和土的复杂性，非饱和土固结理论仍然存在一些问题。
关于非饱和土在多种应力路径下的变形、强度、屈服和水量变化特性已有大量研究[18-19]，然而水-力作用下土的变形与水分迁移特性的同步性（变形与含水率随时间变化规律）研究鲜有报道。针对上述问题，采用非饱和土三轴仪实时监测水-力作用下土的变形和含水率，探究在吸力平衡、等向固结和三轴剪切过程中黏土的体变和含水率随时间的变化规律，为非饱和土本构模型的完善提供试验和理论基础。
1. 试验概况
1.1 试验材料和设备
试验材料选用南阳膨胀土，取自南水北调中线工程市南阳段卧龙区卧姜沟乡。首先清除地表1 m左右的杂质，然后提取土样，并迅速放进保鲜袋中进行封存，带回实验室后测量原状样的天然含水率、干密度以及一些土性指标，其基本物理性质指标如表 1所示。采用筛分法和密度计法对南阳膨胀土进行颗粒大小测量，其颗粒级配累积曲线如图 1所示。根据建筑规范对土的分类，综合考虑土的自由膨胀率和液塑限等指标，鉴定是弱膨胀土，并命名为南阳膨胀土。
表 1 南阳膨胀土基本物理指标Table 1. Physical properties of Nanyang weakly expansive soil相对质量
密度液限/
%塑限/
%塑性指数 最大干密度/
(g·cm−3)缩限/
%最优含水率/% 自由膨胀率/% 原状样干密度/(g·cm−3) 2.74 38.8 17.2 21.6 1.69 10.5 18.2 53.8 1.45 ![]()
图 1 南阳膨胀土颗粒级配曲线Figure 1. Grain-size distribution curve of Nanyang weakly expansive soil试验仪器采用的是吸力控制的GDS非饱和土三轴仪。试样体变采用双压力室量测方法，其原理是根据内压力室水位的压力差推算试样体变。试验过程中含水率的变化通过反压控制器进行测量。
1.2 试验方案
（1）试样制备
三轴试验采用击实样，首先把现场取的土过0.5 mm筛，并调配含水率约为20%，干密度约为1.25 g/cm3，密封静置36 h，使水分充分平衡。三轴试样模具尺寸为直径38 mm，高76 mm，将分布均匀的土进行4层击实，每层达到控制高度时进行刮毛处理，以保证试样干密度均匀。
（2）试验方案
为了研究不同水-力路径下土样含水率与体变的滞后效应，对初始状态相同的试样施加不同吸力，并进行一系列等净围压和等吸力的三轴固结和剪切试验。所有试验的初始试样状态相同，把制备好的三轴试样装进压力室，然后依次按照试验方案进行吸力平衡、固结平衡和三轴剪切。三轴试验的吸力等级为50，200，400 kPa，净围压等级为100，200 kPa。吸力平衡采用轴平移技术，三轴仪底部嵌有进气值为500 kPa的陶土板，可以通过施加吸力值使试样进行吸湿或者脱湿；吸力平衡后施加净围压进行等净围压和等吸力固结；固结平衡后进行剪切试验（控制剪切速率）。吸力平衡和固结平衡的条件是同时满足含水率和体变达到平衡（吸/排水变化速率小于0.05 cm3/12 h；体积变化率小于0.1 cm3/12 h）。
试验路径如图 2所示，分别进行净围压为100，200 kPa的吸力平衡、固结平衡和三轴剪切试验。对于试验1，首先施加净围压20 kPa（O→A），使橡皮膜与试样充分接触；稳定后施加吸力50 kPa（A→B）；吸力平衡后（含水率和体积基本稳定）施加净围压100 kPa（B→C）进行固结；固结稳定后开始三轴剪切（剪切速率为0.00189 mm/min）（C→D）。对于试验2，首先同样施加净围压20 kPa（O→A）；稳定后施加吸力200 kPa（A→G）；吸力平衡后施加净围压100 kPa（G→H）进行固结；固结平衡后进行三轴剪切。对于试验3，首先施加20 kPa净围压进行预固结（O→A）；平衡后施加吸力400 kPa（A→L）；吸力平衡后施加净围压100 kPa进行固结（L→M）；固结稳定后开始三轴剪切。对于试验4、5和6，试验方法与上述3个试验相同，只是固结净围压变为200 kPa。所有试验在每个阶段都实时测量含水率和体变。
2. 试验结果比较与分析
2.1 吸力平衡过程
图 3~5为不同目标吸力平衡过程中土样含水率和体变随时间变化的规律。可以看出，吸力平衡初期，土体排水和收缩变形速率都比较大，随着吸力进一步增大，两者变化速率都有所降低，直到吸力达到平衡（含水率和体变的变化不明显）。在吸力平衡过程中，相比较含水率的变化，3个目标吸力下土样的变形都率先达到平衡状态。而且吸力达到平衡后，土体的含水率和收缩变形仍有轻微变化，含水率变化相对明显，收缩变形更加趋于稳定。
![]()
图 3 吸力50 kPa平衡过程土样吸水量和体变量变化Figure 3. Variation of drainage and deformation of soil samples with suction of 50 kPa during consolidation![]()
图 4 吸力200 kPa平衡过程土样吸水量和体变量变化Figure 4. Variation of drainage and deformation of soil samples with suction of 200 kPa during consolidation![]()
图 5 吸力400 kPa平衡过程土样吸水量和体变量变化Figure 5. Variation of drainage and deformation of soil samples with suction of 400 kPa during consolidation2.2 固结平衡过程
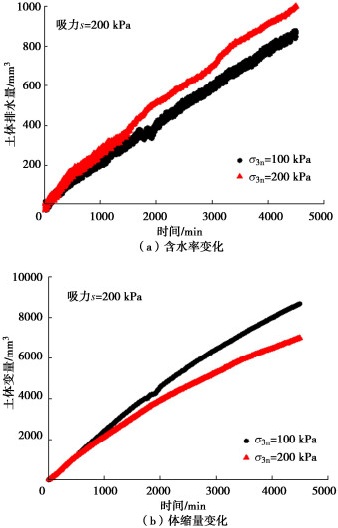
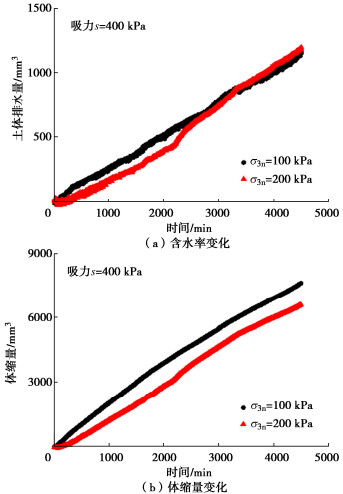
图 6~8给出了固结过程中土样含水率和体积变化规律。对比图 6（a），7（a），8（a）可以看出，对于同一个固结压力（净围压），经过湿化和干化过的土样含水率变化规律不同，吸力为50 kPa土样相对容易达到含水率平衡状态，且平衡后含水率随时间变化很小；吸力200和400 kPa土样含水率平衡时间较慢，而且达到平衡后仍然存在一定的含水率变化。对于同一吸力，不同固结压力的土样，固结压力越大，土体排水量也越大，而且达到平衡的时间也越长；对于高吸力的试样（吸力为200和400 kPa），在净围压为200 kPa的固结压力下，其含水率很难达到平衡，即使达到相对平衡状态，含水率仍然有一定变化。
![]()
图 6 吸力50 kPa土样固结过程排水量和体变量变化Figure 6. Variation of drainage and deformation of soil samples withsuction of 50 kPa during consolidation![]()
图 7 吸力200 kPa土样固结过程排水量和体变量变化Figure 7. Variation of drainage and deformation of soil samples with suction of 200 kPa during consolidation![]()
图 8 吸力400 kPa土样固结过程排水量和体变量变化Figure 8. Variation of drainage and deformation of soil samples with suction of 400 kPa during consolidation对比图 6（b），7（b），8（b）可以看出，在固结过程中，土体变形达到平衡的时间相对很短，一般在300~500 min范围。对于同一固结压力，随着吸力增大，固结过程中压缩变形量增大，但是达到平衡所需时间没有明显规律；对于相同吸力，随着固结压力增大，固结过程中压缩变形也增大，但是达到平衡所需时间相差不大。
图 6中吸力为50 kPa试样在200 kPa净围压下固结试验采用分级加载（分为6个等级加载到200 kPa净围压，每级达到平衡再进行下一级），可以看出施加每一级净围压，土体变形在短时间内可以达到平衡，但是土体中水一直持续稳定排出，并没有出现明显波动。整个固结过程，由于分级加载，变形呈现明显“台阶”式增加，但是含水率变化一直很平稳。对比图 6~8可以看出，对于3个吸力大小的土样，在等围压固结过程中，试样的体变率先达到平衡，而土体中含水率达到平衡所需时间更长，而且在最后阶段仍有微小增加。
2.3 剪切过程
图 9~11给出了三轴剪切过程中土样含水率和体积变化规律。对比图 9（a），10（a），11（a）可以发现在相同净围压下，随着吸力增大，排水曲线越来越直线化，只有低吸力50 kPa土样的排水曲线有达到平衡的趋势；但是随着吸力增大，土样最终排水量总体上呈减小趋势。对于吸力50 kPa的土样，随着净围压增大，排水量反而降低；对于吸力200 kPa的土样，随着净围压增大，排水量也增大；对于吸力400 kPa的土样，随着净围压增大，排水量基本一致。
![]()
图 9 吸力50 kPa土样在剪切过程排水量和体变量变化Figure 9. Variation of drainage and deformation of soil samples with suction of 50 kPa during shear![]()
图 10 吸力200 kPa土样在剪切过程排水量和体变量变化Figure 10. Variation of drainage and deformation of soil samples with suction of 200 kPa during shear![]()
图 11 吸力400 kPa土样在剪切过程排水量和体变量变化Figure 11. Variation of drainage and deformation of soil samples with suction of 400 kPa during shear对比图 9（b），10（b），11（b），可以发现在相同净围压下，吸力50 kPa土样的体变曲线最低，说明吸力50 kPa土样的刚度比较大；吸力200和400 kPa土样的体变曲线相差不大。对于3个吸力的土样，随着净围压增大，其体变曲线都降低。
综合分析图 9~11得到，非饱和土三轴剪切过程中其体变量大于排水量，说明整个剪切过程并没有使土样达到饱和。对于相同净围压，随着吸力增大，在三轴剪切过程中土样体变量与排水量的差异越大。然而对于相同吸力，随着净围压增大，在三轴剪切过程中土样体变量与排水量的差异变化不大。
3. 水-力路径下非饱和土含水率变化与变形滞后机理探讨
忽略温度和化学影响，土中水的变化主要受变形和吸力控制，而变形主要受水-力作用影响。土中含水率变化与变形又是耦合作用，因此，水-力作用下非饱和土含水率变化、变形特性尤为复杂。Bishop有效应力提出以后，人们试图利用这一单一应力变量描述非饱和土的力学特性。但是单一应力变量模型有一些弊端，首先不能模拟土体的湿陷和剪胀等力学特性，而且不能很好地描述土体变形特性。后续许多学者尝试利用双应力变量模型描述非饱和土水-力特性。Houlsby[16]根据非饱和土输入功率方程提出了功共轭应力与应变变量的概念：
L=ns˙Sr+{sij−[Sruw+(1−Sr)ua]σij}˙εij。 (1) 式中：L为非饱和土输入功率；n为土体的孔隙率；s为吸力；Sr为饱和度；σij为应力张量；uw为孔隙水压；ua为孔隙气压；εij为应变张量。Wheeler等[17]在此基础上提出用Bishop有效应力和有效饱和度（或者等效吸力）组成的双应力变量参数在p-q-Sr空间中建立水-力耦合模型，见图 12。
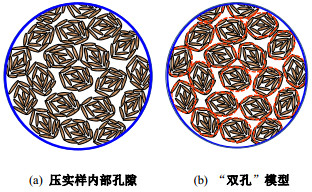
黏土孔隙一般可以分为集聚体间孔隙和集聚体内孔隙[18-21]，两种孔隙结构受水-力作用响应不同，普遍认为有效应力作用在集聚体内小孔隙上，小孔隙的变形导致集聚体间大孔隙的变化，即“双孔”模型，如图 13所示。大量试验数据表明（例如图 14），含水率的增加会使集聚体崩解或者使集聚在一起的土颗粒分开，孔隙结构最终趋于均匀化，但随着含水率的减少，土颗粒又会重新聚拢在一起形成集聚体，并呈现双峰孔隙结构[20, 22-24]；外力荷载只影响土中集聚体间孔隙，集聚体内孔隙基本上不受影响[9, 20-21, 25]。基于上述试验结果，建立了水-力作用下土孔隙演化模型，详见图 15，16。
![]()
图 14 不同水-力作用下孔径分布Figure 14. Pore-size distributions of samples under different hydro- mechanical effects![]()
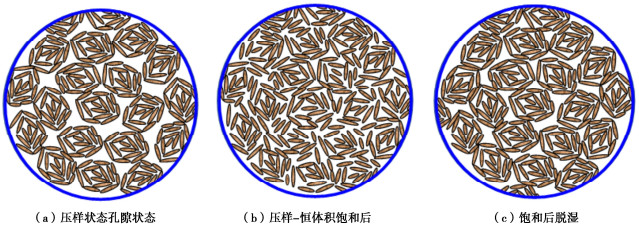
图 15 含水率变化条件下土孔隙演化Figure 15. Evolution of pore structure during variation of water content在吸力平衡过程中，从力学角度分析，土体在脱湿过程会发生收缩变形（图 4，5所示）主要原因是吸力增加了土颗粒间的Bishop有效应力，导致颗粒发生重新排列而变得更密实，因此吸力是导致土体收缩变形的内在力学机制，如图 15（b），（c）所示。从水力学角度分析，吸力变化会导致土中亲水性黏土矿物水化膜厚度改变。当土体含水率较高时，黏土颗粒外围包裹一层很厚的水化膜，颗粒间距较大，在干燥过程中，水分逐渐被蒸发，水化膜逐渐变薄，土颗粒逐渐靠拢，孔隙不断减小，从而土体体积发生收缩变形。吸力平衡过程实际是孔压消散过程，在这个过程中会有孔隙水流动和孔隙变形。比如脱湿过程，如图 17所示，孔隙水中的毛细水优先排出，随着不断排出，孔隙水不再连续，而且毛细水减少，导致后半阶段孔隙水排出速度变小，但是由于孔压没有完全耗散，排水仍然进行。由于排水导致土体应力场发生变化（骨架应力或者有效应力），在力的作用下使土孔隙发生变形，变形主要发生在吸力平衡的前半阶段，说明自由水变化对土变形影响相对较大。整体而言，吸力平衡导致孔隙水排出量一般大于土孔隙变形量。
固结过程中，由于净围压的施加，导致作用在土骨架上的应力增加，导致集聚体间大孔隙被压缩（机理如图 16所示），土体发生体缩（图 6~8所示），同时也导致部分孔隙水排出，一般土体变形量大于孔隙水排出量。外力作用使土体变形在很短时间内达到平衡，但是孔隙水达到平衡仍然比较慢，尤其是吸力较大的土样。有效应力直接作用在土骨架上，导致集聚体间孔隙被压缩，土体变形响应更加灵敏，如果土孔隙水不连续或者主要以吸附水存在，那么此时孔隙水迁移速度比较慢，耗费很长时间达到孔隙水平衡，而且饱和度越低，这种现象越明显。另外，固结会改变孔隙结构，导致吸力不再平衡，但试验是等吸力固结控制，因此吸力需要重新达到平衡，含水率平衡时间较长。同时，非饱和黏土孔隙水多以吸附水形式存在，相对于自由水其流动性相对较差，使吸力平衡更加困难。
剪切过程中，剪切应力直接作用在土骨架导致土体迅速发生变形，土孔隙被挤压会导致土孔隙水排出（如图 9~11所示），而且土孔隙变形导致孔压发生变化，孔压消散也会导致孔隙水迁移；与此同时，孔隙水迁移也会使土颗粒发生重新排列，导致土孔隙变形。因此，土的变形和孔隙水变化是相互耦合作用，又同时受水（含水率变化）-力（有效应力）作用控制。饱和土的含水率变化可以由变形表述，而非饱和土中含水率变化主要受吸力和变形影响。吸力平衡过程，一方面吸力导致含水率变化，另外在此过程会发生有效应力变化，导致土体变形，进而引起土体含水率变化。
通过式（1）看出，土体变形主要受有效应力和饱和度变化控制。有效应力和含水率变化对土体变形的影响机制不同，有效应力主要控制集聚体间孔隙变形，而含水率变化主要影响颗粒与颗粒之间孔隙（集聚体内孔隙），在吸力平衡过程，吸力和饱和度变化导致有效应力变化，导致土体发生变形，同时含水率变化会导致土颗粒发生移动，进而导致土体发生变形。土中含水率变化和变形是相互耦合作用，相对于变形来说，含水率变化比较缓慢。
4. 结论
通过对非饱和膨胀土开展吸力平衡、等向固结和三轴剪切试验，探究了水-力作用下非饱和土变形和含水率随时间变化特性，并从微观角度讨论了这些差异的原因，得到以下4点结论。
（1）吸力平衡过程中，土体的含水率和体积变化同步发生，含水率和体变都很难达到绝对平衡，但是体变比含水率变化率先达到相对平衡；在整个过程中，而且随着目标吸力增大，达到相对平衡时间越长。
（2）等向固结过程中，体变在相对较短时间内达到平衡，含水率却很难达到平衡；吸力和净围压对含水率达到平衡时间影响较大，对体变达到平衡所用时间影响不大。
（3）三轴剪切过程，土体排水和变形一直增加，总体而言，净围压越大，土体排水量和变形越小。
（4）改进“双孔模型”理论，外力对集聚体间孔隙影响显著，对集聚体内孔隙基本不影响；含水率变化会导致土颗粒重新排列（集聚体内小孔隙），继而影响集聚体间大孔隙。集聚体间孔隙水优先流动，集聚体内孔隙水（颗粒表面吸附水）相对迁移缓慢，导致在水-力作用下土的含水率达到稳定比体变达到稳定慢很多。
-
![]()
图 1 南阳膨胀土颗粒级配曲线
Figure 1. Grain-size distribution curve of Nanyang weakly expansive soil
![]()
图 3 吸力50 kPa平衡过程土样吸水量和体变量变化
Figure 3. Variation of drainage and deformation of soil samples with suction of 50 kPa during consolidation
![]()
图 4 吸力200 kPa平衡过程土样吸水量和体变量变化
Figure 4. Variation of drainage and deformation of soil samples with suction of 200 kPa during consolidation
![]()
图 5 吸力400 kPa平衡过程土样吸水量和体变量变化
Figure 5. Variation of drainage and deformation of soil samples with suction of 400 kPa during consolidation
![]()
图 6 吸力50 kPa土样固结过程排水量和体变量变化
Figure 6. Variation of drainage and deformation of soil samples withsuction of 50 kPa during consolidation
![]()
图 7 吸力200 kPa土样固结过程排水量和体变量变化
Figure 7. Variation of drainage and deformation of soil samples with suction of 200 kPa during consolidation
![]()
图 8 吸力400 kPa土样固结过程排水量和体变量变化
Figure 8. Variation of drainage and deformation of soil samples with suction of 400 kPa during consolidation
![]()
图 9 吸力50 kPa土样在剪切过程排水量和体变量变化
Figure 9. Variation of drainage and deformation of soil samples with suction of 50 kPa during shear
![]()
图 10 吸力200 kPa土样在剪切过程排水量和体变量变化
Figure 10. Variation of drainage and deformation of soil samples with suction of 200 kPa during shear
![]()
图 11 吸力400 kPa土样在剪切过程排水量和体变量变化
Figure 11. Variation of drainage and deformation of soil samples with suction of 400 kPa during shear
![]()
图 14 不同水-力作用下孔径分布
Figure 14. Pore-size distributions of samples under different hydro- mechanical effects
![]()
图 15 含水率变化条件下土孔隙演化
Figure 15. Evolution of pore structure during variation of water content
表 1 南阳膨胀土基本物理指标
Table 1 Physical properties of Nanyang weakly expansive soil
相对质量
密度液限/
%塑限/
%塑性指数 最大干密度/
(g·cm−3)缩限/
%最优含水率/% 自由膨胀率/% 原状样干密度/(g·cm−3) 2.74 38.8 17.2 21.6 1.69 10.5 18.2 53.8 1.45 
下载: 导出CSV
-
[1] 李昆鹏, 陈永贵, 叶为民, 等. 高压实膨润土孔隙结构特征研究进展[J]. 岩土工程学报, 2022, 44(3): 399-408. LI Kunpeng, CHEN Yonggui, YE Weimin, et al. Advances in studies on pore structure of highly compacted bentonite[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(3): 399-408. (in Chinese)
[2] MAŠÍN D. Double structure hydromechanical coupling formalism and a model for unsaturated expansive clays[J]. Engineering Geology, 2013, 165: 73-88. doi: 10.1016/j.enggeo.2013.05.026
[3] 陈正汉, 刘祖典. 黄土的湿陷变形机理[J]. 岩土工程学报, 1986, 8(2): 1-12. http://cge.nhri.cn/cn/article/id/9384 CHEN Zhenghan, LIU Zudian. Mechanism of collapsible deformation of loess[J]. Chinese Journal of Geotechnical Engineering, 1986, 8(2): 1-12. (in Chinese) http://cge.nhri.cn/cn/article/id/9384
[4] DONG S, LIU Z D. Plastic constitutive relation for slumping loess[C]//Proceedings of International Conference on Engineering Problems of Regional Soils. Beijing, 1998.
[5] 蔡国庆, 韩博文, 韦靖威, 等. 复杂水-力路径下非饱和砂质黄土增湿变形特性[J]. 岩石力学与工程学报, 2022, 41(增刊1): 3073-3080. CAI Guoqing, HAN Bowen, WEI Jingwei, et al. Wetting deformation characteristics of unsaturated sandy loess under complex hydro-mechanical paths[J]. Chinese Journal of Rock Mechanics and Engineering, 2022, 41(S1): 3073-3080. (in Chinese)
[6] 谈云志, 胡莫珍, 周玮韬, 等. 荷载-干湿循环共同作用下泥岩的压缩特性[J]. 岩土力学, 2016, 37(8): 2165-2171. TAN Yunzhi, HU Mozhen, ZHOU Weitao, et al. Effects of drying-wetting cycle and loading on compressive property of mudstone[J]. Rock and Soil Mechanics, 2016, 37(8): 2165-2171. (in Chinese)
[7] 陈康, 刘先峰, 袁胜洋, 等. 饱和红层泥岩填料累积变形特性及安定界限研究[J]. 岩土力学, 2022, 43(5): 1261-1268. CHEN Kang, LIU Xianfeng, YUAN Shengyang, et al. Experimental study of accumulative deformation behaviour and shakedown limit of saturated red mudstone fill material[J]. Rock and Soil Mechanics, 2022, 43(5): 1261-1268. (in Chinese)
[8] 宋朝阳, 韦昌富, 赵成刚. 考虑物理化学作用的饱和黏土统一压缩模型及验证[J]. 岩石力学与工程学报, 2021, 40(增刊1): 2888-2895. SONG Zhaoyang, WEI Changfu, ZHAO Chenggang. Unified virgin compression model for saturated clay considering physico-chemical effects and its verification[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(S1): 2888-2895. (in Chinese)
[9] 刘樟荣, 叶为民, 张召, 等. 膨润土颗粒混合物的堆积性质与水-力特性研究进展[J]. 工程地质学报, 2020, 28(2): 294-305. LIU Zhangrong, YE Weimin, ZHANG Zhao, et al. A review on packing and hydro-mechanical behaviour of bentonite pellet mixtures[J]. Journal of Engineering Geology, 2020, 28(2): 294-305. (in Chinese)
[10] DONG Y, LU N, FOX P J. Drying-induced consolidation in soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(9): 04020092. doi: 10.1061/(ASCE)GT.1943-5606.0002327
[11] NIU G, CUI Y J, PEREIRA J M, et al. Determining Bishop's parameter χ based on pore size distribution[J]. Géotechnique Letters, 2021, 11(1): 1-28.
[12] 郭剑峰, 陈正汉, 郭楠. 延安新区高填方工程的变形与水分迁移耦合分析[J]. 岩土工程学报, 2021, 43(增刊1): 143-148. GUO Jianfeng, CHEN Zhenghan, GUO Nan. Application of incremental nonlinear consolidation theory for unsaturated soil in high fill projects[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(S1): 143-148. (in Chinese)
[13] 高游, 孙德安, 张俊然, 等. 考虑孔隙比和水力路径影响的非饱和土土水特性研究[J]. 岩土工程学报, 2019, 41(12): 2191-2196. GAO You, SUN Dean, ZHANG Junran, et al. Soil-water characteristics of unsaturated soils considering initial void ratio and hydraulic path[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(12): 2191-2196. (in Chinese)
[14] ZHOU B C, LU N. Assessments of water sorption methods to determine soil's specific surface area[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2021, 147(8): 04021066. doi: 10.1061/(ASCE)GT.1943-5606.0002579
[15] 周葆春, 孔令伟, 陈伟, 等. 荆门膨胀土土-水特征曲线特征参数分析与非饱和抗剪强度预测[J]. 岩石力学与工程学报, 2010, 29(5): 1052-1059. ZHOU Baochun, KONG Lingwei, CHEN Wei, et al. Analysis of characteristic parameters of soil-water characteristic curve(swcc) and unsaturated shear strength prediction of Jingmen expansive soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(5): 1052-1059. (in Chinese)
[16] 陶高梁, 孔令伟. 基于微观孔隙通道的饱和/非饱和土渗透系数模型及其应用[J]. 水利学报, 2017, 48(6): 702-709. TAO Gaoliang, KONG Lingwei. A model for determining the permeability coefficient of saturated and unsaturated soils based on micro pore channel and its application[J]. Journal of Hydraulic Engineering, 2017, 48(6): 702-709. (in Chinese)
[17] 汪磊, 张立婷, 沈思东, 等. 分段循环荷载作用下非饱和土轴对称固结特性研究[J]. 岩土力学, 2022, 43(增刊1): 203-212. WANG Lei, ZHANG Liting, SHEN Sidong, et al. Axisymmetric consolidation characteristics for unsaturated soils under piece-wise cyclic load[J]. Rock and Soil Mechanics, 2022, 43(S1): 203-212. (in Chinese)
[18] 陈正汉. 重塑非饱和黄土的变形、强度、屈服和水量变化特性[J]. 岩土工程学报, 1999, 21(1): 82-90. CHEN Zhenghan. Deformation, strength, yield and moisture change of a remolded unsaturated loess[J]. Chinese Journal of Geotechnical Engineering, 1999, 21(1): 82-90. (in Chinese)
[19] 陈正汉. 非饱和土与特殊土力学[M]. 北京: 中国建筑工业出版社, 2022. CHEN Zhenghan. Mechanics for unsaturated and special soils[M]. Beijing: China Architecture & Building Press, 2022. (in Chinese)
[20] HOULSBY G T. The work input to an unsaturated granular material[J]. Géotechnique, 1997, 47(1): 193-196. doi: 10.1680/geot.1997.47.1.193
[21] WHEELER S J, SHARMA R S, BUISSON M S R. Coupling of hydraulic hysteresis and stress–strain behaviour in unsaturated soils[J]. Géotechnique, 2003, 53(1): 41-54. doi: 10.1680/geot.2003.53.1.41
[22] ALONSO E E, VAUNAT J, GENS A. Modelling the mechanical behaviour of expansive clays[J]. Engineering Geology, 1999, 54(1/2): 173-183.
[23] DELAGE P, AUDIGUIER M, CUI Y J, et al. Microstructure of a compacted silt[J]. Canadian Geotechnical Journal, 1996, 33(1): 150-158. doi: 10.1139/t96-030
[24] ROMERO E, DELLA VECCHIA G, JOMMI C. An insight into the water retention properties of compacted clayey soils[J]. Géotechnique, 2011, 61(4): 313-328. doi: 10.1680/geot.2011.61.4.313
[25] LLORET A, VILLAR M V, SÁNCHEZ M, et al. Mechanical behaviour of heavily compacted bentonite under high suction changes[J]. Géotechnique, 2003, 53(1): 27-40. doi: 10.1680/geot.2003.53.1.27
[26] 牛庚, 邵龙潭, 孙德安, 等. 土-水特征曲线测量过程中孔隙分布的演化规律探讨[J]. 岩土力学, 2020, 41(4): 1195-1202. NIU Geng, SHAO Longtan, SUN Dean, et al. Evolution law of pore-size distribution in soil-water retention test[J]. Rock and Soil Mechanics, 2020, 41(4): 1195-1202. (in Chinese)
[27] CUI Y J, LOISEAU C, DELAGE P. Microstructure changes of a confined swelling soil due to suction controlled hydration[J]. Proceedings of the 3nd International Conference on Unsaturated Soils, 2002, 2: 593-598.
[28] QIONG W, CUI Y J, TANG A M, et al. Time- and density-dependent microstructure features of compacted bentonite[J]. Soils and Foundations, 2014, 54(4): 657-666. doi: 10.1016/j.sandf.2014.06.021
[29] MIAO L C, HOUSTON S L, CUI Y, et al. Relationship between soil structure and mechanical behavior for an expansive unsaturated clay[J]. Canadian Geotechnical Journal, 2007, 44(2): 126-137. doi: 10.1139/t06-108
[30] 牛庚. 基于双孔模型的非饱和土水-力特性研究[D]. 大连: 大连理工大学, 2021. NIU Geng. Study on Hydro-mechanical Behavior of Unsaturated Soil based on Double Pore Structure Model[D]. Dalian: Dalian University of Technology, 2021. (in Chinese)
-
期刊类型引用(0)
其他类型引用(1)
-
其他相关附件
计量
- 文章访问数: 290
- HTML全文浏览量: 26
- PDF下载量: 102
- 被引次数: 1
