Constitutive theory of geomaterials saturated with salt solution and its application in clay
-
摘要: 盐溶液中离子的化学活性会改变饱和岩土的力学性质,诱发其工程性能出现劣化甚至失效等岩土工程问题。为了研究化学活性对饱和岩土水力与变形特性的影响,基于混合物理论与热力学溶液理论,建立了盐溶液饱和岩土材料的本构理论框架。与以往研究不同,该理论将固相应变分解为孔隙率变化引起的骨架应变、固相材料变形引起的基质应变以及化学反应等物质交换引起的质量交换应变,用以凸显孔隙率在水-力-化学多场耦合机制中的关键作用;采用溶质的现时质量分数作为化学状态变量来反映化学活性的影响;利用自由能和耗散势分别建立弹性和塑性本构关系。根据该理论框架建立了NaCl溶液饱和黏土的固相、流相本构关系以及溶质的渗流-扩散方程,并得到了已有试验数据的验证,表明该框架可以指导盐溶液饱和岩土的本构建模工作。Abstract: The chemical activity of ions in salt solution will change the mechanical properties of saturated geomaterials, inducing geotechnical problems such as deterioration or even failure of engineering properties. In order to study the effects of chemical activity on the hydraulic and deformation properties of saturated geomaterials, a constitutive theory framework for geomaterials saturated with salt solution is established based on the mixture theory and thermodynamic solution theory. Different from the previous studies, the solid phase strain is decomposed into the skeleton one caused by porosity change, the matrix one caused by solid material deformation, and the mass exchange one caused by material exchange such as chemical reaction, to highlight the key role of porosity in the hydro-mechanical-chemo multi-field coupling mechanism. This theory adopts the current mass fraction of solute as the chemical state variable to reflect the effects of chemical activity. The free energy and dissipation potential are used to establish the elastic and plastic constitutive relations, respectively. Based on the above theoretical framework, the constitutive relations of solid and fluid phases for the clay saturated with NaCl solution and the seepage-diffusion equation for the solute are established. The constitutive model is validated by the experimental data, which proves that the framework can guide the establishment of the constitutive model for the geomaterials saturated with salt solution.
-
0. 引言
在核废料处置库、垃圾填埋场、石油和天然气储油层以及海洋工程等涉及环境和岩土相互作用的工程建设领域,经常会遇到盐溶液饱和岩土材料[1-13]。与普通饱和岩土相比,盐溶液饱和岩土中的可溶盐分在溶液中分解出阴阳离子。这些离子具有化学活性,能够降低矿物表面双电层的厚度,改变岩土颗粒间的距离[7],进而引起岩土材料渗透、变形和强度性质发生变化,诱发其工程性能劣化甚至失效。因此研究盐溶液饱和岩土材料的化学活性和工程力学特性的耦合作用具有重要的理论和工程实践意义。
目前国内外学者已经较系统地开展了盐溶液饱和岩土材料工程特性的试验研究[4-6],并已开始着手盐溶液饱和岩土材料的本构建模研究工作[8-13]。Guimarães等[8]基于唯象理论,采用盐溶液中离子摩尔浓度和渗透压作为化学状态变量来建立非饱和黏土的本构模型。徐永福[3]用表面分形学来完善双电层理论,利用渗透压修正有效应力,以此计算NaCl溶液饱和膨润土的膨胀变形。Dominijanni等[9]基于固相骨架电荷与孔隙溶液离子之间的电荷平衡条件,引入渗透压作为化学状态变量来建立理论模型。Bennethum等[10]在Hassanizadeh等[11]所创立的复合混合物理论基础之上,定义了与经典热力学相容的化学势,通过应变在各组分自由能之间的耦合作用来反映多孔介质的吸附作用,建立了膨胀多孔骨架的本构理论框架。Wei[2]和Ma等[12]从混合物理论出发,推导了考虑表面势的粒间应力公式,进而利用渗透压来修正有效应力,建立了考虑化学活性影响的白垩石吸水本构模型。上述成果有力地推动了饱和与非饱和岩土材料在力学-渗流-化学多场耦合研究领域的发展。
在当前考虑化学活性的研究中,大多数学者选用渗透压作为化学状态变量来反映饱和岩土材料中的水-力-化学之间的耦合作用。然而,渗透压的物理含义是半透膜达到热力学平衡时两侧存在的压力差[3]。但在饱和岩土固结过程中,孔隙流体存在渗流速度,因而未达到热力学平衡状态,与渗透压的物理含义略有不符。除此之外,也有学者如Loret等[13]基于热力学理论,选用组分的化学势与摩尔分数作为化学状态变量建立了饱和黏土的化学-力学耦合本构模型。但在该理论中,摩尔分数定义在初始构形的摩尔浓度之上,而在试验中能够直接测量的是现时构形的摩尔浓度,这给试验测量带来一定的困难。因此,需要基于现时构形,开展考虑力学-渗流-化学多场耦合的理论建模研究工作。
另外,作为多孔介质,饱和岩土中的孔隙率反映了颗粒组成结构,在水-力-化学耦合机制中起到至关重要的作用[14]。然而,对于岩土材料中的裂隙岩体,岩石材料本身的变形不可忽略[15-16],故对于一般的岩土材料,固相应变包含了固相材料变形引起的基质应变和孔隙变化引起的骨架应变[15-16],它们具有不同的力学性质和本构关系。因此需要把基质应变和骨架应变从固相应变中单独区分开来,以便揭示孔隙结构在多孔介质水-力-化学作用过程中的关键作用。此外,当前盐溶液饱和岩土材料的本构研究多侧重于固相组分的本构模型,而忽略了流相组分的本构模型和溶质渗流-扩散控制方程。事实上,饱和岩土的本构关系不仅应包含固相的本构关系,还应包含流相的本构关系以及溶质的渗流-扩散控制方程[17-19]。由于变形过程中流固两相的体积分数之和必须等于1,同时建立固相和流相的本构模型可以很容易发现它们均包含骨架体积应变,因此更有利于直观揭示流固两相的几何耦合机制[15-16, 18-19]。
在以往的饱和岩土材料本构模型研究历史中,Collins等[20]、Borja[21]、陈正汉[22-23]、赵成刚等[24]、刘艳等[25]和胡亚元[15-16]在混合物理论与非平衡态热力学理论框架下,从热力学第一定律所蕴含的自由能和热力学第二定律所蕴含的耗散势中出发,成功地建立了考虑力学-渗流耦合的饱和岩土弹塑性本构理论。其中自由能决定材料的弹性性质,耗散势则决定材料的塑性性质。本文将在上述研究基础上,把热力学溶液理论[26]引入混合物理论与非平衡态热力学理论框架,建立考虑力学-渗流-化学多场耦合过程的盐溶液饱和多孔介质的本构理论。
1. 体积分数和密度
盐溶液饱和多孔介质包括固相与孔隙流相两相,为简便分析,把固相视为单一组分构成,流相视为溶质与溶剂两种组分构成。由于可能存在溶解(或析出)、吸附和化学反应等物理化学作用,为不失一般性,假定固相与流相之间以及流相中各组分之间存在质量交换。令α={S, F}为相的指征变量,固相用S表示,流相用F表示;φα表示α相的现时体积分数,ρα为α相的表观密度[27](有些文献也称为组分密度),ρRα为α相的真实密度(或称材料密度)且满足ρα=φαρRα。则饱和多孔介质的总密度为ρ=ρS+ρF。根据体积分数的定义有φS+φF=1。
孔隙流相中包含溶质与溶剂两种组分,根据经典热力学溶液理论[26]可知,溶质与溶剂相互融合,很难区分出其各自所占体积,因此可认为溶质与溶剂具有与流相相同的体积。令β={L, c}为流相中组分的指征变量,溶剂用L表示,溶质用c表示,ρβF为流相中β组分的表观密度[27],根据表观密度的定义有
ρF=∑β=L, cρβF=ρLF+ρcF。 (1) 2. 平衡方程
2.1 质量守恒
根据混合物理论[17]可知,盐溶液饱和多孔介质的固相和流相连续,并共享混合物的空间位置。令α相的初始位置为Xα,t时刻的空间位置为x,则α相的运动方程可表示为x=xα(Xα,t),令vα为α相的速度,则饱和多孔介质混合物的相平均速度为v=(ρSvS+ρFvF)/ρ;α相相对于多孔介质混合物的相对速度为uα=vα−v。选择固相作为盐溶液饱和多孔介质的参考构形,令WF=νF−νS为流相相对于固相的扩散速度。考虑到可能存在的溶解(或析出)和化学反应等物理化学作用,固流两相之间以及溶剂与溶质之间可能存在质量交换,令ˆcS与ˆcF分别为固相和流相之间的质量交换率,ˆcLF与ˆccF分别为流相中溶剂、溶质与固相组分之间的质量交换率。定义质量交换率以质量供给为正。根据以往研究,在考虑固流两相质量交换情况下可得固流两相的质量守恒方程为[15, 17]
φSρRSdSρRSdt+dSφSdt−φS∇⋅vS−ˆcSρRS=0,φFρRFdFρRFdt+dSφFdt−φF∇⋅vS−φF∇⋅WF−WF⋅∇φF−ˆcFρRF=0。} (2) 式(2)满足ˆcS+ˆcF=0[17],同理,可得流相中各组分的质量守恒方程为[10]
ρFdLFcLF/dt−∇⋅(ρLFuLF)=ˆcLF−cLFˆcF,ρFdcFccF/dt−∇⋅(ρcFucF)=ˆccF−ccFˆcF。} (3) 式中:ˆcLF+ˆccF=ˆcF[10];cβF=ρβF/ρF为流相中β组分关于现时构形的质量分数;vβF为流相中β组分的速度;uβF=vβF−vF为流相中β组分相对于流相的相对速度。
令σα(α∈{S, F})为α相的表观应力(有些文献也称为组分应力),σ为总应力,为了更好地应用于岩土工程,根据岩土力学规定,应力张量和应变张量均以受压为正。根据混合物理论[17]与复杂介质的平均应力定理[28]可得
σ=σS+σF。 (4) 令总压力为PT=σ:I/3,PS=σS:I/(3φS)为固相基质压力;PF=σF:I/(3φF)为流相基质压力或称为孔压。则根据式(4)有PT=φSPS+φFPF。
2.2 能量平衡
令qα,rα以及ˆεα分别为α相的热流向量、外热供给量以及能量供给量,ξα为内能密度;bβF为外体力密度,则固相与流相的能量平衡方程为[15-17]
ρSdSξSdt=σS:∇vS−∇⋅qS+ρSrS+ˆεS,ρFdFξFdt=σF:∇vF−∇⋅qF+ρFrF+ˆεF+∑β=L,cρβFuβF⋅bβF。} (5) 令DS=[∇vS+(∇vS)T]/2为固相变形率;根据混合物理论[17]可知,式(5)中的ˆεα满足方程:
∑α=S,F[ˆεα+uα⋅ˆpα+ˆcα(ξα+u2α/2)]=0。 (6) 孔隙率在多孔介质中反映微观结构的变化,在多孔介质变形中占据着关键地位[14]。在土力学中,把与孔隙率变化存在一一对应关系的体积应变称为骨架应变[15-16]。因此,有必要将孔隙率变化相关的骨架应变从固相应变中分离开来。然而下面的分析将会看到,式(5)1中的∇vS不仅取决于骨架应变,还取决于固相基质应变和固相质量交换所产生的应变,因此式(5)1中的∇vS与骨架应变并不是一一对应的关系。为了分析孔隙率对水-力-化学耦合的重要影响,需要利用式(2),(4)~(6)将固相应变分解为骨架应变、基质应变和固相质量交换所引起的应变。
利用Terzaghi有效应力˜σ=σ−PFI和φS+φF=1,并结合式σF=φFPFI,WF=vF−vS与式(2)可得
∑α=S,Fσα:∇vα=˜σ:∇vS+PFφSdSρRS/(ρRSdt)−PFWF⋅∇φF+PFφFdFρRF/(ρRFdt)−PF(ˆcS/ρRS+ˆcF/ρRF)。 (7) 定义α相材料的体应变为ϑα=ln(ρRα/ρRα0),ρRα0为α相的初始材料密度,材料体应变ϑα以受压为正。将ϑα=ln(ρRα/ρRα0)代入式(7),则式(7)等式右侧第二项变为PFφSdSρRS/(ρRSdt)=φSPFdSϑS/dt,即此时固相材料(基质)体应变与流相孔压呈功共轭对,然而,固相材料(基质)体应变应该取决于固相基质压力。因此,需要将这一项的功共轭对进行变换以获得更符合多孔介质受力特征的能量平衡表达式。
将固相质量交换所引起的固相变形称为质量交换变形,记为εc,其速率定义式为
dεc/dt=−ˆcS/ρS。 (8) 定义DH为
DH=Ds−dsϑSI/(3dt)−dεcI/(3dt)。 (9) 由式DS=[∇vS+(∇vS)T]/2,式(2)1和(9)得
trDH=trDS−dSϑS/dt−dεc/dt=dSφS/(φSdt)。 (10) trDH的物理含义是体应变速率,即式(10)表明与trDH所对应的体积变形仅取决于固相体积分数,而固相体积分数与孔隙率一一对应,所以与DH所对应的变形为骨架变形,DH为固相骨架变形率。采用DH来建立饱和多孔介质本构模型要比DS更加简便。
令固相基质压力为PS=(PT−φFPF)/φS,利用DS=[∇vS+(∇vS)T]/2,φS+φF=1,式(9)以及ϑα=ln(ρRα/ρRα0),则式(7)可表示为
∑α=S,Fσα:∇vα=˜σ:DH+∑α=S,FφαPαdαϑα/dt−PFWF⋅∇φF−(PSˆcS/ρRS+PFˆcF/ρRF)。 (11) 式(11)表明,当采用DH与有效应力˜σ作为功共轭对时,与固相基质体应变ϑS呈共轭对的是固相基质压力,这与固相基质体应变取决于固相基质压力的力学规律一致,因而式(11)比式(7)更容易反映多孔介质各组分的力学规律。在试验中,固相基质压力无法直接测量,可通过测量总应力PT、孔压PF和孔隙率φF并根据式PS = (PT−φFPF)/(1−φF)来计算。
令Wα=uα−uS,将式(5)中的两个方程相加,再将式(6),(11)代入可得
∑α=S,Fραdαξα/dt=˜σ:DH+∑α=S,FφαPαdαϑα/dt+∑α=S,F(−∇⋅qα+ραrα)−WF⋅(PF∇φF+ˆpF)−∑α=S,Fˆcα(ξα+W2α/2+Pα/ρRα)+∑β=L,cρβFuβF⋅bβF。 (12) 其中ˆpα为α相的动量供给量。令: FS=∂x/∂XS, JS=detFS,ES=(FTS⋅FS−I)/2,JRS=ρRS/ρRS0, Jc=exp(∫t0ˆcS/ρSdt),FH=[Jc/JRS]1/3FS,EH=(FTH. FH−I)/2,˜TH=F−1H⋅˜σ⋅F−TH。其中FS为固相变形梯度; ES为固相Green应变; FH为固相骨架的变形梯度; EH为固相骨架Green应变; ˜TH为Piola-Kirchhoff有效应力。将˜TH与EH代入式(12) 可得
∑α=S,Fραdαξαdt=(˜TH:dSEHdt+φSPSdSϑSdt)+φFPFdFϑFdt+∑α=S,F(−∇⋅qα+ραrα)−WF⋅(PF∇φF+ˆpF)−∑α=S,Fˆcα(Pα/ρRα+W2α/2+ξα)+∑β=L,cρβFuβF⋅bβF。 (13) 式(13)便是考虑化学活性时的盐溶液饱和多孔介质的能量平衡方程。
3. 熵流与熵产
根据式(9)可得
DS=DH+dSϑSI/(3dt)+dεcI/(3dt)。 (14) 式(14)表明多孔固体总变形率DS包括3个部分:固相基质体积变形率dSϑS/dt,固相骨架变形率DH以及质量交换变形率dεc/dt。式(13)表明EH,ϑS与ϑF分别与˜TH,φSPS与φFPF呈功共轭关系。根据热力学理论,可选取EH、ϑS和ϑF作为饱和多孔介质本构模型的应变状态变量;选取˜TH、φSPS和φFPF作为应力状态变量。此外,在考虑化学活性时,还应选取各相各组分的质量分数及其化学势作为本构模型的化学状态变量。当本构模型需要描述塑性行为时,在内能表达式中还需选取塑性应变作为内变量,它的功共轭量称为耗散应力[15]。在考虑化学活性的本构方程中,应选取两个塑性Green应变,分别为应力加载产生的骨架塑性应变Ep1H和化学加载产生的化学塑性应变Ep2H。假定固流两相具有相同温度,考虑到水溶剂或溶质与固相之间的吸附作用,流相的内能将受到骨架应变的影响。因此根据非平衡态热力学[29],式(13)中固相和流相的内能可分别表示为ξS(ηS,EH,Ep1H,Ep2H,ϑS)和ξF(ηF,EH,Ep1H,Ep2H,ϑF,cLF,ccF),其中ηα是α相的熵密度,cLF=ρLF/ρF与ccF=ρcF/ρF分别为流相中溶剂与溶质的质量分数。由此可得内能的全微分为
∑α=S,Fραdαξαdt=ρS∂ξS∂ηSdSηSdt+ρF∂ξF∂ηFdFηFdt+(ρS∂ξS∂EH+ρF∂ξF∂EH):dSEHdt+(ρS∂ξS∂EplH+ρF∂ξF∂Ep1H)dSEp1Hdt+(ρS∂ξS∂Ep2H+ρF∂ξF∂Ep2H)dSEp2Hdt+ρS∂ξS∂ϑSdSϑSdt+ρF∂ξF∂ϑFdFϑFdt+(ρF∂ξF∂EH:∇EH+ρF∂ξF∂EplH:∇Ep1H+ρF∂ξF∂Ep2H:∇Ep2H)⋅WF+ρF∂ξF∂cLFdFcLFdt+ρF∂ξF∂ccFdFccFdt。 (15) 根据热力学局部平衡假定,对比式(13)与(15)可得
θ=∂ξS∂ηS=∂ξF∂ηF;˜TH=ρS∂ξS∂EH+ρF∂ξF∂EH; (16a) PS=ρRS∂ξS/∂ϑS;PF=ρRF∂ξF/∂ϑF。 (16b) 令:
ˉμLF=∂ξF/∂cLF;ˉμcF=∂ξF/∂ccF (16c) ˜Tp1H=−ρS∂ξS/∂Ep1H−ρF∂ξF/∂Ep1H (16d) ˜Tp2H=−ρS∂ξS/∂Ep2H−ρF∂ξF/∂Ep2H。 (16e) 式中:ˉμLF,ˉμcF分别为与质量分数cLF与ccF呈功共轭关系的化学势;˜Tp1H和˜Tp2H为Piola-Kirchhoff耗散有效应力。根据试验成果获得内能表达式后,依据式(16a)~(16e)可获得有限应变条件下以内能形式表示的饱和多孔介质的弹性本构方程。
设α相的Helmholtz自由能ψα=ξα−θηα。令
ˆpA=ρF∂ξF∂EH:∇EH+ρF∂ξF∂EpH:∇Ep1H+ρF∂ξF∂Ep2H:∇Ep2H。 (17) 将Helmholtz自由能定义式、式(13),(17)代入(15)并结合式(16a)~(16e)得
θ∑α=S,Fραdαηαdt=−ρFˉμLFdFcLFdt−ρFˉμcFdFccFdt+˜Tp1HdSEp1Hdt+˜Tp2HdSEp2Hdt+∑α=S,F(−∇⋅qα+ραrα)−(PF∇φF+ˆpF+ˆpA)⋅WF−∑α=S,Fˆcα(Pα/ρRα+W2α/2+ψα+θηα)+∑β=L,cρβFuβF⋅bβF。 (18) 根据混合物理论[17]有
ρdηdt=∑α=S,F[ραdαηαdt+∇⋅(ραηαuα)+ˆcαηα]。 (19) 令ˉμF=cLFˉμLF+ccFˉμcF,并将式(3)与(18)代入式(19),并利用b∇⋅a=∇⋅(ba)−a⋅∇b可得
ρdηdt=∇⋅[−∑α=S,F(−ραηαuα+qαθ)−∑β=L,c1θˉμβFρβFuβF]+∑α=S,Fραrαθ+∑α=S,Fqα⋅∇1θ+˜Tp1HθdSEp1Hdt+˜Tp2HθdSEp2Hdt+∑β=L,cρβFuβF⋅∇(ˉμβFθ)−PF∇φF+ˆpF+ˆpAθ⋅WF+ˆcFˉμFθ−∑α=S,Fˆcαθ(ψα+12W2α+PαρRα)−∑β=L,cˉμβFˆcβFθ+∑β=L,cρβFuβFθ⋅bβF。 (20) 根据热力学的熵分解理论[29],由式(20)可得熵流项为
ρdηr/dt=∇⋅[−∑α=S,F(−ραηαuα+qα/θ)−∑β=L,cˉμβFρβFuβF/θ]+∑α=S,Fραrα/。 (21) 熵产项为
ρdηidt=∑α=S,Fqα⋅∇1θ+˜Tp1HθdSEp1Hdt+˜Tp2HθdSEp2Hdt−PF∇φF+ˆpF+ˆpAθ⋅WF+∑β=L,cρβFuβF⋅[∇(ˉμβFθ)+bβFθ]−∑α=S,Fˆcαθ(ψα+12W2α+PαρRα)+ˆcFˉμFθ−∑β=L,cˉμβFˆcβFθ。 (22) 在式(22)的右侧,第一项是热传导引起的熵产;第二项和第三项是塑性行为引起的熵产;第四项是渗流引起的熵产;第五项是由于在流体中扩散引起的熵产;第六项和第七项是由于固体和流体之间化学作用引起的熵产;最后一项是由于流相组分之间化学作用引起的熵产。根据热力学第二定律[29],熵产项应大于等于0。根据vF=(ρLFvLF+ρcFvcF)/ρF和uβF=vβF−vF可得ρLFuLF=−ρcFucF,将其代入式(22),即耗散率势函数为
ς=ρθdηi/dt=∑α=S,Fqα⋅θ∇(1/θ)+˜Tp1H:(dSEp1H/dt)+˜Tp2H:(dsEp2H/dt)−(PF∇φF+ˆpF+ˆpA)⋅WF+ρcFucF⋅[θ∇(ˉμcF−ˉμLFθ)+bcF−bLF]+ˆcFˉμF−∑α=S,Fˆcα(ψα+Pα/ρRα+W2α/2)−∑β=L,cˉμβFˆcβF⩾0。 (23) 4. 小应变条件下的一般本构方程
令εS与εH分别为固相应变张量ES与骨架应变张量EH在小应变条件下的近似值[30]; εp1H与εp2H分别为骨架塑性应变张量Ep1H与化学塑性应变张量Ep2H在小应变条件下的近似值 [30]。小应变条件下有DS=dεs/dt, DH=dεH/dt,ρα≈ρα0,ρRα≈ρRα0,˜TH≈˜σ, ˜Tp1H≈˜σp1与˜Tp2H≈˜σp2, 由式(14) 可得
εS=εH+ϑsI/3+εcI/3。 (24) 式(24)表明,在小应变条件下,盐溶液饱和岩土材料的固相应变εS可以分解为εH、ϑS以及εc之和。
令εSV与εHV分别为固相体应变与固相骨架体应变,对式(24)取迹得
εSV=εHV+ϑS+εc。 (25) 由式(10)和DS=dεS/dt可得在小应变条件下有εHV=ln(φS/φS0),注意到ln(φS0/φS)泰勒展开式中的高次项在小应变条件下可忽略,得
εHV=(φS−φS0)/φS0。 (26) 式中,φS0为固相初始体积分数。同理,根据ϑα=ln(ρRα/ρRα0)可得基质(材料)小应变表达式为
ϑα=(ρRα−ρRα0)/ρRα0。 (27) 在小应变条件下, 式(16a)~(16e) 中的固相的内能变为ξS(ηS,εH,εp1H,εp2H,ϑS), 流相的内能变为ξF(ηF,εH,εp1H,εp2H,ϑF,cLF,ccF), 则以内能势函数表示的一般弹性本构方程式(16a)~(16e) 表示为
θ=∂ξS∂ηS=∂ξF∂ηF,˜σ=∂(ρS0ξS+ρF0ξF)∂εH,˜σp1=−∂(ρS0ξS+ρF0ξF)∂εpH,˜σp2=−∂(ρS0ξS+ρF0ξF)∂εpH,PS=∂(ρRS0ξS)/∂ϑS,PF=∂(ρRF0ξF)/∂ϑF,ˉμLF=∂ξF/∂cLF,ˉμcF=∂ξF/∂ccF。} (28) 其中˜σp1和˜σp2是与εp1H和εp2H对应的耗散应力[15, 17]。引入Helmholtz自由能为ρα0ψα=ρα0ξα−ρα0θηα, α∈{S,F}, 此时固相Helmholtz自由能的表达式为ψS(θ,εH,εp1H,εp2H,ϑS), 流相Helmholtz自由能表达式为ψF(θ,εH,εp1H,εp2H,ϑF,cLF,ccF), 对ρα0ψα=ρα0ξα−ρα0θηα求全微分后将式(28) 代入得
ηS=−∂ψS∂θ,ηF=−∂ψF∂θ,˜σ=∂(ρS0ψS+ρF0ψF)∂εH,˜σp1=−∂(ρS0ψS+ρF0ψF)∂εp1H,˜σp2=−∂(ρS0ψS+ρF0ψF)∂εp2H,PS=∂(ρR0ξS)/∂ϑS,PF=∂(ρRF0ξF)/∂ϑF,ˉμLF=∂ξF/∂cLF,ˉμcF=∂ξF/∂ccF。} (29) 由于固流两相的温度相同且恒定,自由能ψS和ψF表达式中的温度θ可被省略。在大多数情况下,固相Helmholtz自由能可被简化为两部分:①固相材料体积变形所产生的自由能ψRS(ϑS);②固相骨架变形所产生的自由能ψHS(εH,εp1H,εp2H)。根据式cLF=1−ccF,流相Helmholtz自由能ψF(εH,εp1H,εp2H,ϑF,cLF,ccF)可表达为ψF(εH,εp1H,εp2H,ϑF,ccF),也可被简化为两部分:①流相基质(材料)的体积变形以及化学活性的作用而产生的自由能ψRF(ϑF,ccF);②由于流相与固相之间的吸附作用而产生的自由能ψHF(εH,εp1H,εp2H)。令ΨHF(εH,εp1H,εp2H)=ρF0ψHF(εH,εp1H,εp2H),ΨHS(εH,εp1H,εp2H)=ρS0ψHS(εH,εp1H,εp2H),ΨRS(ϑS)=ρRS0ψRS(ϑS),ΨRF(ϑF,ccF)=ρRF0ψRF(ϑF,ccF),根据上述分析由式(29)可得
˜σ=∂[ΨHS(εH,εp1H,εp2H)+ΨHF(εH,εplH,εp2H)]∂εH,˜σp1=−∂[ΨHS(εH,εp1H,εp2H)+ΨHF(εH,εp1H,εp2H)]∂εpH,˜σp2=−∂[ΨHS(εH,εp1H,εp2H)+ΨHF(εH,εp1H,εp2H)]∂εpH,PS=∂ΨRS(ϑS)/∂ϑS;PF=∂ΨRF(ϑF,ccF)/∂ϑF,ˉμcF−ˉμLF=∂ΨRF(ϑF,ccF)/(ρRF0∂ccF)。} (30) 式(30)是在小应变条件下以自由能势函数表示的一般弹性本构方程。由于考虑到温度恒定,则耗散率势函数式(23)在小应变条件下可表示为
ς=˜σp1:dεp1Hdt+˜σp2:dεp2Hdt−(PF∇φF+ˆpF+ˆpA)⋅WF+ρcFucF⋅[∇(ˉμcF−ˉμLF)+bcF−bLF]+ˆcFˉμF−∑α=S,Fˆcα(ψα+Pα/ρRα+W2α/2)−∑β=L,cˉμβFˆcβF⩾0。 (31) 当以下关系成立时,式(31)显然成立。
˜σp1:dεp1H/dt⩾0;˜σp2:dεp2H/dt⩾0,−(PF∇φF+ˆpF+ˆpA)⋅WF⩾0,ρcFucF⋅[∇(ˉμcF−ˉμLF)+bcF−bLF]⩾0。} (32a) ˆcFˉμF−∑α=S,Fˆcα(ψα+12W2α+PαρRα)−∑β=L,cˉμβFˆcβF=−ˆcF(ψF+12W2F+PαρRα−ˉμF+ˉμLF−ψS−PSρRS)−(ˉμcF−ˉμLF)ˆccF⩾0。 (32b) Collins等[20]认为,一般可假定耗散势存在:
˜σp1=∂Θp1(dεp1H/dt)∂(dεp1H/dt);˜σp2=∂Θp2(dεp2H/dt)∂(dεp2H/dt), (33a) PF∇φF+ˆpF+ˆpA=−∂Θw(WF)/∂WF, (33b) ∇(ˉμcF−ˉμLF)+bcF−bLF=∂Θd(ρcFucF)/∂(ρcFucF), (33c) ψF+12W2F+PFρRF−ˉμF+ˉμLF−ψS−PSρRS=−∂Θc(ˆcF)∂ˆcF, (33d) ˉμcF−ˉμLF=−∂Θcf(ˆccF)/∂ˆccF。 (33e) 式(33a)~(33e)基于热力学第二定律的耗散势建立,反映了多孔介质非弹性、扩散和化学反应等不可逆过程,其塑性本构方程与渗流-扩散控制方程可据此获得。
5. 算例验证
上面所建立的是盐溶液饱和岩土的一般本构规律。具体建模时,在上述一般本构规律指导下,可以结合黏土的微细观结构,从物理意义的角度出发确定具体材料的本构方程;也可以结合试验成果,通过拟合试验数据来建立具体材料的本构方程。本文结合颜荣涛等[5]开展的NaCl溶液饱和黏土的等向压缩试验来建立饱和黏土的等向压缩本构模型。
为了验证上述盐溶液饱和岩土的本构框架的实用性,现结合具体试验成果来建立NaCl溶液饱和黏土的本构建模。试验用土取自南宁的五象新区某工地,为高液限黏土[5]。黏土试样由NaCl溶液饱和,试验过程为等向加压到1200 kPa后卸压回弹至100 kPa。结合试样在去离子水和质量分数为3%,11%的NaCl溶液饱和下的等向压缩试验数据,确定模型参数。利用该模型参数模拟了试样在质量分数分别为0.6%和6%的NaCl溶液饱和时的等向压缩力学行为。
在等向压缩试验中,剪应力为0,试样在平均有效应力作用下只产生体应变,因此式(30)可退化为
˜P=∂[ΨHS(εHV,εp1HV,εp2HV)+ΨHF(εHV,εp1HV,εp2HV)]∂εHV,˜Pp1=−∂[ΨHS(εHV,εp1HV,εp2HV)+ΨHF(εHV,εp1HV,εp2HV)]∂εp1HV,˜Pp2=−∂[ΨHS(εHV,εp1HV,εp2HV)+ΨHF(εHV,εp1HV,εp2HV)]∂εp2HV,PS=∂ΨRS(ϑS)/∂ϑS,PF=∂ΨRF(ϑF,ccF)/∂ϑF,ˉμcF−ˉμLF=∂ΨRF(ϑF,ccF)/(ρRF0∂ccF)。} (34) 式中:˜P为平均有效应力;˜Pp1和˜Pp2为反映第1和第2屈服面的耗散有效应力;εp1HV,εp2HV分别为骨架塑性体应变与化学塑性体应变。式(34)表明对于饱和多孔介质的本构关系包含固相和流相本构关系,这与Biot固结理论以及陈正汉的研究成果相一致[18-19, 28]。同时式(34)中与化学活性相关的状态变量是无量纲的质量分数而不是摩尔浓度,这与当前采用摩尔浓度作为状态变量的盐溶液饱和岩土本构模型有所区别。此外,化学势在试验中不易定量,因此采用质量分数作为化学变量来建立土体固相本构模型则更为方便。
根据以往研究可知,对于大多数弹塑性问题,耗散有效应力˜Pp1和˜Pp2与Terzaghi有效应力大小相等˜Pp1=˜Pp2=˜P,因此˜Pp1和˜Pp2也被称为Terzaghi耗散有效应力[15-16]。
目前在关于盐溶液饱和黏土的实际工程应用与研究中,通常不考虑固相与液相之间以及流相中各组分之间的质量交换。因此有ˆcF=ˆcS=0,ˆcLF=ˆccF=0与εc=0。则根据式(25)可得土体固相的体应变为
εSV=εHV+ϑS。 (35) 在等向压缩试验中,(33a)~(33c)可写为
˜Pp1=∂Θp1( dεp1HV/dt)∂(dεp1HV/dt),˜Pp2=∂Θp2( dεp2HV/dt)∂(dεp2HV/dt),PF∂φF/∂z+ˆpF+ˆpA=−∂Θw(WF)/∂WF,∂∂z(ˉμcF−ˉμLF)+bcF−bLF=∂Θd(ρcFucF)∂(ρcFucF)。} (36) 式(36)表明盐溶液饱和黏土的本构关系还应包括塑性本构关系与流体的渗流规律以及溶质的扩散方程。
5.1 固体基质(土颗粒)的本构关系
在土力学中,固相基质的变形即为土体颗粒的变形。当土骨架破坏时,一般认为固相基质仅产生弹性应变。对于线弹性模型,固相基质的Helmholtz自由能由式(34)4可表示为
ΨRS(ϑS)=KRSϑ2S/2。 (37) 式中,KRS为土颗粒的体积模量,将式(37)代入式(34)4得:
PS=KRSϑS。 (38) 5.2 土骨架的弹性本构关系
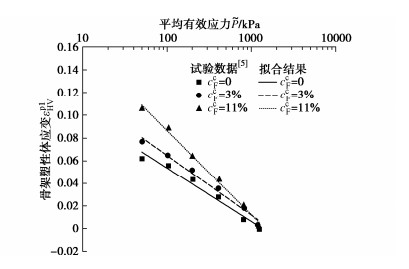
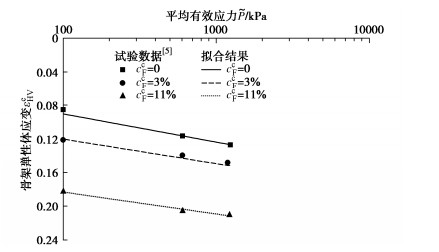
设骨架弹性体应变为εeHV=εHV−εp1HV−εp2HV,根据本文理论框架,重新整理试验数据可以得到土体骨架弹性应变[5],如图 1所示。土骨架的Helmholtz自由能ΨHS(εHV,εp1HV,εp2HV)与ΨHF(εHV,εp1HV,εp2HV)可表示为εeHV的函数[16],结合式(34),进一步可表示为
ΨHS=˜P0λe(expεeHVλe−1),ΨHF=˜P0λe[expεeHV−εHmaxλe−expεeHVλe−exp−εHmaxλe+1]。} (39) 式中:˜P0为初始有效应力;λe为回弹曲线斜率;试验结果表明,随着NaCl溶液的质量分数增加,λe基本保持不变[5]。εHmax为试样去离子水饱和条件下,平均有效应力为˜P0时由于吸附作用而产生的最大膨胀应变。饱和土的体积分数与含水率w之间的关系为φS=dF/(1+wdS),dF与dS分别是流相和固相的相对密度,因此最大膨胀应变εHmax与最大含水率wmax之间关系为εHmax=(φS0+φS0dSwmax−dF)/(φS0+φS0dSwmax)。将式(39)代入式(34)1可得
˜P=˜P0exp[(εeHV−εHmax)/λe]。 (40) 式(40)还可进一步表示为
εeHV=εHmax+λeln(˜P/˜P0)。 (41) 5.3 土骨架的塑性本构关系
根据试验结果[5]和骨架的弹性体应变,可以得到骨架塑性体应变随着平均有效应力的变化,如图 2所示。根据图 2,并结合式(36)1,Θp1可表示为
Θp1(dεp1HVdt)=[˜P0expεp1HV−εp1HV0(ccF)λp(ccF)]dεp1HVdt。 (42) 将式(42)代入式(36)1得
˜P=˜Pp1=∂Θp1∂(dεp1HV/dt)=˜P0expεp1HV−εp1HV0(ccF)λp(ccF)。 (43) 为了使(32a)1成立,即当dεp1HV/dt⩾0时,d˜P= d˜Pp1>0,式(43)可进一步表示为
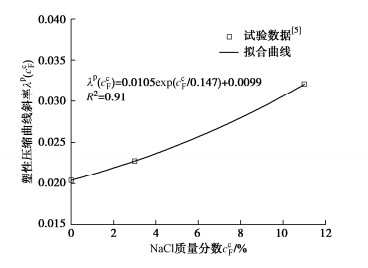
εp1HV=εp1HV0(ccF)+λp(ccF)ln(˜P/˜P0)。 (44) 式中:εp1HV0(ccF)为质量分数为ccF的NaCl溶液饱和黏土骨架的初始塑性体应变;λp(ccF)是塑性压缩曲线斜率,它与溶液质量分数有关,如图 3所示。塑性压缩曲线斜率与溶液质量分数的关系为
λp(ccF)=λp1exp(−ccF/λp2)+λp3, (45) 式中,λp1,λp2以及λp3为塑性压缩参数,可根据试验结果拟合获得。与式(45)不同,Loret等[13]采用化学势ˉμcF代替质量分数ccF来建立塑性压缩参数公式。
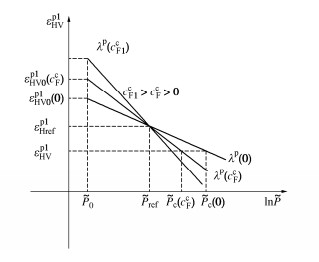
图 4为在εp1HV - ln˜P平面上盐溶液饱和黏土的塑性压缩曲线示意图,类比于孙德安等[31]开展的吸力对非饱和土压缩曲线影响的研究,可认为不同质量分数的NaCl溶液饱和黏土的塑性压缩曲线相交于一点。其中˜Pc(ccF)和˜Pc(0)分别为NaCl溶液饱和与去离子水饱和黏土的屈服应力;˜Pref与εp1Href分别为参考应力与应变;当初始有效应力˜P0 = ˜Pref,则有εp1HV0(ccF)=εp1Href。根据式(44)和图 4可得
εp1HV=εp1Href+λp(ccF)ln[˜Pc(ccF)/˜Pref]=εp1Href+λp(0)ln[˜Pc(0)/˜Pref ]。 (46) 即可得屈服应力为
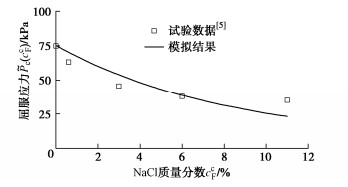
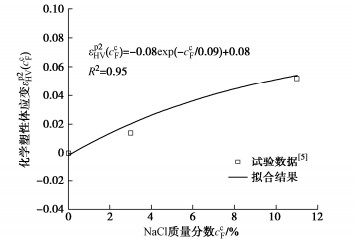
˜Pc(ccF)=˜Pref[˜Pc(0)/˜Pref]λp(0)/λp(ccF)。 (47) 将式(45)代入式(47),得到的计算结果与试验数据进行对比,如图 5所示。图 5表明,实测数据与计算结果基本一致。
从饱和黏土的等向压缩试验数据可以看出,在相同的等向应力荷载作用下,溶液质量分数的变化(即化学加载)会产生化学塑性体应变εp2HV(ccF),此塑性变形可采用第二个屈服面来模拟。根据NaCl溶液饱和黏土等向压缩试验所体现的化学塑性变形变化规律[5],第二屈服面的耗散势函数表示为
Θp2(dεp2HVdt)={˜P−εp2HV(ccF)+εcp[exp(−λcccF)−1]}dεp2HVdt。 (48) 其中,εcp与λc为塑性应变参数,把式(48)代入式(36)2得
˜P=˜Pp2=∂Θp2/∂(dεp2HV/dt)=˜P−εp2HV(ccF)+εcp[exp(−λcccF)−1]。 (49) 根据式(49)可得
εp2HV(ccF)=εcp[exp(−λcccF)−1]。 (50) 在等向压缩试验中,˜Pp2=˜P>0,由式(32a)2所要求的不等式˜Pp2dεp2HV⩾0可得第二屈服面的塑性变形存在的条件是εp2HV需满足dεp2HV⩾0。基于等向压缩试验成果[5],可以获得化学塑性体应变随NaCl溶液质量分数的变化规律,如图 6所示。
5.4 土体固相的本构模型
根据式(35),(38),(42),(44),(50)可得NaCl溶液饱和黏土的固相应变为
dεSV=λd˜P/˜P−εcpλcexp(−λcccF)dccF+dPS/KRS。 (51) 参数λc与λ取值情况如表 1所示,其中ccFc为化学加载达到塑性屈服的临界值。
表 1 参数λc与λ取值情况Table 1. Values of parametersλcandλ取值 ccF<ccFc
˜P<˜PcccF⩾ccFc
˜P<˜PcccF⩾ccFc
˜P⩾˜PcccF<ccFc
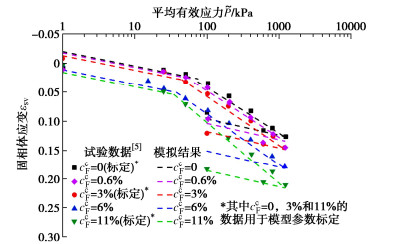
˜P⩾˜Pcλ λe λe λe+λp(ccF) λe+λp(ccF) λc 0 λc λc 0 利用去离子水、3%与11% NaCl溶液饱和黏土试样的试验数据来标定模型参数,由此获取的模型参数如表 2所示。利用表 2的模型参数和本构方程理论模拟0.6%和6%试样的应变特性,并与试验数据相对比以验证本文本构方程的合理性,模拟结果与试验数据对比如图 7所示。从图 7可以看出该模型能有效地反映NaCl溶液对黏性土等向压缩行为的影响,从而表明采用混合物理论[17]与经典热力学溶液理论[26]所建立的盐溶液饱和岩土的本构理论可以指导盐溶液饱和黏土固相本构模型的建立。
表 2 等向压缩试验的模型参数选取Table 2. Model parameters for isotropic compression testsλp1 λp2 λp3 λc λe 0.0105 -0.147 0.0099 1/0.09 0.014 εcp εHmax ˜Pref/kPa ˜Pc(0)/kPa KRS/GPa -0.08 0.02 5 75 20 5.5 流相材料的应力应变关系
在以往研究中,流相基质本构关系也称为流相材料的本构关系[15-16]。本文假定流相为无黏性流体,流相材料Gibbs自由能为GRF(ϑF,ccF)=ΨRF(ϑF,ccF)−PFϑF,根据式(34)5和式(34)6得
ϑF=−∂GRF(PF,ccF)∂PF;ˉμcF−ˉμLF=1ρRF0∂GRF(ϑF,ccF)∂ccF。 (52) 根据式(52)可得
dϑF=−∂2GRF(PF,ccF)∂P2F dPF−∂2GRF(PF,ccF)∂PF∂ccFdccF=∂ϑF∂PFdPF−ρRF∂(ˉμcF−ˉμLF)∂PFdccF。 (53) 根据经典热力学溶液理论[26]可知,溶质与溶剂的化学势之差可表示为
ˉμcF−ˉμLF=ˉμc0F(θ,P0)−ˉμL0F(θ,P0)+RθMcFln[MLFccFMcF+(MLF−McF)ccF]−RθMLFln[1−MLFccFMcF+(MLF−McF)ccF]+ˉVF(PF−P0)。 (54) 式中:ˉμc0F(θ,P0)与ˉμL0F(θ,P0)分别为标准状态下NaCl溶质与水溶剂的化学势;McF与MLF分别为NaCl溶质与水溶剂的的摩尔质量;R为气体通用常数。通常认为理想溶液的偏摩尔容积−ˉVF保持不变[26],对式(54)关于PF求偏导,将其代入式(53)可得
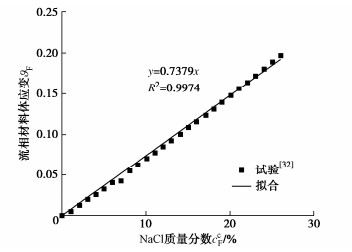
dϑF=dPF/KF−ρRF0ˉVFdccF。 (55) 式中,KF为NaCl溶液的体积模量,图 8给出了NaCl溶液的体应变随着NaCl质量分数的变化关系[32]。
根据式(55)可得
ϑF=PF/KF−ρRF0ˉVFccF。 (56) 式(56)表明溶液体应变ϑF是由孔隙水压力PF与NaCl质量分数ccF所共同决定,其中任何一个因素改变都将会影响流相材料的应变。
5.6 流相渗流的达西定律与一维固结控制方程
在等向压缩试验中,试样在上下两端双面排水,因此可认为流相主要发生竖直方向的渗流。令式(37)2 Θw(WF) = γwφF0φFW2F/(2kF),其中,kF为渗透系数,γw为水的重度。将Θw(WF)代入式(37)2可得
PF∂φF/∂z+ˆpF+ˆpA=−γwφF0φFWF/kF。 (57) NaCl溶液的动量平衡方程为[10]
∂(φFPF)/∂z+ˆpF=0。 (58) 将式(58)代入式(59)可得
kF∂PF/(γw∂z)−kFˆpA/(γwφF)−φF0WF=0。 (59) 在小应变条件下,由式(17)有
ˆpA=∂(ρF0ξF)∂ϵHV∂ϵHV∂z+∂(ρF0ξF)∂ϵp1HV∂ϵp1HV∂z+∂(ρF0ξF)∂ϵp2HV∂ϵp2HV∂z 。 (60) 根据∂(ρF0ξF)/∂εHV=∂ΨHF/∂εHV,∂(ρF0ξF)/∂εp1HV=∂ΨHF/∂εp1HV,∂(ρF0ξF)/∂εp2HV=∂ΨHF/∂εp2HV,再结合εeHV=εHV−εp1HV−εp2HV,式(60)可表示为
ˆpA=∂ΨHF∂εHV∂(εHV−εp1HV−εp2HV)∂z=∂ΨHF(εeHV)∂εeHV∂εeHV∂z。 (61) 根据式(39)~(41)以及(50)得
∂ΨHF∂εeHV=−˜P[expεHmax+εp2HV(ccF)λe−1]。 (62) 将式(61),(62)代入式(59)可得
kFγw∂PF∂z+kFγwφF˜P[expεHmax+εp2HV(ccF)λe−1]∂εeHV∂z−φF0WF=0。 (63) 式(63)为广义达西定律。当不考虑由于溶质与水的吸附作用而产生的膨胀变形时,有εHmax+εp2HV(ccF)=0,式(63)即可退化为经典的达西定律。
在实际工程中,岩土工程界关心的是流体从多孔固体中的流出或流入量。根据混合物理论和文献[16],可得流体渗入量为
ζF=φF0(εSV−εFV)=εSV−φS0ϑS−φF0ϑF。 (64) 将φF0+φS0=1与式(38),(51)与(55)代入式(64)可得
dζFdt=λ˜Pd˜P dt−εcPλcexp(−λcccF)dccFdt+φF0KRSdPSdt−φF0KFdPFdt+ρF0ˉVFdccFdt。 (65) 利用ζF=φF0(εSV−εFV)和WF=vF−vS可得∂(φF0WF)/ ∂z=−∂ζF/∂t,再结合式(63)和(65)可得
λ˜Pd˜P dt−εcpλcexp(−λcccF)dccFdt+φF0KRSdPSdt−φF0KFdPFdt+ρF0ˉVFdccFdt=−∂∂z(kFγw∂PF∂z)−∂∂z{kFγwφF˜P[expεHmax+εp2HV(ccF)λc−1]∂εeHV∂z}。 (66) 式(66)是考虑固体基质(土颗粒)可压缩和化学活性的饱和黏土一维固结控制方程。
5.7 NaCl溶质的渗流-扩散方程
令Θd(ρcFucF)=kd(ρcFucF)2/2,式(37)3可表示为
∂(ˉμcF−ˉμLF)∂z+bcF−bLF=∂Θd(ρcFucF)∂(ρcFucF)=kdρcFucF。 (67) 其中kd为扩散系数,z为扩散距离。在小应变条件下,有vS≈0,ρF≈ρF0,将式(67)代入式(3)2,并利用式vcF=ucF+vF=ucF+WF+vS可得
∂ccF∂t−WF∂ccF∂z−1kdρcF0[∂(ˉμcF−ˉμLF)∂z+bcF−bLF]∂ccF∂z−1ρF0∂∂z[∂(ˉμcF−ˉμLF)kd∂z+bcF−bLFkd]=0。 (68) 将式(54)代入式(68)可得
∂ccF∂t−WF∂ccF∂z−1kdρcF0[Rθ/ccF/(1−ccF)McF+(MLF−McF)ccF∂ccF∂z+ˉVF∂PF∂z+bcF−bLF]∂ccF∂z−1ρF0∂∂z[Rθ/ccF/(1−ccF)kd[McF+(MLF−McF)ccF]∂ccF∂z+ˉVFkd∂PF∂z+bcF−bLFkd]=0。 (69) 式(69)即为NaCl溶质在饱和黏土中的渗流-扩散方程。
5.8 渗透压
为了使式(69)在WF=0时∂ccF/∂t=0成立,即渗流量为零时质量分数保持不变,需满足以下关系:
Rθ/ccF/(1−ccF)McF+(MLF−McF)ccF∂ccF∂z+ˉVF∂PF∂z+bcF−bLF=0。 (70) 根据热力学溶液理论[26],对于理想的NaCl溶液,其溶剂的化学势可表示为
ˉμL=FˉμL0F(θ,P0)+RθMLFln[1−MLFccFMcF+(MLF−McF)ccF]+ˉVm,LMLF(PF−P0)。 (71) 式中,ˉVm, L为水溶剂的偏摩尔容积。将式(54)代入式(71)得
ˉμcF=ˉμc0F(θ,P0)+RθMcFln[MLFccFMcF+(MLF−McF)ccF]+ˉVm,L+MLFˉVFMLF(PF−P0)。 (72) 半透膜阻止溶质穿过半透膜扩散,相当于NaCl溶质在半透膜上承受一个阻力使其达到化学势平衡,即bcF=−∂ˉμcF/∂z。当外载荷满足bcF=−∂ˉμcF/∂z,则相当于半透膜作用。将式bcF=−∂ˉμcF/∂z与式(72)代入式(70)得
Rθ/(1−ccF)McF+(MLF−McF)ccF∂ccF∂z−ˉVm, LMLF∂PF∂z−bLF=0。 (73) 对式(73)积分,先利用PF+∫z0(bLFMLF/ˉVm, L) dz=0,再根据ccF非常小时可略去对数函数泰勒展开的高次项,最后采用ccF=ρcF/ρF代替ccF,可得水溶剂化学势平衡的表达式为
PF+∫z0MLFˉVm,LbLFdz=RθˉVm,LMLFccFMcF+(MLF−McF)ccF=RθˉVm,L[(ρcF/McF)+(ρLF/MLF)]ρcFMcF。 (74) 式中:ρcF/McF,ρLF/MLF分别为溶质与溶剂的摩尔数,故式(74)即为广义渗透压的一般表达式。广义渗透压不仅与溶质的质量分数有关,还与所受外荷载有关。当流相动量达到平衡WF=0和流相中组分的化学势达到热力学平衡∂ccF/∂t=0时,式(74)就变成了经典渗透压公式。饱和土在外荷载作用下会产生固结,此时WF≠0,故经典渗透压公式在饱和多孔介质固结过程中不成立。
6. 结论
(1)把固相变形分解为骨架变形、固相基质变形和质量交换变形,以凸显孔隙率和化学活性在水-力-化学多场耦合中的关键作用;采用现时质量分数作为化学状态变量来反映饱和岩土孔隙溶液的化学活性,改变了以往采用渗透压和溶质摩尔浓度作为化学状态变量建立模型的传统思路。
(2)研究表明,弹性本构方程可以通过自由能势函数推导而得;塑性本构方程、广义达西定律可以通过耗散势函数推导而得。采用混合物理论和热力学溶液理论建立的盐溶液饱和多孔介质本构理论框架可以用来指导创建本构模型。
(3)在上述理论指导下,结合NaCl溶液饱和黏土的等向压缩试验成果,建立了考虑水-力-化学耦合特性的NaCl溶液饱和黏土本构模型。该本构模型包括固流两相本构方程和溶质渗流-扩散方程。经典渗透压公式需同时满足流相动量守恒方程和热力学平衡条件才成立。
致谢: 感谢美国华盛顿州立大学数学与统计系Lynn Schreyer (原名Lynn Schreyer Bennethum) 教授在建构和完善化学本构理论方面的帮助和指导。 -
表 1 参数与取值情况
Table 1 Values of parametersand
取值 0 0 表 2 等向压缩试验的模型参数选取
Table 2 Model parameters for isotropic compression tests
0.0105 -0.147 0.0099 1/0.09 0.014 /kPa /kPa /GPa -0.08 0.02 5 75 20 -
[1] 陈云敏. 环境土工基本理论及工程应用[J]. 岩土工程学报, 2014, 36(1): 1-46. doi: 10.11779/CJGE201401001 CHEN Yunmin. A fundamental theory of environmental geotechnics and its application[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(1): 1-46. (in Chinese) doi: 10.11779/CJGE201401001
[2] WEI C F. A theoretical framework for modeling the chemomechanical behavior of unsaturated soils[J]. Vadose Zone Journal, 2014, 13(9): 1-21.
[3] 徐永福. 考虑渗透吸力影响膨润土的修正有效应力及其验证[J]. 岩土工程学报, 2019, 41(4): 631-638. doi: 10.11779/CJGE201904005 XU Yongfu. Modified effective stress induced by osmotic suction and its validation in volume change and shear strength of bentonite in saline solutions[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(4): 631-638. (in Chinese) doi: 10.11779/CJGE201904005
[4] YE W M, ZHANG F, CHEN B, et al. Effects of salt solutions on the hydro-mechanical behavior of compacted GMZ01 Bentonite[J]. Environmental Earth Sciences, 2014, 72(7): 2621-2630. doi: 10.1007/s12665-014-3169-x
[5] 颜荣涛, 赵续月, 于明波, 等. 盐溶液饱和黏土的等向压缩特性[J]. 岩土力学, 2018, 39(1): 129-138. YAN Rongtao, ZHAO Xuyue, YU Mingbo, et al. Isotropic compression characteristics of clayey soil saturated by salty solution[J]. Rock and Soil Mechanics, 2018, 39(1): 129-138. (in Chinese)
[6] DI MAIO C, SANTOLI L, SCHIAVONE P. Volume change behaviour of clays: the influence of mineral composition, pore fluid composition and stress state[J]. Mechanics of Materials, 2004, 36(5/6): 435-451.
[7] SRIDHARAN A. Engineering behavior of clays: influence of mineralogy[C]//Chemo-mechanical Coupling in Clays: From Nano-scale to Engineering Applications. Maratea: Swets and Zeitlinger, 2001.
[8] DO N GUIMARÃES L, GENS A, SÁNCHEZ M, et al. A chemo-mechanical constitutive model accounting for cation exchange in expansive clays[J]. Géotechnique, 2013, 63(3): 211-234.
[9] DOMINIJANNI A, MANASSERO M, PUMA S. Coupled chemical-hydraulic-mechanical behaviour of bentonites[J]. Géotechnique, 2013, 63(3): 191-205. doi: 10.1680/geot.SIP13.P.010
[10] BENNETHUM L S, MURAD M A, CUSHMAN J H. Macroscale thermodynamics and the chemical potential for swelling porous media[J]. Transport in Porous Media, 2000, 39(2): 187-225. doi: 10.1023/A:1006661330427
[11] HASSANIZADEH M, GRAY W G. General conservation equations for multi-phase systems: 1. Averaging procedure[J]. Advances in Water Resources, 1979, 2: 131-144. doi: 10.1016/0309-1708(79)90025-3
[12] MA T, WEI C, CHEN P, et al. Chemo-mechanical coupling constitutive model for chalk considering chalk–fluid physicochemical interaction[J]. Géotechnique, 2019, 69(4): 308-319. doi: 10.1680/jgeot.17.P.115
[13] LORET B, HUECKEL T, GAJO A. Chemo-mechanical coupling in saturated porous media: elastic-plastic behaviour of homoionic expansive clays[J]. International Journal of Solids and Structures, 2002, 39(10): 2773-2806. doi: 10.1016/S0020-7683(02)00151-8
[14] CHENG A H D. Poroelasticity[M]. Berlin: Springer, 2016.
[15] 胡亚元. 饱和多孔介质的超黏弹性本构理论研究[J]. 应用数学和力学, 2016, 37(6): 584-598. HU Yayuan. Study on the super viscoelastic constitutive theory for saturated porous media[J]. Applied Mathematics and Mechanics, 2016, 37(6): 584-598. (in Chinese)
[16] 胡亚元. 基于混合物理论的饱和岩石弹塑性模型[J]. 岩土工程学报, 2020, 42(12): 2161-2169. doi: 10.11779/CJGE202012001 HU Yayuan. Elastoplastic model for saturated rock based on mixture theory[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(12): 2161-2169. (in Chinese) doi: 10.11779/CJGE202012001
[17] BOWEN R M. Theory of Mixtures[M]. Amsterdam: Elsevier, 1976: 1-127.
[18] 陈正汉. 固-液-气三相多孔介质相互作用的动力学理论[C]//. 全国首届结构与介质相互作用的理论及其应用学术研讨会文集. 南京: 河海大学出版社, 1993: 134-147. CHEN Zhenghan. Dynamics theory of solid-liquid-gas three-phase porous media interaction[C]// Proceedings of the First National Symposium on Theory and Application of Interaction between Structure and Medium. Nanjing: Hohai University Press, 1993: 134-147. (in Chinese)
[19] CHEN Zhenghan. A dynamical theory of interaction of triphase porous media[C]// Proc 2nd lnt Conf on Non-Linear Mechanics. Beijing: Peking Univ Press, 1993: 889-892.
[20] COLLINS I F, HOULSBY G T. Application of thermomechanical principles to the modelling of geotechnical materials[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1997, 453: 1975-2001. doi: 10.1098/rspa.1997.0107
[21] BORJA R I. On the mechanical energy and effective stress in saturated and unsaturated porous continua[J]. International Journal of Solids and Structures, 2006, 43(6): 1764-1786.
[22] 陈正汉. 非饱和土与特殊土力学的基本理论研究[J]. 岩土工程学报, 2014, 36(2): 201-272. CHEN Zhenghan. On basic theories of unsaturated soils and special soils[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(2): 201-272. (in Chinese)
[23] 陈正汉. 岩土力学的公理化理论体系[J]. 应用数学和力学, 1994, 15(10): 901-910. CHEN Zhenghan. An axiomatics of geomechanics[J]. Applied Mathematics and Mechanics, 1994, 15(10): 901-910. (in Chinese)
[24] 赵成刚, 刘艳. 连续孔隙介质土力学及其在非饱和土本构关系中的应用[J]. 岩土工程学报, 2009, 31(9): 1324-1335. ZHAO Chenggang, LIU Yan. Continuum porous medium soil mechanics and its application in constitutive relationship of unsaturated soils[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(9): 1324-1335. (in Chinese)
[25] 刘艳, 赵成刚, 蔡国庆. 理性土力学与热力学[M]. 北京: 科学出版社, 2016. LIU Yan, ZHAO Chenggang, CAI Guoqing. Rational Soil Mechanics and Thermodynamics[M]. Beijing: Science Press, 2016. (in Chinese)
[26] 苏长荪, 谭连城, 刘桂玉. 高等工程热力学[M]. 北京: 高等教育出版社, 1987. SU Changsun, TAN Liancheng, LIU Guiyu. Advanced Engineering Thermodynamics[M]. Beijing: Higher Education Press, 1987. (in Chinese)
[27] BOWEN R M. Compressible porous media models by use of the theory of mixtures[J]. International Journal of Engineering Science, 1982, 20(6): 697-735.
[28] 陈正汉. 非饱和土与特殊土力学[M]. 北京: 中国建筑工业出版社, 2022: 502-509. CHEN Zhenghan. Mechanics for Unsaturated and Special Soils[M]. Beijing: China Architecture & Building Press, 2022: 502-509. (in Chinese)
[29] 李如生. 非平衡态热力学和耗散结构[M]. 北京: 清华大学出版社, 1986. LI Rusheng. Non-equilibrium ThermoDynamics and Dissipative Structure[M]. Beijing: Tsinghua University Press, 1986. (in Chinese)
[30] 黄筑平. 连续介质力学基础[M]. 2版. 北京: 高等教育出版社, 2012: 83-121. HUANG Zhuping. Fundamentals of Continuum Mechanics[M]. 2nd ed. Beijing: Higher Education Press, 2012: 83-121. (in Chinese)
[31] 孙德安, 孙文静, 孟德林. 膨胀性非饱和土水力和力学性质的弹塑性模拟[J]. 岩土工程学报, 2010, 32(10): 1505-1512. http://cge.nhri.cn/cn/article/id/8363 SUN De'an, SUN Wenjing, MENG Delin. Elastoplastic modelling of hydraulic and mechanical behaviour of unsaturated expansive soils[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(10): 1505-1512. (in Chinese) http://cge.nhri.cn/cn/article/id/8363
[32] SIMIONA I, GRIGORAS C G, ROSU A M, et al. Mathematical modelling of density and viscosity of NaCl aqueous solutions[J]. Journal of Agroalimentary Processes and Technologies, 2015, 21(1): 41-52.
-
期刊类型引用(3)
1. 陈敏. 基于BP神经网络的边坡可靠度分析. 黑龙江交通科技. 2024(07): 31-34 .  百度学术
百度学术
2. 汪卫,廖志浩,廖杰林. 基于随机场模型的土石坝失效概率分析研究进展. 人民珠江. 2024(10): 114-123 .  百度学术
百度学术
3. 彭宗桓 ,盛建龙 ,叶祖洋 ,李硕 . 基于t-SNE-AMARS-MPM的空间变异性边坡可靠度分析及大变形破坏模式研究. 力学学报. 2024(11): 3274-3289 .  百度学术
百度学术
其他类型引用(4)
-
其他相关附件



 下载:
下载: