浑水入渗对粗粒土柱孔隙及渗透性影响试验研究

毛海涛; 张超; 袁古城; 何涛; 谷易

doi:10.11779/CJGE20221233

浑水入渗对粗粒土柱孔隙及渗透性影响试验研究 English Version

毛海涛^{1, 2,},
张超^{1, 2, ,},
袁古城¹,
何涛²,
谷易²

1.
山西农业大学城乡建设学院, 山西太原 030000
2.
重庆三峡学院土木工程学院, 重庆 404120

基金项目:

山西省自然科学基金面上项目 202103021223132

山西省自然科学基金面上项目 202103021224151

国家自然科学青年基金项目 42207102

山西农业大学211省改革高层次人才引进项目 2021XG009

山西省水利科学技术研究与推广项目 2024GM33

详细信息

作者简介:
毛海涛(1980—)，男，博士，教授，主要从事水利工程渗流相关问题的研究。E-mail: maohaitao1234@163.com

通讯作者:
张超, E-mail: zhangch688@163.com

中图分类号: TU432
计量
- 文章访问数: 235
- HTML全文浏览量: 33
- PDF下载量: 62
出版历程
- 收稿日期: 2022-10-07
- 网络出版日期: 2024-09-28
- 刊出日期: 2024-12-31

Experimental study on influences of seepage of muddy water on porosity and permeability of coarse-grained soil columns

MAO Haitao^{1, 2,},
ZHANG Chao^{1, 2, ,},
YUAN Gucheng¹,
HE Tao²,
GU Yi²

1.
College of Urban and Rural Construction, Shanxi Agricultural University, Taiyuan 030000, China
2.
School of Civil Engineering, Chongqing Three Gorges University, Chongqing 310058, China

摘要

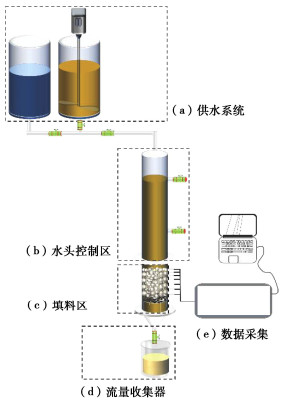
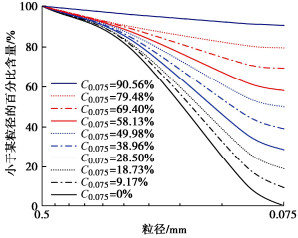
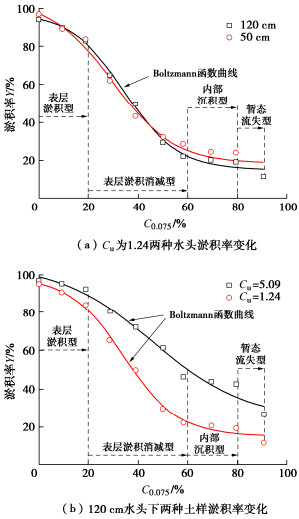
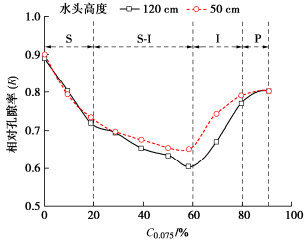
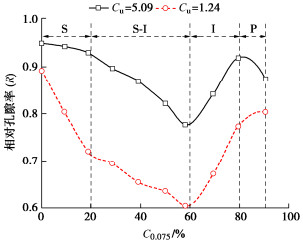
摘要: 浑水渗流在水利工程的反滤设计、浑水浇灌、堤坝渗流控制等方面都有较大影响，目前理论多采用稳定渗流计算方法，忽略了渗流过程中粗细颗粒与水力的耦合作用。自制渗流装置，将不同控制粒径浑水、不均匀系数粗粒土柱和水头等作为基本控制因素，研究不同工况下浑水中悬浮颗粒对粗粒土土柱中的渗透特性影响；推导了变渗透系数浑水渗流计算微分方程，通过对比验证和公式修正，结果表明：粗粒土中颗粒淤积率与控制粒径C_0.075含量符合Boltzmann函数关系；C_0.075是重要的影响因子，浑水颗粒在粗粒土柱的运移、沉积和淤堵形态过程大致可分为4种形态：表层堆积淤堵形态（S型）；表层-内部双重淤堵形态（S-I型）；内部孔隙淤堵形态（I型）；暂态孔隙淤堵形态（P型）。土柱C_u越大，孔隙度越小，浑水颗粒在粗粒土中运移也越困难，土柱填充性就越差；水头加剧了颗粒在土柱内部运移的速度，但也加速了其在顶部的沉积并封堵；S型时土柱0~2 cm渗透系数下降速率最大，封堵时总体渗透系数最小，2 cm以下相对孔隙率及随深度逐渐减小；S-I和I型土柱下部渗透系数明显滞后于上部，相对孔隙率存在临界深度（约为4~6 cm）；P型时土柱整体相对孔隙率基本无变化。
- 颗粒 /
- 渗流 /
- 粗粒土 /
- 浑水 /
- 堵塞
Abstract: The seepage of muddy water has significant influences on the anti-filtration design in hydraulic engineering, muddy water irrigation and seepage control in embankments. At present, the theoretical approaches are predominantly stable seepage methods, neglecting the coupled effects between coarse and fine particles during seepage process. In this study, a seepage apparatus is fabricated to investigate the infiltration characteristics of particles in coarse-grained soil columns under various combinations of factors, including muddy water with different compositions, coarse-grained soil columns with non-uniform coefficient, and hydraulic heads. A differential equation for calculating the seepage with variable permeability coefficients in muddy water is derived. Through comparative validation and formula modification, it is revealed that the particle deposition rate in coarse-grained soil and the content of particles with the control size C_0.075 follow a Boltzmann function relationship. C_0.075 is a significant influencing factor, dictating the migration, deposition and clogging morphology of particles in the coarse-grained soil columns. Four predominant morphologies are identified: surface accumulation clogging (S type), surface-internal dual clogging (S-I type), internal pore clogging (I type), and transient pore clogging (P type). As the value of C_u of the coarse-grained soil columns increases and the porosity decreases, the migration of particles in the coarse-grained soil becomes more difficult, and the filling characteristics of the coarse-grained soil columns are poor. The hydraulic head intensifies the migration velocity of particles in the coarse-grained soil columns but also accelerates their deposition and clogging at the top. During the S type phase, the rate of decrease in the permeability coefficient from 0 to 2 cm in depth is the highest, resulting in the overall minimum permeability coefficient during clogging, with a gradual reduction in the relative porosity under the depth below 2 cm. For the S-I and I type columns, the permeability coefficient in the lower part lags significantly behind that in the upper part, with the critical depth of the relative porosity (approximately 4~6 cm). The overall relative porosity is basically unchanged for the P type columns.
- particle /
- seepage /
- coarse-grained soil /
- muddy water /
- clogging

HTML全文

0. 引言

地表局部地形对地震波的传播有显著影响，当地震波遇到高山、峡谷等，会产生散射波、入射波和反射波等复杂波场，并引起地面运动的放大或衰减，称为地形效应。目前针对地形效应已有了相应的研究（表 1），主要包含了数值模拟和解析分析两种。解析主要运用的是波函数展开法，Wong等^[1]提出了半圆形峡谷对地震SH波散射的波函数级数解，随后众多学者提出了多种圆弧形峡谷的解析解^[2-6]，Gao等^[7]提出了通过坐标变换求解V形对称峡谷引起的圆柱形SH波二维散射和衍射波函数的级数解。数值方法包含了有限差分法^[8]，谱元法等^[9]等，数值方法可实现复杂地形地震波传播模拟，具备边界和复杂几何处理的灵活性，但在计算精度方面往往需要解析解的校准。

表 1 复杂地形效应近场波动模拟研究现状

Table 1. Researches on near-field fluctuation problems

模拟方法	应用场景	时间	文献
解析法	平面SH波在半圆柱型峡谷的散射	1972年	[1]
	平面SH波在半圆柱型冲击峡谷的散射	1971年	[2]
	平面SH波在半椭圆形冲击峡谷的散射	1974年	[3]
	平面SH波在圆弧形峡谷的散射	2009年	[4]
	平面SH波在截断峡谷的散射	2009年	[5]
	U型峡谷引起的地形放大对地震波的影响	2012年	[6]
	柱面SH波在对称V型峡谷的反射和散射	2013年	[7]
有限差分法	极坐标尺度不规则地形FEM方法	2021年	[8]
谱元法	入射平面SV波作用下梯田形山丘的表面运动	2017年	[9]
PINN	近场波动数值模拟	2022年	[30]

下载: 导出CSV

| 显示表格

近场波动在数学上可归结为偏微分方程的初值、边值问题，偏微分方程的数值离散化在模拟多物理场问题方面取得了很大的进展，但通过使用经典的分析或计算工具来建模和预测非线性多尺度系统的演化较困难，面对复杂网络剖分、参数化偏微分方程控制的高维问题等。

近年来的研究发现，物理信息神经网络（PINN）可以用于对控制物理系统的偏微分方程进行建模，通过嵌入物理信息解决了传统神经网络算法对于求解方面的局限性，例如高度依赖数据驱动，缺乏物理可解释性、易陷入过拟合以及可获取数据的稀疏性等。PINN方法仅依赖于少量甚至零标记的数据集，并实现数据稀缺、物理约束的学习。嵌入物理公式为可训练参数提供约束，缓解过拟合问题，减少对大型训练数据集的需求，从而提高训练模型的鲁棒性，以实现可靠的预测。Raissi等^[10]利用深度学习神经网络（DNN）的强表达性，开发了通用PINN框架，解决了涉及小数据集甚至没有任何标记数据的非线性偏微分方程系统的正逆问题。最近几年PINN方法在地球物理学^[11-13]、固体力学^[14-16]、流体动力学^[17-20]、热传导^[21-22]等方面有了相应的研究。众多学者针对不同的偏微分方程，让PINN方法更好地适应不同的物理问题^[23-29]。也有了少数利用物理信息神经网络求解波动方程的工作，Rao等^[19]通过DNN复合方案以硬嵌入的方式强制满足初值、边值条件，在截断域的波传播问题上进行了模拟。陈苏等^[30]结合了数值模拟原理和物理驱动深度学习建立了波动模拟方法，提出了可以提高网络训练效率的迁移学习方法。

在前人研究的基础上，提出通过物理信息神经网络模拟圆柱形SH波在不规则地形下的散射和衍射方法。通过新的参数加载代理建模策略，在给定初始时刻稀疏地震位移波场，模拟地震波在半无限域的传播，通过对比解析解和PINN预测解来评估所提出的规则地形下PINN模型的性能。通过PINN模型模拟不规则地形下圆柱形SH波的二维散射和衍射，证明该方法具有良好的泛化性。

1. 物理驱动深度学习原理

深度学习神经网络（DNN）具备出色的计算表达能力，在图像识别和自然语言处理等领域获得了较多应用。前馈全连接神经网络可以假设为输入层、多个隐藏层和输出层的堆栈。相邻两层之间的连接，例如从第i−1层到第i层，可用张量的形式简单表示为

$\boldsymbol{Y}_i=\alpha\left(\boldsymbol{W}_i \boldsymbol{Y}_{i-1}+\boldsymbol{b}_i\right) \quad(1 \leqslant i \leqslant n+1) 。$

(1)

式中：n为隐层总数；σ(·)为按元素作用的激活函数； ${\boldsymbol{Y}_0}$ 和 ${\boldsymbol{Y}_{n + 1}}$ 分别为输入张量和输出张量； ${\boldsymbol{W}_i}$ ， ${\boldsymbol{b}_i}$ 为第i层的可训练权重矩阵和偏置向量。DNN作为弹性动力学问题的参数化近似解，其中时空位置X = (x, t)为自变量。通过最优逼近物理系统理论解，获取训练参数，需设计嵌入物理定律的损失函数作为训练目标，网络训练中需评估物理场对时空变量的偏导数，Tensorflow和Pytorch框架中可完成自动微分功能。以前馈神经网络为例，网络以变量x为输入，在式（1）中定义的非线性变换后输出f，表示第i个隐藏层中第j个神经元的输出。由于输出f可以表示为x的嵌套函数，应用链式法则，可以计算每一层之间的梯度关系，通过构建损失函数和误差的反向传播，每训练一步后更新权重和偏置，如图 1所示，权重和偏置的更新计算为

图 1 DNN网络自动微分简图

Figure 1. Automatic differential diagram of DNN network

下载: 全尺寸图片幻灯片

$\omega_{1 \mathrm{f}}^{\prime}=\omega_{1 \mathrm{f}}-\alpha \frac{\partial l}{\partial \omega_{1 \mathrm{f}}} ,$

(2)

$\frac{\partial l}{\partial \omega_{\mathrm{1f}}}=\frac{\partial l}{\partial f} \cdot \frac{\partial f}{\partial \omega_{\mathrm{1f}}},$

(3)

$f=\sigma\left(\sum_i^n \omega_{i \mathrm{f}} y_i^{(2)}+b_i\right),$

(4)

$\frac{\partial f}{\partial \omega_{1 \mathrm{f}}}=\sigma y_1^{(2)}。$

(5)

式中： $\alpha$ 为DNN网络的学习率；l为期望值h与网络输出值f构建的损失函数。

损失函数L可以求得 $\tfrac{{\partial l}}{{\partial f}}$ 的值，式（4）中节点 $y_1^{(2)}$ 与输出f之间关系可以求得 $\tfrac{{\partial f}}{{\partial {\omega _\text{1f}}}}$ ，再通过式（2），（3）求得更新后的权重 ${\omega '_\text{1f}}$ 。偏置 ${b'_\text{1f}}$ 的计算同理，网络参数更新过后采用梯度下降最快的策略，使得损失函数L减小到0，最终输出值f与期望值h以及两者的导数实现强形式的相等，如图 1所示。

从函数逼近论角度，具有单一隐藏层的神经网络可精确逼近任何线性或非线性连续函数，因此可以将神经网络作为非线性函数逼近器。Rassi等^[10]通过训练全连接神经网络来逼近偏微分方程的解，用神经网络逼近方程的各阶偏导数，实现将PDE残差以及初、边值条件作为正则项加入损失函数中。

以一维杆件中波的传播为例，介绍物理驱动深度学习方法求解偏微分方程的可行性。杆件长10 m，在杆左端施加Ricker子波，波速为1 m/s。一维标量波动方程形式为

$\frac{{{\partial ^2}u}}{{{\partial ^2}t}} - c\frac{{{\partial ^2}u}}{{{\partial ^2}x}} = 0{\text{ }}\left( {x \in [0, 10], t \in [0, 20]} \right),$

(6)

Ricker子波公式 $:$

$u_{\mathrm{r}}=\left[\frac{2 \pi^2\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}}。$

(7)

Ricker子波从x=0处输入，所以在x=0处的边界条件可以表示为

$u(0, t)=\left[\frac{2 \pi^2\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_{\mathrm{s}}\right)^2}{t_{\mathrm{s}}^2}}。$

(8)

式中：c为波速， ${t_\text{s}}$ 为Ricker波的半周期，根据波动传播理论，得到

$u=f\left(t+\frac{x}{c}\right)=\left[\frac{2 \pi^2\left(t-t_\text{s}\right)^2}{t_\text{s}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_\text{s}\right)^2}{t_\text{s}^2}}。$

(9)

化简后易得上述波动方程解析解：

$u(x, t)=\left[\frac{2 \pi^2\left(t-t_{\mathrm{s}}-\frac{x}{c}\right)^2}{t_{\mathrm{s}}^2}-1\right] \mathrm{e}^{-\pi_2 \frac{\left(t-t_{\mathrm{s}}-\frac{x}{c}\right)^2}{t_{\mathrm{s}}^2}}。$

(10)

此案例满足如下形式的偏微分方程：

$\left. \begin{array}{l}\begin{gathered} \boldsymbol{D}(u(x, t) ; \lambda)=f(x, t) \quad(x \in \varOmega, t \in[0, T]), \\ u(x, t)=\boldsymbol{B}_D(t) \quad\left(x \in \partial \varOmega_D, t \in[0, T]\right), \\ \nabla u(x, t)=\boldsymbol{B}_N(t) \quad\left(x \in \partial \varOmega_N, t \in[0, T]\right), \\ u(0, t)=\boldsymbol{B}_0(t) \quad(t \in[0, T]), \\ u(x, 0)=\boldsymbol{J}_0(x) \quad(x \in \varOmega) 。 \end{gathered}\end{array} \right\}$

(11)

式中： $u(x, t)$ 为偏微分方法的解； $\boldsymbol{D}( \cdot )$ 为带参数 $\lambda$ 的微分算子；x为域 $\varOmega \in {R^d}$ 中的空间变量， $d = 1, 2, \ldots n$ ；域边界 $\partial \varOmega$ 由Dirichlet边界 $\partial {\varOmega _D}$ 和Neumann边界 $\partial {\varOmega _N}$ 组成； $t \in [0, T]$ 为时间变量； ${\boldsymbol{B}_D}(t), {\boldsymbol{B}_N}(t)$ 分别为偏微分方程的初边值问题中的Dirichlet、Neumann边界条件函数； ${\boldsymbol{B}_0}(t)$ 为在x=0处的边界条件函数； ${\boldsymbol{J}_0}(x)$ 为初始条件函数。

对于这些初、边值函数，通过设计损失函数 $\sum (\theta )$ 架构并训练神经网络：

$\sum (\theta ) = {\sum _{\text{p}}}(\theta ) + {\sum _{{\text{bc}}}}(\theta ) + {\sum _{{\text{ic}}}}(\theta ) ,$

(12)

$\left. \begin{array}{l}\begin{aligned} \sum\nolimits_{\mathrm{bc}}(\theta)= & \frac{1}{N_{\mathrm{d}}} \sum\nolimits_i^{N_{\mathrm{p}}}\left\|\nabla \boldsymbol{N} \boldsymbol{N}\left(x_i, t_i ; \theta\right)-\boldsymbol{B}_D(t)\right\|_{\partial \varOmega_D \times[0, T]}^2+ \\ & \frac{1}{N_{\mathrm{n}}} \sum\nolimits_i^{N_{\mathrm{n}}}\left\|\nabla \boldsymbol{N} \boldsymbol{N}\left(x_i, t_i ; \theta\right)-\boldsymbol{B}_N(t)\right\|_{\partial \varOmega_N \times[0, T]}^2, \\ \sum\nolimits_{\mathrm{ic}}(\theta)= & \frac{1}{N_{\mathrm{ic}}} \sum\nolimits_i^{N_{\mathrm{ic}}}\left(\left\|\nabla \boldsymbol{N} \boldsymbol{N}\left(x_i, 0 ; \theta\right)-\boldsymbol{J}_0(t)\right\|_{\varOmega \times\{t=0\}}^2+\right. \\ & \left.\left\|\nabla \boldsymbol{N} \boldsymbol{N}_t\left(x_i, 0 ; \theta\right)-\boldsymbol{J}_1(t)\right\|_{\varOmega \times\{t=0\}}^2\right), \\ \sum\nolimits_{\mathrm{p}}(\theta)= & \frac{1}{N_{\mathrm{p}}} \sum\nolimits_i^{N_{\mathrm{p}}}\left(\left\|\boldsymbol{D}\left(\boldsymbol{N} \boldsymbol{N}\left(x_i, t_i ; \theta\right) ; \lambda\right)-f\left(x_i\right)\right\|_{\varOmega \times[0, T]}^2\right.。 \end{aligned}\end{array} \right\}$

(13)

使用Sobol序列算法分别生成PDE残差损失项、初始条件损失项的时空采样点。采用8个隐藏层、每层20个神经元的全连接神经网络，使用Adam优化器训练40000步，波场云图及PINN的预测解与解析解对比如图 2所示，PINN预测值与解析解之间的绝对误差最大值为0.007 m，表明经过训练的神经网络已具备较强逼近波动方程真解的能力。

图 2 波场云图及PINN预测与解析对比图

Figure 2. Comparison of wavefield clouds and PINN prediction and resolution

下载: 全尺寸图片幻灯片

2. 物理驱动人工智能波动模拟方法

2.1 方法介绍

以SH波在平面内和地表及峡谷处的散射反射为例，二维波动方程为

$\frac{{{\partial ^2}u}}{{{\partial ^2}t}} - c\left( {\frac{{{\partial ^2}u}}{{{\partial ^2}x}} + \frac{{{\partial ^2}u}}{{{\partial ^2}z}}} \right) = f。$

(14)

式中： $u(x, z, t)$ 为出平面波动位移；c为介质物理波速； $f(x, z, t)$ 为外荷载，令 $f \equiv 0$ ，并通过给定初始波场等效施加外力。

根据陈苏等^[30]提出的二维波动方程PINN求解框架，指定时空坐标 $X = (x, z, t)$ 的3个分量为网络的输入值，位移场 $Y = u(x, z, t)$ 为网络的输出值，通过Pytorch的自动微分功能，得到位移对于各分量的微分值，即 $\tfrac{{{\partial ^2}u}}{{{\partial ^2}t}}, \tfrac{{{\partial ^2}u}}{{{\partial ^2}x}}, \tfrac{{{\partial ^2}u}}{{{\partial ^2}z}}$ ，并构建损失函数。

Gao等^[7]提出了对称V形峡谷引起的柱面SH波二维散射和衍射的波函数级数解。峡谷模型如所示，采用半径为a（峡谷壁长度）的圆弧作为辅助边界，将整个空间分成两个子区域。子区域①中为驻波波场，子区域②中包含没有牵引边界的自由波场和因为峡谷存在而产生的散射波场。要求波源的位置位于子区域②中，通过波函数展开法和坐标变换得到了此模型下二维圆柱SH波的反射结果，即半平面内的位移场 ${Y_\text{reli}} = {u_\text{reli}}(x, z, t)$ 。本文采用解析计算得到的 ${t_1}, {t_2}$ 时刻的两个早期位移场作为初始条件，通过两帧波场快照 ${\boldsymbol{u}_1}, {\boldsymbol{u}_2}$ 约束震源的位置、形状和SH波的传播方向。垂直地表的应力为零的边界条件可通过损失函数中的Neumann边界条件 $\nabla u(x, z = {z_\text{top}}, t) = 0$ 表示。

图 3 对称V型峡谷模型示意图

Figure 3. Schematic diagram of a symmetrical V-shaped canyon model

下载: 全尺寸图片幻灯片

$\boldsymbol{L}(\theta)=\lambda_1 \boldsymbol{L}_{\mathrm{p}}(\theta)+\lambda_2 \boldsymbol{L}_{\mathrm{bc}}(\theta)+\lambda_3 \boldsymbol{L}_{\mathrm{ic}}(\theta) ,$

(15)

$\left. \begin{array}{l}\boldsymbol{L}_{\text{p}}(\theta )=\frac{1}{{N}_{\text{p}}}{\displaystyle {\sum }_{i}^{{N}_{\text{p}}}}\Vert \frac{{\partial }^{2}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})}{\partial {t}_{i}^{2}}-{c}_{i}^{2}(\frac{{\partial }^{2}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})}{\partial {x}_{i}^{2}}+\\ {\text{ }\frac{{\partial }^{2}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})}{\partial {z}_{i}^{2}})\Vert }_{\varOmega \times [0, T]}^{2}, \\ \boldsymbol{L}_{\text{ic}}(\theta )=\frac{1}{{N}_{\text{ic1}}}{\displaystyle {\sum }_{i}^{{N}_{\text{ic}1}}}\Vert {\Vert \stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})-{U}_\text{rel1}({x}_{i}, {z}_{i}, {t}_{i})\Vert }_{\varOmega \times \{t={t}_{1}\}}^{2}+\\ {\text{ }\frac{1}{{N}_{\text{ic2}}}{\displaystyle {\sum }_{i}^{{N}_{\text{ic2}}}}\stackrel{⌢}{u}({x}_{i}, {z}_{i}, {t}_{i})-{U}_\text{rel2}({x}_{i}, {z}_{i}, {t}_{i})\Vert }_{\varOmega \times \{t={t}_{2}\}}^{2}, \\ \boldsymbol{L}_{\text{bc}}(\theta )=\frac{1}{{N}_{\text{bc}}}{\displaystyle {\sum }_{i}^{{N}_{\text{bc}}}{\Vert \nabla \stackrel{⌢}{u}({x}_{i}, {z}_{i}={z}_\text{top}, {t}_{i})\Vert }_{\varOmega \times [0, T]}^{2}。}\end{array} \right\}$

(16)

式中： $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}$ 为PINN逼近的偏微分方程的解， $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} (x, z, t) =$ $\boldsymbol{NN}(x, z, t;\theta )$ 。

根据式（15），（16），在半无限区域的二维波动问题中，损失函数由PDE残差损失项、初始条件损失项和边界条件损失项组成，其中 ${\lambda _1}$ ， ${\lambda _2}$ ， ${\lambda _3}$ 为损失分配系数。求解二维波动方程的物理信息神经网络架构如图 4所示。选择Tanh激活函数作为神经网络的非线性激活函数，以确保网络非零二阶导数存在，并实现高效收敛。采用Adam和L-BFGS共同作用的优化策略。其中Adam优化算法可实现全域快速收敛，接L-BFGS优化获得高精度解。使用Xavier初始化对神经网络中的可训练参数进行初始化。

图 4 物理驱动神经网络架构图

Figure 4. Diagram of PINN architecture

下载: 全尺寸图片幻灯片

2.2 方法验证

半无限均匀介质内的SH波动模型如图所示，模型区域为宽1500 m，深1500 m，峡谷深度d=50 m，峡谷宽度b=150 m。介质物理波速c=3000 m/s，输入波位移时程采用主频为10 Hz的Ricker源时间函数，源位置处于模型中心x = 750 m， z = -750 m。

使用解析计算得到的 ${t_1} = 0.05{\text{ s}}$ ， ${t_2} = 0.1{\text{ s}}$ 的位移场作为初始条件参与训练，其余时刻的结果与PINN的计算结果进行对比验证。解析计算中时间步长为0.01 s，计算总时长为1 s。训练前根据模型的几何数据，定义顶部边界为宽150 m，深50 m的对称V型峡谷，在此边界上添加应力为0的Neumann边界条件。采用Sobol序列算法在整个域中生成用于计算PDE残差损失项的采样点和初始条件采样点。在V型峡谷处的采样点布设做局部加密，在顶部两侧水平边界布设200个采样点，在V型边界布设1000个采样点，删除峡谷上部PDE残差损失项采样点，调整后采样点数 ${N_{\text{p}}} = 9954$ ， ${N_{{\text{ic1}}}} = 500$ ， ${N_{{\text{ic2}}}} = 500$ ， ${N_{{\text{top}}}} = 1400$ 。设置4个隐藏层，每层30个神经元的全连接神经网络。

根据时间域分解策略，首先对模型采取预训练（热启动），波场时刻从 ${t_1} = 0.05{\text{ s}}$ 开始算起，预测总时间 $T = 0.1{\text{ s}}$ ，根据经验设置损失分配系数 ${\lambda _1} = {10^{ - 5}}$ ， ${\lambda _2} = 1$ ， ${\lambda _3} = {10^{ - 1}}$ 。调用学习率为6×10^-3的Adam优化器训练20000步，再使用L-BFGS优化器训练200000步。损失分配系数的神经网络会根据初始条件项损失项、边界条件损失项、PDE残差损失项的顺序进行训练，预训练时的SH波还未传播到顶部边界，能够观测到PINN方法很好地预测了柱面SH波的传播过程。保存预训练后的网络结构进行二次训练，调整损失分配系数 ${\lambda _1} = {10^{ - 3}}$ ， ${\lambda _2} = 1$ ， ${\lambda _3} = {10^{ - 1}}$ ，预测总时间 $T =$ $0.3{\text{ s}}$ 。调用L-BFGS优化器训练100000步，进一步优化PDE残差损失项，训练完成后保存网络结构进行最终训练，损失分配系数不变，设置预测总时间T=0.6 s，调用L-BFGS优化器训练200000步。训练完成后，可对任意分辨率下任意时空点的波动方程解及解的各阶偏导进行预测，图 5给出了4个时刻的PINN模拟波场和解析波场的对比。

图 5 半无限空间波动问题: PINN与解析波场快照对比

Figure 5. Semi-infinite space fluctuation problem: PINN vs. analytical wave snapshot

下载: 全尺寸图片幻灯片

由于此模型的波源位于中心位置，所以可在 $x = 300$ 外布设传感器，观测入射波、反射波和散射波经过的过程，验证PINN在预测柱面SH波在半无限空间内传播和反射特性，给出x坐标同为300 m，z坐标关于 $z = - 750$ 对称点位的时程数据，其中z坐标600 m与z坐标900 m是相对于 $z = - 750$ 的对称坐标，由于t=0 s时刻区域内已存在点源散发出的波场，在0~0.6 s时刻内，在坐标 $z = - 600$ 处和 $z = - 900$ 处有入射波和反射波经过，可以看出PINN方法在此模型下的入射波传播和边界反射的预测值与解析真值基本一致。同时z坐标-300 m与z坐标-1200 m是相对于 $z = - 750$ 的对称坐标，在0~0.6 s时刻内，坐标 $z = - 300$ 处和 $z = - 1200$ 处除入射波和反射波外，还有因峡谷而产生的散射波，可以看出PINN方法在预测柱面SH波在峡谷出的散射值与解析真值基本一致。在 $x = 300$ 布设的位移传感器和预测位移时程结果图 7所示。

图 6 对称位置PINN与解析波场时程对比

Figure 6. Comparison of time histories of symmetrical position PINN and analytical wave field

下载: 全尺寸图片幻灯片

图 7 PINN模拟时程图（x=300）

Figure 7. Time histories of PINN analog (x=300)

下载: 全尺寸图片幻灯片

3. 不同工况深切峡谷波动模拟

为保证PINN方法在处理对称V型峡谷波动模拟问题的有效性，考虑不同波速、不同主频的Ricker波在V型半无限空间内的波动问题。模型区域为宽1500 m，高1500 m，峡谷深度d=50 m，峡谷宽度b=150 m，输入波位移时程采用Ricker源时间函数，源位置处于模型中心x = 750 m，z = -750 m。

本文所有工况的模型参数和训练参数如表 2所示，工况二和工况三的预测结果与解析值的对比云图如图 8所示，由此可见PINN方法在对称V型峡谷的地形下，能够较好地预测不同频率不同波速下柱面SH波的反射和散射。

表 2 不同工况PINN模型参数

Table 2. Parameters of PINN model under different working conditions

参数	工况一（图 5）		工况二（图 8(a)）	工况三（图 8(b)）
主频 $\omega {\text{/Hz}}$		10	8	5
波速 $c{\text{/}}$ ${\text{(m}} \cdot {{\text{s}}^{ - 1}}{\text{)}}$		3000	3000	2000
第一帧快照时间 ${t_0}{\text{/s}}$		0.20	0.15	0.30
第二帧快照时间 ${t_1}{\text{/s}}$		0.22	0.20	0.40
传播时间 $T{\text{/s}}$		0.60	0.65	1.00
采样点	${N_{\text{p}}} = 9954$ ， ${N_{{\text{ic1}}}} = 500$ ， ${N_{{\text{ic2}}}} = 500$ ， ${N_{{\text{top}}}} = 1400$
预训练损失分配系数	${\lambda _1} = {10^{ - 5}}$ , ${\lambda _2} = 1$ , ${\lambda _3} = {10^{ - 1}}$
后续损失分配系数	${\lambda _1} = {10^{ - 3}}$ , ${\lambda _2} = 1$ , ${\lambda _3} = {10^{ - 1}}$
优化策略	Adam20000步+ LBFGS500000步		Adam20000步+ LBFGS300000步	Adam20000步+ LBFGS300000步

下载: 导出CSV

| 显示表格

图 8 PINN预测与解析真值云图对比

Figure 8. Comparison of PINN prediction and ground truth under condition 3

下载: 全尺寸图片幻灯片

对比不同工况下的预测精度，定义在某一点PINN与解析波场之间的相对 ${L_2}$ 范数误差为

$\varepsilon (\boldsymbol{u}) = \frac{{\sqrt {\sum\nolimits_{i = 1}^N {{{\left\| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ({x_0}, {z_0}, {t_i}) - {u_\text{ref}}({x_0}, {z_0}, {t_i})} \right\|}^2}} } }}{{\sqrt {\sum\nolimits_{i = 1}^N {{{\left\| {{u_\text{ref}}({x_0}, {z_0}, {t_i})} \right\|}^2}} } }}。$

(17)

式中： ${x_0}$ ， ${z_0}$ 为采样点的坐标位置； $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ({x_0}, {z_0}, {t_i})$ 为PINN方法预测得到的该采样点的位移时程； ${u_{ref}}({x_0}, {z_0}, {t_i})$ 为相同位置的解析位移时程；N为计算点数。

给出3种工况预测模型在 $x = 300$ 不同位置的相对范数误差。在x相同时，相对 ${L_2}$ 范数误差与纵坐标z有关，越靠近地表，由于散射波和衍射波的叠加，相对 ${L_2}$ 范数误差会增大，但都保持在0.03以内。表明PINN方法处理对称V型峡谷反射波和散射波的有效性，可实现复杂地形模拟分析。分别给出不同频率下PINN预测的峡谷地表及附近各位置峰值位移分布。由可知：不同SH波（5，8，10 Hz）条件下，V型峡谷地形效应总体上呈现出“M”型分布，中心V型峡谷底端及邻区SH波发生衰减与振荡，在谷肩及地表SH波放大，峡谷边缘出现了显著放大。3种工况下地表处最大峰值位移的相对 ${L_2}$ 误差范数分别为0.0009，0.0006，0.001，由此可见PINN方法在预测低频SH波峡谷处地形效应时更为准确。

图 9 不同工况相对

${L_2}$ 范数误差（x=300）

Figure 9. Relative norm errors under different working conditions (x=300)

下载: 全尺寸图片幻灯片

图 10 地表峰值位移对比

Figure 10. Comparison of peak displacements on surface

下载: 全尺寸图片幻灯片

4. 结论

通过物理信息驱动神经网络（PINN）的自动微分功能求解了二维波动方程，并计算了柱面SH波在对称V型峡谷下的反射和散射。通过与解析值的对比，验证了PINN方法在求解波动问题上的精度。得到3点结论。

（1）物理驱动深度学习（PINN）方法可通过稀疏初始波场数据，模拟柱面SH波在对称V型峡谷下的反射和散射，具备“无网格、强耦合”等特性，可适应不同地形与波源。

（2）对比不同工况的训练结果，发现越靠近地表位置，波场叠加越复杂，相对 ${L_2}$ 误差范数也会越大。且同一模型下，相对 ${L_2}$ 范数误差与柱面SH波的主频关系不大。

（3）对比不同工况下解析与PINN预测的地表峰值位移大小关系，柱面SH波在V型峡谷底端发生衰减现象，在其他位置发生放大现象。其中在V型峡谷边缘处放大现象最明显，且PINN方法在预测低频SH波在峡谷处地形效应时更为准确。

图 1 试验装置

Figure 1. Test devices

下载: 全尺寸图片幻灯片

图 2 球型陶瓷颗粒

Figure 2. Spherical ceramic particles

下载: 全尺寸图片幻灯片

图 3 粗粒土柱颗粒级配曲线

Figure 3. Grain-size distribution curves of coarse-grained soil

下载: 全尺寸图片幻灯片

图 4 浑水中颗粒组成

Figure 4. Particle composition in muddy water

下载: 全尺寸图片幻灯片

图 5 各组分颗粒级配曲线

Figure 5. Grain-size distribution curves of various particle component

下载: 全尺寸图片幻灯片

图 6 不同控制粒径下土柱典型淤堵形态

Figure 6. Typical clogging forms of coarse-grained soil columns under different controlled particle sizes

下载: 全尺寸图片幻灯片

图 7 各工况下淤积率变化规律

Figure 7. Variation laws of deposition rate under various working conditions

下载: 全尺寸图片幻灯片

图 8 不同水头下相对孔隙率变化曲线

Figure 8. Variation curves of relative porosity under different water heads

下载: 全尺寸图片幻灯片

图 9 两种粗粒土相对孔隙率变化曲线

Figure 9. Variation curves of relative porosity of two kinds of coarse-grained soil

下载: 全尺寸图片幻灯片

图 10 土柱不同深度相对孔隙率变化规律

Figure 10. Variation laws of relative porosity at different depths of soil columns

下载: 全尺寸图片幻灯片

图 11 不同形态下土柱不同深度渗透系数变化规律

Figure 11. Variations law of permeability coefficient of soil columns at different depths under different forms

下载: 全尺寸图片幻灯片

图 12 4种淤堵形态下整体渗透系数试验与理论值对比

Figure 12. Test and theoretical overall permeability curves under four clogging conditions

下载: 全尺寸图片幻灯片

图 13 阶段2试验与式(18)改进渗透系数结果对比

Figure 13. Comparison between stage 2 tests and improved permeability coefficient results by Formula (18)

下载: 全尺寸图片幻灯片

图 14 阶段2试验与式（19）改进渗透系数结果对比

Figure 14. Comparison between stage 2 tests and improved permeability coefficient results by Formula (19)

下载: 全尺寸图片幻灯片

图 15 权重系数与控制粒径的线性拟合关系

Figure 15. Linear fitting relationship between weight coefficient and control particle size

下载: 全尺寸图片幻灯片

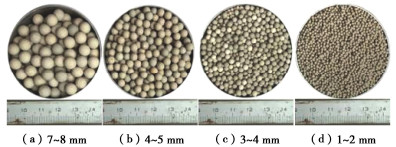
表 1 粗粒土柱物理力学参数

Table 1 Physical and mechanical parameters of coarse-grained soil columns

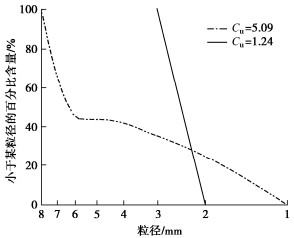
工况	粒径	不均匀系数 C_u	等效颗粒粒径d_e/mm	干密度ρ_d/(g·cm^-3)	初始孔隙率n₀	有效孔隙直径D_e/mm	渗透系数k/(cm·s^-1)
土样1	2~3 mm	1.24	2.45	2.53	0.397	0.56~0.70	4.76
土样2	1~8 mm	5.09	1.72	2.40	0.357	0.36~0.46	2.97

下载: 导出CSV

表 2 各颗粒组分的干密度和渗透系数

Table 2 Dry densities and permeability coefficients of various particle components

C_0.075/%	干密度ρ_d/(g·cm^-3)	渗透系数k/(cm·s^-1)
0	2.41	3.00×10^-2
9.17	2.40	6.78×10^-3
18.73	2.37	1.09×10^-3
28.50	2.33	5.56×10^-4
38.96	2.31	5.09×10^-4
49.98	2.30	4.01×10^-4
58.13	2.25	9.68×10^-5
69.40	2.22	8.63×10^-5
79.48	2.18	6.27×10^-5
90.56	2.16	3.41×10^-5

下载: 导出CSV

表 3 粗粒土淤堵形态判别

Table 3 Discrimination of clogging forms of coarse-grained soil

淤堵形态	表层淤积淤堵形态（S）	表层-内部双重淤堵形态（S-I）	内部孔隙淤堵形态（I）	暂态孔隙淤堵形态（P）
C_0.075	≤20%	20%~60%	60%~80%	＞80%

下载: 导出CSV

表 4 土体计算参数

Table 4 Soil parameters

C_0.075	阶段	决定系数R²	均方根误差 RMSE
0	阶段1	0.99	0.04
	阶段2	0.85	0.404
	阶段3	0.98	0.086
28.5	阶段1	0.43	2.04
	阶段2	0.68	0.41
	阶段3	0.99	0
58.13	阶段1	-1.02	2.78
	阶段2	0.92	0.22
	阶段3	1.00	0
79.49	阶段1	-1.82	3.13
	阶段2	0.97	0.26
	阶段3	1.00	0
90.56	阶段1	-1.27	2.53
90.56	阶段2	0.98	0.27

下载: 导出CSV

表 5 改进式与试验渗透系数误差指标

Table 5 Error indexes of permeability coefficient by improved formula and tests

工况	阶段	R²	RMSE
未改进	阶段1	0.99	0.04
	阶段2	0.85	0.404
	阶段3	0.98	0.086
改进	阶段1	0.99	0.04
	阶段2	0.96	0.09
	阶段3	0.98	0.086

下载: 导出CSV

表 6 改进式与试验渗透系数误差指标

Table 6 Error indexes of permeability coefficient by improved formula and test

改进与未改进	阶段	R²	RMSE
未改进	阶段1	-1.02	2.78
	阶段2	0.92	0.22
	阶段3	1	0
改进	阶段1	1	0
	阶段2	0.99	0.008
	阶段3	1	0

下载: 导出CSV

参考文献(21)

[1]	FARSHBAF AGHAJANI H, SHAHBAZI P, SALIMI M, et al. The effect of a defective permeable zone inside the clay core of an earthfill dam with regard to the seepage aspect[J]. SN Applied Sciences, 2020, 2(9): 1544. doi: 10.1007/s42452-020-03352-3
[2]	YOUSIF O S Q, KARAKOUZIAN M, RAHIM N O A, et al. Physical clogging of uniformly graded porous media under constant flow rates[J]. Transport in Porous Media, 2017, 120(3): 643-659. doi: 10.1007/s11242-017-0946-5
[3]	费良军, 王锦辉. 泥沙粒度组成对浑水膜孔灌单向交汇入渗特性的影响[J]. 农业机械学报, 2016, 47(4): 105-112. FEI Liangjun, WANG Jinhui. Effect of clay and sand grades on single-line interference infiltration characteristics of muddy water film hole irrigation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(4): 105-112. (in Chinese)
[4]	刘杰, 罗玉再. 高土石坝心墙裂缝的自愈机理与反滤层的防护作用[J]. 水利学报, 1987, 18(7): 20-29. LIU Jie, LUO Yuzai. The mechanism of crack healing in core and the protective functions of filters in high earth-rock dams[J]. Journal of Hydraulic Engineering, 1987, 18(7): 20-29. (in Chinese)
[5]	TRZASKAA, SOBOWSKA K. Effect of colmatage on the magnitude of the discharge of flow during bore-hole exploitation of water[J]. Archiwwm Gornictwa, 1988, 33(1): 34-38.
[6]	党发宁, 刘云贺, 陈军强, 等. 浑水渗流理论及其工程应用[J]. 中国科学E辑: 技术科学, 2006, 36(9): 1029-1036. DANG Faning, LIU Yunhe, CHEN Junqiang, et al. Muddy water seepage theory and its engineering application[J]. Science in China (Series E (Information Sciences)), 2006, 36(9): 1029-1036. (in Chinese)
[7]	姚锋杰. 基于浑水渗流理论的某斜心墙土石坝渗流稳定机理研究[J]. 水力发电, 2012, 38(10): 24-27. YAO Fengjie. Study on seepage stability mechanism of an inclined-wall earth and rockfill dam based on muddy water seepage theory[J]. Water Power, 2012, 38(10): 24-27. (in Chinese)
[8]	许尚杰, 党发宁, 程素珍. 浑水渗流理论及平原水库防渗技术研究[J]. 岩土力学, 2011, 32(7): 2093-2098. XU Shangjie, DANG Faning, CHENG Suzhen. Research of muddy water seepage theory and anti-seepage technique for plain reservoirs[J]. Rock and Soil Mechanics, 2011, 32(7): 2093-2098. (in Chinese)
[9]	赵军, 张程远, 刘泉声. 水源热泵回灌井悬浮颗粒运移和沉积物理特性试验模型研究[J]. 岩石力学与工程学报, 2014, 33(2): 257-263. ZHAO Jun, ZHANG Chengyuan, LIU Quansheng. Test study of physical properties of suspended particles migration and deposition in water source heat pump injection well[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2): 257-263. (in Chinese)
[10]	SEN T K, KHILAR K C. Review on subsurface colloids and colloid-associated contaminant transport in saturated porous media[J]. Advances in Colloid and Interface Science, 2006, 119(2/3): 71-96.
[11]	周永潮, 许恒磊, 陈佳代, 等. 渗流作用下多孔介质内颗粒迁移与堵塞规律研究[J]. 岩土工程学报, 2022, 44(2): 255-263. doi: 10.11779/CJGE202202006 ZHOU Yongchao, XU Henglei, CHEN Jiadai, et al. Particle migration and clogging in porous media with seepage[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(2): 255-263. (in Chinese) doi: 10.11779/CJGE202202006
[12]	路莹, 杜新强, 迟宝明, 等. 地下水人工回灌过程中多孔介质悬浮物堵塞实验[J]. 吉林大学学报(地球科学版), 2011, 41(2): 448-454. LU Ying, DU Xinqiang, CHI Baoming, et al. The porous media clogging due to suspended solid during the artificial recharge of groundwater[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(2): 448-454. (in Chinese)
[13]	李识博, 王常明, 王钢城, 等. 粗粒土淤堵模式判别及最优淤堵粒径区间确定[J]. 水利学报, 2013, 44(10): 1217-1224. LI Shibo, WANG Changming, WANG Gangcheng, et al. Clogging types distinguishing of coarse-grained soil and determination of optimal range of clogging grain size[J]. Journal of Hydraulic Engineering, 2013, 44(10): 1217-1224. (in Chinese)
[14]	朱国胜, 张家发, 陈劲松, 等. 宽级配粗粒土渗透试验尺寸效应及边壁效应研究[J]. 岩土力学, 2012, 33(9): 2569-2574. ZHU Guosheng, ZHANG Jiafa, CHEN Jinsong, et al. Study of size and wall effects in seepage test of broadly graded coarse materials[J]. Rock and Soil Mechanics, 2012, 33(9): 2569-2574. (in Chinese)
[15]	土工试验方法标准: GB/T 50123—2019[S]. 北京: 中国计划出版社, 2019. Standard for Geotechnical Testing Method: GB/T 50123—2019[S]. Beijing: China Planning Press, 2019. (in Chinese)
[16]	党发宁, 周玫, 李玉涛, 等. 黏性土地基流土破坏的临界水力坡降研究[J]. 岩土工程学报, 2021, 43(增刊1): 1-6. doi: 10.11779/CJGE2021S1001 DANG Faning, ZHOU Mei, LI Yutao, et al. Critical hydraulic gradient of soil flow failure in cohesive soil foundation[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(S1): 1-6. (in Chinese) doi: 10.11779/CJGE2021S1001
[17]	陈星欣, 白冰, 于涛, 等. 粒径和渗流速度对多孔介质中悬浮颗粒迁移和沉积特性的耦合影响[J]. 岩石力学与工程学报, 2013, 32(增刊1): 2840-2845. CHEN Xingxin, BAI Bing, YU Tao, et al. Coupled effects of particle size and flow rate on characteristics of particle transportation and deposition in porous media[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S1): 2840-2845. (in Chinese)
[18]	李广信. 对"论土骨架与渗透力" 讨论的答复[J]. 岩土工程学报, 2017, 39(2): 387-388. doi: 10.11779/CJGE201702026 LI Guangxin. Reply to discussion on "On soil skeleton and seepage force"[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(2): 387-388. (in Chinese) doi: 10.11779/CJGE201702026
[19]	土的工程分类标准: GB/T 50145—2007[S]. 北京: 中国计划出版社, 2008. Standard for Engineering Classification of Soil: GB/T 50145—2007[S]. Beijing: China Planning Press, 2008. (in Chinese)
[20]	张鹏远, 白冰, 蒋思晨. 孔隙结构和水动力对饱和多孔介质中颗粒迁移和沉积特性的耦合影响[J]. 岩土力学, 2016, 37(5): 1307-1316. ZHANG Pengyuan, BAI Bing, JIANG Sichen. Coupled effects of hydrodynamic forces and pore structure on suspended particle transport and deposition in a saturated porous medium[J]. Rock and Soil Mechanics, 2016, 37(5): 1307-1316. (in Chinese)
[21]	毛昶熙. 渗流计算分析与控制[M]. 北京: 水利电力出版社, 1990. MAO Changxi. Seepage Calculation Analysis and Control[M]. Beijing: Hydropower and Electric Power Publishing, 1990. (in Chinese)