Method and apparatus for measuring in-situ gas diffusion coefficient and permeability coefficient of unsaturated soils
-
摘要: 气体扩散系数Dg和渗透系数Kg是研究非饱和土中气体运移的两个重要参数。推导了稳态条件下,非饱和土中气体运移参数的计算理论。该理论基于示踪气体浓度C与气体流量q1之间及压力梯度P与气体流量q2之间的变化规律,分别确定非饱和土的Dg,Kg。依据推导的理论公式,设计并研制了一种原位测量非饱和土的Dg,Kg的装置。开展土柱试验,利用新装置测量非饱和土的Dg,Kg,并采用单元试验和数值模拟验证新方法和装置的有效性。研究表明新方法测量的非饱和土的Dg,Kg与单元试验及数值模拟结果吻合良好。基于数值模拟开展的敏感性分析结果揭示:Dg测量准确度随土体的质量含水率w减少而降低,而Kg的测量准确度受含水量的影响不显著;非饱和土的Dg,Kg的测量准确度均随着注气球半径增加而降低,但是注气球半径对Kg的测量准确度的影响更为显著,当注气球半径增加到0.05 m时,其准确度约为55%;土体各向异性降低测量准确度,当竖向与水平向的气体运移参数的比值Dgv/Dgh和Kgv/Kgh均为0.1时,Dg,Kg的测量准确度仍可达到40%以上。Abstract: The gas diffusion (Dg) and permeability (Kg) coefficients are the two important parameters for the study on gas transport in unsaturated soils. In the present study, the theory of calculating Dg and Kg for unsaturated soils under steady state is derived. Dg and Kg of unsaturated soils are determined based on the relationship between tracer gas concentration (C) and gas flow rate (q1) and that between pressure gradient (p) and gas flow rate (q2), respectively. A device for in-situ measurement of Dg and Kg in unsaturated soils is designed and developed. The soil column tests are conducted to measure Dg and Kg of unsaturated soils with different water contents. Thereafter, the element tests and numerical simulation analysis are used to verify the effectiveness of the new method and device. It is found that Dg and Kg obtained by the new method are in good agreement with the results of the element tests and numerical simulations. The results of the sensitivity analysis show that the measurement accuracy of Dg reduces as the soil water content decreases, while the measurement accuracy of Kg is independent of water content of soil. The measurement accuracies of both Dg and Kg decrease with the increase of the radius of the aeration bulb, but the measurement of Kg is more sensitive to the change of the radius. The measurement accuracy of Kg is about 55% of the true value, when the radius of the aeration bulb is 0.05 m. The soil anisotropy reduces the measurement accuracy; when the values of Dgv/Dgh and Kgv/Kgh is 0.1, the measurement accuracies of Dg and Kg can still reach more than 40%.
-
0. 引言
随着环境污染治理得到普遍重视,气体在非饱和土中的运移受到了广泛的关注,如填埋气的排放、土中微生物-植物的呼吸作用、尾矿氧化及地下管廊泄漏等[1-3]。扩散和渗透是非饱和土中气体运移的两个重要机理[4]。扩散由气体浓度梯度控制,气体从高浓度区域向低浓度区域运移[4]。渗透则受到气体压力梯度影响,气体从高压区迁移到低压区。确定气体扩散系数和渗透系数是研究非饱和土中气体运移的关键问题。此外,研究发现,气体扩散系数对描述土体微观结构、孔隙特征及估算酸性尾矿中氧气通量等具有重要意义[5-8],气体渗透系数则是估算气体排放速率的关键因素[9-11]。
非饱和土的气体扩散系数测量受到了众多学者的关注。McIntyre等[12]提出了通量室法,该方法较为简单,但仅适用于表层土体。Lai等[13]研发了单井法,此方法可快速获得现场土体的气体扩散系数。试验前只需将少量的示踪气体注入近地表土中,随后抽取少量气体样本,检测示踪气体浓度随时间的变化情况,最后通过对测量的示踪气体浓度与理论值进行最佳拟合,实现气体扩散系数的测量。Nicot等[14]发现可以通过监测注气点一定距离r处的示踪气体浓度来确定土体的气体扩散系数。该方法对土体扰动较小,但需要大量的示踪气体,且测试持续时间长(约4 d左右),容易受到天气变化而影响测量结果的准确度。同时,Weeks等[15]依据大气示踪法来确定气体扩散系数,该方法基于分子扩散理论,考虑土体密度、孔隙度、充气孔隙度等参数的影响,需进行大量测量,耗费时间较多,且测量过程复杂。上述测量方法中扩散系数的计算相当复杂,大都需要已知土体的充气孔隙度(土体中气体体积与土体总体积之比),然而在现场测量该参数较困难,尤其在测量点较深时。当前缺乏能够克服扩散系数计算复杂且需输入众多参数的计算理论,也亟需研发具有如下优点的新的测量装置:对现场土体扰动较小、测量深度不受限制及测量时间较短。
非饱和土的气体渗透系数一般通过气体渗透装置[16-23]或大规模的现场注气/抽气试验[24-26]获得。研究发现在一定干密度和气体压梯度下,土体的气体渗流速度随着土体含水量增加而降低(苗强强等[18])。增湿时含水率变化对气体渗透系数的影响大于减湿(陈存礼等[17])。陈正汉等[27]研发了土筒桩渗气装置,发现土的密度对渗气性有显著影响,而湿度对渗气性影响不大。大部分测量仪器为圆柱体空腔(直径为0.1~0.2 m),测量范围受空腔长度控制,干燥条件下易产生侧壁优势流。目前已有的装置难以同时测量非饱和土的气体扩散和渗透系数,工程中若要确定土体的气体渗透和扩散系数,则需要布置两套甚至多种测量装置。综上,当前亟需一种能够同时测量非饱和土的气体渗透系数与气体扩散系数的简便高效的装置。
本研究旨在研发一种非饱和土的气体扩散系数和渗透系数的测量方法及装置。首先,推导非饱和土的气体扩散系数计算理论,克服现有计算方法复杂且需众多土体参数的缺陷;其次,依据新的计算方法,研发测量装置,克服现有装置测量周期长、准确度低、对现场土壤扰动大等缺点。然后,开展土柱试验测量非饱和土气体扩散系数和渗透系数,并采用室内单元试验和数值模拟验证新的计算方法及装置的有效性。最后,基于数值模拟开展了一系列敏感性分析,探究装置尺寸、埋置深度和土体各向异性对气体扩散系数及渗透系数测量准确度的影响。
1. 新装置的测量原理及设计
1.1 测量原理
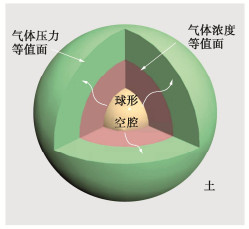
如图 1所示,假设在无限、均匀、各向同性且刚性的土体中存在半径为r0的球形空腔。
通过球心以恒定流量向球形空腔内泵入示踪气体(如惰性气体、CO2等),示踪气体向周围土体运移并逐步达到稳定状态,使得示踪气体浓度和气体压力等值线为球形等值线。此时,非饱和土体中溶解于水和水相释放到气相的气体总量平衡,土颗粒吸附和释放的示踪气体总量也相等。故稳态下,不考虑非饱和土的气体溶解、吸附和释放的影响。假定土中气压和温度恒定,基于理想气体定律,气体密度可为
ρa=PwaRT。 (1) 式中:ρa为气体密度(kg/m3);P为绝对气体压力(Pa);wa为空气的摩尔质量(0.029 kg/mol);R为摩尔气体常数(8.314 J/(mol K));T为热力学温度(K)。
(1)非饱和土的气体扩散系数测量原理
测量扩散系数时,通过控制低进气流量,维持气压恒定(增量小于0.01 kPa),此时可以忽略气体的压缩性。基于理想气体方程,在气压恒定、温度恒定条件下,可假定气体的密度不变,扩散控制土中气体的运移。根据质量守恒,稳态扩散条件下(气体浓度及浓度梯度不随时间变化),任一球形截面的示踪气体扩散量相等的:
dqdr=0。 (2) 式中:q为任一截面的示踪气体扩散量(m3/s);r为球体的半径(m)。
q=−4πr2DgdCdr。 (3) 式中:π为圆周率;Dg为扩散系数(m2/s);C为示踪气体浓度(m3/m3)。
在无限、均匀、各向同性且不考虑变形的土体假设下,土体的扩散系数Dg恒定,将式(3)代入式(2)可得
−4πDg(2rdCdr+r2d2C dr2)=0。 (4) 在球形腔体内壁,边界条件为
r=r0,C=C0。 (5) 式中:r0为球形腔体半径(m);C0为腔体内示踪气体浓度(m3/m3)。
基于式(4),(5)计算可得
C=C0+B(r−r0)4πDgr0r。 (6) 式中:B为待定常数(m3/s)。
对式(6)求导可得
dCdr=B4πDgr2。 (7) 将式(7)代入式(3)可得
B=−q。 (8) 将式(8)代入式(6)可得
C=C0−q4πDgr0+q4πDgr。 (9) 由式(9)可知,示踪气体浓度C随着半径r增大而降低。无限远处,示踪气体浓度等于环境中该气体的背景浓度Ch(m3/m3)。
不考虑环境温度与气压的影响,依据式(9)可得气体扩散系数为
Dg=q14πr0(C0−Ch)。 (10) 式中:q1为示踪气体进气流量(m3/s);r0为球形腔体半径(m);C0为稳态下球形腔体内示踪气体浓度(m3/m3);Ch为土中初始示踪气体浓度(m3/m3)。
当环境中示踪气体的初始浓度为0时(即Ch=0 m3/m3), 气体扩散系数为
Dg=q14πr0C0。 (11) 需要指出式(11)适用于测量示踪气体在空气中的二元气体扩散系数,气体扩散的机理为气体分子碰撞引起的体相扩散,并未考虑气体分子与土颗粒之间碰撞引起的努森扩散[11]。这是由于努森扩散主要发生在气体的平均自由程(标准状态下约为10-8 m)与土体孔隙的大小相当的时候,因此努森扩散主要影响饱和度很高的细粒土体(如膨润土)的气体运移,在大多数情况下可以忽略[11]。
(2)非饱和土的气体渗透系数测量原理
扩散系数测量后,通过增大进气流量,使得层流控制土中气体运移。此时要避免由于气体流量过大而产生湍流。稳定状态下,当雷诺数Re≤1[28]时,非饱和土中气体流动为层流。届时可用达西定律描述气体在土中运移,则气体渗透系数为[29]
Kg=P2q2gρa2πr0(P22−Patm2)。 (12) 式中:q2为示踪气体进气流量(m3/s);P2为球形空腔内的绝对气压值(Pa);g为重力加速度;Patm为环境大气压(Pa);Kg为气体渗透系数(m/s)。
1.2 测量装置设计
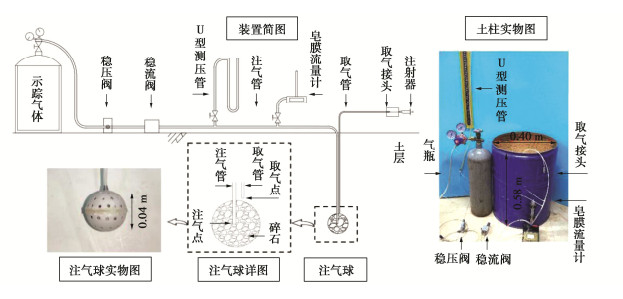
基于前文推导的非饱和土的气体扩散系数和渗透系数的计算理论,研发了一种原位测量气体扩散系数和渗透系数的装置。如图 2所示,该装置主要由进气管,镂空注气球(半径为0.02 m)和取气管组成。镂空注气球腔内填满了用尼龙网包裹的直径为3~4 mm的碎石,球体表面均匀分布直径为1.5 mm间距为3 mm的小孔。进气管(外径3 mm)一端位于注气球球心,另一端与气源相连,沿着导气管分别布置有稳压阀、稳流阀、皂膜流量计和U型管。试验过程中,调节稳压阀和稳流阀,向镂空注气球内通入恒定流量的示踪气体。分别采用皂膜流量计和U型管测量试验过程中气体流量和气体压强变化,其精度分别为0.1mL/min和0.01 kPa。取气管(外径3 mm)一端紧挨注气球边缘,另一端连接由橡胶密封的取气接口。通过注射器在取气口抽取一定量的气体,利用气相色谱仪检测示踪气体浓度。
1.3 测量方法
测量装置使用前,将注气球埋至目标深度(本研究中注气球中心深度为0.35 m),采用的示踪气体是纯CO2。首先,测量土中示踪气体的初始浓度(Ch为0.03%~0.04%)。接着,向注气球中注入示踪气体,开始测量土体的扩散系数。调节进气流量值(如1 mL/min),使得注气球腔内的相对气压小于0.01 kPa,待示踪气体浓度稳定后,记录此时示踪气体浓度与进气流量q1。试验过程中,每隔30 min,抽取3 mL气体样本,测量CO2浓度,若两次连续测量结果之差小于0.5%,则视为CO2扩散达到稳定。再次调节稳压阀和稳流阀,改变进气流量,重复上述试验步骤。值得注意的是,每次取气前,先抽取1.5 mL气体避免取气管内空气对示踪气体浓度的影响,然后再抽取气体开展试验。试验过程中需记录进气流量、示踪气体浓度、气体压强随时间的变化规律,确保气体在土中扩散处于稳定状态。最后,依据式(10),计算非饱和土的气体扩散系数Dg。扩散系数测量完毕后,提高进气流量(如100 mL/min),测量非饱和土气体渗透系数Kg。此时采用空气作为气源,调节稳流阀,增大气体流量(200~400 mL/min),从而提高土体的气压,待U型管读数稳定后(约1~2 min),记录此时气体压强(P2<5 kPa)和对应的进气流量q2,每隔30 min记录一次数据。非饱和土气体渗透系数Kg可通过式(12)计算得到。为了保证测量的准确性,对于每个测量点采用不同的气体流量,至少重复测量3次。
2. 土柱试验
2.1 试验用土
试验用土取自福建省福州市红庙岭垃圾卫生填埋场,为粉砂(SM)(ASTM D2487,2017)。土壤风干后,过2 mm筛,去除粗颗粒和植物根系等杂质,过筛后的土壤放入105 ℃恒温烘箱中连续烘干至少24 h。烘干后的土壤,均匀喷水至目标质量含水率(w为12.5%,18%,21%),然后将湿土再次过2 mm筛以减少土壤团聚。最后,将湿土放入密封袋中封存48 h使其水分平衡。土壤的基本性质见表 1。所有试验均在温度(25±1℃)和湿度(RH=45%)恒定的实验室内开展。
表 1 土柱试验用土的基本性质Table 1. Index properties of soils used in column tests基本性质 土柱试验 参考文献 土的分类 SM ASTM D 2487 相对质量密度 2.66 ASTM D 854 颗粒组成 ASTM D 422 粗砂(2~4.75 mm)/% 0 中砂(0.425~2 mm)/% 53.60 细砂(0.075~0.425 mm)/% 26.13 粉粒(0.002~0.075 mm)/% 15.87 黏粒(<0.002 mm)/% 4.40 液塑限 ASTM D 4318 液限/% 37.8 塑限/% 28.2 塑性指数 9.6 最优含水率/% 17.12 ASTM D 698 最大干密度/(g·cm-3) 1.84 ASTM D 698 2.2 土柱装置
室内土柱试验装置如图 2所示。土柱直径为0.40 m,高度为0.58 m。压实土体前,在土柱内壁涂抹一层凡士林,避免土样与土柱内壁产生优势流[1]。土体压实度为90%。为保证土体的均匀性,采用分层压实,每层土厚度为0.04 m,合计13层,总高0.52 m。每层土压实完毕后刮毛,确保土层间压实紧密。当从下往上压实第四层土时,预埋测量装置(注气球中心深度为0.35 m)。土柱压实完成后,通过导气管连接气瓶、稳压阀、稳流阀、U型管、皂膜流量计与注气球进气管。
2.3 试验流程
土柱搭建完成后,依次测量非饱和土的气体扩散系数和渗透系数。本研究制备3组不同含水率(w为12.5%,18%,21%)的土柱。首先测量土体的气体扩散系数,扩散是气体从高浓度区域向低浓度区域运移的过程,由气体浓度梯度控制,进气流量较小,分别为1,2,4 mL/min。试验中确保U型测压管(精度为0.01 kPa)测量的相对气压小于0.01 kPa。扩散系数测量完成后,调节稳流阀,增大进气流量,实现非饱和土中气体迁移的层流控制。进气流量分别提高至200,300,400 mL/min,测定非饱和土气体渗透系数。土体气体扩散系数和渗透系数测定试验完毕后,用环刀(高度20 mm、内径79.8 mm)取测量点附近的原状土样,开展单元试验测量土样的气体扩散系数和渗透系数(详见下文)。取土前,在环刀内壁涂抹一层凡士林,以降低环刀内壁与土体间优势流。此外,从每个测量点均取3个土样,并测量其含水率、干密度和孔隙度。
3. 单元试验
采用双腔室测量装置[30-31]获得土柱中测量点周围土样的气体扩散系数和渗透系数。该测量装置由主动腔室、被动腔室和中间的土样品腔室组成,各腔室内径分别为80,80,90 mm[31]。首先,测量土体的气体扩散系数。打开被动扩散腔的进气口和取气口,将纯氮气注入被动腔室进行洗气。然后,拉出塑料隔膜并开始计时,此时,氧气通过土体扩散,记录氧气浓度随时间变化规律,通过计算可获得气体扩散系数。最后,改变进气流量,开展气体渗透系数测定试验。试验中记录气体压力与流量的变化值。应当注意,为保证试验的准确性,所有试验均重复测量3次,试验细则及计算方法详见Chen等[3]和赵能凯[31]的工作。
4. 数值模拟
采用有限元分析软件COMSOL Multiphysics的用户自定义模块偏微分方程接口,求解相应控制方程(式(13),(16)),获得稳定状态下土柱中示踪气体浓度与压强分布,验证新装置测量结果,并研究注气球尺寸、埋置深度、土体各向异性对测量结果的影响。
4.1 理论模型
基于质量守恒,用于测量扩散系数的示踪气体运移控制方程如下[32-33]:
∂∂t[θgCg+θwHw]=−∇(VgCg)−∇Ng。 (13) 式中:Cg为气体的摩尔浓度(mol/m3);θg为土体体积含气量(m3/m3);θw为土体体积含水量;Hw为气体溶解于水中的摩尔浓度(mol/m3);Ng为气体扩散通量(mol/(m2 s));Vg为气体对流速度(m/s)。
式(13)左侧第一项和第二项分别表示气体的气相摩尔量和溶于水的气体摩尔量随时间的变化;式(13)右侧第一项表示气体通过对流产生的变化,第二项则表示气体扩散量变化。
根据亨利定律,气体溶解于水的摩尔浓度可为[34]
Hw=KhCg。 (14) 式中:Kh为气体的亨利系数(无量纲),本研究示踪气体为二氧化碳,其值为0.81[35]。
通过控制实验中气压增量较小(小于5 kPa),可以忽略气体压缩对其密度的影响[29]。因此,基于混合气质量守恒,土中示踪气体与空气组成的混合气的运移控制方程为
∂∂t(ρmix θg)=−∇(ρmix Vg)。 (15) 式中:ρmix 为混合气的密度(kg/m3)。由于混合气的气压达到稳定所需的时间(约1~2 min)远小于示踪气体浓度稳定的时间(约2~3 h),因此式(15)可以进一步简化为稳态情况:
∇Vg=0。 (16) 根据Darcy定律,非饱和土中的气体对流速度Vg为[36]
Vg=−Kg(∇Pgγg+1)。 (17) 式中:Vg为非饱和土中气体重度(N/m3);Pg为气体压力(Pa)。
气体扩散通量可通过Fick定律由下式计算:
Ng=−Dg∇Cg。 (18) 式中:Dg为气体扩散系数(m2/s)。
当模拟土体气体扩散系数测量时,需要求解控制方程(13),(16),从而反演得到土体中示踪气体浓度分布及压强变化。而模拟测量土体的气体渗透系数时候,仅求解式(16)。
当开展土柱试验的数值反演时,先模拟测量土体的气体渗透系数,通过调整输入的Kg,使得数值模拟得到的不同流量下的气压的计算值与实测值最为接近,此时得到了反演的Kg值。确定Kg后,通过调整输入的Dg值,使得数值计算得到的不同气体流量下非饱和土中示踪气体浓度与时间变化规律与实测值最为接近,此时得到了反演的Dg值。
4.2 数值模拟模型
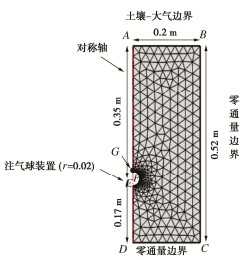
二维轴对称数值模拟示意图如图 3所示,模型尺寸与土柱试验一致。其中,AB是土体-大气界面,设置为狄利克雷边界条件[37],对于式(16)其边界为恒定相对大气压(0 Pa),对于式(13)为恒定气体浓度(CO2摩尔浓度0.0178 mol/mL)。AD是轴对称边界,DC和BC分别为土柱底部和侧壁,均为零通量边界,GFE为气体通量边界,对式(13),(16)其值分别为试验中施加的注气球单位表面积气体摩尔通量与气体体积通量。根据前述注气球装置,数值模拟中示踪气体浓度与混合气体气压的监测点为图 3中G点(即注气球的顶点)。
4.3 敏感性分析
土柱试验验证完成后,开展一系列的敏感性分析,分别研究注气球半径r0、注气球埋置深度和土体各向异性对气体扩散与渗透系数测量准确度的影响,模拟工况详见表 2。基于数值模拟得到的稳态下给定的气体流量下非饱和土中示踪气体浓度值,代入本文新推导的式(10)即可得到气体扩散系数。同样的,将模拟得到的气体流量与对应的压强差值,代入式(12)亦可获得气体渗透系数。
表 2 敏感性分析模拟工况Table 2. Summary of sensitivity analysis系列 r0/
m注气球埋置深度/m Kgv/
(10-7 m·s)Dgv/
(10-7 m·s)土体各向异性(Dgv/Dgh,Kgv/Kgh)① 1 0.01~0.05 0.35 6.43, 4② 4.54, 1.43 31.0, 7.46, 2.71 1 2 0.02 0.05~0.45 1 3 0.01 0.35 0.1~1 注:①Dgv,Dgh分别为竖向与水平向的土体的气体扩散系数,Kgv,Kgh分别为竖向与水平向的土体的气体渗透系数。②w=12.5%时,Kgv=6.43×10-7 m/s,Dgv=31.0×10-7 m2/s;w=18.0%时,Kgv=4.54×10-7 m/s,Dgv=7.46×10-7 m2/s;w=21.0%时,Kgv=1.43×10-7 m/s,Dgv=2.71×10-7 m2/s。 5. 结果与讨论
5.1 土柱试验、单元试验及数值模拟结果
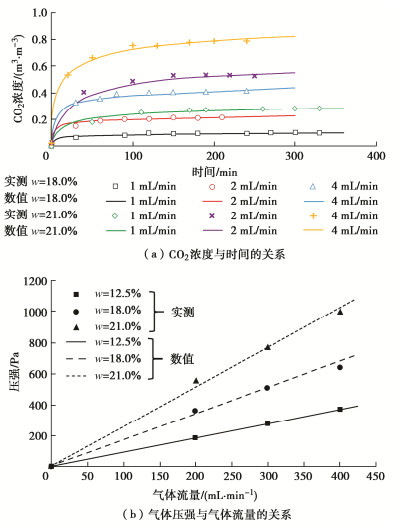
土柱试验的实测数据(w=12.5%,饱和度Sr=54%)分别如图 4(a),(b)所示。气体扩散系数测量试验中,CO2浓度随时间缓慢增加,约2 h后气体浓度趋于稳定。然而,在气体渗透系数测量试验中(如图 4(b)所示),气体压强在短时间内(大约3 min)基本达到稳定状态。试验结果与Qiu等[29]测量现场土体的气体渗透系数的试验结果吻合。这是由于测量气体渗透系数时施加的气体流量(200~400 mL/min)远大于测量扩散系数的流量(1~4 mL/min),使得气体压力梯度较大,能较快地达到稳定状态[38-39]。而测量扩散系数施加的流量较小,导致浓度梯度较小,达到稳定状态所需时间较长[39]。
土柱试验中CO2浓度-时间及压强-进气流量变化规律的实测值和数值模拟计算值如图 5所示。总体上,气体浓度随时间变化的实测值与计算值吻合良好,整体偏差在10%以内,表明数值模拟能够准确地模拟试验中气体浓度变化。试验初期,CO2浓度迅速增加,2 h左右达到峰值并趋于稳定。其中,土体含水率越高,气体浓度趋于稳定所需时间越长。这是因为土体含水量增加,饱和度提高,孔隙连通度降低[40-41],不利于气体扩散,气体浓度达到稳定状态所需的时间更长。
由图 5(b)可知,气压随着气体流量增加成线性增长,实测值与数值模拟结果匹配良好。一定气体流量下(如200 mL/min),气体压力随着土体含水率的增加逐渐提高。土体含水率越高对气体压强的影响越明显。主要原因是土体含水率增加,气体流动通道减少,土体的气体渗透系数降低,导致气体压力提高[42]。
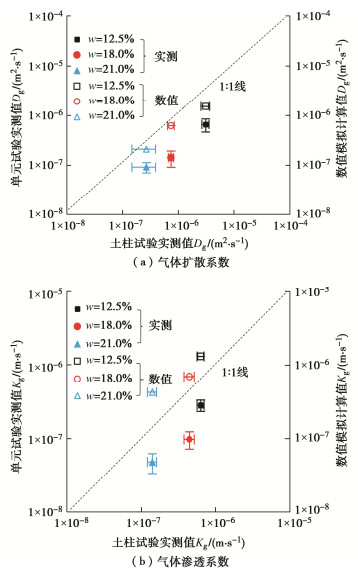
图 6(a), (b)分别对比了土柱试验、单元试验与数值模拟得到的非饱和土的气体扩散系数和渗透系数。如图 6(a)所示,总体上气体扩散系数随着土体含水率的增加而降低,这与众多研究结果一致[29]。土柱试验得到的气体扩散系数与数值模拟结果吻合良好,但均大于单元试验值。总体上,土体含水率越低,土柱试验与单元试验得到的土体的气体扩散系数差值越大。这是由于单元试验土样尺寸较小,容易受到土柱中压实的土样的不均匀性影响,从而影响试验结果[37]。因此,为克服小尺寸土样的“局限性”带来的测量结果偏差,必须进行多次的重复试验。此外,单元试验中取样过程中也会对土样造成一定的扰动,影响测量结果。综上,土柱试验、单元试验和数值模拟得到的气体扩散系数吻合较好,表明新推导的计算方法和新装置能够准确地得到非饱和土的气体扩散系数。
气体渗透系数与土体含水率之间关系如图 6(b)所示。非饱和土气体渗透系数随着土体含水率提高而降低,这与Zhan等[9]的试验结果一致。当土含水率21%时,土体饱和度较高(Sr=91%),土体孔隙连通度降低,导致土体的气体渗透系数骤减。与扩散系数相同,单元试验得到的气体渗透系数小于土柱试验值,仅为土柱试验值的30%左右。这可能是因为单元试验土样尺寸较小,不能完全表征土体结构及潜在优势流的影响[25]。然而,土柱试验得到的气体渗透系数小于数值模拟计算结果。土体含水率越高,土柱试验结果与数值模拟值差别越大,当土体含水率为21%时(Sr=91%),土柱试验获得的气体渗透系数仅为数值模拟值的35%。原因之一是土柱边界扭曲了球形气压轮廓,测量气体压力偏大,从而导致渗透系数偏小。总体上,试验值和数值模拟结果吻合较好,表明新推导的理论及研发的装置可以有效地得到非饱和土气体扩散系数和渗透系数。后续还应当开展现场试验,进一步的验证装置的有效性。
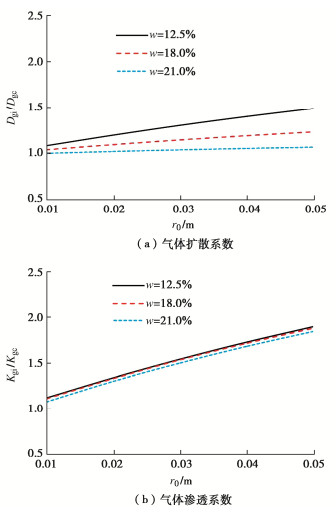
5.2 注气球半径对测量准确度的影响
注气球半径对测量气体扩散系数和渗透系数的影响分别如图 7(a), (b)所示。气体扩散系数的计算值与真实值(数值模拟中输入值为3.10×10-6,7.46×10-7,2.71×10-7 m2/s)的比值随着注气球半径增大而降低,说明注气球的半径越大测量准确度越低。其中,土体含水率越低,影响越明显。注气球半径为0.01 m时,扩散系数的计算值约为真实值的95%(标准差为±1.64×10-8),且基本不受土体含水率的影响。注气球直径增加到0.05 m时,较干燥的土体中(w=12.5%,Sr=54%)气体扩散系数的计算值约为真实值的58%。这是因为土体饱和度越低,气体更容易向周围土体扩散,受到零通量边界条件的影响(图 3中BC,CD边界),示踪气体更容易聚集导致浓度更大,致使扩散系数的计算值偏小。
由图 7(b)可知,非饱和土气体渗透系数的测量准确度随着注气球半径增加而降低,但其对含水率变化不敏感(土体Sr为54%~91%)。当注气球半径为0.01 m时,计算值约为真实值(6.43×10-7,4.54×10-7,1.43×10-7 m/s)的90%(标准差为±3.32×10-8)。然而,当注气球半径增加到0.05 m时,气体渗透系数被严重低估,其计算值约为真实值的55%。这主要是因为在一定的进气流量下,减小注气球半径将会减少周围土体中的气压影响区,从而提高测量结果的准确性[29]。由此可见,注气球半径越小,相应的边界效应也会减弱,不仅可提高装置的测量准确度,同时也能用于浅层土体。但应当注意的是,在一定的进气流量下,直径越小的注气球中会产生更大的气体压力值,此种情况下,应当加强气压监测,避免气体在周围土壤中产生湍流(即Re>1)。
上述结果表明非饱和土的气体扩散系数和渗透系数的测量准确度均随着注气球半径的增加而降低。注气球半径对渗透系数测量准确度的影响更加明显。这不同于Feng等[43]的结论:气体扩散系数受边界效应的影响大于气体渗透系数。这是由于Feng等[43]采用含有8%浓度示踪气体的混合气测量土体的扩散系数,使得混合气的对流显著影响示踪气体运移,即示踪气体的对流与扩散均受到边界条件的影响,而本文采用纯的CO2作为示踪气体,测量扩散时候,气体的扩散是气体运移的主要方式,降低了边界效应的影响。此外,图 7(a)表明当土体含水率较高时(w=21%, Sr= 91%),注气球半径对扩散系数测量准确度的影响不显著。
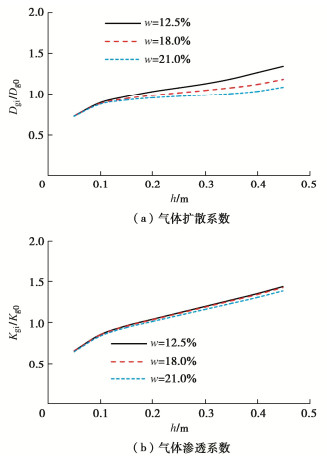
5.3 装置埋置深度对测量准确度的影响
注气球(r=0.02 m)埋置深度对气体扩散系数和渗透系数测量准确度的影响如图 8所示。计算结果表明,当注气球埋深0.05 m时,气体扩散系数的计算值最大,约为真实值的1.6倍。计算值随埋深的增加而逐步减小,在埋深0.3 m左右接近真实值。这是因为当测量点接近土体表面时(h=0.05 m),示踪气体容易向浓度更低的空气扩散,稳定状态下,测量点处的浓度偏低,导致扩散系数被高估[37]。反之,距离土柱底面较近时(h=0.45 m),受到土柱底部边界的影响,阻碍了示踪气体的扩散,使得稳定状态下测量点处的浓度偏大,导致扩散系数被低估。值得注意的是,土体含水率越低(w=12.5%, Sr=54%),注气球深度对测量准确度的影响越明显。因此,在干旱地区要特别注意仪器埋设深度,以提高测量准确度。
气体渗透系数的计算值与真实值的变化规律与扩散系数相同(图 8(b))。测量点深度较浅时(h=0.05 m),土体的气体渗透系数被高估,其值约为真实值的2倍。然而,测量点深度靠近土柱底部边界时(h=0.45 m),气体渗透系数的计算值约为真实值的70%。其原因主要是测量点接近土体表面时,气体压力偏小,导致气体渗透系数被高估。当注气点接近底面边界时,稳定状态下,气体压力差偏大,致使计算得到的渗透系数偏小。因此,实际工程中,注气球埋置深度不宜太浅。对比注气球埋置深度对气体渗透和扩散系数的影响,可知,埋置深度较浅,扩散和渗透系数均大于实际值,埋置深度靠近场地中的土-岩石界面都会导致计算值偏小。但是,渗透系数对埋置深度更加敏感。因此,在现场或试验中应注意注气球埋置深度,以减少测量误差。
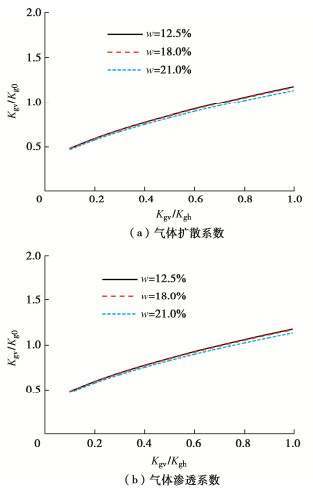
5.4 土体各向异性对测量准确度的影响
土体各向异性对测量气体扩散系数和渗透系数的影响分别如图 9(a),(b)所示(r0=0.01 m)。考虑土体各向异性(Dgv/Dgh≠1)会导致计算得到的扩散系数偏离实际值。如图 9(a)所示,当土体各向异性较大时(Dgv/Dgh=0.1),由式(10)计算得到的气体扩散系数约为真实值(Dgv)的2倍,气体扩散系数被高估。其原因主要是各向异性下,气体浓度等值曲面为椭球面与假定的球形气体浓度等值曲不符,实际浓度值与理想状态下不同,导致扩散系数的准确度降低。另外,含水率对气体扩散系数的变化趋势有一定的影响。总体上,含水率越高,土体为各向同性时(Dgv/Dgh=1),计算获得的扩散系数的准确度越高。
本文提出的新方法与测量装置得到的气体渗透系数的计算准确度随着土体各向异性(Kgh/Kgv≠1)增加而降低,其变化规律如图 9(b)所示。本研究结果与Qiu等[29]类似。主要原因是土体Kgh与Kgv值不同,导致气体等压线从理想球形变为椭球形,实际气体压力差与理想状态下气压差不等。比较土体各向异性对气体扩散和渗透系数的影响可得到,计算值均随着土体各向异性的增加而增大,各向异性越明显,测量准确度越低。当Dgv/Dgh和Kgv/Kgh比值介于0.5~1.0,扩散和渗透系数的计算值为真实值(Dgv或Kgv)的75%~120%。
6. 结论
推导了非饱和土中气体运移参数的计算方法,克服了传统方法需已知土体众多参数且计算复杂的缺点。依据推导的计算方法,研发了一种原位测量装置,可测量非饱和土的气体扩散系数与渗透系数。
(1)土柱试验、单元试验与数值模拟得到的气体扩散系数和渗透系数吻合良好,验证了新推导的计算方法的正确性与新装置的有效性。
(2)注气球半径越大,非饱和土气体扩散系数和渗透系数的测量准确度越低,但其对气体渗透系数的影响更为明显。当注气球半径为0.05 m时,气体扩散系数与渗透系数的计算值仅为真实值的55%左右。
(3)边界条件影响装置的测量准确度,实际工程中,注气球埋置深度不宜过浅,宜为0.3 m左右。
(4)气体扩散和渗透系数的测量准确度随着土体各向异性增加而降低,当Dgv/Dgh和Kgv/Kgh介于0.5~1.0,新方法得到的气体扩散系数和渗透系数为真实值(Dgv或Kgv)的75%~120%。
-
表 1 土柱试验用土的基本性质
Table 1 Index properties of soils used in column tests
基本性质 土柱试验 参考文献 土的分类 SM ASTM D 2487 相对质量密度 2.66 ASTM D 854 颗粒组成 ASTM D 422 粗砂(2~4.75 mm)/% 0 中砂(0.425~2 mm)/% 53.60 细砂(0.075~0.425 mm)/% 26.13 粉粒(0.002~0.075 mm)/% 15.87 黏粒(<0.002 mm)/% 4.40 液塑限 ASTM D 4318 液限/% 37.8 塑限/% 28.2 塑性指数 9.6 最优含水率/% 17.12 ASTM D 698 最大干密度/(g·cm-3) 1.84 ASTM D 698 表 2 敏感性分析模拟工况
Table 2 Summary of sensitivity analysis
系列 r0/
m注气球埋置深度/m Kgv/
(10-7 m·s)Dgv/
(10-7 m·s)土体各向异性(Dgv/Dgh,Kgv/Kgh)① 1 0.01~0.05 0.35 6.43, 4② 4.54, 1.43 31.0, 7.46, 2.71 1 2 0.02 0.05~0.45 1 3 0.01 0.35 0.1~1 注:①Dgv,Dgh分别为竖向与水平向的土体的气体扩散系数,Kgv,Kgh分别为竖向与水平向的土体的气体渗透系数。②w=12.5%时,Kgv=6.43×10-7 m/s,Dgv=31.0×10-7 m2/s;w=18.0%时,Kgv=4.54×10-7 m/s,Dgv=7.46×10-7 m2/s;w=21.0%时,Kgv=1.43×10-7 m/s,Dgv=2.71×10-7 m2/s。 -
[1] ALLAIRE S E, LAFOND J A, CABRAL A R, et al. Measurement of gas diffusion through soils: comparison of laboratory methods[J]. Journal of Environmental Monitoring, 2008, 10(11): 1326-1336. doi: 10.1039/b809461f
[2] LIPIEC J, HORN R, PIETRUSIEWICZ J, et al. Effects of soil compaction on root elongation and anatomy of different cereal plant species[J]. Soil and Tillage Research, 2012, 121: 74-81. doi: 10.1016/j.still.2012.01.013
[3] CHEN F Q, ZHAO N K, FENG S, et al. Effects of biochar content on gas diffusion coefficient of soil with different compactness and air contents[J]. Environmental Science and Pollution Research, 2020, 27(17): 21497-21505. doi: 10.1007/s11356-020-08594-7
[4] FREDLUND D G, RAHARDJO H. Soil Mechanics for Unsaturated Soils[M]. New York: Wiley, 1993.
[5] KUNCORO P H, KOGA K, SATTA N, et al. A study on the effect of compaction on transport properties of soil gas and water: I Relative gas diffusivity, air permeability, and saturated hydraulic conductivity[J]. Soil and Tillage Research, 2014, 143: 172-179. doi: 10.1016/j.still.2014.02.006
[6] MOLDRUP P, OLESEN T, KOMATSU T, et al. Tortuosity, diffusivity, and permeability in the soil liquid and gaseous phases[J]. Soil Science Society of America Journal, 2001, 65(3): 613-623. doi: 10.2136/sssaj2001.653613x
[7] DESUTTER T M, SAUER T J, PARKIN T B, et al. A subsurface, closed-loop system for soil carbon dioxide and its application to the gradient efflux approach[J]. Soil Science Society of America Journal, 2008, 72(1): 126-134. doi: 10.2136/sssaj2006.0101
[8] PINGINTHA N, LECLERC M Y, BEASLEY J P, et al. Assessment of the soil CO2 gradient method for soil CO2 efflux measurements: comparison of six models in the calculation of the relative gas diffusion coefficient[J]. Tellus B: Chemical and Physical Meteorology, 2010, 62(1): 47. doi: 10.1111/j.1600-0889.2009.00445.x
[9] ZHAN T L T, YANG Y B, CHEN R, et al. Influence of clod size and water content on gas permeability of a compacted loess[J]. Canadian Geotechnical Journal, 2014, 51(12): 1468-1474. doi: 10.1139/cgj-2014-0126
[10] 姚志华, 陈正汉, 黄雪峰, 等. 非饱和Q3黄土渗气特性试验研究[J]. 岩石力学与工程学报, 2012, 31(6): 1264-1273. doi: 10.3969/j.issn.1000-6915.2012.06.023 YAO Zhihua, CHEN Zhenghan, HUANG Xuefeng, et al. Experimental research on gas permeability of unsaturated Q3 loess[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(6): 1264-1273. (in Chinese) doi: 10.3969/j.issn.1000-6915.2012.06.023
[11] 陈云敏. 环境土工基本理论及工程应用[J]. 岩土工程学报, 2014, 36(1): 1-46. doi: 10.11779/CJGE201401001 CHEN Yunmin. A fundamental theory of environmental geotechnics and its application[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(1): 1-46. (in Chinese) doi: 10.11779/CJGE201401001
[12] MCINTYRE D S, PHILIP J R. A field method for measurement of gas diffusion into soils[J]. Soil Research, 1964, 2(2): 133. doi: 10.1071/SR9640133
[13] LAI S H, TIEDJE J M, ERICKSON A E. In situ measurement of gas diffusion coefficient in soils[J]. Soil Science Society of America Journal, 1976, 40(1): 3-6. doi: 10.2136/sssaj1976.03615995004000010006x
[14] NICOT J P, BENNETT P C. Shallow subsurface characterization of gas transport in a playa wetland[J]. Journal of Environmental Engineering, 2015, 124(11): 1038-1046.
[15] WEEKS E P, EARP D E, THOMPSON G M. Use of atmospheric fluorocarbons F-11 and F-12 to determine the diffusion parameters of the unsaturated zone in the Southern High Plains of Texas[J]. Water Resources Research, 1982, 18(5): 1365-1378. doi: 10.1029/WR018i005p01365
[16] 秦冰, 陆飏, 张发忠, 等. 考虑Klinkenberg效应的压实膨润土渗气特性研究[J]. 岩土工程学报, 2016, 38(12): 2194-2202. doi: 10.11779/CJGE201612007 QIN Bing, LU Yang, ZHANG Fazhong, et al. Gas permeability of compacted bentonite considering Klinkenberg effect[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(12): 2194-2202. (in Chinese) doi: 10.11779/CJGE201612007
[17] 陈存礼, 张登飞, 张洁, 等. 等向应力条件下原状Q3黄土的渗气特性研究[J]. 岩土工程学报, 2017, 39(2): 287-294. doi: 10.11779/CJGE201702012 CHEN Cunli, ZHANG Dengfei, ZHANG Jie, et al. Gas permeability of intact Q3 loess under isotropic stresses[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(2): 287-294. (in Chinese) doi: 10.11779/CJGE201702012
[18] 苗强强, 陈正汉, 张磊, 等. 非饱和黏土质砂的渗气规律试验研究[J]. 岩土力学, 2010, 31(12): 3746-3750, 3757. doi: 10.3969/j.issn.1000-7598.2010.12.009 MIAO Qiangqiang, CHEN Zhenghan, ZHANG Lei, et al. Experimental study of gas permeability of unsaturated clayey sand[J]. Rock and Soil Mechanics, 2010, 31(12): 3746-3750, 3757. (in Chinese) doi: 10.3969/j.issn.1000-7598.2010.12.009
[19] 陈正汉. 非饱和土与特殊土力学[M]. 北京: 中国建筑工业出版社, 2022. CHEN Zhenghan. Mechanics for Unsaturated and Special Soils[M]. Beijing: China Architecture & Building Press, 2022. (in Chinese)
[20] CHEN R, HUANG J W, ZHOU C, et al. A new simple and low-cost air permeameter for unsaturated soils[J]. Soil and Tillage Research, 2021, 213(12): 105083.
[21] MOHAMMADI M H, VANCLOOSTER M. A simple device for field and laboratory measurements of soil air permeability[J]. Soil Science Society of America Journal, 2019, 83(1): 58-63. doi: 10.2136/sssaj2018.03.0114
[22] JALBERT M, DANE J H. A handheld device for intrusive and nonintrusive field measurements of air permeability[J]. Vadose Zone Journal, 2003, 2(4): 611-617. doi: 10.2136/vzj2003.6110
[23] IVERSEN B V, SCHJøNNING P, POULSEN T G, et al. In situ, on-site and laboratory measurements of soil air permeability: boundary conditions and measurement scale [J]. Soil Science, 2001, 166(2): 97-106. doi: 10.1097/00010694-200102000-00003
[24] SHAN C, FALTA R W, JAVANDEL I. Analytical solutions for steady state gas flow to a soil vapor extraction well[J]. Water Resources Research, 1992, 28(4): 1105-1120. doi: 10.1029/91WR02986
[25] OLSON M S, TILLMAN F D, CHOI J W, et al. Comparison of three techniques to measure unsaturated-zone air permeability at Picatinny Arsenal, NJ[J]. Journal of Contaminant Hydrology, 2001, 53(1/2): 1-19.
[26] ZHAN L T, QIU Q W, XU W J, et al. Field measurement of gas permeability of compacted loess used as an earthen final cover for a municipal solid waste landfill[J]. Journal of Zhejiang University-Science A (Applied Physics & Engineering), 2016, 17(7): 541-552.
[27] 陈正汉, 谢定义, 王永胜. 非饱和土的水气运动规律及其工程性质研究[J]. 岩土工程学报, 1993, 15(3): 9-20. doi: 10.3321/j.issn:1000-4548.1993.03.002 CHEN Zhenghan, XIE Dingyi, WANG Yongsheng. Experimental studies of laws of fluid motion, suction and pore pressures in unsaturated soil[J]. Chinese Journal of Geotechnical Engineering, 1993, 15(3): 9-20. (in Chinese) doi: 10.3321/j.issn:1000-4548.1993.03.002
[28] ROUF M A, SINGH R M, BOUAZZA A, et al. Gas permeability of partially hydrated geosynthetic clay liner under two stress conditions[J]. Environmental Geotechnics, 2016, 3(5): 325-333. doi: 10.1680/envgeo.14.00009
[29] QIU Q W, ZHAN L T, LEUNG A K, et al. A new method and apparatus for measuring in situ air permeability of unsaturated soil[J]. Canadian Geotechnical Journal, 2021, 58(4): 514-530. doi: 10.1139/cgj-2019-0733
[30] SCHJØNNING P, EDEN M, MOLDRUP P, et al. Two-chamber, two-gas and one-chamber, one-gas methods for measuring the soil-gas diffusion coefficient: validation and inter-calibration[J]. Soil Science Society of America Journal, 2013, 77(3): 729-740. doi: 10.2136/sssaj2012.0379
[31] 赵能凯. 根系特征对非饱和土体气体渗透与扩散的影响规律[D]. 福州: 福州大学, 2021. ZHAO Nengkai. Influence of Root Characteristics on Gas Permeation and Diffusion in Unsaturated Soils[D]. Fuzhou: Fuzhou University, 2021. (in Chinese)
[32] MOLINS S, MAYER K U. Coupling between geochemical reactions and multicomponent gas and solute transport in unsaturated media: a reactive transport modeling study[J]. Water Resources Research, 2007, 43(5): 687-696.
[33] NG C W W, FENG S, LIU H W. A fully coupled model for water-gas-heat reactive transport with methane oxidation in landfill covers[J]. Science of the Total Environment, 2015, 508: 307-319. doi: 10.1016/j.scitotenv.2014.11.037
[34] REID R C, PRAUSNITZ J M, POLING B E. The Properties of Gases and Liquids[M]. 4th ed. New York: McGraw-Hill, 1987.
[35] ALBERTY R A, SILBEY R J. Physical Chemistry[M]. New York: Wiley, 1992.
[36] PARKER J C. Multiphase flow and transport in porous media[J]. Reviews of Geophysics, 1989, 27(3): 311-328. doi: 10.1029/RG027i003p00311
[37] LAEMMEL T, MAIER M, SCHACK‐KIRCHNER H, et al. An in situ method for real‐time measurement of gas transport in soil[J]. European Journal of Soil Science, 2017, 68(2): 156-166. doi: 10.1111/ejss.12412
[38] BARRAL C, OXARANGO L, PIERSON P. Characterizing the gas permeability of natural and synthetic materials[J]. Transport in Porous Media, 2010, 81(2): 277-293. doi: 10.1007/s11242-009-9398-x
[39] AUBERTIN M, AACHIB M, AUTHIER K. Evaluation of diffusive gas flux through covers with a GCL[J]. Geotextiles and Geomembranes, 2000, 18(2/3/4): 215-233.
[40] MOLDRUP P, OLESEN T, SCHJØNNING P, et al. Predicting the gas diffusion coefficient in undisturbed soil from soil water characteristics[J]. Soil Science Society of America Journal, 2000, 64(1): 94-100. doi: 10.2136/sssaj2000.64194x
[41] HAMAMOTO S, MOLDRUP P, KAWAMOTO K, et al. Effect of particle size and soil compaction on gas transport parameters in variably saturated, sandy soils[J]. Vadose Zone Journal, 2009, 8(4): 986-995. doi: 10.2136/vzj2008.0157
[42] 施建勇, 赵义. 气体压力和孔隙对垃圾土体气体渗透系数影响的研究[J]. 岩土工程学报, 2015, 37(4): 586-593. doi: 10.11779/CJGE201504002 SHI Jianyong, ZHAO Yi. Influence of air pressure and void on permeability coefficient of air in municipal solid waste(MSW)[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(4): 586-593. (in Chinese) doi: 10.11779/CJGE201504002
[43] FENG S, SUN J X, ZHAN L T, et al. A new method and instrument for measuring in situ gas diffusion coefficient and gas coefficient of permeability of unsaturated soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2023, 149(7): 04023041. doi: 10.1061/JGGEFK.GTENG-10871
-
其他相关附件



 下载:
下载: