Practical solutions for complex variable function for radius of tunnel plastic zone under non-hydrostatic pressures and their application extension
-
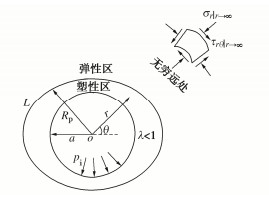
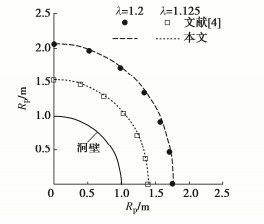
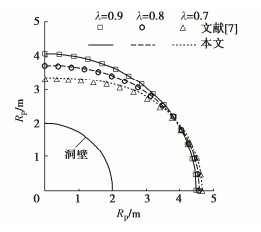
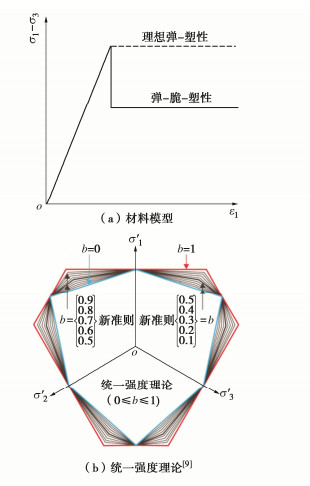
摘要: 针对非静水压力作用下圆形巷道的非圆塑性区边界线求解，首先通过类比提出围岩弹性区应力的简洁复变函数，基于理想弹−塑性模型和Mohr-Coulomb准则并利用围岩弹塑性交界线处的应力连续条件，建立了巷道塑性区半径的复变函数实用解答，其次采用弹−脆−塑性模型和统一强度理论以考虑围岩强度的峰后脆性下降与中间主应力效应，推导了巷道塑性区半径的复变函数扩展解答，最后给出所得解答的适用条件，并与文献理论解答和实测结果进行对比。研究结果表明：所得复变函数实用解答具有显式解析表达和易于计算分析等优点，其正确性与精度得到文献摄动解和高精度复变函数解的充分性验证；所得扩展解答保留了原实用解答的所有优点，能合理描述围岩强度的峰后脆性下降与中间主应力效应而工程应用前景广阔，与深埋巷道实测松动圈吻合良好。Abstract: In order to address the non-circular plastic boundary of rock circular tunnels under non-hydrostatic pressures, a simple complex variable function for the stress in an elastic zone is firstly introduced by using the analogy method. Based on the elastic perfectly-plastic model and the Mohr-Coulomb criterion, a practical solution for complex variable function for the radius of tunnel plastic zone is then derived under the stress continuity at the elastic-plastic boundary of surrounding rocks. Additionally, an extended solutions for complex variable function for the radius of tunnel plastic zone is proposed by adopting the elastic-brittle-plastic model and the unified strength theory to take into consideration both the post-peak brittle decrease and the effect of the intermediate principal stress of rock strength. Finally, the application conditions for the proposed solutions are provided, and they are compared with the available theoretical solutions and the measured data in the literatures. The results show that the practical solution for complex variable function has the advantages of explicitly analytical formulation as well as convenient calculation and analysis, whose validity and accuracy are sufficiently demonstrated by the perturbed solution and high-precision solution for complex variable function in the literatures. The extended solution retains all the advantages of the original practical solution and has good consistency with the measured loosening depth of a deep tunnel. Moreover, the extended solution has a broad application prospect due to the fact that it reasonably accounts for the post-peak brittle decrease and the effect of the intermediate principal stress of rock strength.
-
0. 引言
随着中国煤炭资源开采大范围向深部转移，冲击矿压（也称“冲击地压”）灾害日益凸显，严重影响煤矿安全生产[1]。冲击矿压主要是由采矿活动引起的煤岩结构局部应力集中引起，大量研究表明，在应力异常集中区（如断层、褶曲、煤柱区等），更容易发生冲击矿压[2]。
此外，相变构造区似乎也会增加煤层的异常应力集中[3]。国内外学者针对相变构造区诱发冲击矿压的研究，大多集中在煤层厚度变化诱发冲击矿压方面，针对坚硬覆岩厚度变化导致应力异常及诱冲效应的研究较少。孙振武[4]根据地应力场测量和矿压观测结果，发现在局部煤层厚度变化的区域往往会发生构造应力异常现象；Álvarez-Fernández等[5]运用数值模拟分析了分段崩落法开采煤层时，由于煤层厚度变薄导致在某超前巷道应力显著增大、变形较大的具体情况；Zhu等[6]通过现场观测和数值分析，研究了煤厚变化区初始应力场及采动应力场的分布规律；南存全等[7]研究发现，当工作面接近煤厚变异区时，煤厚变异区对工作面超前支承压力分布特征影响显著；王勇等[8]分析了不同煤层厚度变化条件下应力及能量分布规律；赵同彬等[9]研究了煤层厚度变化对超前支承压力及能量演化规律的影响，揭示了煤厚变异区冲击矿压发生的力学机制。
关于坚硬覆岩厚度变化与煤层厚度变化诱发冲击矿压机理的问题，其实质都是在厚度变化区产生局部应力集中，但是覆岩厚度变化不像煤厚变化能随着工作面的推进直观表现出来，只能从部分钻孔了解覆岩的分布情况。因此，坚硬覆岩厚度变化诱发冲击矿压的问题很难引起研究人员的注意。
针对现有研究成果的局限性，本文针对中国内蒙深部矿区坚硬覆岩厚度变化区煤层开采诱发冲击矿压机理问题，采用弹性力学理论对坚硬覆岩厚度变化区的构造应力特征进行力学分析，试图揭示覆岩厚度变化区应力异常分布的成因机制；并利用FLAC3D数值模拟研究覆岩厚度变化区工作面超前支承压力分布特征以及煤壁前方的能量演化规律，进一步探讨坚硬覆岩厚度变化区煤层开采诱发冲击矿压的机理。
1. 覆岩厚度变化区煤层应力异常形成机制
当煤岩体的应力不超过弹性范围时，最适宜用弹性力学的方法解析煤岩地下工程的力学行为[10]。原岩应力条件下，煤层及顶底板未受采掘扰动影响，假设煤岩体均未超过其弹性范围，可将覆岩厚度变化区简化为覆岩1、覆岩2两个组合的弹性元件[9]。其整体力学属性由两个弹性元件串联、并联组合表示，模型如图 1所示。
由图 1可知，在覆岩厚度变化区，区域一、区域二、区域三的弹性模量均为覆岩1、覆岩2的弹性模量串联组成，其等效弹性模量E为
1E=H1H⋅ER1+H2H⋅ER2， (1) 式中：H1，H2分别为区域一覆岩1、覆岩2的厚度；ER1，ER2分别为覆岩1、覆岩2的弹性模量。
根据煤岩体应力应变关系可知：
σ=Eε。 (2) 本模型内区域一、区域二、区域三相互并联，故区域一、区域二、区域三的应变εa，εb，εc相等；同时串联部分应力相等，联立式（1），式（2）可得覆岩变化区下方煤层应力关系为
σaσc=E1E3=H′2⋅ER1+H′1⋅ER2H2⋅ER1+H1⋅ER2， (3) 式中：σa，σc为区域一、区域三覆岩厚度变化区下方的应力，H′1，H′2为区域三覆岩1、覆岩2的厚度。
为了定性分析覆岩厚度变化区下方的应力分布情况，假设区域一覆岩1和覆岩2的厚度H1和H2保持不变，将式（3）优化为ER2/ER1和H1'/H1的函数：
σaσc=[HH1 + H′1H1⋅(ER2ER1−1)]/[HH1 + (ER2ER1−1)]。 (4) 对于坚硬顶板赋存条件ER1＞ER2，区域一坚硬覆岩厚度H1大于区域三坚硬覆岩厚度H′1。由式（4）可知，区域一所受的应力σa大于区域三所受的应力σc，即覆岩变厚区的构造应力比覆岩变薄区大。
为研究ER2/ER1与H′1/H1变化对σa/σc的影响，控制式（4）中的自变量，将H/H1设为定值；同时ER2/ER1与H′1/H1的数值仅代表覆岩性质及厚度变化的一个趋势，不做实际情况下精确数值的讨论。图 2（a）为覆岩厚度比值一定的情况下，构造应力比值与覆岩弹性模量比值关系图，H1'/H1一定，σa/σc随ER2/ER1增加呈反比例关系，即两覆岩性质相差越大，构造应力变化越大。图 2（b）为覆岩性质一定的情况下，构造应力比值与覆岩厚度变化关系图，当ER2/ER1一定，σa/σc随H1'/H1增加呈线性递减关系，说明坚硬覆岩厚度变化越大，构造应力变化越大。
![]()
图 2 构造应力比值与覆岩性质/厚度变化关系图Figure 2. Relationship between tectonic stress ratio and roof properties or variation of roof thickness2. 覆岩厚度变化区煤层开采应力与能量分布特征
2.1 覆岩厚度变化区煤层开采数值模型建立
为研究坚硬覆岩厚度及性质变化对煤层应力分布特征的影响，本文以某矿煤层基本顶的厚度及性质变化为例，利用FLAC3D建立覆岩厚度变化区煤层开采数值计算模型。模型尺寸x×y×z为300 m×400 m ×150 m，覆岩变化区为y轴中部100 m范围，其它模型参数如图 3所示。初始应力状态下，假设煤岩均处于线弹性状态，模型本构设置为Elastic弹性模型[11]。
许家林等[12]基于岩层控制关键层理论指出，只有关键层上部的载荷可以简化为均布载荷。因此，本文在模型顶部设置一层20 m厚的关键层；模拟煤层埋深约700 m，在模型顶部施加15 MPa的均布载荷，重力加速度为10 m/s2；底部固定x，y，z方向的位移；x，y方向为固定边界，并在x，y方向施加水平渐变应力，x，y方向应力系数分别设为1.0和1.5。
模型材料参数以某矿实际的煤岩力学参数为基准，对材料参数进行简化处理[13]，如表 1所示。模拟方案主要为：方案一：模拟H1=60 m，H′1=30 m，ER2=10 GPa，ER1为15，20，25，30，35 GPa 5种情况下，覆岩性质变化对煤层初始应力分布特征的影响；方案二：模拟ER1=30 GPa，ER2=10 GPa，H1=60 m，H1'为10，20，30，40，50 m 5种情况下，覆岩厚度变化对煤层初始应力分布特征的影响。
表 1 模型选用参数Table 1. Model parameters序号 岩性 厚度/m 密度/(kg·m-3) 弹性模量/GPa 泊松比 1 细粒砂岩 20 2400 20 0.20 2 中粒砂岩 30* 2500 30* 0.15 砂质泥岩 30* 2200 10 0.25 3 砂质泥岩 10 2200 10 0.25 4 细粒砂岩 20 2400 20 0.20 5 煤层 6 1400 5 0.30 6 砂质泥岩 14 2200 10 0.25 7 细粒砂岩 20 2400 20 0.20 注：表中带“*”参数为方案一、方案二中的可变量。 2.2 覆岩厚度变化区煤层初始应力分布特征
图 4所示为不同方案下煤层内初始应力分布规律，由图 4（a）可知，由覆岩较薄区至覆岩较厚区，煤层内初始应力由均布状态逐渐减小，然后随着覆岩厚度的增加而增加，当处于覆岩较厚区时，初始应力又逐渐减小，最终恢复至均布状态；并且最大（最小）应力值随覆岩弹性模量比的增加而增加（减小）。由图 4（b）可知，初始应力分布规律与方案一相似，最大（最小）应力值随覆岩厚度变化率的增加而增加（减小）。
由于在模型顶部施加了15 MPa的均布载荷，因此，坚硬覆岩性质及其厚度变化对煤层初始应力的影响程度为煤层内的应力值减模型顶部均布载荷之后的比值，如图 5所示。方案一中H′1/H1不变，覆岩弹性模量ER2/ER1由10/35增加至10/15时，煤层内应力变化比值呈反比例函数由1.70降到1.21；方案二中ER2/ER1不变，覆岩厚度情况H′1/H1由1/6增加至5/6，煤层内应力变化比值呈线性关系由2.14递减至1.22。这与理论分析式（4）所得规律一致。
![]()
图 5 覆岩性质及厚度变化对应力变化率的影响Figure 5. Influences of properties and thickness of overburden on change of stress rate2.3 覆岩厚度变化区煤层采动应力分布特征
煤岩体所受应力在采动应力影响下会超过其峰值应力，煤岩体进入全应力应变曲线的峰后阶段，而应变软化模型能很好的反映煤岩体的峰后破坏阶段[14]。因此，将工作面回采过程中的煤岩体本构模型设置为应变软化模型，煤岩体应变软化参数的设置参考文献[14]，如表 2所示，其余模型参数见表 1。
表 2 煤岩体应变软化参数Table 2. Strain-softening parameters of coal and rock塑性应变 中粒砂岩 砂质砂岩 黏聚力/MPa 摩擦角/(°) 剪胀角/(°) 黏聚力/MPa 摩擦角/(°) 剪胀角/(°) 0 10.00 36 18 5.00 28 12 1×10-4 6.00 32 10 3.00 24 6 2×10-4 4.00 28 5 2.00 22 2 5×10-4 2.00 24 0 1.00 20 0 1 2.00 24 0 1.00 20 0 塑性应变 细粒砂岩 煤层 黏聚力/MPa 摩擦角/(°) 剪胀角/(°) 黏聚力/MPa 摩擦角/(°) 剪胀角/(°) 0 8.00 32 16 4.00 25 10 1×10-4 5.00 28 8 2.00 22 5 2×10-4 3.00 24 4 1.00 20 2 5×10-4 1.50 22 0 0.50 18 0 1 1.50 22 0 0.50 18 0 为研究覆岩厚度变化对工作面回采的影响，采用的开挖模型为：H1=H1'=60 m，覆岩厚度不变；H1= 2H′1=60 m，覆岩厚度发生改变。煤层回采方式包括沿覆岩由厚向薄推进和沿覆岩由薄向厚推进，如图 6所示。为消除边界效应对工作面回采的影响，在工作面两侧留50 m的边界煤柱。此外，工作面每开挖20 m，计算一次平衡。
工作面回采过程中，煤岩体内应力重新分布并在工作面超前区域形成应力集中区。为研究覆岩厚度变化对工作面回采超前支承压力的影响，在煤层中部，x=150 m，z=37 m处布置一条测线，将工作面沿覆岩由薄向厚回采、由厚向薄回采与沿覆岩厚度不变回采的超前支承压力进行对比分析。定义应力突变系数为工作面沿覆岩厚度变化推进的超前支承压力与沿覆岩厚度不变推进的超前支承压力之比。限于篇幅，本文选用超前工作面10，20，30，40，50 m处的支承压力进行对比分析，如图 7所示。
![]()
图 7 不同推进方式工作面超前支承压力突变规律Figure 7. Abrupt change of abutment pressure in advance of working faces with different mining modes由图 7（a）可以看出，当工作面沿覆岩由薄向厚推进时，应力突变系数呈先减小后升高再减小的趋势。工作面在覆岩较厚区，应力突变系数最大，平均为1.042；在覆岩较薄区，应力突变系数最小为0.947，同时超前距离越近，应力突变系数越接近1，表明距离回采位置越近，受超前支承压力影响越大，受覆岩厚度变化影响较小。
由图 7（b）可得，当工作面沿覆岩由厚向薄推进时，超前工作面的应力突变系数有先增加后降低再升高的趋势。工作面在覆岩较厚区，应力突变系数最大约为1.039；在覆岩较薄区，应力突变系数最小为0.943，同时超前距离越近，受超前支承压力影响越大，受覆岩厚度变化影响较小。
通过分析可知，应力突变系数最大的区域，均在覆岩较厚区至覆岩变化区范围，当工作面推进至此区域时，超前支承压力与突变的构造应力进行叠加，增加了冲击矿压发生的可能性。因此，工作面在坚硬覆岩厚度变化区推进时，在覆岩较厚区至覆岩变化区应力集中系数最大，当工作面推进至此区域时，因重点关注此区域的应力异常情况，必要时进行卸压处理。
2.4 覆岩厚度变化区煤层开采能量分布特征
谢和平等[15]指出，处于三向应力状态下的工程岩体常常面临卸载破坏的危险，并且煤岩体单元在卸载过程中释放的弹性能密度为
WE=σ21+σ22+σ23−2ν⋅σ1⋅σ2−2ν⋅σ2⋅σ3−2ν⋅σ1⋅σ32E， (5) 式中：σ1，σ2，σ3为最大、中间、最小主应力；E为弹性模量；ν为泊松比。
为研究覆岩厚度变化对工作面回采煤壁前方积聚弹性应变能演化规律的影响，由式（5）得出了工作面回采过程中模型内储存的弹性能密度。为了更直观地反映工作面回采过程中煤层内的能量聚积情况，将工作面回采过程中每一步的弹性能密度云图进行切片（切片取z=37 m）、组合处理，如图 8所示。
![]()
图 8 不同推进方式下煤层弹性能密度切片云图Figure 8. Section cloud diagram of elastic energy density in different mining modes工作面沿覆岩由薄向厚推进时，除了在工作面开挖附近出现了能量聚积区，还在覆岩较厚区出现第二个能量聚积区；随工作面继续向覆岩厚度变化区推进，能量聚集区范围增加，冲击危险性增加。工作面沿覆岩由厚向薄推进时，仅在工作面前方出现一个能量聚集区，该能量聚集区在覆岩较厚区至覆岩变化区范围较大，冲击危险性更高；随工作面继续推进，能量聚集区范围逐渐减小。
3. 覆岩厚度变化区煤层开采诱发冲击矿压机理
冲击矿压发生的“动静载叠加诱冲原理”表示，采掘空间周围煤岩体中的静载荷与矿震形成的动载荷叠加超过煤岩体发生冲击的最小载荷时，就容易诱发冲击矿压[16-17]，即
σs+σd⩾σbmin， (6) 式中：σs为煤岩体静载应力，σd为矿震动载，σbmin为冲击矿压的临界应力。
根据覆岩厚度变化区煤层开采过程中超前支承压力分布特征及动静载叠加诱冲原理，得出了不同回采方式下覆岩厚度变化区煤层开采诱发冲击矿压的机理，如图 9所示。
![]()
图 9 冲击矿压动静载叠加诱发机理示意图Figure 9. Schematic diagram of induced mechanism of dynamic and static load superposition under rock burst pressure当工作面沿覆岩由薄向厚推进时，超前支承压力由变薄区向变厚区传递，煤层中的静载应力相比覆岩厚度不变时有先减小后升高的趋势，在覆岩较厚区会形成应力的第二峰值区。当工作面前方覆岩破断诱发动载时，动载荷与静载荷相互叠加，可能会出现两个冲击矿压潜在发生区，即：工作面前方超前支承压力峰值区和应力第二峰值区与动载荷叠加诱冲区。其中第二峰值区与动载荷叠加诱冲区位于工作面前方，产生的冲击能量将主要向工作面两巷或者工作面临空面释放，冲击矿压影响范围增加。
当工作面沿覆岩由厚向薄推进时，超前支承压力由变厚区向变薄区传递，煤层中的静载应力相比覆岩厚度不变时先升高后减小，仅在超前支承压力影响范围与覆岩较厚区形成一个峰值应力；与动载荷叠加时，形成一个冲击矿压潜在发生区，但是该区域相对覆岩厚度不变时影响范围更大、冲击能量更高。
因此，工作面在覆岩较厚区至覆岩厚度变化区回采时，煤壁前方超前支承压力与突变的构造应力进行叠加，积聚的弹性能增加，更容易诱发冲击矿压。冲击矿压防治的主要工作是降低覆岩变化区第二峰值应力，将应力集中区向煤岩体深部转移。
4. 覆岩厚度变化区工程案例分析
4.1 工作面沿覆岩由薄向厚推进案例分析
（1）工程概况
伊泰某矿103工作面为矿井一采区的第2个回采工作面，东南侧为实体煤；西北侧为101采空区，两者留有两个30 m宽的双煤柱；东北邻南翼辅运大巷；西南方向开切眼为实体煤柱。工作面设计推进长度2480 m，宽度210 m，主采3-1煤层，煤层埋深平均706.3 m，煤层厚度约6.7 m，倾角1°~3°，平均倾角2°，为近水平煤层。
统计103工作面附近的钻孔，并绘制出覆岩厚度变化等值线图，发现在3-1煤层上方近200 m范围主要存在一层较厚的坚硬顶板，该覆岩位于煤层上方20 m左右，层厚在60~110 m；经计算可知，该岩层为工作面覆岩结构的关键层。随着工作面的推进，该覆岩由薄变厚，如图 10所示。
![]()
图 10 伊泰某矿103工作面覆岩厚度等值线及微震平面定位图Figure 10. Contours of roof thickness and distribution map of microseismic plane location of working face 103 in Yitai Mine（2）案例分析
103工作面自2018年3月开始回采以来，大能量事件频发，103辅运顺槽出现了不同程度的动力显现，造成巷道多次破坏和设备损坏，破坏以巷道底板的瞬间开裂、底鼓为主。通过分析微震监测数据，可判断煤岩体的应力分布状态及覆岩运移规律[18]。统计分析103工作面回采期间的微震数据与坚硬覆岩厚度变化的关系，以103临空顺槽做剖面，如图 11所示。
![]()
图 11 沿覆岩由薄向厚推进覆岩厚度变化与微震关系图Figure 11. Relationship between variation of roof thickness and microseismicity when working face advancing from thin to thick along roof103工作面回采期间，位于工作面前方的微震事件频次占比87.7%，微震能量占比91.0%，表明103工作面回采期间微震事件与工作面前方煤岩体应力分布状态关系较大。同时，微震频次、能量的分布情况与覆岩厚度变化存在一定的对应关系，工作面沿覆岩由薄向厚推进时，工作面推进位置前方微震能量、频次均处于较大的水平，工作面冲击危险性较高，此时对应于冲击矿压的潜在发生区Ⅰ，主要由工作面采动引起的超前支承压力造成；在坚硬覆岩较厚区域，微震频次及＜103 J的微震总能量存在极大值，此时对应于冲击矿压的潜在发生区Ⅱ，主要受超前支承压力与突变的构造应力叠加影响。
4.2 工作面沿覆岩由厚向薄推进案例分析
（1）工程概况
中煤某矿3102工作面为矿井第2个回采工作面，主采3-1煤层，工作面走向长5540 m，倾向宽300 m，东侧为实体煤，西侧与3101采空区相邻，南侧为井田边界，北侧为3-1煤辅助回风巷，区段煤柱宽度35 m。该工作面煤层埋深690~700 m，煤层厚度4.35~5.47 m，倾角1°~4°，平均倾角2°，为近水平煤层。
统计3102工作面附近的钻孔，并绘制出覆岩厚度变化等值线图，发现在3-1煤层上方近200 m范围主要存在一层厚度变化较大的坚硬顶板，该覆岩位于煤层上方40 m左右，层厚在40~60 m。随着工作面的推进，该覆岩由厚变薄，如图 12所示。
![]()
图 12 中煤某矿3102工作面覆岩厚度等值线及微震平面定位图Figure 12. Contours of roof thickness and distribution map of microseismic plane location of working face3102 in China Coal Mine（2）案例分析
3102工作面自2017年8月开始回采，大能量事件频发，3102回风巷出现了不同程度的帮鼓、顶板下沉、底鼓、单体损坏等冲击显现情形。统计分析3102工作面回采期间所有的微震数据与坚硬厚度变化的关系，以3102临空巷做剖面，见图 13。
![]()
图 13 沿覆岩由厚向薄推进覆岩厚度变化与微震关系图Figure 13. Relationship between variation of roof thickness and microseismicity when working face advancing from thick to thin along roof3102工作面回采期间，微震事件大多位于工作面前方，其中微震事件频次占比62.3%，微震能量占比87.1%。工作面沿覆岩由厚向薄推进时，在坚硬覆岩较厚区至覆岩厚度变化区，微震总频次分布较多，极大值分布在坚硬覆岩厚度较大的区域；并且小于103 J的微震总能量与微震频次具有相似的分布规律。表明在覆岩较厚区至覆岩厚度变化区的冲击危险性较高，此时对应于工作面沿覆岩由厚向薄推进时的冲击矿压潜在发生区，主要受超前支承压力与突变的构造应力叠加影响。
以上分析可知，工作面沿覆岩厚度变化区回采期间，微震事件大多分布在工作面前方，与煤岩体应力分布状态关系较大；同时，微震频次及能量小于103 J的微震总能量与坚硬覆岩厚度变化相关性较好。工作面受超前支承压力与突变的构造应力叠加影响，静载应力较大，煤岩体产生较多的微裂隙，导致坚硬覆岩厚度变化区至覆岩较厚区微震事件频发。这与前文研究成果相符。
5. 结论
（1）基于弹性力学理论分析了坚硬覆岩厚度变化区的力学机制，结果表明，覆岩变厚区的构造应力比覆岩变薄区大，覆岩厚度变化越大或覆岩之间弹性模量相差越大，覆岩厚度变化区构造应力变化越大。
（2）采用数值模拟方法研究了坚硬覆岩厚度及物理力学性质变化对煤层构造应力分布特征的影响，结果表明，自覆岩较薄区到覆岩较厚区，构造应力均有先减小后增大再减小的趋势，覆岩厚度变化越大或覆岩物理力学性质差异越大，应力变化比值越大。
（3）工作面在覆岩厚度变化区开采时，受超前支承压力与突变的构造应力叠加影响，覆岩厚度变化区至覆岩较厚区应力集中程度较大，该区域积聚的弹性能主要向工作面前方巷道释放，冲击危险性更大；冲击矿压防治思路是降低覆岩变化形成的第二应力峰值区。
（4）现场案例表明，工作面沿覆岩由薄向厚推进或沿覆岩由厚向薄推进时，在坚硬覆岩厚度变化区及变化区向较厚区过渡时微震能量、频次较高，冲击矿压危险上升，与理论与模拟分析较为吻合。
-
![]()
图 4 对比高精度复变函数解
Figure 4. Comparison with high-precision solution for complex variable function
-
[1] 曾开华, 李学军, 鹿守山, 等. 两向不等压圆形隧道塑性统一解及其应用[J]. 岩土工程学报, 2022, 44(10): 1772-1779. doi: 10.11779/CJGE202210002 ZENG Kaihua, LI Xuejun, LU Shoushan, et al. Unified plastic solutions to a circular tunnel under two-way unequal pressures and their applications[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(10): 1772-1779. (in Chinese) doi: 10.11779/CJGE202210002
[2] HU Z P, AN X X, LI F T, et al. The shape characteristics of circular tunnel surrounding rock plastic zone in the complex stress field[J]. Arabian Journal of Geosciences, 2022, 15(2): 150. doi: 10.1007/s12517-021-08567-1
[3] 张常光, 李宗辉, 关港辉, 等. 采用总荷载不变法的非静水压隧道摄动拓展解[J]. 哈尔滨工业大学学报, 2022, 54(6): 71-82. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX202306009.htm ZHANG Changguang, LI Zonghui, GUAN Ganghui, et al. Extended perturbation solutions of a non-hydrostatic pressure tunnel based on total load invariant method[J]. Journal of Harbin Institute of Technology, 2022, 54(6): 71-82. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX202306009.htm
[4] 魏悦广. 两向不等压作用下圆形巷道弹塑性分析摄动解[J]. 岩土工程学报, 1990, 12(4): 11-20. http://www.cgejournal.com/cn/article/id/9385 WEI Yueguang. Perturbation solutions for elasto-piastic analysis of circular tunnel under unequal compression in two directions[J]. Chinese Journal of Geotechnical Engineering, 1990, 12(4): 11-20. (in Chinese) http://www.cgejournal.com/cn/article/id/9385
[5] SHENG Y M, ZOU J F, DONG Y P, et al. Novel perturbation solutions for deep-buried non-circular tunnels under biaxial in situ stress field based on Mohr-Coulomb criterion[J]. Applied Mathematical Modelling, 2022, 110: 408-440. doi: 10.1016/j.apm.2022.06.006
[6] 张常光, 李宗辉, 关港辉, 等. 基于统一强度理论的非静水压圆形隧道塑性区半径的脆塑性摄动解[J]. 力学学报, 2022, 54(7): 1994-2007. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202207021.htm ZHANG Changguang, LI Zonghui, GUAN Ganghui, et al. Brittle plastic perturbation solutions of plastic zone radius for circular tunnels under non-hydrostatic pressures based on the unified strength theory[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(7): 1994-2007. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202207021.htm
[7] 吕爱钟, 张晓莉, 王少杰. 两向不等压圆形隧洞弹塑性解析分析[J]. 岩石力学与工程学报, 2018, 37(1): 14-22. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201801002.htm LÜ Aizhong, ZHANG Xiaoli, WANG Shaojie. Analytic method for elasto-plastic analysis of circular tunnels under non-axisymmetric stresses[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(1): 14-22. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201801002.htm
[8] LÜ Z T, XIA C C, LIU W P. Analytical solution of frost heaving force and stress distribution in cold region tunnels under non-axisymmetric stress and transversely isotropic frost heave of surrounding rock[J]. Cold Regions Science and Technology, 2020, 178: 103117.
[9] 俞茂宏, 武霞霞, 史俊, 等. 确定土体破坏准则的一个新方法[J]. 西安交通大学学报, 2020, 54(8): 1-10. https://www.cnki.com.cn/Article/CJFDTOTAL-XAJT202008002.htm YU Maohong, WU Xiaxia, SHI Jun, et al. A new strategy for determining failure criteria of soil[J]. Journal of Xi'an Jiaotong University, 2020, 54(8): 1-10. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAJT202008002.htm
[10] 经纬. 圆形巷道围岩变形分区的理论与试验研究[D]. 淮南: 安徽理工大学, 2017. JING Wei. Theoretical and Experimental Research on Deformation Partition of Circular Roadway[D]. Huainan: Anhui University of Science and Technology, 2017. (in Chinese)
-
期刊类型引用(2)
1. 周斌，张弘，林春秀，付冬平. 降雨条件下基坑坡度和平台宽度对稳定性的影响. 广东土木与建筑. 2025(02): 28-31 . 
百度学术
2. 樊鸿志，王光进，蓝蓉，刘明生. 露天矿山岩质边坡软弱夹层赋存状态影响边坡稳定性规律研究. 重庆大学学报. 2024(04): 22-33 . 百度学术
其他类型引用(2)
-
其他相关附件
下载:
计量
- 文章访问数: 394
- HTML全文浏览量: 36
- PDF下载量: 121
- 被引次数: 4
