Multiscale finite element method–triple grid model for simulation of groundwater flows
-
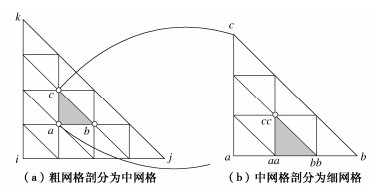
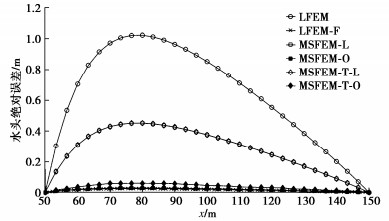
摘要: 传统有限元法在模拟地下水流问题时常需要精细剖分描述含水介质的非均质性以保证精度，导致计算消耗过高。传统多尺度有限元法（MSFEM）能缓解这一问题，但在处理高计算量问题时仍需较高消耗来构造基函数。提出了一种用于模拟地下水流的三重尺度有限元模型（MSFEM-T），该方法在MSFEM的粗、细两种尺度网格之间引入中网格，从而可以在粗网格单元内基于中、细两种尺度网格应用MSFEM本身替代有限元法构造基函数，能够显著降低基函数的构造消耗以提高整体计算效率。此外，MSFEM-T还提出了一种基于粗、中、细三重网格的超样本技术，可以进一步提升其计算精度。数值算例结果显示MSFEM-T的精度与MSFEM和精细剖分有限元法（LFEM-F）的精度相近，且计算效率更高。Abstract: The traditional finite element method often requires fine element grids to describle the heterogeneity of medium to ensure the accuracy for numerical modeling of groundwater, which leads to a large amount of calculation consumption. The multiscale finite element method can alleviate this problem, but it still needs a high cost to formulate the basis function when dealing with high computational complexity. A multiscale finite element method-triple grid model (MSFEM-T) is proposed for the simulation of groundwater flows. The MSFEM-T introduces an intermediate grid between the coarse grid and the fine grid, so that the basis function in the coarse grid can be established using the MSFEM instead of the FEM based on the intermediate and fine grids, therefore reducing the construction consumption of the basis function and improving the overall calculation efficiency. Moreover, the MSFEM-T uses an over-sampling method based on the coarse, intermediate and fine grids, which can further improve its calculation accuracy. The results show that the accuracy of the MSFEM-T is similar to that of the MSFEM and the finite element method of fine elements (LFEM-F), but the computational efficiency is much higher.
-
0. 引言
中国大规模和超大深度地下空间、综合交通枢纽和城市地下综合体建设越来越多[1],这些地下工程建设中常面临地下水丰富（“水”）、地层软弱（“软”）和开挖岩土体变形难以预测（“变形难以预测”）的3大难题。常规地层加固处理技术有时也很难彻底预防水害和变形失控难题,由此造成生命财产损失的事故时有发生。人工地层冻结法（简称冻结法）可为解决地下工程建设中“水、软、变形难以预测”3大难题提供一种灵活可靠的绿色技术方案。
冻结法工程应用已有近160 a的历史。中国自1955年首次采用冻结法建设开滦煤矿林西矿风井至今,已有1000多个矿山竖井和斜井采用了冻结法施工,并在220多个地铁和市政工程建设中得到应用,中国地层冻结技术已处于国际领先地位[2-3]。然而,冻结法除了有其他工法应用的一定风险外,还因其主要材料——冻土的强度必须在地下工程施工中得到维持,而维系维系冻土强度的冰具有特殊性质,这就增加了冻结法比其他工法更多的变数。此外,人工冻土多场耦合作用机制认识尚不全面,工程勘察和试验精准度、设计与施工系统性与智能化水平尚有待提升,冻结法工程建设的不确定性与风险仍始终存在。
本文将基于冻土中水的相变过程及其动态平衡、冻结土体水分迁移、冻土内部联结作用的基本原理,分析人工冻土特点及冻结法工程风险的物理本质,并进一步从工程设计条件输入、建设质量控制、运行维护3方面,阐述冻结法工程风险预控方法与技术,为其在今后地下工程建设中的推广应用提供指引。
1. 人工冻土特点与冻结法工程风险
1.1 冻土形成及其水的相变与动态平衡
人工冻土形成过程的典型温度-时间特征曲线如图1所示[4]。在冷却段和过冷段都仅是地层温度下降,并无析冰现象。当过冷段土体中某点过冷水遇到凝结核后,便在凝结核上富集、扩散而形成冰晶,冰晶接触过冷水分子后便随即与之结合,并不断增大,从而开始析冰。析冰过程释放潜热使土体温度短时间内急剧上升,产生温度跃升,直至达到冻结温度并于稳定,土中孔隙水持续冻结成冰,土体进入稳定冻结段,人工冻土逐渐形成。随着冷量持续输入地层,土体进入冻结降温段,冻土强度不断提高,冻结范围不断扩大,直至冻土结构形成。
对特定土体而言,其冻结过冷温度和冻结温度一般随土体矿物成分、含水率、含盐量及其类型而变化。此外,土体中水可分为强结合水、弱结合水和自由水,且各自冰点温度不同。对正冻土和已冻土而言,未冻水总是存在,且其含量主要取决于冻结土体负温及其所受应力水平。在外荷载作用下,土体高应力区的冰因挤压和错动而融化成水,并向低应力区转移。同时,低应力区未冻水也不断冻结成冰,形成了土体中冰和未冻水的相互转化。若低应力区未冻水冻结成冰速度大于或等于高应力区冰融化成未冻水速度,则冻土强度趋于稳定；反之,冻土则处于不稳定状态。
人工冻土形成过程中,水是核心,负温是关键,两者相互作用并决定了冻土及冻土结构的形成过程。冻土中水的相变过程以及未冻水的数量、成分与性质均随冻土负温和冻土应力水平而变化,并处于动态平衡,这既决定了冻土结构的强度与稳定性,也决定了冻结法工程应用的经济性及其风险程度。
1.2 冻结土体水分迁移与冻胀融沉
土体中水冻结冰,其原位体积增大约9%。当增加的体积足以造成土颗粒相对位移时,就形成了地层冻胀。此时,若冻胀受到建（构）筑物限制,则对建（构）筑物产生相应法向和切向冻胀力。反之,温度升高,冻土中冰融化成水,其体积将原位减小约8.3%。
冻土形成过程中往往伴随着水分向冻结面转移的现象。同时,当温度、含水率、渗透压力、矿物颗粒表面能等外部条件变化时,冻土中水的相态平衡发生变化,并伴随水分迁移。水分迁移是冻土物理力学过程的基本规律。水分迁移量的大小直接决定了冻结地层的冻胀融沉特性,因为冻结土体冻胀由土中原有水分冻结和迁移水冻结两部分组成,前者称为原位冻胀,后者称为迁移水冻胀或分凝冻胀。冻结地层原位冻胀很难消除,而迁移水冻胀则容易使地层冻胀量急剧增加。因此,应尽可能减少迁移水冻胀。对冻土工程而言,冻胀和融沉具有正相关联性,抑制了地层土体冻胀,也就相应地减少了地层土体的融沉。
冻结土体水份迁移及其冻胀性与土体性质、水的补给条件、冻结温度、冻结速度等因素有关。如果对冻胀融沉机理以及由此引起冻土与工程建（构）筑物相互作用规律的认识不足,再加上冻胀融沉控制措施使用不当,都将会引起地层冻结过程中产生不均匀的冻胀融沉变形,破坏邻近建筑物与设施,造成经济损失,甚至导致冻结工程失败[5]。因此,冻结法应用过程中始终面临着地层冻胀和融沉风险。
1.3 冻土内部联结作用及其蠕变和应力松弛
冻土流变性主要表现为外荷载作用下冻土变形随时间增长而增大（蠕变）和强度随时间增长而弱化（应力松弛）,其实质是冻土中土颗粒（骨架）-可变胶结体（冰）-不稳定活化液体（未冻水）-活动催化体（气体、冻土组构）之间相互转化与作用过程[2-3, 6]。
冻土由土颗粒、冰、未冻水和空气四相材料组成,其内部联结作用主要有土颗粒间静电引力作用、冰的胶结作用以及冻土组构（团聚体、孔隙等）构造联结作用等。在外荷载作用下,冻土中一些颗粒间接触受挤压而引起应力集中,并由此产生温升而导致其间胶结冰部分融化、塑性流动和冰晶重新定向,部分融化水将补充冻土中的未冻水,从而打破了原有的冰-未冻水-气体之间的平衡,融化水和未冻水在应力梯度和温度梯度的作用下,借助气体的边缘效应,由高应力区和高温区向低应力和低温区迁移,并在低应力和低温区重新冻结,使冰-未冻水-气体达到新的平衡。当冻土结构应力水平较小时,上述动态变化过程表现为冻土内部“结构强化”占优势,冻土呈衰减型蠕变。然而,一旦外应力水平或者荷载作用时间超过某一界限值,使冻土内部“结构弱化”处于优势,将产生不可逆的非衰减型蠕变,直至冻土结构变形或失稳破坏,且应力水平越高,冻土达到破坏变形所需时间越短。
与此同时,冻土受荷载作用后,其强度随时间增长迅速衰减,一般需经过6～10 h后才能进入缓慢衰减阶段,达到冻土长期强度极限值,而该值多数情况下仅为其瞬时强度值的1/3～1/2,且在仅荷载作用初期的10 h内,冻土强度即可能从瞬时强度降低约1/5～1/4。冻土蠕变和应力松弛的流变性特征以及可能由此导致的冻结工程风险,应引起工程界高度重视。
2. 冻结法风险预控
冻结法的本质是通过人工降温技术把地层温度降到冰点以下,使地层中的水冻结成冰并胶结土体颗粒,形成具有高强度和大弹性模量的冻土结构（密闭冻结壁或连续冻土墙）,以抵抗水土压力,隔绝地下水与待开挖地下空间的水力联系,从而确保地下空间岩土体开挖和永久支护的施工作业安全[2-3]。水是冻结法的核心,负温是关键控制条件,二者相互作用并决定着人工冻土形成、扩展以及冻土结构的安全稳定性。
基于前述人工冻土特点与冻结法工程风险分析,结合图2所示的冻结法施工的主要流程及其关键点,可将冻结法应用的工程风险概括为3大方面：①冻土结构能否形成且满足施工全过程的安全稳定性要求；②地层土体冻胀及其工后融沉变形能否可控且满足施工全过程中周围建（构）筑物和设施的安全与环境要求；③地层冻结法应用能否具有经济性与安全性的统一。为了实现对冻结法工程应用风险的预防和控制,需从设计条件输入、建设质量控制、运行维护3方面入手。
![]()
图 2 冻结法施工主要流程及其关键点Figure 2. Typical construction processes and key points of artificial ground freezing2.1 严格设计输入数据可靠关
（1）水文地质勘察及其可靠性
采用人工制冷方法将地层中的水冻结成冰是冻结法的核心,水文地质条件决定了冻结设计的各个参数,也是冻结法成功应用的关键。因此,冻结地层的含水率、含盐量以及水的流速、流向、水温、地下水位变化等区域水文地质条件至关重要。
首先,应掌握冻结地层土体含水率,这决定了冻土含冰量多少。冻结土体含水率一般不宜低于5.0%,但含水率增加也将直接影响冻土强度特性,如黏土层含水率超过其液限后,含水率增加会降低冻土强度,而砂土层达到饱和含水率后,含水率增加会降低其冻结强度,若比饱和含水率大很多时,冻土强度会降低至与冰的强度差不多,甚至仅为冰的强度。
其次,应查明地下含水层赋存情况,如流速、流向、水温以及冻结范围的内外水力联系（通道）等[7-8]。水流速度大于5 m/d或水位变化大于等于2 m/d都将影响冻结效果,推迟冻土结构交圈时间,严重时冻土不能交圈[9]。当冻结地层流水速度较大或水位变化明显时,应对地层预先采取排水或封堵水措施,待水流速度降低后再进行地层冻结。否则,除难以形成稳定可靠的冻土结构外,还容易产生“天窗”漏水酿成冻结失败的重大事故风险。
再次,需明确地下水的含盐类型及其含量,这直接决定了土体冻结温度,并影响冻土强度。冻结地层地下水的含盐量一般不宜大于3%。含盐量越高,土体冻结温度越低,所需制冷量越多,土体冻结与冻土结构交圈（封闭）所需时间越长,冻结成本也越高。此时,采用若继续采用冻结法施工,就要降低冷媒温度,开展冻土物理力学试验,优化设计参数。
最后,还应了解地层冻结施工范围以及与其直接接触地层下面是否存在承压水以及承压水的压力、承压水与外部水源的水力联系等,应取承压水压力和计算水土压力二者之大值作为冻土结构设计荷载。此外,还应掌握冻结地层的隔水层位置、厚度及其物理力学性质等,以合理确定冻土结构设计的边界条件。
（2）工程地质勘察与地层信息的可靠性
首先,对冻结范围内地层,尤其要对冻结管可能布置范围内地层,进行详细的地质勘察。钻孔深度应超过冻结范围并穿过可能作为隔水或围护结构的地层。应全面掌握关键地层信息,需特别关注冻结地层范围内是否有诸如孤石、杂物等影响冻结孔布置与钻进的物体?是否有过施工扰动或采用土体固化剂进行加固处理的历史?是否有气体分布或气体聚积而影响冻土物理力学性质甚至加速冻土破坏进程的情形?
其次,天然地层性质一定程度上决定了人工冻土的工程性质。因此,需全面掌握冻结地层范围内土体的类型与分布、矿物成分及其颗粒级配等,这些都决定了冻结土体未冻水含量、土冻结水分迁移及其冻胀融沉特性、冻土内部联结作用及其流变性特征等。
此外,需准确分析施工范围及其关联地层是否有其他地下热源的影响,掌握冻结地层初始温度以及土体的导热系数、比热、潜热、热容量等热物理参数,这些都直接决定了冻结效果与冻结交圈时间,也将影响冻土结构稳定性和工程冻结费用。工程设计时,一般应取最不利条件作为参考。
最后,应对工程地质勘察过程中的所有钻孔进行完全充填封闭,防止冻土开挖时涌水。同时,可将所有水文地质和工程勘探成果描绘在同一钻孔柱状图上,并逐一表述清楚,以便冻结设计时将所有可能不利于冻结设计和施工的因素考虑周全。
（3）选择最恰当的冻土结构型式及其计算模型
冻土结构选型与设计至关重要。首先,应根据地下工程建设情况,明确拟建冻土结构功能需求,分析与其关联结构（已有地下结构体、隔水地层、其他工法即将形成的结构）之间联系的紧密程度与可靠性,按表1确定冻土结构类别、冻土帷幕平均温度及其对应安全系数[2],确保地下工程施工安全,避免周围环境与建（构）筑物受到冻结工程施工的影响。
表 1 冻土结构类别及其设计要求Table 1. Styles of frozen soil walls and their design requirements结构类别 冻土帷幕功能要求 冻土帷幕平均温度/℃ 安全系数 抗压 抗折 抗剪 Ⅰ 仅止水,无承载要求 ≤-8.0 — — — Ⅱ 仅承载,无止水要求 ≤-10.0 1.8 2.7 1.8 Ⅲ 既要承载,又要止水 ≤-10.0 2.0 3.0 2.0 在此基础上,需进一步根据冻土结构类别与功能要求,全面分析影响冻土强度及冻土结构稳定的因素,确定地层冻结施工全过程中冻土结构的荷载特征与受力状态,从而选择能正确反映其承载过程物理本质的设计计算模型,这将决定冻结工程的成败。
冻土结构设计主要包括热工计算和静力设计两部分。热工计算是确定冻土结构温度场,以形成冻结方案。静力设计是基于弹性、弹塑性、塑性以及大变形弹塑性冻土结构设计理论[10-13],确定冻土结构尺寸,并满足其在极限状态下的强度和变形要求。
（4）冻土强度指标与冻土结构受力状态的符合性
首先,冻土强度指标参数选取,特别是-10℃左右的冻土强度参数,对冻结法设计最为重要。因此,应根据待建冻土结构埋深与受力情况,合理确定冻土强度试验的温度、荷载和时间等参数并开展相应试验,确定包括冻土单轴（三轴）抗压、抗拉和抗剪强度以及变形模量、泊松比等参数,并掌握这些参数随温度、含水率、荷载和时间变化规律。显然,试验方法直接决定了冻土强度参数取值的准确性和合理性[14]。冻土强度指标参数选用时,一定要分析试验方法与冻土结构受力状态、计算模型、施工过程的一致性。如冻土瞬时强度试验多采用加载方式,而冻结法施工中,冻土结构受力主要是卸载过程,由加载方式得到的试验参数显然不符合冻土结构实际受力过程与状态。
其次,城市地下工程及矿山凿井工程的冻结法施工中,冻土和结构物间往往会形成较大接触面积。如盾构机在冻土加固区推进时,需克服冻土接触面极限冻结强度。因此,分析冻土与结构物接触面冻结强度影响因素,建立合理的冻土接触面本构模型,准确预估接触面冻结强度,从而保障冻结工程顺利施工[15-16]。
此外,随着地层冻结法在深厚表土层凿井工程及城市复杂地下工程中推广应用,越来越多地涉及到深部冻土力学问题[17-18]。冻结土层埋深增加,将导致冻土结构所受侧向土压力的增大。由于深层土体原位取样后,应力释放将导致土体体积和重度发生变化,这种变化在冻土强度试验时必须考虑。为此,冻结土体试验前,应根据试样所在地层侧向土压力大小,先对试样进行排气不排水固结,达到固结点后,将试样冻结到试验温度并恒温至少24 h,再进行加载或卸载试验。反之,则冻土强度指标与实际情况相差甚远。同时,当冻结深度范围存在不同性质土层时,应对不同层位土体强度和变形试验结果分别进行校核,并关注高围压作用下冻土的蠕变特征及其长期强度。正确认识高围压固结和有压冻结条件下深部冻土的流变性特征,将是深土冻结设计的关键与前提。
最后还需要说明,重大地下工程设计前,有针对性地开展冻结工程的物理模型试验或数值模拟试验,将对提升冻结工程本质安全水平具有重要意义。
2.2 严把冻结系统各关键环节质量关
冻结系统主要包括冻结孔施工、冻结管安装和密封、供液和回液管路的安装与密封、盐水系统等。冻结系统各关键环节质量是冻结法成功的重要保证。
（1）冻结孔（管）施工与设计符合性及质量控制
首先,冻结孔（管）布置应与冻土结构设计一致,孔位、开孔间距、成孔间距、孔深及其偏斜等施工参数应与冻土的交圈时间、扩展厚度、平均温度等冻土结构形成参数的要求相一致。否则,易导致冻土结构局部强度低,甚至达不到设计要求。以基坑工程冻结帷幕为例[2],当冻结孔单排布置时,其成孔间距应满足表2规定的要求,且不宜大于冻结帷幕的设计厚度,相应的冻结孔偏斜值也不应大于表2的规定值。当采用多排冻结孔布置时,内部冻结孔的间距可适当增大。
表 2 单排冻结孔间距与最大允许偏斜值Table 2. Spacings and maximum biases of single-row freezing holes冻结孔深度/m 成孔间距/mm 最大偏斜/mm ≤20 ≤1300 150 20~40 ≤1600 225 40~60 ≤1800 300 其次,应选用最合适的钻孔机具和钻孔测斜与纠偏设备,并确定合理的冻结孔施工顺序,做好承压含水层的孔口防喷涌与漏浆处理措施。对影响冻结孔布置的地方,要适当移位或适当增加冻结管。冻结孔深度必须达到设计要求,从而保证冻结管底部能够安放到设计深度处,避免出现没有完全冻结的开窗情况。
最后,做好冻结孔（管）施工质量的检验与验收,主要包括孔位、孔深、钻孔偏斜、冻结管规格与长度的检验与验收以及冻结管耐压试验等。
（2）冻结制冷、冷媒和冷却水3大系统安全可靠
首先,应根据地下工程建设实际,合理确定地层冻结的制冷方法。地层冻结一般有直接制冷法（消耗制冷剂系统）和间接制冷法（循环冷媒系统）两种[2]。直接制冷法的地层冻结温度一般较低,如液氮可达-190℃,冻土结构可在几小时内迅速形成,冻结速度快、操作方便、冻土结构承载力高,主要适合于工程事故处理或重要建（筑）物下施工。间接制冷法则是较为传统和普遍使用的方法,主要包括冷冻站和地层冻结系统两部分,二者之间通过蒸发器组合在一起。一般采用液氨或氟里昂作为制冷剂,氯化钙水溶液作为循环盐水（冷媒剂）,并可根据冻土结构平均温度设计要求,按表3确定循环盐水的最低温度。
表 3 循环盐水的最低温度Table 3. Minimum temperature of circulating saline water冻土结构平均温度/℃ 循环盐水最低温度/℃ -8.0~-10.0 -28.0~-30.0 ≤-10.0 ≤-30.0 其次,冷冻站应符合防火规定,通风良好,避免雨淋和阳光直射。冷冻站的计算制冷能力,应满足冻结工程设计需求。冷冻机型号及其数量,应根据计算的制冷能力以及冷媒循环系统的冷凝温度、蒸发温度等综合确定,冷冻机组的总制冷能力不应小于冷冻站的计算制冷能力。同时,需根据建设工程的重要程度,确定冷冻机组、盐水泵和冷却水泵的备用数量。
再次,盐水管路应符合设计要求且安全可靠。供液管、盐水干管和集配液管的管径,应按盐水流速计算确定,盐水在冻结器环形空间内流速宜取0.1～0.3 m/s,在供液管宜取0.6～1.5 m/s,在干管及配、集液管宜取1.5～2.0 m/s。盐水干管及配、集液管可选用普通低碳钢无缝钢管或焊接钢管,管壁厚度不宜小于4.5 mm。供液管宜选用钢管或聚乙烯增强塑料管,供液管接头应有足够强度。所有管路应可靠连接。
最后,应做好冻结系统试运转,并确保冻结制冷、冷媒和冷却水3大系统在积极冻结期、维持冻结期和解冻期均具有足够的安全可靠性。
2.3 严守冻结和开挖全过程安全运行维护关
（1）信息化智能化的全过程检测监测与预警
采用新型感知技术,自动、实时、远程获取准确可靠的监测数据,对冻土形成、发展和冻结体交圈（封闭）全过程进行信息化、智能化的检测监测与预警,也是冻结法工程风险防控的关键之一。
在积极冻结阶段,应重点关注冻结站内的盐水液面变化,如液面有变化一定要进行检测。同时,需对盐水温度和盐水去、回路温差,冻土帷幕温度以及冻土体和地表位移进行监测。此外,还要通过水文观测孔,对水位、温度、水压等进行实时监测,并结合图乘法[19]、地质雷达探测法[20]、超声波透射法[21-22]对冻土结构形成情况及其强度特性进行检测监测与判断。
冻土开挖和支护结构施工阶段,应监测冻土结构变形,其大小标志着冻土结构稳定性程度。应实时观测开挖地层水文变化,同时对支撑结构轴力与衬砌温度、支护结构受力和位移、混凝土水化热等进行监测。
在冻结解冻过程,应继续对盐水液面,盐水去、回路温差,冻土温度、衬砌温度以及地层工后变形、永久结构稳定性进行必要的跟踪监测。
最后,应基于冻结工程建设全过程检测监测结果,对冻结工程进行反演分析和可视化管理,形成冻结工程可视化平台,加快冻结工程智慧工地建设,确保影响冻结法施工全过程的安全质量环节的关键要素始终可控、能控、在控,不断提升冻结工程建设水平。
（2）快速应急抢险抢修预案与工程技术
冻结工程的快速应急抢险抢修预案及其技术,是实现冻结工程安全及其风险防控的重要保障。
首先,应运用科学管理方法、先进技术手段、有效制度流程,建立安全长效机制,使冻结工程的全体管理者树立人本安全观,让全体工程施工人员掌握规避风险、预防事故的专业知识和技能。
其次,对冻结工程中的重要风险,应做好应急抢险抢修预案。如冻结工程过程中,凡涉及到人身和重大财产安全的,都必须有应急能力储备（如备用液氮槽车等抢险设备）。再如,应采用双回路供电,防止冷冻机停机。此外,施工作业面应准备一定量的水泥、水玻璃等抢险材料,一旦开挖掘砌施工中发生涌砂漏水险情,应立即组织人员进行封堵。必要时,采用液氮加强冻结,从而迅速有效维护整个冻土结构稳定。
最后,应做好防止地层冻胀和融沉的技术预案。可采用压力释放孔、注浆充填、工作面释放水、强制解冻融沉注浆等措施,有效预防和解决地层冻胀融沉风险[23]。必要时,可设置预留注浆孔,在冻结地层融化过程进行跟踪注浆,控制地层融沉量。
3. 结语
国内外工程实践表明,冻结法仍是当前解决地下工程建设面临“水、软、变形难以预测”3大难题的一种灵活可靠绿色技术。水冻结成冰,是冻结法的核心,而水的入侵则是冻结法的最主要风险来源。总体上看,充分认识人工冻土特点及冻结法工程风险的物理本质,针对冻结法施工全流程及其关键节点,严格设计输入数据可靠关、严把冻结系统各关键环节质量关、严守冻结和开挖全过程安全运行维护关,将是冻结法成功应用与风险防控的关键。
基于传统与新型感知技术,综合应用原位测试、室内试验、数值模拟和大数据深度学习方法,形成冻结工程人工智能系统与平台,准确获取冻结工程范围内地质体的物理力学性质,揭示冻土中未冻水和冰的动平衡状态、水分迁移以及冻土流变性特征随温度和荷载变化物理本质,基于时空观阐明冻土结构与周围地质体相互作用的协调机制以及冻结工程建设与环境效应作用规律,将是冻结法工程风险防控的发展方向。
-
![]()
图 2 MSFEM粗网格剖分方式
Figure 2. Sketch map of standard subdivision of coarse element of MSFEM
![]()
图 3 MSFEM-T粗网格剖分方式
Figure 3. Sketch map of standard subdivision of coarse element of MSFEM-T
![]()
图 4 y=100 m处各数值方法水头绝对误差图
Figure 4. Absolute errors of hydraulic heads of different methods, with y=100 m
![]()
图 5 不同放大倍数时水头绝对误差图
Figure 5. Absolute errors of hydraulic heads with different magnifications
![]()
图 6 不同单元数时的计算用时和计算绝对误差图
Figure 6. CPU time and absolute errors of methods with different element numbers
![]()
图 7 各数值方法在y=5000 m时的水头值
Figure 7. Calculated heads of different methods, with y=5000 m
![]()
图 8 不同单元数时的计算用时和计算绝对误差图
Figure 8. CPU time and absolute errors of methods with different element numbers
![]()
图 9 不同单元数时的基函数计算用时图
Figure 9. CPU time of basics function of MSFEM-L and MSFEM-T-L with different element numbers
-
[1] 陈雄, 张岩, 王艺伟, 等. 苏北沿海三市三维地下水流数值模拟[J]. 吉林大学学报(地球科学版), 2018, 48(5): 1434–1450. https://www.cnki.com.cn/Article/CJFDTOTAL-CCDZ201805036.htm CHEN Xiong, ZHANG Yan, WANG Yi-wei, et al. Numerical simulation of three dimensional groundwater flow in three coastal cities of north Jiangsu[J]. Journal of Jilin University (Earth Science Edition), 2018, 48(5): 1434–1450. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CCDZ201805036.htm
[2] YE S J, LUO Y, WU J C, et al. Three-dimensional numerical modeling of land subsidence in Shanghai, China[J]. Hydrogeology Journal, 2016, 24(3): 695–709. doi: 10.1007/s10040-016-1382-2
[3] 李宁, 杨敏, 李国锋. 再论岩土工程有限元方法的应用问题[J]. 岩土力学, 2019, 40(3): 1140–1148, 1157. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201903035.htm LI Ning, YANG Min, LI Guo-feng. Revisiting the application of finite element method in geotechnical engineering[J]. Rock and Soil Mechanics, 2019, 40(3): 1140–1148, 1157. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201903035.htm
[4] 薛禹群, 谢春红. 地下水数值模拟[M]. 北京: 科学出版社, 2007. XUE Yu-qun, XIE Chun-hong. Numerical Simulation for Groundwater[M]. Beijing: Science Press, 2007. (in Chinese)
[5] 周杰, 汪德爟. 有限元水流计算中内存和运行效率初探[J]. 水科学进展, 2004, 15(5): 593–597. doi: 10.3321/j.issn:1001-6791.2004.05.010 ZHOU Jie, WANG De-guan. Exploration on memory requirement and operation efficiency of finite element method in flow calculation[J]. Advances in Water Science, 2004, 15(5): 593–597. (in Chinese) doi: 10.3321/j.issn:1001-6791.2004.05.010
[6] 张丙印, 朱京义, 王昆泰. 非饱和土水气两相渗流有限元数值模型[J]. 岩土工程学报, 2002, 24(6): 701–705. doi: 10.3321/j.issn:1000-4548.2002.06.006 ZHANG Bing-yin, ZHU Jing-yi, WANG Kun-tai. Finite element modeling of two-phase seepage in unsaturated soil[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(6): 701–705. (in Chinese) doi: 10.3321/j.issn:1000-4548.2002.06.006
[7] HOU T Y, WU X H. A multiscale finite element method for elliptic problems in composite materials and porous media[J]. Journal of Computational Physics, 1997, 134(1): 169–189. doi: 10.1006/jcph.1997.5682
[8] YE S J, XUE Y Q, XIE C H. Application of the multiscale finite element method to flow in heterogeneous porous media[J]. Water Resources Research, 2004, 40(9): 337–348.
[9] 范颖, 王磊, 章青. 多尺度有限元法及其应用研究进展[J]. 水利水电科技进展, 2012, 32(3): 90–94. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD201203025.htm FAN Ying, WANG Lei, ZHANG Qing. Research progress and application of multiscale finite element method[J]. Advances in Science and Technology of Water Resources, 2012, 32(3): 90–94. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD201203025.htm
[10] CHEN J, CHUNG E T, HE Z K, et al. Generalized multiscale approximation of mixed finite elements with velocity elimination for subsurface flow[J]. Journal of Computational Physics, 2020, 404: 109133. doi: 10.1016/j.jcp.2019.109133
[11] CHEN Z M, HOU T. A mixed multiscale finite element method for elliptic problems with oscillating coefficients[J]. Mathematics of Computation, 2003, 72(242): 541–576.
[12] JENNY P, LEE S H, TCHELEPI H A. Multi-scale finite-volume method for elliptic problems in subsurface flow simulation[J]. Journal of Computational Physics, 2003, 187(1): 47–67. doi: 10.1016/S0021-9991(03)00075-5
[13] 贺新光, 任理. 求解非均质多孔介质中非饱和水流问题的一种自适应多尺度有限元方法: Ⅰ. 数值格式[J]. 水利学报, 2009, 40(1): 38–45, 51. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200901007.htm HE Xin-guang, REN Li. Adaptive multi-scale finite element method for unsaturated flow in heterogeneous porous media I. Numerical scheme[J]. Journal of Hydraulic Engineering, 2009, 40(1): 38–45, 51. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200901007.htm
[14] 贺新光, 任理. 求解非均质多孔介质中非饱和水流问题的一种自适应多尺度有限元方法: Ⅱ. 数值结果[J]. 水利学报, 2009, 40(2): 138–144. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200902003.htm HE Xin-guang, REN Li. Adaptive multi-scale finite element method for unsaturated flow in heterogeneous porous media Ⅱ. Numerical results[J]. Journal of Hydraulic Engineering, 2009, 40(2): 138–144. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200902003.htm
[15] 黄梦杰, 贺新光. 求解非均质多孔介质中随机水流问题的多尺度有限元降基方法[J]. 水资源与水工程学报, 2019, 30(6): 86–95. https://www.cnki.com.cn/Article/CJFDTOTAL-XBSZ201906014.htm HUANG Meng-jie, HE Xin-guang. Reduced multiscale finite element basis method for solving the stochastic water flow problems in heterogeneous porous media[J]. Journal of Water Resources and Water Engineering, 2019, 30(6): 86–95. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XBSZ201906014.htm
[16] SHI L S, ZHANG D X, LIN L, et al. A multiscale probabilistic collocation method for subsurface flow in heterogeneous media[J]. Water Resources Research, 2010, 46(11): 386.
[17] 谢一凡, 吴吉春, 王益, 等. 一种模拟节点达西流速的多尺度有限元-有限元模型[J]. 岩土工程学报, 2022, 44(1): 107–114, 202. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202201010.htm XIE Yi-fan, WU Ji-chun, WANG Yi, et al. Multiscale finite element-finite element model for simulating nodal Darcy velocity[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(1): 107–114, 202. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202201010.htm
[18] SHI X Q, WU J C, YE S J, et al. Regional land subsidence simulation in Su-Xi-Chang area and Shanghai City, China[J]. Engineering Geology, 2008, 100(1/2): 27–42.
[19] XIE Y F, WU J C, XUE Y Q, et al. Modified multiscale finite-element method for solving groundwater flow problem in heterogeneous porous media[J]. Journal of Hydrologic Engineering, 2014, 19(8): 04014004.
[20] XIE Y F, WU J C, XUE Y Q, et al. Efficient triple-grid multiscale finite element method for solving groundwater flow problems in heterogeneous porous media[J]. Transport in Porous Media, 2016, 112(2): 361–380.
[21] DEUTSCH C V. GSLIB: Geostatistical Software Library and User's Guide[M]. 2nd ed. Oxford: Oxford University Press, 1998.
-
期刊类型引用(2)
1. 江博. 长源水电站大坝坝肩破坏成因分析研究. 陕西水利. 2025(03): 11-14 . 
百度学术
2. 王顿，裴丽欣，张礼中，樊连杰，卢丽，李习文，刘潇桐，李俊楠，梁林德，白雪冬. 基于文献计量学近20年国内外地下水数值模拟研究进展及展望. 环境工程. 2023(S1): 240-247 . 百度学术
其他类型引用(6)
下载:
计量
- 文章访问数: 154
- HTML全文浏览量: 41
- PDF下载量: 18
- 被引次数: 8
