长距离深埋岩石地层顶管摩阻力计算方法研究

钟祖良; 刁小军; 刘新荣

doi:10.11779/CJGE202211012

长距离深埋岩石地层顶管摩阻力计算方法研究 English Version

钟祖良^{1, 2,},
刁小军¹,
刘新荣^{1, 2}

1.
重庆大学土木工程学院, 重庆 400045
2.
库区环境地质灾害防治国家地方联合工程研究中心(重庆大学), 重庆 400045

基金项目:

重庆市技术创新与应用示范专项社会民生类重点研发项目 cstc2018jscx-mszdX0071

详细信息

作者简介:
钟祖良(1980—)，男，副教授，博士，博士生导师，主要从事地下工程研究工作。E-mail: haiou983@126.com

中图分类号: TU43
计量
- 文章访问数: 176
- HTML全文浏览量: 46
- PDF下载量: 35
出版历程
- 收稿日期: 2021-10-19
- 网络出版日期: 2022-12-08
- 刊出日期: 2022-10-31

Method for calculating frictional resistance of long-distance pipejacking in deeply buried rock strata

1.
School of Civil Engineering, Chongqing University, Chongqing 400045, China
2.
National Joint Engineering Research Center for Prevention and Control of Environmental Geological Hazards in the TGR Area (Chongqing University), Chongqing 400045, China

摘要

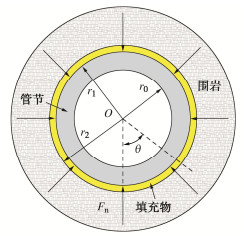
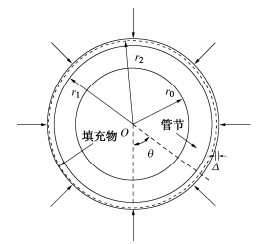
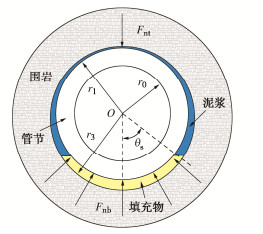
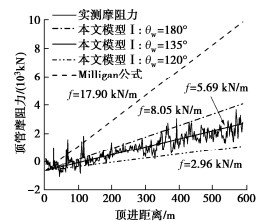
摘要: 顶管法具有掘进效率高、安全环保、质量可靠等优点，在土质地层中得到广泛推广。为满足水利及市政工程快速建设的需求，顶管法也在岩石地层中进行应用，但对于长距离深埋岩石顶管摩阻力计算方法的研究较为匮乏。依托国内首个采用长距离岩石顶管法施工的重庆观景口水利枢纽工程，通过现场顶力测试试验研究发现，管节–围岩间摩阻力主要受管外间隙填充物和注入的润滑泥浆的影响，且前者的影响较大。根据顶管超挖间隙中沉渣填充程度的不同，提出了3种管节–围岩接触力学模型，并基于围岩弹塑性理论以及管节与填充物之间的协调变形，推导了各力学模型的顶管摩阻力计算公式。通过将摩阻力计算值与实测值对比，验证了摩阻力公式在岩石地层顶管顶力计算中的适用性。
- 顶管 /
- 岩石地层 /
- 摩阻力 /
- 顶力 /
- 计算公式
Abstract: The pipe jacking method has the advantages of high efficiency, safety, environmental protection and reliable quality, and is widely used in soil strata. In order to meet the demand for rapid construction of water conservancy projects and municipal projects, pipe jacking is also used in rocky strata, but there is a lack of research on the calculation of the frictional resistance of long-distance pipe jacking in deeply buried rock. Based on the first long-distance pipe jacking case in rock in China, Guanjingkou water conservancy project of Chongqing, through the field tests on jacking force it is found that the pipe- rock friction resistance is mainly affected by the filling of over-excavation gap and the injected lubricating mud, and the former has a greater impact. According to different degrees of the filling of the over-excavated gap with sediment, three mechanical models for the contact between pipe and rock are proposed, and based on the elastic-plasticity theory and the coordinated deformation between the pipe and the filling, the formulae for calculating the frictional resistance of the pipe are derived for each mechanical model. The applicability of the formulae for the frictional resistance in deeply buried rock strata is verified by comparing the calculated values of the frictional resistance with the measured ones.
- pipe jacking /
- rock stratum /
- frictional resistance /
- jacking force /
- formula

HTML全文

0. 引言

随着中国基础设施建设的快速发展，在非饱和盐渍土地区进行盐渍土的改良以及工程土障建设中，均涉及到水-热-气-传质等多物理场多相的耦合作用。Reshetin等^[1]基于扩散定律和温度、湿度和蒸汽含量之间的函数关系，建立了关于温度场与湿度场的动力学数学模型，但数学模型中没有考虑非饱和土中水力梯度变化对耦合作用的影响。Jia等^[2]在建立传热传质耦合模型时，考虑到水蒸汽对传热传质效应的影响。基于压力梯度和温度梯度等多种驱动因素建立了多种有关非饱和多孔介质的水-热耦合的数学模型，但忽略了非饱和多孔介质中水力梯度随时间和空间的变化规律且对气相的组分划分较为笼统^[3-6]，Mohammad等^[7]考虑干燥气体与水蒸气的迁移对能量守恒的影响，但在在能量迁移的方式中忽略了对流作用影响。He等^[8]在非饱和土水-热-力多场耦合的数学模型，没有考虑多场多相耦合作用中溶质的存在对多孔介质中水分场、温度场迁移规律的影响。

多孔介质中水-热-盐迁移现象是各影响因素相互耦合的过程，且迁移规律随时间和空间不断变化。Cleall等^[9]，HERNÁNDEZ-LÓPEZ等^[10]通过试验孔隙的曲率因子和土体温度梯度的增强因子对水蒸汽通量有较大影响，Chen等^[11]发现随着盐分在一端的大量聚集，溶液中的盐分会在盐分梯度作用下继续向该处迁移。周凤玺等^[12-13]建立了完善热-湿-盐多物理场多相耦合的数学模型。但模型仅考虑均质非饱和多孔介质中的热湿盐多场耦合，并没有对复合非饱和土中的水-热-盐迁移规律进行进一步的研究且缺乏试验验证。

本文全面研究了复合非饱和土中的液态水、液相中的干燥气体和盐分以及孔隙中水蒸气等对水分场、盐分场和温度场随时间变化在空间上的分布规律的影响，并在能量守恒中考虑盐分、干燥气体以及各组分导热系数等分项对温度场的影响，建立了非稳态条件下复合非饱和土中多场多相耦合的状态方程。通过试验分单层验证了数学模型的准确性而后对复合非饱和土中水-盐-热的多场耦合问题进行参数分析。

1. 数学模型

1.1 质量守恒方程

组分α在π相中的质量守恒方程表示为^[12-13]

， ，

$\frac{\partial ({\phi }^{\pi }{\rho }_{\alpha }^{\pi })}{\partial t}+\nabla \cdot ({\phi }^{\pi }{\rho }_{\alpha }^{\pi }{\boldsymbol{v}}^{\alpha })+\nabla \cdot {\boldsymbol{j}}_{\alpha }^{\pi }={\dot{m}}_{\alpha }^{\pi }\text{，} \text{，}$

(1)

式中， ${\boldsymbol{j}}_\alpha ^\pi$ 为α组分在π相的非对流通量矢量， ${\phi ^\pi }$ 为π相的体积分数， $\rho _\alpha ^\pi$ 为α组分在π相的质量分数， ${{\boldsymbol{v}}^\alpha }$ 为α组分的速度矢量^[12-13]。

由式（1）可得水分平衡方程为

$\frac{{\partial (n{S^{\text{l}}}\rho _{\text{w}}^{\text{l}})}}{{\partial t}} + \frac{{\partial (n{S^{\text{g}}}\rho _{\text{w}}^{\text{g}})}}{{\partial t}} + \nabla\cdot {\text{(}}n{S^{\text{g}}}\rho _{\text{w}}^{\text{g}}{{\boldsymbol{v}}^{\text{g}}}{\text{)}} + \nabla\cdot {\boldsymbol{j}}_{\text{w}}^{\text{g}} + \\ \;\;\;\;\;\nabla \cdot (n{S}^{\text{l}}{\rho }_{\text{w}}^{\text{l}}{\boldsymbol{v}}^{\text{l}})+\nabla \cdot ({\rho }_{\text{w}}^{\text{l}}{q}^{\text{l}})+\nabla \cdot ({\rho }_{\text{w}}^{\text{g}}{q}^{\text{g}})=0\text{ }\text{，}$

(2)

式中，饱和度 ${S^{\text{l}}}$ 为孔隙水压力P_l与孔隙气压力P_g的函数，存在表达式P_l + P_g = 1。液相、气相通量^[12-13]存在表达式：

${q^{\bf{l}}} =- {K^{\bf{l}}}(\nabla {P_{\bf{l}}} + \rho _{\text{w}}^{\bf{l}}g) \text{，}$

(3)

${q^\text{g}} =- {K^\text{g}}(\nabla {P_\text{g}} + {\rho ^\text{g}}g) \text{，}$

(4)

式中，K^l，K^g为水动力参数^[12-13]，g为重力加速度矢量。

非对流水通量遵循Philip等^[14]所建立的模型，气相中水蒸汽非对流通量的变化可以归因于系统中水分的变化和系统中温度的变化：

${\boldsymbol{j}}_{\text{w}}^{\text{g}} = {\boldsymbol{j}}_{{\text{vw}}}^{\text{g}} + {\boldsymbol{j}}_{{\text{vT}}}^{\text{g}} =- {D_{{\text{vw}}}}\nabla {P_{\text{l}}} + {D_{{\text{vw}}}}\nabla {P_{\text{g}}} - {D_{{\text{vT}}}}\nabla T 。$

(5)

其中由温度和水分引起的分子扩散系数存在表达式^[12-13]：

${D_{{\text{vT}}}} = n{S^{\text{g}}}\rho _{\text{w}}^{\text{g}}{D_{{\text{atm}}}}v\tau {f_{{\text{Tv}}}}\left[ {\frac{{4974.0}}{{{T^2}}} + \frac{{{M_{\text{w}}}\psi }}{{R{T^2}\rho _{\text{w}}^{\text{l}}}}} \right] \text{，}$

(6)

${D_{{\text{vw}}}} = n{S^{\text{g}}}\rho _{\text{w}}^{\text{g}}{D_{{\text{atm}}}}v\tau \frac{{{M_{\text{w}}}}}{{RT\rho _{\text{w}}^{\text{l}}}} \text{，}$

(7)

式中，D_atm为水蒸汽分子的扩散系数，D_atm = 2.16×10^-5(T/273.15)^1.8，τ为曲率因子^[12-13]。

结合式（1）可得干燥气体的质量平衡方程为

$\frac{{\partial (nH{S^{\text{l}}}\rho _{\text{a}}^{\text{l}})}}{{\partial t}} + \nabla\cdot ({\phi ^{\text{l}}}\rho _{\text{a}}^{\text{l}}{{\boldsymbol{v}}^{\text{l}}}) + \nabla\cdot {\boldsymbol{j}}_{\text{a}}^{\text{l}} +\\ \;\;\;\;\;\; \frac{\partial (n{S}^{\text{g}}{\rho }_{\text{a}}^{\text{g}})}{\partial t}+\nabla \cdot ({\phi }^{\text{g}}{\rho }_{\text{a}}^{\text{g}}{v}^{\text{g}})+\nabla \cdot {j}_{\text{a}}^{\text{g}}=0\text{ }。$

(8)

干燥气体在液相中不发生扩散，即 ${\boldsymbol{j}}_{\text{a}}^{\text{l}} = 0$ 。非对流项中的干燥气体的非对流通量与水蒸气的非对流通量存在表达式 ${\boldsymbol{j}}_{\text{a}}^{\text{g}} =- {\boldsymbol{j}}_{\text{w}}^{\text{g}}$ ，水中气体的密度存在^[12-13]：

$\rho _{\text{a}}^{\text{l}} \approx \rho _{\text{a}}^{\text{g}} = {\rho _{\text{a}}} = \frac{{{M_{\text{a}}}}}{{RT}}({P_{\text{g}}} - {P_{\text{v}}}) \text{，}$

(9)

式中，P_v为水蒸气压力，M_a为干气摩尔质量，R为气体常数。

结合式（1）可以得出液相中盐分的质量守恒方程为

$\frac{{\partial ({\phi ^{\text{l}}}\rho _{\text{p}}^{\text{l}})}}{{\partial t}} + \nabla\cdot (\rho _{\text{w}}^{\text{l}}\omega {q^{\text{l}}}) + \nabla\cdot {\boldsymbol{j}}_{\text{p}}^{\text{l}} = 0 。$

(10)

由于研究土壤液相中盐分得浓度较低，不考虑溶质的溶解与析出。液相中溶质非对流通量 ${\boldsymbol{j}}_{\text{p}}^{\text{l}}$ 可以表示为

${\boldsymbol{j}}_{\text{p}}^{\text{l}} =- n{S^{\text{l}}}\rho _{\text{w}}^{\text{l}}\tau {D_{\text{p}}}\nabla \omega \text{，}$

(11)

式中，D_p为溶质的扩散系数^[12-13]。

1.2 能量平衡方程

系统中能量平衡的一般形式为^[15]

$\frac{{\partial {\mathit{\Phi} _\text{h}}}}{{\partial t}} + Q + \nabla\cdot {q_\text{h}} = 0 \text{，}$

(12)

式中，Φ_h为内能，Q为潜热， $\nabla\cdot {q_\text{h}}$ 表示热对流和传导。

考虑局部平衡以及不同组分温度相等的条件下，土壤的内能变化可表示为

$\frac{{\partial {\mathit{\Phi} _\text{h}}}}{{\partial t}} = \left[ {{\text{(}}1 - n{\text{)}}{\rho ^\text{s}}{c_\text{s}} + nH{S^\text{l}}{\rho _\text{a}}{c_\text{a}} + } \right. \\ \;\;\;\;\;\;\;\; n{S}^{\text{g}}{\rho }_{\text{a}}{c}_{\text{a}}+n{S}^{\text{l}}{\rho }_{\text{w}}^{\text{l}}{c}_{\text{w}}^{\text{l}}+n{S}^{\text{g}}{\rho }_{\text{w}}^{\text{g}}{c}_{\text{w}}^{\text{g}}]\frac{\partial T}{\partial t}\text{ }。$

(13)

在非饱和土中由汽化和凝结引起的能量变化可表示为

$Q = \dot m_\text{w}^\text{g}{H_{\text{gw}}} \text{，}$

(14)

式中， ${H_\text{gw}}$ 为液相中水分的汽化焓^[16]， ${H_{\text{gw}}} = {L_{\text{gw}}} -$ $(c_\text{w}^\text{l} - c_\text{w}^\text{g})$ $(T - {T_0})$ ， $\dot m_\text{w}^\text{g}$ 为蒸发率。

热流方程包括固相热传导、液相对流、气相对流，存在表达式^[14]：

$\begin{aligned} q_{\mathrm{h}}= & q^{\mathrm{T}}+\rho_\alpha^\pi E_{\mathrm{T} \alpha}^\pi q^\alpha+E_{\mathrm{T} \alpha}^\pi {\boldsymbol{j}}_\alpha^\pi \\ = & -\left(\lambda_{\mathrm{s}}^{1-n} \lambda_{\mathrm{w}}^{n S^l} \lambda_{\mathrm{p}}^{n S^{\mathrm{p}}}\right) \nabla T+\left(\rho_a c_a+\rho_{\mathrm{w}}^{\mathrm{g}} c_{\mathrm{w}}^{\mathrm{g}}\right)\left(T-T_0\right) q^{\mathrm{g}}+ \\ & \left(c_{\mathrm{w}}^{\mathrm{g}}-c_a\right)\left(T-T_0\right) {\boldsymbol{j}}_{\mathrm{w}}^{\mathrm{g}}+c_{\mathrm{p}}^1 \boldsymbol{j}_{\mathrm{p}}^{\mathrm{1}}\left(T-T_0\right)+ \\ & \left(\rho_a c_a H+\rho_{\mathrm{w}}^1 c_{\mathrm{w}}^1\right)\left(T-T_0\right) q^1。 \end{aligned}$

(15)

以往的研究忽略温度对溶液热容与导热系数的影响，溶液热容和导热系数与溶质的浓度有关^[17]

$\left.\begin{array}{l} c_{\mathrm{w}}^{\prime}=\beta_2 c_{\mathrm{s}}+c_{\mathrm{w}}, \\ \lambda_{\mathrm{w}}=\beta_3 c_{\mathrm{s}}+\lambda_{\mathrm{l}}, \end{array}\right\}$

(16)

式中， ${\beta _2}$ = -167， ${\beta _3}$ = 0.00493。

1.3 复合非饱和土非稳态问题求解

方程（2），（8），（10），（12）给出了复合非饱和土中水-气-盐-热多场耦合过程的控制方程，耦合方程是将孔隙水压力、孔隙气压力、温度、含盐率及其一阶偏导为未知量的封闭方程。将控制方程进行拉普拉斯变换后通过数值方法计算可得控制方程的频域解，而后基于Hausdoff矩问题将频域解 $u(x)$ 转化为时域解 ${q_N}(t)$ 。

Hausdoff矩问题存在积分关系式

${\displaystyle {\int }_{0}^{1}{x}^{n}u(x)\text{d}x={\mu }_{n}}\text{ (}n=0,1,2,\cdot \cdot \cdot \text{) }。$

(17)

Hausdorff矩问题是一个典型的不适定问题， $u(x)$ 的正则化近似解为

${p_N}(x) = \sum\limits_{i = 0}^N {{\lambda _i}{L_i}(x)} 。$

(18)

最终Laplace逆变换的近似解为

${q_N}{\text{(}}t{\text{)}} \equiv {p_N}({{\text{e}}^{ - t}}) = \sum\limits_{i = 0}^N {{\lambda _i}{L_i}({{\text{e}}^{ - t}})} 。$

(19)

基于式（19）Hausdoff矩问题的稳定化算法获得Laplace逆变换的解。

2. 试验验证

试验采用的土样是取自甘肃省兰州市的粉质黏土，该土样的颗粒相对质量密度为2.70 g/cm³，渗透系数约为2.89×10^-6 m/s。将土样压制成高为280 mm、直径为200 mm，试验土柱的孔隙率n为0.3。初始时刻试验土柱的温度为25℃，顶板与底板的温度分别设为30，15℃。两端的孔隙气压力为101 kPa、初始质量含水率为10 %、初始含盐率为7%。

表 1，2分别给出了试验粉质黏土土样各物理成分的热力学参数和Van Genuchten（VG）模型^[13，15]参数。经试验和计算可得粉质黏土土样在VG模型中所对应的拟合参数分别为n_vg=1.69，m_vg=0.0147。图 1~3分别给出了试样中水分，盐分和温度的分布规律，并与本文所提出的教学模型进行验证，两者吻合较好。

表 1 多孔介质中各物理成分的热力学参数

Table 1. Thermodynamic parameters of physical components in porous media

参数	数值	参数	数值
${c_{\text{a}}}$ /(J·kg^-1·K^-1)	1000	${L_{{\text{gw}}}}$ /(J·kg^-1)	2413000
$c_{\text{w}}^{\text{l}}$ /(J·kg^-1·K^-1)	4180	${k_0}$ /(m·s^-1)	2.89×10^-6
$c_{\text{w}}^{\text{g}}$ /(J·kg^-1·K^-1)	1900	g/(m·s^-2)	9.8
$c_{\text{p}}^{\text{l}}$ /(J·kg^-1·K^-1)	3750	$\rho _{\text{w}}^{\text{g}}$ /(kg^-1·m^-3)	1000
${\lambda _{\text{g}}}$ /(W·m^-1·K^-1)	0.024	${M_{\text{a}}}$ /(kg^-1·mol^-1）	0.0288
${\lambda _{\text{s}}}$ /(W·m^-1·K^-1)	2.93	${M_{\text{w}}}$ /(kg^-1·mol^-1)	0.018016
${\lambda _{\text{l}}}$ /(W·m^-1·K^-1)	0.56	$R$ /(J·mol^-1·K^-1)	8.3144

下载: 导出CSV

| 显示表格

表 2 粉质黏土VG模型参数

Table 2. VG model parameters of silty clay

参数	数值	参数	数值
$n$	0.3	${n_{{\text{vg}}}}$	1.698
$S_{{\text{res}}}^{\text{l}}$	0.15	v	1.4
$S_{{\text{sat}}}^{\text{l}}$	0.85	${f_{\tau {\text{v}}}}$	1.2
${m_{{\text{vg}}}}$	0.411	${P_{\text{s}}}$ /kPa	68

下载: 导出CSV

| 显示表格

图 1 体积含水率的对比验证

Figure 1. Comparative verification of volume water content

下载: 全尺寸图片幻灯片

图 2 含盐率的对比验证

Figure 2. Comparative verification of salt content

下载: 全尺寸图片幻灯片

图 3 温度的对比验证

Figure 3. Comparative verification of temperature

下载: 全尺寸图片幻灯片

3. 参数分析

表 2，3^[18]分别给出了粉质黏土与砂土的VG模型参数。非饱和黏土上覆非饱和砂土的高度为300 mm保持不变，对砂土不同厚度、渗透系数等条件下复合非饱和土中的水分、盐分随时间变化的分布情况以及变化规律进行分析。砂土的孔隙率为0.5，上覆粉质黏土的孔隙率为0.3、土体上下边界的温度分别为27℃，3℃，上下边界的孔隙气压力均为102 kPa。复合非饱和土初始时刻的温度为15℃、初始时刻的孔隙气压力为102 kPa，为了让迁移规律更加明显砂土与黏土中初始的孔隙水压力设为-800 kPa、含盐率为0.12%。

表 3 砂土的VG模型参数

Table 3. VG model parameters of sand soil

参数	数值	参数	数值
n	0.5	${n_{{\text{vg}}}}$	2.45
$S_{{\text{res}}}^{\text{l}}$	0.07	v	2
$S_{{\text{sat}}}^{\text{l}}$	0.93	${f_{\tau {\text{v}}}}$	1.4
${m_{{\text{vg}}}}$	0.59	${P_{\text{s}}}$ /kPa	32

下载: 导出CSV

| 显示表格

图 4，5分别给出了在砂土厚度分别为50，100，150 mm，且复合非饱和土厚度始终为300 mm条件下，复合土体中孔压和溶质的分布情况。从图 4中可以明显地看出随着砂土厚度的增加，复合土体中砂土中的盐分是降低的。图 5给出了距热端25，75，125，75，225，275 mm位置处复合非饱和土孔隙水压力随时间的变化情况。随着砂土厚度增大，相同位置处复合非饱和土热端的孔隙水压力越小，继而含水率越小。当孔隙率为0.5的砂土厚度越大，砂土对复合非饱和土中盐分迁移和水分迁移阻碍能力就越大。

图 4 不同砂土厚度下含盐率的变化

Figure 4. Variation of salt content under different sand thicknesses

下载: 全尺寸图片幻灯片

图 5 不同砂土厚度下不同位置处孔隙水压力随时间变化

Figure 5. Variation of pore water pressure with time at different locations under different sand thicknesses

下载: 全尺寸图片幻灯片

为了分析砂土渗透系数对复合非饱和土中水-热-盐耦合行为的影响，当砂土与粉质黏土的孔隙率以及复合非饱和土体的边界和初始条件保持不变。图 6绘出了砂土厚度为100 mm，复合非饱和土厚度为300 mm，砂土的渗透系数分别为1.2×10^-4，4.2×10^-4，8.2×10^-4 m/s条件下，复合非饱和土体中盐分的变化情况。由图中曲线可以看出：随着砂土渗透系数的增大，复合非饱和土热端处溶液中的盐分浓度是增加。图 7给出了距低温端25，75，125，175，225，275 mm位置处孔隙水压力随时间的变化情况，随着砂土渗透系数增大，相同位置处复合非饱和土热端处的孔隙水压力越小，继而含水率越小。

图 6 不同渗透系数下含盐率的变化

Figure 6. Change of salt content under different permeability coefficients

下载: 全尺寸图片幻灯片

图 7 不同渗透系数下不同位置处孔隙水压力随时间变化

Figure 7. Change of pore water pressure with time at different positions under different permeability coefficients

下载: 全尺寸图片幻灯片

4. 结论

文章建立了完善的双层非饱和多孔介质中水-热-盐耦合运移的数学模型，并进行相应的参数分析和试验研究。

（1）复合非饱和土中，盐分在温度梯度的作用下逐渐向热端聚集，水分在温度梯度的作用下逐渐向冷端聚集。

（2）随着砂土厚度的增大，复合非饱和土低温端聚集的水分是逐渐增加的，高温端的水分是逐渐减少的。高温端砂土中聚集的盐分会随着砂土厚度的增大而逐渐降低，低温端粉质黏土中的盐分随着砂土厚度的增大而增加。

（3）随着砂土渗透系数的增大，复合非饱和土低温端的水分降低。高温端砂土中聚集的盐分会随着砂土渗透系数的增大而逐渐增加，低温端粉质黏土中的盐分随着砂土渗透系数的增大而减小。

图 1 ^#6隧洞工程地质纵剖面图

Figure 1. Geological longitudinal section of tunnel No. 6

下载: 全尺寸图片幻灯片

图 2 管节结构示意图

Figure 2. Schematic diagram of pipe structure

下载: 全尺寸图片幻灯片

图 3 ^#6隧洞顶管顶进阻力与顶进距离关系曲线

Figure 3. Relationship between jacking resistance and jacking distance of tunnel No. 6

下载: 全尺寸图片幻灯片

图 4 模型Ⅰ：管节–围岩点接触模型

Figure 4. ModelⅠ: point contact model for pipe-surrounding rock

下载: 全尺寸图片幻灯片

图 5 模型Ⅱ：管节–围岩全接触模型

Figure 5. Model II: full contact model for pipe-surrounding rock

下载: 全尺寸图片幻灯片

图 6 双层圆筒模型

Figure 6. Double-layer cylinder model

下载: 全尺寸图片幻灯片

图 7 模型Ⅲ：管节–围岩部分接触模型

Figure 7. Model III: partial contact model for pipe-surrounding rock

下载: 全尺寸图片幻灯片

图 8 ^#6隧洞Ⅰ段摩阻力对比

Figure 8. Comparison of friction resistance for section Ⅰ of tunnel No. 6

下载: 全尺寸图片幻灯片

图 9 ^#6隧洞Ⅱ段摩阻力对比

Figure 9. Comparison of friction resistance for section Ⅱ of tunnel No. 6

下载: 全尺寸图片幻灯片

图 10 ^#6隧洞Ⅲ段摩阻力对比

Figure 10. Comparison of friction resistance for section Ⅲ of tunnel No. 6

下载: 全尺寸图片幻灯片

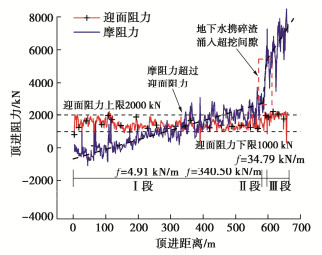
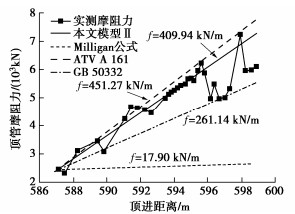
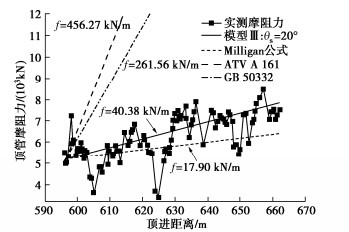
表 1 现场各段摩阻力实测值与计算值之比

Table 1 Ratios of measured to calculated frictional resistance

摩擦系数	实测值/计算值
摩擦系数	Ⅰ段	Ⅱ段	Ⅲ段
0.2	0.41	28.65	2.93
0.3	0.28	19.10	1.95
0.4	0.21	14.32	1.46
0.5	0.16	11.46	1.17

下载: 导出CSV

表 2 ^#6隧洞工程参数

Table 2 Parameters of tunnel No. 6

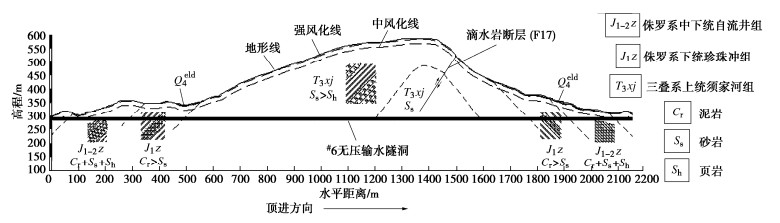
工程参数	Ⅰ段	Ⅱ段	Ⅲ段
顶进距离/m	0~586	586~599	599~662
隧洞埋深/m	16~77	77~81	81~109
地层岩性	泥岩	砂岩	砂岩
围岩分类	Ⅳ级	Ⅲ级	Ⅲ级

下载: 导出CSV

表 3 现场围岩、管节和填充物力学参数

Table 3 Mechanical parameters of surrounding rock, pipe and filling

项目	密度 /(g·cm^-3)	弹性模量/GPa	泊松比	内摩擦角/(°)	黏聚力/MPa
砂岩	2.54	2.5	0.31	30.5	0.50
泥岩	2.51	1.5	0.35	26.1	0.25
管节	2.50	34.5	0.20	—	—
填充物	—	1.5×10^-3	0.35	—	—

下载: 导出CSV

参考文献(23)

[1]	SOFIANOS A I, LOUKAS P, CHANTZAKOS C. Pipe jacking a sewer under Athens[J]. Tunnelling and Underground Space Technology, 2004, 19(2): 193–203. doi: 10.1016/S0886-7798(03)00108-1
[2]	MILLIGAN G W E, NORRIS P. Pipe-soil interaction during pipe jacking[J]. Proceedings of the Institution of Civil Engineers Geotechnical Engineering, 1999, 137(1): 27–44. doi: 10.1680/gt.1999.370104
[3]	HASLEM R F. Pipe-jacking forces: from practice to theory[J]. Thomas Telford, 1986: 173.
[4]	叶艺超, 彭立敏, 杨伟超, 等. 考虑泥浆触变性的顶管顶力计算方法[J]. 岩土工程学报, 2015, 37(9): 1653–1659. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201509016.htm YE Yi-chao, PENG Li-min, YANG Wei-chao, et al. Calculation of jacking force for pipe-jacking considering mud slurry thixotropy[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(9): 1653–1659. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201509016.htm
[5]	王双, 夏才初, 葛金科. 考虑泥浆套不同形态的顶管管壁摩阻力计算公式[J]. 岩土力学, 2014, 35(1): 159–166, 174. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201401024.htm WANG Shuang, XIA Cai-chu, GE Jin-ke. Formulae of lateral friction resistance for pipe-jacking considering different forms of mud screen[J]. Rock and Soil Mechanics, 2014, 35(1): 159–166, 174. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201401024.htm
[6]	张鹏, 谈力昕, 马保松. 考虑泥浆触变性和管土接触特性的顶管摩阻力公式[J]. 岩土工程学报, 2017, 39(11): 2043–2049. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201711014.htm ZHANG Peng, TAN Li-xin, MA Bao-song. Formulae for frictional resistance considering mud thixotropy and pipe-soil contact characteristics[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(11): 2043–2049. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201711014.htm
[7]	TERZAGHI K T. Theoretical Soil Mechanics[M]. New York: John Wiley & Sons Inc, 1943.
[8]	给水排水工程管道结构设计规范: GB 50332—2002[S]. 2003. Structural design code for pipelines of water supply and waste water engineering: GB 50332—2002[S]. 2003. (in Chinese)
[9]	Standard Practice for Direct Design of Precast Concrete Pipe for Jacking in Trenchless Construction[S]. Virginia: The American Society of Civil Engineers, 2001.
[10]	ATV-A 161 E-90 Structural Calculation of Driven Pipes[S]. Hennef: German ATV Rules and Standards, 1990.
[11]	Pipe-Jacking Application[S]. Tokyo: Japan Micro Tunneling Association, 2000.
[12]	ZHANG H F, ZHANG P, ZHOU W, et al. A new model to predict soil pressure acting on deep burial jacked pipes[J]. Tunnelling and Underground Space Technology, 2016, 60: 183–196. doi: 10.1016/j.tust.2016.09.005
[13]	ATKINSON, J H, POTTS, D M. Stability of a shallow circular tunnel in cohesionless soil[J]. Géotechnique, 1977, 27(2): 203–215. doi: 10.1680/geot.1977.27.2.203
[14]	STAHELI K. Jacking Force Prediction: An Interface Friction Approach Based on Pipe Surface Roughness[D]. Atlanta: Georgia Institute of Technology, 2006.
[15]	BARLA M, CAMUSSO M, AIASSA S. Analysis of jacking forces during microtunnelling in limestone[J]. Tunnelling and Underground Space Technology, 2006, 21(6): 668–683. doi: 10.1016/j.tust.2006.01.002
[16]	SHEIL B B, CURRAN B G, MCCABE B A. Experiences of utility microtunnelling in Irish limestone, mudstone and sandstone rock[J]. Tunnelling and Underground Space Technology, 2016, 51: 326–337. doi: 10.1016/j.tust.2015.10.019
[17]	ONG D E L, CHOO C S. Assessment of non-linear rock strength parameters for the estimation of pipe-jacking forces. Part 1. Direct shear testing and backanalysis[J]. Engineering Geology, 2018, 244: 159–172.
[18]	ZHONG Z L, LI C, LIU X R, et al. Assessment of experimental friction parameters and contact property of pipe string for the estimation and verification of a solution for pipe stuck in the China's first rock pipe jacking[J]. Tunnelling and Underground Space Technology, 2021, 107: 103671.
[19]	LI C, ZHONG Z L, LIU X R, et al. The investigation of ultra-long-distance concrete pipe stuck in quartz sandstone formation using numerical simulation[J]. Arabian Journal of Geosciences, 2018, 11(21): 1–17.
[20]	STEIN D, MÖLLERS K, BIELECKI R, et al. Microtunnelling: Installation and Renewal of Nonman-Size Supply and Sewage Lines by the Trenchless Construction Method[M]. Berlin: Ernst & Sohn Verlag fur Architektur und technische Wissenschaften, 1989.
[21]	CHOO C S, ONG D E L. Evaluation of pipe-jacking forces based on direct shear testing of reconstituted tunneling rock spoils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2015, 141(10): 4015044.
[22]	YU Xue-fu. Stability Analysis of Surrounding Rock of Underground Engineering[M]. Beijing: China Coal Industry Publishing House, 1983. (in Chinese)
[23]	VLACHOPOULOS N, DIEDERICHS M S. Improved longitudinal displacement profiles for convergence confinement analysis of deep tunnels[J]. Rock Mechanics and Rock Engineering, 2009, 42(2): 131–146.

施引文献(10)

期刊类型引用(6)

1.	白雪. 煤矿顶管掘进参数实测分析与控制方法研究. 煤矿机械. 2025(02): 65-68 . 百度学术
2.	李博，刘宇翔，陈建国，杨耀红，张哲. 基于物理信息神经网络的长距离顶管施工顶力预测. 人民长江. 2025(01): 147-155 . 百度学术
3.	钟祖良，米朝阳，范一飞，李超，刘新荣. 软岩蠕变作用下顶管顶力计算方法研究. 岩石力学与工程学报. 2025(02): 292-302 . 百度学术
4.	钟祖良，杜传烨，刘新荣，李超. 岩石顶管穿越深大断层破碎带摩阻力计算方法研究. 岩土力学. 2025(03): 943-954 . 百度学术
5.	叶生华，陆俊，明攀，王涛，聂叙平. 复杂岩溶地层大口径DRCP顶管施工试验研究. 人民长江. 2024(08): 166-173 . 百度学术
6.	钱朋亮. 三圆咬合顶管顶推力计算方法研究. 铁道建筑技术. 2024(10): 71-76 . 百度学术